Mathematics
A solid sphere is cut into identical hemispheres.
Statement 1 : The total volume of two hemispheres is equal to the volume of the original sphere.
Statement 2 : The total surface area of two hemispheres together is equal to the surface area of the original sphere.
Which of the following is valid ?
Both the statements are true
Both the statements are false
Statement 1 is true, and statement 2 is false
Statement 1 is false, and statement 2 is true
Mensuration
ICSE Sp 2025
17 Likes
Answer
When a solid sphere is cut into identical hemispheres.
Let radius of sphere be r.
Volume of a sphere =
Volume of hemisphere =
Volume of 2 hemisphere = .
The total volume of two hemispheres is equal to the volume of the original sphere.
Surface area of sphere = 4πr2
Surface area of hemisphere = 3πr2
Surface area of 2 hemisphere = 2 × 3πr2 = 6πr2.
The surface area of two hemispheres is not equal to the surface area of the original sphere.
Hence, Option 3 is the correct option.
Answered By
10 Likes
Related Questions
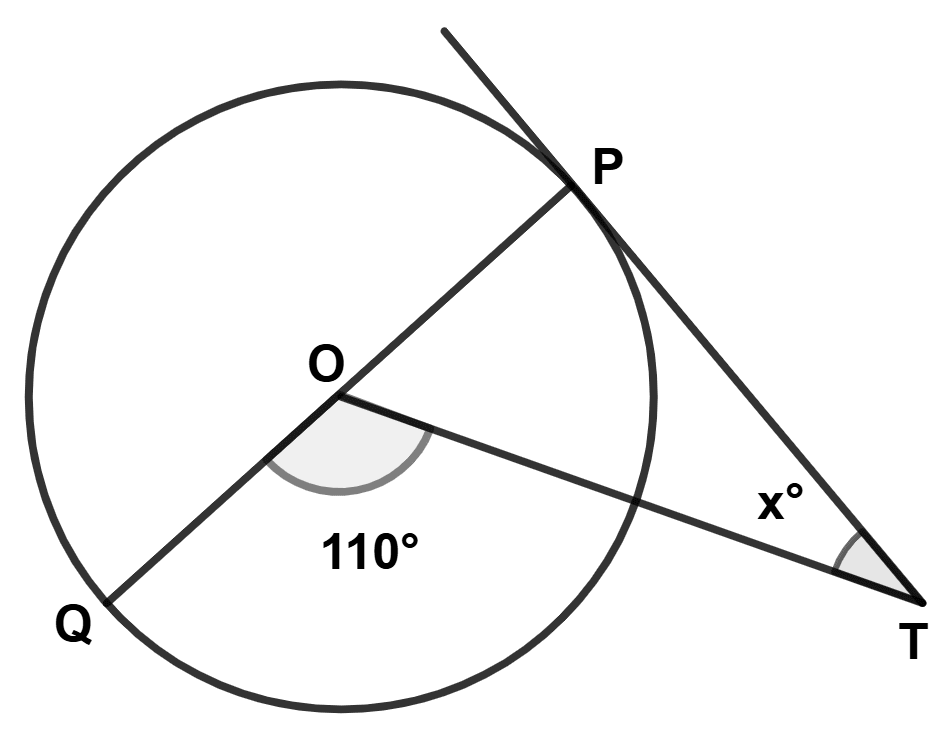
In the adjoining diagram, O is the center of the circle and PT is a tangent. The value of x is :
20°
40°
55°
70°
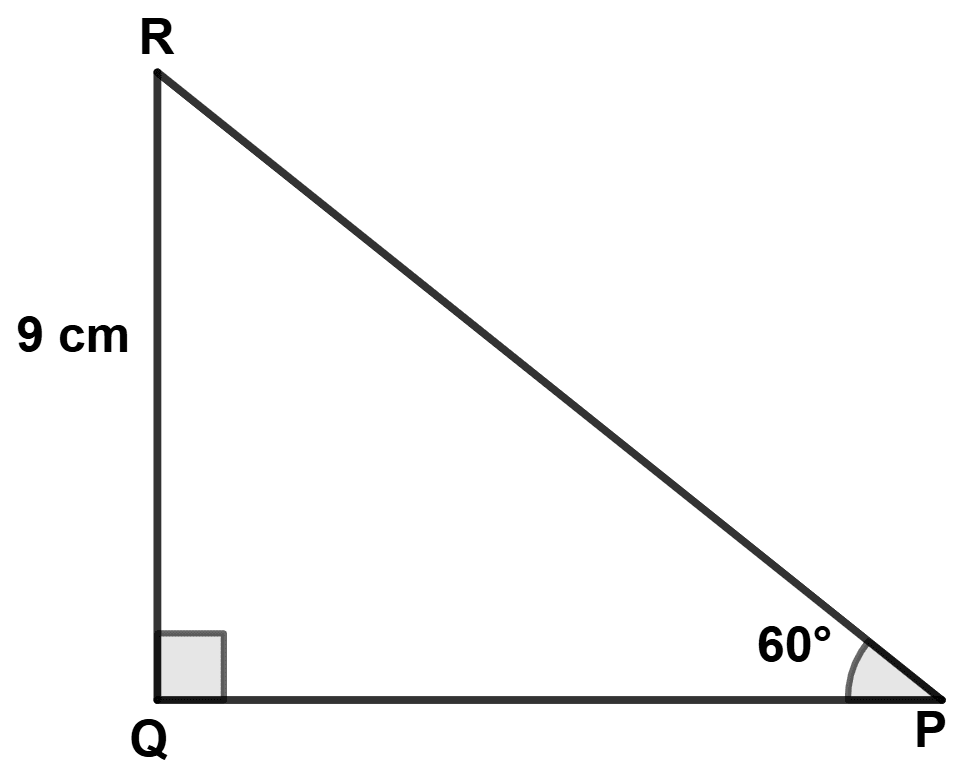
In the adjoining diagram the length of PR is :
cm
cm
cm
18 cm
Given that the sum of the squares of the first seven natural numbers is 140, then their mean is :
20
70
280
980
A bag contains 3 red and 2 blue marbles. A marble is drawn at random. The probability of drawing a black marble is :
0