Mathematics
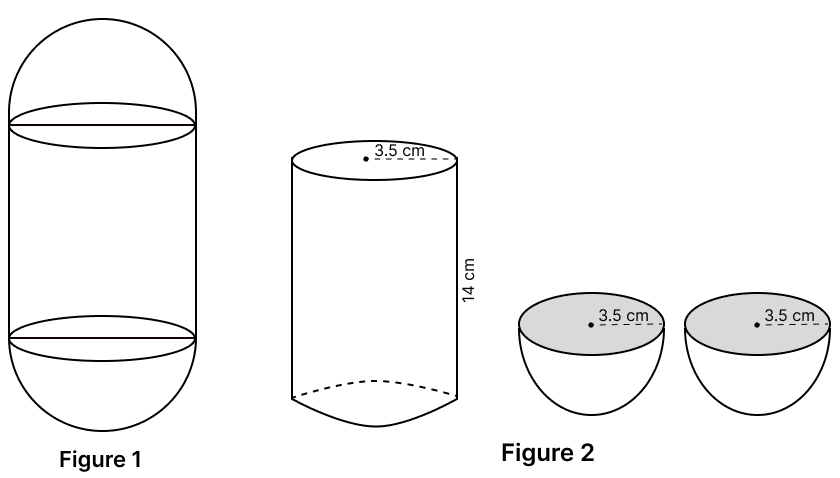
A solid wooden capsule is shown in Figure 1. The capsule is formed of a cylindrical block and two hemispheres.
Find the sum of total surface area of the three parts as shown in Figure 2. Given, the radius of the capsule is 3.5 cm and the length of the cylindrical block is 14 cm.
(Use )
Mensuration
24 Likes
Answer
From figure,
Radius of cylindrical block = radius of hemispheres = r = 3.5 cm
Height of cylindrical block = h = 14 cm.
By formula,
Total surface area of cylinder = 2πr(h + r)
Total surface area of a hemisphere = 3πr2
Total surface area = Total surface area of cylinder + Total surface area of 2 hemispheres
= 2πr(h + r) + 2 × 3πr2
= 2πrh + 2πr2 + 6πr2
= 2πrh + 8πr2
= 2πr(h + 4r).
Substituting values, we get :
Hence, the total surface area = 616 cm2.
Answered By
9 Likes
Related Questions
Using properties of proportion, find the value of ‘x’:
It is given that (x − 2) is a factor of polynomial 2x3 − 7x2 + kx − 2.
Find:
(a) the value of ‘k’.
(b) hence, factorise the resulting polynomial completely.
Use a graph paper for this question taking 2 cm = 1 unit along both axes.
(a) Plot A(1, 3), B(1, 2) and C(3, 0).
(b) Reflect A and B on the x-axis and name their images as E and D respectively. Write down their coordinates.
(c) Reflect A and B through the origin and name their images as F and G respectively.
(d) Reflect A, B and C on the y-axis and name their images as J, I and H respectively.
(e) Join all the points A, B, C, D, E, F, G, H, I and J in order and name the closed figure so formed.
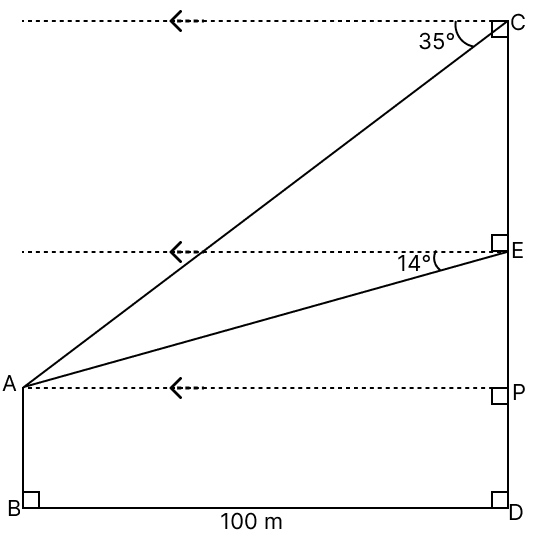
In the given diagram, AB is a vertical tower 100 m away from the foot of a 30 storied building CD. The angles of depression from the point C and E, (E being the mid-point of CD), are 35° and 14° respectively. (Use mathematical table for the required values rounded off correct to two places of decimals only.)
Find the height of the:
(a) tower AB
(b) building CD