Solve graphically the following equations: x + 2y = 4, 3x - 2y = 4.

Take 2 cm = 1 unit on each axis. Write down the area of the triangle formed by the lines and the y-axis. Also, find the area of the triangle formed by the lines and the x-axis.

Given,

⇒ x + 2y = 4

⇒ 2y = 4 - x

⇒ y = $\dfrac{4 - x}{2}$ ………………….(1)

When x = 0, y = $\dfrac{4 - 0}{2} = \dfrac{4}{2}$ = 2,

x = 2, y = $\dfrac{4 - 2}{2} = \dfrac{2}{2}$ = 1,

x = 4, y = $\dfrac{4 - 4}{2} = \dfrac{0}{2}$ = 0.

Table of values for equation (1)

Steps of construction :

1. Plot the points (0, 2), (2, 1) and (4, 0).

2. Join the points.

Given,

⇒ 3x - 2y = 4

⇒ 2y = 3x - 4

⇒ y = $\dfrac{3x - 4}{2}$ ………………(2)

When x = 0, y = $\dfrac{3 \times 0 - 4}{2} = \dfrac{0 - 4}{2} = \dfrac{-4}{2}$ = -2,

x = 2, y = $\dfrac{3 \times 2 - 4}{2} = \dfrac{6 - 4}{2} = \dfrac{2}{2}$ = 1,

x = 4, y = $\dfrac{3 \times 4 - 4}{2} = \dfrac{12 - 4}{2} = \dfrac{8}{2}$ = 4.

x = $\dfrac{4}{3}, y = \dfrac{3 \times \dfrac{4}{3} - 4}{2} = \dfrac{4 - 4}{2} = \dfrac{0}{2}$ = 0.

Table of values for equation (2)

Steps of construction :

1. Plot the points (0, -2), (2, 1), (4, 4) and $\Big(\dfrac{4}{3}, 0\Big)$.

2. Join the points.

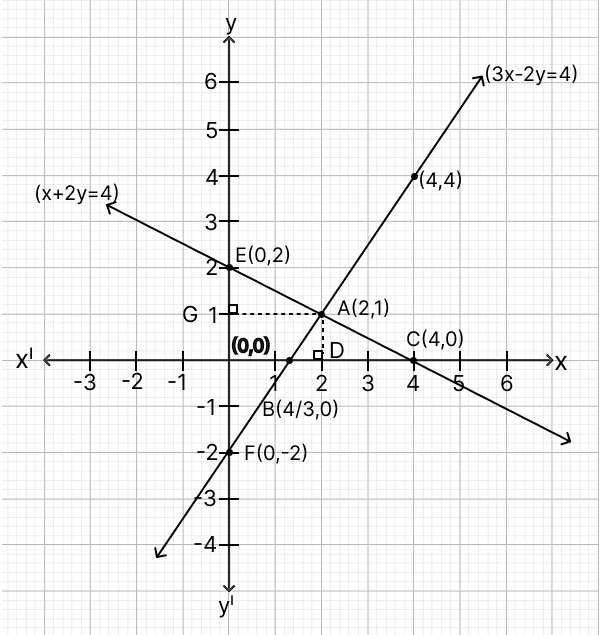
From graph,

A(2, 1) is the point of intersection of lines.

AEF is the triangle between lines and y-axis.

From A, draw AG perpendicular to EF.

Using distance formula, distance = $\sqrt{(x$2 - x1)^2 + (y2 - y1)^2}

Distance between E (0, 2) and F (0, -2)

= $\sqrt{(0 - 0)^2 + \Big(2 - (-2)\Big)^2} = \sqrt{(2 + 2)^2} = \sqrt{4^2} = 4$ units

From graph,

AG = 2 units

EF = 4 units

Area of triangle = $\dfrac{1}{2}$ x base x height

= $\dfrac{1}{2}$ x EF x AG

= $\dfrac{1}{2}$ x 4 x 2

= 1 x 4

= 4 sq. units.

And, ABC is the triangle between lines and x-axis.

Using distance formula, distance = $\sqrt{(x$2 - x1)^2 + (y2 - y1)^2}

Distance between B $\Big(\dfrac{4}{3}, 0\Big)$ and C (4, 0)

= $\sqrt{\Big(4 - \dfrac{4}{3}\Big)^2 + (0 - 0)^2} = \sqrt{\Big(\dfrac{12 - 4}{3}\Big)^2} = \sqrt{\Big(\dfrac{8}{3}\Big)^2} = \dfrac{8}{3}$

From A, draw AD perpendicular to BC.

AD = 1 unit

BC = $\dfrac{8}{3}$ units

Area of triangle = $\dfrac{1}{2}$ x base x height

$\text{Area of triangle ABC} = \dfrac{1}{2} \times BC \times AD \\[1em] = \dfrac{1}{2} \times \dfrac{8}{3} \times 1 \\[1em] = \dfrac{4}{3} \text{sq. units}$

Hence, point of intersection of lines is x = 2, y = 1 and area of the triangle formed by the lines and the y-axis = 4 sq. unit and area of the triangle formed by the lines and the x-axis = $\dfrac{4}{3}$ sq units.