Mathematics
Statement 1: AD is median of triangle ABC and DE is parallel to BA.
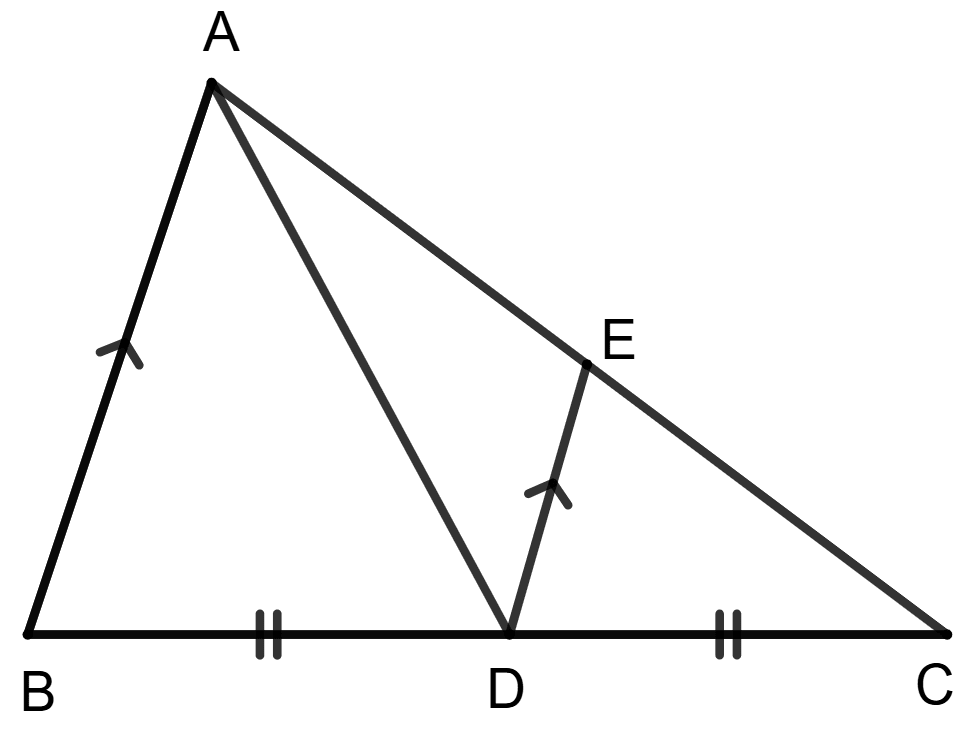
Statement 2: DE is median of triangle ADC.
Both the statements are true.
Both the statements are false.
Statement 1 is true, and statement 2 is false.
Statement 1 is false, and statement 2 is true.
Mid-point Theorem
2 Likes
Answer
In △ ABC,
From figure,
BD = DC.
∴ D is the mid-point of BC.
A median of a triangle is a line segment that connects a vertex of the triangle to the midpoint of the opposite side.
So, AD is the median of triangle ABC.
So, statement 1 is true.
By converse of mid-point theorem,
The straight line drawn through the mid-point of one side of a triangle parallel to another, bisects the third side.
Since, D is mid-point of BC and AB || DE
∴ E is the mid-point of AC.
Thus, DE is a median of triangle ADC.
So, statement 2 is true.
∴ Both the statements are true.
Hence, option 1 is the correct option.
Answered By
1 Like
Related Questions
In rhombus PQRS; A, B and C are mid-points of sides PQ, QR and RS respectively. If ∠P = 60°, the angle PQR is equal to:
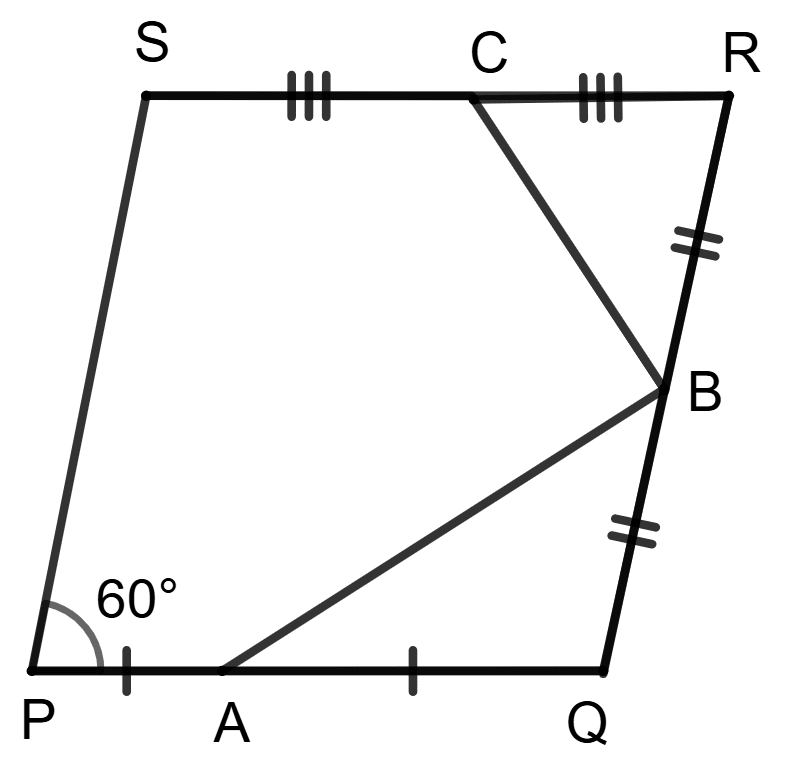
60°
90°
120°
none of these
Statement 1: The diagonals of a quadrilateral are perpendicular to each other; P, Q, R and S are the midpoints of sides AB, BC, CD and DA respectively.
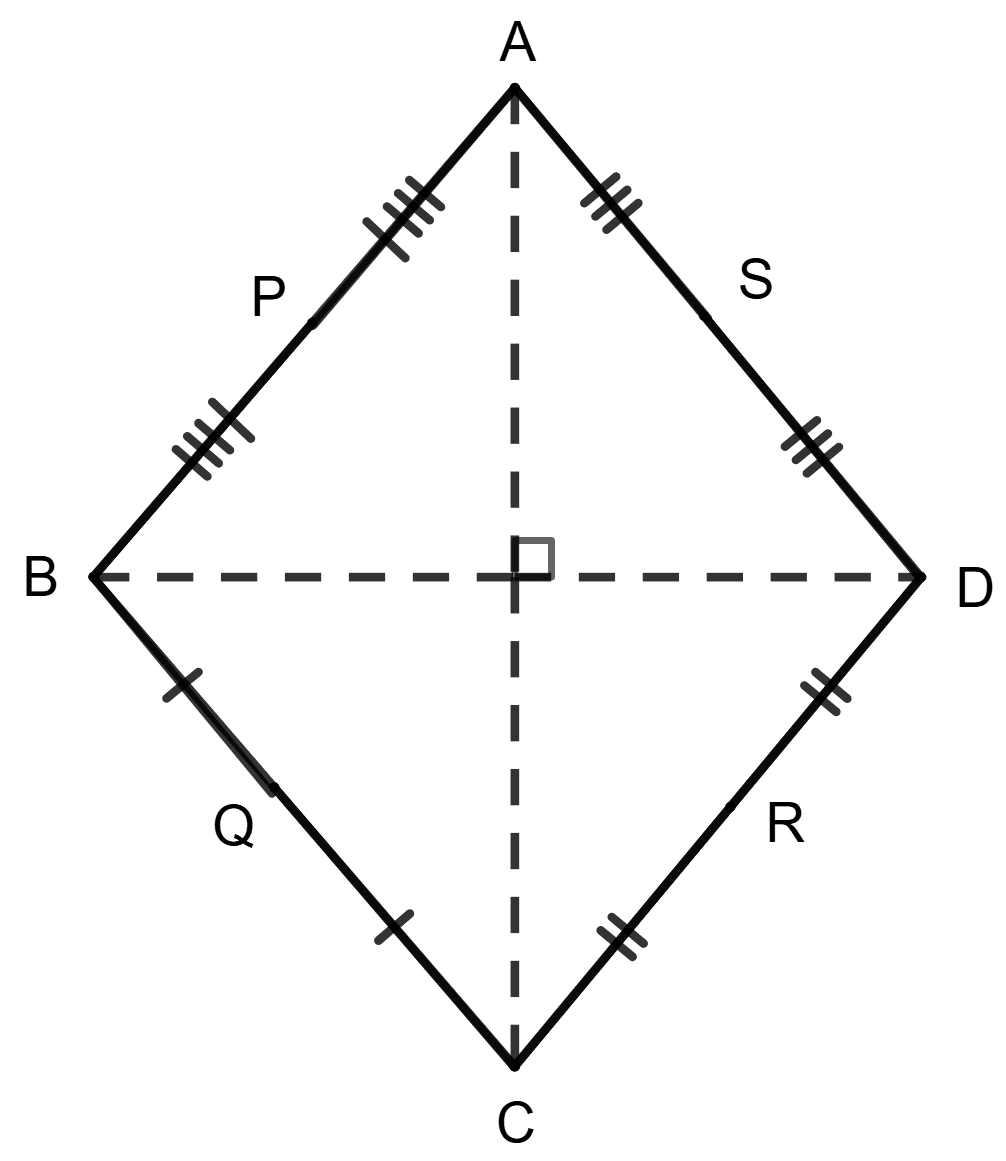
Statement 2: Quadrilateral PQRS is a square.
Both the statements are true.
Both the statements are false.
Statement 1 is true, and statement 2 is false.
Statement 1 is false, and statement 2 is true.
Assertion (A): The figure formed by joining the mid-points of the sides of a quadrilateral ABCD is a square.
Reason (R): Diagonals of quadrilateral ABCD are not equal and are not perpendicular to each other.
A is true, but R is false.
A is false, but R is true.
Both A and R are true, and R is the correct reason for A.
Both A and R are true, and R is the incorrect reason for A.
Assertion (A): R, S, D and E are mid-points of OC, OB, AB and AC respectively, then DERS is a parallelogram.
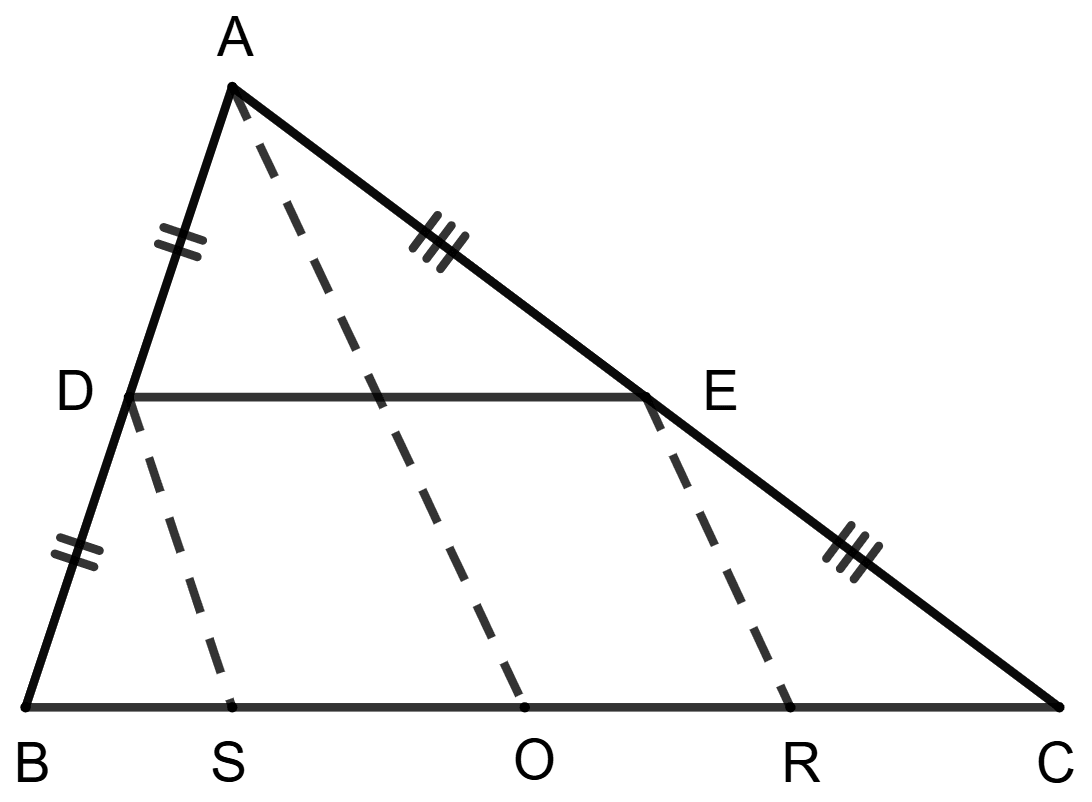
Reason (R): DS ∥ AO ∥ ER and DS = ER = .
A is true, but R is false.
A is false, but R is true.
Both A and R are true, and R is the correct reason for A.
Both A and R are true, and R is the incorrect reason for A.