Mathematics
Statement 1: A rhombus shaped sheet with perimeter 40 cm has one diagonal 12 cm and the other diagonal is 16 cm.
Statement 2: If the other diagonal of this rhombus = x cm, x = 102 - 62.
Both the statements are true.
Both the statements are false.
Statement 1 is true, and statement 2 is false.
Statement 1 is false, and statement 2 is true.
Mensuration
1 Like
Answer
Given,
The perimeter of a rhombus = 40 cm.
One diagonal = 12 cm.
As we know, the perimeter of the rhombus = 4 x side
⇒ 4 x side = 40 cm
⇒ side = cm
⇒ side = 10 cm

Let ABCD be a rhombus. From figure,
AB = 10 cm
Let diagonal AC = 12 cm
We know that,
Diagonals of rhombus bisect each other.
Then, OA = OC = = 6 cm
Let OB be a cm.
Since the diagonal of a rhombus bisect at 90°.
Applying pythagoras theorem in triangle AOB, we get:
⇒ AB2 = OA2 + OB2
⇒ (10)2 = (6)2 + a2
⇒ a2 = (10)2 - (6)2
⇒ a2 = 100 - 36
⇒ a2 = 64
⇒ a =
⇒ a = 8
So, OB = 8 cm
BD = 2 x OB = 2 x 8 cm = 16 cm.
∴ Statement 1 is true.
As solved above,
If the other diagonal of this rhombus = x cm,
Then will be equal to 102 - 62.
∴ Statement 2 is false.
∴ Statement 1 is true, and statement 2 is false.
Hence, option 3 is the correct option.
Answered By
1 Like
Related Questions
If the area of a trapezium is 32 cm2 and distance between its parallel sides is 8 cm; the sum of length of its parallel side is :
4 cm
16 cm
8 cm
12 cm
Statement 1: The side of a triangular board are 8 cm, 6 cm and 10 cm; the cost of painting it at the rate of ₹ 10 per square cm is x 6 x 8 x ₹ 10.
Statement 2: 102 = 82 + 62
⇒ Sides of the triangle are 8 cm and 6 cm.
Both the statements are true.
Both the statements are false.
Statement 1 is true, and statement 2 is false.
Statement 1 is false, and statement 2 is true.
Assertion (A): The perimeter of the adjoining figure is (32 + x) cm.
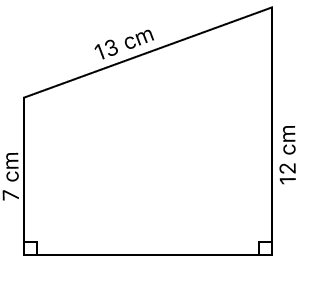
Reason (R): x2 = 132 - 52 = 144 and x = 12 cm.
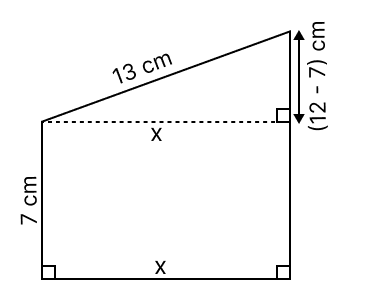
Perimeter = (32 + 12) cm
A is true, but R is false.
A is false, but R is true.
Both A and R are true, and R is the correct reason for A.
Both A and R are true, and R is the incorrect reason for A.
Assertion (A): If BC = 14 cm, AB = 14 x 4 cm
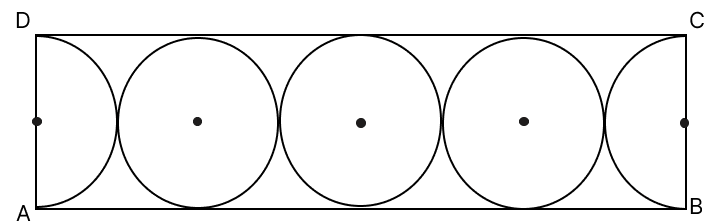
Reason (R): AB = 4 x 2r = 4 x 14 cm
A is true, but R is false.
A is false, but R is true.
Both A and R are true, and R is the correct reason for A.
Both A and R are true, and R is the incorrect reason for A.