Mathematics
Statement 1: Through a vertex of a polygon, 3 diagonals can be drawn.
Statement 2: The polygon is hexagon.
Both the statements are true.
Both the statements are false.
Statement 1 is true, and statement 2 is false.
Statement 1 is false, and statement 2 is true.
Rectilinear Figures
3 Likes
Answer
It is possible through a vertex of a polygon, to draw 3 diagonals.
The number of diagonals from a single vertex in a polygon with n sides is n - 3.
3 = n - 3
n = 3 + 3 = 6.
A polygon with 6 sides is a hexagon.
∴ Both the statements are true.
Hence, option 1 is the correct option.
Answered By
2 Likes
Related Questions
In parallelogram ABCD, diagonal AC and BD intersect each other at point O. Then:
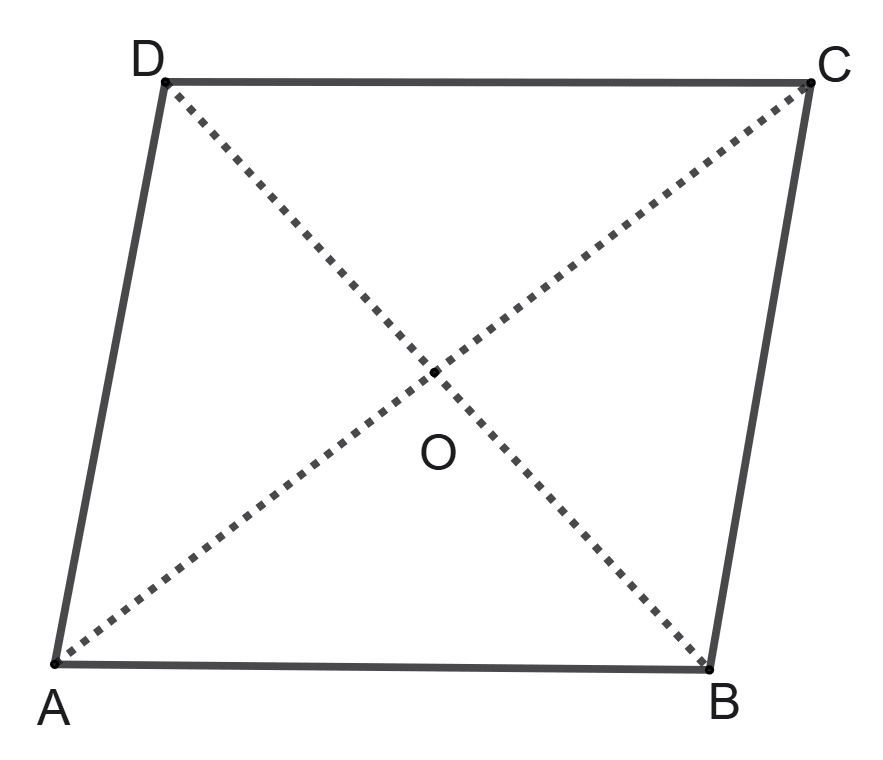
AC = BD
∠AOB = 90°
The four triangles formed are congruent
AC and BD bisect each other
Statement 1: The sum of the interior angles of a regular polygon is twice of the sum of its exterior angles.
Statement 2: Number of sides(n) of the polygon is 6.
Both the statements are true.
Both the statements are false.
Statement 1 is true, and statement 2 is false.
Statement 1 is false, and statement 2 is true.
Assertion (A): The diagonal of a quadrilateral bisect each other at right angle.
Reason (R): The quadrilateral is square.
A is true, but R is false.
A is false, but R is true.
Both A and R are true, and R is the correct reason for A.
Both A and R are true, and R is the incorrect reason for A.
Assertion (A): In parallelogram ABCD, PD bisects ∠ADC and PC bisects angle DCB, then ∠DPC = 90°.
Reason (R): ∠PDC = x ∠ADC
∠PCD = x ∠BCD
∠PDC + ∠PCD = x (∠ADC + ∠BCD)
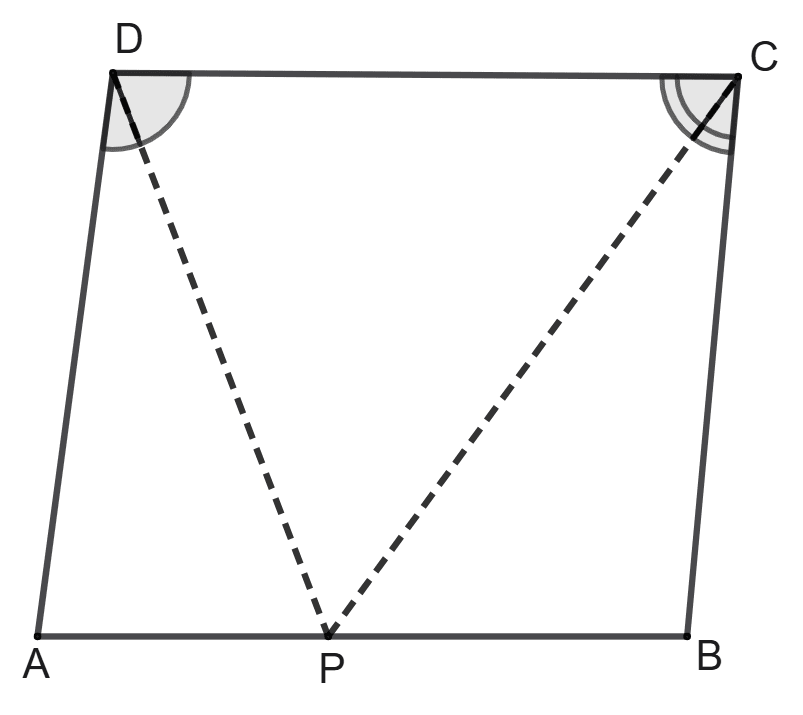
A is true, but R is false.
A is false, but R is true.
Both A and R are true, and R is the correct reason for A.
Both A and R are true, and R is the incorrect reason for A.