Mathematics
Assertion (A) : In the figure below, O is the center of the circle and ∠AOC = 160°. Then x = 100° and y = 80°.
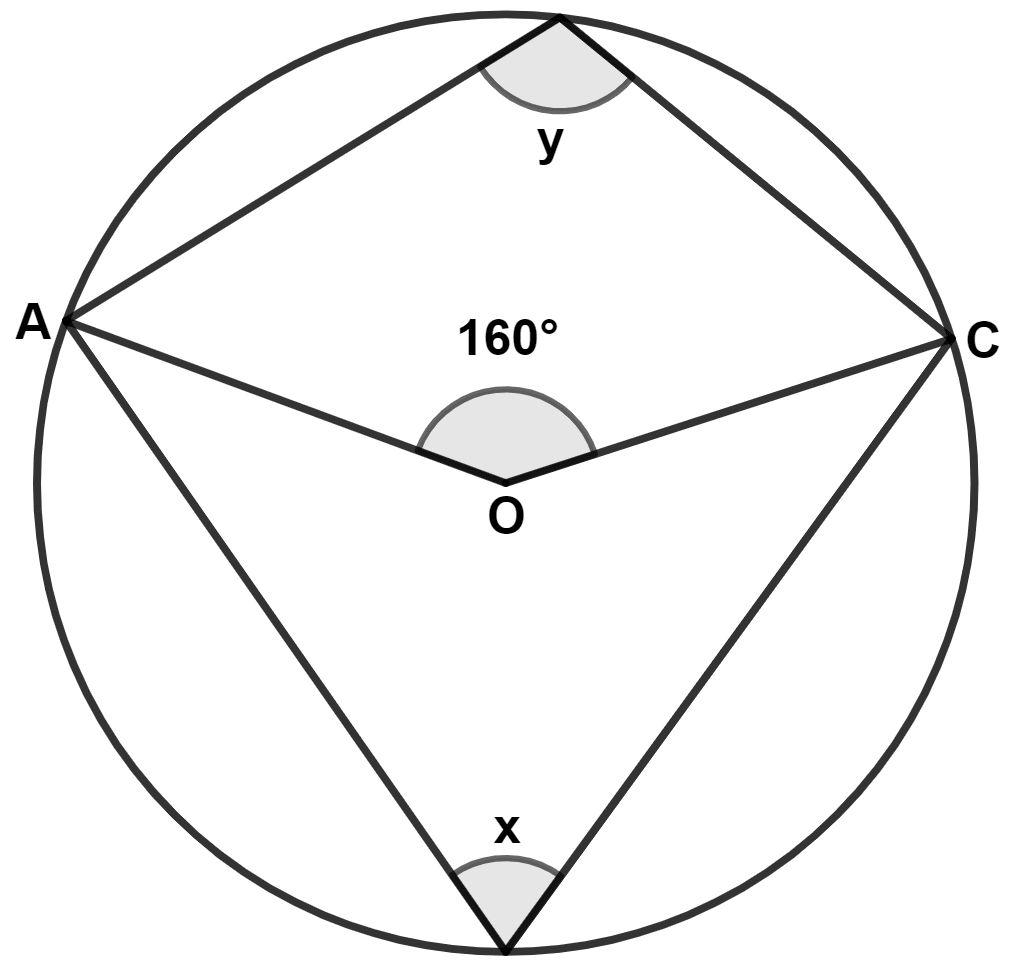
Reason (R) : The angle, which an arc of a circle subtends at the centre of the circle is double that which it subtends at any point on the remaining part of the circumference.
A is true, R is false.
A is false, R is true.
Both A and R are true.
Both A and R are false.
Circles
1 Like
Answer
We know that,
The angle, which an arc of a circle subtends at the centre of the circle is double that which it subtends at any point on the remaining part of the circumference.
From figure,
⇒ 2x = ∠AOC
⇒ 2x = 160°
⇒ x = = 80°.
We know that,
Sum of opposite angles in a cyclic quadrilateral = 180°.
⇒ x + y = 180°
⇒ 80° + y = 180°
⇒ y = 180° - 80° = 100°.
∴ Assertion (A) is false and Reason (R) is true.
Hence, Option 2 is the correct option.
Answered By
2 Likes
Related Questions
Assertion (A) : Locus of points which are at equal distances from three non-collinear points does not exist.
Reason (R) : Locus of non-collinear points A, B and C is the circumference of triangle ABC.
A is true, R is false.
A is false, R is true.
Both A and R are true.
Both A and R are false.
Assertion (A) : The locus of the mid-points of all equal chords in a circle is the circumference of the circle concentric with the given circle and having radius equal to the distance of equal chords from the center.
Reason (R) : Locus of all points at a fixed distance from a fixed point is a circle with the fixed point as center and fixed distance as radius.
A is true, R is false.
A is false, R is true.
Both A and R are true.
Both A and R are false.
Assertion (A) : In the figure below, CD = 7.8 cm, PD = 5 cm, PB = 4 cm, then PT = 8 cm.
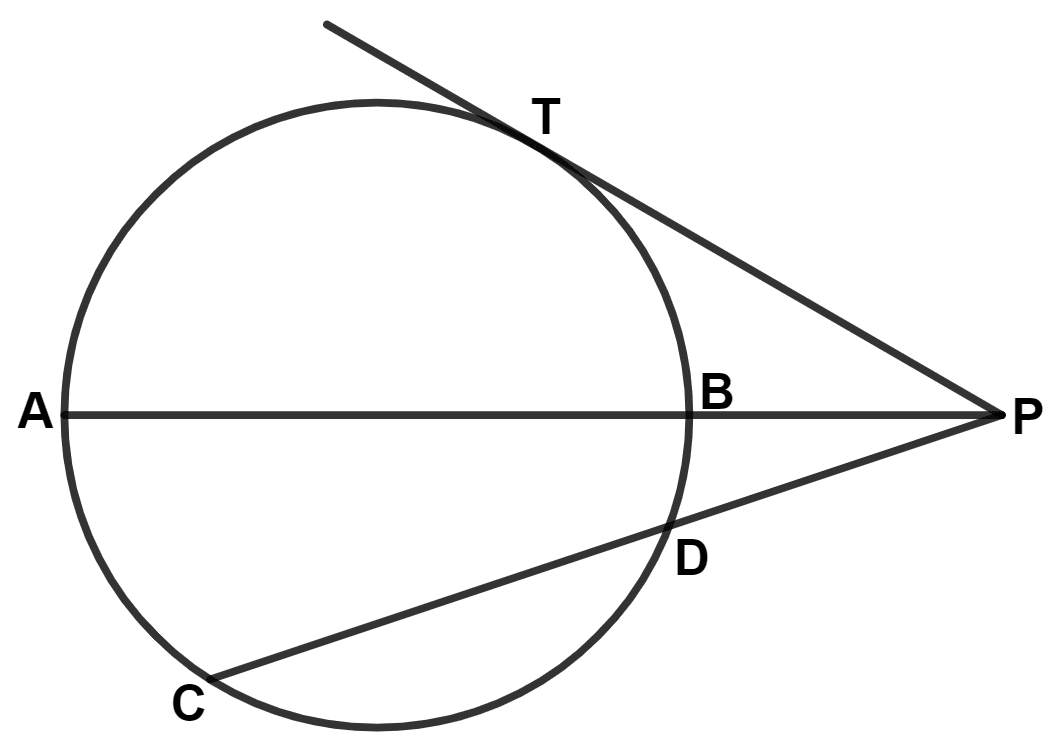
Reason (R) : If two chords of a circle intersect internally or externally then the product of the lengths of their segments is equal.
A is true, R is false.
A is false, R is true.
Both A and R are true.
Both A and R are false.
Assertion (A) : The length of a cylinder is 21 cm and radius of its cross-section is 2 cm. Area covered by the cylinder in one revolution is 264 cm2.
Reason (R) : Distance travelled by the cylinder in 1 round = circumference of its cross-section.
A is true, R is false.
A is false, R is true.
Both A and R are true.
Both A and R are false.