Mathematics
Assertion (A) : In the figure given below the measurement of x = 12 cm.
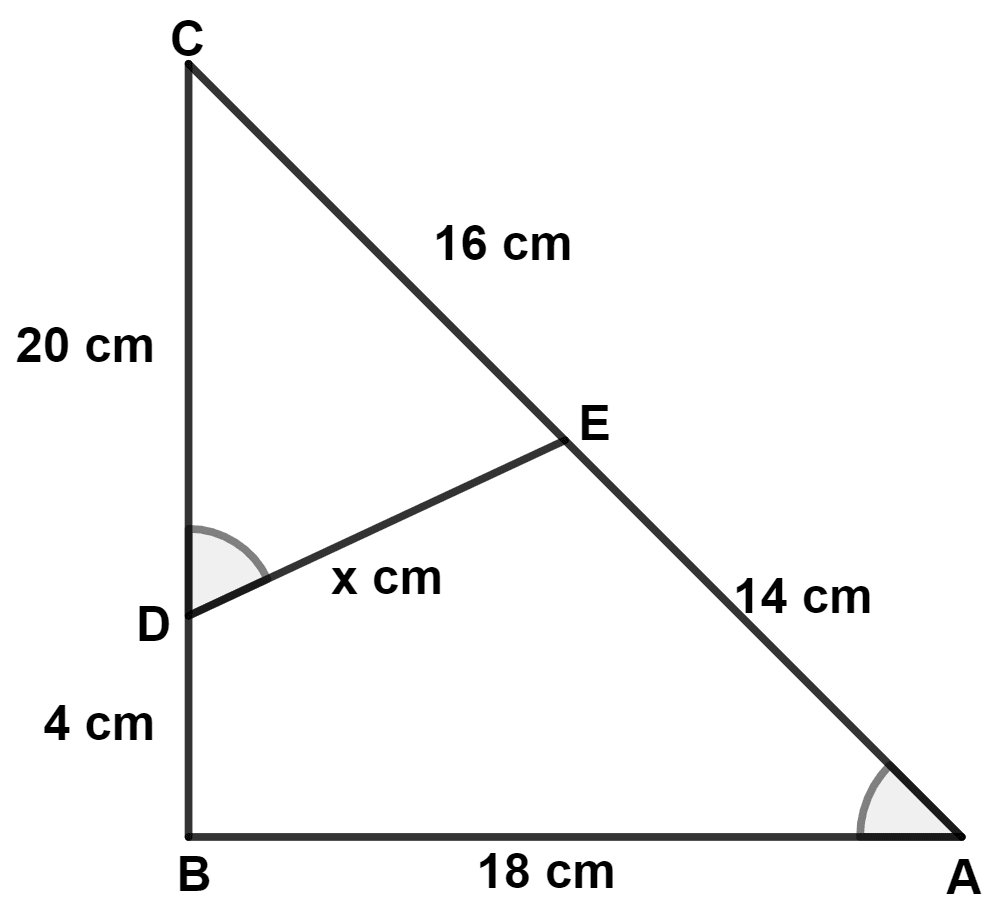
Reason (R) : In similar triangles, the corresponding sides are in proportion.
A is true, R is false.
A is false, R is true.
Both A and R are true.
Both A and R are false.
Similarity
2 Likes
Answer
We know that,
In similar triangles, the corresponding sides are in proportion.
From figure,
In △ CDE and △ CBA,
⇒ ∠CDE = ∠CAB (Given)
⇒ ∠DCE = ∠BCA (Common angle)
∴ △ CDE ~ △ CBA (By A.A. axiom)
∴
= 12 cm.
∴ Assertion (A) and Reason (R) are true.
Hence, Option 3 is the correct option.
Answered By
1 Like
Related Questions
Assertion (A) : If (3a, 4) is the mid-point of the line segment joining points (-6, 5) and (-2, 3); then a = -4.
Reason (R) : The mid-point of the line segment joining the points (x1, y1) and (x2, y2) is .
A is true, R is false.
A is false, R is true.
Both A and R are true.
Both A and R are false.
Assertion (A) : Given two straight lines 3x - 2y = 5 and 2x + ky + 7 = 0 are perpendicular to each other when k = 3.
Reason (R) : Let AB and CD be two mutually perpendicular lines and their inclinations be α and θ respectively, then tan θ = -cot α.
A is true, R is false.
A is false, R is true.
Both A and R are true.
Both A and R are false.
Assertion (A) : The perpendicular drawn from the vertex of the right angle of a right-angled triangle divides the triangle into two triangles similar to each other.
Reason (R) : Triangles, which are similar to the same triangle, are similar to each other.
A is true, R is false.
A is false, R is true.
Both A and R are true.
Both A and R are false.
Assertion (A) : Locus of points which are at equal distances from three non-collinear points does not exist.
Reason (R) : Locus of non-collinear points A, B and C is the circumference of triangle ABC.
A is true, R is false.
A is false, R is true.
Both A and R are true.
Both A and R are false.