Science
Study the data given below showing the focal length of three concave mirrors A, B and C and the respective distances of objects placed in front of the mirrors:
| Case | Mirror | Focal Length (cm) | Object Distance (cm) |
|---|---|---|---|
| 1 | A | 20 | 45 |
| 2 | B | 15 | 30 |
| 3 | C | 30 | 20 |
(a) In which one of the above cases the mirror will form a diminished image of the object? Justify your answer.
(b) List two properties of the image formed in case 2.
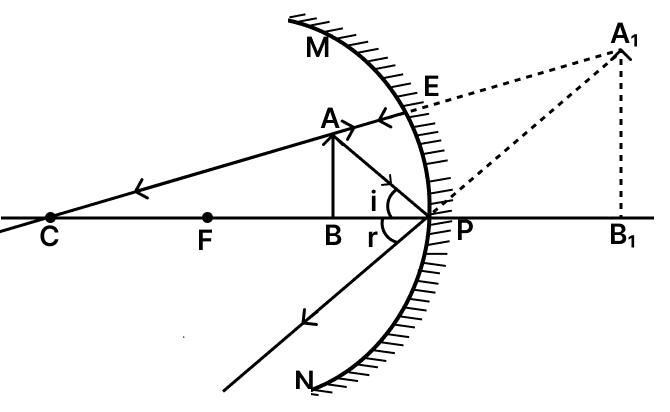
(c) What is the nature and size of the image formed by mirror C? Draw ray diagram to justify your answer.
OR
(c) An object is placed at a distance of 18 cm from the pole of a concave mirror of focal length 12 cm. Find the position of the image formed in this case.
Reflection of Light
1 Like
Answer
(a) Case 1 (Mirror A) will form a diminished image.
Explanation : The object (45 cm) is beyond C (40 cm) and for a concave mirror an object beyond C produces a real, inverted and diminished image located between f and C.
(b) Two properties of the image formed in case 2 (Mirror B) where object is at C :
- The image is real and inverted.
- The image is of the same size as the object and is formed at C (30 cm) on the other side of the mirror.
(c) For mirror C (f = 30 cm, object at 20 cm) :
- Nature of image : Virtual and erect (since the object lies between pole and focus).
- Size of image: Magnified (appears larger than the object).
- Where formed : Behind the mirror (cannot be projected on a screen).
The ray diagram of the above arrangement is shown below :
OR
(c)
Given,
- Object distance () = -18 cm
- Focal length of the mirror () = -12 cm
Here, negative sign indicates that object is in front of the mirror and parallel rays after reflection converges in front of the mirror.
Let, image distance be ''.
From mirror formula,
Hence, the image is formed at a distance of 36 cm in front of the mirror.
Answered By
1 Like
Related Questions
(a) Define electric power. Express it in terms of potential difference (V) and resistance (R).
(b) An electric oven is designed to work on the mains voltage of 220 V. This oven consumes 11 units of electrical energy in 5 hours. Calculate :
- power rating of the oven
- current drawn by the oven
- resistance of the oven when it is red hot
(a) Write the relation between resistance and electrical resistivity of the material of a conductor in the shape of cylinder of length and area of cross-section . Hence derive the SI unit of electrical resistivity.
(b) The resistance of a metal wire of length 3 m is 60 Ω. If the area of cross-section of the wire is 4 × 107 m2, calculate the electrical resistivity of the wire.
(c) State how would electrical resistivity be affected if the wire (of part 'b') is stretched so that its length is doubled. Justify your answer.
The metals produced by various reduction processes are not very pure. They contain impurities, which must be removed to obtain pure metals. The most widely used method for refining impure metals is electrolytic refining.
(a) What is the cathode and anode made of in the refining of copper by this process ?
(b) Name the solution used in the above process and write its formula.
(c) How copper gets refined when electric current is passed in the electrolytic cell?
OR
(c) You have two beakers 'A' and 'B' containing copper sulphate solution. What would you observe after about 2 hours if you dip a strip of zinc in beaker 'A' and a strip of silver in beaker ‘B’? Give reason for your observations in each case.
Mendel worked out the rules of heredity by working on garden pea using a number of visible contrasting characters. He conducted several experiments by making a cross with one or two pairs of contrasting characters of pea plant. On the basis of his observations he gave some interpretations which helped to study the mechanism of inheritance.
(a) When Mendel crossed pea plants with pure tall and pure short characteristics to produce F1 progeny, which two observations were made by him in F1 plants?
(b) Write one difference between dominant and recessive trait.
(c) In a cross with two pairs of contrasting characters
RRYY (Round Yellow) X rryy (Wrinkled Green)
Mendel observed 4 types of combinations in F2 generation. By which method did he obtain F2 generation? Write the ratio of the parental combinations obtained and what conclusions were drawn from this experiment.
OR
(c) Justify the statement : "It is possible that a trait is inherited but may not be expressed."