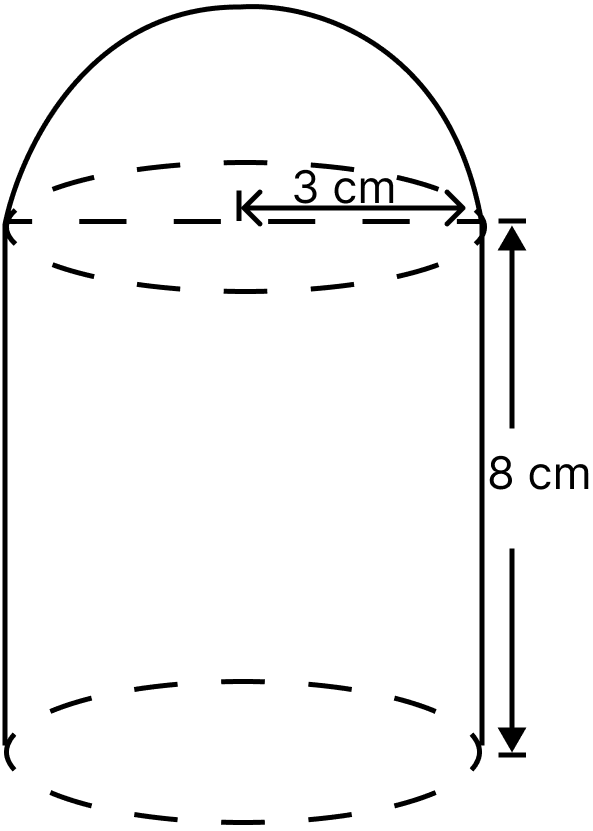
The adjoining figure shows a model of a solid consisting of a cylinder surmounted by a hemisphere at one end. If the model is drawn to a scale of 1 : 200, find

(i) the total surface area of the solid in π m².

(ii) the volume of the solid in π litres.

(i) In the given figure,

Height of cylindrical portion (H) = 8 cm.

Radius of cylindrical portion = radius of hemispherical portion = (r) = 3 cm.

Scale = 1 : 200

∴ k = 200.

Total surface area (S) = Curved surface area of hemisphere + Curved surface area of cylinder + Area of base of cylinder

= 2πr² + 2πrH + πr²

= 3πr² + 2πrH

= πr(3r + 2H)

= 3π(3 × 3 + 2 × 8)

= 3π(9 + 16)

= 3π × 25

= 75π cm².

∴ Surface area of solid = 75π × k²

= 75π × (200)²

= 75π × 40000 cm²

= 75π × $\dfrac{40000}{100 \times 100}$ m²

= 300π m².

Hence, the surface area of solid = 300π m².

(ii) Volume (V) = Volume of hemisphere + Volume of cylinder

= $\dfrac{2}{3}πr^3 + πr^2H$.

Substituting values we get :

$V = πr^2\Big(\dfrac{2}{3}r + H\Big) \\[1em] = πr^2\Big(\dfrac{2}{3} \times 3 + 8\Big) \\[1em] = π \times 3^2 \times (2 + 8) \\[1em] = 9π \times 10 \\[1em] = 90π \text{ cm}^3$

∴ Volume of solid = 90π × k³

= 90π × (200)³

= 90π × 8000000

= 720000000π cm³

= $\dfrac{720000000π}{100 \times 100 \times 100}$ m³

= 720π m³.

As, 1 m³ = 1000 litres

∴ Volume of solid = 720π × 1000 = 720000π litres.

Hence, the volume of solid = 720000π litres.