Mathematics
The area of a rectangle is 640 m2. Taking its length as x m; find, in terms of x, the width of the rectangle. If the perimeter of the rectangle is 104 m; find its dimensions.
Mensuration
3 Likes
Answer
Given:
Area of the rectangle = 640 m2
Length = x meters
Let b be the width of the rectangle.
Area of the rectangle = l x b
⇒ x × b = 640
⇒ b = m
By formula,
Perimeter of the rectangle = 2(l + b)
⇒ = 104
⇒
⇒ = 52
⇒ x2 + 640 = 52x
⇒ x2 - 52x + 640 = 0
⇒ x2 - 32x - 20x + 640 = 0
⇒ x(x - 32) - 20(x - 32) = 0
⇒ (x - 20)(x - 32) = 0
⇒ x - 20 = 0 or x - 32 = 0
⇒ x = 20 m or x = 32 m.
Now,
⇒ b =
Case 1 : x = 20 m
⇒ b = = 32 m.
Case 2 : x = 32 m
⇒ b = = 20 m.
Hence, the width of rectangle is and the dimensions of the rectangle are 20 m and 32 m.
Answered By
2 Likes
Related Questions
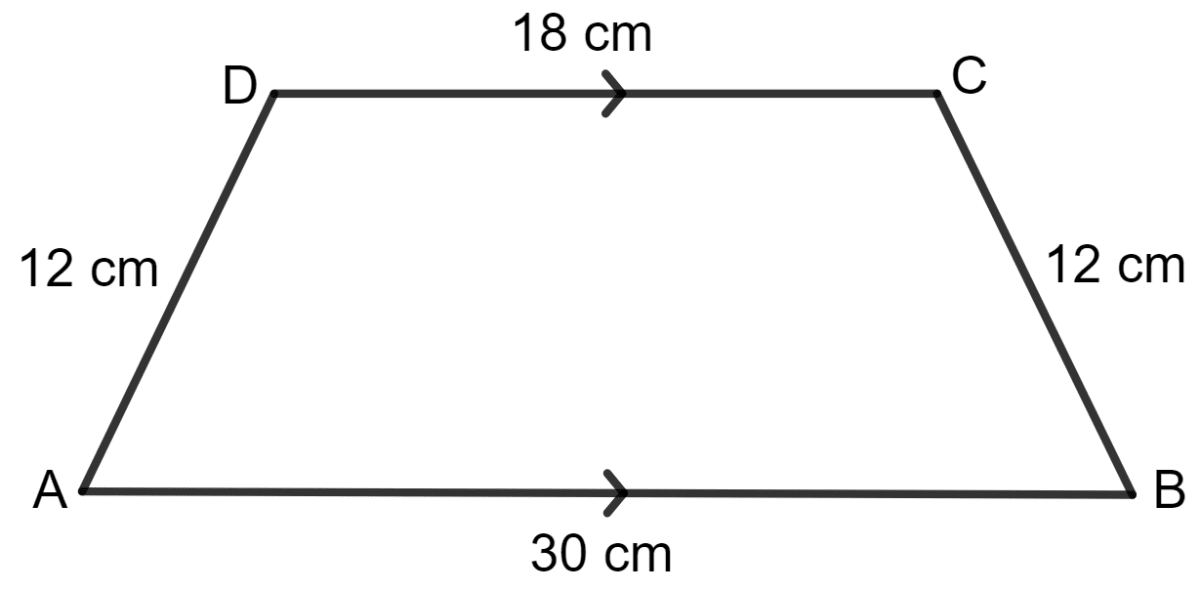
For the trapezium given below; find its area.
The perimeter of a rectangular board is 70 cm. Taking its length as x cm, find its width in terms of x.
If the area of the rectangular board is 300 cm2; find its dimensions.
The length of a rectangle is twice the side of a square and its width is 6 cm greater than the side of the square. If area of the rectangle is three times the area of the square; find the dimensions of each.
ABCD is a square with each side 12 cm. P is a point on BC such that area of Δ ABP : area of trapezium APCD = 1 : 5. Find the length of CP.