The base BC of an equilateral triangle ABC lies on y-axis. The coordinates of the point C are (0, -3). If origin is the mid-point of the base BC, find the coordinates of the points A and B.

Given, base BC of an equilateral triangle ABC lies on y-axis and coordinates of the point C are (0, -3).

Let coordinates of B be (x, y). Since, origin is the mid-point of the BC. So, by mid-point formula,

$\Rightarrow 0 = \dfrac{x + 0}{2} \text{ and } \dfrac{y - 3}{2} = 0 \\[1em] \Rightarrow \dfrac{x}{2} = 0 \text{ and } y - 3 = 0 \\[1em] \Rightarrow x = 0 \text{ and } y - 3 = 0 \\[1em] \Rightarrow x = 0 \text{ and } y = 3.$

∴ Coordinates of B are (0, 3).

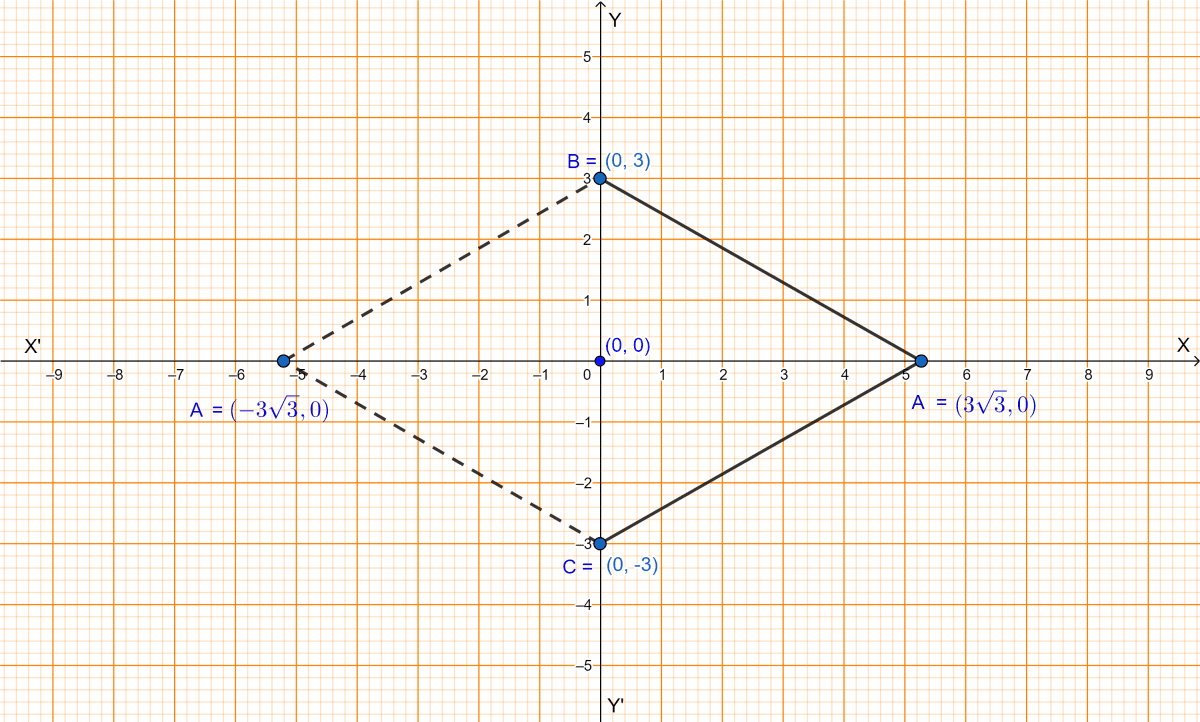
From graph we can see that BC = 6 units. Since, ABC is an equilateral triangle so, AB = BC = AC.

Let coordinates of A be (a, 0) as it lies on x-axis.

AB = $\sqrt{(a - 0)^2 + (0 - 3)^2}$

Since AB = 6 units,

$\therefore \sqrt{(a - 0)^2 + (0 - 3)^2} = 6 \\[1em] \Rightarrow \sqrt{a^2 + 9} = 6 \\[1em] \Rightarrow a^2 + 9 = 36 \\[1em] \Rightarrow a^2 = 36 - 9 \\[1em] \Rightarrow a^2 = 27 \\[1em] \Rightarrow a = \sqrt{27} \\[1em] \Rightarrow a = ±3\sqrt{3}.$

∴ Coordinates of A are $(±3\sqrt{3}, 0)$.

Hence, coordinates of A are $(±3\sqrt{3}, 0)$ and of B are (0, 3).