Mathematics
The circumference of a circular field is 308 m. Find its :
(i) radius
(ii) area.
Mensuration
17 Likes
Answer
(i) Let r be the radius of the circle.
The circumference of a circle = 308 m
As we know, the circumference of a circle = 2πr
Hence, the radius of a circle is 49 m.
(ii) Area of a circle = πr2
Hence, the area of a circle is 7,546 m2.
Answered By
10 Likes
Related Questions
The radii of two circles are 14 cm and 28 cm. If the area of the shaded portion is :
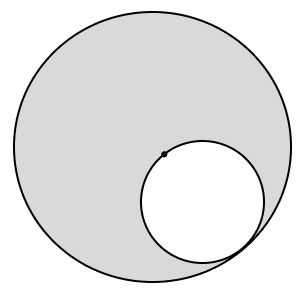
1848 cm2
1644 cm2
486 cm2
702 cm2
The diameter of a circle is 28 cm. Find its :
(i) circumference
(ii) area
The sum of the circumference and diameter of a circle is 116 cm. Find its radius.
The radii of two circles are 25 cm and 18 cm. Find the radius of the circle which has circumference equal to the sum of circumferences of these two circles.