Mathematics
The diagonals of a quadrilateral ABCD are perpendicular. Show that the quadrilateral formed by joining the mid-points of its adjacent sides is a rectangle.
Mid-point Theorem
42 Likes
Answer
From figure,
ABCD is a quadrilateral in which diagonals AC and BD are perpendicular to each other. P, Q, R and S are mid-points of AB, BC, CD and DA.
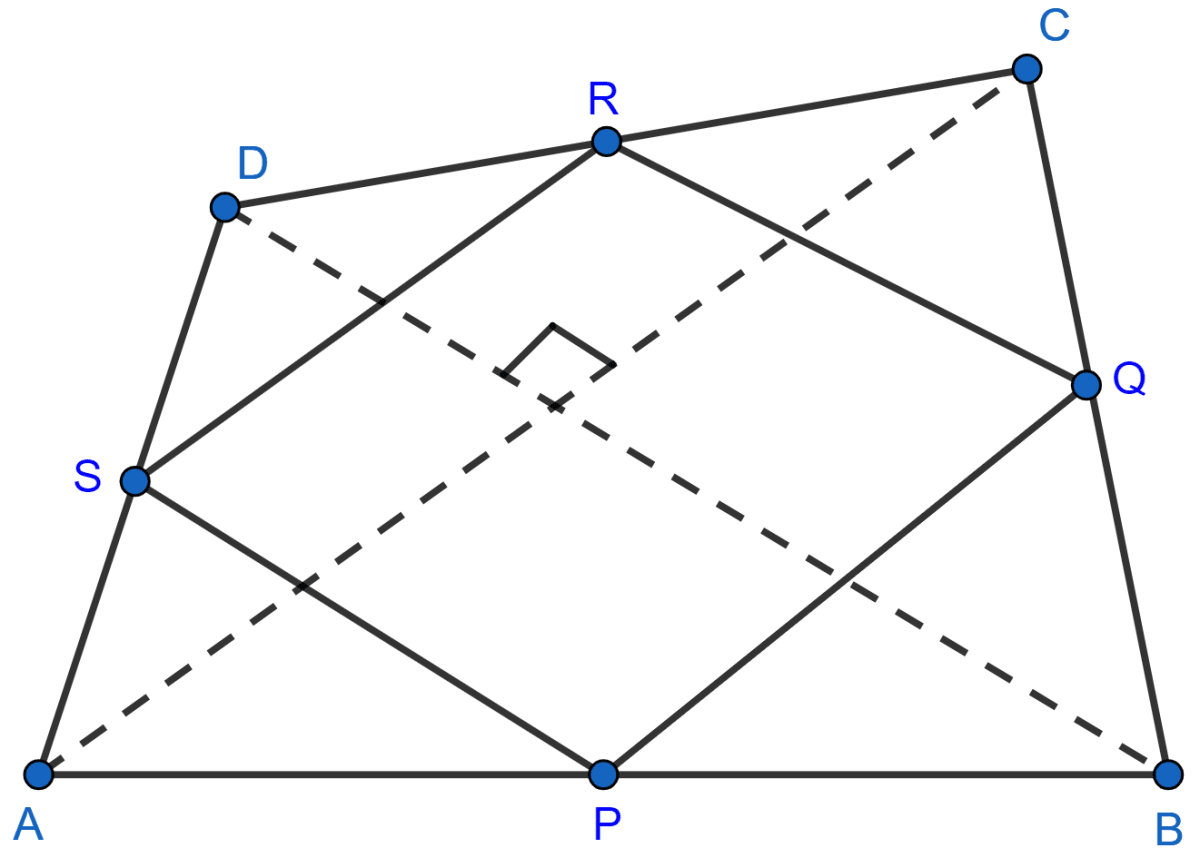
In △ABC,
P and Q are mid-points of AB and BC respectively,
PQ || AC and PQ = AC …….(1) (By mid-point theorem)
In △ADC,
S and R are mid-points of AD and DC respectively,
SR || AC and SR = AC ………(2) (By mid-point theorem)
Using eqn. 1 and 2 we get,
PQ || SR and PQ = SR.
So, PQRS is a parallelogram.
In △ABD,
S and P are mid-points of AD and AB respectively,
SP || BD and SP = BD ………(3) (By mid-point theorem)
Given,
AC and BD intersect at right angles,
From 3 we get,
SP || BD.
∴ SP ⊥ AC
From 2 we get,
SR || AC
∴ SP ⊥ SR i.e. ∠RSP = 90°.
∴ PQRS is a rectangle.
Hence, proved that the quadrilateral formed by joining the mid-points of its adjacent sides is a rectangle.
Answered By
19 Likes
Related Questions
Assertion (A): Refer to the adjoining figure. Three lines p, q, r are parallel to each other and PQ = QR = 1 cm. Then we conclude that AB = AC.
Reason (R): If a tranversal makes equal intercepts on three parallel lines, then another transversal will also make equal intercepts.
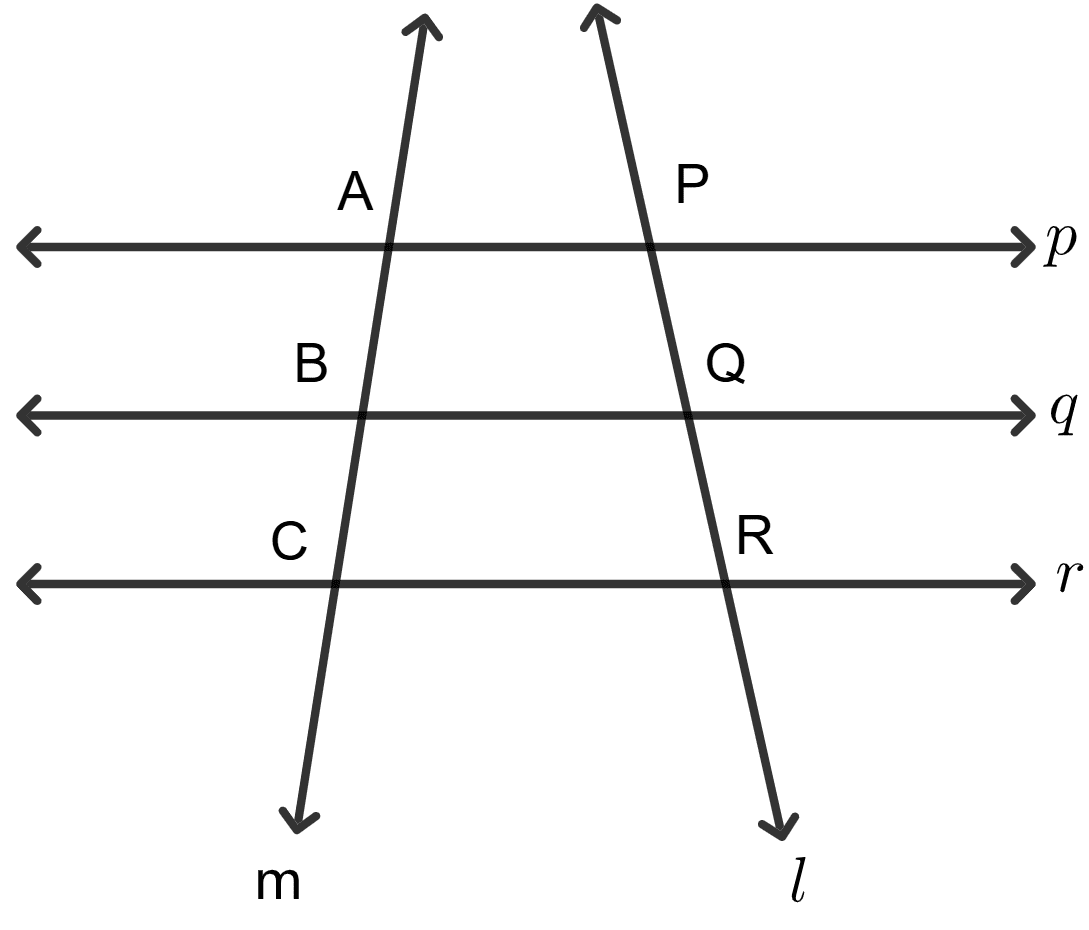
Assertion (A) is true, Reason (R) is false.
Assertion (A) is false, Reason (R) is true.
Both Assertion (A) and Reason (R) are true, and Reason (R) is the correct reason for Assertion (A).
Both Assertion (A) and Reason (R) are true, but Reason (R) is not the correct reason (or explanation) for Assertion (A).
ABCD is a rhombus with P, Q and R as mid-points of AB, BC and CD respectively. Prove that PQ ⊥ QR.
If D, E and F are mid-points of the sides BC, CA and AB respectively of a △ABC, prove that AD and FE bisect each other.
In △ABC, D and E are mid-points of the sides AB and AC respectively. Through E, a straight line is drawn parallel to AB to meet BC at F. Prove that BDEF is a parallelogram. If AB = 8 cm and BC = 9 cm, find the perimeter of the parallelogram BDEF.