Mathematics
The difference between an exterior angle of (n - 1) sided regular polygon and an exterior angle of (n + 2) sided regular polygon is 6°. Find the value of n.
Rectilinear Figures
14 Likes
Answer
Exterior angle of (n - 1) sided regular polygon =
Exterior angle of (n + 2) sided regular polygon =
Given,
Difference between an exterior angle of (n - 1) sided regular polygon and an exterior angle of (n + 2) sided regular polygon is 6°.
Since, no. of sides cannot be negative.
∴ n = 13.
Hence, n = 13.
Answered By
7 Likes
Related Questions
Assertion (A): The diagonal of a quadrilateral bisect each other at right angle.
Reason (R): The quadrilateral is square.
A is true, but R is false.
A is false, but R is true.
Both A and R are true, and R is the correct reason for A.
Both A and R are true, and R is the incorrect reason for A.
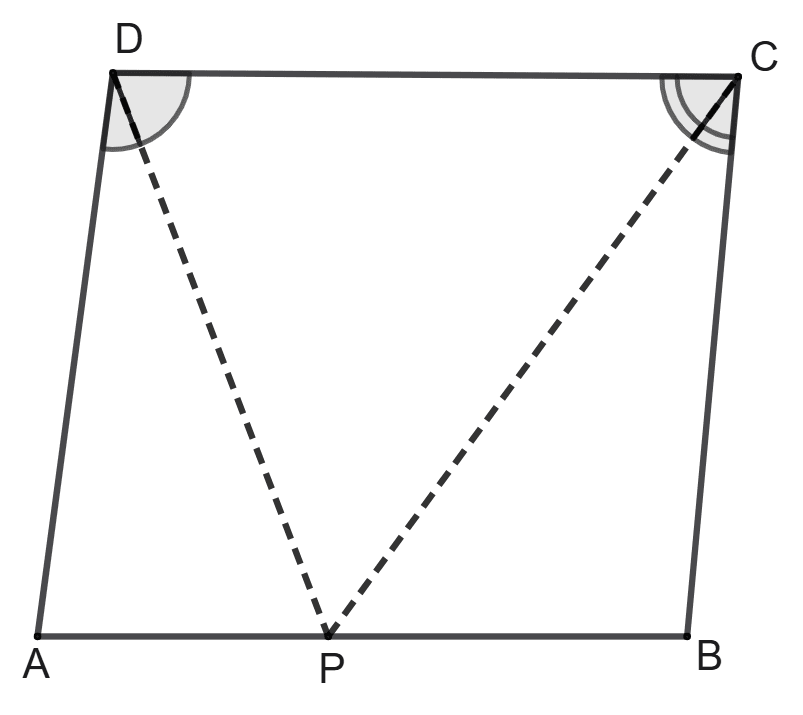
Assertion (A): In parallelogram ABCD, PD bisects ∠ADC and PC bisects angle DCB, then ∠DPC = 90°.
Reason (R): ∠PDC = x ∠ADC
∠PCD = x ∠BCD
∠PDC + ∠PCD = x (∠ADC + ∠BCD)
A is true, but R is false.
A is false, but R is true.
Both A and R are true, and R is the correct reason for A.
Both A and R are true, and R is the incorrect reason for A.
Two alternate sides of a regular polygon, when produced, meet at right angle. Find :
(i) the value of each exterior angle of the polygon;
(ii) the number of sides in the polygon.
In parallelogram ABCD, AP and AQ are perpendiculars from vertex of obtuse angle A as shown. If ∠x : ∠y = 2 : 1; find the angles of the parallelogram.
