Mathematics
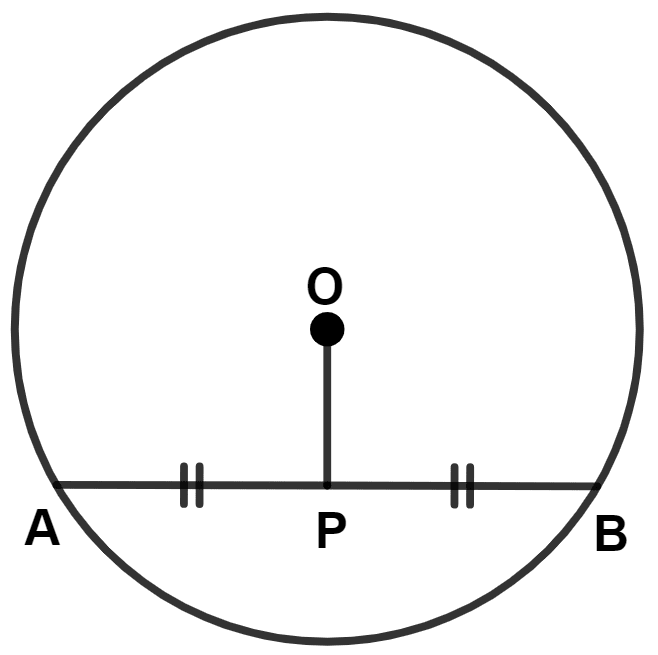
The given figure shows a circle with center O. P is mid-point of chord AB. Show that OP is perpendicular to AB.
Related Questions
In triangles ABC and DEF, AB = DE and AC = EF, then to make these two triangles congruent, we must have :
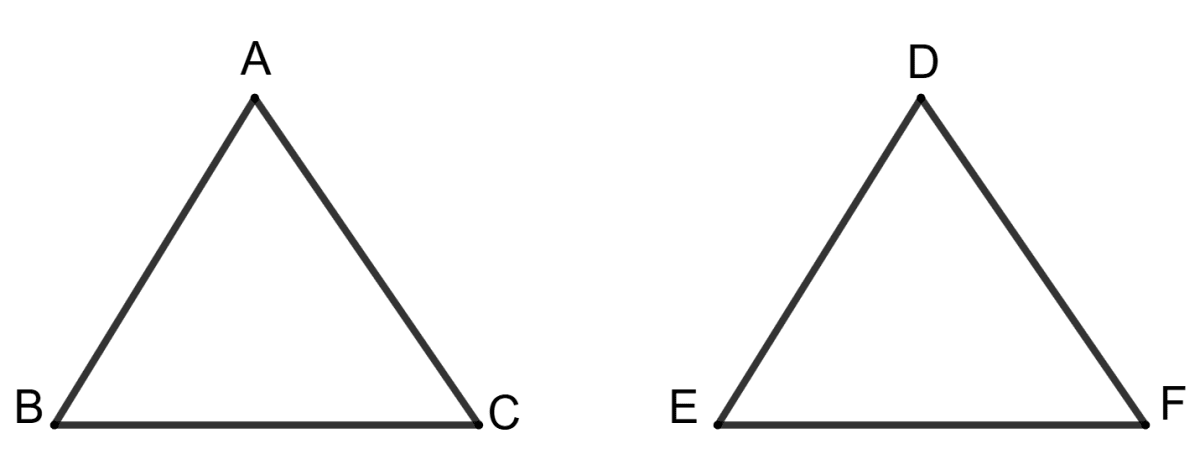
BC = DF
∠A = ∠E
any of (1) and (2)
none of (1) and (2)
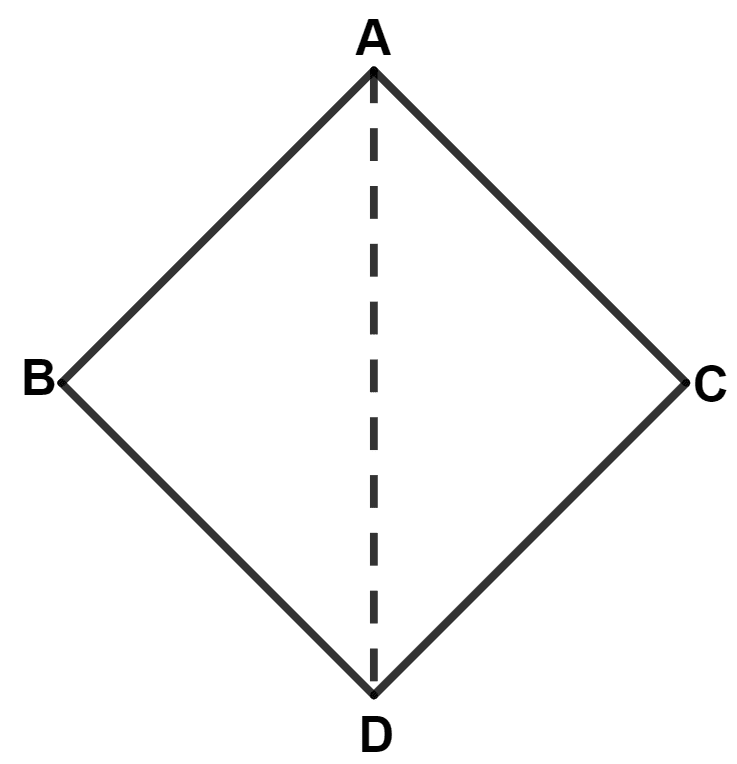
In quadrilateral ABCD, AB = AC and BD = CD, then AD bisects :
angle ADC
angle BAD
angle BAC
angle ABC
A triangle ABC has ∠B = ∠C. Prove that :
(i) the perpendiculars from the mid-point of BC to AB and AC are equal.
(ii) the perpendicular from B and C to the opposite sides are equal.
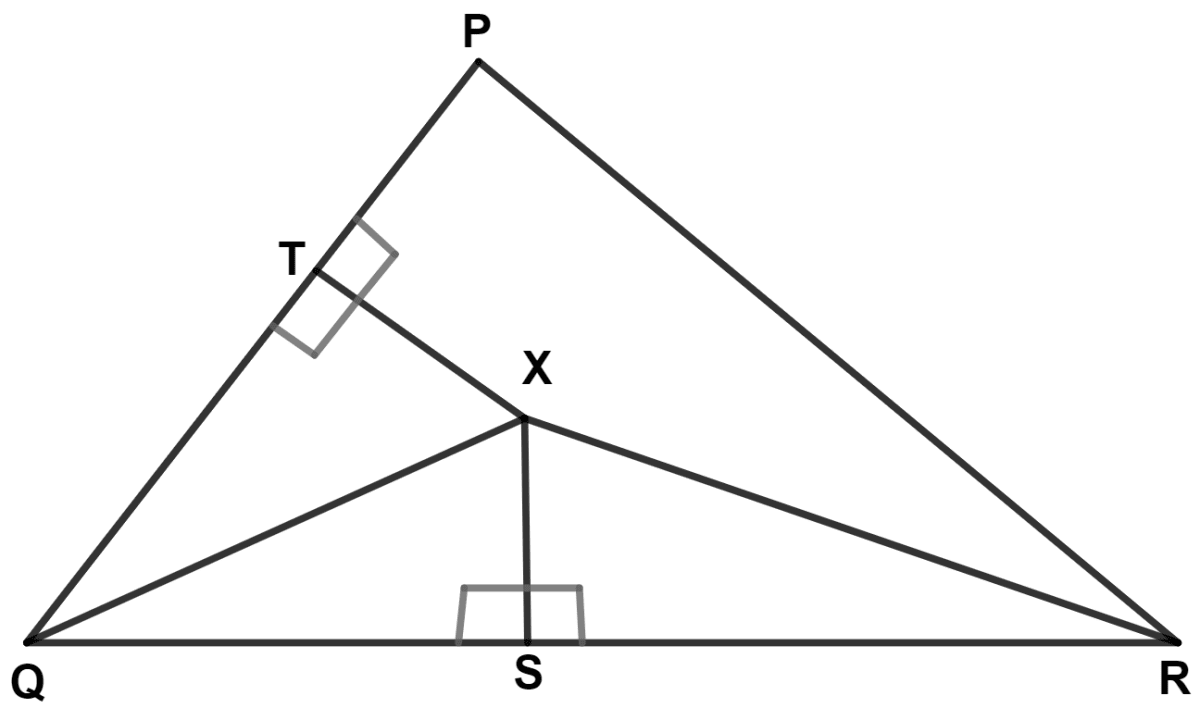
In the adjoining figure, QX and RX are the bisectors of the angles Q and R respectively of the triangle PQR. If XS ⊥ QR and XT ⊥ PQ; prove that :
(i) △ XTQ ≅ △ XSQ
(ii) PX bisects angle P.