Mathematics
The given figure shows a semi-circle with center O and diameter PQ. If PA = AB and ∠BCQ = 140°; find measures of angles PAB and AQB. Also, show that AO is parallel to BQ.
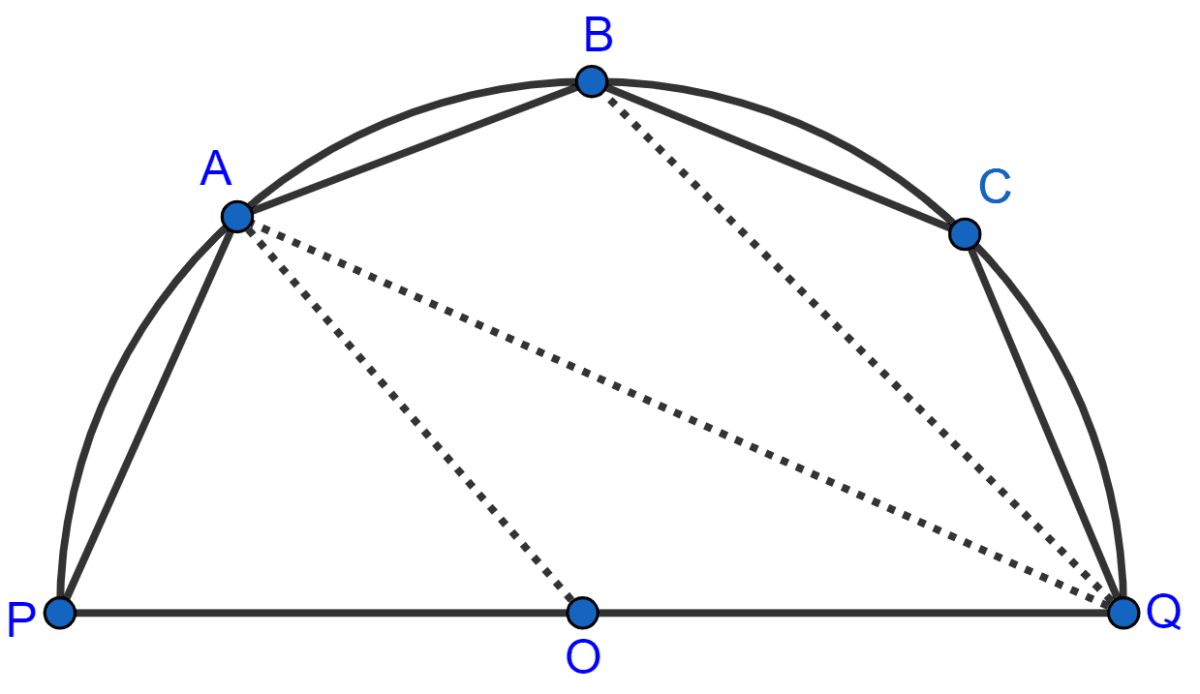
Circles
10 Likes
Answer
Join PB.
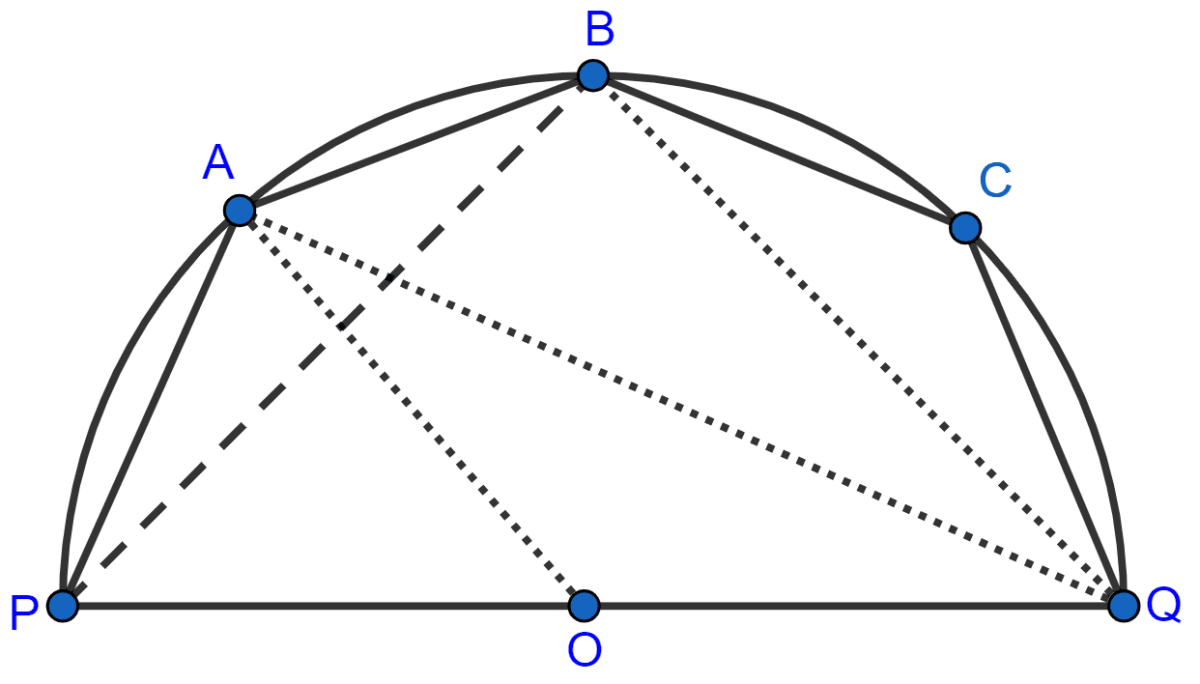
In cyclic quadrilateral PBCQ,
⇒ ∠BPQ + ∠BCQ = 180° [Sum of opposite angles of a cyclic quadrilateral = 180°]
⇒ ∠BPQ + 140° = 180°
⇒ ∠BPQ = 180° - 140°
⇒ ∠BPQ = 40° …………(1)
In △PBQ,
∠PBQ = 90° [Angle in a semi-circle is a right angle.]
⇒ ∠PBQ + ∠BPQ + ∠PQB = 180° [Angle sum property of triangle]
⇒ 90° + 40° + ∠PQB = 180°
⇒ 130° + ∠PQB = 180°
⇒ ∠PQB = 180° - 130°
⇒ ∠PQB = 50°.
In cyclic quadrilateral PQBA,
⇒ ∠PQB + ∠PAB = 180° [Sum of opposite angles of a cyclic quadrilateral = 180°]
⇒ 50° + ∠PAB = 180°
⇒ ∠PAB = 180° - 50°
⇒ ∠PAB = 130°.
In △PAB,
⇒ ∠PAB + ∠PBA + ∠BPA = 180° [Angle sum property of triangle]
⇒ 130° + ∠PBA + ∠BPA = 180°
⇒ ∠PBA + ∠BPA = 180° - 130°
⇒ ∠PBA + ∠BPA = 50° …………….(2)
Given, PA = PB
Angles opposite to equal sides are equal.
∴ ∠PBA = ∠BPA = x (let)
Substituting above value in (2), we get :
⇒ x + x = 50°
⇒ 2x = 50°
⇒ x =
⇒ x = 25°.
From figure,
∠AQB = ∠APB = 25° [Angles in same segment are equal.]
∠APQ = ∠APB + ∠BPQ = 25° + 40° = 65.
We know that,
Angle subtended by an arc at the center is twice the angle subtended at any other point of circumference.
Arc AQ subtends ∠AOQ at the center and ∠APQ at the remaining part of the circle.
∠AOQ = 2∠APQ = 2 × 65° = 130°.
In △AOQ,
OA = OQ [Radii of same circle]
As, angles opposite to equal sides are equal.
∠OAQ = ∠OQA = y (let)
⇒ ∠OAQ + ∠OQA + ∠AOQ = 180° [Angle sum property of triangle]
⇒ y + y + 130° = 180°
⇒ 2y = 180° - 130°
⇒ 2y = 50°
⇒ y =
⇒ y = 25°.
∴ ∠OAQ = 25°.
Since, ∠OAQ = ∠AQB = 25°.
∠OAQ and ∠AQB are alternate angles.
Thus, AO and BQ are parallel.
Hence, ∠AQB = 25° and ∠PAB = 130°.
Answered By
3 Likes
Related Questions
ABCDE is a cyclic pentagon with centre of its circumcircle at point O such that AB = BC = CD and angle ABC = 120°.
Calculate :
(i) ∠BEC
(ii) ∠BED
In the adjoining figure, O is the centre of the circle. Tangents to the circle at A and B meet at C. If ∠ACO = 30°, find
(i) ∠BCO
(ii) ∠AOB
(iii) ∠APB

The given figure shows a circle with center O such that chord RS is parallel to chord QT, angle PRT = 20° and angle POQ = 100°. Calculate :
(i) angle QTR
(ii) angle QRP
(iii) angle QRS
(iv) angle STR

TA and TB are tangents to a circle with center O from an external point T. OT intersects the circle at point P. Prove that AP bisects the angle TAB.