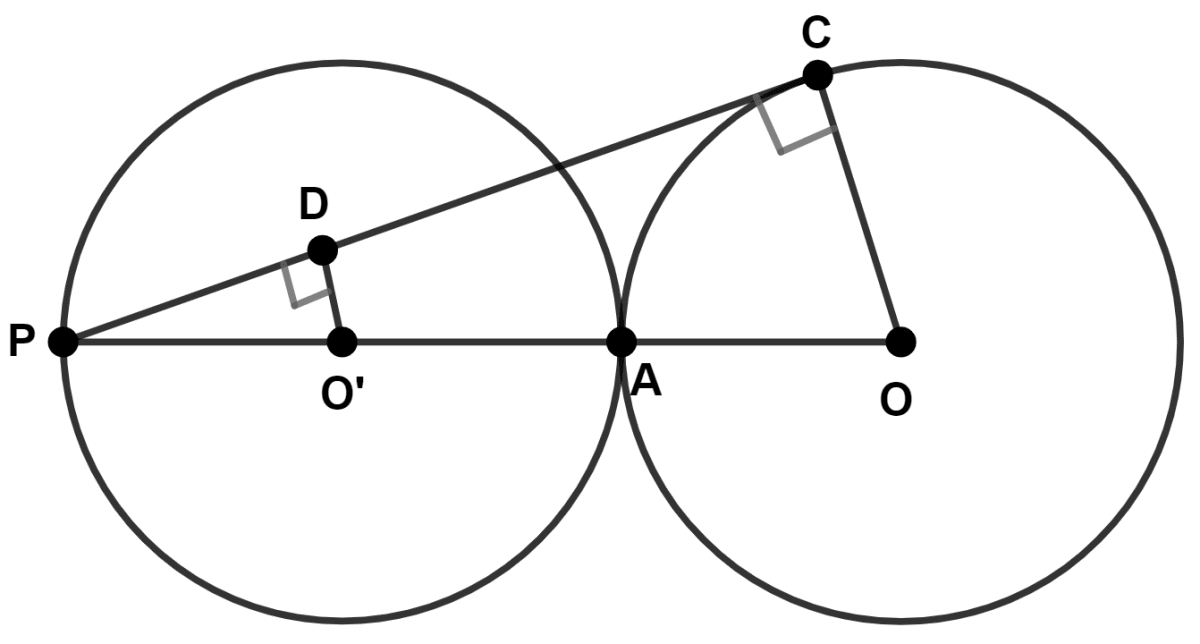
The given figure shows two congruent circles touching each other externally and with centers O' and O as shown. PC is tangent to the circle with center O. Find :

(i) $\dfrac{PO'}{PO}$

(ii) $\dfrac{\text{area (△PDO')}}{\text{area (△PCO)}}$

(i) Given, circles are congruent, so radius of both circles with be equal.

Let radius of both circles be r.

∴ PO' = AO = r

From figure,

PO = PO' + O'A + AO = r + r + r = 3r.

$\dfrac{PO'}{PO} = \dfrac{r}{3r} = \dfrac{1}{3}$.

Hence, $\dfrac{PO'}{PO} = \dfrac{1}{3}$.

(ii) In △PDO' and △PCO,

∠PDO = ∠PCO = 90°

∠DPO' = ∠CPO (Common)

∴ △PDO' ~ △PCO (By A.A. axiom)

We know that,

The ratio of the areas of two similar triangles is equal to the square of the ratio of their corresponding sides.

$\therefore \dfrac{\text{area (△PDO')}}{\text{area (△PCO)}} = \Big(\dfrac{\text{PO'}}{PO}\Big)^2\\[1em] = \Big(\dfrac{1}{3}\Big)^2 \\[1em] = \dfrac{1}{9}.$

Hence, $\dfrac{\text{area (△PDO')}}{\text{area (△PCO)}} = \dfrac{1}{9}$.