The length and the breadth of a conference hall are in the ratio 7 : 4 and its perimeter is 110 m. Find :

(i) area of the floor of the hall.

(ii) number of tiles, each a rectangle of size 25 cm x 20 cm, required for flooring of the hall.

(iii) the cost of the tiles at the rate of ₹ 1,400 per hundred tiles.

(i) Given:

The length and the breadth of a conference hall are in the ratio 7 : 4.

The perimeter of the hall = 110 m

Let the length of the conference hall be 7a and the breadth be 4a.

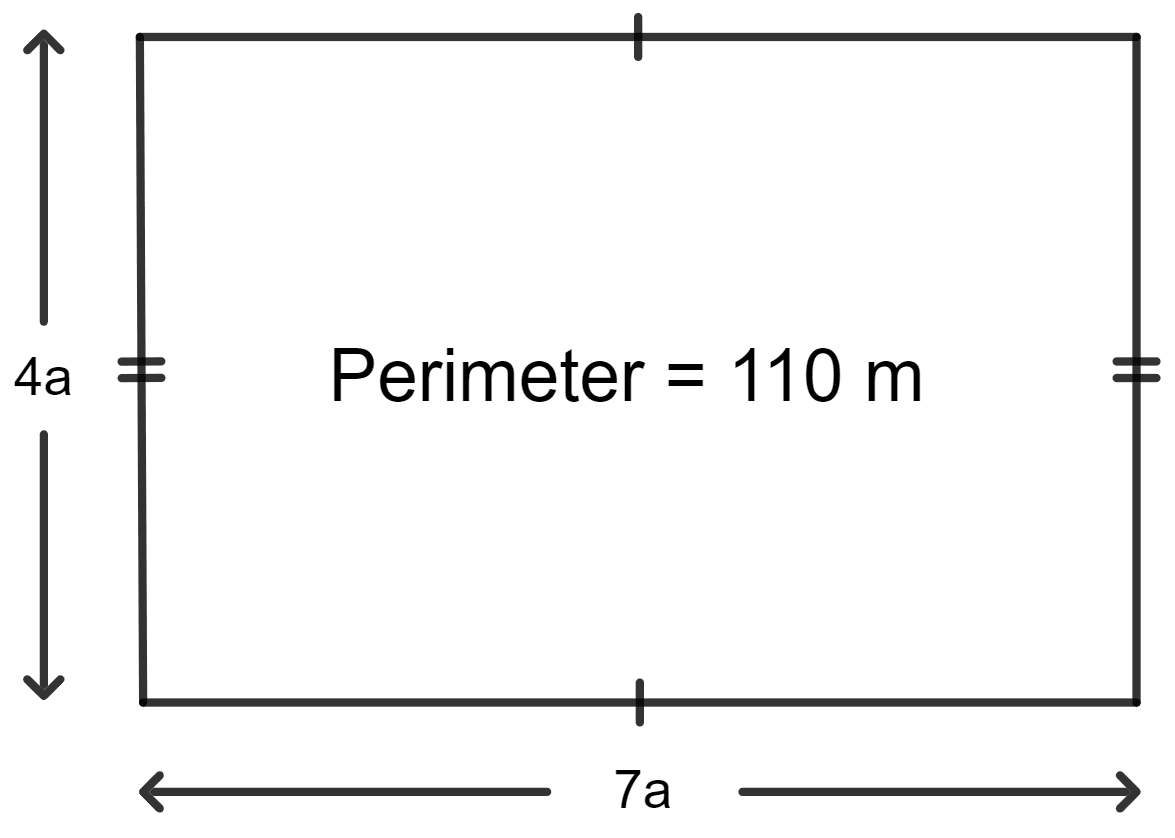
As we know, the perimeter of the hall = 2(length + breadth)

⇒ 2(7a + 4a) = 110

⇒ 2 x 11a = 110

⇒ 22a = 110

⇒ a = $\dfrac{110}{22}$

⇒ a = 5

So, the length of the hall = 7a

= 7 x 5 m

= 35 m

And, the breadth of the hall = 4a

= 4 x 5 m

= 20 m

Area of the hall = length x breadth

= 35 x 20 m²

= 700 m²

Hence, the area of the conference hall is 700 m².

(ii) Given:

Length of the tile = 25 cm

= $\dfrac{25}{100}$ m

= $\dfrac{1}{4}$ m

Breadth of the tile = 20 cm

= $\dfrac{20}{100}$ m

= $\dfrac{1}{5}$ m

Area of the tile = length x breadth

= $\dfrac{1}{4} \times \dfrac{1}{5}$ m²

= $\dfrac{1}{20}$ m²

Area of hall = Area of tiles x Number of tiles

⇒ 700 = $\dfrac{1}{20}$ x Number of tiles

⇒ Number of tiles = 700 x 20

⇒ Number of tiles = 14,000

Hence, the number of tiles = 14,000.

(iii) Cost of tiles = ₹ 1,400 per 100 tiles

Total cost = $\dfrac{14,000 \times 1400}{100}$

= ₹ 1,96,000

Hence, the cost of tiles = ₹ 1,96,000.