Mathematics
The length of a rectangular verandah is 3 m more than its breadth. The numerical value of its area is equal to the numerical value of its perimeter.
(i) Taking x as the breadth of the verandah, write an equation in x that represents the above statement.
(ii) Solve the equation obtained in (i) above and hence find the dimensions of the verandah.
Mensuration
36 Likes
Answer
(i) Given:
Breadth of the verandah = x
Length of the verandah = x + 3
It is also given that the numerical value of the area is equal to the numerical value of the perimeter.
⇒ l x b = 2(l + b)
⇒ x(x + 3) = 2(x + x + 3)
⇒ x2 + 3x = 2(2x + 3)
⇒ x2 + 3x = 4x + 6
⇒ x2 + 3x - 4x - 6 = 0
⇒ x2 - x - 6 = 0
Hence, the equation is x2 - x - 6.
(ii) From (i),
⇒ x2 - x - 6 = 0
⇒ x2 - 3x + 2x - 6 = 0
⇒ x(x - 3) + 2(x - 3) = 0
⇒ (x - 3)(x + 2) = 0
⇒ x = 3 or - 2
Since breadth cannot be negative, x = 3 m.
Length = x + 3 = 3 + 3 m = 6 m
Hence, length = 6 m and breadth = 3 m.
Answered By
19 Likes
Related Questions
The cost of enclosing a rectangular garden with a fence all round, at the rate of 75 paise per metre, is ₹ 300. If the length of the garden is 120 metres, find the area of the field in square metres.
The width of a rectangular room is of its length, x, and its perimeter is y. Write an equation connecting x and y. Find the length of the room when the perimeter is 4400 cm.
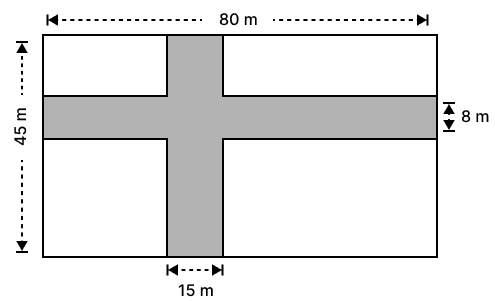
The diagram, given below, shows two paths drawn inside a rectangular field 80 m long and 45 m wide. The widths of the two paths are 8 m and 15 m as shown. Find the area of the shaded portion.
The rate for a 1.20 m wide carpet is ₹ 40 per metre; find the cost of covering a hall 45 m long and 32 m wide with this carpet. Also, find the cost of carpeting the same hall if the carpet, 80 cm wide, is at ₹ 25 per metre.