Mathematics
The ordinate of a point lying on the line joining the points (6, 4) and (7, -5) is -23. Find the co-ordinates of that point.
Straight Line Eq
4 Likes
Answer
Let point A = (6, 4) and B = (7, -5).
Let the point P be (a, -23).
By formula,
Slope =
Slope of AB = = -9.
By point-slope form,
⇒ y - y1 = m(x - x1)
⇒ y - 4 = -9(x - 6)
⇒ y - 4 = -9x + 54
⇒ 9x + y = 54 + 4
⇒ 9x + y = 58.
Since, P lies on AB so it will satisfy the equation.
Substituting values of P in equation we get,
⇒ 9(a) + (-23) = 58
⇒ 9a - 23 = 58
⇒ 9a = 58 + 23
⇒ 9a = 81
⇒ a =
⇒ a = 9.
∴ P = (a, -23) = (9, -23).
Hence, co-ordinates of the required point are (9, -23).
Answered By
1 Like
Related Questions
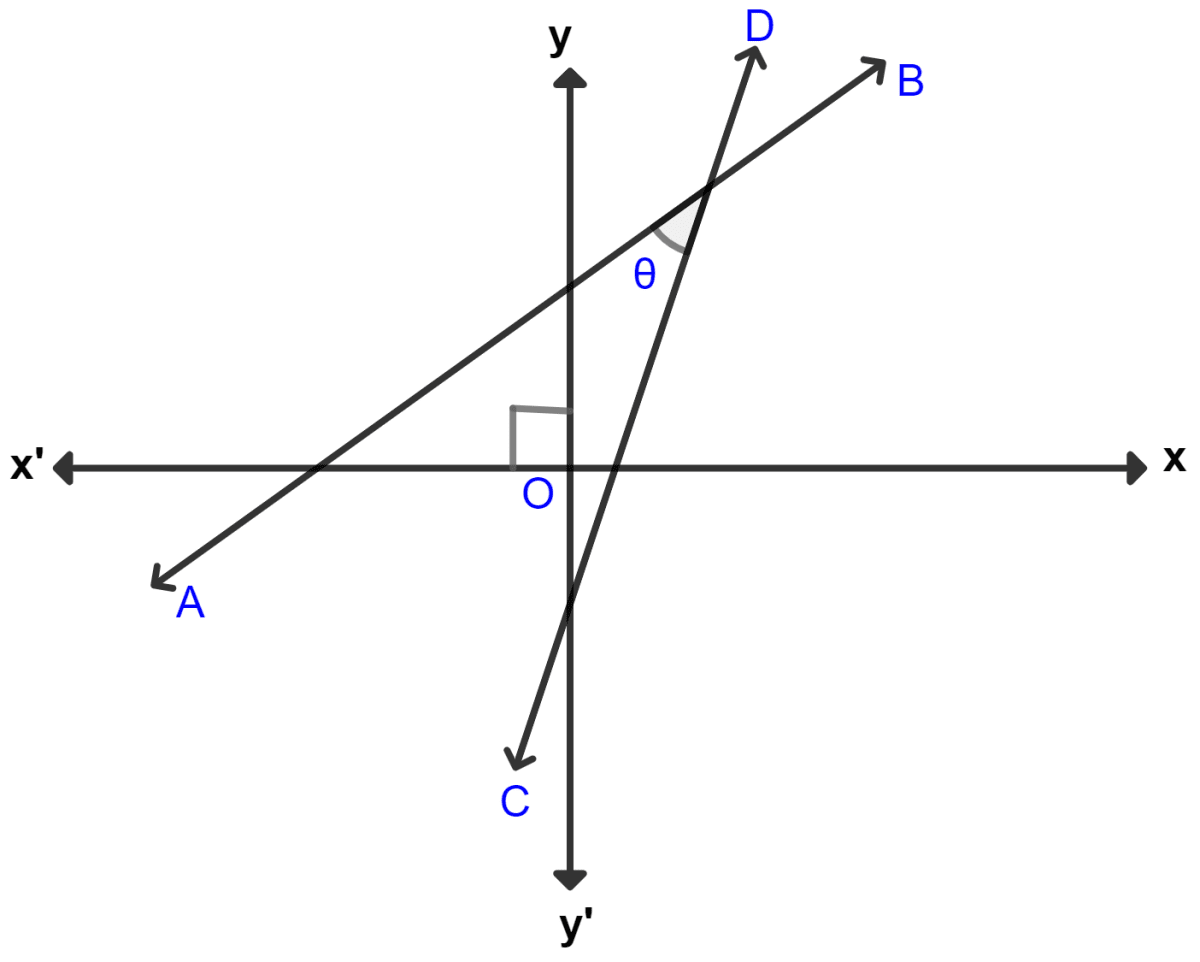
The given figure (not drawn to scale) shows two straight lines AB and CD. If equation of the line AB is : y = x + 1 and equation of line CD is : y = x - 1. Write down the inclination of lines AB and CD; also, find the angle θ between AB and CD.
Write down the equation of the line whose gradient is and which passes through P, where P divides the line segment joining A(-2, 6) and B(3, -4) in the ratio 2 : 3.
Point A and B have co-ordinates (7, -3) and (1, 9) respectively. Find :
(i) the slope of AB.
(ii) the equation of perpendicular bisector of the line segment AB.
(iii) the value of 'p' if (-2, p) lies on it.
A and B are the two points on the x-axis and y-axis respectively. P(2, -3) is the mid-point of AB.

Find :
(i) the coordinates of A and B.
(ii) the slope of the line AB.
(iii) the equation of the line AB.