Mathematics
The parallel sides of a trapezium are in the ratio 3 : 4. If the distance between the parallel sides is 9 dm and its area is 126 dm2, find the lengths of its parallel sides.
Area Trapezium Polygon
11 Likes
Answer
Given:
The parallel sides of a trapezium are in the ratio 3 : 4.
The distance between the parallel sides = 9 dm
The area = 126 dm2
Let the parallel sides of trapezium be 3a and 4a.
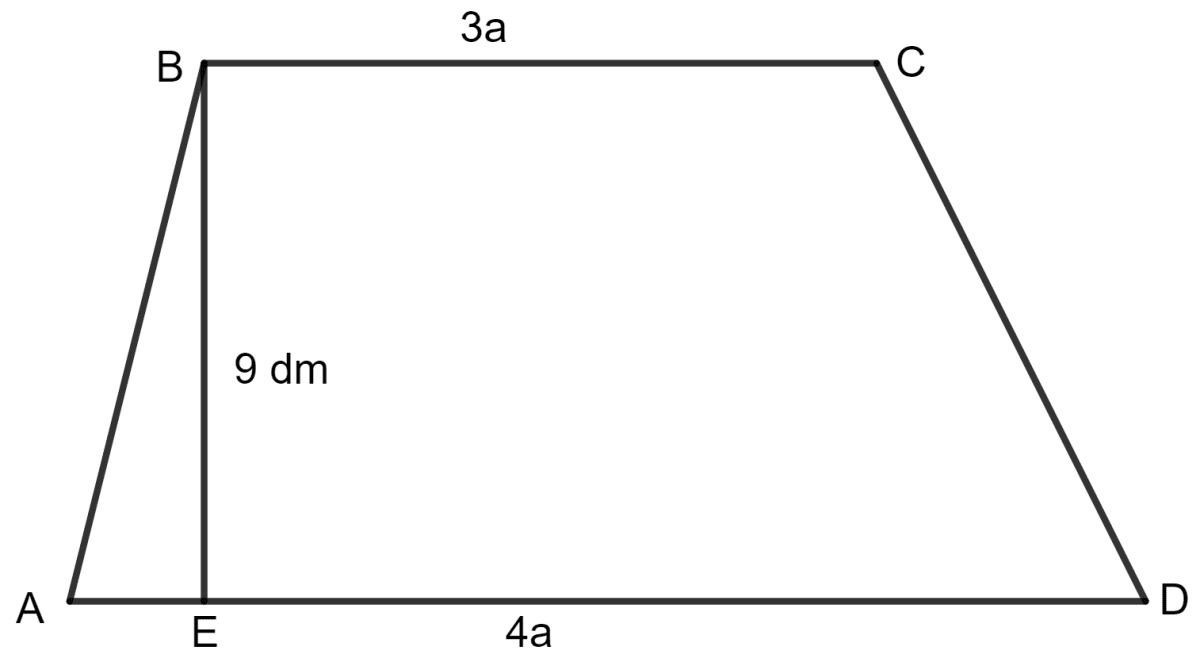
As we know, the area of a trapezium = x (sum of parallel side) x height
⇒ x (3a + 4a) x 9 = 126
⇒ x 7a x 9 = 126
⇒ x 63a = 126
⇒ 63a = 126 x 2
⇒ 63a = 252
⇒ a =
⇒ a = 4
So, the parallel sides of the trapezium are:
For 3a:
= 3 x 4 dm = 12 dm
And, for 4a:
= 4 x 4 dm = 16 dm
Hence, the lengths of its parallel sides are 12 dm and 16 dm.
Answered By
5 Likes
Related Questions
The diagonal of a rhombus is 15 cm and its area is 60 cm2; the other diagonal of the rhombus is :
4 cm
8 cm
12 cm
16 cm
The following figure shows the cross-section ABCD of a swimming pool which is a trapezium in shape.
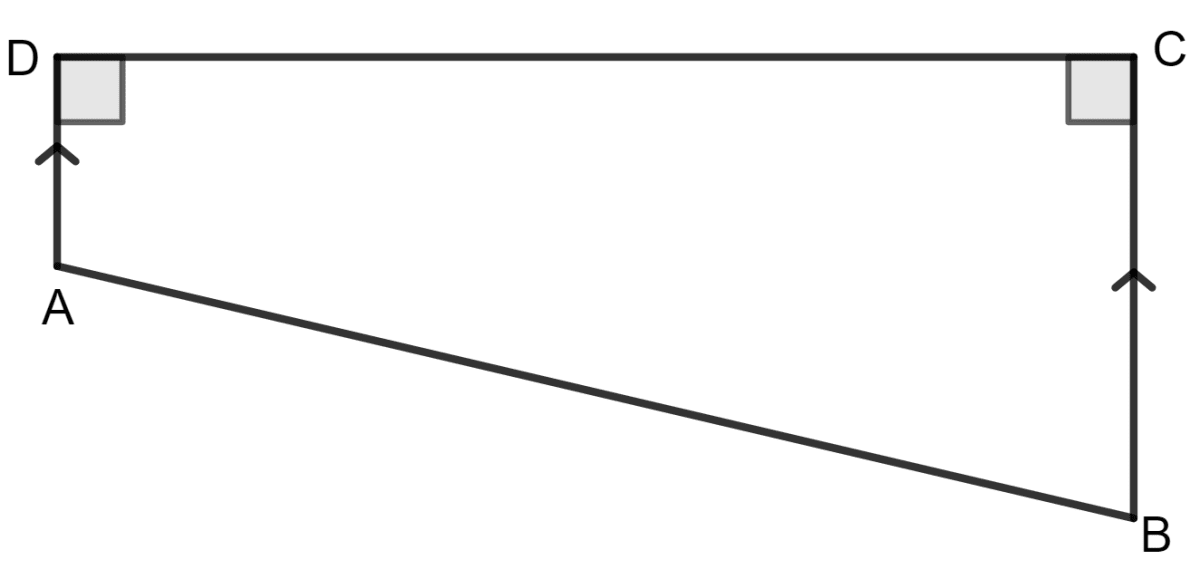
If the width DC of the swimming pool is 6.4 m, depth (AD) at the shallow end is 80 cm and depth (BC) at the deepest end is 2.4 m, find its area of cross-section.
The two parallel sides and the distance between them are in the ratio 3 : 4 : 2. If the area of the trapezium is 175 cm2, find its height.
The adjacent sides of a parallelogram are 21 cm and 28 cm. If its one diagonal is 35 cm, find the area of the parallelogram.