Mathematics
The quadrilateral obtained by joining the mid-points (in order) of the sides of quadrilateral ABCD is :
rectangle
rhombus
parallelogram
square
Mid-point Theorem
22 Likes
Answer
Let ABCD be the quadrilateral. P, Q, R and S are the mid-points of sides AB, BC, CD and DA.
Join PQRS, AC and BD.
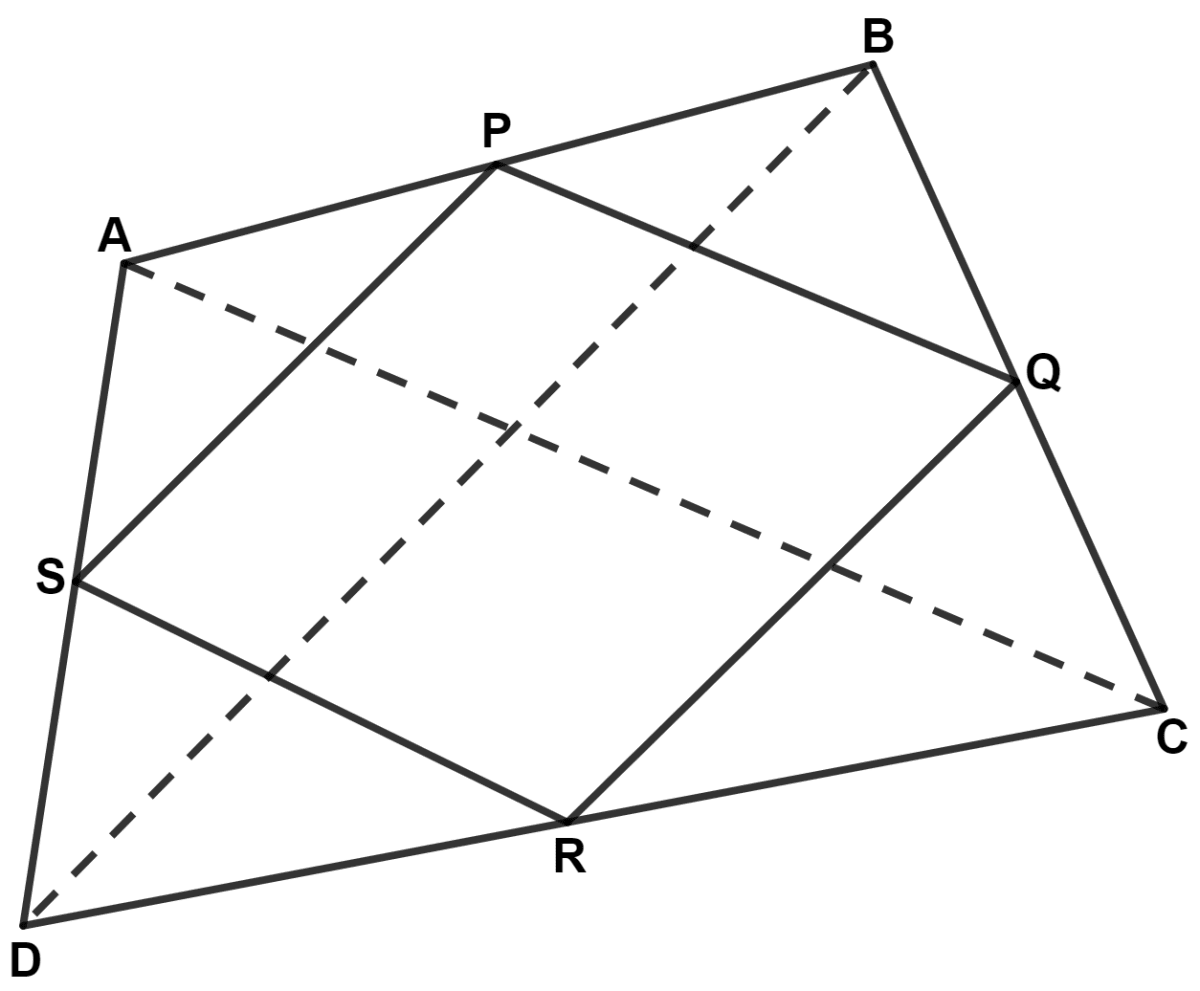
By mid-point theorem,
The line segment joining the mid-points of any two sides of a triangle is parallel to the third side and is equal to half of it.
In △ ABC,
P and Q are mid-points of sides AB and BC respectively.
∴ PQ || AC and PQ = (By mid-point theorem) …….(1)
In △ ADC,
S and R are mid-points of sides AD and DC respectively.
∴ SR || AC and SR = (By mid-point theorem) ……..(2)
From equations (1) and (2), we get :
⇒ PQ = SR and PQ || SR.
In △ ABD,
P and S are mid-points of sides AB and AD respectively.
∴ SP || BD and SP = (By mid-point theorem) …….(3)
In △ CBD,
Q and R are mid-points of sides BC and DC respectively.
∴ QR || BD and QR = (By mid-point theorem) ……..(4)
From equations (3) and (4), we get :
⇒ SP = QR and SP || QR.
Since, opposite sides are parallel and equal.
∴ PQRS is a parallelogram.
Hence, Option 3 is the correct option.
Answered By
13 Likes
Related Questions
In the given figure, ABCD is a rectangle. As per the given information, the length of PQ is :
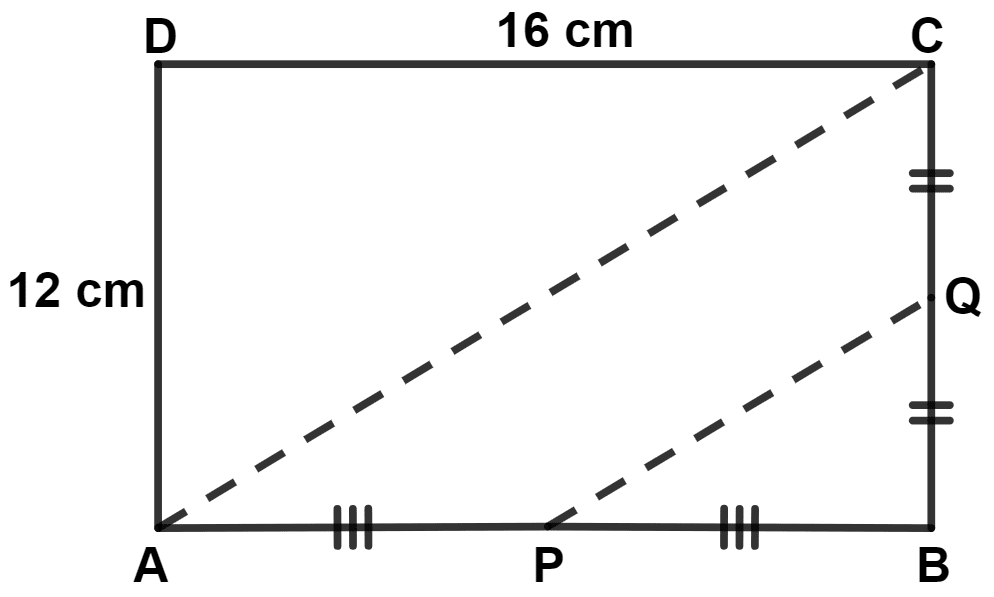
12 cm
14 cm
20 cm
10 cm
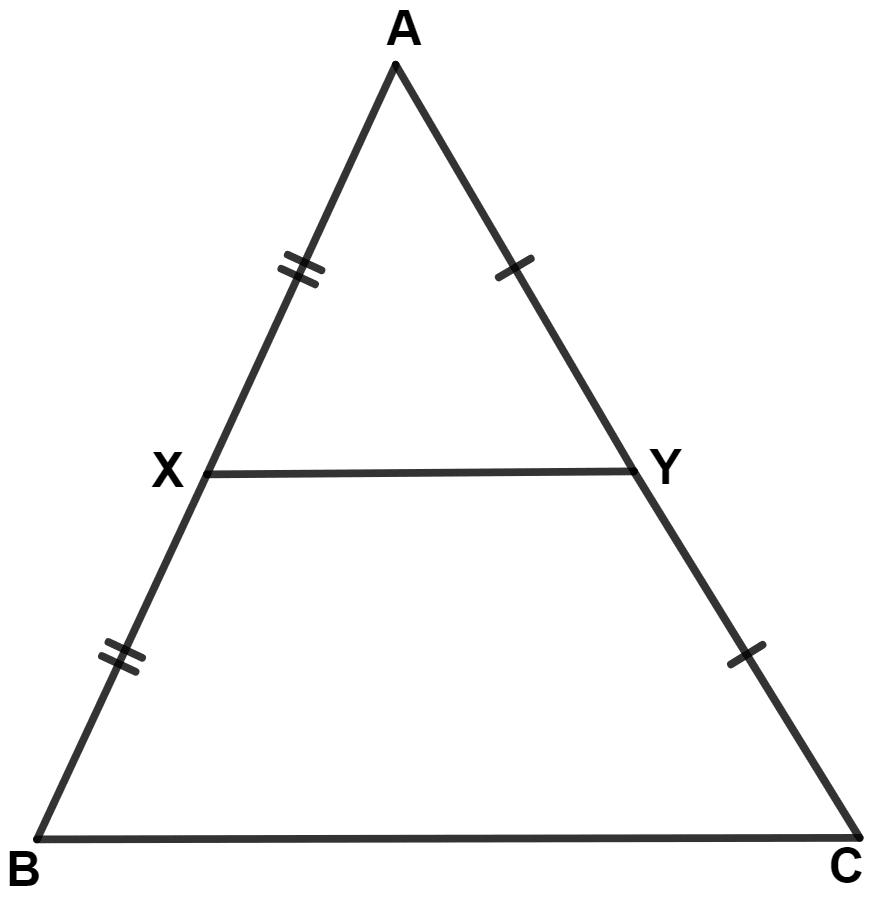
If BC = 12 cm, AB = 14.8 cm, AC = 12.8 cm, the perimeter of quadrilateral BCYX is :
31.8 cm
15.9 cm
29.8 cm
32.8 cm
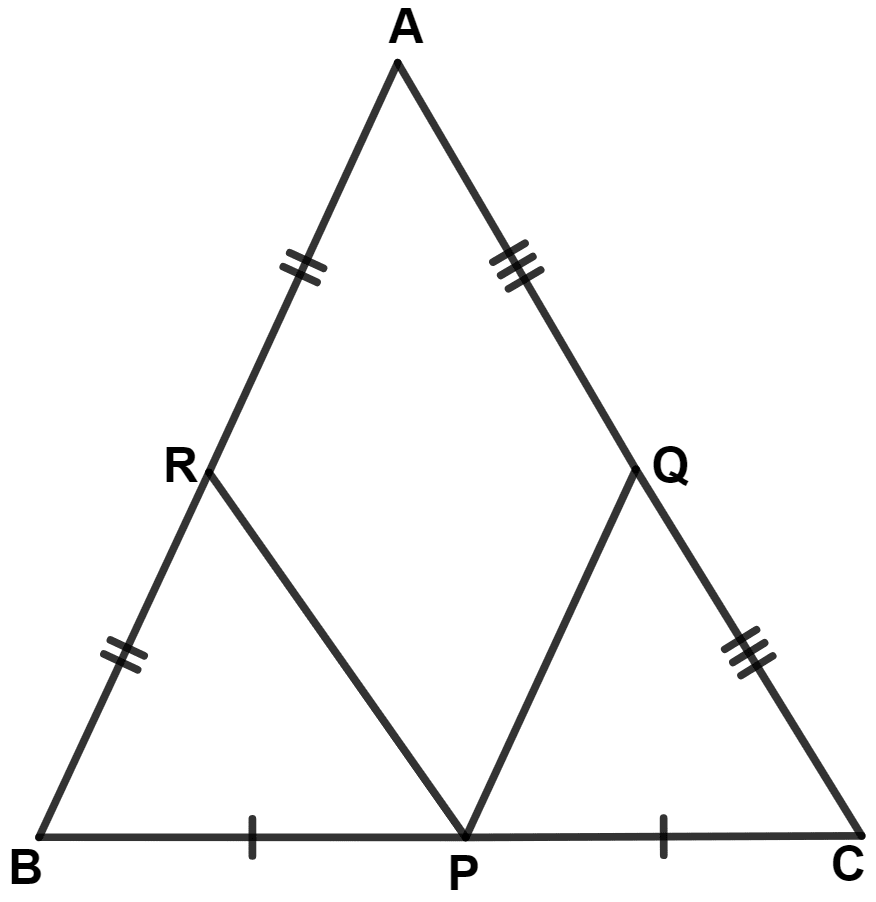
In the given figure, AB = AC, P, Q and R are mid-points of sides BC, CA and AB respectively, then △ PQR is :
scalene
isosceles
equilateral
obtuse angled
P, Q, R and S are the mid-points of sides AB, BC, CD and DA respectively of rectangle ABCD, then quadrilateral PQRS is :
rectangle
rhombus
square
parallelogram