Mathematics
The radii of two concentric circles are 6 cm and 10 cm respectively. Find the length of the chord of the bigger circle which is tangent to smaller circle.
Circles
12 Likes
Answer
From figure,
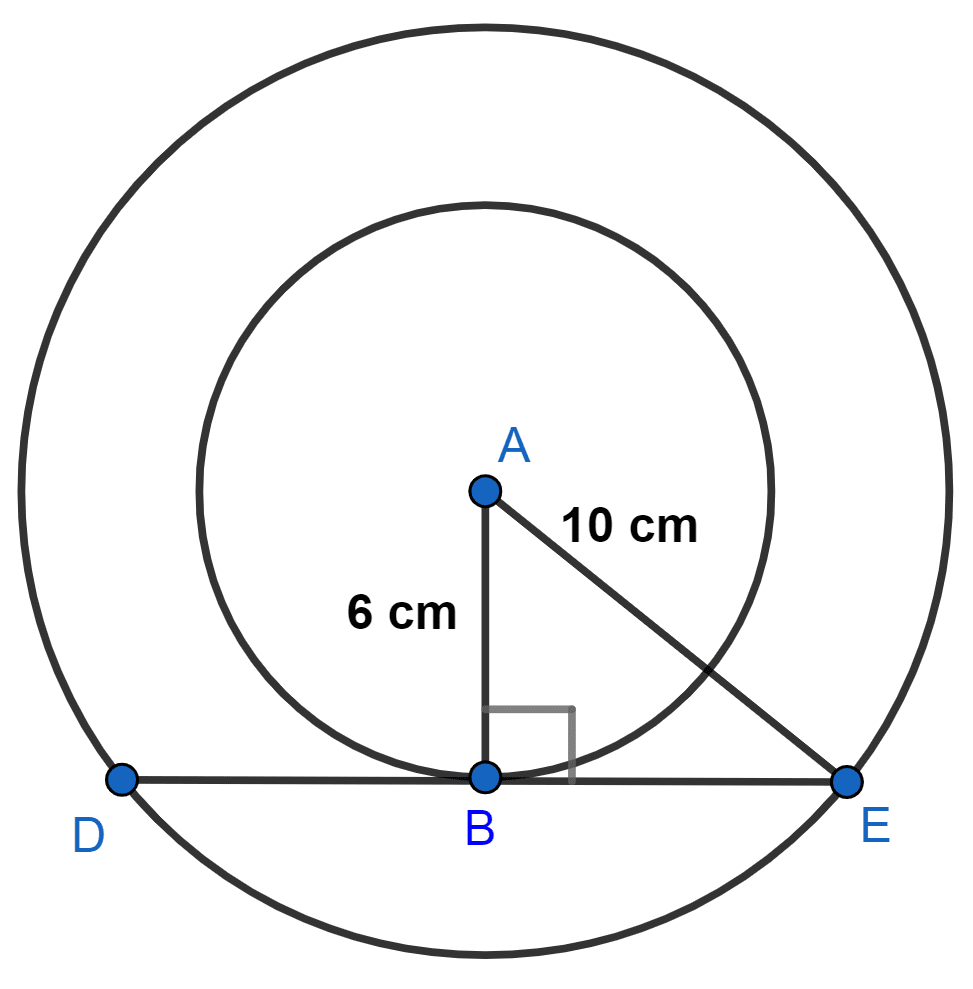
There are two circles with center A and radius AE = 10 cm and AB = 6 cm.
In △ABE,
⇒ AE2 = AB2 + BE2
⇒ 102 = 62 + BE2
⇒ 100 = 36 + BE2
⇒ BE2 = 100 - 36
⇒ BE2 = 64
⇒ BE = = 8 cm.
We know that,
The perpendicular from the centre to a chord bisect the chord.
DE = 2BE = 2 × 8 = 16 cm.
Hence, length of chord of bigger circle which is tangent to smaller circle = 16 cm.
Answered By
9 Likes
Related Questions
The following table shows the marks obtained (out of 100) by different students of class X.
Marks No. of students 50-60 8 60-70 16 70-80 28 80-90 38 90-100 10 Taking suitable scales on both the axes, draw a histogram and use it to estimate mode.
If matrix M = , find M2 + 3I.
If x2 - 3x + 2 is a factor of x3 - ax2 + b, find the values of a and b.
In the given figure, P(-3, -4) is the mid-point of the line segment AB.
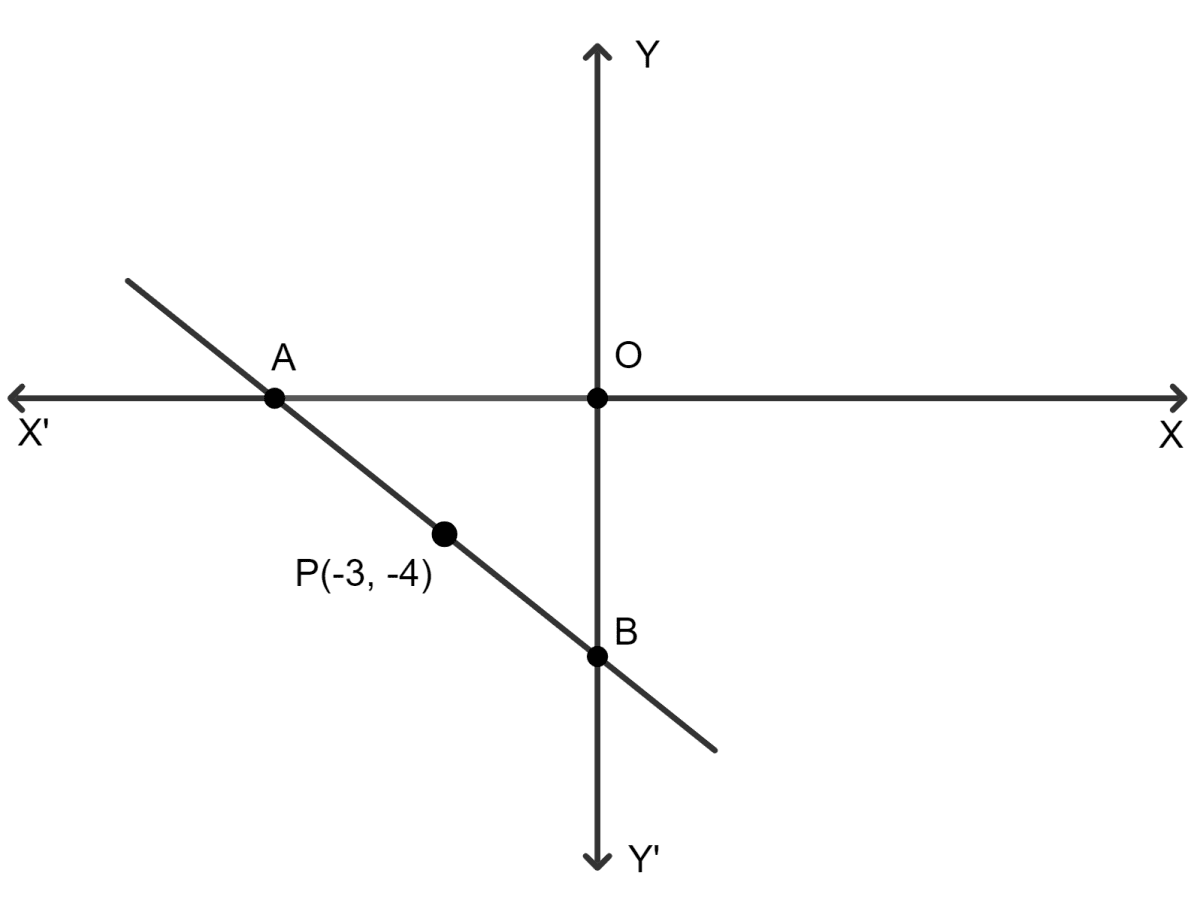
Find the coordinates of points A and B. Also, find the equation of the line passing through the point P and also perpendicular to line-segment AB.