Mathematics
The rational number between and is:
Rational Numbers
1 Like
Answer
For any two rational numbers and , is also a rational number with its value lying between and .
Hence, Option 3 is the correct option.
Answered By
1 Like
Related Questions
In the following number line, points A and B represent:
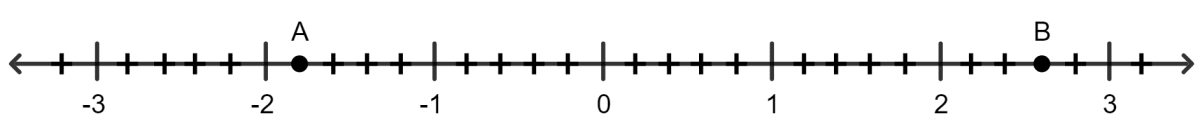
and
and
and
and
Using the number line, given below; the length of line segment AB is:
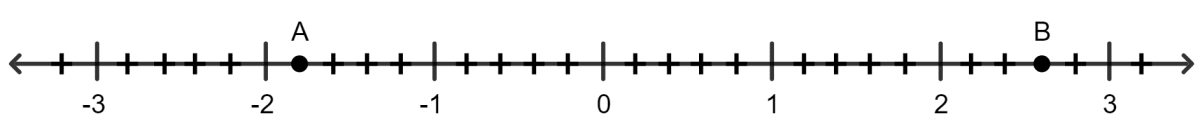
=
=
The rational number between and is:
and
and 0
and
and
The rational numbers and are represented by:
B and E respectively
C and D respectively
C and E respectively
B and F respectively