Mathematics
The shaded region of the given diagram represents the lawn in the form of a house. On the three sides of the lawn there are flower-beds having a uniform width of 2 m.
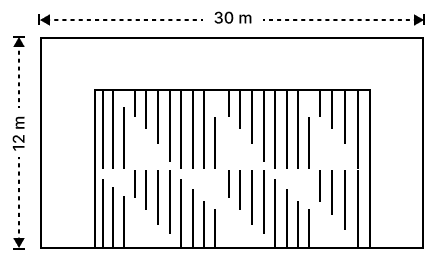
(i) Find the length and the breadth of the lawn.
(ii) Hence, or otherwise, find the area of the flower-beds.
Mensuration
13 Likes
Answer
Given:
Length of the lawn = 30 m
Breadth of the lawn = 12 m
Width of flowerbed = 2 m
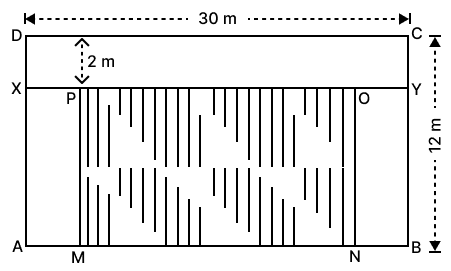
New length of lawn = 30 - 2 - 2 m = 30 - 4 m = 26 m
New breadth of lawn = 12 - 2 m = 10 m
Hence, the length of lawn = 26 m and the breadth of lawn = 10 m.
(ii) Area of flowerbed = Area of AMPX + Area of XDCY + Area of NBYO
Area of AMPX = l x b = AM x MP
= 10 x 2 m2
= 20 m2
Area of XDCY = l x b = XD x DC
= 30 x 2 m2
= 60 m2
Area of NBYO = l x b = NB x BY
= 10 x 2 m2
= 20 m2
Area of flowerbed = 20 + 60 + 20 m2
= 100 m2
Hence, the area of flowerbed is 100 m2.
Answered By
10 Likes
Related Questions
The rate for a 1.20 m wide carpet is ₹ 40 per metre; find the cost of covering a hall 45 m long and 32 m wide with this carpet. Also, find the cost of carpeting the same hall if the carpet, 80 cm wide, is at ₹ 25 per metre.
Find the area and perimeter of a square plot of land, the length of whose diagonal is 15 metres. Give your answer correct to 2 places of decimals.
A floor which measures 15 m x 8 m is to be laid with tiles measuring 50 cm x 25 cm. Find the number of tiles required.
Further, if a carpet is laid on the floor so that a space of 1 m exists between its edges and the edges of the floor, what fraction of the floor is left uncovered.
Two adjacent sides of parallelogram are 24 cm and 18 cm. If the distance between the longer sides is 12 cm; find the distance between the shorter sides.