Mathematics
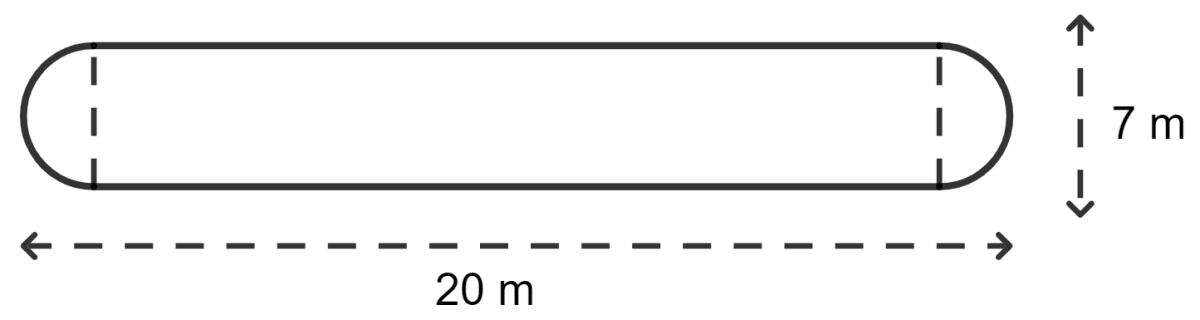
The shape of a garden is rectangular in the middle and semicircular at each end as shown in the figure. Find the area and perimeter of the garden.
Area Trapezium Polygon
6 Likes
Answer
Given:
Total length of garden = 20 m
Radius of the circle = m
Length of rectangle = total length - 2 x radius of the circle
= 20 - 2 x m
= 20 - 7 m
= 13 m
Perimeter of the figure = l + l + 2 x x circumference of semicircle
As we know that circumference of the circle = 2πr
= 13 + 13 + 2 x x 2πr
= 26 + 2 x
= 26 +
= 26 + 22
= 48 m
Area of the figure = Area of rectangle + 2 x Area of semicircle
As we know that area of rectangle = length x breadth
And, area of the circle = πr2
So, area
Hence, the area of the garden is 129.5 m2 and the perimeter is 48 m.
Answered By
4 Likes
Related Questions
Assertion (A) : The area of trapezium with base 10 cm, height 5 cm and the side parallel to the given base being 6 cm is 40 cm2.
Reason (R) : The area of trapezium = x (sum of non parallel sides) x height.
Both A and R are correct, and R is the correct explanation for A.
Both A and R are incorrect.
A is true, but R is false.
A is false, but R is true.
The perimeter of a trapezium is 52 cm. If its non-parallel sides are 10 cm each and its altitude is 8 cm, find the area of the trapezium.
Each side of rhombus is 13 cm and one of its diagonals is 10 cm. Find :
(i) the length of its other diagonal
(ii) its area.
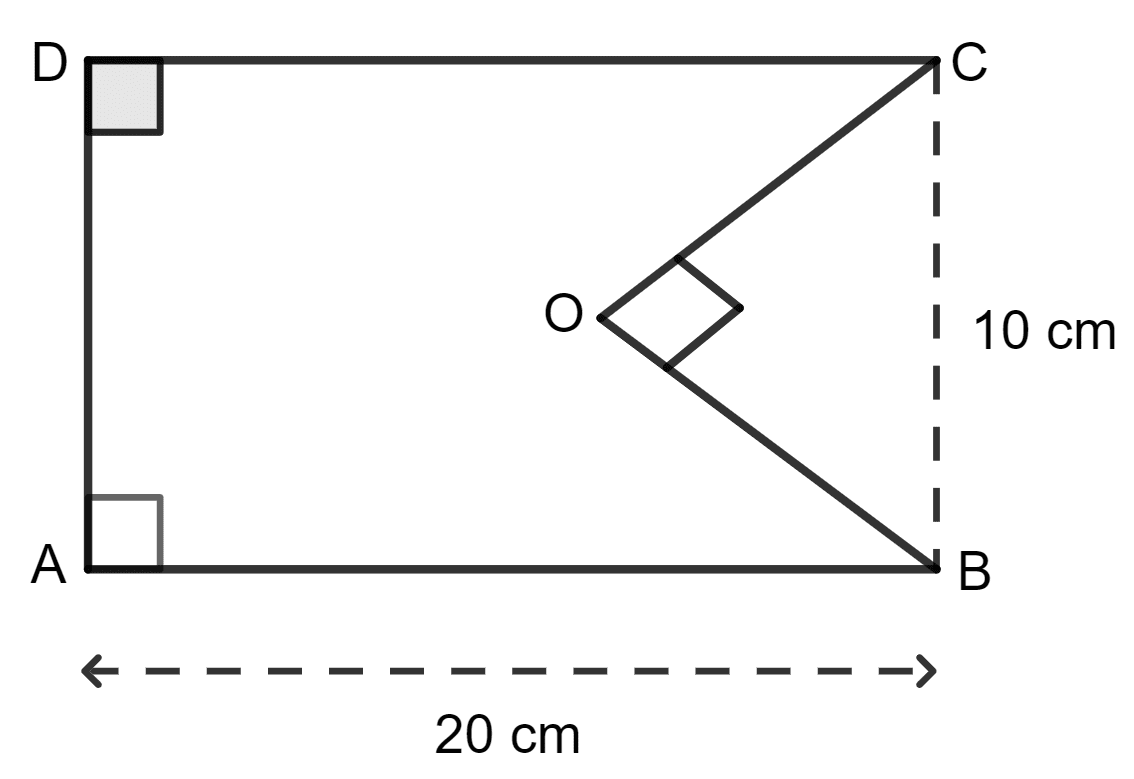
The given figure shows a rectangle ABCD and a right triangle BOC. Find the area of the shaded portion.