Mathematics
Three equal cubes are placed adjacently in a row. Find the ratio of the total surface area of the resulting cuboid to that of the sum of the total surface areas of the three cubes.
Mensuration
47 Likes
Answer
Given:
Let a be the side of each cube.
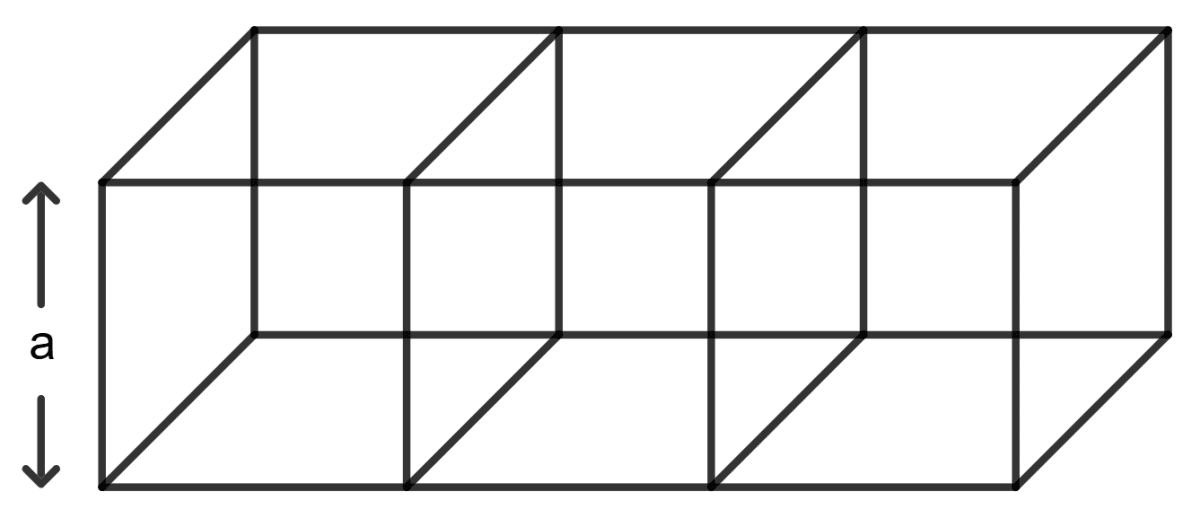
When the cubes are placed adjacently, they form a cuboid with the following dimensions:
Length of cuboid = a + a + a = 3a
Breadth of cuboid = a
Height of cuboid = a
The ratio =
Hence, the ratio of the total surface area of the resulting cuboid to that of the sum of the total surface areas of the three cubes is 7:9.
Answered By
18 Likes
Related Questions
The edges of three cubes of metal are 3 cm, 4 cm and 5 cm. They are melted and formed into a single cube. Find the edge of the new cube.
Three cubes, whose edges are x cm, 8 cm and 10 cm respectively, are melted and recast into a single cube of edge 12 cm. Find 'x'.
The cost of papering the four walls of a room at 75 paise per square metre is ₹ 240. The height of the room is 5 metres. Find the length and the breadth of the room, if they are in the ratio 5 : 3.
The area of a playground is 3650 m2. Find the cost of covering it with gravel 1.2 cm deep, if the gravel costs ₹ 6.40 per cubic metre.