Mathematics
Through the mid-point M of the side CD of a parallelogram ABCD, the line BM is drawn intersecting diagonal AC in L and AD produced in E. Prove that : EL = 2BL.
Similarity
14 Likes
Answer
The parallelogram ABCD is shown in the figure below:
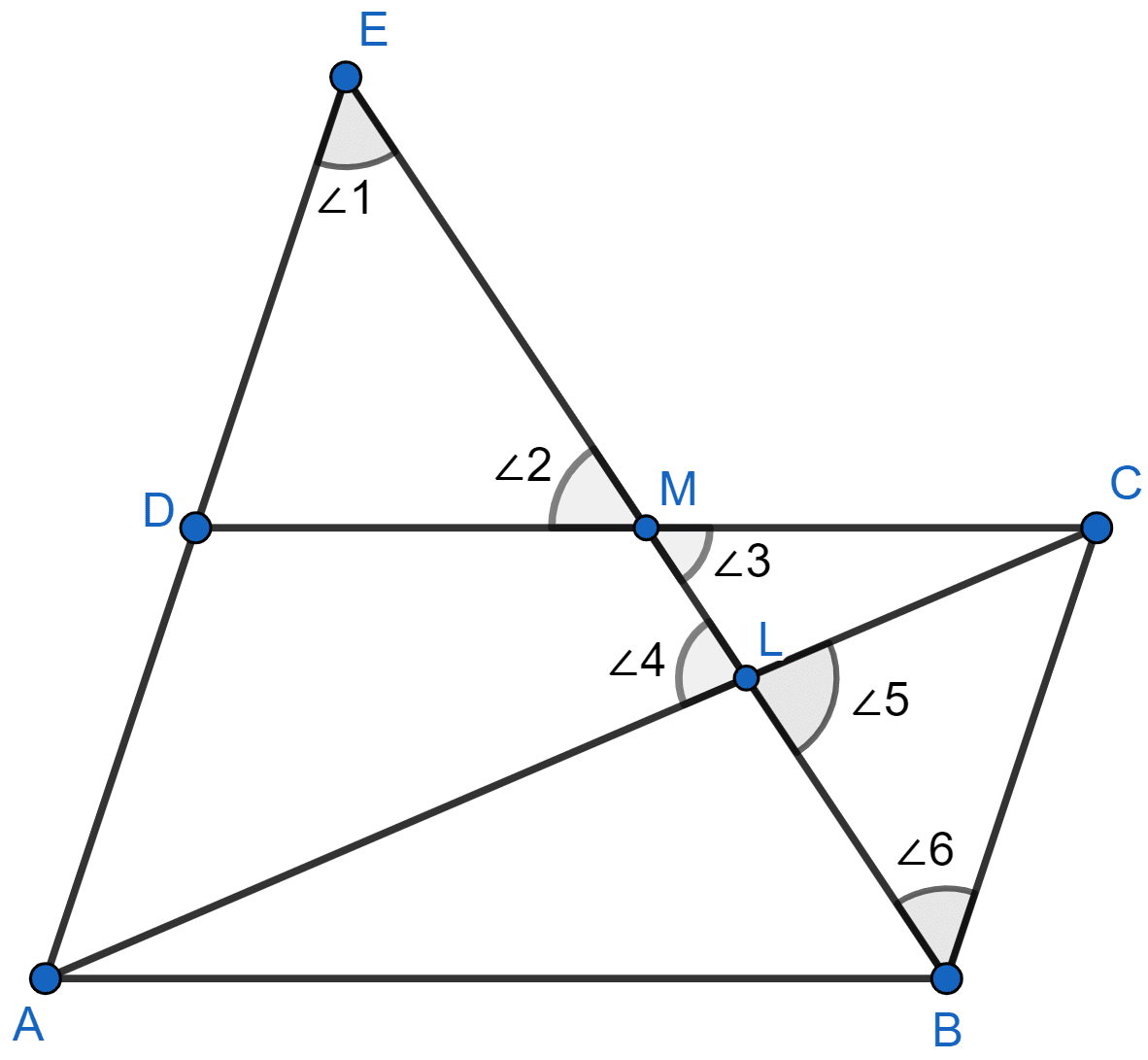
∠1 = ∠6 (Alternate angles)
∠2 = ∠3 (Vertically opposite angles)
DM = MC (M is the mid-point of CD)
△DEM ≅ △CBM (By AAS axiom)
∴ DE = BC (By C.P.C.T)
Also, AD = BC (As opposite sides of parallelogram are equal.)
From figure,
AE = AD + DE = BC + BC = 2BC.
Now,
∠1 = ∠6 (Proved above)
∠4 = ∠5 (Vertically opposite angles)
∴ △ELA ~ △BLC (By AA)
Since, corresponding sides of similar triangle are proportional to each other.
Hence, proved that EL = 2BL.
Answered By
10 Likes
Related Questions
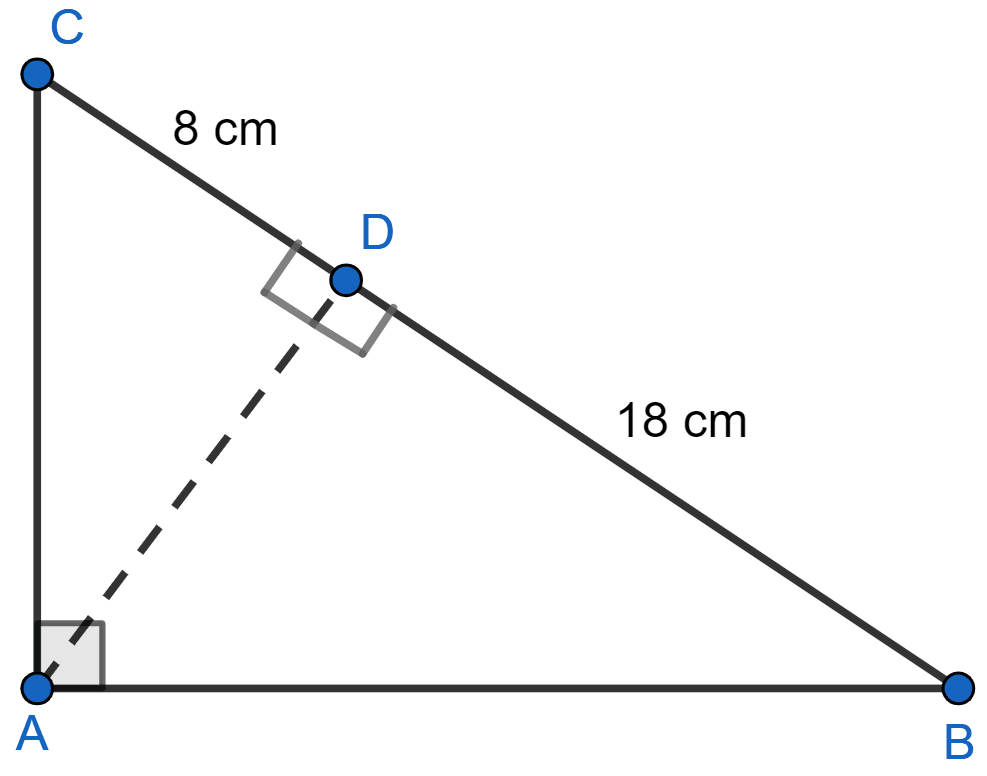
In the given figure, ABC is a right angled triangle with ∠BAC = 90°.
(i) Prove that : △ADB ~ △CDA.
(ii) If BD = 18 cm and CD = 8 cm, find AD.
(iii) Find the ratio of the area of △ADB is to area of △CDA.
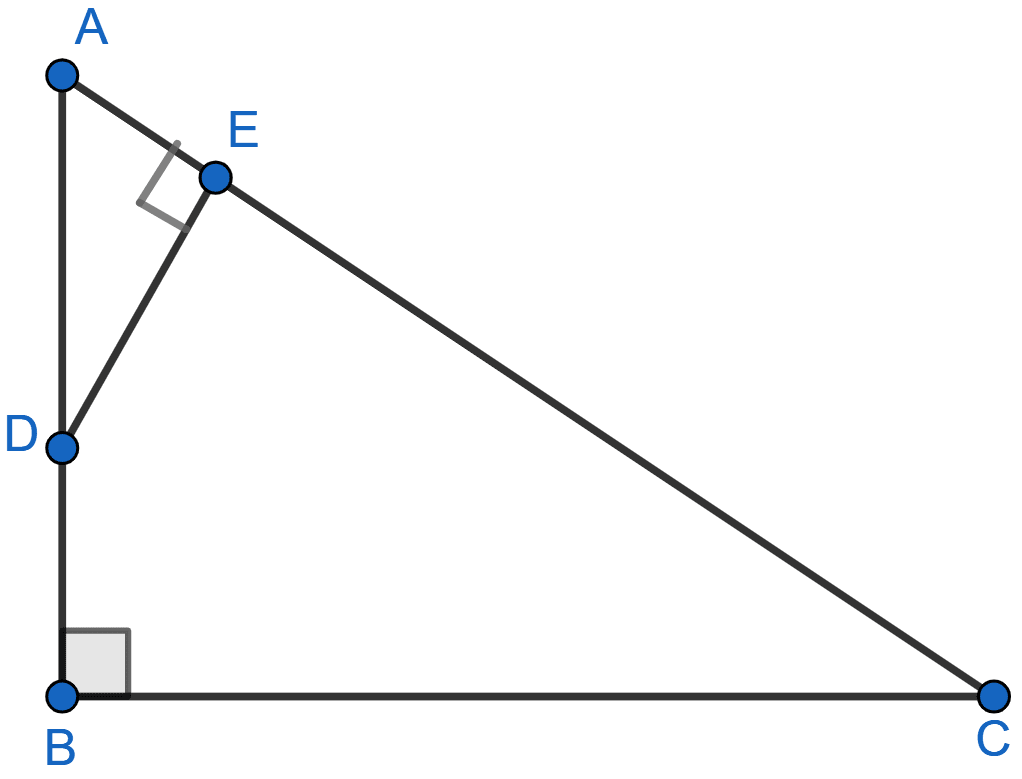
ABC is a right angled triangle with ∠ABC = 90°. D is any point on AB and DE is perpendicular to AC. Prove that :
(i) △ADE ~ △ACB
(ii) If AC = 13 cm, BC = 5 cm and AE = 4 cm. Find DE and AD.
(iii) Find, area of △ADE : area of quadrilateral BCED.
Given : AB || DE and BC || EF. Prove that :
(i)
(ii) △DFG ~ △ACG.

PQR is a triangle. S is a point on the side QR of △PQR such that ∠PSR = ∠QPR. Given QP = 8 cm, PR = 6 cm and SR = 3 cm.
(i) Prove △PQR ~ △SPR.
(ii) Find the lengths of QR and PS.
(iii)
