Mathematics
In triangle ABC and DEF, ∠A = ∠D and then prove that Δ ABC ∼ Δ DEF.
Similarity
59 Likes
Answer
Given,
⇒
In Δ ABC and Δ DEF,
⇒ ∠A = ∠D (Given)
⇒
∴ Δ ABC ∼ Δ DEF (By SAS postulate)
Hence, proved that Δ ABC ∼ Δ DEF.
Answered By
37 Likes
Related Questions
In the given figure, OA = 5, OB = 6, OC = 3 and OD = 10, then
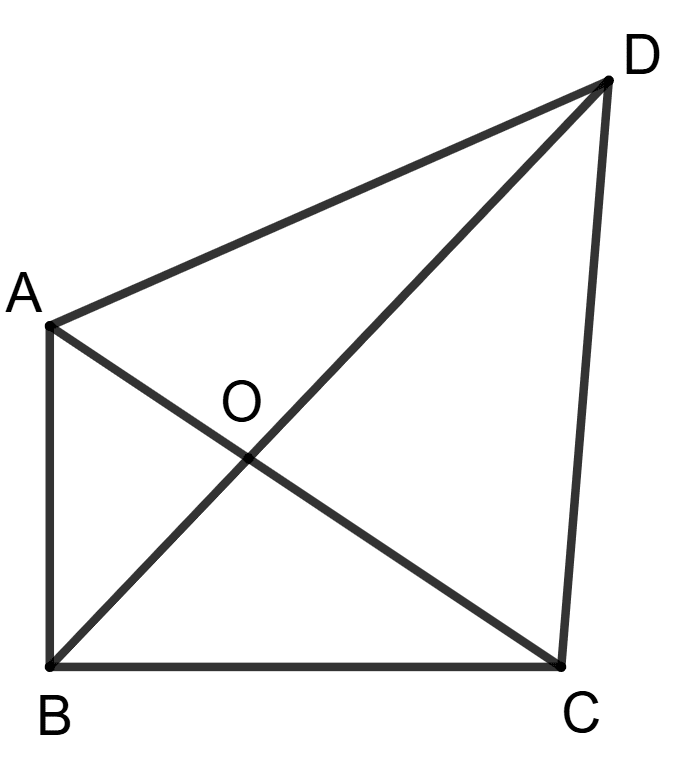
Δ AOB ∼ Δ AOB
Δ AOB ∼ Δ BOC
Δ BOC ∼ Δ COD
Δ AOD ∼ Δ COB
In the given figure, the value of x is:
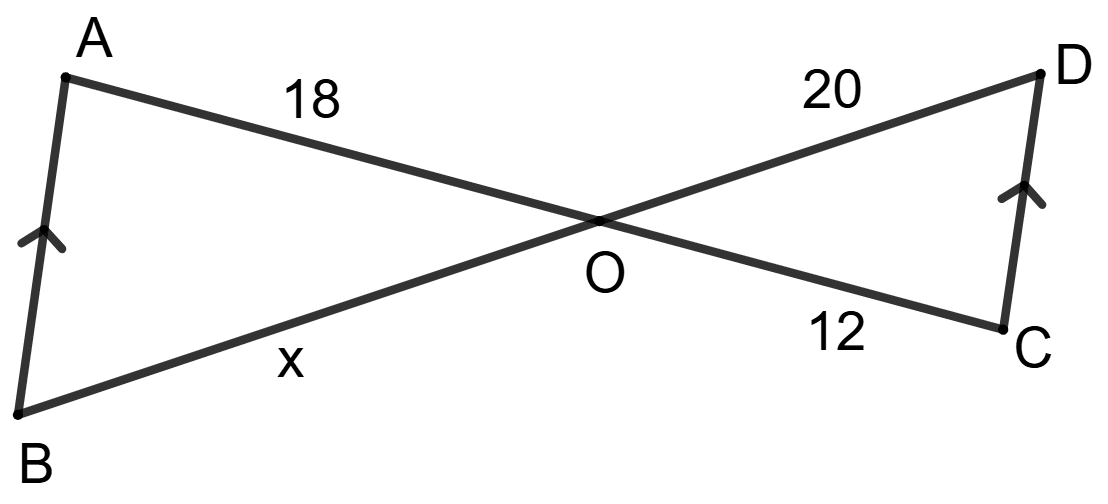
15
30
36
40
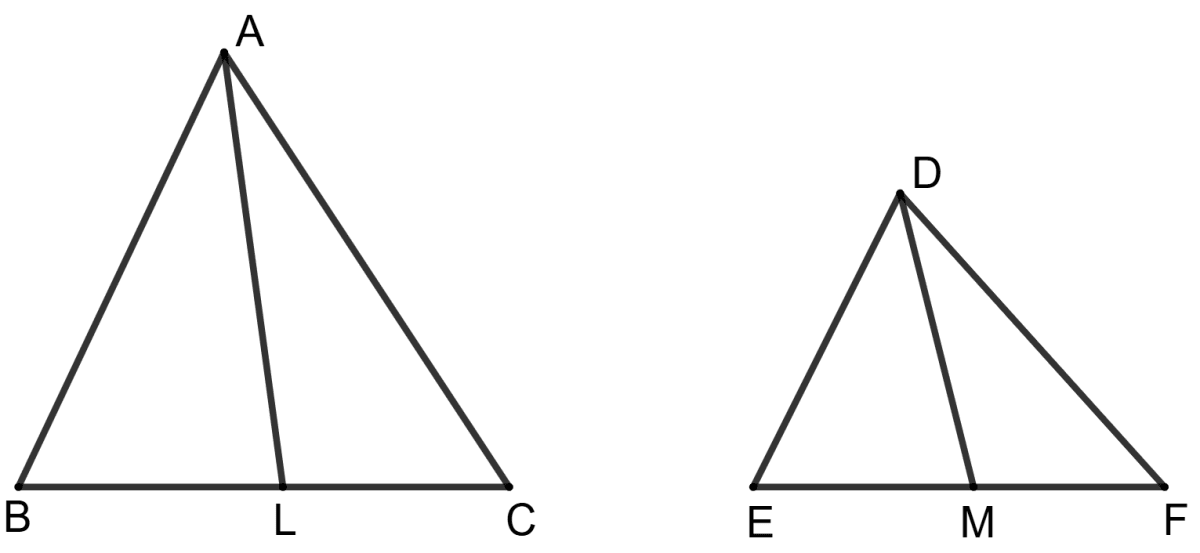
In triangle ABC and DEF, ∠A = ∠D, ∠B = ∠E and ∠C = ∠F. Also, AL and DM are medians. Prove that .
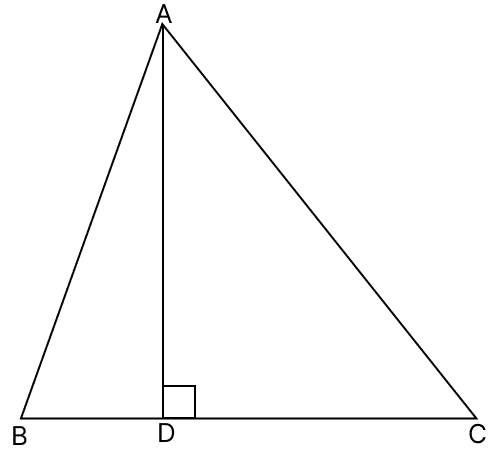
In triangle ABC, AD is perpendicular to side BC and AD2 = BD × CD.
prove that angle BAC = 90°.