Mathematics
Answer
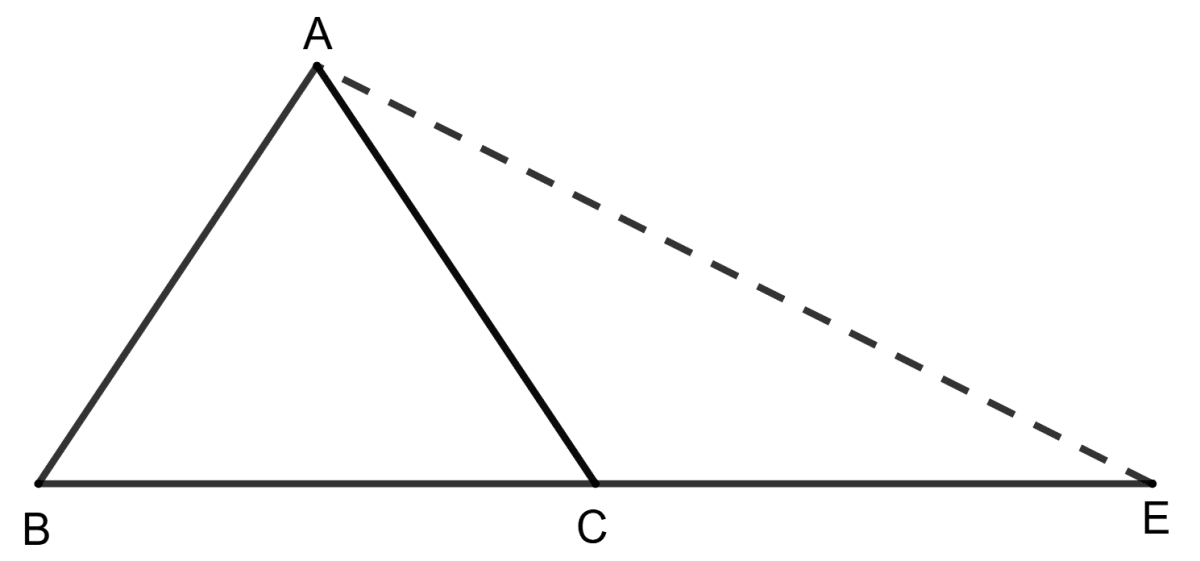
Since, ABC is an equilateral triangle, ∠A = ∠B = ∠C = 60°.
From figure,
⇒ ∠ACB + ∠ACE = 180° [Linear pairs]
⇒ 60° + ∠ACE = 180°
⇒ ∠ACE = 120°.
From figure, BC = CE (Given) ………………..(1)
⇒ BC = AC (Side of equilateral triangle) ……………….(2)
⇒ AC = CE (From equation (1) and (2))
⇒ ∠AEC = ∠CAE = y (let) [As angles opposite to equal sides of a triangle are equal]
By angle sum property in triangle AEC,
⇒ ∠AEC + ∠CAE + ∠ACE = 180°
⇒ y + y + 120° = 180°
⇒ 2y = 60°
⇒ y = 30°.
∴ ∠AEC = 30°.
Hence, option 3 is the correct option.
Related Questions
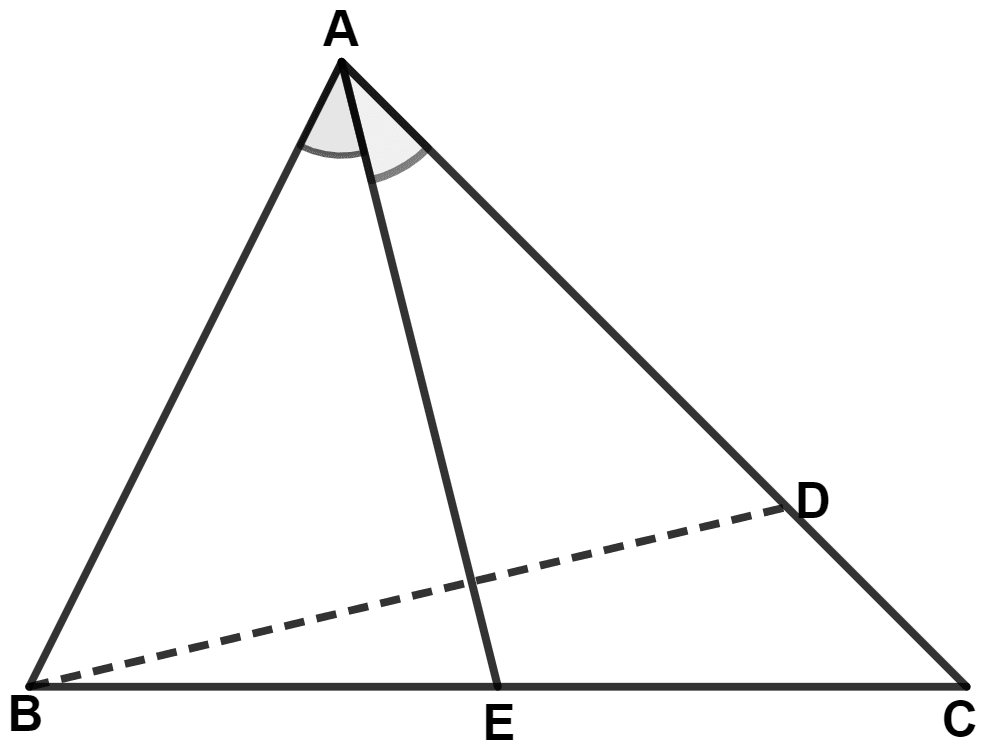
In the following diagram; AD = AB and AE bisects angle A. Prove that :
(i) BE = DE
(ii) ∠ABD > ∠C
∠ABC = 90° and P is a point on side AC. Then:
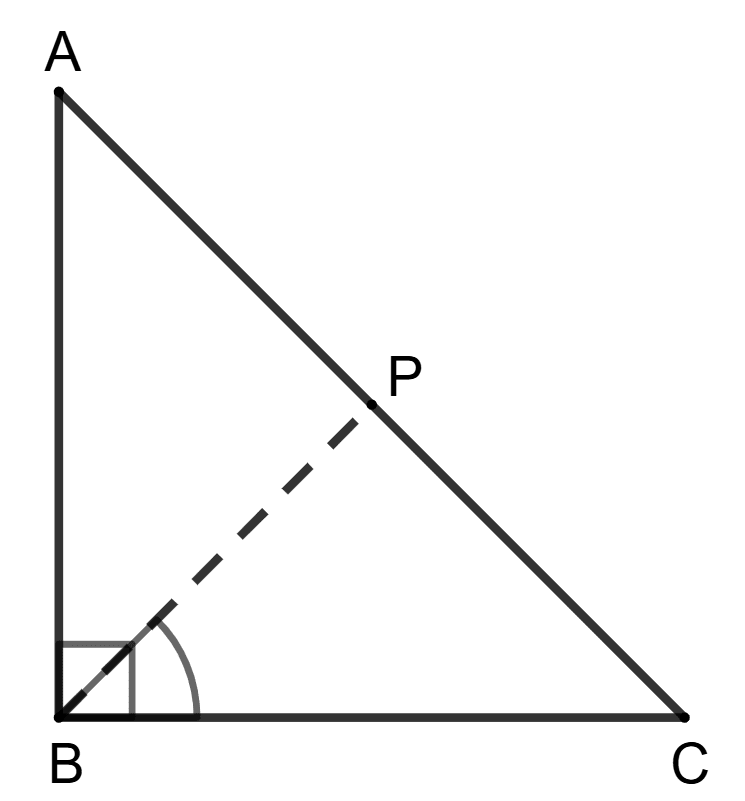
PA = PB
PA > PB
PA < PB
none of these
Side BA is produced upto point D and side BC upto point E such that ∠DAC = 110° and ∠ACE = 125°. Then the largest side of the triangle ABC is
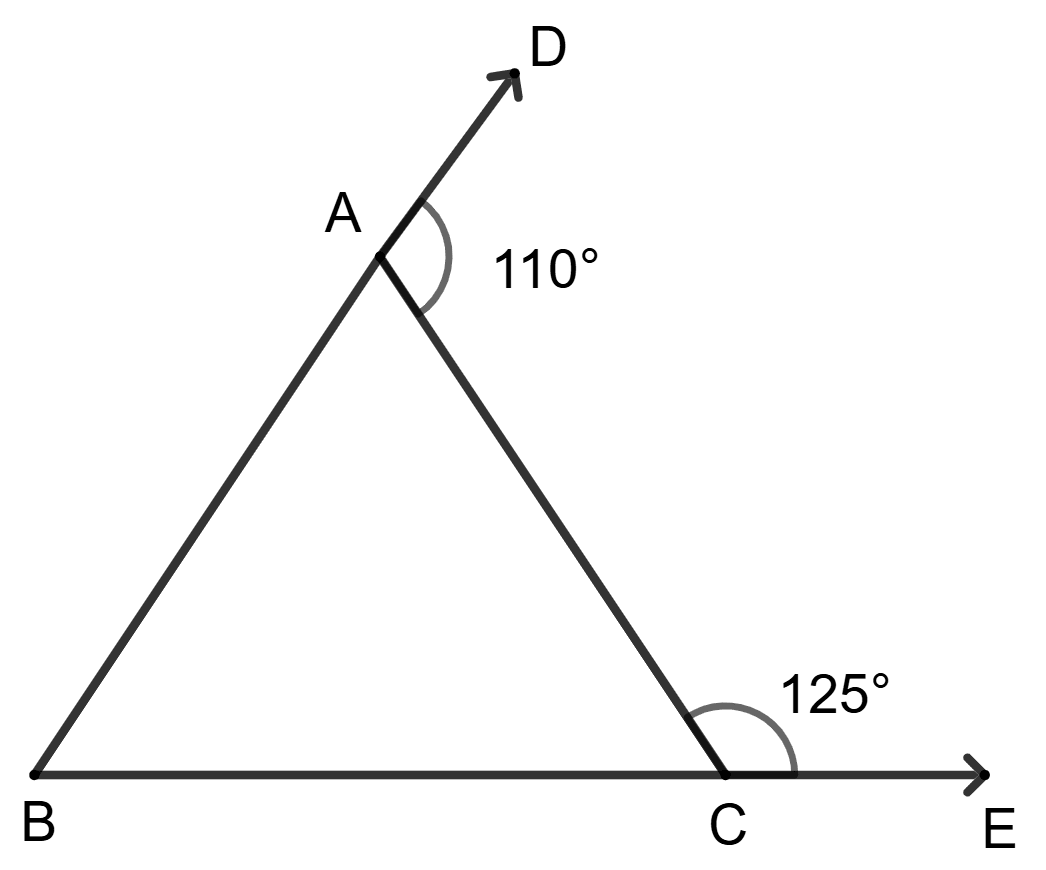
AB
BC
AC
none of these
In the given figure,
AC = CD
AB > CD
AB < CD
none of these