Mathematics
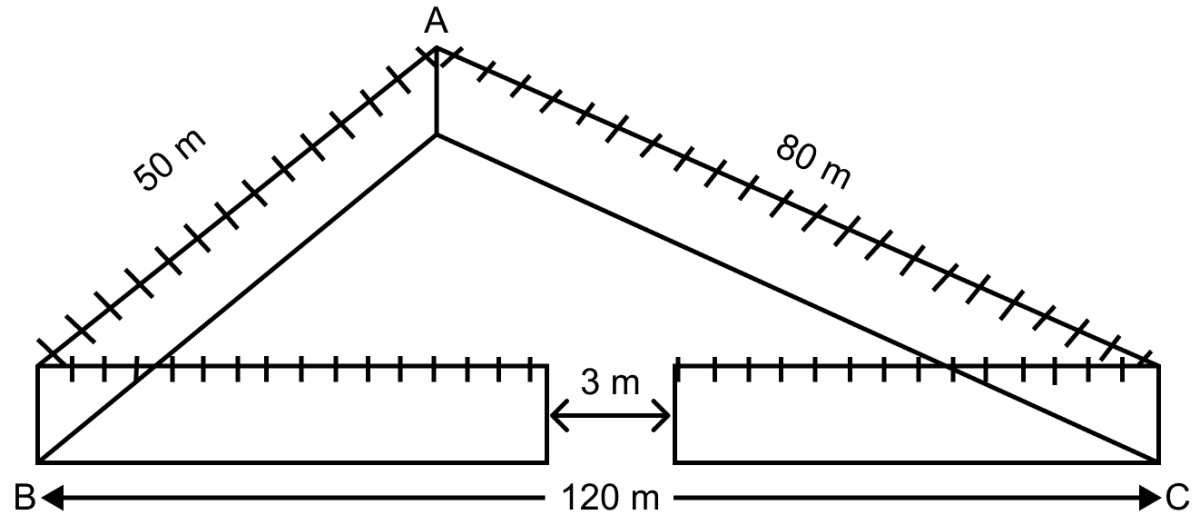
A triangular park ABC has sides 120 m, 80 m and 50 m (as shown in the adjoining figure). A gardner Dhania has to put a fence around it and also plant grass inside. How much area does she need to plant? Find the cost of fencing it with barbed wire at the rate of ₹ 200 per metre leaving a space 3 m wide for a gate on one side.
Mensuration
17 Likes
Answer
It is given that,
ABC is a triangular park with sides 120 m, 80 m and 50 m.
Here, the perimeter of △ABC = 120 + 80 + 50 = 250 m
Portion at which a gate is built = 3 m
Remaining perimeter = 250 – 3 = 247 m.
So, the length of the fence required around the park = 247 m.
Rate of fencing = ₹ 200 per metre
Total cost of fencing = 200 × 247 = ₹ 49,400.
We know that,
Semi perimeter (s) = = 125 m.
By formula,
Area of triangle (A) =
Substituting values we get,
Hence, area needed for plantation = m2 and cost of fencing = ₹49,400.
Answered By
12 Likes
Related Questions
If the area of an isosceles triangle is 60 cm2 and the length of each of its equal sides is 13 cm, find its base.
The base of a triangular field is 3 times its height. If the cost of cultivating the field at the rate of ₹25 per 100 m2 is ₹60000, find its base and height.
An umbrella is made by stitching 10 triangular pieces of cloth of two different colors (shown in the adjoining figure), each piece measuring 20 cm, 50 cm and 50 cm. How much cloth of each colour is required for the umbrella?

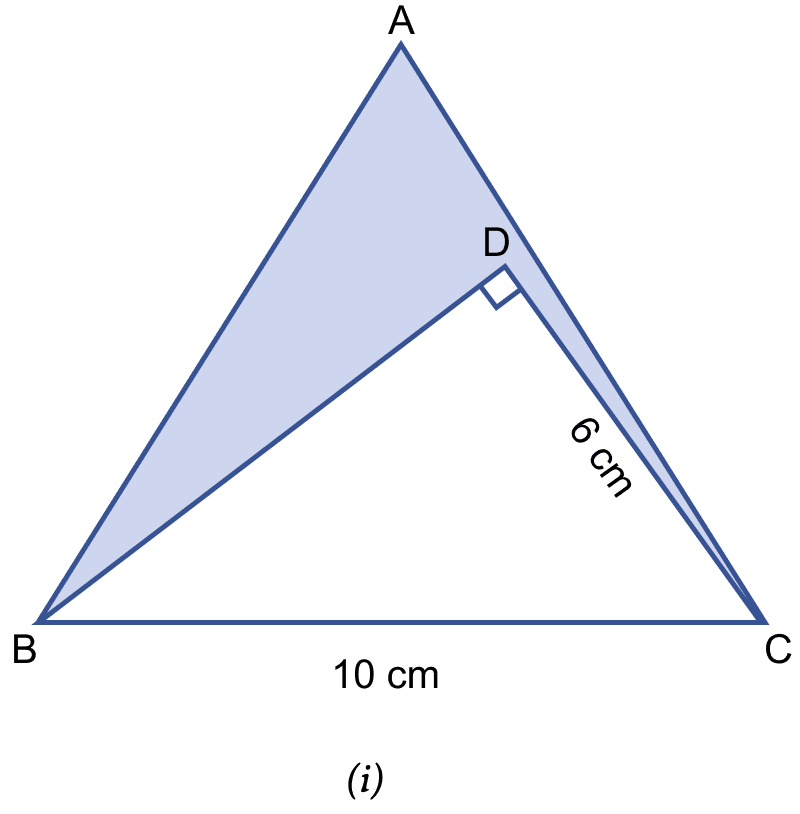
In the figure (i) given below, ABC is an equilateral triangle with each side of length 10 cm. In △BCD, ∠D = 90° and CD = 6 cm. Find the area of the shaded region. Give your answer correct to one decimal place.