Mathematics
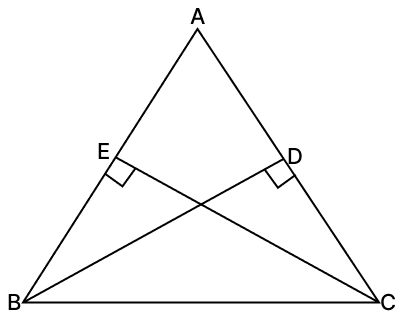
If two altitudes of a triangle are equal, prove that it is an isosceles triangle.
Triangles
2 Likes
Answer
Given,
CE = BD [Altitudes of △ABC are equal]
In △ABD and △ACE,
⇒ ∠ADB = ∠AEC [Each equal to 90°]
⇒ CE = BD [Given]
⇒ ∠DAB = ∠EAC [Common angle]
∴ △ABD ≅ △ACE (∵ A.A.S. axiom)
⇒ AB = AC [Corresponding parts of congruent triangles are equal]
Since, two sides are equal.
Hence, △ABC is an isosceles triangle with AB = AC.
Answered By
1 Like
Related Questions
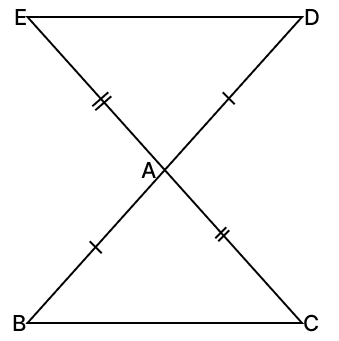
In the given figure, the sides BA and CA of △ABC have been produced to D and E such that BA = AD and CA = AE. Prove that, ED || BC.
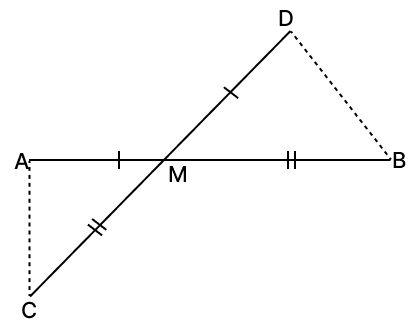
In the given figure, the line segments AB and CD intersect at a point M in such a way that AM = MD and CM = MB. Prove that, AC = BD but AC may not be parallel to BD.
In the given figure, ∠BAC = ∠CDB and ∠BCA = ∠CBD. Prove that AB = CD.
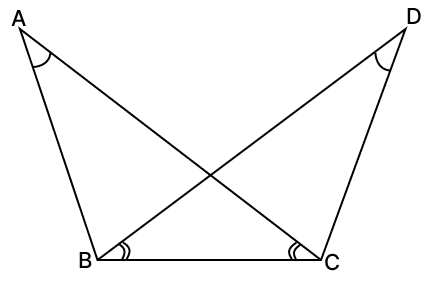
In the given figure, ∠ABD = ∠EBC, BD = BC and ∠ACB = ∠EDB. Prove that AB = BE.