Mathematics
Two circles of radii 10 cm and 17 cm intersecting each other at two points and the distance between their centres is 21 cm. Find the length of the common chord.
Circles
6 Likes
Answer
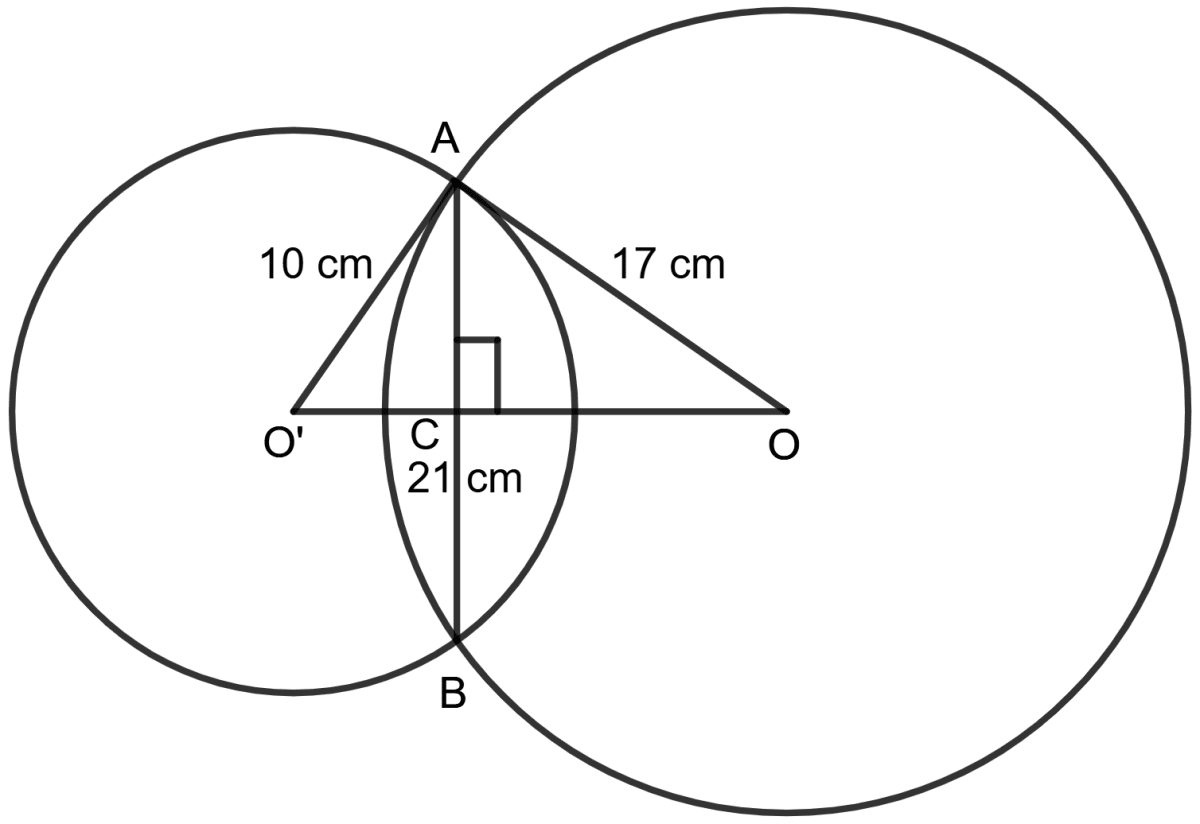
Let the length of OC be x cm and that of O'C be (21 - x)cm.
Since the perpendicular to a chord from the center of a circle bisects the chord, we use the Pythagorean theorem in two right triangles.
From the right triangle OAC, we have:
⇒ OA2 = OC2 + AC2 (By pythagoras theorem)
⇒ 172 = x2 + AC2
⇒ AC2 = 289 - x2 ……………….(1)
From the right triangle O'AC, we have:
⇒ O'A2 = O'C2 + AC2 (By pythagoras theorem)
⇒ 102 = (21 - x)2 + AC2
⇒ 100 = 441 + x2 - 42x + AC2
Using the equation (1):
⇒ 100 = 441 + x2 - 42x + 289 - x2
⇒ 100 = 730 - 42x
⇒ 42x = 730 - 100
⇒ 42x = 630
⇒ x = = 15
Thus, OC = 15 cm and O'C - 21 - 15 = 6 cm.
Substituting the value of x in equation (1), we get:
⇒ AC2 = 289 - x2
⇒ AC2 = 289 - 152
⇒ AC2 = 289 - 225 = 64
⇒ AC = = 8
Since the chord is bisected, length of common chord = 2 AC = 2 AC = 16 cm.
Hence, the length of the common chord = 16 cm.
Answered By
2 Likes
Related Questions
Equal chords of a circle subtend equal angles at the centre, prove it.
A line segment AB is of length 8 cm. Draw a circle of radius 5 cm that passes through A and B.
Can you draw a circle of radius 3 cm passing through A and B ? Give reason in support of your answer.
In the given circle, arc APB and arc BQC are in the ratio 2 : 5 and O is centre of the circle.
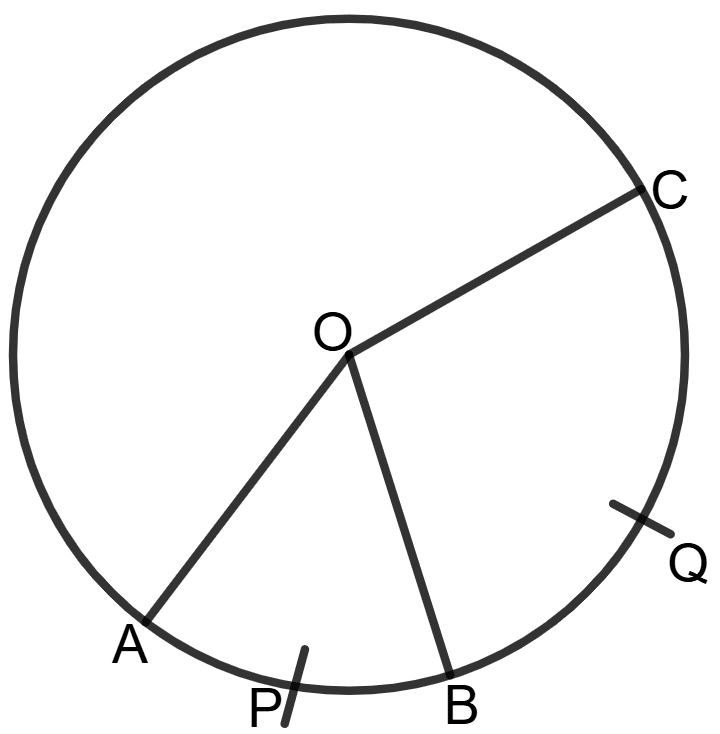
If angle AOB = 44°; find angle AOC.
The given figure shows two congruent circles with centres P and Q. R is mid-point of PQ and ABRCD is a straight line.
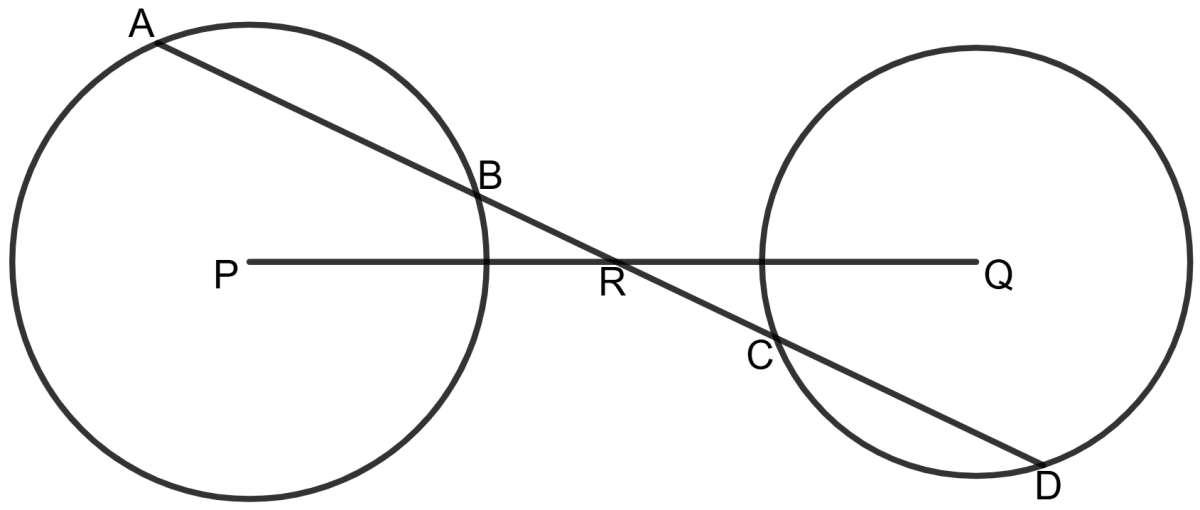
Prove that : AB = CD.