Mathematics
Two circles touch each other internally. Show that the tangents drawn to the two circles from any point on the common tangent are equal in length.
Answer
We know that,
If two tangents are drawn to a circle from an exterior point, the tangents are equal in length.

Let Q be the point on the common tangent from which, two tangents QA and QP are drawn to the circle with centre O.
So, QA = QP ………. (1)
Similarly, from point Q, QB and QP are two tangents to the circle with centre O’
So, QB = QP ………. (2)
From (1) and (2), we have
QA = QB
Hence, proved that the tangents are equal.
Related Questions
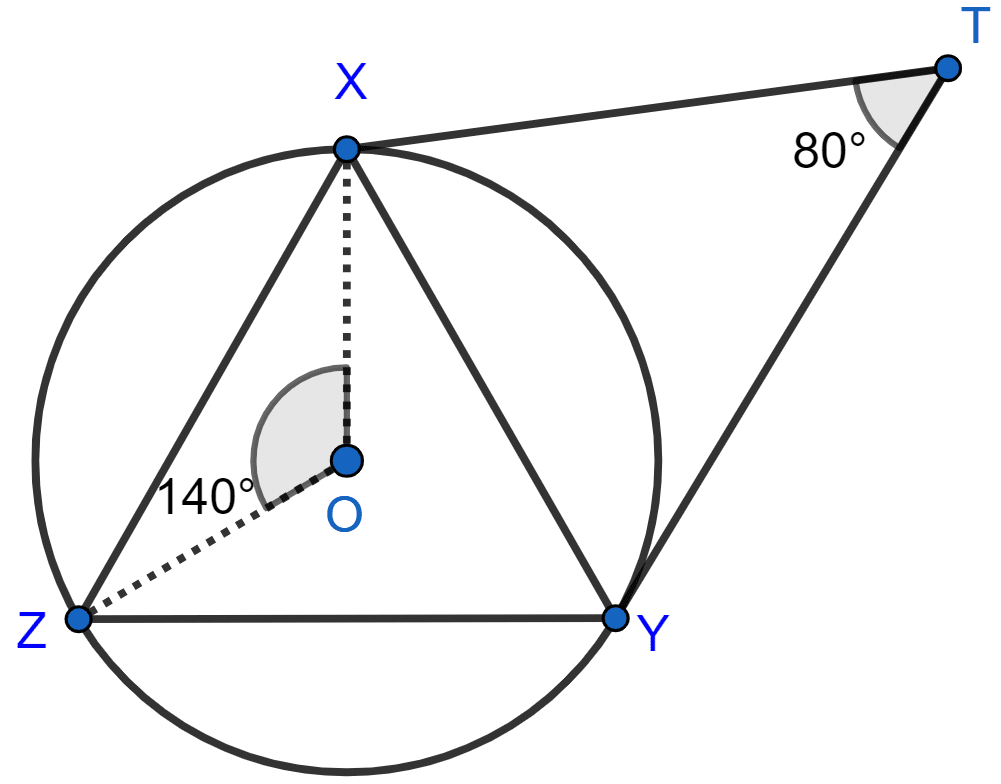
In the figure, given below, O is the center of the circumcircle of triangle XYZ. Tangents at X and Y intersect at point T. Given ∠XTY = 80° and ∠XOZ = 140°, calculate the value of ∠ZXY.
In the given figure, AE and BC intersect each other at point D. If ∠CDE = 90°, AB = 5 cm, BD = 4 cm and CD = 9 cm, find AE.

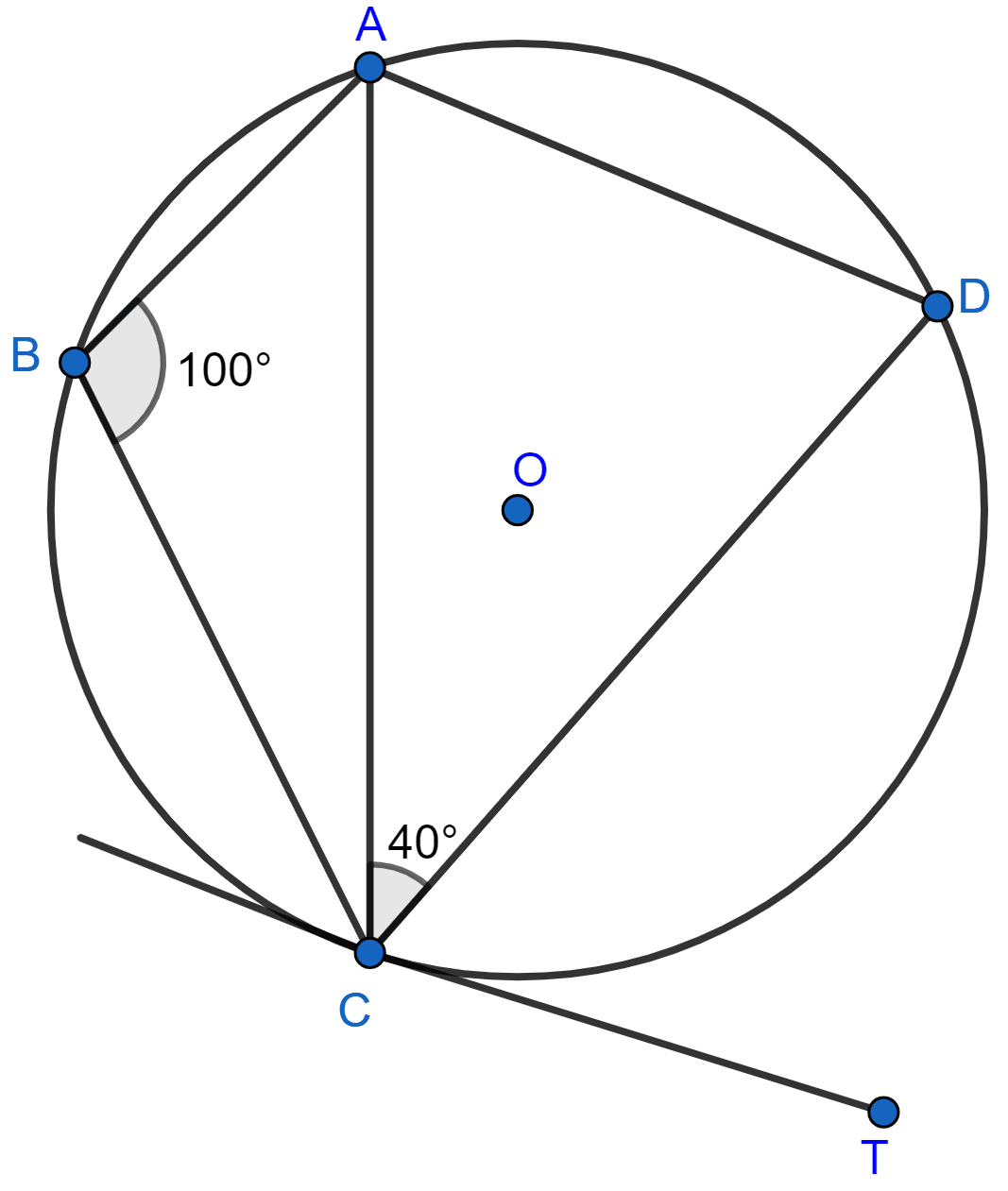
In the given circle with centre O, angle ABC = 100°, ∠ACD = 40° and CT is a tangent to the circle at C. Find ∠ADC and ∠DCT.
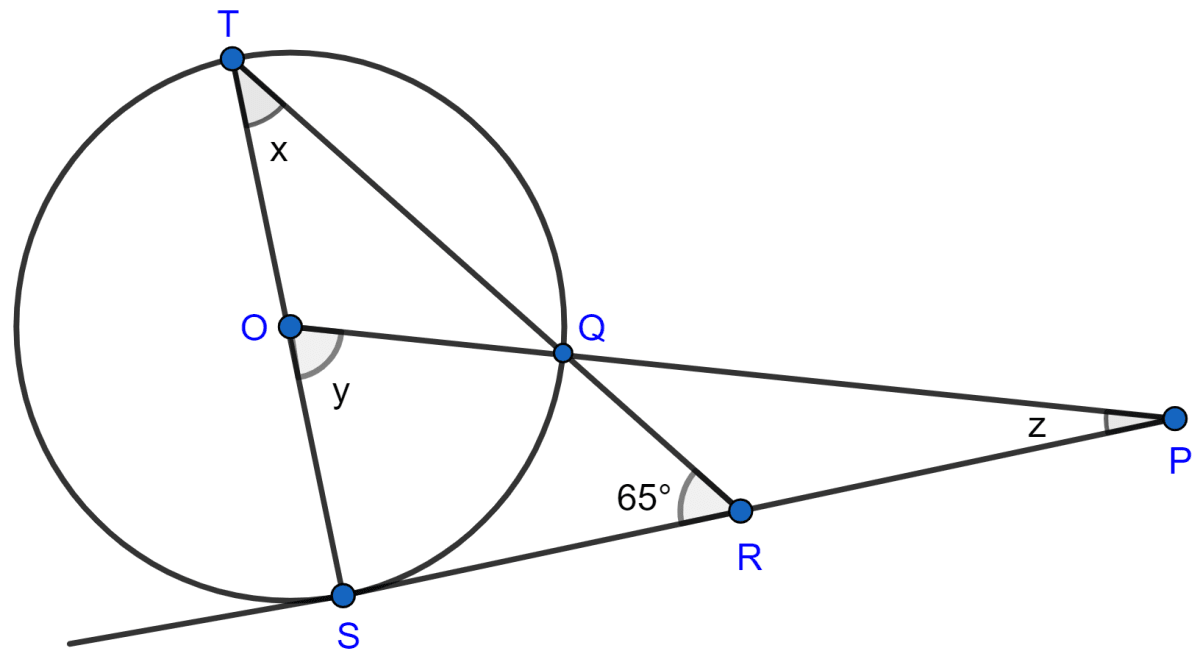
In the figure given below, O is the center of the circle and SP is a tangent. If ∠SRT = 65°, find the values of x, y and z.