Mathematics
Two poles of heights 6 m and 11 m stand vertically on a plane ground. If the distance between their feet is 12 m; find the distance between their tips.
Pythagoras Theorem
24 Likes
Answer
Let AB and CD be two poles of height 6 m and 11 m respectively.
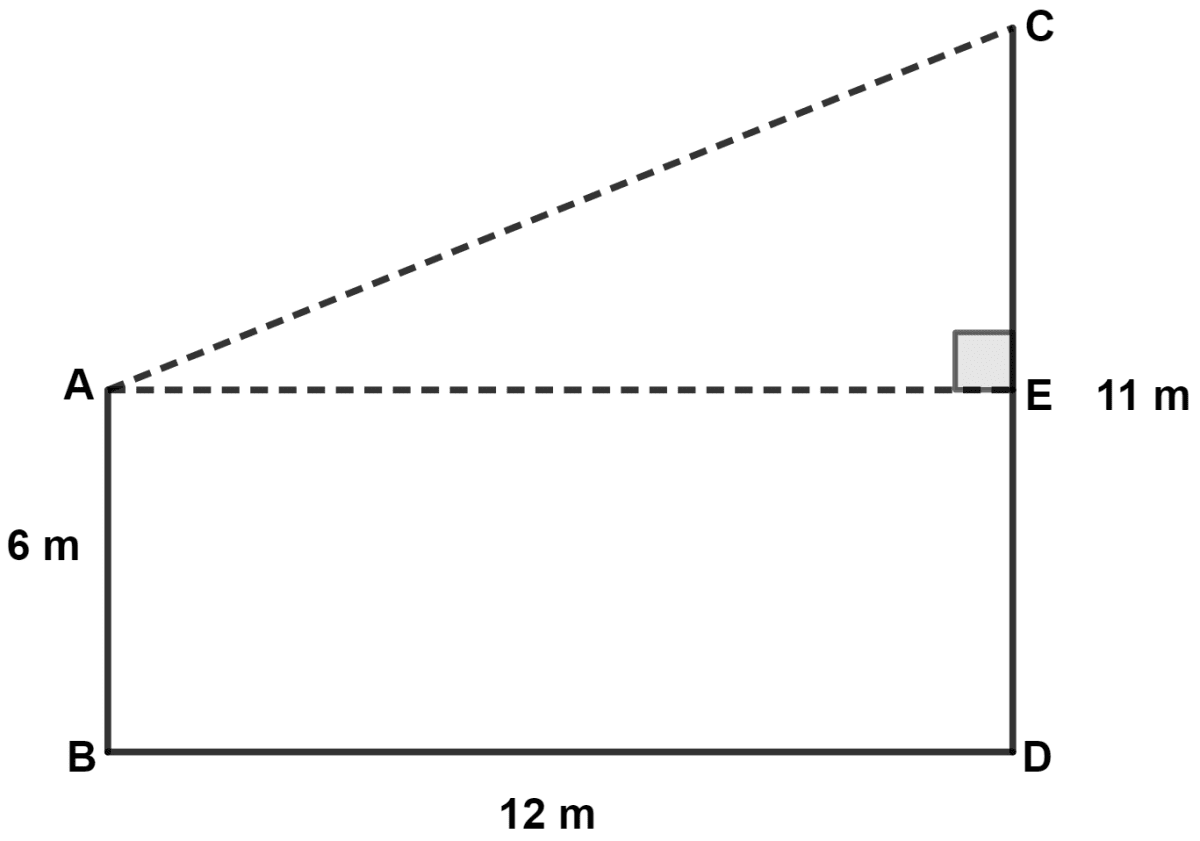
From figure,
ABDE is a rectangle.
∴ AE = BD = 12 m and ED = AB = 6 m.
From figure,
CE = CD - ED = 11 - 6 = 5 m.
In right-angled triangle,
By pythagoras theorem,
⇒ (Hypotenuse)2 = (Perpendicular)2 + (Base)2
⇒ AC2 = CE2 + AE2
⇒ AC2 = 52 + 122
⇒ AC2 = 25 + 144
⇒ AC2 = 169
⇒ AC = = 13 m.
Hence, the distance between the tips of two poles is 13 m.
Answered By
16 Likes
Related Questions
In triangle ABC,
AB = AC = x; BC = 10 cm and the area of the triangle is 60 cm2. Find x.
If the sides of a triangle are in the ratio 1 : : 1, show that it is a right-angled triangle.
In △ ABC, ∠C = 90° and AC = BC, then AB2 is equal to :
AC2
2AC2
BC2
2BC2 - AC2
In the given diagram, AE2 + BD2 is equal to :
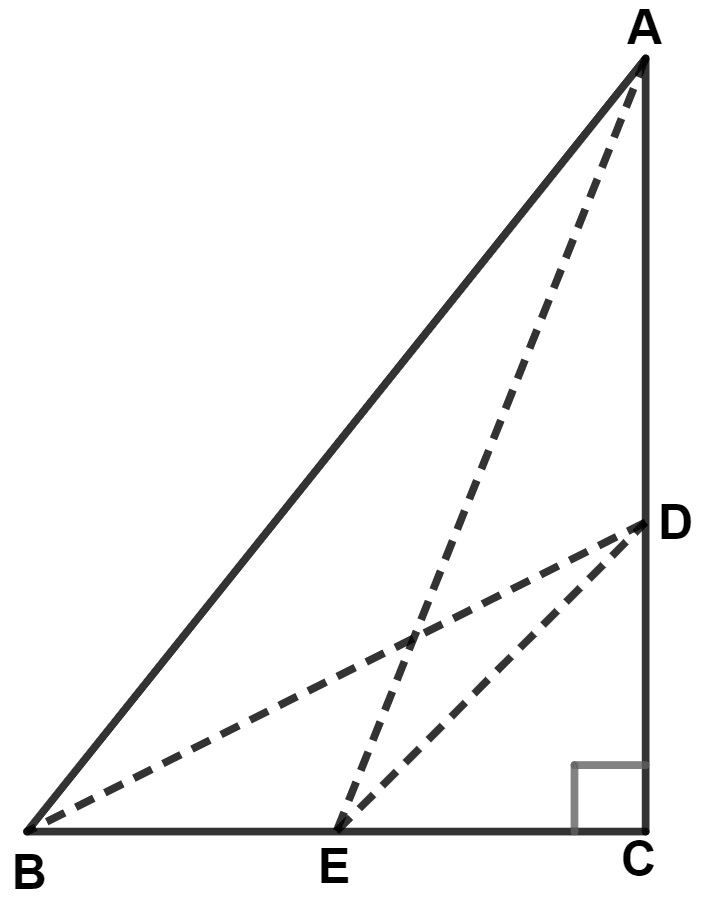
AB2 - DE2
DE2 - AB2
AB2 + DE2
DE × AB