Mathematics
Two trains leave a railway station at same time. The first train travels due west and the second train due north. The first train travels 5 km/hr faster than the second train. If after 2 hours, they are 50 km apart, find the speed of each train.
Quadratic Equations
19 Likes
Answer
Let speed of second train be x km/hr and first be (x + 5) km/hr.
According to figure,
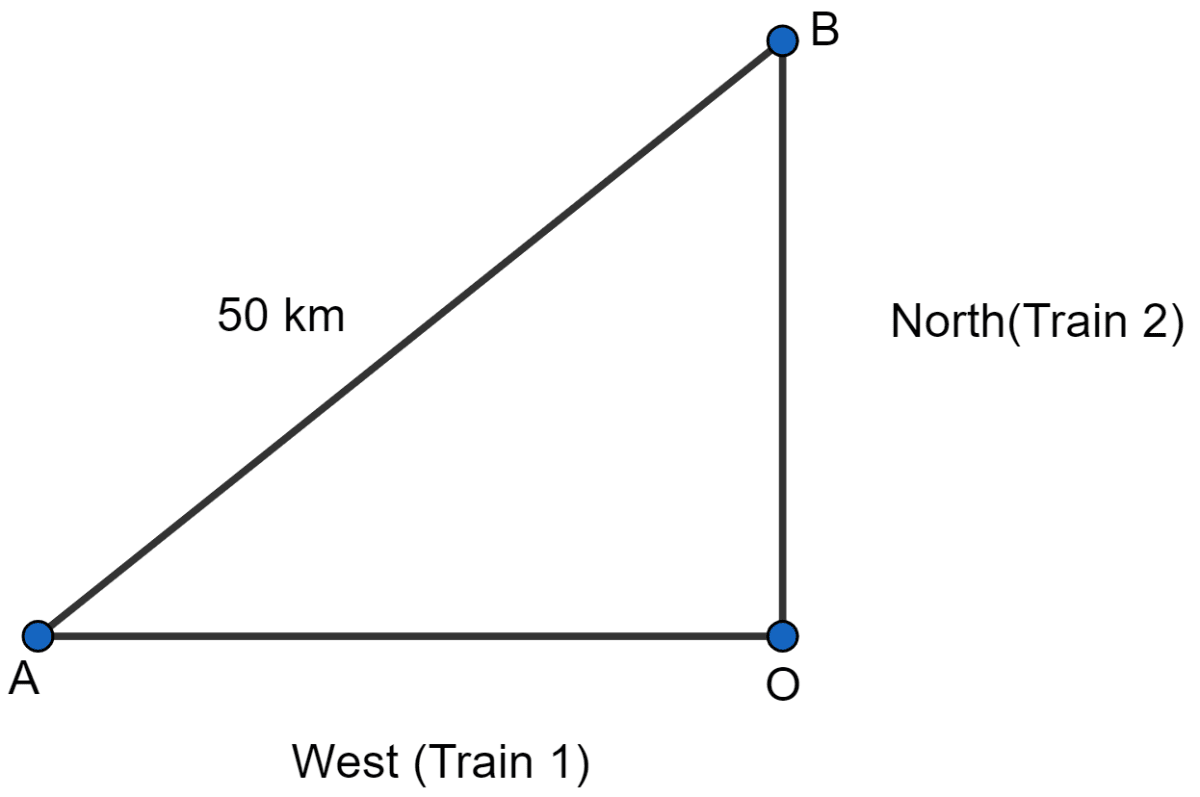
Let O be the position where trains leave
Distance travelled by first train OA = 2(x + 5) km
Distance travelled by second train OB = 2x km
By pythagoras theorem we get,
⇒ AB2 = OA2 + OB2
⇒ 502 = [2(x + 5)]2 + (2x)2
⇒ 502 = 4(x + 5)2 + 4x2
⇒ 2500 = 4(x2 + 25 + 10x) + 4x2
⇒ 2500 = 4x2 + 100 + 40x + 4x2
⇒ 8x2 + 40x - 2400 = 0
⇒ 8(x2 + 5x - 300) = 0
⇒ x2 + 5x - 300 = 0
⇒ x2 + 20x - 15x - 300 = 0
⇒ x(x + 20) - 15(x + 20) = 0
⇒ (x - 15)(x + 20) = 0
⇒ x - 15 = 0 or x + 20 = 0
⇒ x = 15 or x = -20.
Since, speed cannot be negative,
∴ x ≠ -20.
∴ x = 15 and x + 5 = 20
Hence, speed of first train = 20 km/hr and second train = 15 km/hr.
Answered By
13 Likes
Related Questions
In an auditorium, seats were arranged in rows and columns. The number of rows was equal to number of seats in each row. When the number of rows was doubled and the number of seats in each row was reduced by 10, the total number of seats increased by 300. Find :
(i) the number of rows in the original arrangement.
(ii) the number of seats in the auditorium after re-arrangement.
In a certain positive fraction , the denominator is greater than the numerator by 3. If 1 is subtracted from both the numerator and denominator , the fraction is decreased by . Find the fraction.
A two digit number contains the largest digit at ten's place. The product of the digits is 27 and the difference between two digits is 6. Find the number.
₹480 is divided equally among 'x' children. If the number of children were 20 more, then each would have got ₹12 less . Find 'x'.