Mathematics
The upper part of a tree is broken over by the wind and makes an angle of 42° with the ground. The horizontal distance from the root of the tree to the point where the top of tree meets the ground is 20 m. Find the height of the tree before it was broken.
Give your answer correct to the nearest whole number.
Heights & Distances
8 Likes
Answer
Let AC be the broken part of tree.
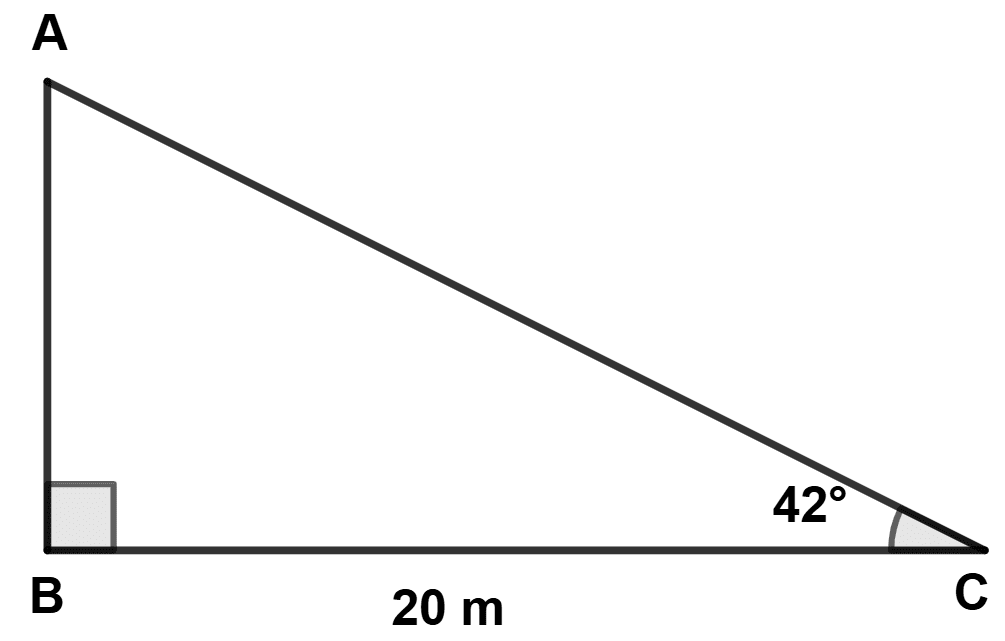
In △ ABC,
⇒ tan 42° =
⇒ 0.9004 =
⇒ AB = 20 × 0.9004 = 18.008 m
⇒ cos 42° =
⇒ AC =
⇒ AC = = 26.914 m
Height of tree = AB + AC = 18.008 + 26.914 = 44.9 ≈ 45 m.
Hence, height of tree = 45 m.
Answered By
5 Likes
Related Questions
A semicircular sheet of metal of radius 14 cm is bent to form an open conical cup of the largest size. Find the capacity of the cup. (Take )
P and Q are two points on the x-axis and y-axis respectively. M(3, 2) divides the line segment PQ in the ratio 2 : 3. Find :
(i) the co-ordinates of the points P and Q
(ii) the slope of line segment PQ
(iii) the equation of the line through point P and perpendicular to PQ.
Solve the following inequation and represent the solution set on a number line :
; x ∈ R.
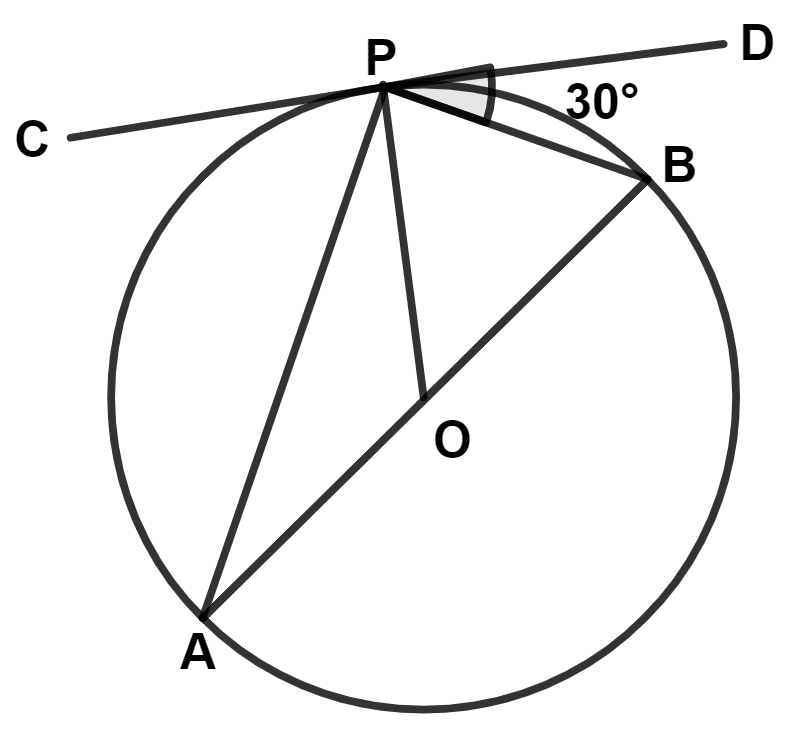
In the given figure, O is the center of the circle, AB is diameter and CPD is a tangent to the circle at P. If ∠BPD = 30°, find :
(i) ∠APC
(ii) ∠BOP
(iii) ∠OAP