Mathematics
Use graph paper for this question (take 2cm = 1 unit along both x and y axis). ABCD is a quadrilateral whose vertices are A(2, 2), B(2, -2), C(0, -1) and D(0, 1).
(i) Reflect quadrilateral ABCD on the y-axis and name it as A'B'CD.
(ii) Write down the coordinates of A' and B'.
(iii) Name two points which are invariant under the above reflection.
(iv) Name the polygon A'B'CD.
Answer
(i) Reflected quadrilateral A'B'CD is shown in the graph below:
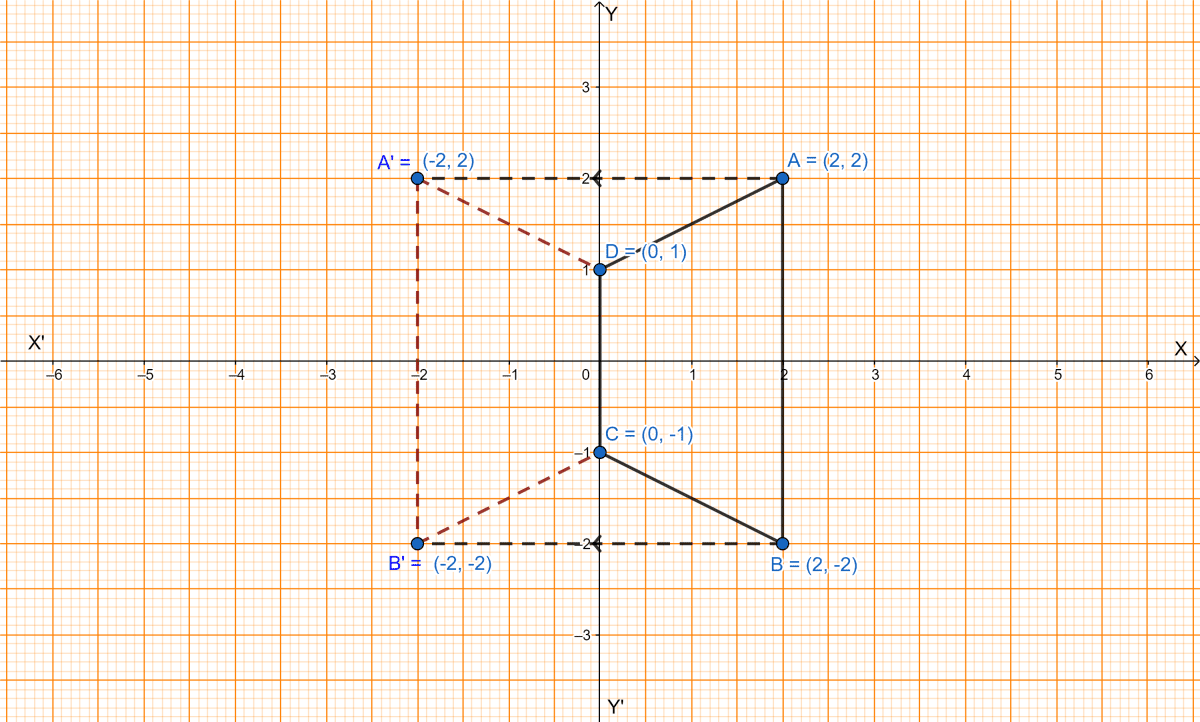
(ii) From graph we get,
The coordinates of A' and B' are (-2, 2) and (-2, -2) respectively.
(iii) From graph we get,
The two points which are invariant under the above reflection are C and D.
(iv) From graph we get,
The polygon(A'B'CD) formed is an isosceles trapezium.
Related Questions
Use graph paper for this question.
Take 2 cm = 1 unit on both the axes.
(i) Plot the points A(0, 4), B(2, 2), C(5, 2) and D(4, 0), E(0, 0) is the origin.
(ii) Reflect B, C, D on the y-axis and name them as B', C' and D' respectively.
(iii) Join the points ABCDD'B'C' and A in order and give a geometrical name to the closed figure.
Use graph paper for this question.
Take 1 cm = 1 unit on both the axes.
(i) Plot the following points on your graph sheet:
A(-4, 0), B(-3, 2), C(0, 4), D(4, 1) and E(7, 3)
(ii) Reflect the points B, C, D and E on the x-axis and name them as B', C', D' and E' respectively.
(iii) Join A, B, C, D, E, E', D', C', B' and A in order.
(iv) Name the closed figure.
Use a graph sheet for this question. Take 1cm = 1 unit along both x and y-axes.
(i) Plot the points : A(0, 5), B(3, 0), C(1, 0) and D(1, -5).
(ii) Reflect the points B, C and D on the y-axis and name them as B', C' and D' respectively.
(iii) Write down the coordinates of B', C' and D'.
(iv) Join the points A, B, C, D, D', C', B', A in order and give a name to the closed figure ABCDD'C'B'.
Use graph paper for this question.
(i) The point P(2, -4) is reflected about the line x = 0 to get the image Q. Find the coordinates of Q.
(ii) Point Q is reflected about the line y = 0 to get the image R. Find the coordinates of R.
(iii) Name the figure PQR.
(iv) Find the area of the figure PQR.