Mathematics
Use a graph paper for this question taking 2 cm = 1 unit along both axes.
(a) Plot A(1, 3), B(1, 2) and C(3, 0).
(b) Reflect A and B on the x-axis and name their images as E and D respectively. Write down their coordinates.
(c) Reflect A and B through the origin and name their images as F and G respectively.
(d) Reflect A, B and C on the y-axis and name their images as J, I and H respectively.
(e) Join all the points A, B, C, D, E, F, G, H, I and J in order and name the closed figure so formed.
Answer
Steps of Construction:
Plot the given points: A(1, 3), B(1, 2) and C(3, 0).
Reflect points A and B in x-axis.The image of A under reflection in x-axis is E(1, -3) and image of B under reflection in x-axis is D(1, -2).
Reflect points A and B through the origin.The image of A under reflection through origin is F(-1, -3) and image of B under reflection through origin is G(-1, -2).
Reflect points A, B, and C in y-axis. The image of A under reflection in y-axis is is J(-1, 3),the image of B under reflection in y-axis is I(-1, 2) and the image of C under reflection in y-axis is H(-3, 0).
Join the points in order A, B, C, D, E, F, G, H, I, J and finally back to A to obtain the required closed figure ABCDEFGHIJ. The figure formed is a decagon.
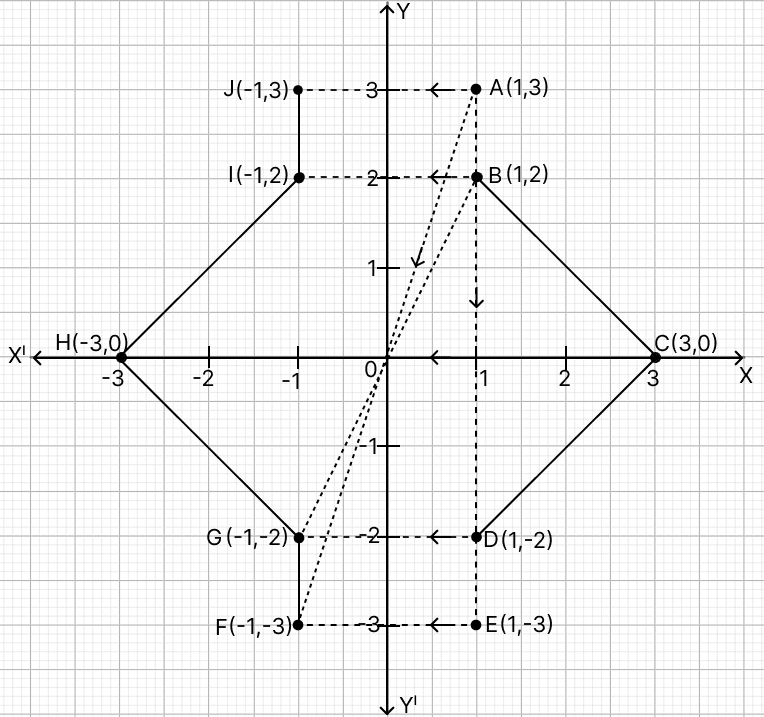
Hence, the figure formed is a decagon.
Related Questions
It is given that (x − 2) is a factor of polynomial 2x3 − 7x2 + kx − 2.
Find:
(a) the value of ‘k’.
(b) hence, factorise the resulting polynomial completely.
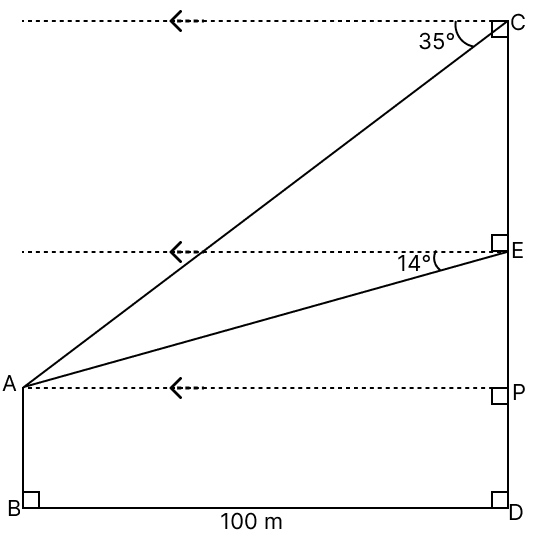
In the given diagram, AB is a vertical tower 100 m away from the foot of a 30 storied building CD. The angles of depression from the point C and E, (E being the mid-point of CD), are 35° and 14° respectively. (Use mathematical table for the required values rounded off correct to two places of decimals only.)
Find the height of the:
(a) tower AB
(b) building CD
Use a graph paper for this question. (Take 2 cm = 10 Marks along one axis and 2 cm = 10 students along another axis). Draw a Histogram for the following distribution which gives the marks obtained by 164 students in a particular class and hence find the Mode.
Marks Number of students 30 - 40 10 40 - 50 26 50 - 60 40 60 - 70 54 70 - 80 34