Mathematics
Use the graphical method to show that the straight lines given by the equations and pass through the same point.
Coordinate Geometry
2 Likes
Answer
First equation : x + y = 2
Step 1:
Give at least three suitable values to the variable x and find the corresponding values of y.
Let x = -1, then (-1) + y = 2 ⇒ y = 3
Let x = 0, then 0 + y = 2 ⇒ y = 2
Let x = 1, then 1 + y = 2 ⇒ y = 1
Let x = 3, then 3 + y = 2 ⇒ y = -1
Step 2:
Make a table (as given below) for the different pairs of the values of x and y:
| x | -1 | 0 | 1 | 3 |
|---|---|---|---|---|
| y | 3 | 2 | 1 | -1 |
Step 3:
Plot the points, from the table, on a graph paper and then draw a straight line passing through the points plotted on the graph.
Second equation : x - 2y = 5
Step 1:
Give at least three suitable values to the variable x and find the corresponding values of y.
Let x = -1, then (-1) - 2y = 5 ⇒ y = -3
Let x = 0, then 0 - 2y = 5 ⇒ y = -2.5
Let x = 1, then 1 - 2y = 5 ⇒ y = -2
Let x = 3, then 3 - 2y = 5 ⇒ y = -1
Step 2:
Make a table (as given below) for the different pairs of the values of x and y:
| x | -1 | 0 | 1 | 3 |
|---|---|---|---|---|
| y | -3 | -2.5 | -2 | -1 |
Step 3:
Plot the points, from the table, on a graph paper and then draw a straight line passing through the points plotted on the graph.
Third equation :
Step 1:
Give at least three suitable values to the variable x and find the corresponding values of y.
Let x = -3, then ⇒ y = 1
Let x = 0, then ⇒ y = 0
Let x = 3, then ⇒ y = -1
Step 2:
Make a table (as given below) for the different pairs of the values of x and y:
| x | -3 | 0 | 3 |
|---|---|---|---|
| y | 1 | 0 | -1 |
Step 3:
Plot the points, from the table, on a graph paper and then draw a straight line passing through the points plotted on the graph.
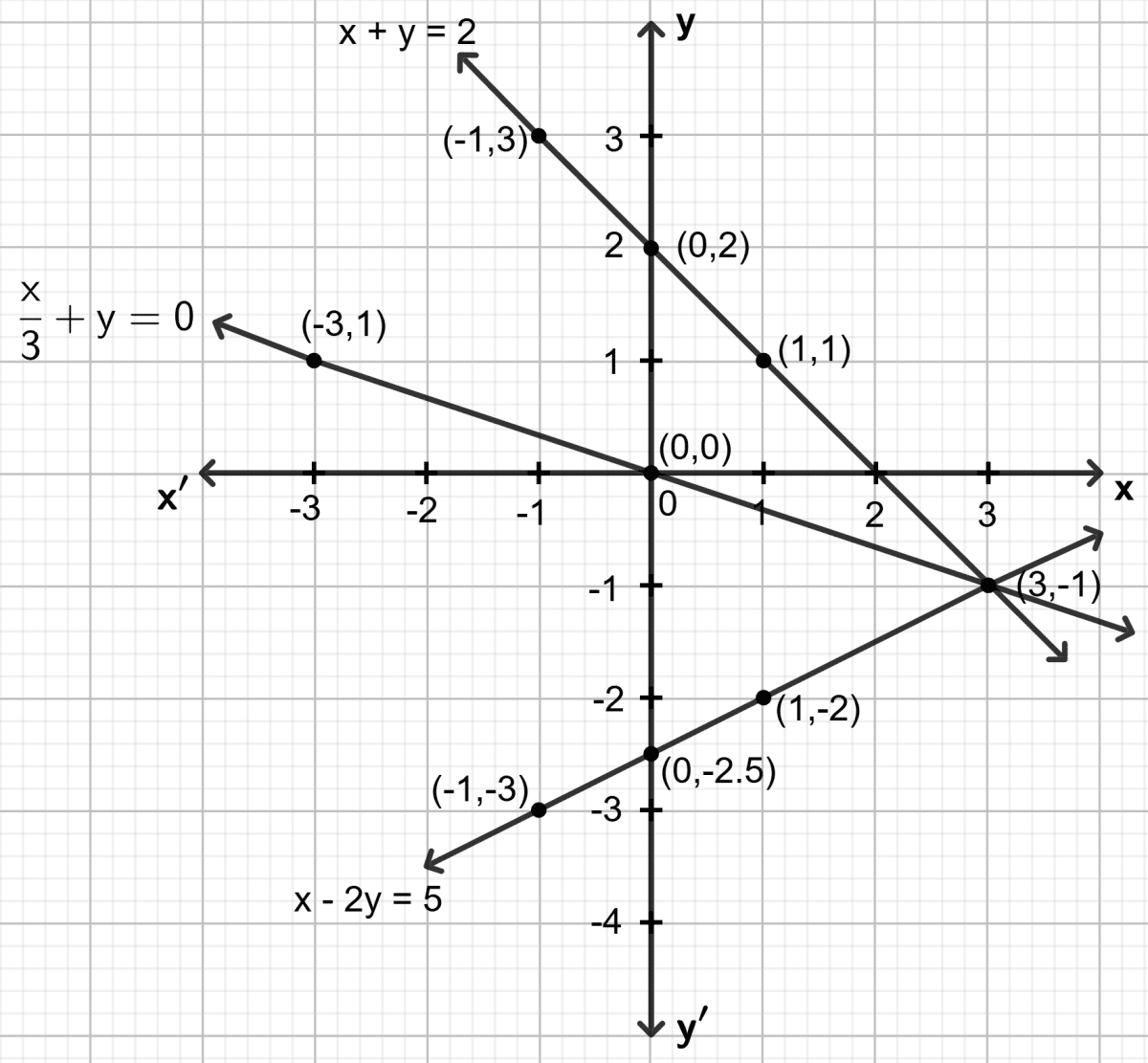
Hence, the three straight lines pass through the same point.
Answered By
1 Like
Related Questions
Draw the graph of equation 3x - 4y = 12. Use the graph drawn to find :
(i) y1, the value of y, when x = 4
(ii) y2, the value of y, when x = 0.
Draw the graph of equation . Use the graph drawn to find :
(i) x1, the value of x, when y = 10
(ii) y1, the value of y, when x = 8.
Draw the graph of line x + y = 5. Use the graph paper drawn to find the inclination and the y-intercept of the line.
Draw the graph of line 2x + y = 5.