Mathematics
Write the slope of the line whose inclination is:
(i) 0°
(ii) 30°
(iii) 45°
(iv) 60°
Coordinate Geometry
8 Likes
Answer
(i) 0°
The inclination of a line is 0°, then θ = 0°.
The slope of the line = m = tan 0° = 0
Hence, the slope of the line whose inclination is 0° is 0.
(ii) 30°
The inclination of a line is 30°, then θ = 30°.
The slope of the line = m = tan 30° =
Hence, the slope of the line whose inclination is 30° is .
(iii) 45°
The inclination of a line is 45°, then θ = 45°.
The slope of the line = m = tan 45° = 1
Hence, the slope of the line whose inclination is 45° is 1.
(iv) 60°
The inclination of a line is 60°, then θ = 60°.
The slope of the line = m = tan 60° =
Hence, the slope of the line whose inclination is 60° is .
Answered By
7 Likes
Related Questions
In the following, find the inclination of line AB :
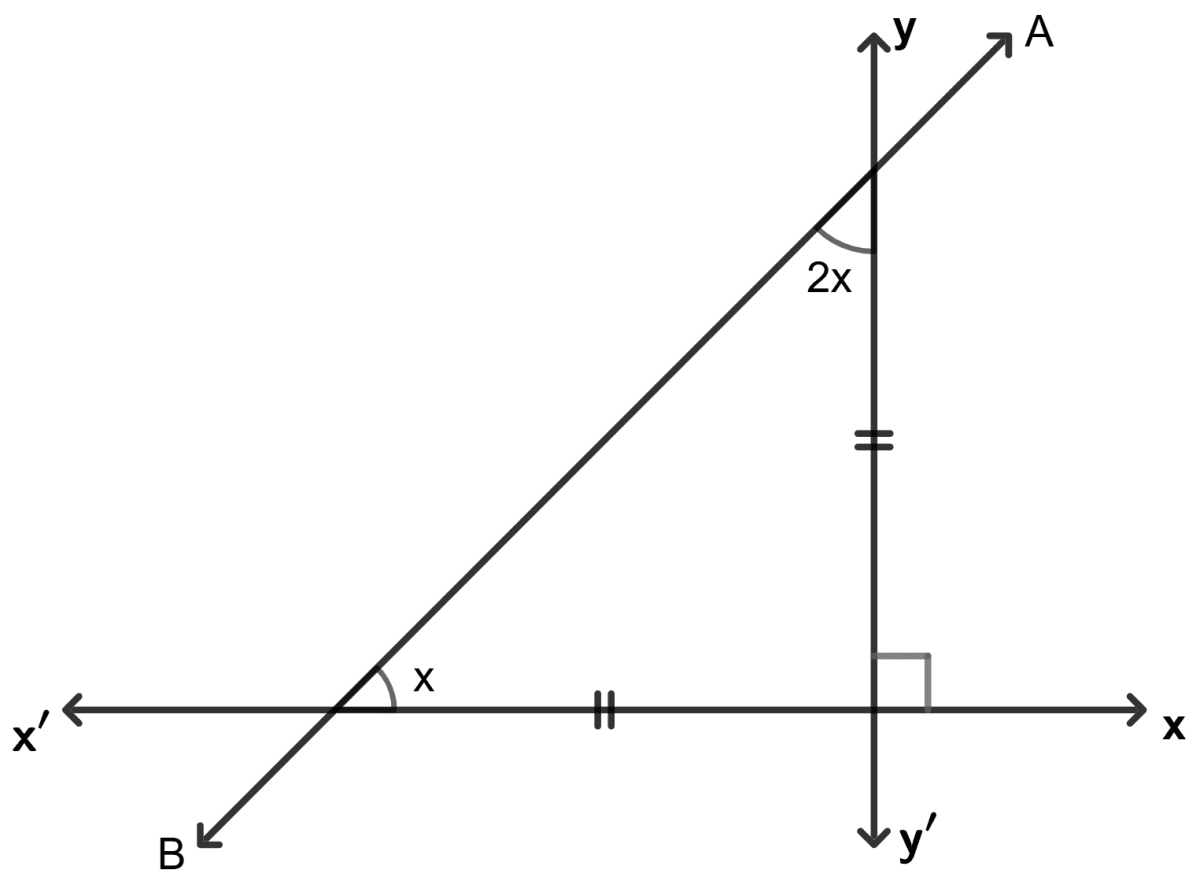
Write the inclination of a line which is :
(i) parallel to x-axis.
(ii) perpendicular to x-axis.
(iii) parallel to y-axis.
(iv) perpendicular to y-axis.
Find the inclination of the line whose slope is:
(i) 0
(ii) 1
(iii)
(iv)
Write the slope of the line which is :
(i) parallel to x-axis.
(ii) perpendicular to x-axis.
(iii) parallel to y-axis.
(iv) perpendicular to y-axis.