Chapter 15: Similarity (With Applications to Maps and Modules)

Exercise 15(A)

Question 1(a)

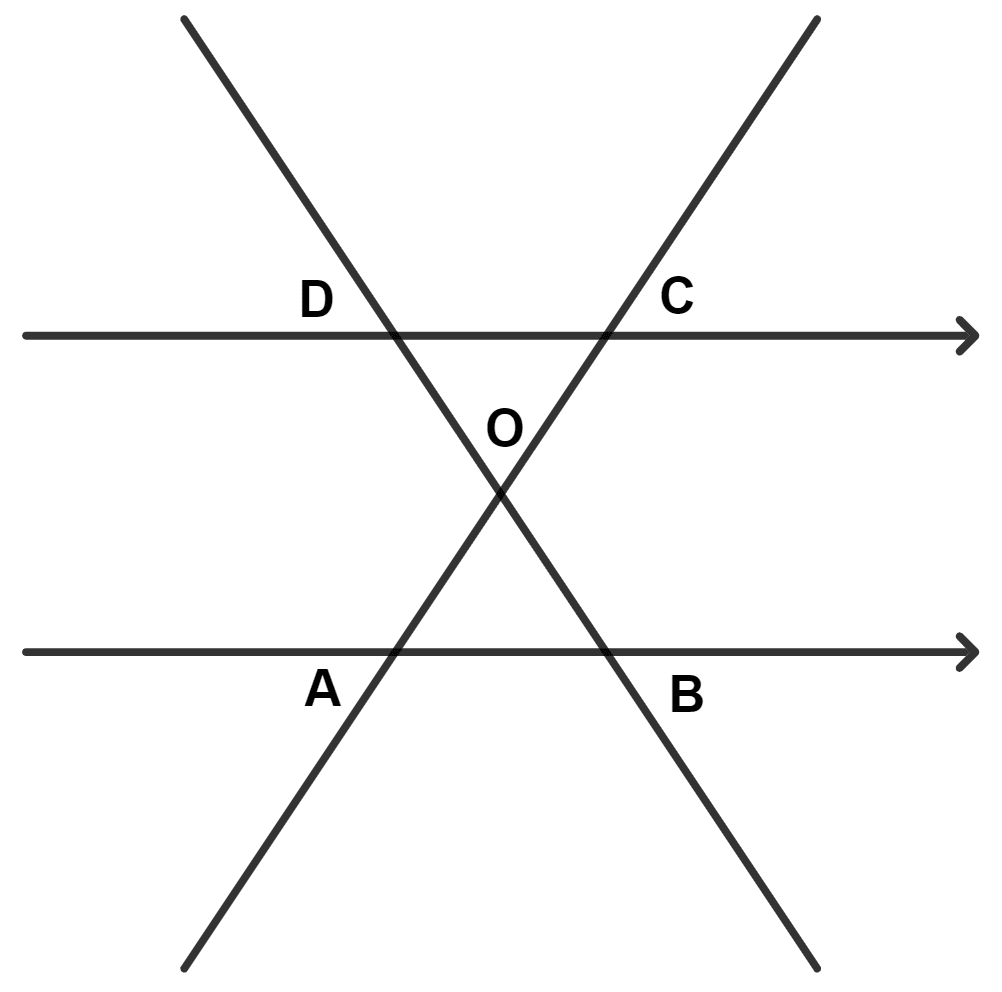
In the given diagram OC = 1.5 × OA, then OB is equal to :

3 × OD
1.5 × OD
$\dfrac{2}{3}$ × OD
OD

Answer

From figure,

In △ OAB and △ OCD,

⇒ ∠AOB = ∠COD (Vertically opposite angles are equal)

⇒ ∠OAB = ∠OCD (Alternate angles are equal)

⇒ ∠OBA = ∠ODC (Alternate angles are equal)

∴ △ OAB ~ △ OCD (By A.A.A. postulate)

Given,

⇒ OC = 1.5 × OA

⇒ $\dfrac{OA}{OC} = \dfrac{1}{1.5} = \dfrac{2}{3}$ .

We know that,

Corresponding sides of similar triangle are in proportion.

$\therefore \dfrac{OB}{OD} = \dfrac{OA}{OC} \\[1em] \Rightarrow \dfrac{OB}{OD} = \dfrac{2}{3} \\[1em] \Rightarrow OB = \dfrac{2}{3} \times OD.$

Hence, Option 3 is the correct option.

Question 1(b)

Are the given triangles similar?

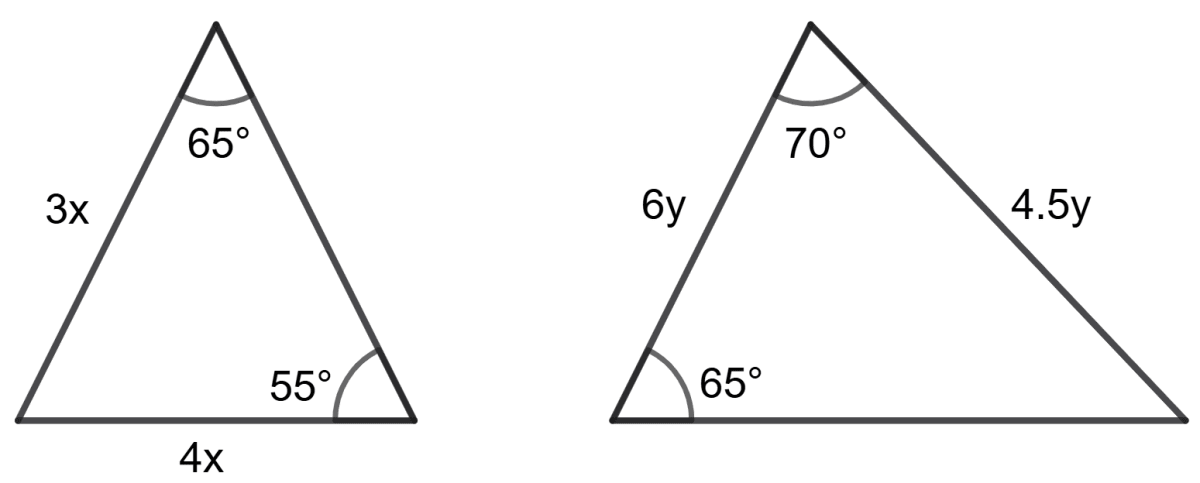
Yes
No
None of these

Answer

As we know that sum of all angles of a triangle is 180°.

In first triangle,

⇒ 65° + 55° + third angle = 180°

⇒ 120° + third angle = 180°

⇒ third angle = 180° - 120°

⇒ third angle = 60°

In second triangle,

⇒ 65° + 70° + third angle = 180°

⇒ 135° + third angle = 180°

⇒ third angle = 180° - 135°

⇒ third angle = 45°

Since, the in the given triangles neither corresponding angles are equal nor their corresponding sides are in proportion.

Hence, option 2 is the correct option.

Question 1(c)

In the given figure, OA = 5, OB = 6, OC = 3 and OD = 10, then

Δ AOB ∼ Δ AOB
Δ AOB ∼ Δ BOC
Δ BOC ∼ Δ COD
Δ AOD ∼ Δ COB

Answer

Given,

OA = 5, OB = 6, OC = 3 and OD = 10.

$\Rightarrow \dfrac{OA}{OC} = \dfrac{5}{3} \\[1em] \Rightarrow \dfrac{OD}{OB} = \dfrac{10}{6} = \dfrac{5}{3} \\[1em] \therefore \dfrac{OA}{OC} = \dfrac{OD}{OB}$

From figure,

∠AOD = ∠BOC (Vertically opposite angles are equal)

∴ △ AOD ∼ △ COB (By S.A.S. axiom)

Hence, option 4 is the correct option.

Question 1(d)

In the given figure, the value of x is:

Answer

In Δ AOB and Δ DOC

⇒ ∠AOB = ∠DOC (Vertically opposite angles are equal)

⇒ ∠BAO = ∠DCO (Alternate angles are equal)

⇒ ∠ABO = ∠CDO (Alternate angles are equal)

∴ Δ AOB ∼ Δ COD (By AAA postulate)

We know that,

Corresponding sides of similar triangles are proportional.

$\therefore \dfrac{AO}{CO} = \dfrac{OB}{OD}\\[1em] \Rightarrow \dfrac{18}{12} = \dfrac{x}{20}\\[1em] \Rightarrow x = \dfrac{18 \times 20}{12}\\[1em] \Rightarrow x = \dfrac{360}{12}\\[1em] \Rightarrow x = 30$

Hence, option 2 is the correct option.

Question 2

In triangle ABC and DEF, ∠A = ∠D and $\dfrac{\text{AB}}{\text{AC}} = \dfrac{\text{DE}}{\text{DF}}$ then prove that Δ ABC ∼ Δ DEF.

Answer

Given, $\dfrac{\text{AB}}{\text{AC}} = \dfrac{\text{DE}}{\text{DF}}$

⇒ $\dfrac{\text{AB}}{\text{DE}} = \dfrac{\text{AC}}{\text{DF}}$

In Δ ABC and Δ DEF,

⇒ ∠A = ∠D (Given)

⇒ $\dfrac{\text{AB}}{\text{DE}} = \dfrac{\text{AC}}{\text{DF}}$

∴ Δ ABC ∼ Δ DEF (By SAS postulate)

Hence, proved that Δ ABC ∼ Δ DEF.

Question 3

In triangle ABC and DEF, ∠A = ∠D, ∠B = ∠E and ∠C = ∠F. Also, AL and DM are medians. Prove that $\dfrac{\text{BC}}{\text{EF}} = \dfrac{\text{AL}}{\text{DM}}$ .

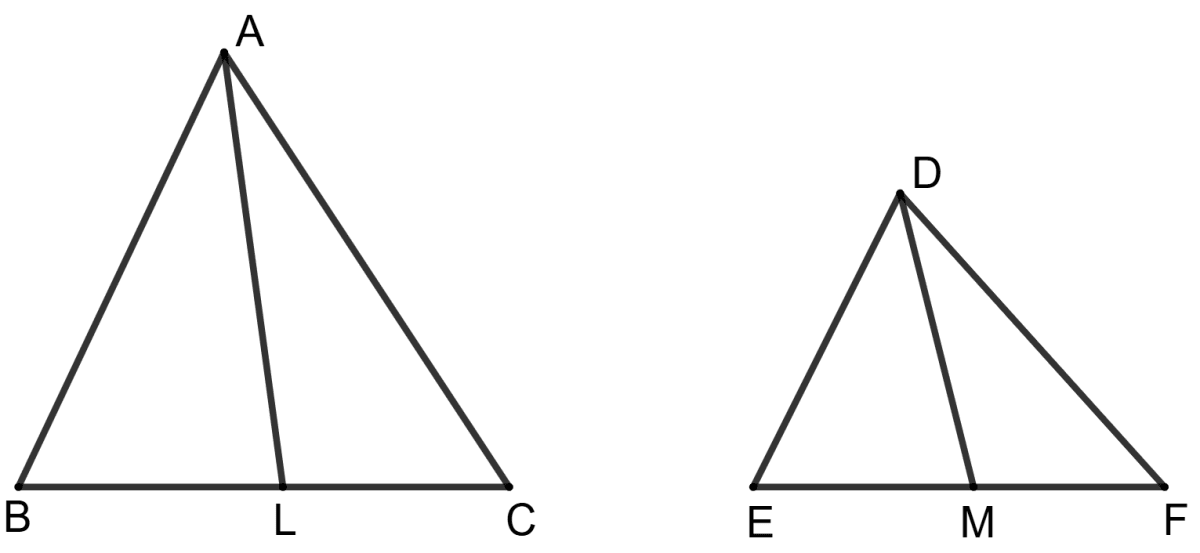
In triangle ABC and DEF, ∠A = ∠D, ∠B = ∠E and ∠C = ∠F. Also, AL and DM are medians. Prove that BC/EF = AL/DM. Concise Mathematics Solutions ICSE Class 10.

Answer

In Δ ABC and Δ DEF,

⇒ ∠A = ∠D (Given)

⇒ ∠B = ∠E (Given)

⇒ ∠C = ∠F (Given)

∴ Δ ABC ∼ Δ DEF (By AAA postulate)

Since, AL and DM are medians of triangles ABC and DEF respectively.

∴ BL = $\dfrac{1}{2}BC$ and EM = $\dfrac{1}{2}EF$

We know that,

Corresponding sides of similar triangles are proportional.

$\therefore \dfrac{AB}{DE} = \dfrac{BC}{EF}....................(1)\\[1em] \Rightarrow \dfrac{AB}{DE} = \dfrac{\dfrac{1}{2}BC}{\dfrac{1}{2}EF}\\[1em] \Rightarrow \dfrac{AB}{DE} = \dfrac{BL}{EM} .........................(2)$

In Δ ABL and Δ DEM,

⇒ ∠B = ∠E (Given)

⇒ $\dfrac{AB}{DE} = \dfrac{BL}{EM}$ [From equation (2)]

∴ Δ ABL ∼ Δ DEM (By SAS postulates)

As, corresponding sides of similar triangles are proportional.

$\therefore \dfrac{AB}{DE} = \dfrac{AL}{DM}$ .........(3)

From equation (1) and (3), we get :

$\Rightarrow \dfrac{\text{BC}}{\text{EF}} = \dfrac{\text{AL}}{\text{DM}}$

Hence, proved that $\dfrac{\text{BC}}{\text{EF}} = \dfrac{\text{AL}}{\text{DM}}$

Question 4

In triangle ABC, AD is perpendicular to side BC and AD² = BD × CD.

Show that angle BAC = 90°.

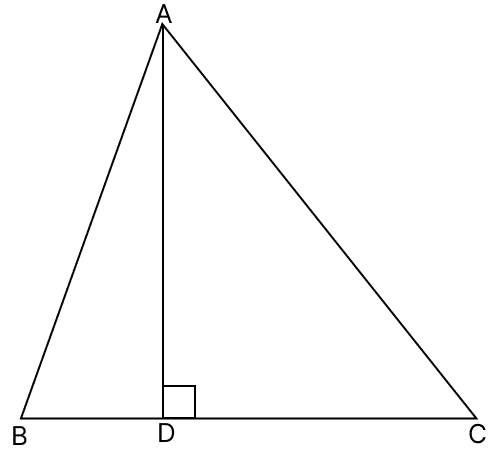
Answer

Triangle ABC is shown in the figure below:

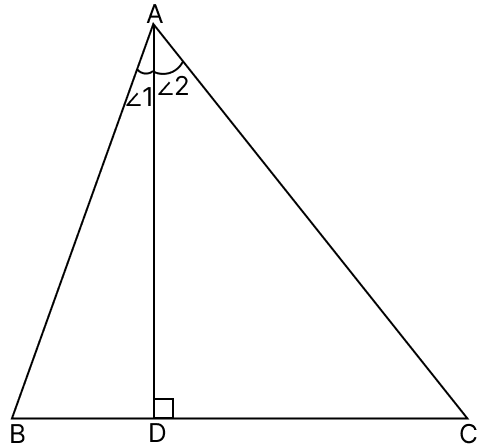
Given :

AD² = BD × DC

⇒ $\dfrac{AD}{DC} = \dfrac{BD}{AD}$

∠ADB = ∠ADC [Both = 90°]

∴ △DBA ~ △DAC (By SAS).

Since, triangles are similar they will be equiangular.

∴ ∠1 = ∠C and ∠2 = ∠B

⇒ ∠1 + ∠2 = ∠B + ∠C

⇒ ∠A = ∠B + ∠C

By angle sum property :

⇒ ∠A + ∠B + ∠C = 180°

⇒ ∠A + ∠A = 180°

⇒ 2∠A = 180°

⇒ ∠A = 90°.

From figure,

⇒ ∠BAC = ∠A = 90°.

Hence, proved that ∠BAC = 90°.

Question 5

In the given figure, Δ ABC and Δ DEF are similar, BM and EN are their medians. If Δ ABC is similar to Δ DEF, prove that :

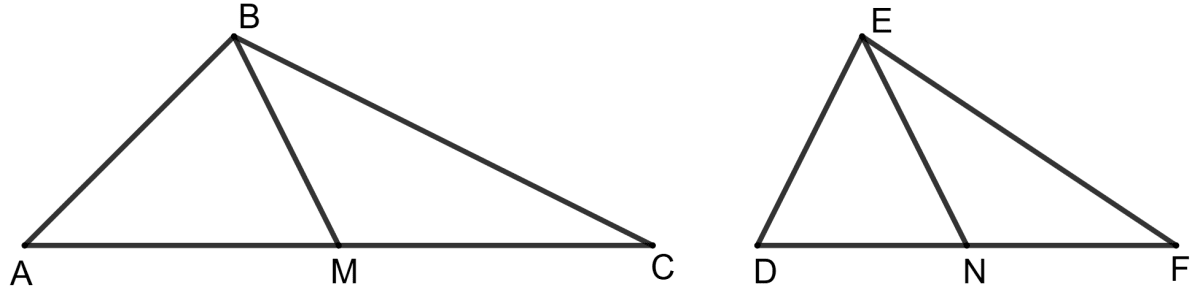
(i) Δ AMB ∼ Δ DNE

(ii) Δ CMB ∼ Δ FNE

(iii) $\dfrac{BM}{EN} = \dfrac{AC}{DF}$

Answer

(i) Given,

Since, BM and EN are medians of triangles ABC and DEF respectively.

∴ AM = $\dfrac{1}{2}AC$ and DN = $\dfrac{1}{2}DF$

Given,

Δ ABC ∼ Δ DEF

∴ ∠A = ∠D (Corresponding angles of similar triangles are equal)

We know that,

Corresponding sides of similar triangles are proportional.

$\therefore \dfrac{AB}{DE} = \dfrac{AC}{DF} ....................(1)\\[1em] \Rightarrow \dfrac{AB}{DE} = \dfrac{\dfrac{1}{2}AC}{\dfrac{1}{2}DF}\\[1em] \Rightarrow \dfrac{AB}{DE} = \dfrac{AM}{DN} .........................(2)$

In Δ AMB and Δ DNE,

⇒ ∠A = ∠D (Proved above)

⇒ $\dfrac{AB}{DE} = \dfrac{AM}{DN}$ [From equation (2)]

∴ Δ AMB ∼ Δ DNE (By SAS postulate)

Hence, proved that Δ AMB ∼ Δ DNE.

(ii) Given,

Since, BM and EN are medians of triangles ABC and DEF respectively.

∴ MC = $\dfrac{1}{2}AC$ and NF = $\dfrac{1}{2}DF$

Given,

Δ ABC ∼ Δ DEF

⇒ ∠C = ∠F (Corresponding angles of similar triangles are equal)

Since, corresponding sides of similar triangles are proportional.

$\therefore \dfrac{BC}{EF} = \dfrac{AC}{DF} ....................(3)\\[1em] \Rightarrow \dfrac{BC}{EF} = \dfrac{\dfrac{1}{2}AC}{\dfrac{1}{2}DF}\\[1em] \Rightarrow \dfrac{BC}{EF} = \dfrac{MC}{NF} .........................(4)$

In Δ CMB and Δ FNE,

⇒ ∠C = ∠F (Proved above)

⇒ $\dfrac{BC}{EF} = \dfrac{MC}{NF}$ [From equation (4)]

∴ Δ CMB ∼ Δ FNE (By SAS postulate)

Hence, proved that Δ CMB ∼ Δ FNE.

(iii) Given,

Δ ABC ∼ Δ DEF

We know that,

Corresponding sides of similar triangles are proportional.

$\therefore \dfrac{AB}{DE} = \dfrac{AC}{DF}$ .......(5)

Δ AMB ∼ Δ DNE

We know that,

Corresponding sides of similar triangles are proportional.

$\therefore \dfrac{BM}{EN} = \dfrac{AB}{DE}$ ......(6)

From equation (5) and (6), we get :

$\Rightarrow \dfrac{BM}{EN} = \dfrac{AC}{DF}$

Hence, proved that $\dfrac{BM}{EN} = \dfrac{AC}{DF}$ .

Question 6

In the given figure, Δ ABC is isosceles and AP x BQ = AC², prove that Δ ACP ∼ Δ BCQ.

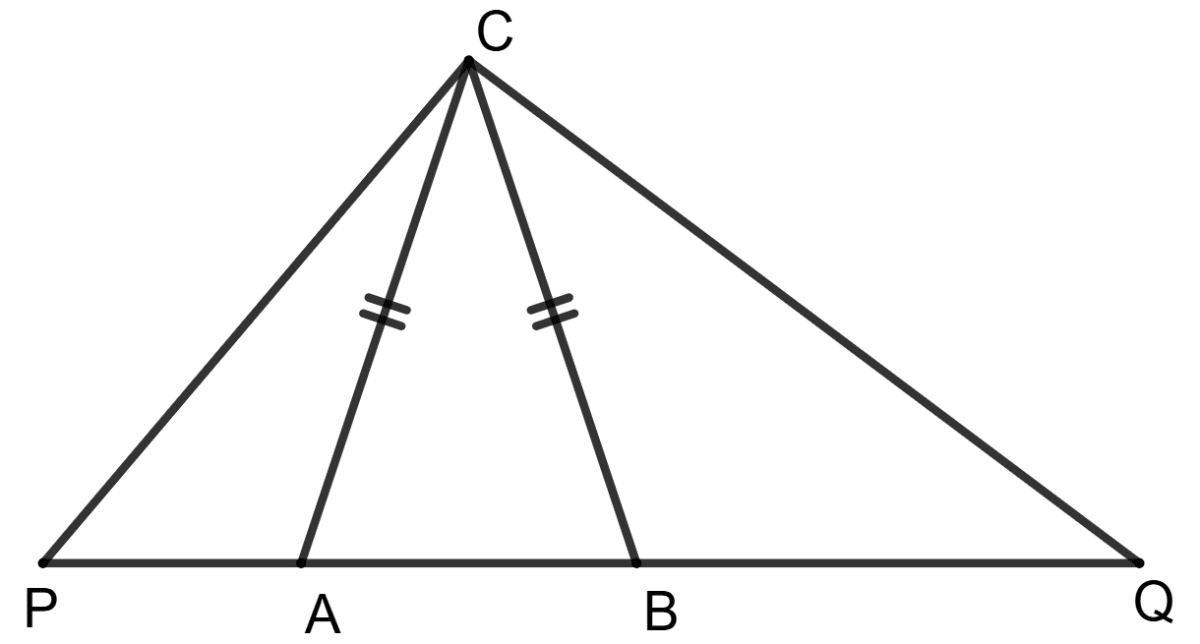
Answer

Given,

⇒ AP x BQ = AC²

⇒ AP x BQ = AC x AC

⇒ AP x BQ = AC x BC (From figure, AC = BC)

⇒ $\dfrac{AP}{BC} = \dfrac{AC}{BQ}$ ........................(1)

Since, AC = BC

⇒ ∠CAB = ∠CBA ...............(2) [Angles opposite to equal sides are equal]

⇒ 180° - ∠CAB = 180° - ∠CBA

⇒ ∠CAP = ∠CBQ ...................(3)

In Δ ACP and Δ BCQ,

⇒ ∠CAP = ∠CBQ [From equation (3)]

⇒ $\dfrac{AP}{BC} = \dfrac{AC}{BQ}$ [From equation (1)]

∴ Δ ACP ∼ Δ BCQ (By SAS postulates)

Hence, proved that Δ ACP ∼ Δ BCQ.

Exercise 15(B)

Question 1(a)

In triangle ABC, ∠BAC = 90° and AD is perpendicular to side BC. Triangle ABD is similar to triangle CBA by :

Answer

In △ CBA and △ ABD,

In triangle ABC, ∠BAC = 90° and AD is perpendicular to side BC. Triangle ABD is similar to triangle CBA by : Similarity, Concise Mathematics Solutions ICSE Class 10.

⇒ ∠CAB = ∠ADB (Both equal to 90°)

⇒ ∠CBA = ∠DBA (Common angles)

Since, two angles of two triangles are equal so third angle of both the triangle will also be equal.

⇒ ∠ACB = ∠DAB.

∴ △ CBA ~ △ ABD (By A.A.A. postulate)

Hence, Option 3 is the correct option.

Question 1(b)

If AE = 10 cm, BD = 8 cm and BC = 10 cm, then AB is equal to :

5 cm
25 cm
12.5 cm
2.5 cm

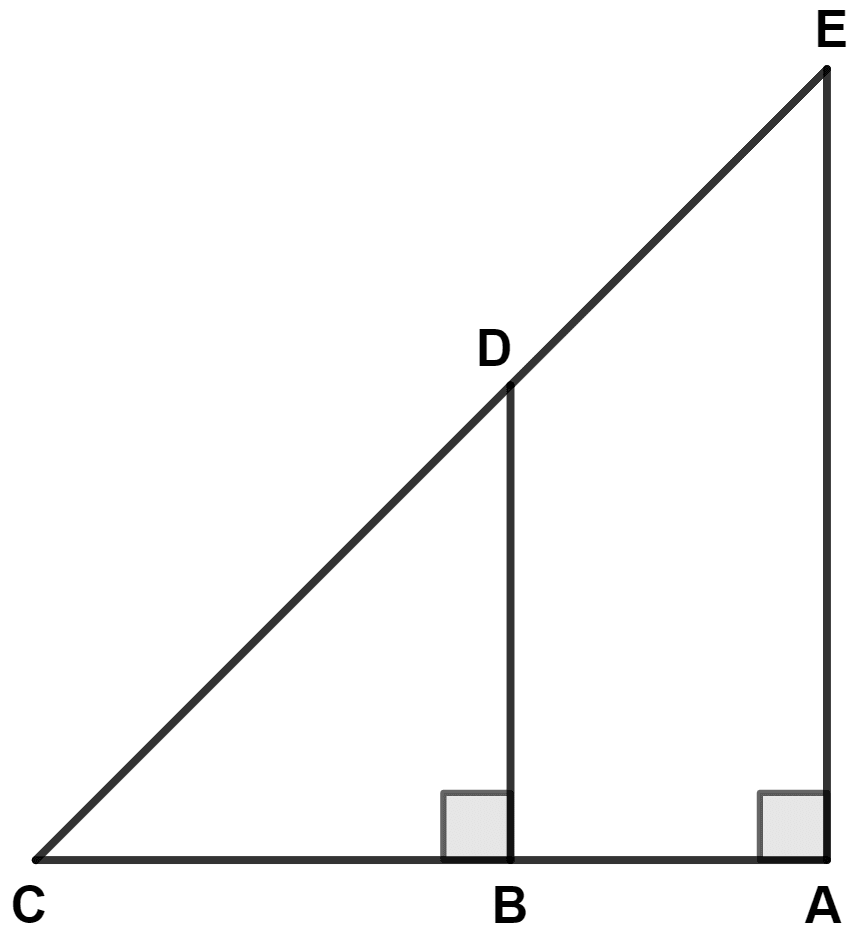
Answer

From figure,

In △ ACE and △ BCD,

⇒ ∠CAE = ∠CBD (Both equal to 90°)

⇒ ∠ACE = ∠BCD (Common angles)

Since, two angles of two triangles are equal so third angle of both the triangle will also be equal.

⇒ ∠CEA = ∠CDB.

∴ △ ACE ~ △ BCD (By A.A.A. postulate)

We know that,

Corresponding sides of similar triangle are in proportion.

$\therefore \dfrac{AC}{BC} = \dfrac{AE}{BD} \\[1em] \Rightarrow \dfrac{AC}{10} = \dfrac{10}{8} \\[1em] \Rightarrow AC = \dfrac{100}{8} = 12.5 \text{ cm}.$

From figure,

AB = AC - BC = 12.5 - 10 = 2.5 cm.

Hence, Option 4 is the correct option.

Question 1(c)

In the given figure :

△ ABE ~ △ ADE
△ ADE ~ △ ABC
△ ADE ~ △ BAC
△ ADE ~ △ CAB

Answer

From figure,

⇒ ∠BAE = x (let)

⇒ ∠DAB = ∠EAC = y (let)

⇒ ∠AED = ∠ACB = z (let)

⇒ ∠DAE = ∠DAB + ∠BAE = y + x

⇒ ∠BAC = ∠BAE + ∠EAC = x + y

⇒ ∠DAE = ∠BAC = x + y

In △ ABC and △ ADE,

⇒ ∠DAE = ∠BAC (Proved above)

⇒ ∠AED = ∠ACB (Both equal to z)

∴ △ ADE ~ △ ABC (By A.A. axiom)

Hence, Option 2 is the correct option.

Question 1(d)

The value of x is :

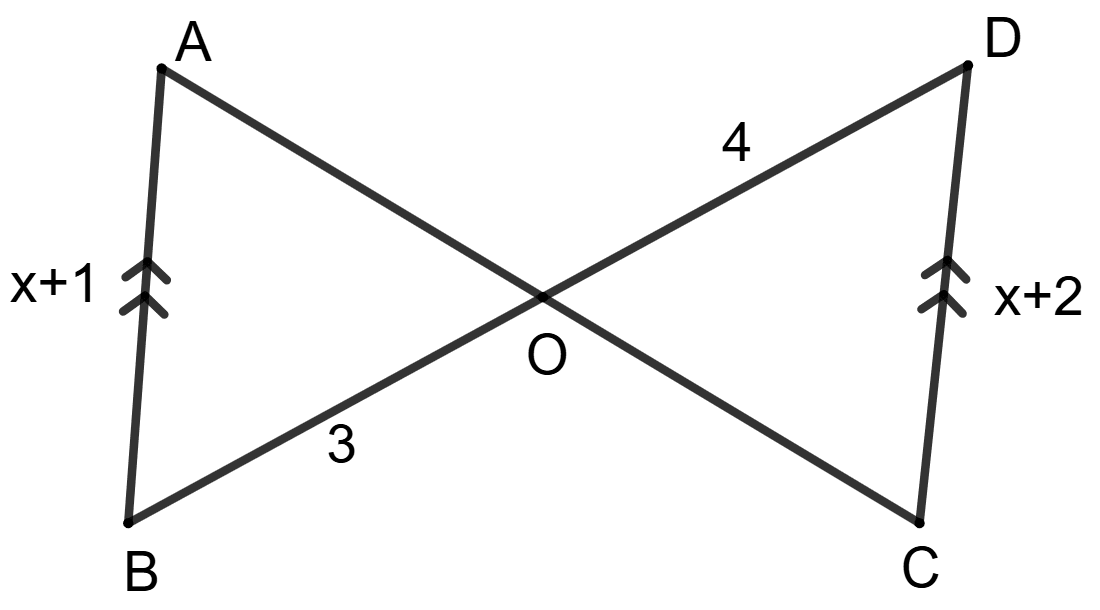
2
3
1
none of these

Answer

In Δ AOB and Δ DOC

⇒ ∠AOB = ∠DOC (Vertically opposite angles are equal)

⇒ ∠BAO = ∠DCO (Corresponding angles are equal)

⇒ ∠ABO = ∠CDO (Corresponding angles since AB ∥ CD and BD is a transversal)

∴ Δ AOB ∼ Δ COD (By AAA postulates)

We know that,

Corresponding sides of similar triangles are proportional.

$\therefore \dfrac{OB}{OD} = \dfrac{AB}{CD}\\[1em] \Rightarrow \dfrac{3 }{4} = \dfrac{x + 1}{x + 2}\\[1em] \Rightarrow 3(x + 2) = 4(x + 1)\\[1em] \Rightarrow 3x + 6 = 4x + 4\\[1em] \Rightarrow 4x - 3x = 6 - 4\\[1em] \Rightarrow x = 2\\[1em]$

Hence, option 1 is the correct option.

Question 2

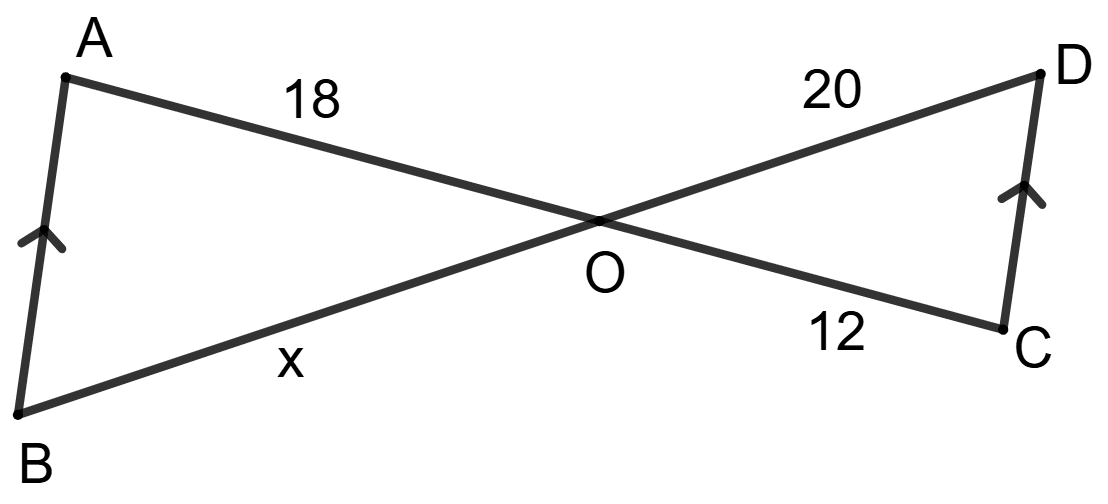
In the figure, given below, straight lines AB and CD intersect at P; and AC || BD. Prove that:

(i) ∆APC and ∆BPD are similar.

(ii) If BD = 2.4 cm, AC = 3.6 cm, PD = 4.0 cm and PB = 3.2 cm; find the lengths of PA and PC.

Answer

(i) In ∆APC and ∆BPD, we have

∠APC = ∠BPD [Vertically opposite angles are equal]

∠ACP = ∠BDP [Alternate angles (as, AC || BD) are equal]

∴ ∆APC ~ ∆BPD [By A.A.]

Hence, proved that ∆APC ~ ∆BPD.

(ii) In similar triangles the ratio of corresponding sides are equal.

$\dfrac{\text{AC}}{\text{BD}} = \dfrac{\text{PA}}{\text{PB}}$ ..............(1) and,

$\dfrac{\text{AC}}{\text{BD}} = \dfrac{\text{PC}}{\text{PD}}$ ...............(2)

Solving (1) we get,

$\Rightarrow \dfrac{\text{AC}}{\text{BD}} = \dfrac{\text{PA}}{\text{PB}} \\[1em] \Rightarrow \dfrac{3.6}{2.4} = \dfrac{\text{PA}}{3.2} \\[1em] \Rightarrow \text{PA} = \dfrac{3.6}{2.4} \times 3.2 \\[1em] \Rightarrow \text{PA} = \dfrac{3}{2} \times 3.2 \\[1em] \Rightarrow \text{PA} = 4.8 \text{ cm}.$

Solving (2) we get,

$\Rightarrow \dfrac{\text{AC}}{\text{BD}} = \dfrac{\text{PC}}{\text{PD}} \\[1em] \Rightarrow \dfrac{3.6}{2.4} = \dfrac{\text{PC}}{4} \\[1em] \Rightarrow \text{PC} = \dfrac{3.6}{2.4} \times 4 \\[1em] \Rightarrow \text{PC} = \dfrac{3}{2} \times 4 \\[1em] \Rightarrow \text{PC} = 6 \text{ cm}.$

Hence, PA = 4.8 cm and PC = 6 cm.

Question 3

In the given figure, AB || DC, BO = 6 cm and DQ = 8 cm; find: BP x DO.

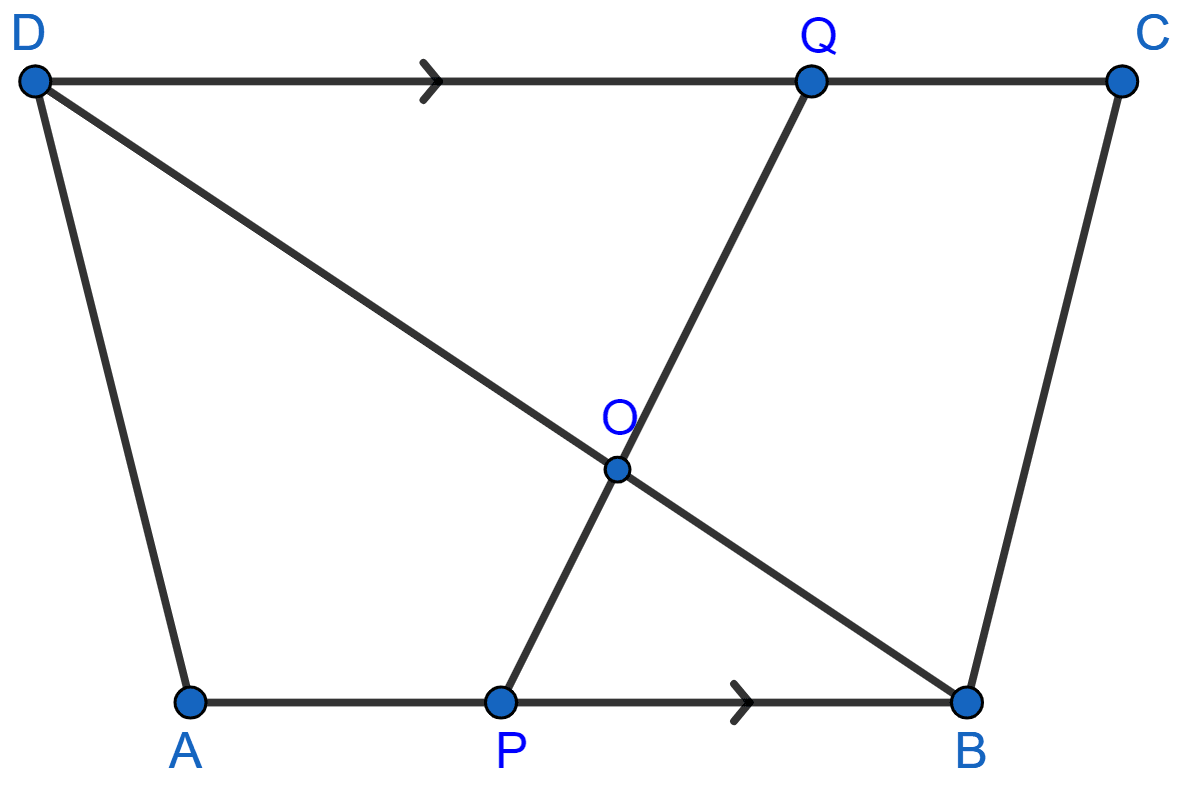
In the figure, AB || DC, BO = 6 cm and DQ = 8 cm; find: BP x DO. Similarity, Concise Mathematics Solutions ICSE Class 10.

Answer

In ΔDOQ and ΔBOP,

As AB || DC so, PB || DQ and BD is transversal.

∴ ∠QDO = ∠PBO [Alternate angles]

∠DOQ = ∠BOP [Vertically opposite angles are equal]

Hence, ∆DOQ ~ ∆BOP [By AA]

Since, corresponding sides of similar triangles are proportional we have :

$\Rightarrow \dfrac{DO}{BO} = \dfrac{DQ}{BP} \\[1em] \Rightarrow \dfrac{DO}{6} = \dfrac{8}{BP} \\[1em] \Rightarrow BP \times DO = 8 \times 6 = 48 \text{ cm}^2. \\[1em]$

Hence, BP x DO = 48 cm².

Question 4

In ΔABC, BM ⊥ AC and CN ⊥ AB; show that:

$\dfrac{AB}{AC} = \dfrac{BM}{CN} = \dfrac{AM}{AN}$

Answer

ΔABC is shown in the figure below:

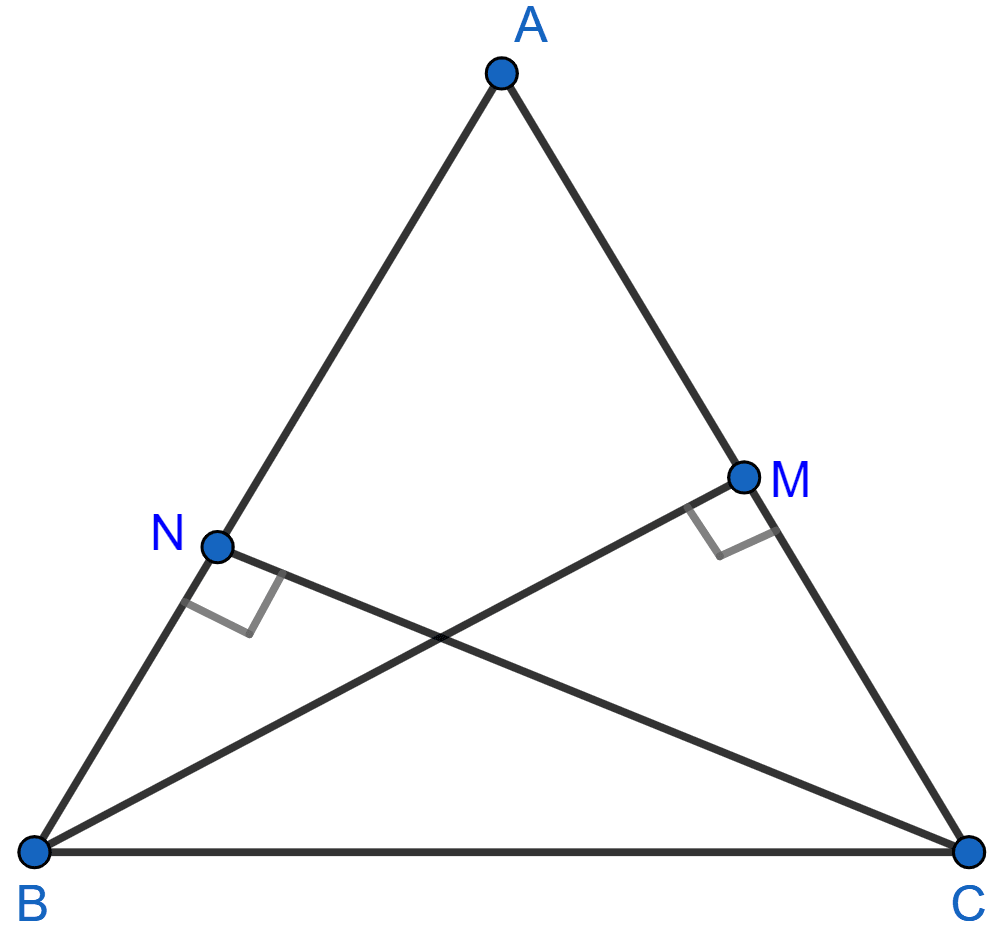
In ΔABC, BM ⊥ AC and CN ⊥ AB; show that: AB/AC = BM/CN = AM/AN. Similarity, Concise Mathematics Solutions ICSE Class 10.

In ΔABM and ΔACN,

∠AMB = ∠ANC [Since, BM ⊥ AC and CN ⊥ AB]

∠BAM = ∠CAN [Common angle]

∴ ∆ABM ~ ∆ACN [By A.A.]

Since corresponding sides of similar triangles are proportional we have,

⇒ $\dfrac{AB}{AC} = \dfrac{BM}{CN} = \dfrac{AM}{AN}$

Hence, proved that $\dfrac{AB}{AC} = \dfrac{BM}{CN} = \dfrac{AM}{AN}$ .

Question 5

Given: ∠GHE = ∠DFE = 90°, DH = 8, DF = 12, DG = 3x – 1 and DE = 4x + 2.

Find: the lengths of segments DG and DE.

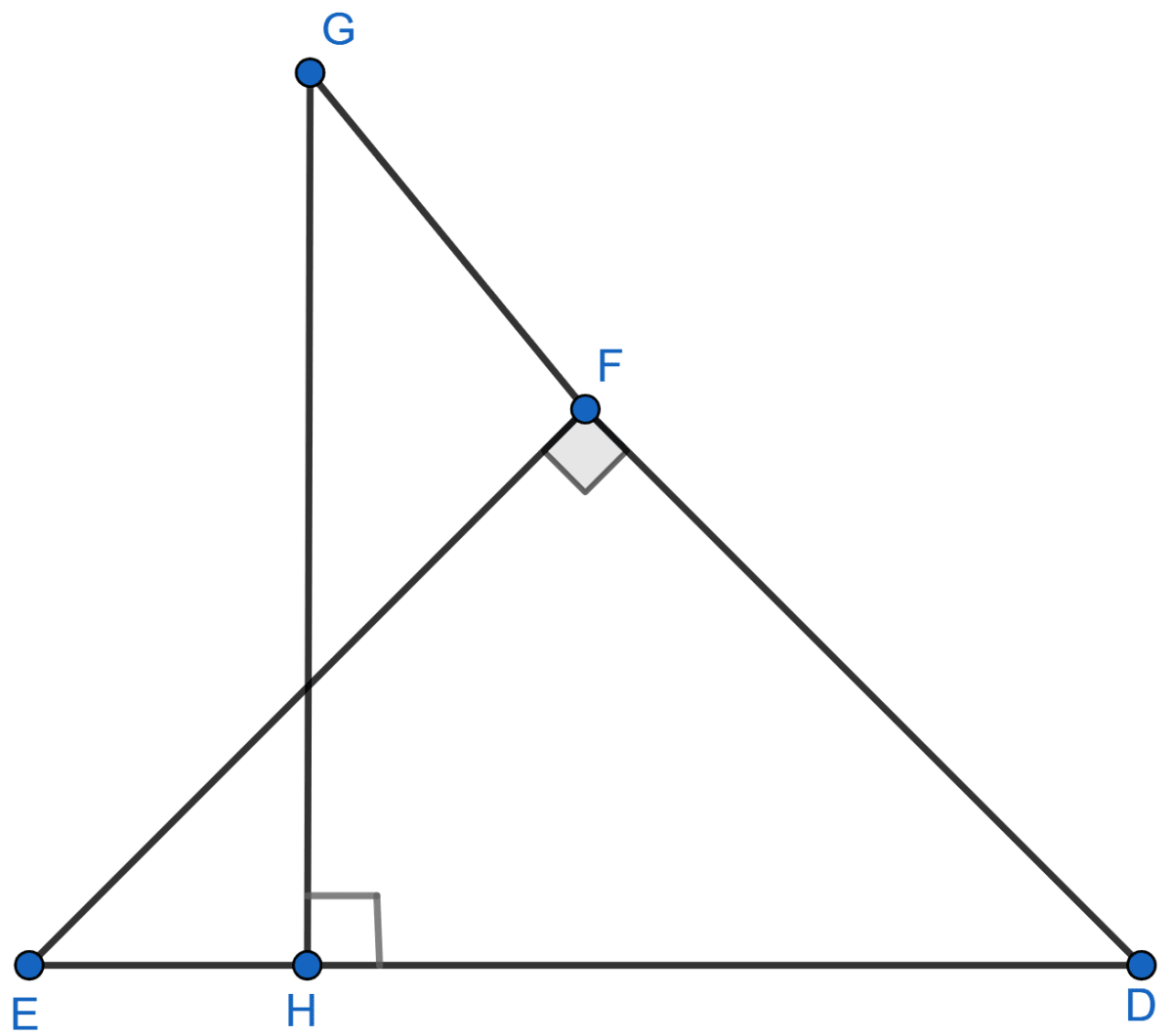
Answer

In ΔDHG and ΔDFE,

⇒ ∠GHD = ∠DFE = 90°

⇒ ∠D = ∠D [Common]

Thus, ∆DHG ~ ∆DFE [By AA]

Since, corresponding sides of similar triangles are proportional we have :

$\Rightarrow \dfrac{DH}{DF} = \dfrac{DG}{DE} \\[1em] \Rightarrow \dfrac{8}{12} = \dfrac{(3x – 1)}{(4x + 2)} \\[1em] \Rightarrow 8(4x + 2) = 12(3x – 1) \\[1em] \Rightarrow 32x + 16 = 36x - 12 \\[1em] \Rightarrow 36x - 32x = 12 + 16 \\[1em] \Rightarrow 4x = 28 \\[1em] \Rightarrow x = 7.$

DG = 3x - 1 = 3(7) - 1 = 21 - 1 = 20,

DE = 4x + 2 = 4(7) + 2 = 28 + 2 = 30.

Hence, DG = 20 and DE = 30.

Question 6

In △PQR, ∠Q = 90° and QM is perpendicular to PR. Prove that :

(i) PQ² = PM × PR

(ii) QR² = PR × MR

(iii) PQ² + QR² = PR²

Answer

△PQR is shown in the figure below:

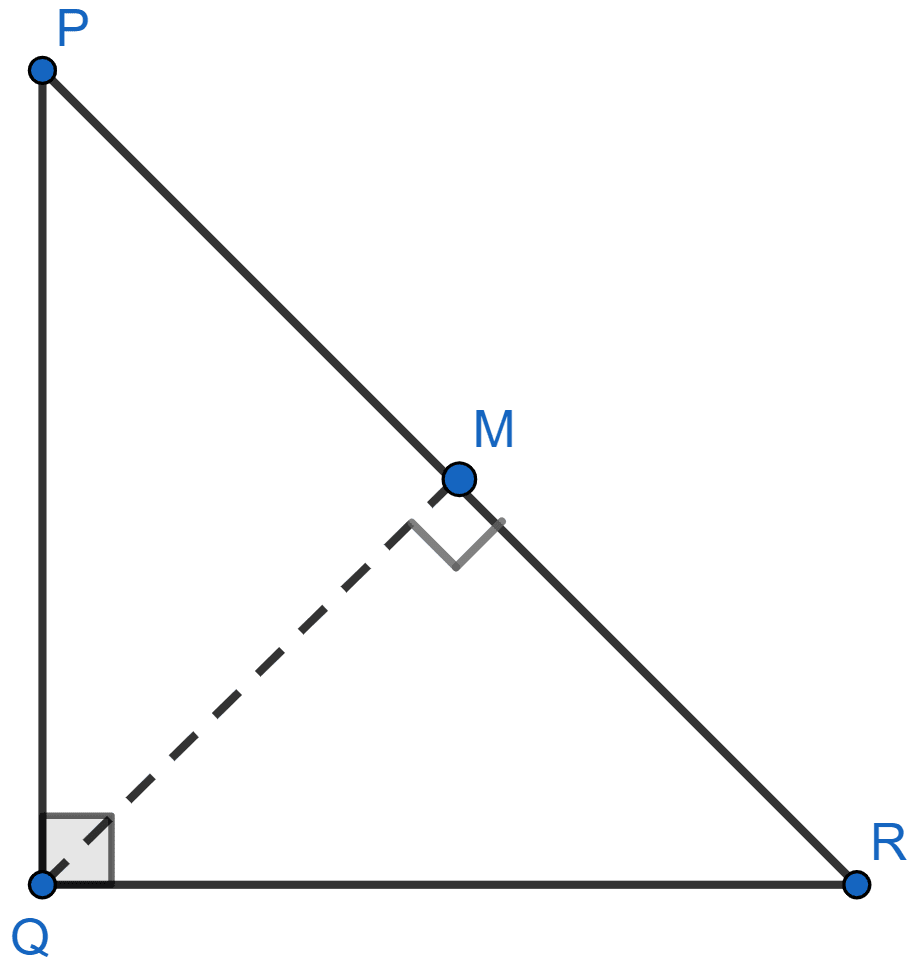
In △PQR, ∠Q = 90° and QM is perpendicular to PR. Prove that (i) PQ^2 = PM × PR (ii) QR^2 = PR × MR (iii) PQ^2 + QR^2 = PR^2. Similarity, Concise Mathematics Solutions ICSE Class 10.

(i) In △PQR and △PMQ,

⇒ ∠PMQ = ∠PQR [Both = 90°]

⇒ ∠QPM = ∠RPQ [Common]

∴ △PQR ~ △PMQ [By AA]

Since, corresponding sides of similar triangles are proportional we have :

⇒ $\dfrac{PQ}{PR} = \dfrac{PM}{PQ}$

⇒ PQ² = PM × PR

Hence, proved that PQ² = PM × PR.

(ii) In △QRM and △PRQ,

⇒ ∠QMR = ∠PQR [Both = 90°]

⇒ ∠QRM = ∠QRP [Common]

∴ △QRM ~ △PRQ [By AA]

Since, corresponding sides of similar triangles are proportional we have :

⇒ $\dfrac{QR}{PR} = \dfrac{MR}{QR}$

⇒ QR² = PR × MR

Hence, proved that QR² = PR × MR.

(iii) Adding equations from (i) and (ii) we get,

⇒ PQ² + QR² = PM × PR + PR × MR .........(1)

⇒ PQ² + QR² = PR(PM + MR)

From figure,

PM + MR = PR

⇒ PQ² + QR² = PR².

Hence, proved that PQ² + QR² = PR².

Question 7

In △ABC, ∠B = 90° and BD ⊥ AC.

(i) If CD = 10 cm and BD = 8 cm; find AD.

(ii) If AC = 18 cm and AD = 6 cm; find BD.

(iii) If AC = 9 cm and AB = 7 cm; find AD.

Answer

△ABC is shown in the figure below:

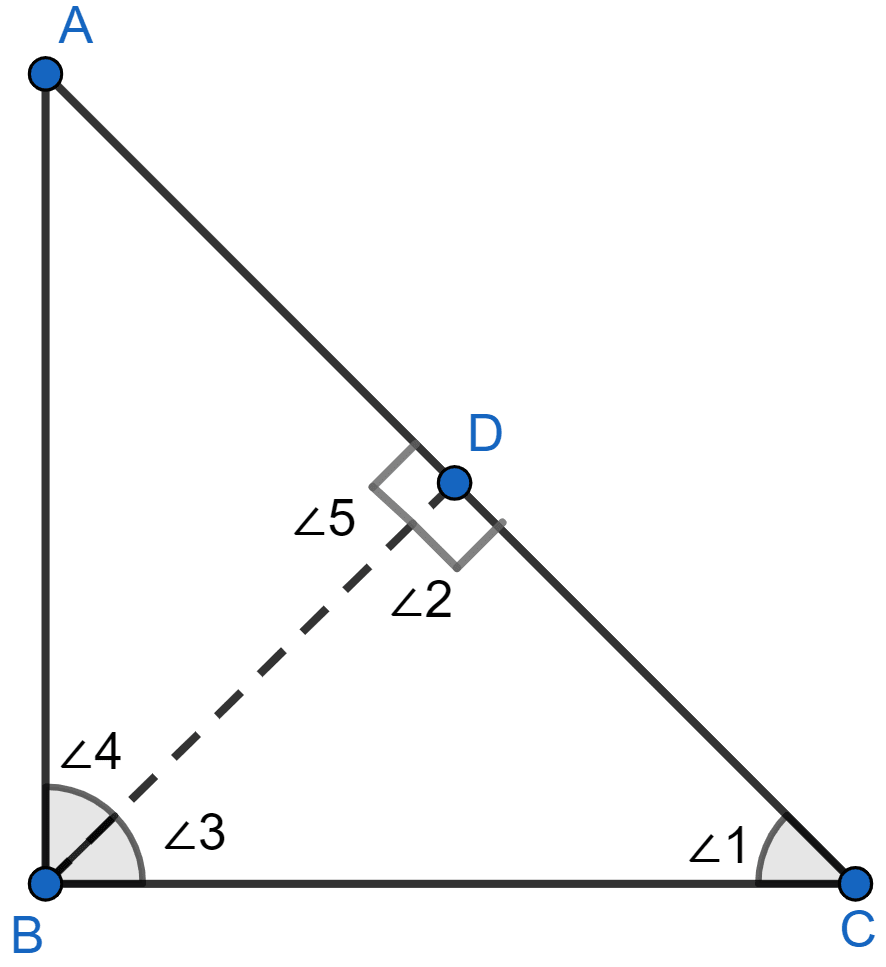
In △ABC, ∠B = 90° and BD ⊥ AC. (i) If CD = 10 cm and BD = 8 cm; find AD. (ii) If AC = 18 cm and AD = 6 cm; find BD. Similarity, Concise Mathematics Solutions ICSE Class 10.

(i) In △CDB,

⇒ ∠1 + ∠2 + ∠3 = 180° (Sum of angles of triangle = 180°)

⇒ ∠1 + ∠3 + 90° = 180°

⇒ ∠1 + ∠3 = 90° ..........(1)

From figure,

⇒ ∠B = 90°

⇒ ∠3 + ∠4 = 90° ..........(2)

From (1) and (2) we get,

⇒ ∠1 + ∠3 = ∠3 + ∠4

⇒ ∠1 = ∠4.

From figure,

⇒ ∠2 = ∠5 [Both = 90°]

∴ △CDB ~ △BDA [By AA]

Since, corresponding sides of similar triangles are proportional we have :

$\dfrac{CD}{BD} = \dfrac{BD}{AD}$ ..........(3)

Substituting values we get :

$\Rightarrow \dfrac{10}{8} = \dfrac{8}{AD} \\[1em] \Rightarrow AD = \dfrac{8^2}{10} \\[1em] \Rightarrow AD = \dfrac{64}{10} = 6.4 \text{ cm}.$

Hence, AD = 6.4 cm.

(ii) From figure,

CD = AC - AD = 18 - 6 = 12 cm.

Substituting values in (3) we get :

$\Rightarrow \dfrac{12}{BD} = \dfrac{BD}{6} \\[1em] \Rightarrow BD^2 = 12 \times 6 \\[1em] \Rightarrow BD^2 = 72 \\[1em] \Rightarrow BD = \sqrt{72} = 6\sqrt{2} = 8.5\text{ cm}.$

Hence, BD = 8.5 cm.

(iii) In △ABC and △ABD,

⇒ ∠ADB = ∠ABC [Both = 90°]

⇒ ∠ABD = ∠ACB [As ∠1 = ∠4]

∴ △ABC ~ △ABD [By AA]

Since, corresponding sides of similar triangles are proportional we have :

$\Rightarrow \dfrac{AD}{AB} = \dfrac{AB}{AC} \\[1em] \Rightarrow \dfrac{AD}{7} = \dfrac{7}{9} \\[1em] \Rightarrow AD = 7 \times \dfrac{7}{9} = \dfrac{49}{9} = 5\dfrac{4}{9} \text{ cm}.$

Hence, AD = $5\dfrac{4}{9}$ cm.

Question 8

In the right-angled triangle QPR. PM is an altitude.

Given that QR = 8 cm and MQ = 3.5 cm, calculate the value of PR.

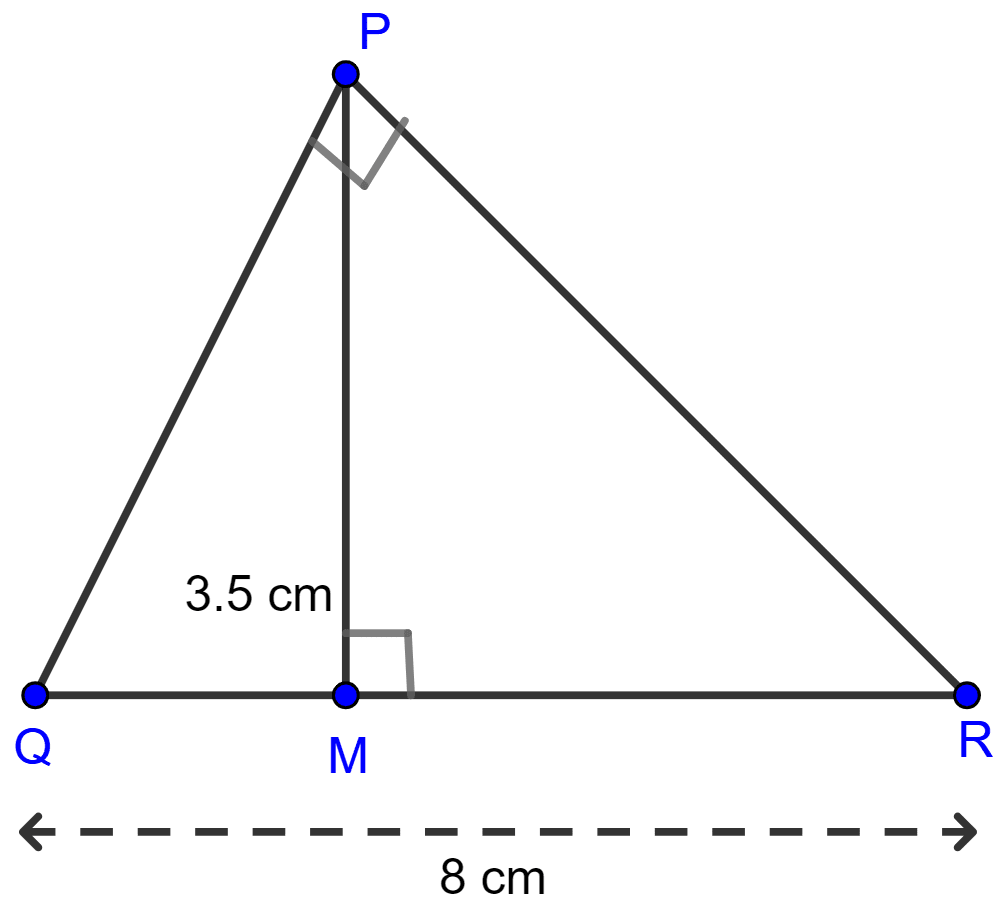
Answer

In △PQR and △MPR,

∠QPR = ∠PMR = 90°

∠PRQ = ∠PRM (Common)

∴ △PQR ~ △MPR [By AA]

Since, corresponding sides of similar triangle are proportional to each other.

$\therefore \dfrac{QR}{PR} = \dfrac{PR}{MR} \\[1em] \Rightarrow PR^2 = QR \times MR \\[1em] \Rightarrow PR^2 = 8 \times (8 - 3.5) \\[1em] \Rightarrow PR^2 = 8 \times 4.5 = 36 \\[1em] \Rightarrow PR = \sqrt{36} = 6 \text{ cm}.$

Hence, PR = 6 cm.

Exercise 15(C)

Question 1(a)

In the given figure, OD = 2 × OB, OC = 2 × OA and CD = 2 × AB then △ AOB ~ △ COD by :

Answer

Given,

⇒ OD = 2 × OB

⇒ $\dfrac{OD}{OB}$ = 2 .......(1)

⇒ OC = 2 × OA

⇒ $\dfrac{OC}{OA}$ = 2 .......(2)

⇒ CD = 2 × AB

⇒ $\dfrac{CD}{AB}$ = 2 .......(3)

From equation (1), (2) and (3), we get :

⇒ $\dfrac{OD}{OB} = \dfrac{OC}{OA} = \dfrac{CD}{AB}$

∴ △ AOB ~ △ COD (By S.S.S. postulate)

Hence, Option 4 is the correct option.

Question 1(b)

Are the two congruent triangles always similar?

yes
no
none of these

Answer

Two congruent triangles have equal corresponding angles, and equal corresponding sides (same lengths).

Two similar triangles only require equal corresponding angles and proportional corresponding sides (not necessarily equal).

Hence, option 1 is the correct option.

Question 1(c)

If $\dfrac{\text{AB}}{\text{DE}} = \dfrac{\text{BC}}{\text{EF}} = \dfrac{\text{AC}}{\text{DF}}$ , then :

Δ ABC ∼ Δ EDF
Δ ABC ∼ Δ DEF
Δ ABC ∼ Δ FDE
none of these

Answer

In Δ ABC and Δ DEF,

$\dfrac{\text{AB}}{\text{DE}} = \dfrac{\text{BC}}{\text{EF}} = \dfrac{\text{AC}}{\text{DF}}$

From above equation, we can conclude

AB corresponds to DE, BC corresponds to EF and AC corresponds to DF.

∴ Δ ABC ∼ Δ DEF (By SSS postulates)

Hence, option 2 is the correct option.

Question 1(d)

If Δ ABC ∼ Δ DEF, then

$\dfrac{\text{AB}}{\text{EF}} = \dfrac{\text{AC}}{\text{DF}}$
$\dfrac{\text{AB}}{\text{DE}} = \dfrac{\text{BC}}{\text{DF}}$
$\dfrac{\text{AC}}{\text{DF}} = \dfrac{\text{AB}}{\text{DE}}$
$\dfrac{\text{BC}}{\text{EF}} = \dfrac{\text{AC}}{\text{DE}}$

Answer

$\dfrac{\text{AC}}{\text{DF}} = \dfrac{\text{AB}}{\text{DE}}$

Reason

In Δ ABC ∼ Δ DEF, we can conclude :

AB corresponds to DE, BC corresponds to EF and AC corresponds to DF.

We know that,

Corresponding sides of similar triangles are equal.

$\therefore \dfrac{\text{AB}}{\text{DE}} = \dfrac{\text{BC}}{\text{EF}} = \dfrac{\text{AC}}{\text{DF}} \\[1em] \Rightarrow \dfrac{AB}{DE} = \dfrac{AC}{DF}.$

Hence, option 3 is the correct option.

Question 2

Sides AB, BC and median AD of the triangle ABC are respectively proportional to sides PQ, QR and median PM of triangle PQR.

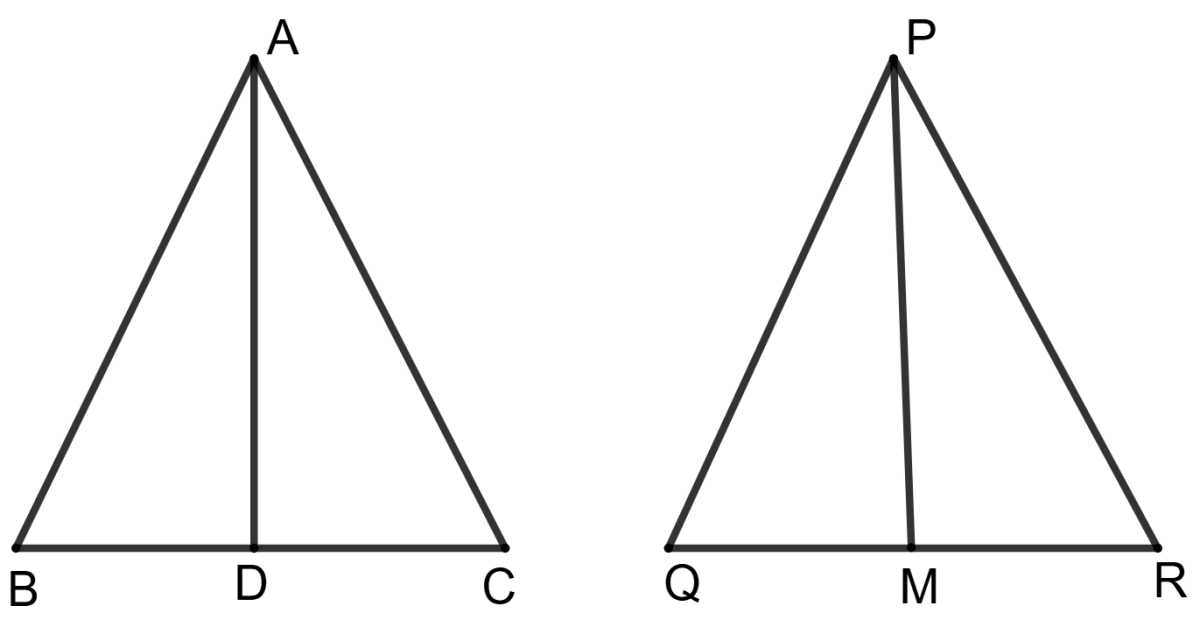
Prove that:

(i) Δ ABD ∼ Δ PQM

(ii) Δ ABC ∼ Δ PQR

Answer

(i) Given, AB, BC and median AD of the triangle ABC are respectively proportional to sides PQ, QR and median PM of triangle PQR.

$\dfrac{\text{AB}}{\text{PQ}} = \dfrac{\text{BC}}{\text{QR}} = \dfrac{\text{AD}}{\text{PM}}$

AD is median of triangle ABC.

∴ BD = DC = $\dfrac{1}{2}$ BC

PM is median of triangle PQR.

∴ QM = RM = $\dfrac{1}{2}$ QR

In Δ ABD and Δ PQM,

$\Rightarrow \dfrac{\text{AB}}{\text{PQ}} = \dfrac{\text{BC}}{\text{QR}} = \dfrac{\text{AD}}{\text{PM}}\\[1em] \Rightarrow \dfrac{\text{AB}}{\text{PQ}} = \dfrac{\dfrac{1}{2}\text{BC}}{\dfrac{1}{2}\text{QR}} = \dfrac{\text{AD}}{\text{PM}}\\[1em] \Rightarrow \dfrac{\text{AB}}{\text{PQ}} = \dfrac{BD}{QM} = \dfrac{\text{AD}}{\text{PM}}\\[1em]$

∴ Δ ABD ∼ Δ PQM (By SSS postulates)

Hence, Δ ABD ∼ Δ PQM.

(ii) From (i), Δ ABD ∼ Δ PQM

Corresponding angles of similar triangles are equal.

∴ ∠ABD = ∠PQM ................(1)

In Δ ABC and Δ PQR,

⇒ ∠ABC = ∠PQR [From equation (1)]

$\Rightarrow \dfrac{\text{AB}}{\text{PQ}} = \dfrac{\text{BC}}{\text{QR}}$

∴ Δ ABC ∼ Δ PQR (By SAS postulate)

Hence, Δ ABC ∼ Δ PQR.

Question 3

Find the value of x, if ∠B = ∠E.

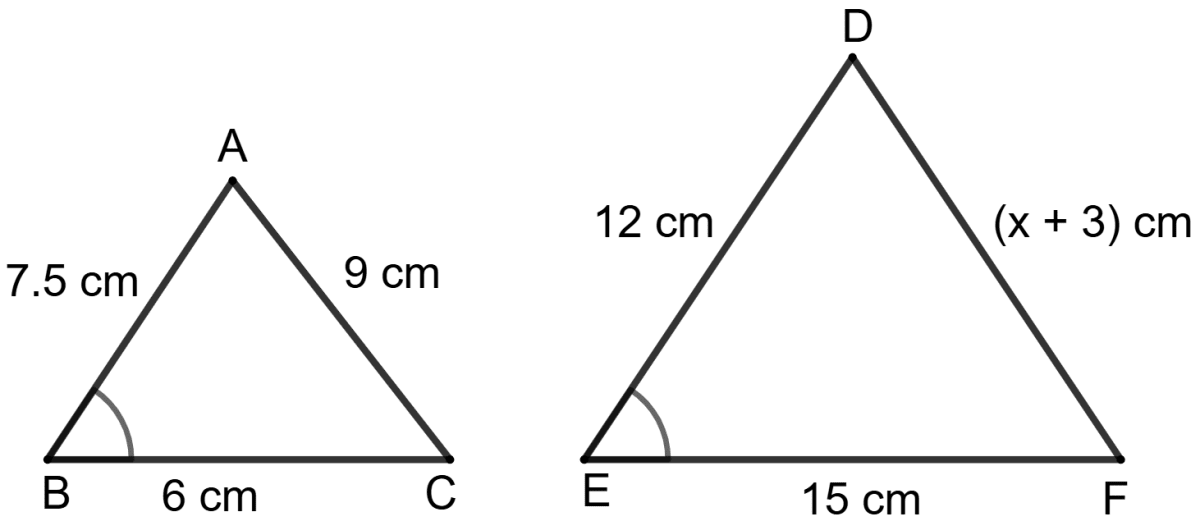
Answer

Given, ∠B = ∠E ...................(1)

$\Rightarrow \dfrac{\text{BC}}{\text{ED}} = \dfrac{6}{12} = \dfrac{1}{2}\\[1em] \Rightarrow \dfrac{\text{AB}}{\text{EF}} = \dfrac{7.5}{15} = \dfrac{1}{2}\\[1em] \therefore \dfrac{\text{BC}}{\text{ED}} = \dfrac{\text{AB}}{\text{EF}} \text{ ..........(2)}$

From (1) and (2), we get :

⇒ ∠B = ∠E

⇒ $\dfrac{\text{BC}}{\text{ED}} = \dfrac{\text{AB}}{\text{EF}}$

∴ Δ BAC ∼ Δ EFD (By SAS postulate)

We know that,

The corresponding sides of similar triangles are proportional.

$\Rightarrow \dfrac{\text{AC}}{\text{FD}} = \dfrac{\text{BC}}{\text{ED}}\\[1em] \Rightarrow \dfrac{9}{x + 3} = \dfrac{6}{12}\\[1em] \Rightarrow \dfrac{9}{x + 3} = \dfrac{1}{2}\\[1em] \Rightarrow 9 \times 2 = 1 \times (x + 3)\\[1em] \Rightarrow 18 = x + 3\\[1em] \Rightarrow x = 18 - 3\\[1em] \Rightarrow x = 15$

Hence, the value of x = 15.

Question 4

In the given figure, Δ ABC ∼ Δ DEF. Find the lengths of the sides of both the triangles (Each side is in cm).

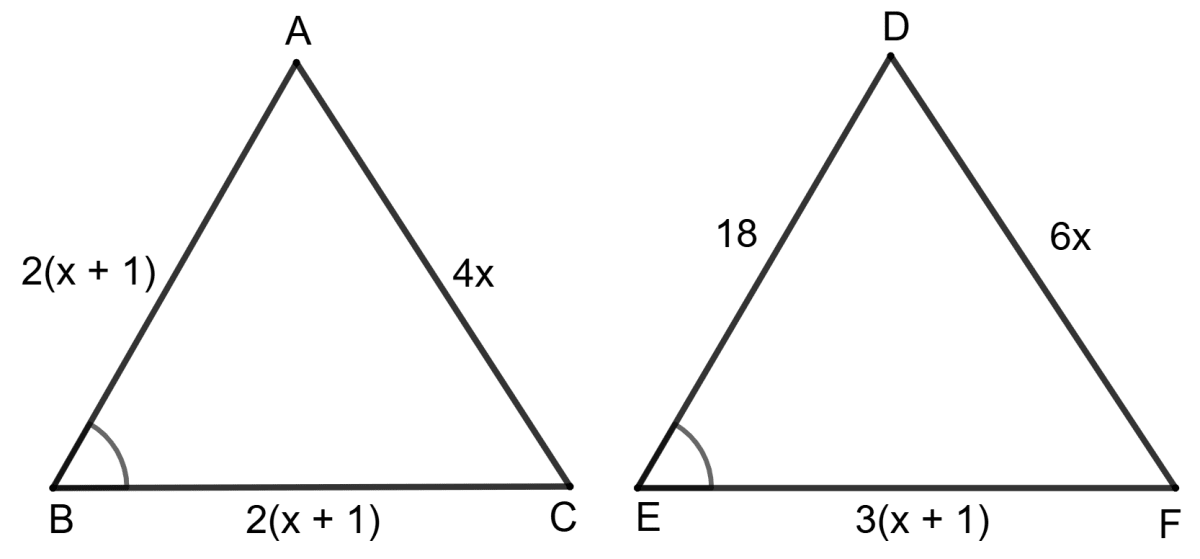
Answer

Given, Δ ABC ∼ Δ DEF

We know that,

Corresponding sides of similar triangles are proportional.

$\Rightarrow \dfrac{\text{AB}}{\text{DE}} = \dfrac{\text{BC}}{\text{EF}}\\[1em] \Rightarrow \dfrac{(2x + 1)}{18} = \dfrac{2(x + 1)}{3(x + 1)}\\[1em] \Rightarrow \dfrac{(2x + 1)}{18} = \dfrac{2}{3}\\[1em] \Rightarrow (2x + 1) \times 3 = 18 \times 2\\[1em] \Rightarrow 6x + 3 = 36\\[1em] \Rightarrow 6x = 36 - 3\\[1em] \Rightarrow 6x = 33\\[1em] \Rightarrow x = \dfrac{33}{6}\\[1em] \Rightarrow x = \dfrac{11}{2}$

Now, in Δ ABC, AB = 2x + 1 = 2 × $\dfrac{11}{2}$ + 1 = 11 + 1 = 12 cm

BC = 2(x + 1) = $2\Big(\dfrac{11}{2} + 1\Big) = 2 × \Big(\dfrac{11 + 2}{2}\Big) = 2 × \dfrac{13}{2} = 13$ cm

AC = 4x = 4 × $\Big(\dfrac{11}{2}\Big)$ = 22 cm

Now, in Δ DEF, DE = 18 cm

EF = 3(x + 1) = $3\Big(\dfrac{11}{2} + 1\Big) = 3 × \Big(\dfrac{11 + 2}{2}\Big) = 3 × \dfrac{13}{2} = \dfrac{39}{2}$ cm

DF = 6x = 6 × $\Big(\dfrac{11}{2}\Big)$ = 33 cm

Hence, AB = 12 cm, BC = 13 cm, AC = 22 cm, DE = 18 cm, EF = $\dfrac{39}{2}$ cm and DF = 33 cm.

Question 5

In Δ ABC and Δ DEF, AB = 3 x DF, BC = 3 x DE and AC = 3 x EF. Show that the given triangle are similar. Name the two similar triangle on a proper way.

Answer

Given, AB = 3 x DF, BC = 3 x DE and AC = 3 x EF

$\Rightarrow \dfrac{\text{AB}}{\text{DF}} = 3, \dfrac{\text{BC}}{\text{DE}} = 3 \text{ and } \dfrac{\text{AC}}{\text{EF}} = 3\\[1em] \Rightarrow \dfrac{\text{AB}}{\text{DF}} = \dfrac{\text{BC}}{\text{DE}} = \dfrac{\text{AC}}{\text{EF}}$

∴ Δ ABC ∼ Δ FDE (By SSS postulates)

Hence, Δ ABC ∼ Δ FDE by SSS.

Question 6

In a trapezium ABCD, side AB is parallel to side DC; and the diagonals AC and BD intersect each other at point P. Prove that:

(i) ΔAPB is similar to ΔCPD.

(ii) PA x PD = PB x PC.

Answer

Trapezium ABCD is shown in the figure below:

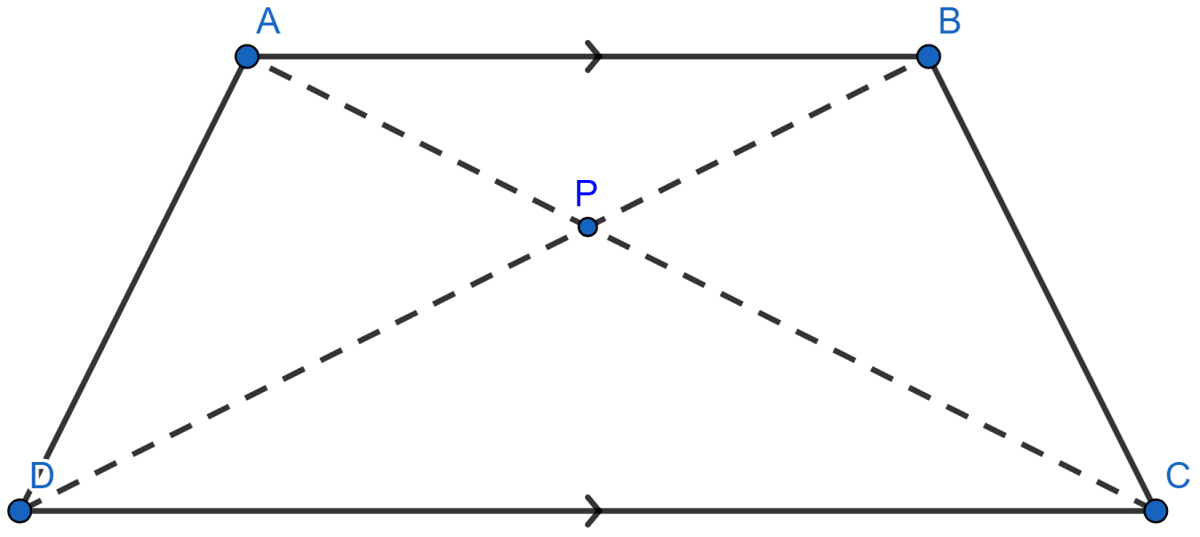
In a trapezium ABCD, side AB is parallel to side DC; and the diagonals AC and BD intersect each other at point P. Prove that (i) ΔAPB is similar to ΔCPD. (ii) PA x PD = PB x PC. Similarity, Concise Mathematics Solutions ICSE Class 10.

(i) In ∆APB and ∆CPD, we have

∠APB = ∠CPD [Vertically opposite angles]

∠ABP = ∠CDP [Alternate angles (as AB||DC) are equal]

∴ ∆APB ~ ∆CPD [By A.A.]

Hence, proved that ∆APB ~ ∆CPD.

(ii) We know that,

In similar triangles the ratio of corresponding sides are equal.

$\therefore \dfrac{\text{PA}}{\text{PC}} = \dfrac{\text{PB}}{\text{PD}} \\[1em] \Rightarrow \text{PA} \times \text{PD} = \text{PB} \times \text{PC}.$

Hence, proved that PA x PD = PB x PC.

Question 7

P is a point on side BC of a parallelogram ABCD. If DP produced meets AB produced at point L, prove that:

(i) DP : PL = DC : BL.

(ii) DL : DP = AL : DC.

Answer

Parallelogram ABCD is shown in the figure below:

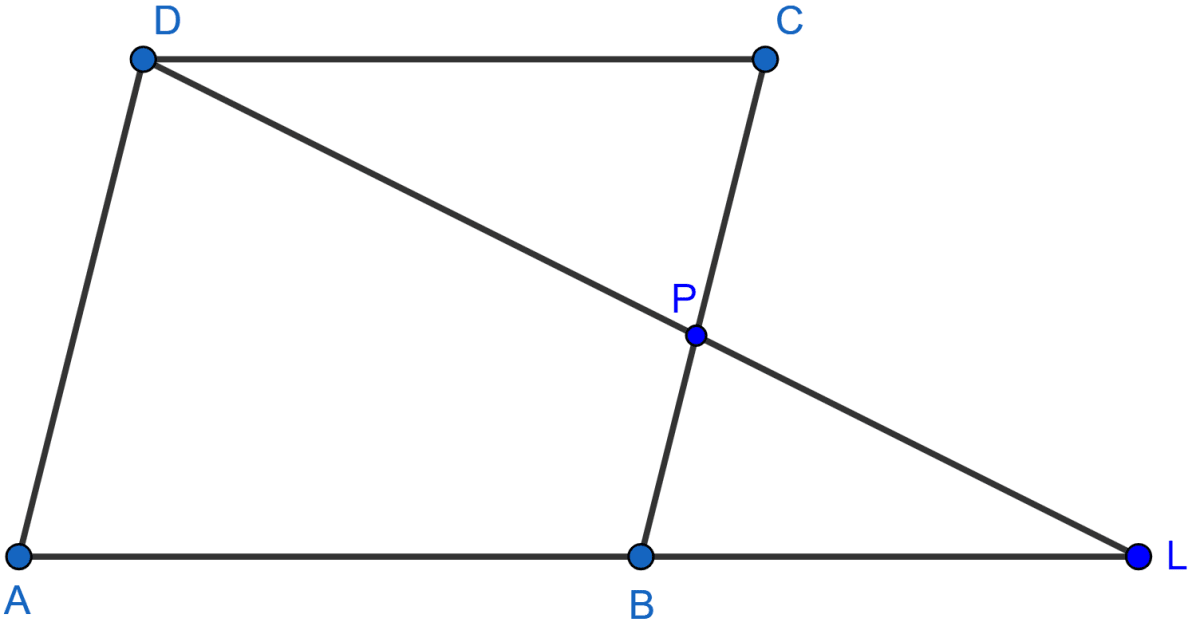
P is a point on side BC of a parallelogram ABCD. If DP produced meets AB produced at point L, prove that (i) DP : PL = DC : BL. (ii) DL : DP = AL : DC. Similarity, Concise Mathematics Solutions ICSE Class 10.

(i) In ∆DPC and ∆BPL, we have

∠DPC = ∠BPL [Vertically opposite angles area equal]

∠DCP = ∠PBL [Alternate angles (as AB || DC) are equal]

∴ ∆DPC ~ ∆BPL [By A.A.]

Since, corresponding sides of similar triangles are proportional.

$\therefore \dfrac{DP}{PL} = \dfrac{DC}{BL}$ .

i.e., DP : PL = DC : BL.

Hence, proved that DP : PL = DC : BL.

(ii) From part (i) we get,

$\Rightarrow \dfrac{DP}{PL} = \dfrac{DC}{BL} \\[1em] \Rightarrow \dfrac{PL}{DP} = \dfrac{BL}{DC} \\[1em] \Rightarrow \dfrac{PL}{DP} + 1 = \dfrac{BL}{DC} + 1 \\[1em] \Rightarrow \dfrac{PL + DP}{DP} = \dfrac{BL + DC}{DC} \\[1em] \Rightarrow \text{Since, AB = DC as ABCD is a || gm} \\[1em] \Rightarrow \dfrac{PL + DP}{DP} = \dfrac{BL + AB}{DC} \\[1em] \Rightarrow \dfrac{DL}{DP} = \dfrac{AL}{DC}.$

Hence, proved that DL : DP = AL : DC.

Question 8

In ΔABC, angle ABC is equal to twice the angle ACB, and bisector of angle ABC meets the opposite side at point P. Show that :

(i) CB : BA = CP : PA

(ii) AB x BC = BP x CA

Answer

ΔABC is shown in the figure below:

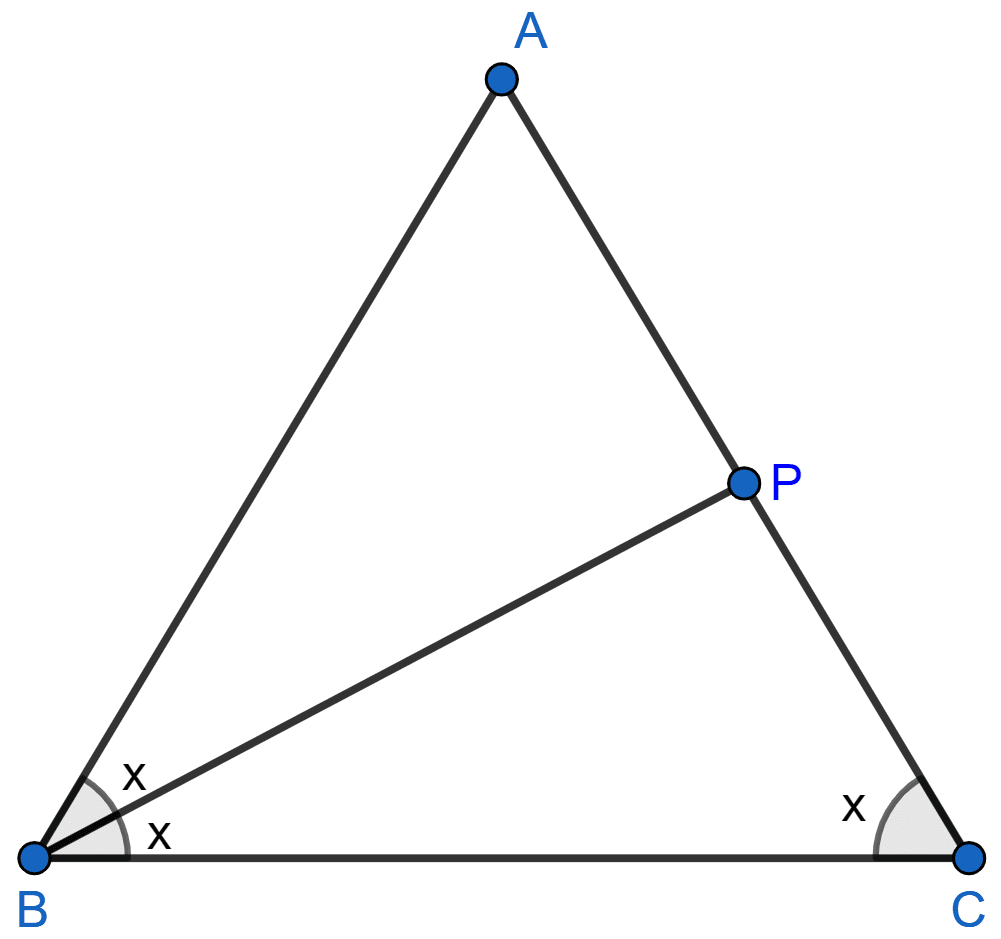
In ΔABC, angle ABC is equal to twice the angle ACB, and bisector of angle ABC meets the opposite side at point P. Show that (i) CB : BA = CP : PA. (ii) AB x BC = BP x CA. Similarity, Concise Mathematics Solutions ICSE Class 10.

(i) Let ∠ACB = x, so ∠ABC = 2x.

Since, BP is the bisector of ∠ABC.

So, ∠ABP = ∠PBC = x.

By angle bisector theorem,

The internal bisector of an angle of a triangle divides the opposite side internally in the ratio of the sides containing the angle.

$\therefore \dfrac{CB}{BA} = \dfrac{CP}{PA}$

i.e. CB : BA = CP : PA.

Hence, proved that CB : BA = CP : PA.

(ii) From figure,

∠APB = ∠PBC + ∠PCB = 2x. [Exterior angle is equal to the sum of opposite two interior angles].

∴ ∠APB = ∠ABC

∠BCP = ∠ABP [Both = x]

∴ △ABC ~ △APB [By A.A.]

Since corresponding sides of similar triangles are proportional we have,

⇒ $\dfrac{CA}{AB} = \dfrac{BC}{BP}$

⇒ AB x BC = BP x CA

Hence, proved that AB x BC = BP x CA.

Question 9

In the given figure, DE || BC, AE = 15 cm, EC = 9 cm, NC = 6 cm and BN = 24 cm.

(i) Write all possible pairs of similar triangles.

(ii) Find the lengths of ME and DM.

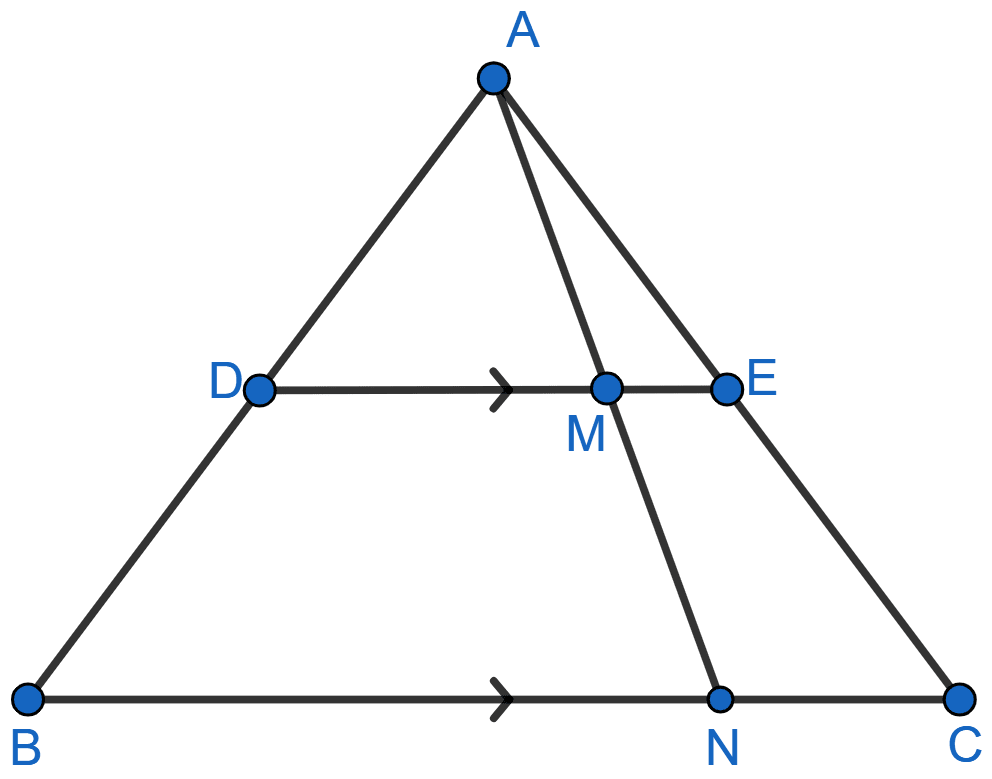
Answer

(i) In ΔAME and ΔANC,

⇒ ∠AME = ∠ANC [Since DE || BC so, ME || NC and AN is transversal]

⇒ ∠MAE = ∠NAC [Common angle]

∴ ∆AME ~ ∆ANC [By AA]

In ΔADM and ΔABN,

⇒ ∠ADM = ∠ABN [Since DE || BC so, DM || BN and AB is transversal]

⇒ ∠DAM = ∠BAN [Common angle]

∴ ∆ADM ~ ∆ABN [By AA]

In ΔADE and ΔABC,

⇒ ∠ADE = ∠ABC [Since DE || BC and AB is transversal]

⇒ ∠AED = ∠ACB [Since DE || BC and AC is transversal]

∴ ∆ADE ~ ∆ABC [By AA]

Hence, ∆ADM ~ ∆ABN, ∆AME ~ ∆ANC and ∆ADE ~ ∆ABC.

(ii) Since, ∆AME ~ ∆ANC

We know that,

Corresponding sides of similar triangles are proportional.

$\Rightarrow \dfrac{ME}{NC} = \dfrac{AE}{AC} \\[1em] \Rightarrow \dfrac{ME}{6} = \dfrac{15}{15 + 9} \\[1em] \Rightarrow ME = \dfrac{15}{24} \times 6 \\[1em] \Rightarrow ME = 3.75 \text{ cm}.$

Since, ∆ADE ~ ∆ABC [Proved above]

We know that,

Corresponding sides of similar triangles are proportional.

$\dfrac{AD}{AB} = \dfrac{AE}{AC} = \dfrac{15}{24}$ ......... (1)

Also, ∆ADM ~ ∆ABN [Proved above]

$\therefore \dfrac{DM}{BN} = \dfrac{AD}{AB} = \dfrac{15}{24} ........[From (1)] \\[1em] \therefore \dfrac{DM}{BN} = \dfrac{15}{24} \\[1em] DM = \dfrac{15}{24} \times BN = \dfrac{15}{24} \times 24 = 15 \text{ cm}.$

Hence, ME = 3.75 cm and DM = 15 cm.

Question 10

In the given figure, AD = AE and AD² = BD x EC. Prove that: triangles ABD and CAE are similar.

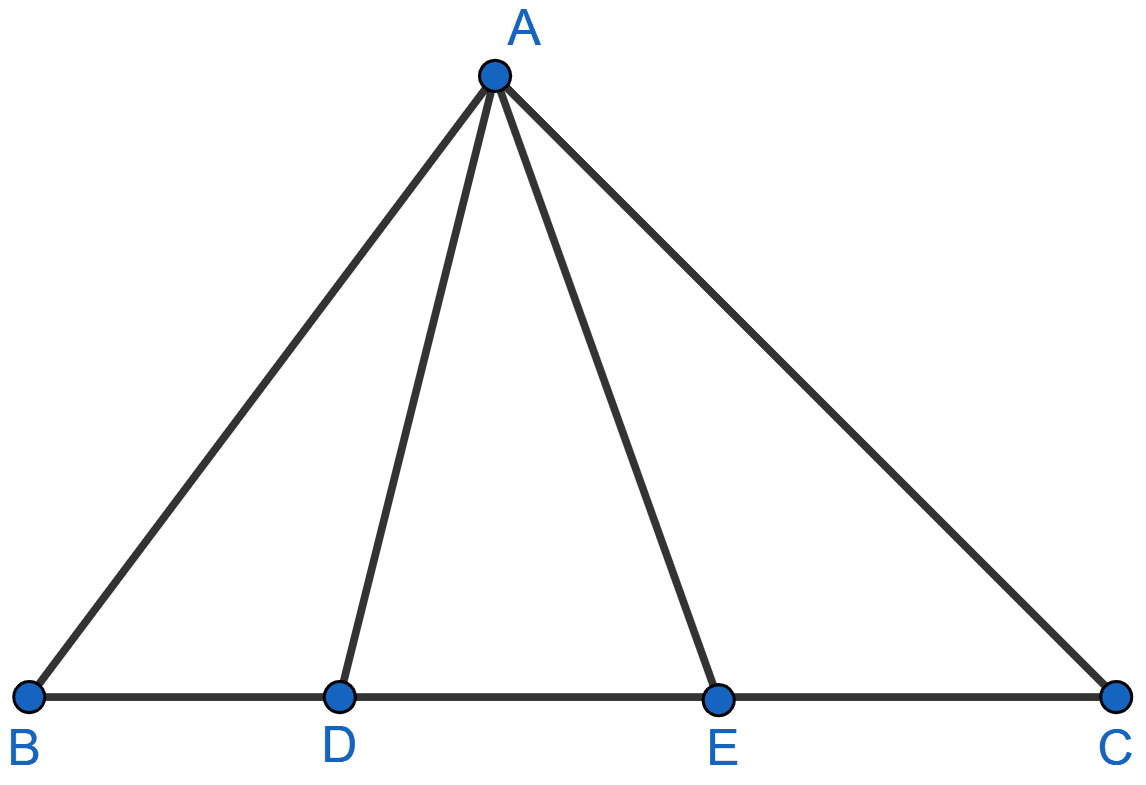
In the given, AD = AE and AD^2 = BD x EC. Prove that: triangles ABD and CAE are similar. Similarity, Concise Mathematics Solutions ICSE Class 10.

Answer

From figure,

⇒ ∠ADE = ∠AED [Angles opposite to equal sides of a triangle are equal].

⇒ 180° - ∠ADE = 180° - ∠AED

⇒ ∠ADB = ∠AEC

Given,

⇒ AD² = BD x EC

⇒ AD x AD = BD x EC

⇒ AD x AE = BD x EC

⇒ $\dfrac{AD}{EC} = \dfrac{BD}{AE}$

∴ △ABD ~ △CAE [By SAS]

Hence, proved that △ABD ~ △CAE.

Question 11

State, true or false:

(i) Two similar polygons are necessarily congruent.

(ii) Two congruent polygons are necessarily similar.

(iii) All equiangular triangles are similar.

(iv) All isosceles triangles are similar.

(v) Two isosceles-right triangles are similar.

(vi) Two isosceles triangles are similar, if an angle of one is congruent to the corresponding angle of the other.

(vii) The diagonals of a trapezium, divide each other into proportional segments.

Answer

(i) False

(ii) True

(iii) True

(iv) False

(v) True

(vi) True

(vii) True

Question 12

D is a point on the side BC of triangle ABC such that angle ADC is equal to angle BAC. Prove that: CA² = CB x CD.

Answer

In ΔADC and ΔBAC,

D is a point on the side BC of triangle ABC such that angle ADC is equal to angle BAC. Prove that: CA^2 = CB x CD. Similarity, Concise Mathematics Solutions ICSE Class 10.

⇒ ∠ADC = ∠BAC [Given]

⇒ ∠ACD = ∠ACB [Common]

∴ ∆ADC ~ ∆BAC [By AA]

Since, corresponding sides of similar triangles are proportional we have :

⇒ $\dfrac{CA}{CB} = \dfrac{CD}{CA}$

⇒ CA² = CB x CD.

Hence, proved that CA² = CB x CD.

Question 13

In the given figure, ΔABC and ΔAMP are right angled at B and M respectively.

Given AC = 10 cm, AP = 15 cm and PM = 12 cm.

(i) Prove that : ∆ABC ~ ∆AMP.

(ii) Find AB and BC.

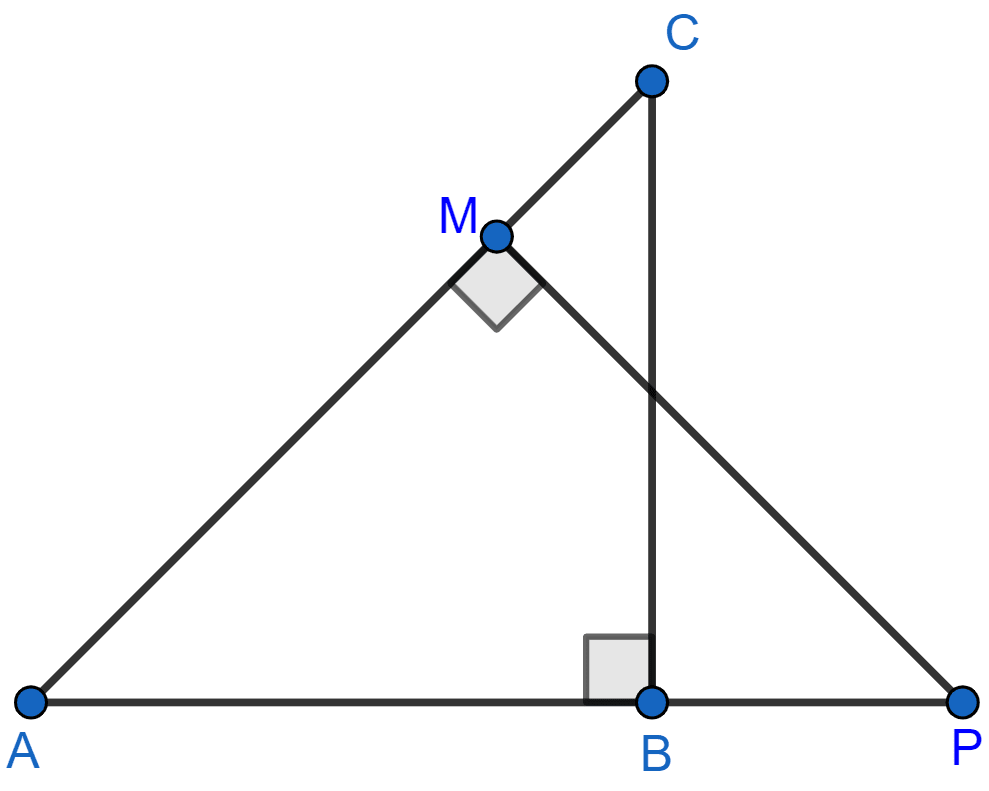
Answer

(i) In ∆ABC and ∆AMP, we have

⇒ ∠BAC = ∠PAM [Common]

⇒ ∠ABC = ∠PMA [Each = 90°]

∴ ∆ABC ~ ∆AMP [By AA]

Hence, proved that, ∆ABC ~ ∆AMP.

(ii) In right angle triangle AMP,

By pythagoras theorem,

⇒ AP² = AM² + MP²

⇒ AM² = AP² - MP²

⇒ AM² = 15² - 12²

⇒ AM² = 225 - 144

⇒ AM² = 81

⇒ AM = $\sqrt{81}$ = 9 cm.

Since, corresponding sides of similar triangles are proportional we have :

$\Rightarrow \dfrac{AB}{AM} = \dfrac{AC}{AP} \\[1em] \Rightarrow \dfrac{AB}{9} = \dfrac{10}{15} \\[1em] \Rightarrow AB = 9 \times \dfrac{10}{15} \\[1em] \Rightarrow AB = 6 \text{ cm}.$

Also,

$\Rightarrow \dfrac{BC}{MP} = \dfrac{AC}{AP} \\[1em] \Rightarrow \dfrac{BC}{12} = \dfrac{10}{15} \\[1em] \Rightarrow BC = 12 \times \dfrac{10}{15} \\[1em] \Rightarrow BC = 8 \text{ cm}.$

Hence, AB = 6 cm and BC = 8 cm.

Question 14

In the figure, PQRS is a parallelogram with PQ = 16 cm and QR = 10 cm, L is a point on PR such that RL : LP = 2 : 3. QL produced meets RS at M and PS produced at N. Find the lengths of PN and RM.

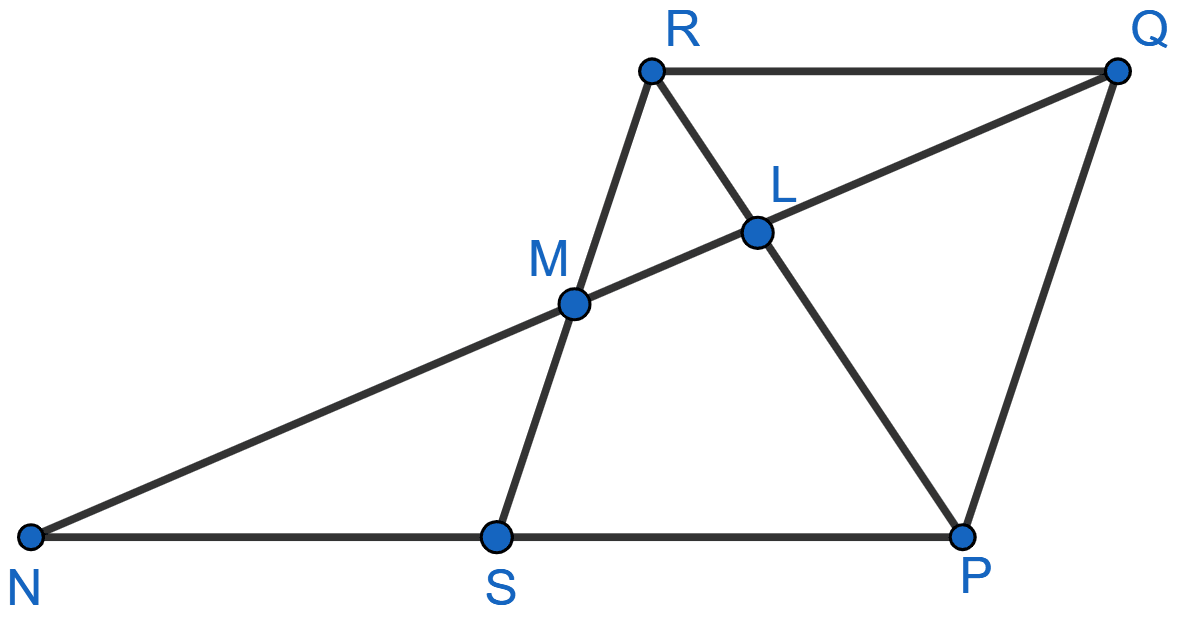
Answer

In △RLQ and △PLN,

⇒ ∠RLQ = ∠PLN [Vertically opposite angles are equal]

⇒ ∠LRQ = ∠LPN [Alternate angles are equal]

∴ △RLQ ~ △PLN [By AA]

Since, corresponding sides of similar triangles are proportional we have :

$\Rightarrow \dfrac{RL}{LP} = \dfrac{RQ}{PN} \\[1em] \Rightarrow \dfrac{2}{3} = \dfrac{10}{PN} \\[1em] \Rightarrow PN = \dfrac{30}{2} = 15 \text{ cm}.$

In △RLM and △PLQ,

⇒ ∠RLM = ∠PLQ [Vertically opposite angles are equal]

⇒ ∠LRM = ∠LPQ [Alternate angles are equal]

∴ △RLM ~ △PLQ [By AA]

Since, corresponding sides of similar triangles are proportional we have :

$\Rightarrow \dfrac{RM}{PQ} = \dfrac{RL}{LP} \\[1em] \Rightarrow \dfrac{RM}{16} = \dfrac{2}{3} \\[1em] \Rightarrow RM = \dfrac{32}{3} = 10\dfrac{2}{3} \text{ cm}.$

Hence, PN = 15 cm and RM = $10 \dfrac{2}{3}$ cm.

Question 15

In the given figure, AB || EF || DC; AB = 67.5 cm, DC = 40.5 cm and AE = 52.5 cm.

(i) Name the three pairs of similar triangles.

(ii) Find the length of EC and EF.

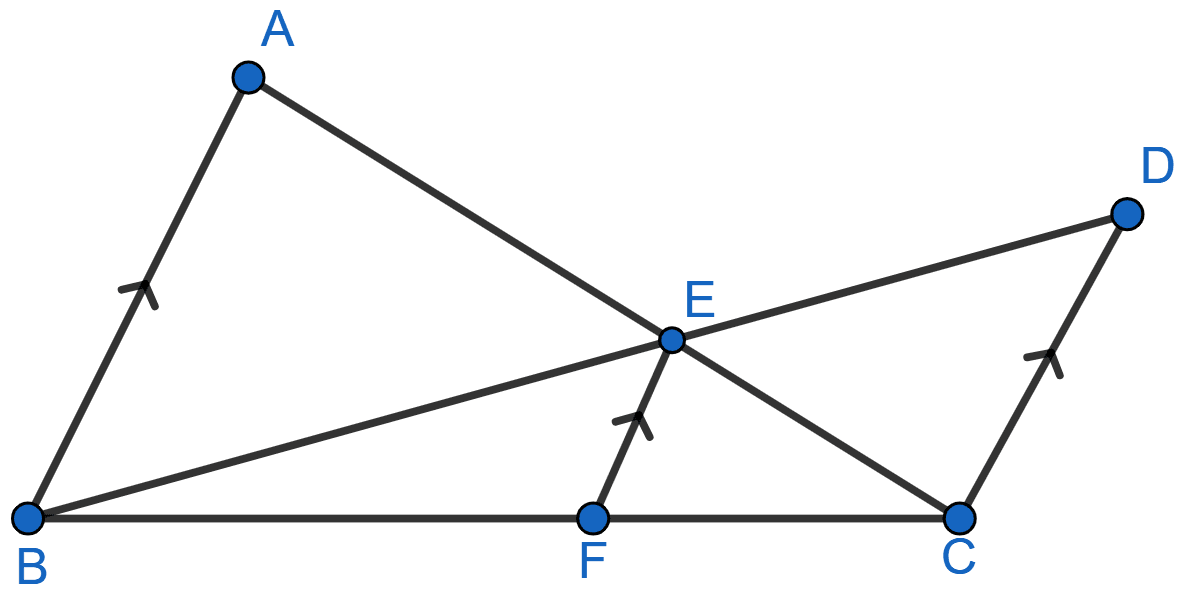
Answer

(i) The three pairs of similar triangle are :

In △BEF and △BDC

⇒ ∠FBE = ∠CBD [Common angle]

⇒ ∠BFE = ∠BCD [Corresponding angles are equal]

∴ △BEF ~ △BDC [By AA]

In △CEF and △CAB

⇒ ∠FCE = ∠BCA [Common angle]

⇒ ∠CFE = ∠CBA [Corresponding angles are equal]

∴ △CEF ~ △CAB [By AA]

In △ABE and △CDE

⇒ ∠AEB = ∠CED [Vertically opposite angles are equal]

⇒ ∠BAE = ∠ECD [Alternate angles are equal]

∴ △ABE ~ △CDE [By AA]

(ii) Since, △ABE and △CDE are similar,

$\therefore \dfrac{AB}{CD} = \dfrac{AE}{CE} \\[1em] \Rightarrow \dfrac{67.5}{40.5} = \dfrac{52.5}{CE} \\[1em] \Rightarrow CE = \dfrac{40.5 \times 52.5}{67.5} \\[1em] \Rightarrow CE = 31.5 \text{ cm}.$

Since, △CEF and △CAB are similar,

$\therefore \dfrac{CE}{CA} = \dfrac{EF}{AB} \\[1em] \Rightarrow \dfrac{31.5}{CE + AE} = \dfrac{EF}{67.5} \\[1em] \Rightarrow \dfrac{31.5}{31.5 + 52.5} = \dfrac{EF}{67.5} \\[1em] \Rightarrow EF = \dfrac{31.5 \times 67.5}{84} \\[1em] \Rightarrow EF = \dfrac{2126.25}{84} \\[1em] \Rightarrow EF = 25\dfrac{5}{16}\text{ cm}.$

Hence, CE = 31.5 cm and EF = $25\dfrac{5}{16}$ cm.

Question 16

In the given figure, P is a point on AB such that AP : PB = 4 : 3. PQ is parallel to AC.

(i) Calculate the ratio PQ : AC, giving reason for your answer.

(ii) In triangle ARC, ∠ARC = 90° and in triangle PQS, ∠PSQ = 90°. Given QS = 6 cm, calculate the length of AR.

Answer

(i) Given,

AP : PB = 4 : 3

Let AP = 4x and PB = 3x.

From figure,

AB = AP + PB = 4x + 3x = 7x.

PB : AB = 3x : 7x = 3 : 7.

In △PQB and △ACB,

QP || AC

∠BPQ = ∠BAC (Corresponding angles are equal)

∠BQP = ∠BCA (Corresponding angles are equal)

△PQB ~ △ACB.

Since, corresponding sides of similar triangle are proportional to each other.

$\therefore \dfrac{PQ}{AC} = \dfrac{PB}{AB} = \dfrac{3}{7}$ .

Hence, PQ : AC = 3 : 7.

(ii) In △ARC and △QSP,

∠ARC = ∠QSP = 90°

∠ACR = ∠SPQ (Alternate angles are equal)

∴ △ARC ~ △QSP [By AA]

Since, corresponding sides of similar triangle are proportional to each other.

$\Rightarrow \dfrac{AR}{QS} = \dfrac{AC}{PQ} \\[1em] \Rightarrow \dfrac{AR}{6} = \dfrac{7}{3} \\[1em] \Rightarrow AR = 6 \times \dfrac{7}{3} \\[1em] \Rightarrow AR = 14 \text{ cm}.$

Hence, AR = 14 cm.

Question 17

In the figure, given below, the medians BD and CE of a triangle ABC meet at G. Prove that :

(i) △EGD ~ △CGB and

(ii) BG = 2GD from (i) above.

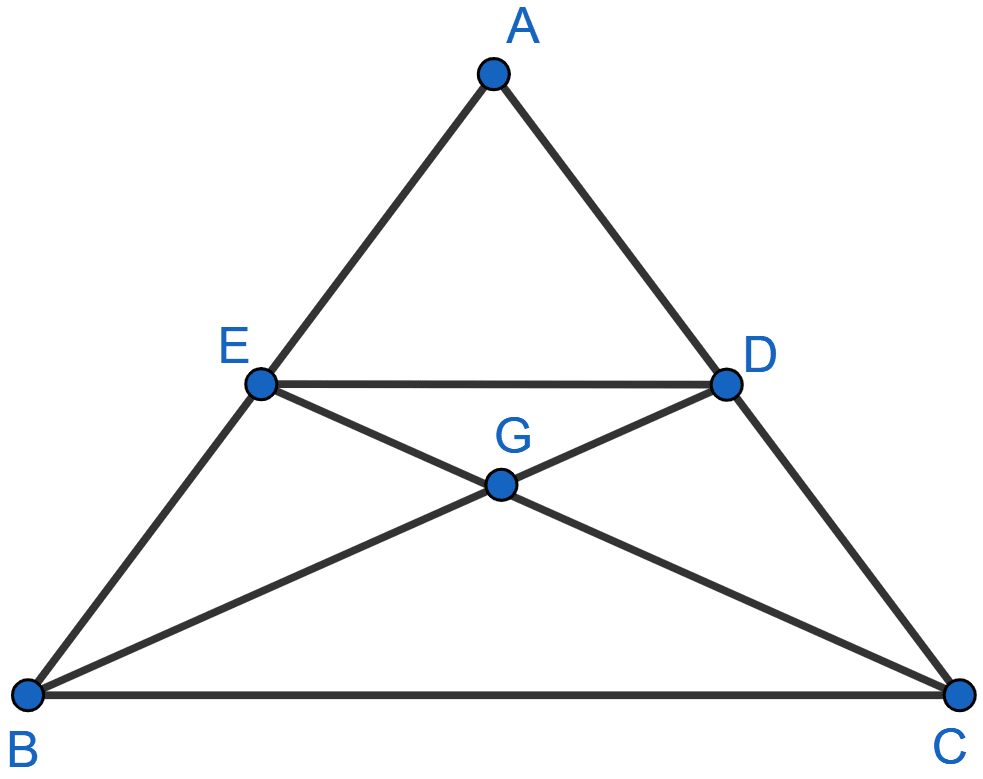
Answer

(i) Since, BD and CE are medians.

So, E is mid-point of AB and D is mid-point of AC.

By converse of mid-point theorem,

ED || BC and ED = $\dfrac{1}{2}$ BC

$\dfrac{ED}{BC} = \dfrac{1}{2}$ .....(1)

In △EGD and △CGB,

∠EGD = ∠BGC (Vertically opposite angles are equal)

∠DEG = ∠GCB (Alternate angles are equal)

∴ △EGD ~ △CGB [By AA].

Hence, proved that △EGD ~ △CGB.

(ii) Since, corresponding sides of similar triangle are proportional to each other.

$\Rightarrow \dfrac{BG}{GD} = \dfrac{ED}{BC} \\[1em] \Rightarrow \dfrac{BG}{GD} = \dfrac{1}{2} \space .....\text{ (From 1)} \\[1em] \Rightarrow BG = 2GD.$

Hence, proved that BG = 2GD.

Exercise 15(D)

Question 1(a)

In the given figure, DE is parallel to BC. If AD : BD = 3 : 5 then DE : BC is :

3 : 8
3 : 5
5 : 3
8 : 3

Answer

From figure,

In △ DAE and △ BAC,

⇒ ∠DAE = ∠BAC (Common angle)

⇒ ∠EDA = ∠CBA (Corresponding angles are equal)

∴ △ DAE ~ △ BAC (By A.A. postulate)

Given,

AD : BD = 3 : 5

Let AD = 3x and BD = 5x.

From figure,

AB = AD + BD = 3x + 5x = 8x.

We know that,

Corresponding sides of similar triangle are in proportion.

$\therefore \dfrac{DE}{BC} = \dfrac{AD}{AB} \\[1em] \Rightarrow \dfrac{DE}{BC} = \dfrac{3x}{8x} \\[1em] \Rightarrow \dfrac{DE}{BC} = \dfrac{3}{8} \\[1em] \Rightarrow DE : BC = 3 : 8.$

Hence, Option 1 is the correct option.

Question 1(b)

If AD = AE and BD = CE then :

△ ADE ~ △ ACB
△ ABC ~ △ ACB
△ ABD ~ △ ABC
△ ADE ~ △ ABC

Answer

Given,

⇒ AD = AE = x (let)

⇒ BD = CE = y (let)

From figure,

⇒ AB = AD + BD = x + y

⇒ AC = AE + EC = x + y

In △ ADE and △ ABC,

⇒ ∠DAE = ∠BAC

⇒ $\dfrac{AD}{AB} = \dfrac{AE}{AC} = \dfrac{x}{x + y}$

∴ △ ADE ~ △ ABC (By S.A.S. postulate)

Hence, Option 4 is the correct option.

Question 1(c)

In the given figure,

AB = 10 cm, CD = 8 cm = OB, then OD is equal to :

10 cm
3.2 cm
6.4 cm
8 cm

Answer

From figure,

In △ AOB and △ COD,

⇒ ∠AOB = ∠COD (Vertically opposite angles are equal)

⇒ ∠OAB = ∠OCD (Alternate angles are equal)

∴ △ AOB ~ △ COD (By A.A. postulate)

We know that,

Corresponding sides of similar triangle are in proportion.

$\therefore \dfrac{OB}{OD} = \dfrac{AB}{CD} \\[1em] \Rightarrow \dfrac{8}{OD} = \dfrac{10}{8} \\[1em] \Rightarrow OD = \dfrac{8 \times 8}{10} \\[1em] \Rightarrow OD = \dfrac{64}{10} = 6.4 \text{ cm}$

Hence, Option 3 is the correct option.

Question 1(d)

In the given figure, AE : EC = 2 : 3 and BC = 20 cm then DE is equal to :

10 cm
12 cm
8 cm
16 cm

Answer

From figure,

In △ ADE and △ ABC,

⇒ ∠DAE = ∠BAC (Common angle)

⇒ ∠ADE = ∠ABC (Corresponding angles are equal)

∴ △ ADE ~ △ ABC (By A.A. postulate)

Given,

AE : EC = 2 : 3

Let AE = 2x and EC = 3x.

From figure,

AC = AE + EC = 2x + 3x = 5x.

We know that,

Corresponding sides of similar triangle are in proportion.

$\therefore \dfrac{DE}{BC} = \dfrac{AE}{AC} \\[1em] \Rightarrow \dfrac{DE}{20} = \dfrac{2x}{5x} \\[1em] \Rightarrow DE = 20 \times \dfrac{2}{5} \\[1em] \Rightarrow DE = \dfrac{40}{5} = 8\text{ cm}.$

Hence, Option 3 is the correct option.

Question 1(e)

Two congruent triangles are :

not equal in area
similar
not similar
not similar but congruent

Answer

We know that,

Two congruent triangles are equal in area as well are similar.

Hence, Option 2 is the correct option.

Question 2

In the following figure, point D divides AB in the ratio 3 : 5. Find:

(i) $\dfrac{\text{AE}}{\text{EC}}$

(ii) $\dfrac{\text{AD}}{\text{AB}}$

(iii) $\dfrac{\text{AE}}{\text{AC}}$

Also if,

(iv) DE = 2.4 cm, find the length of BC.

(v) BC = 4.8 cm, find the length of DE.

In the figure, point D divides AB in the ratio 3 : 5. Find AC/EC, AD/AB, AE/AC, DE = 2.4 cm, find the length of BC, BC = 4.8 cm, find the length of DE. Similarity, Concise Mathematics Solutions ICSE Class 10.

Answer

(i) Given,

$\dfrac{AD}{DB} = \dfrac{3}{5}$ and DE || BC.

By basic proportionality theorem we have :

A line drawn parallel to one side of triangle divides the other two sides proportionally.

$\therefore \dfrac{AE}{EC} = \dfrac{AD}{DB} = \dfrac{3}{5}.$

Hence, AE : EC = 3 : 5.

(ii) Given,

$\dfrac{AD}{DB} = \dfrac{3}{5}$

Let AD = 3x and DB = 5x.

AB = AD + DB = 3x + 5x = 8x.

$\dfrac{AD}{AB} = \dfrac{3x}{8x} = \dfrac{3}{8}$ = 3 : 8.

Hence, AD : AB = 3 : 8.

(iii) Given,

$\Rightarrow \dfrac{AE}{EC} = \dfrac{3}{5} \\[1em] \Rightarrow \dfrac{EC}{AE} = \dfrac{5}{3} \\[1em] \Rightarrow \dfrac{EC}{AE} + 1 = \dfrac{5}{3} + 1 \\[1em] \Rightarrow \dfrac{EC + AE}{AE} = \dfrac{5 + 3}{3} \\[1em] \Rightarrow \dfrac{AC}{AE} = \dfrac{8}{3} \\[1em] \Rightarrow \dfrac{AE}{AC} = \dfrac{3}{8}.$

Hence, AE : AC = 3 : 8.

(iv) In ∆ADE and ∆ABC,

∠ADE = ∠ABC [As DE || BC, Corresponding angles are equal.]

∠A = ∠A [Common angles]

Hence, ∆ADE ~ ∆ABC by AA criterion for similarity.

Since, corresponding sides of similar triangles are proportional we have :

$\Rightarrow \dfrac{AD}{AB} = \dfrac{DE}{BC} \\[1em] \Rightarrow \dfrac{3}{8} = \dfrac{2.4}{BC} \\[1em] \Rightarrow BC = \dfrac{8 \times 2.4}{3} \\[1em] \Rightarrow BC = 6.4 \text{ cm}.$

Hence, BC = 6.4 cm.

(v) Since, ∆ADE ~ ∆ABC by AA criterion for similarity

So, we have

$\Rightarrow \dfrac{AD}{AB} = \dfrac{DE}{BC} \\[1em] \Rightarrow \dfrac{3}{8} = \dfrac{DE}{4.8} \\[1em] \Rightarrow DE = \dfrac{3 \times 4.8}{8} \\[1em] \Rightarrow DE = 1.8 \text{ cm}.$

Hence, DE = 1.8 cm.

Question 3

In the given figure, PQ || AB; CQ = 4.8 cm, QB = 3.6 cm and AB = 6.3 cm. Find :

(i) $\dfrac{CP}{PA}$

(ii) PQ

(iii) If AP = x, then the value of AC in terms of x.

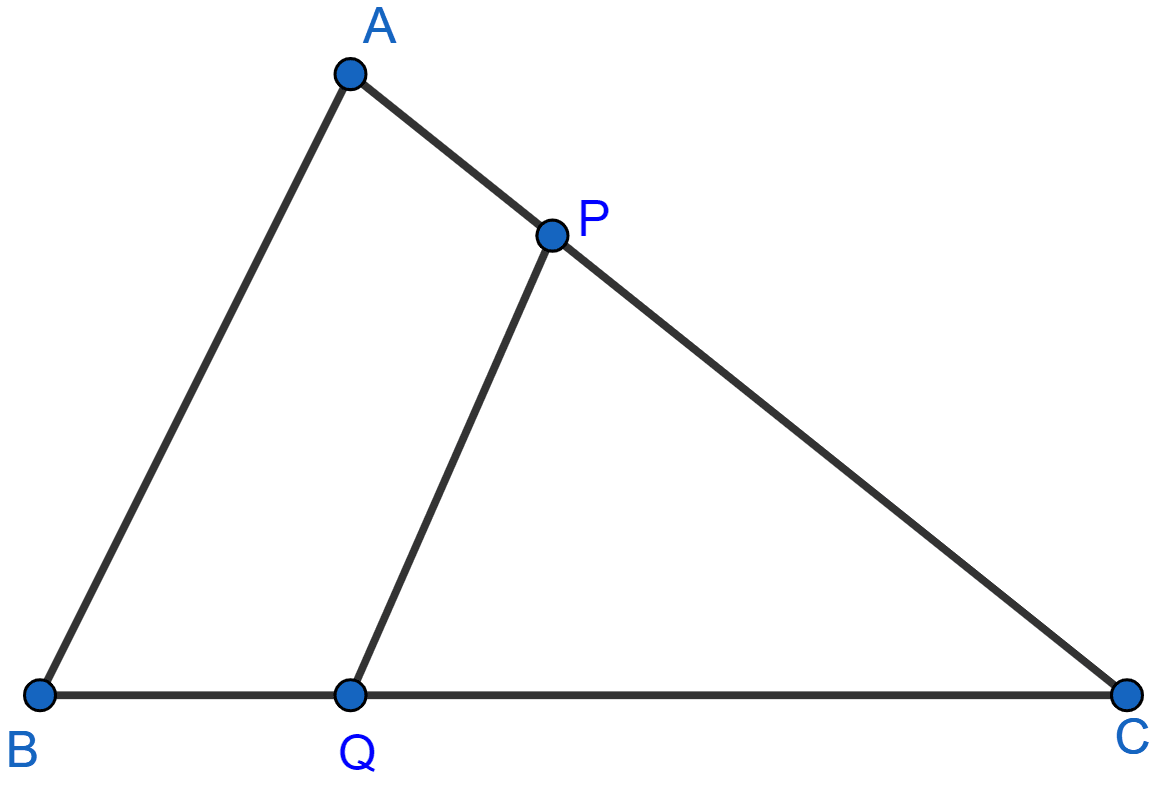
In the figure, PQ || AB; CQ = 4.8 cm, QB = 3.6 cm and AB = 6.3 cm. Find CP/PA, PQ. If AP = x, then the value of AC in terms of x. Similarity, Concise Mathematics Solutions ICSE Class 10.

Answer

(i) Given PQ || AB,

By basic proportionality theorem :

$\therefore \dfrac{CP}{PA} = \dfrac{CQ}{BQ} \\[1em] \Rightarrow \dfrac{CP}{PA} = \dfrac{4.8}{3.6} \\[1em] \Rightarrow \dfrac{CP}{PA} = \dfrac{4}{3}.$

Hence, ratio = 4 : 3.

(ii) In ∆CPQ and ∆CAB,

∠CPQ = ∠CAB [As PQ || AB, corresponding angles are equal.]

∠PCQ = ∠ACB [Common angle]

∴ ∆CPQ ~ ∆CAB [By AA].

From figure,

CB = CQ + QB = 4.8 + 3.6 = 8.4

Since, corresponding sides of similar triangles are proportional we have :

$\therefore \dfrac{PQ}{AB} = \dfrac{CQ}{CB} \\[1em] \Rightarrow \dfrac{PQ}{6.3} = \dfrac{4.8}{8.4} \\[1em] \Rightarrow PQ = 6.3 \times \dfrac{4}{7} = 3.6 \text{ cm}.$

Hence, PQ = 3.6 cm

(iii) As, ∆CPQ ~ ∆CAB.

We have,

$\dfrac{CP}{AC} = \dfrac{CQ}{CB} \\[1em] \dfrac{CP}{AC} = \dfrac{4.8}{8.4} \\[1em] \dfrac{CP}{AC} = \dfrac{4}{7}.$

So, if AC is 7 parts and CP is 4 parts, then PA is 3 parts.

Given, AP = x

or, 3 parts = x

⇒ 1 part = $\dfrac{x}{3}$

⇒ 7 parts = $\dfrac{7x}{3}$ .

Hence, AC = $\dfrac{7x}{3}$ .

Question 4

A line PQ is drawn parallel to the side BC of ΔABC which cuts side AB at P and side AC at Q. If AB = 9.0 cm, CA = 6.0 cm and AQ = 4.2 cm, find the length of AP.

Answer

Let AP = x cm.

From figure,

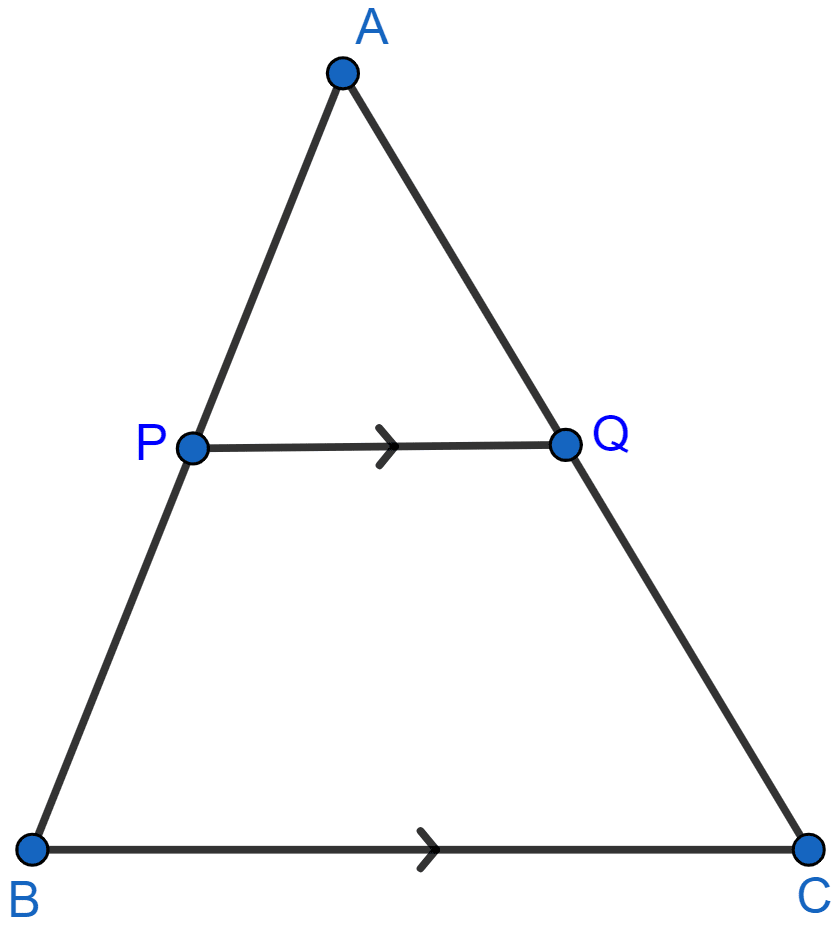
A line PQ is drawn parallel to the side BC of ΔABC which cuts side AB at P and side AC at Q. If AB = 9.0 cm, CA = 6.0 cm and AQ = 4.2 cm, find the length of AP. Similarity, Concise Mathematics Solutions ICSE Class 10.

PB = AB - AP = 9 - x cm.

QC = AC - AQ = 6 - 4.2 = 1.8 cm.

Given PQ || AB,

By basic proportionality theorem :

$\Rightarrow \dfrac{AP}{PB} = \dfrac{AQ}{QC} \\[1em] \Rightarrow \dfrac{x}{9 - x} = \dfrac{4.2}{1.8} \\[1em] \Rightarrow 1.8x = 4.2(9 - x) \\[1em] \Rightarrow 1.8x = 37.8 - 4.2x \\[1em] \Rightarrow 1.8x + 4.2x = 37.8 \\[1em] \Rightarrow 6x = 37.8 \\[1em] \Rightarrow x = 6.3 \text{ cm}.$

Hence, AP = 6.3 cm.

Question 5

In ΔABC, D and E are the points on sides AB and AC respectively.

Find whether DE || BC, if

(i) AB = 9 cm, AD = 4 cm, AE = 6 cm and EC = 7.5 cm.

(ii) AB = 6.3 cm, EC = 11.0 cm, AD = 0.8 cm and EA = 1.6 cm.

Answer

(i) From figure,

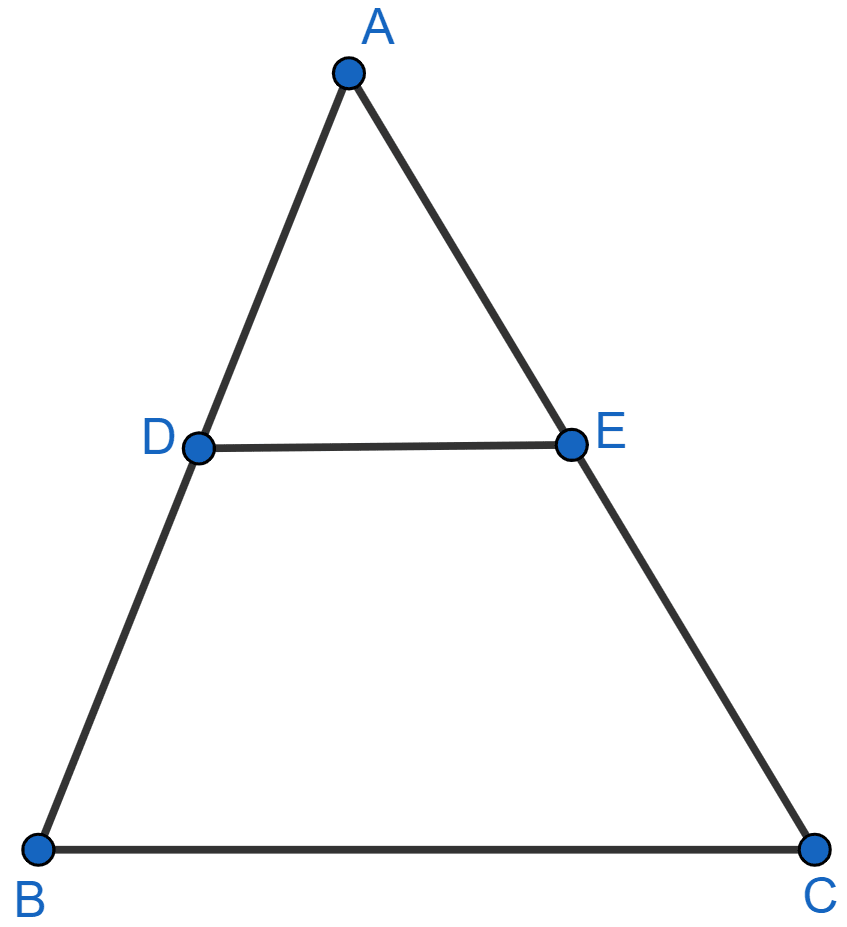
In ΔABC, D and E are the points on sides AB and AC respectively. Find whether DE || BC, if (i) AB = 9 cm, AD = 4 cm, AE = 6 cm and EC = 7.5 cm. (ii) AB = 6.3 cm, EC = 11.0 cm, AD = 0.8 cm and EA = 1.6 cm. Similarity, Concise Mathematics Solutions ICSE Class 10.

BD = AB - AD = 9 - 4 = 5 cm

In ∆ADE and ∆ABC,

$\dfrac{AE}{EC} = \dfrac{6}{7.5} = \dfrac{4}{5} \\[1em] \dfrac{AD}{BD} = \dfrac{4}{5} \\[1em] \text{Since } \dfrac{AE}{EC} = \dfrac{AD}{BD}.$

Hence, DE || BC by the converse of Basic proportionality theorem.

(ii) From figure,

BD = AB - AD = 6.3 - 0.8 = 5.5 cm

In ∆ADE and ∆ABC,

$\dfrac{AE}{EC} = \dfrac{1.6}{11} = \dfrac{0.8}{5.5} \\[1em] \dfrac{AD}{BD} = \dfrac{0.8}{5.5} \\[1em] \text{Since } \dfrac{AE}{EC} = \dfrac{AD}{BD}.$

Hence, DE || BC by the converse of Basic proportionality theorem.

Question 6

In the given figure, ΔABC ~ ΔADE. If AE : EC = 4 : 7 and DE = 6.6 cm, find BC. If 'x' be the length of the perpendicular from A to DE, find the length of perpendicular from A to BC in terms of 'x'.

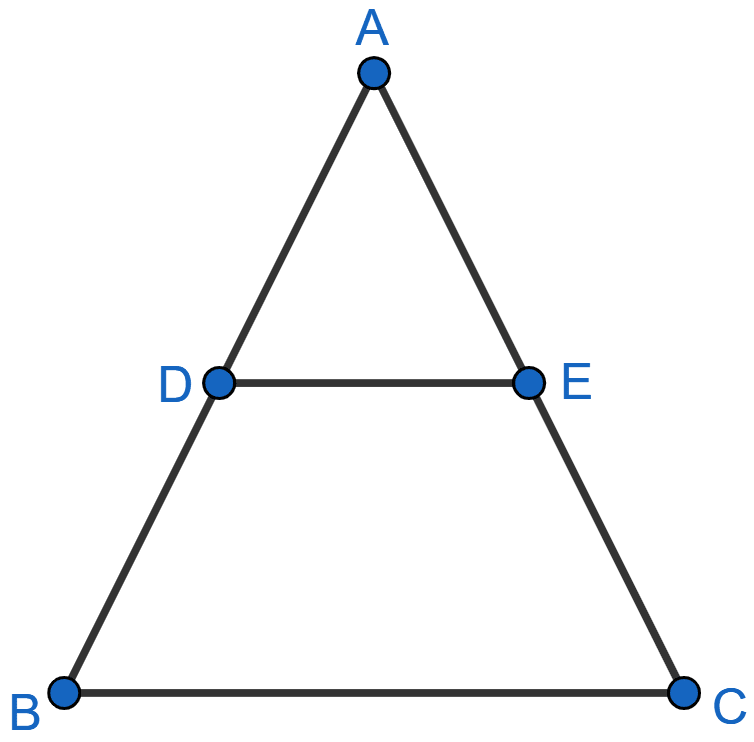
In the figure, ΔABC ~ ΔADE. If AE : EC = 4 : 7 and DE = 6.6 cm, find BC. If x be the length of the perpendicular from A to DE, find the length of perpendicular from A to BC in terms of x. Similarity, Concise Mathematics Solutions ICSE Class 10.

Answer

Given,

ΔABC ~ ΔADE

Given,

AE : EC = 4 : 7

Let AE = 4y and EC = 7y.

So, AC = 4y + 7y = 11y.

From figure,

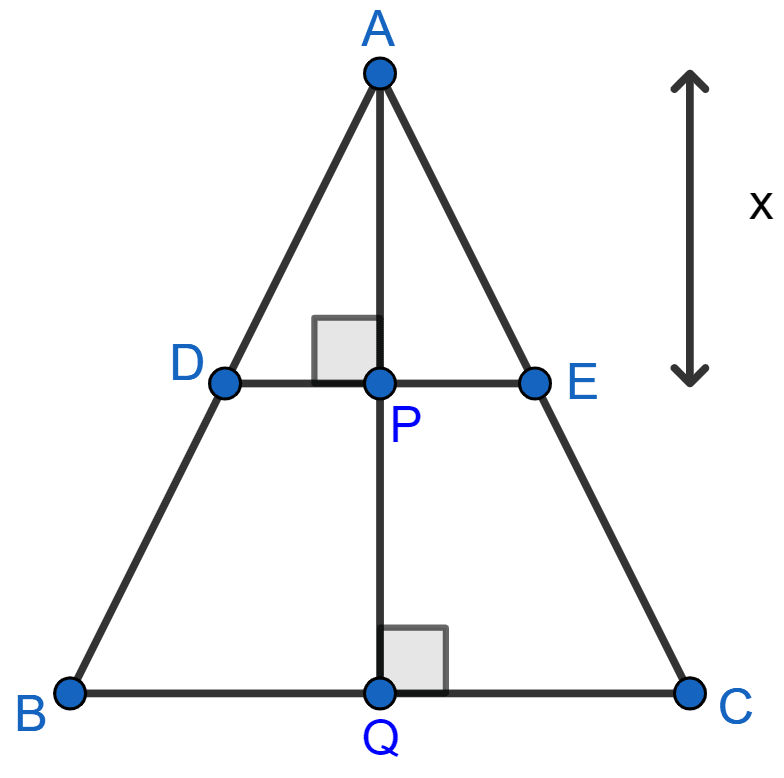
Since, corresponding sides of similar triangles are proportional we have :

$\Rightarrow \dfrac{AE}{AC} = \dfrac{DE}{BC} \\[1em] \Rightarrow \dfrac{4y}{11y} = \dfrac{6.6}{BC} \\[1em] \Rightarrow \dfrac{4}{11} = \dfrac{6.6}{BC} \\[1em] \Rightarrow BC = \dfrac{11 \times 6.6}{4} = 18.15 \text{ cm}$

As ΔABC ~ ΔADE, we have :

∠ABC = ∠ADE and ∠ACB = ∠AED

So, DE || BC as ∠ADE and ∠ABC are corresponding angles.

$\therefore \dfrac{AB}{AD} = \dfrac{AC}{AE} = \dfrac{11y}{4y} = \dfrac{11}{4}$

Let perpendicular from A to DE meet DE at point P. Then,

AP = x

Let perpendicular from A to BC meet BC at point Q.

In ∆ADP and ∆ABQ,

∠ADP = ∠ABQ [Corresponding angles are equal.]

∠APD = ∠AQB [Both = 90°]

∴ ∆ADP ~ ∆ABQ [By AA]

$\Rightarrow \dfrac{AD}{AB} = \dfrac{AP}{AQ} \\[1em] \Rightarrow \dfrac{4}{11} = \dfrac{x}{AQ} \\[1em] \Rightarrow AQ = \dfrac{11}{4}x.$

Hence, BC = 18.15 cm and AQ = $\dfrac{11}{4}x.$

Question 7

A line segment DE is drawn parallel to base BC of ∆ABC which cuts AB at point D and AC at point E. If AB = 5BD and EC = 3.2 cm, find the length of AE.

Answer

Given,

⇒ AB = 5BD

⇒ AD + BD = 5BD

⇒ AD = 5BD - BD

⇒ AD = 4BD

⇒ $\dfrac{\text{AD}}{\text{BD}} = \dfrac{4}{1}$ .

A line segment DE is drawn parallel to base BC of ∆ABC which cuts AB at point D and AC at point E. If AB = 5BD and EC = 3.2 cm, find the length of AE. Similarity, Concise Mathematics Solutions ICSE Class 10.

Given DE || BC,

by basic proportionality theorem :

$\therefore \dfrac{AD}{BD} = \dfrac{AE}{EC} \\[1em] \Rightarrow \dfrac{4}{1} = \dfrac{AE}{3.2} \\[1em] \Rightarrow AE = 4 \times 3.2 = 12.8 \text{ cm}.$

Hence, AE = 12.8 cm

Question 8

In the figure, given below, AB, CD and EF are parallel lines. Given AB = 7.5 cm, DC = y cm, EF = 4.5 cm, BC = x cm and CE = 3 cm, calculate the values of x and y.

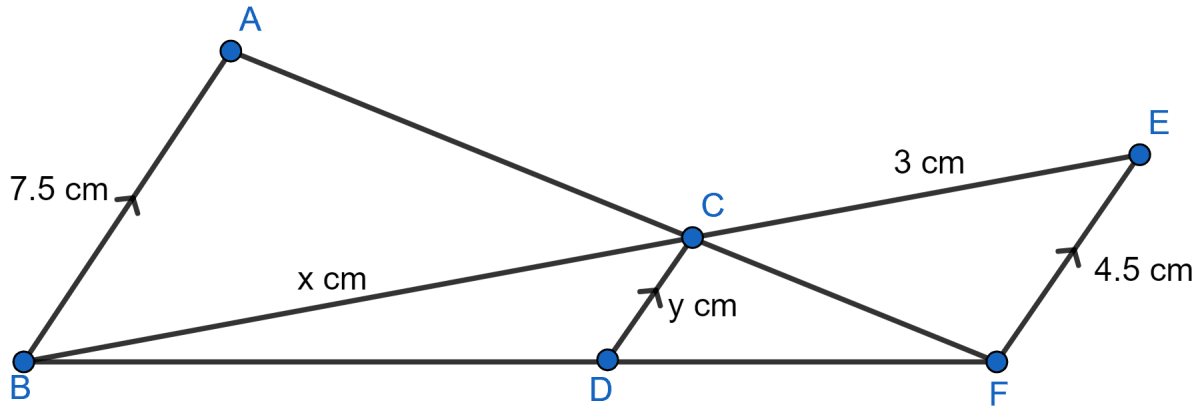
In the figure, AB, CD and EF are parallel lines. Given AB = 7.5 cm, DC = y cm, EF = 4.5 cm, BC = x cm and CE = 3 cm, calculate the values of x and y. Similarity, Concise Mathematics Solutions ICSE Class 10.

Answer

In ∆BEF,

DC || FE

So, by basic proportionality theorem,

$\dfrac{BD}{DF} = \dfrac{BC}{CE} = \dfrac{x}{3}$

$\dfrac{BD}{DF} = \dfrac{x}{3}$ .....(1)

Let BD = ax and DF = 3a.

From figure,

BF = BD + DF = ax + 3a = a(x + 3).

$\dfrac{BF}{DF} = \dfrac{a(x + 3)}{3a} = \dfrac{x + 3}{3}$ .....(2)

In ∆AFB and CDF,

∠AFB = ∠CFD [Common angles]

∠ABF = ∠CDF [Corresponding angles are equal]

∴ ∆AFB ~ ∆CDF [By AA]

Since, corresponding sides of similar triangles are proportional.

$\Rightarrow \dfrac{BF}{DF} = \dfrac{AB}{CD} \\[1em] \Rightarrow \dfrac{BF}{DF} = \dfrac{7.5}{y} .....(3) \\[1em] \text{From (2) and (3) we get}, \\[1em] \Rightarrow \dfrac{x + 3}{3} = \dfrac{7.5}{y} \\[1em] \Rightarrow y = \dfrac{22.5}{x + 3} \space .....(4)$

In ∆BCD and ∆BEF ,

∠FBE = ∠DBC [Common angles]

∠CDB = ∠EFB [Corresponding angles are equal]

∴ ∆BEF ~ ∆BCD [By AA]

Since, corresponding sides of similar triangles are proportional.

$\dfrac{BD}{BF} = \dfrac{CD}{FE} = \dfrac{y}{4.5}$

$\dfrac{BD}{BF} = \dfrac{y}{4.5}$

Let BD = ay and BF = 4.5a

From figure,

DF = BF - BD = 4.5a - ay = a(4.5 - y).

$\therefore \dfrac{BD}{DF} = \dfrac{ay}{a(4.5 - y)} = \dfrac{y}{4.5 - y}$ .....(5)

From (1) and (5) we get,

$\Rightarrow \dfrac{x}{3} = \dfrac{y}{4.5 - y}$

Substituting value of y from (4) in above equation we get,

$\Rightarrow \dfrac{x}{3} = \dfrac{\dfrac{22.5}{x + 3}}{4.5 - \dfrac{22.5}{x + 3}} \\[1em] \Rightarrow \dfrac{x}{3} = \dfrac{\dfrac{22.5}{x + 3}}{\dfrac{4.5x + 13.5 - 22.5}{x + 3}} \\[1em] \Rightarrow \dfrac{x}{3} = \dfrac{22.5}{4.5x - 9} \\[1em] \Rightarrow \dfrac{x}{3} = \dfrac{22.5}{3(1.5x - 3)} \\[1em] \Rightarrow x = \dfrac{22.5}{1.5x - 3} \\[1em] \Rightarrow x = \dfrac{22.5}{1.5(x - 2)} \\[1em] \Rightarrow x = \dfrac{15}{x - 2} \\[1em] \Rightarrow x(x - 2) = 15 \\[1em] \Rightarrow x^2 - 2x - 15 = 0 \\[1em] \Rightarrow x^2 - 5x + 3x - 15 = 0 \\[1em] \Rightarrow x(x - 5) + 3(x - 5) = 0 \\[1em] \Rightarrow (x + 3)(x - 5) = 0 \\[1em] \Rightarrow x = - 3 \text{ or } x = 5.$

Since, side of triangle cannot be negative. So, x = 5 cm.

Substituting value of x in (4) we get,

$\Rightarrow y = \dfrac{22.5}{x + 3} \\[1em] \Rightarrow y = \dfrac{22.5}{5 + 3} \\[1em] \Rightarrow y = \dfrac{22.5}{8} = 2.8125 \text{ cm}$

Hence, x = 5 cm and y = 2.8125 cm

Question 9

In the figure, given below, PQR is a right-angled triangle at Q. XY is parallel to QR, PQ = 6 cm, PY = 4 cm and PX : XQ = 1 : 2. Calculate the lengths of PR and QR.

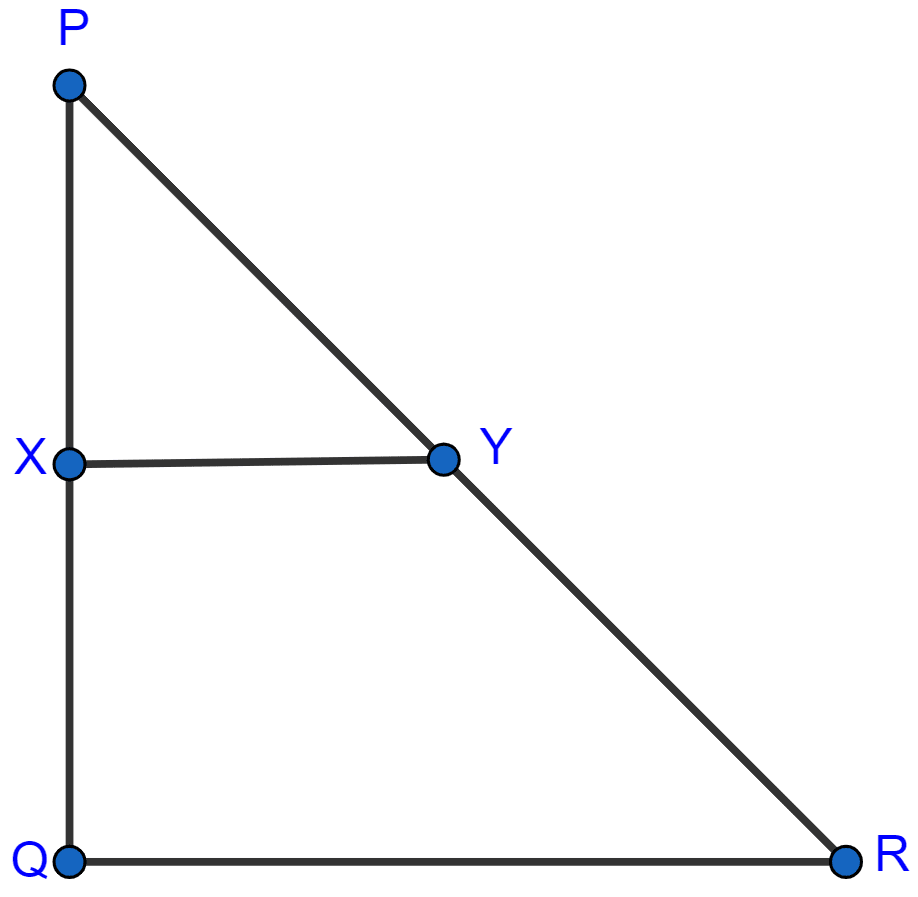
In the figure, PQR is a right-angled triangle at Q. XY is parallel to QR, PQ = 6 cm, PY = 4 cm and PX : XQ = 1 : 2. Calculate the lengths of PR and QR. Similarity, Concise Mathematics Solutions ICSE Class 10.

Answer

Given XY || QR,

By basic proportionality theorem :

$\therefore \dfrac{PX}{XQ} = \dfrac{PY}{YR} \\[1em] \Rightarrow \dfrac{1}{2} = \dfrac{4}{YR} \\[1em] \Rightarrow YR = 4 \times 2 = 8 \text{ cm}.$

From figure,

PR = PY + YR = 4 + 8 = 12 cm.

Since, PQR is a right-angled triangle.

By pythagoras theorem we get,

$\Rightarrow PR^2 = PQ^2 + QR^2 \\[1em] \Rightarrow 12^2 = 6^2 + QR^2 \\[1em] \Rightarrow 144 = 36 + QR^2 \\[1em] \Rightarrow QR^2 = 144 - 36 \\[1em] \Rightarrow QR^2 = 108 \\[1em] \Rightarrow QR = \sqrt{108} = 10.392 \text{ cm}.$

Hence, PR = 12 cm and QR = 10.392 cm.

Question 10

In the following figure, M is the mid-point of BC of a parallelogram ABCD. DM intersects the diagonal AC at P and AB produced at E. Prove that : PE = 2PD.

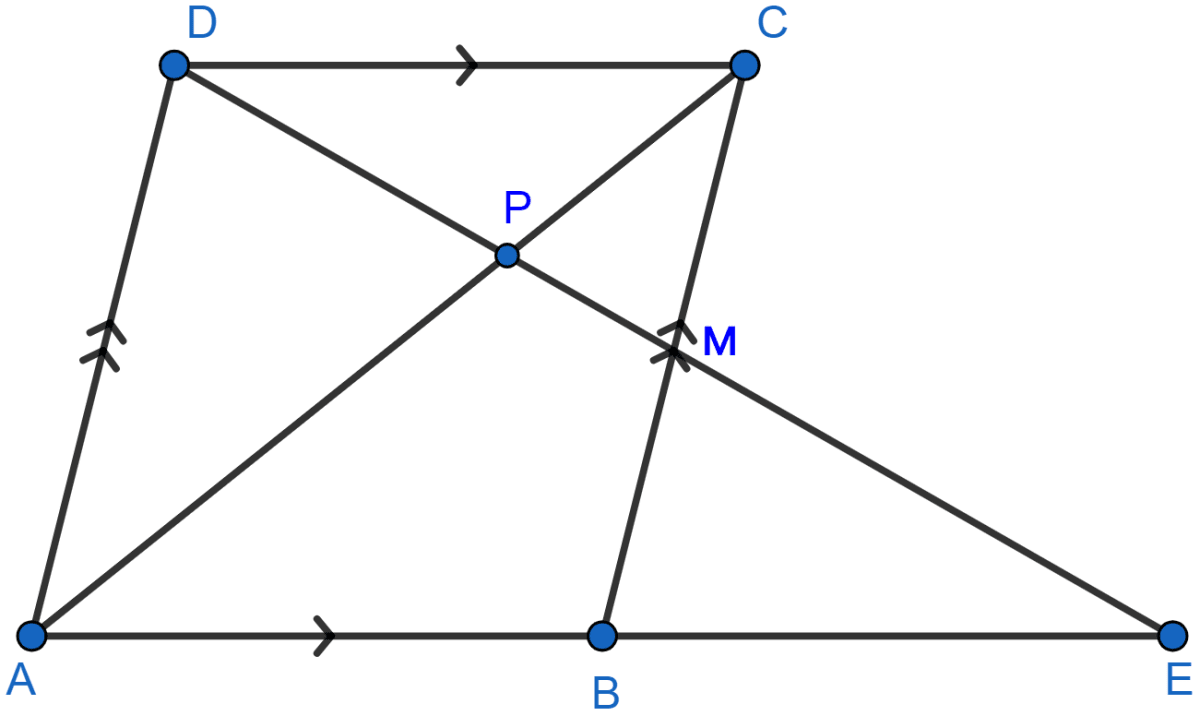
In the figure, M is the mid-point of BC of a parallelogram ABCD. DM intersects the diagonal AC at P and AB produced at E. Prove that : PE = 2PD. Similarity, Concise Mathematics Solutions ICSE Class 10.

Answer

In ∆BME and ∆DMC,

∠BME = ∠CMD [Vertically opposite angles are equal.]

∠MCD = ∠MBE [Alternate angles are equal]

BM = MC [M is mid-point of BC]

∴ ∆BME ≅ ∆DMC [By AAS congruence rule]

∴ BE = DC [By C.P.C.T]

Since, opposite sides of parallelogram are equal.

∴ AB = DC

or, AB = DC = BE. ...........(1)

In ∆DCP and ∆EPA,

∠DPC = ∠EPA [Vertically opposite angles are equal.]

∠CDP = ∠AEP [Alternate angles are equal]

∴ ∆DCP ~ ∆EAP [By AA]

Since, corresponding sides of similar triangles are proportional we have :

$\Rightarrow \dfrac{DC}{EA} = \dfrac{PD}{PE} \\[1em] \Rightarrow \dfrac{EA}{DC} = \dfrac{PE}{PD} \\[1em] \Rightarrow \dfrac{PE}{PD} = \dfrac{AB + BE}{DC} \\[1em] \Rightarrow \dfrac{PE}{PD} = \dfrac{2DC}{DC} \\[1em] \Rightarrow \dfrac{PE}{PD} = 2 \\[1em] \Rightarrow PE = 2PD.$

Hence proved that PE = 2PD.

Question 11

The given figure shows a parallelogram ABCD. E is a point in AD and CE produced meets BA produced at point F. If AE = 4 cm, AF = 8 cm and AB = 12 cm, find the perimeter of the parallelogram ABCD.

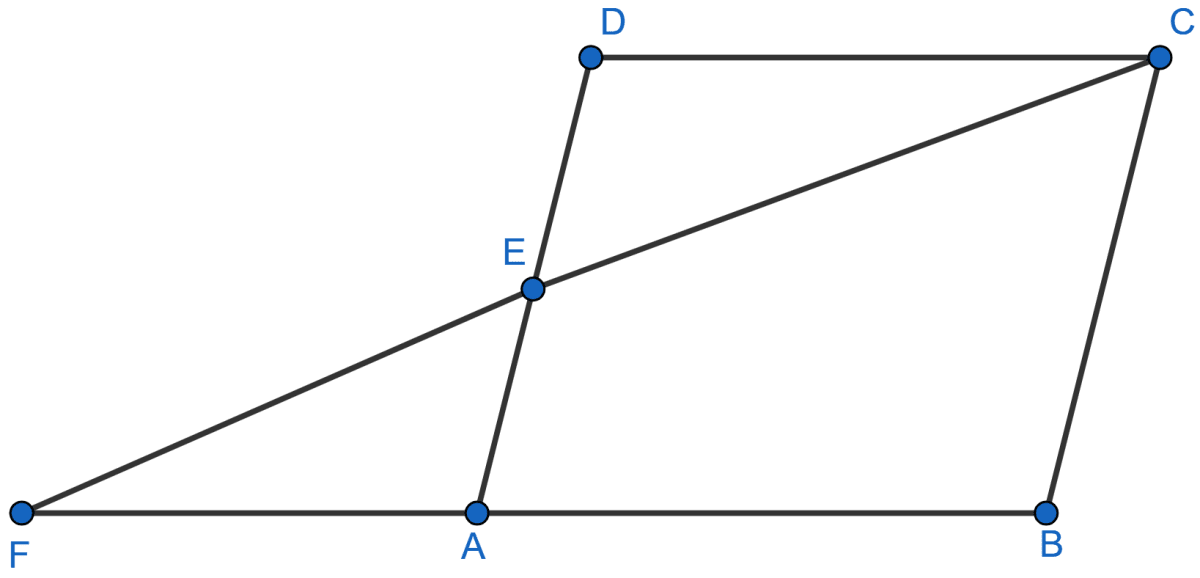
The figure shows a parallelogram ABCD. E is a point in AD and CE produced meets BA produced at point F. If AE = 4 cm, AF = 8 cm and AB = 12 cm, find the perimeter of the parallelogram ABCD. Similarity, Concise Mathematics Solutions ICSE Class 10.

Answer

From figure,

FB = AF + AB = 8 + 12 = 20 cm.

In △DEC and △EAF

⇒ ∠DEC = ∠FEA [Vertically opposite angles are equal]

⇒ ∠EDC = ∠EAF [Alternate angles are equal]

∴ △DEC ~ △EAF [By AA]

Since, corresponding sides of similar triangles are proportional we have :

$\Rightarrow \dfrac{DE}{AE} = \dfrac{DC}{AF} \\[1em] \Rightarrow \dfrac{DE}{AE} = \dfrac{AB}{AF} \space \Big[\because\text{ AB = CD}\Big] \\[1em] \Rightarrow \dfrac{DE}{4} = \dfrac{12}{8} \\[1em] \Rightarrow DE = \dfrac{48}{8} = 6 \text{ cm}.$

Since, ABCD is a ||gm.

AB = CD and BC = AD.

From figure,

AD = AE + ED = 4 + 6 = 10 cm.

Perimeter of ||gm ABCD = AB + BC + CD + AD

= 12 + 10 + 12 + 10

= 44 cm.

Hence, perimeter of ||gm ABCD = 44 cm.

Exercise 15(E)

Question 1(a)

In the given figure, AE = 5 cm and EC = 7 cm, then area of △ ADE : area of △ ABC is :

5 : 7
7 : 5
25 : 144
144 : 25

Answer

From figure,

In △ ADE and △ ABC,

⇒ ∠DAE = ∠BAC (Common angle)

⇒ ∠ADE = ∠ABC (Corresponding angles are equal)

∴ △ ADE ~ △ ABC (By A.A. postulate)

From figure,

AC = AE + EC = 5 + 7 = 12 cm.

We know that,

The areas of two similar triangles are proportional to the squares on their corresponding sides.

$\therefore \dfrac{\text{Area of △ ADE}}{\text{Area of △ ABC}} = \dfrac{AE^2}{AC^2} \\[1em] = \dfrac{5^2}{12^2} \\[1em] = \dfrac{25}{144} \\[1em] = 25 : 144.$

Hence, Option 3 is the correct option.

Question 1(b)

If AD = 5 cm and BD = 2 cm, then area of △ ADE : area of trapezium DBCE is equal to :

5 : 2
2 : 5
24 : 25
25 : 24

Answer

From figure,

In △ ADE and △ ABC,

⇒ ∠DAE = ∠BAC (Common angle)

⇒ ∠ADE = ∠ABC (Corresponding angles are equal)

∴ △ ADE ~ △ ABC (By A.A. postulate)

From figure,

AB = AD + DB = 5 + 2 = 7 cm.

We know that,

The areas of two similar triangles are proportional to the squares on their corresponding sides.

$\therefore \dfrac{\text{Area of △ ADE}}{\text{Area of △ ABC}} = \dfrac{AD^2}{AB^2} \\[1em] = \dfrac{5^2}{7^2} \\[1em] = \dfrac{25}{49} \\[1em] = 25 : 49.$

Let area of △ ADE = 25x and area of △ ABC = 49x.

From figure,

Area of trapezium DBCE = Area of △ ABC - Area of △ ADE = 49x - 25x = 24x.

$\therefore \dfrac{\text{Area of △ ADE}}{\text{Area of trapezium DBCE}} = \dfrac{25x}{24x} = \dfrac{25}{24}$

⇒ Area of △ ADE : Area of trapezium DBCE = 25 : 24.

Hence, Option 4 is the correct option.

Question 1(c)

In the given figure, AD : DB = 2 : 5, then area of △ ODE : area of △ OCB is :

4 : 49
49 : 4
4 : 25
25 : 4

Answer

Given,

AD : DB = 2 : 5

Let AD = 2x and DB = 5x

From figure,

AB = AD + DB = 2x + 5x = 7x.

In △ ADE and △ ABC,

⇒ ∠DAE = ∠BAC (Common angle)

⇒ ∠ADE = ∠ABC (Corresponding angles are equal)

∴ △ ADE ~ △ ABC (By A.A. postulate)

We know that,

Corresponding sides of similar triangles are in proportion.

$\therefore \dfrac{DE}{BC} = \dfrac{AD}{AB} \\[1em] \Rightarrow \dfrac{DE}{BC} = \dfrac{2x}{7x} \\[1em] \Rightarrow \dfrac{DE}{BC} = \dfrac{2}{7}.$

In △ ODE and △ OCB,

⇒ ∠DOE = ∠BOC (Vertically opposite angle are equal)

⇒ ∠ODE = ∠OCB (Alternate angles are equal)

∴ △ ODE ~ △ OCB (By A.A. postulate)

We know that,

The areas of two similar triangles are proportional to the squares on their corresponding sides.

$\Rightarrow \dfrac{\text{Area of △ ODE}}{\text{Area of △ OCB}} = \dfrac{DE^2}{BC^2} \\[1em] = \dfrac{2^2}{7^2} \\[1em] = \dfrac{4}{49} \\[1em] = 4 : 49.$

Hence, Option 1 is the correct option.

Question 1(d)

In the given figure, area of △ ADE : area of trapezium BCED = 25 : 39, then AD : BD is :

5 : 8
8 : 5
3 : 5
5 : 3

Answer

In △ ADE and △ ABC,

⇒ ∠ADE = ∠ABC (Corresponding angles are equal)

⇒ ∠DAE = ∠BAC (Common angle)

∴ △ ADE ~ △ ABC (By A.A. postulate)

Given,

Area of △ ADE : Area of trapezium BCED = 25 : 39

Let area of △ ADE = 25x and area of trapezium BCED = 39x.

From figure,

Area of △ ABC = Area of △ ADE + Area of trapezium BCED = 25x + 39x = 64x.

We know that,

The areas of two similar triangles are proportional to the squares on their corresponding sides.

$\therefore \dfrac{\text{Area of △ ADE}}{\text{Area of △ ABC}} = \dfrac{AD^2}{AB^2} \\[1em] \Rightarrow \dfrac{25x}{64x} = \dfrac{AD^2}{AB^2} \\[1em] \Rightarrow \dfrac{25}{64} = \dfrac{AD^2}{AB^2} \\[1em] \Rightarrow \dfrac{AD}{AB} = \sqrt{\dfrac{25}{64}} = \dfrac{5}{8}.$

Let AD = 5y and AB = 8y.

From figure,

⇒ BD = AB - AD = 8y - 5y = 3y.

⇒ AD : BD = 5y : 3y = 5 : 3.

Hence, Option 4 is the correct option.

Question 1(e)

In the given figure, ∠BAC = 90°, AD is perpendicular to BC, BC = 13 cm and AC = 5 cm, then area of △ ADC : area of △ DBA is :

5 : 13
13 : 5
25 : 144
144 : 25

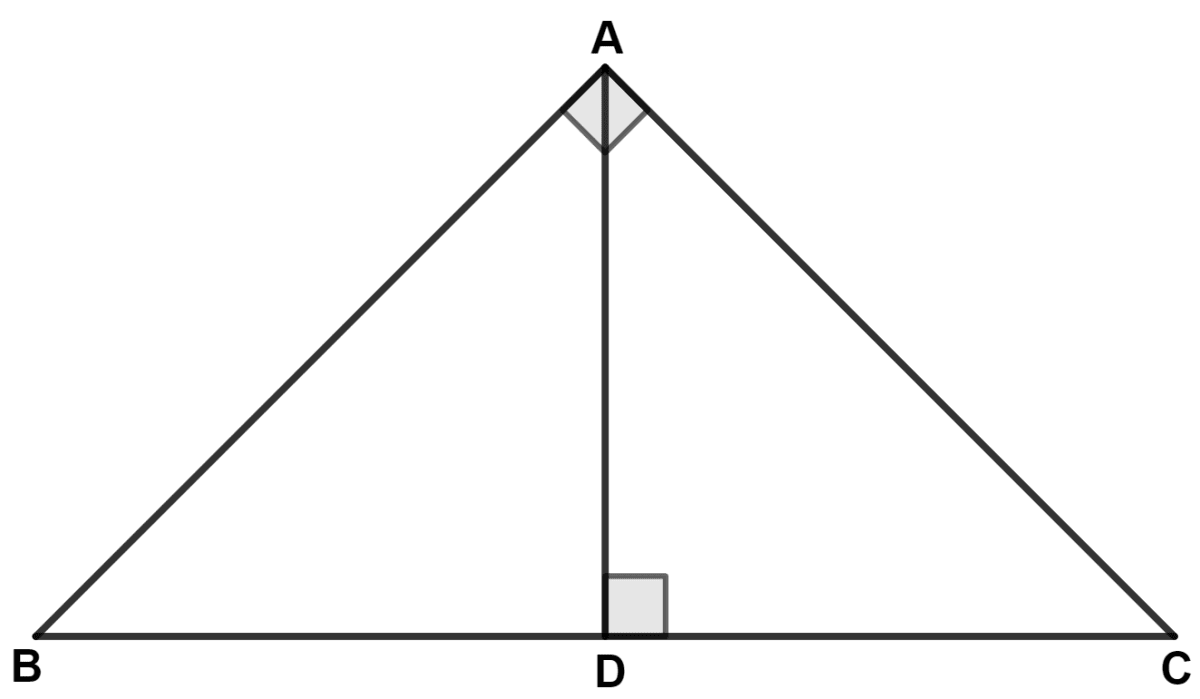
Answer

From figure,

In Δ BAC and Δ ADC,

⇒ ∠BAC = ∠ADC (Both equal to 90°)

⇒ ∠ACB = ∠ACD (Common angle)

∴ Δ BAC ~ Δ ADC (By A.A. postulate)

We know that,

The areas of two similar triangles are proportional to the squares of their corresponding sides.

$\therefore \dfrac{\text{Area of Δ BAC}}{\text{Area of Δ ADC}} = \dfrac{BC^2}{AC^2} \\[1em] \Rightarrow \dfrac{\text{Area of Δ BAC}}{\text{Area of Δ ADC}} = \dfrac{13^2}{5^2} \\[1em] \Rightarrow \dfrac{\text{Area of Δ BAC}}{\text{Area of Δ ADC}} = \dfrac{169}{25}.$

Let, area of Δ BAC = 169x and area of Δ ADC = 25x.

From figure,

Area of Δ DBA = Area of Δ BAC - Area of Δ ADC = 169x - 25x = 144x.

Substituting values we get :

area of △ ADC : area of △ DBA = 25x : 144x = 25 : 144.

Hence, Option 3 is the correct option.

Question 2

A line PQ is drawn parallel to the base BC of ΔABC which meets sides AB and AC at points P and Q respectively. If AP = $\dfrac{1}{3}$ PB; find the value of :

(i) $\dfrac{\text{Area of ΔABC}}{\text{Area of ΔAPQ}}$

(ii) $\dfrac{\text{Area of ΔAPQ}}{\text{Area of trapezium PBCQ}}$

Answer

Given, AP = $\dfrac{1}{3}$ PB

So, $\dfrac{AP}{PB} = \dfrac{1}{3}$

A line PQ is drawn parallel to the base BC of ΔABC which meets sides AB and AC at points P and Q respectively. If AP = 1/3PB; find the value of Area of ΔABC / Area of ΔAPQ. Similarity, Concise Mathematics Solutions ICSE Class 10.

Let AP = x and PB = 3x.

AB = AP + PB = x + 3x = 4x.

$\therefore \dfrac{AP}{AB} = \dfrac{x}{4x} = \dfrac{1}{4}$ .

In ∆APQ and ∆ABC,

∠APQ = ∠ABC and ∠AQP = ∠ACB [Corresponding angles are equal]

Hence, ∆APQ ~ ∆ABC by AA criterion for similarity

(i) We know that,

The ratio of the areas of two similar triangles is equal to the ratio of squares of their corresponding sides.

$\dfrac{\text{Area of ΔABC}}{\text{Area of ΔAPQ}} = \dfrac{\text{AB}^2}{\text{AP}^2} \\[1em] = \dfrac{4^2}{1^2} \\[1em] = \dfrac{16}{1} \\[1em] = 16 : 1$

Hence, $\dfrac{\text{Area of ΔABC}}{\text{Area of ΔAPQ}}$ = 16 : 1.

(ii) From figure,

Area of Trapezium PBCQ = Area of ΔABC – Area of ΔAPQ

From part (i) above we get,

$\dfrac{\text{Area of ΔABC}}{\text{Area of ΔAPQ}} = \dfrac{16}{1}$

Let Area of ΔABC = 16a and Area of ΔAPQ = a

Area of trapezium PBCQ = 16a - a = 15a.

$\dfrac{\text{Area of ΔAPQ}}{\text{Area of trap. PBCQ}} = \dfrac{a}{15a} = \dfrac{1}{15}$ = 1 : 15.

Hence, $\dfrac{\text{Area of ΔAPQ}}{\text{Area of trap. PBCQ}}$ = 1 : 15.

Question 3

The perimeters of two similar triangles are 30 cm and 24 cm. If one side of the first triangle is 12 cm, determine the corresponding side of the second triangle.

Answer

Let the triangles be ∆ABC and ∆DEF.

Given ∆ABC ~ ∆DEF

Since, corresponding sides of similar triangle are proportional to each other.

So, $\dfrac{AB}{DE} = \dfrac{BC}{EF} = \dfrac{AC}{DF}$

Adding numerator and denominator we get :

$\dfrac{AB}{DE} = \dfrac{BC}{EF} = \dfrac{AC}{DF} \\[1em] = \dfrac{AB + BC + AC}{DE + EF + DF} \\[1em] = \dfrac{\text{Perimeter of ΔABC}}{\text{Perimeter of ΔDEF}}$

So,

$\dfrac{\text{Perimeter of ΔABC}}{\text{Perimeter of ΔDEF }} = \dfrac{AB}{DE} \\[1em] \dfrac{30}{24} = \dfrac{12}{DE} \\[1em] DE = \dfrac{24 \times 12}{30} \\[1em] DE = 9.6 \text{ cm}.$

Hence, the length of corresponding side of second triangle is 9.6 cm.

Question 4

In the given figure, AX : XB = 3 : 5.

Find :

(i) the length of BC, if the length of XY is 18 cm.

(ii) the ratio between the areas of trapezium XBCY and triangle ABC.

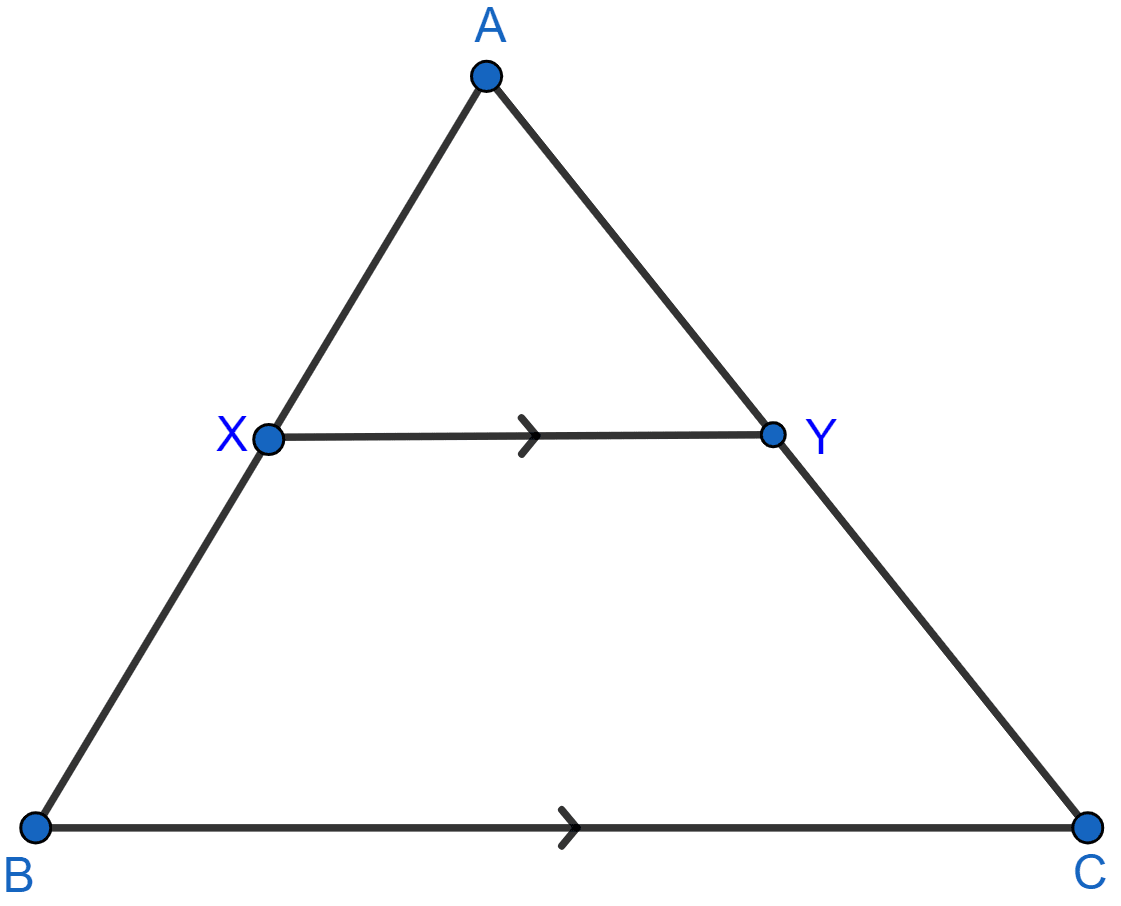
In the given figure, AX : XB = 3 : 5. Find the length of BC, if the length of XY is 18 cm. the ratio between the areas of trapezium XBCY and triangle ABC. Similarity, Concise Mathematics Solutions ICSE Class 10.

Answer

(i) Given, AX : XB = 3 : 5

Let AX = 3a and XB = 5a.

From figure,

AB = AX + XB = 3a + 5a = 8a.

(i) In ΔAXY and ΔABC,

As XY || BC, corresponding angles are equal.

∠AXY = ∠ABC and ∠AYX = ∠ACB

∴ ∆AXY ~ ∆ABC [By AA]

Since, corresponding sides of similar triangle are proportional to each other.

$\therefore \dfrac{AX}{AB} = \dfrac{XY}{BC} \\[1em] \Rightarrow \dfrac{3a}{8a} = \dfrac{18}{BC} \\[1em] \Rightarrow BC = \dfrac{18 \times 8a}{3a} = 48 \text{ cm}.$

Hence, BC = 48 cm.

(ii) We know that,

The ratio of the areas of two similar triangles is equal to the ratio of squares of their corresponding sides.

$\therefore \dfrac{\text{Area of ∆AXY}}{\text{Area of ∆ABC}} = \dfrac{AX^2}{AB^2} \\[1em] = \dfrac{(3a)^2}{(8a)^2} \\[1em] = \dfrac{9a^2}{64a^2} \\[1em] = \dfrac{9}{64}. \\[1em]$

Let area of ∆AXY = 9b and area of ∆ABC = 64b.

From figure,

Area of trapezium XBCY = Area of ∆ABC - Area of ∆AXY

= 64b - 9b = 55b.

$\therefore \dfrac{\text{Area of trap. XBCY}}{\text{Area of ∆ABC}} = \dfrac{55b}{64b} = \dfrac{55}{64}$

Hence, ratio of area of trapezium XBCY and triangle ABC = 55 : 64.

Question 5

ABC is a triangle. PQ is a line segment intersecting AB in P and AC in Q such that PQ || BC and divides triangle ABC into two parts equal in area. Find the value of ratio BP : AB.

Answer

Triangle ABC is shown in the figure below:

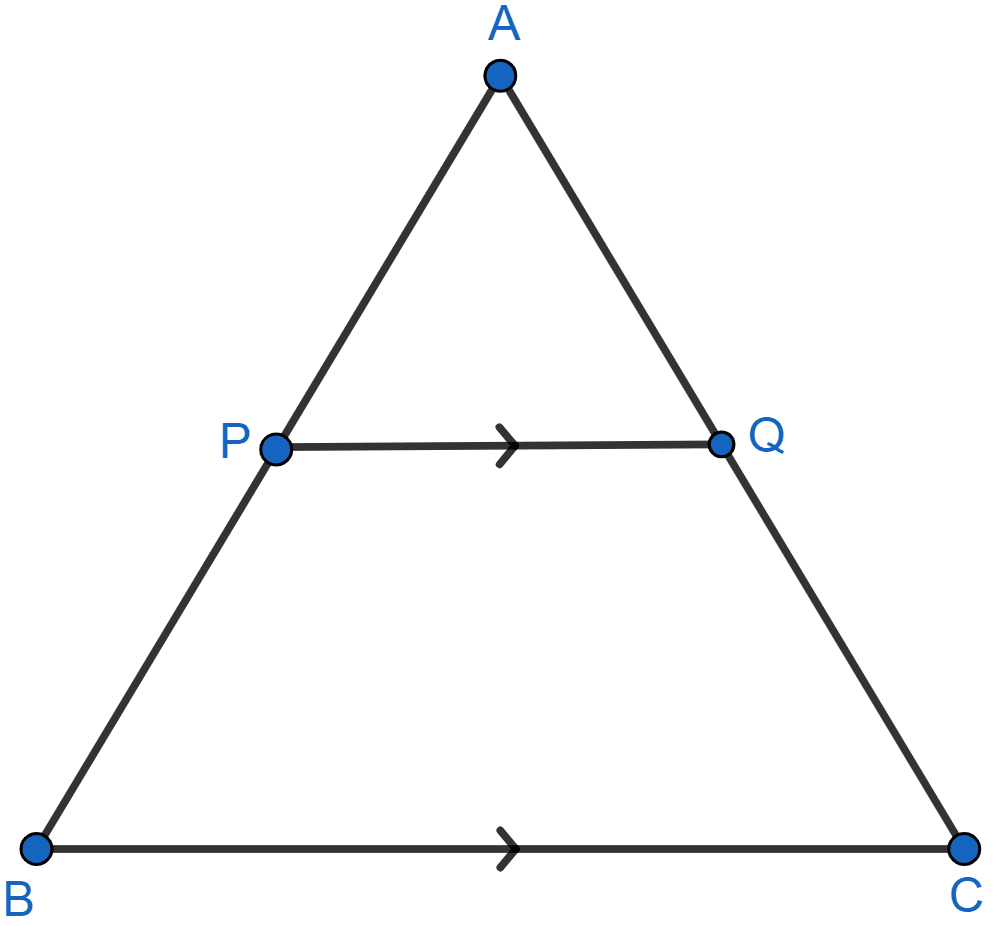
ABC is a triangle. PQ is a line segment intersecting AB in P and AC in Q such that PQ || BC and divides triangle ABC into two parts equal in area. Find the value of ratio BP : AB. Similarity, Concise Mathematics Solutions ICSE Class 10.

In ΔAPQ and ΔABC,

∠PAQ = ∠BAC [Common]

∠APQ = ∠ABC [Corresponding angles are equal]

∴ ΔAPQ ~ ΔABC [By AA].

According to question,

Area of ΔAPQ = $\dfrac{1}{2}$ Area of ΔABC

$\dfrac{\text{Area of ΔAPQ}}{\text{Area of ΔABC}} = \dfrac{1}{2}$

We know that,

The ratio of the areas of two similar triangles is equal to the ratio of squares of their corresponding sides.

$\Rightarrow \dfrac{AP^2}{AB^2} = \dfrac{1}{2} \\[1em] \Rightarrow \dfrac{AP}{AB} = \dfrac{1}{\sqrt{2}}.$

Let AP = x and AB = $\sqrt{2}$ x

From figure,

BP = AB - AP = $\sqrt{2}x - x$

$\therefore \dfrac{BP}{AB} = \dfrac{\sqrt{2}x - x}{\sqrt{2}x} \\[1em] = \dfrac{\sqrt{2} - 1}{\sqrt{2}} \\[1em] = \dfrac{\sqrt{2} - 1}{\sqrt{2}} \times \dfrac{\sqrt{2}}{\sqrt{2}} \\[1em] = \dfrac{2 - \sqrt{2}}{2}.$

Hence, BP : AB = $(\sqrt{2} - 1) : \sqrt{2}$ = $(2 - \sqrt{2}) : 2$ .

Question 6

In the given triangle PQR, LM is parallel to QR and PM : MR = 3 : 4.

Calculate the value of ratio:

(i) $\dfrac{PL}{PQ} \text{ and then } \dfrac{LM}{QR}$

(ii) $\dfrac{\text{ Area of Δ LMN }}{\text{ Area of Δ MNR }}$

(iii) $\dfrac{\text{ Area of Δ LQM }}{\text{ Area of Δ LQN }}$

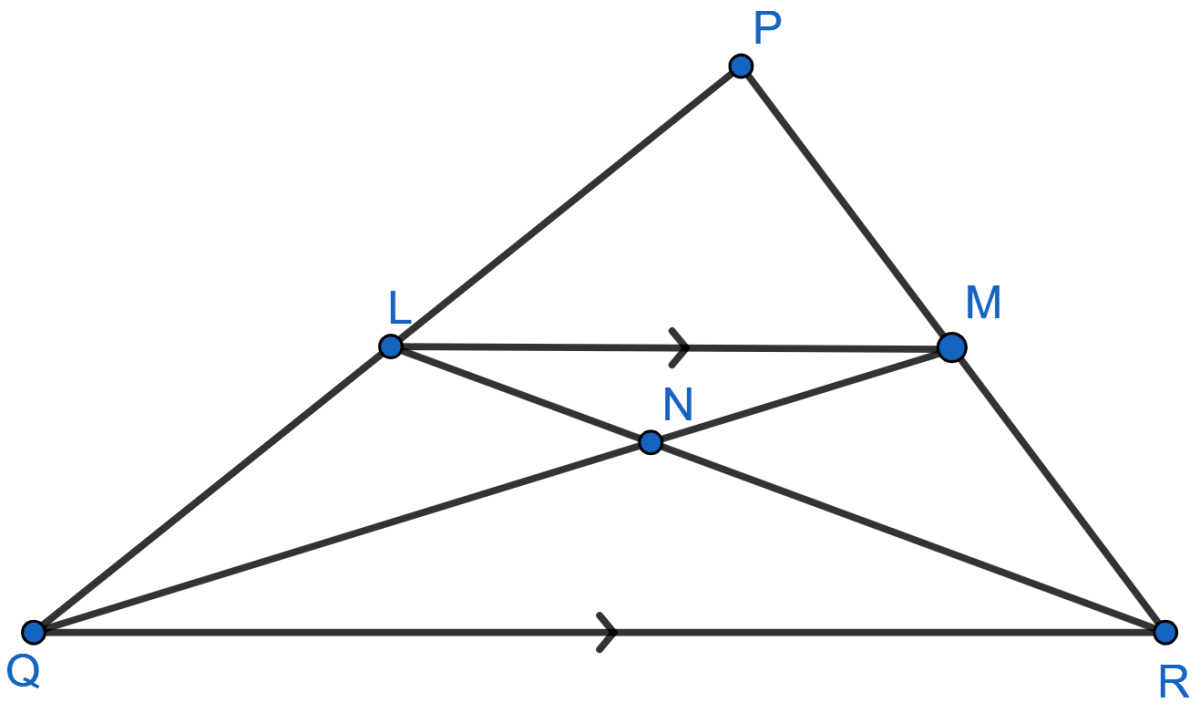
In triangle PQR, LM is parallel to QR and PM : MR = 3 : 4. Calculate the value of ratio PL/PQ LM/QR. Similarity, Concise Mathematics Solutions ICSE Class 10.

Answer

(i) Given,

$\dfrac{PM}{MR} = \dfrac{3}{4}$

Let PM = 3x and MR = 4x.

From figure,

PR = PM + MR = 3x + 4x = 7x.

$\dfrac{PM}{PR} = \dfrac{3x}{7x} = \dfrac{3}{7}$ .

In ΔPLM and ΔPQR,

As LM || QR, corresponding angles are equal.

∠PLM = ∠PQR

∠PML = ∠PRQ

∴ ∆PLM ~ ∆PQR [By AA]

Since, corresponding sides of similar triangles are proportional to each other we have :

$\therefore \dfrac{PL}{PQ} = \dfrac{PM}{PR} = \dfrac{LM}{QR} \\[1em] \therefore \dfrac{PL}{PQ} = \dfrac{LM}{QR} = \dfrac{3}{7}.$

Hence, PL : PQ = 3 : 7 and LM : QR = 3 : 7.

(ii) As ΔLMN and ΔMNR have common vertex at M and their bases LN and NR are along the same straight line.

$\therefore \dfrac{\text{Area of ΔLMN}}{\text{Area of ΔMNR}} = \dfrac{\text{LN}}{\text{NR}}$ .....(1)

Now, in ΔLMN and ΔRNQ we have,

⇒ ∠NLM = ∠NRQ [Alternate angles are equal]

⇒ ∠LMN = ∠NQR [Alternate angles are equal]

∴ ∆LNM ~ ∆RNQ [By AA]

Since corresponding sides of similar triangle are proportional to each other, we have :

$\dfrac{MN}{QN} = \dfrac{LN}{NR} = \dfrac{LM}{QR} = \dfrac{3}{7}$

Substituting value in (1) we get :

$\dfrac{\text{Area of ΔLMN}}{\text{Area of ΔMNR}} = \dfrac{3}{7}$ .

(iii) From part (ii) we get :

$\dfrac{MN}{QN} = \dfrac{3}{7}$

Let MN = 3a and QN = 7a

From figure,

MQ = MN + QN = 3a + 7a = 10a.

As ΔLQM and ΔLQN have common vertex at L and their bases QM and QN are along the same straight line.

$\dfrac{\text{ Area of ΔLQM }}{\text{ Area of ΔLQN }} = \dfrac{QM}{QN} = \dfrac{10a}{7a} = \dfrac{10}{7}$ .

Hence, $\dfrac{\text{ Area of ΔLQM }}{\text{ Area of ΔLQN }} =\dfrac{10}{7}$

Question 7

In the figure, given below, ABCD is a parallelogram. P is a point on BC such that BP : PC = 1 : 2. DP produced meets AB produced at Q. Given the area of triangle CPQ = 20 cm².

Calculate :

(i) area of triangle CDP,

(ii) area of parallelogram ABCD.

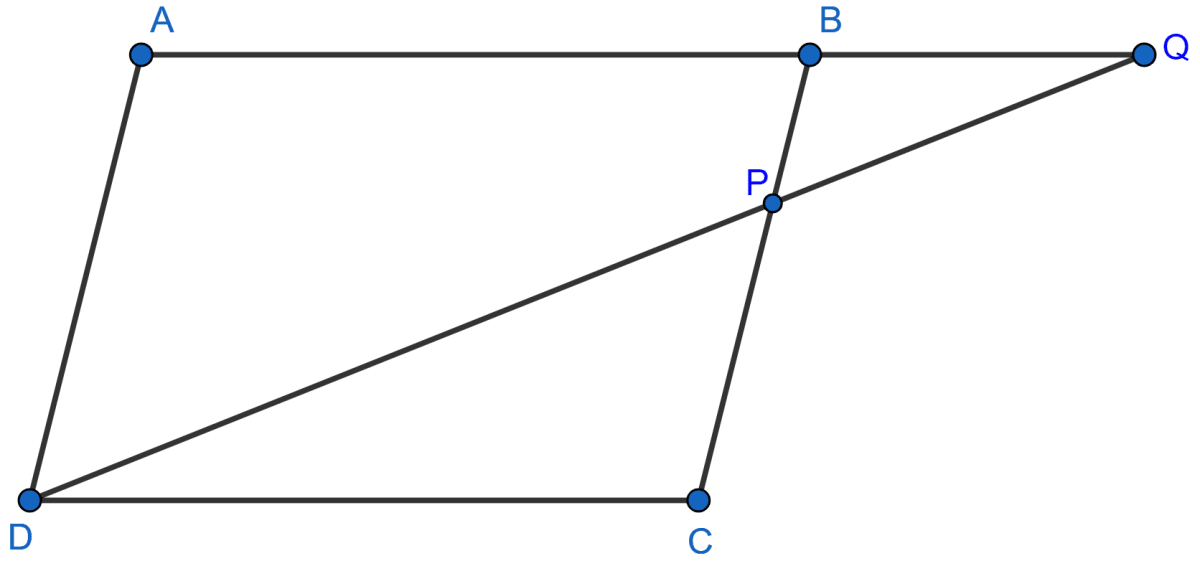
In the figure, ABCD is a parallelogram. P is a point on BC such that BP : PC = 1 : 2. DP produced meets AB produced at Q. Given the area of triangle CPQ = 20 cm^2, Calculate area of triangle CDP, area of parallelogram ABCD. Similarity, Concise Mathematics Solutions ICSE Class 10.

Answer

(i) In △BPQ and △CPD,

⇒ ∠BPQ = ∠CPD [Vertically opposite angles are equal]

⇒ ∠BQP = ∠PDC [Alternate angles are equal]

∴ △BPQ ~ △CPD [By AA]

Since, corresponding sides of similar triangle are proportional to each other.

$\therefore \dfrac{BP}{PC} = \dfrac{PQ}{PD} = \dfrac{BQ}{CD} = \dfrac{1}{2}$ .

As ΔBPQ and ΔCPQ have common vertex at Q and their bases BP and CP are along the same straight line.

So,

$\Rightarrow \dfrac{\text{Area of ΔBPQ}}{\text{Area of ΔCPQ}} = \dfrac{BP}{PC} \\[1em] \Rightarrow \dfrac{\text{Area of ΔBPQ}}{20} = \dfrac{1}{2} \\[1em] \Rightarrow \text{Area of ΔBPQ} = \dfrac{20}{2} \\[1em] \Rightarrow \text{Area of ΔBPQ} = 10 \text{ cm}^2$

We know that,

The ratio of the areas of two similar triangles is equal to the ratio of squares of their corresponding sides.

$\phantom{\Rightarrow} \dfrac{\text{Area of ΔBPQ}}{\text{Area of ΔCPD}} = \dfrac{BP^2}{PC^2} \\[1em] \Rightarrow \dfrac{10}{\text{Area of ΔCPD}} = \dfrac{1^2}{2^2} \\[1em] \Rightarrow \text{ Area of ΔCPD} = \dfrac{10 \times 4}{1} \\[1em] \Rightarrow \text{ Area of ΔCPD} = 40 \text{ cm}^2.$

Hence, area of ΔCPD = 40 cm².

(ii) From part (i),

$\dfrac{PQ}{PD} = \dfrac{1}{2}$

Let PQ = x and PD = 2x.

From figure,

QD = PQ + PD = x + 2x = 3x.

$\dfrac{QD}{QP} = \dfrac{3x}{x} = 3$ ........(1)

In △BPQ and △AQD,

⇒ ∠QBP = ∠QAD [Corresponding angles are equal]

⇒ ∠BQP = ∠AQD [Common]

∴ △BPQ ~ △AQD [By AA]

Since, corresponding sides of similar triangle are proportional to each other.

$\therefore \dfrac{AQ}{BQ} = \dfrac{QD}{QP} = \dfrac{AD}{BP} = 3.$

We know that,

The ratio of the areas of two similar triangles is equal to the ratio of squares of their corresponding sides.

$\therefore \dfrac{\text{Area of △AQD}}{\text{Area of △BPQ}} = \Big(\dfrac{AQ}{BQ}\Big)^2 \\[1em] \Rightarrow \dfrac{\text{Area of △AQD}}{10} = 3^2 \\[1em] \Rightarrow \dfrac{\text{Area of △AQD}}{10} = 9 \\[1em] \Rightarrow \text{Area of △AQD} = 90 \text{ cm}^2.$

Area of trapezium ADPB = Area of △AQD - Area of △BPQ = 90 - 10 = 80 cm².

Area of || gm ABCD = Area of △CDP + Area of trapezium ADPB = 40 + 80 = 120 cm².

Hence, area of || gm ABCD = 120 cm².

Question 8

In the given figure, BC is parallel to DE. Area of triangle ABC = 25 cm², Area of trapezium BCED = 24 cm² and DE = 14 cm. Calculate the length of BC.

Also, find the area of triangle BCD.

In the figure, BC is parallel to DE. Area of triangle ABC = 25 cm^2, Area of trapezium BCED = 24 cm^2 and DE = 14 cm. Calculate the length of BC. Also, find the area of triangle BCD. Similarity, Concise Mathematics Solutions ICSE Class 10.

Answer

Area of △ADE = Area of △ABC + Area of trapezium BCED = 25 + 24 = 49 cm².

Given,

BC || DE.

∠ABC = ∠ADE [Corresponding angles are equal]

∠ACB = ∠AED [Corresponding angles are equal]

∴ △ABC ~ △ADE [By AA]

We know that,

The ratio of the areas of two similar triangles is equal to the ratio of squares of their corresponding sides.

$\therefore \dfrac{\text{Area of △ABC}}{\text{Area of △ADE}} = \dfrac{BC^2}{DE^2}\\[1em] \Rightarrow \dfrac{25}{49} = \dfrac{BC^2}{14^2} \\[1em] \Rightarrow BC^2 = \dfrac{25}{49} \times 196 \\[1em] \Rightarrow BC^2 = 100 \\[1em] \Rightarrow BC = 10 \text{ cm}.$

Let height of trapezium BCED be h cm.

Area = $\dfrac{1}{2}$ × (Sum of || sides) × h

⇒ 24 = $\dfrac{1}{2}$ × (BC + DE) × h

⇒ 24 × 2 = (BC + DE) × h

⇒ 48 = (10 + 14) × h

⇒ 24h = 48

⇒ h = 2 cm.

Area of △BCD = $\dfrac{1}{2}$ × base × height

= $\dfrac{1}{2}$ × BC × h

= $\dfrac{1}{2}$ × 10 × 2

= 10 cm².

Hence, BC = 10 cm and area of △BCD = 10 cm².

Question 9

In the given figure, ABC is a triangle. DE is parallel to BC and $\dfrac{AD}{DB} = \dfrac{3}{2}$ .

(i) Determine the ratios $\dfrac{AD}{AB} \text{ and } \dfrac{DE}{BC}$ .

(ii) Prove that △DEF is similar to △CBF. Hence, find $\dfrac{EF}{FB}$ .

(iii) What is the ratio of the areas of △DEF and △BFC?

In the figure, ABC is a triangle. DE is parallel to BC and AD/DB = 3/2. Determine the ratios AD/AB and DE/BC. Similarity, Concise Mathematics Solutions ICSE Class 10.

Answer

(i) Given,

$\dfrac{AD}{DB} = \dfrac{3}{2}$

Let AD = 3x and BD = 2x.

From figure,

AB = AD + DB = 3x + 2x = 5x.

$\dfrac{AD}{AB} = \dfrac{3x}{5x} = \dfrac{3}{5}$ .

In △ADE and △ABC,

∠A = ∠A [Common]

∠ADE = ∠ABC [Corresponding angles are equal]

∴ △ADE ~ △ABC [By AA]

Since, corresponding sides of similar triangle are proportional to each other.

$\therefore \dfrac{DE}{BC} = \dfrac{AD}{AB} = \dfrac{3}{5}$ ...........(1)

Hence, $\dfrac{AD}{AB} = \dfrac{DE}{BC} = \dfrac{3}{5}$ .

(ii) In △DEF and △CBF,

∠FDE = ∠FCB (Alternate angles are equal)

∠DFE = ∠BFC (Vertically opposite angles are equal)

∴ △DEF ~ △CBF [By AA]

Since, corresponding sides of similar triangle are proportional to each other.

$\therefore \dfrac{EF}{FB} = \dfrac{DE}{BC} = \dfrac{3}{5}$

Hence, $\dfrac{EF}{FB} = \dfrac{3}{5}$ .

(iii) We know that,

The ratio of the areas of two similar triangles is equal to the ratio of squares of their corresponding sides.

$\therefore \dfrac{\text{Area of △DFE}}{\text{Area of △CBF}} = \dfrac{EF^2}{FB^2}\\[1em] = \dfrac{3^2}{5^2} = \dfrac{9}{25}.$

Hence, ratio of the areas of △DEF and △BFC = 9 : 25.

Question 10

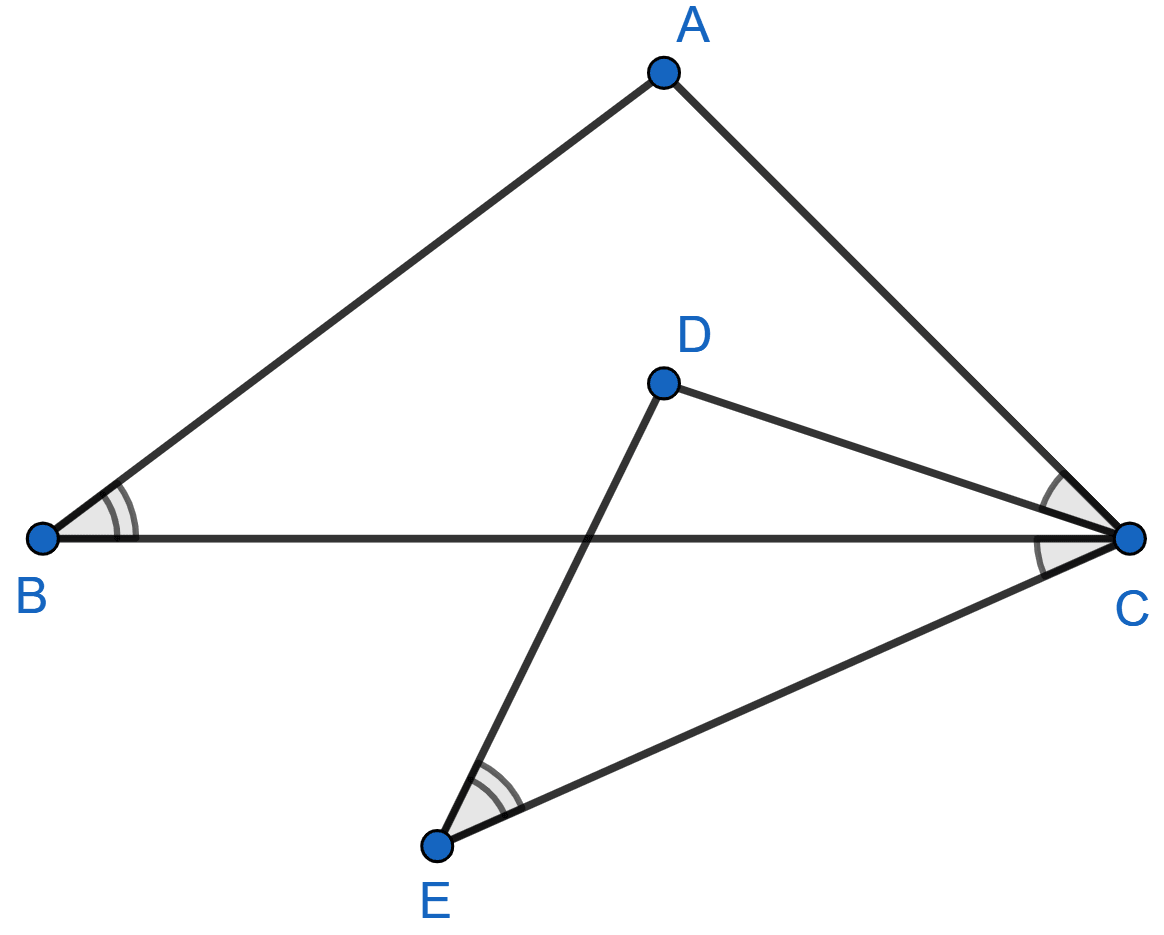
In the given figure,

∠B = ∠E, ∠ACD = ∠BCE, AB = 10.4 cm and DE = 7.8 cm. Find the ratio between areas of the △ABC and △DEC.

Answer

Given,

⇒ ∠ACD = ∠BCE

⇒ ∠ACD + ∠BCD = ∠BCE + ∠BCD

⇒ ∠ACB = ∠DCE

Also, ∠B = ∠E

∴ △ABC ~ △DEC [By AA]

We know that,

The ratio of the areas of two similar triangles is equal to the ratio of squares of their corresponding sides.

$\therefore \dfrac{\text{Area of △ABC}}{\text{Area of △DEC}} = \dfrac{AB^2}{DE^2}\\[1em] = \Big(\dfrac{10.4}{7.8}\Big)^2 = \Big(\dfrac{4}{3}\Big)^2 \\[1em] = \dfrac{16}{9}.$

Hence, ratio between areas of the △ABC and △DEC = 16 : 9.

Exercise 15(F)

Question 1(a)

A model of a vehicle is made to a scale of 1 : 25. If length of the vehicle is 1.6 m; the length of its model is :

6.4 cm
0.64 m
40 cm
15.625 m

Answer

Given,

Scale factor (k) = 1 : 25 or $\dfrac{1}{25}$

By formula,

⇒ Length of model = k × Length of vehicle

⇒ Length of model = $\dfrac{1}{25} \times 1.6$ = 0.064 m = 0.064 × 100 = 6.4 cm.

Hence, Option 1 is the correct option.

Question 1(b)

The length and the breadth of the model of a rectangular object are 12 cm and 7 cm respectively. If the scale factor is 1 : 20, the actual length and breadth of object are :

1 m & 20 m
2.4 m & 1.4 m
12 cm & 140 cm
1.2 m & 0.7 m

Answer

Given,

Scale factor (k) = 1 : 20 or $\dfrac{1}{20}$

By formula,

⇒ Length of model = k × Length of object

⇒ Length of object = $\dfrac{1}{k}$ × Length of model

⇒ Length of object = $\dfrac{1}{\dfrac{1}{20}} \times 12$ = 20 × 12 = 240 cm = $\dfrac{240}{100}$ = 2.4 m.

By formula,

⇒ Breadth of model = k × Breadth of object

⇒ Breadth of object = $\dfrac{1}{k}$ × Breadth of model

⇒ Breadth of object = $\dfrac{1}{\dfrac{1}{20}} \times 7$ = 20 × 7 = 140 cm = $\dfrac{140}{100}$ = 1.4 m.

Hence, Option 2 is the correct option.

Question 1(c)

The length of a boat is 2.4 m and the length of its model is 16 cm. The scale factor is :

15 : 1
2 : 3
1 : 15
3 : 2

Answer

Let scale factor be k.

Given,

Length of model = 16 cm

Length of boat = 2.4 m = 2.4 × 100 = 240 cm.

By formula,

⇒ Length of model = Scale factor × Length of boat

Substituting values we get :

⇒ 16 = k × 240

⇒ k = $\dfrac{16}{240} = \dfrac{1}{15}$ = 1 : 15.

Hence, Option 3 is the correct option.

Question 1(d)

The floor area of a room is 96 m² and area of the floor in the model of the room is 96 cm². The scale factor is :

10 : 1
100 : 1
1 : 10
1 : 100

Answer

Let scale factor be k.

Given,

Floor area of room = 96 m²

Floor area of model = 96 cm² = $\dfrac{96}{100^2} = \dfrac{96}{10000}$ = 96 × 10^-4 m²

By formula,

Floor area of model = (Scale factor)² × Floor area of room

Substituting values we get :

⇒ 96 × 10^-4 = k² × 96

⇒ k² = $\dfrac{96 \times 10^{-4}}{96}$

⇒ k² = 10^-4

⇒ k = $\sqrt{10^{-4}}$

⇒ k = 10^-2 = $\dfrac{1}{10^2} = \dfrac{1}{100}$ = 1 : 100.

Hence, Option 4 is the correct option.

Question 1(e)

A and B are two similar containers with capacities 216 m³ and 1000 m³ respectively. The scale factor of B with respect to A is :

125 : 216
5 : 3
3 : 5
216 : 125

Answer

Let scale factor of B with respect to A be k.

Given,

A and B are two similar containers with capacities 216 m³ and 1000 m³ respectively.

Volume of container B = k³ × Volume of container A

⇒ 1000 = k³ × 216

⇒ k³ = $\dfrac{1000}{216}$

⇒ k³ = $\Big(\dfrac{10}{6}\Big)^3$

⇒ k = $\dfrac{10}{6} = \dfrac{5}{3}$ = 5 : 3.

Hence, Option 2 is the correct option.

Question 2

A triangle ABC has been enlarged by scale factor m = 2.5 to the triangle A' B' C'. Calculate :

(i) the length of AB, if A'B' = 6 cm.

(ii) the length of C'A' if CA = 4 cm.

Answer

Given that, ΔABC has been enlarged by scale factor m of 2.5 to ΔA'B'C'.

(i)

∴ A'B' = m × AB

⇒ 6 = 2.5 × AB

⇒ AB = $\dfrac{6}{2.5} = 2.4$ cm.

Hence, AB = 2.4 cm

(ii)

∴ C'A' = m × CA

⇒ C'A' = 2.5 × 4

⇒ C'A' = 10 cm.

Hence, C'A' = 10 cm.

Question 3

A triangle LMN has been reduced by scale factor 0.8 to the triangle L'M'N'. Calculate:

(i) the length of M'N', if MN = 8 cm.

(ii) the length of LM, if L'M' = 5.4 cm.

Answer

Given, ΔLMN has been reduced by a scale factor (k) = 0.8 to Δ L'M'N'.

(i)

∴ M'N' = k × MN

⇒ M'N' = 0.8 × 8

⇒ M'N' = 6.4 cm

Hence, M'N' = 6.4 cm.

(ii)

∴ L'M' = k × LM

⇒ 5.4 = 0.8 × LM

⇒ LM = $\dfrac{5.4}{0.8} = 6.75$ cm.

Hence, LM = 6.75 cm.

Question 4

A model of an aeroplane is made to a scale of 1 : 400. Calculate :

(i) the length, in cm of the model; if the length of the aeroplane is 40 m.

(ii) the length, in m, of the aeroplane, if length of its model is 16 cm.

Answer

(i) Given,

Scale-factor (k) = $\dfrac{1}{400}$

⇒ Length of model = k × Length of aeroplane

⇒ Length of model = $\dfrac{1}{400} \times 40 = \dfrac{1}{10}$ = 0.1 m = 10 cm.

Hence, length of model = 10 cm.

(ii) Given,

Scale-factor (k) = $\dfrac{1}{400}$

⇒ Length of model = k × Length of aeroplane

⇒ 16 = $\dfrac{1}{400}$ × Length of aeroplane

⇒ 16 × 400 = Length of aeroplane

⇒ Length of aeroplane = 6400 cm = 64 m.

Hence, length of aeroplane = 64 m.

Question 5

The dimensions of the model of a multistorey building are 1.2 m × 75 cm × 2 m. If the scale factor is 1 : 30; find the actual dimensions of the building.

Answer

Dimensions of model = 1.2 m × 75 cm × 2 m = 1.2 m × 0.75 m × 2 m

So,

Length = 1.2 m

Breadth = 0.75 m

Height = 2 m.

$\phantom{\Rightarrow} \dfrac{\text{Length of model}}{\text{Length of building}} = k \\[1em] \Rightarrow \dfrac{1.2}{\text{Length of building}} = \dfrac{1}{30} \\[1em] \Rightarrow \text{Length of building} = 1.2 \times 30 = 36 \text{ m}. \\[2em] \phantom{\Rightarrow} \dfrac{\text{Breadth of model}}{\text{Breadth of building}} = k \\[1em] \Rightarrow \dfrac{0.75}{\text{Breadth of building}} = \dfrac{1}{30} \\[1em] \Rightarrow \text{Breadth of building} = 0.75 \times 30 = 22.5 \text{ m}. \\[2em] \phantom{\Rightarrow} \dfrac{\text{Height of model}}{\text{Height of building}} = k \\[1em] \Rightarrow \dfrac{\text{2}}{\text{Height of building}} = \dfrac{1}{30} \\[1em] \Rightarrow \text{Height of building} = 2 \times 30 = 60 \text{ m}.$

Hence, actual dimension of building = 36 m × 22.5 m × 60 m.

Question 6

On a map drawn to scale of 1 : 2,50,000; a triangular plot of land has the following measurements : AB = 3 cm, BC = 4 cm and angle ABC = 90°.

Calculate :

(i) the actual length of AB and BC in km

(ii) the area of the plot in sq. km.

Answer

(i) Given,

Scale factor for reduction (k) = $\dfrac{1}{250000}$

⇒ Length of AB in model = k × Length of AB

⇒ 3 = $\dfrac{1}{250000}$ × Length of AB

⇒ Length of AB = 3 × 250000 = 750000 cm = $\dfrac{750000}{100 \times 1000}$ = 7.5 km.

⇒ Length of BC in model = k × Length of BC

⇒ 4 = $\dfrac{1}{250000}$ × Length of BC

⇒ Length of BC = 4 × 250000 = 1000000 cm = $\dfrac{1000000}{100 \times 1000}$ = 10 km.

Hence, actual length of AB = 7.5 km and BC = 10 km.

(ii) Area of plot = $\dfrac{1}{2} \times$ base × height

= $\dfrac{1}{2}$ × BC × AB

= $\dfrac{1}{2}$ × 10 × 7.5

= 37.5 sq. km.

Hence, area of plot = 37.5 sq. km.

Question 7

A model of a ship is made to a scale 1 : 300.

(i) The length of the model of the ship is 2 m. Calculate the length of the ship.

(ii) The area of the deck of the ship is 180000 m². Calculate the area of the deck of the model.

(iii) The volume of the model is 6.5 m³. Calculate the volume of the ship.

Answer

(i) Given,

Scale factor (k) = 1 : 300 = $\dfrac{1}{300}$

$\phantom{\Rightarrow} \dfrac{\text{Length of model of ship}}{\text{Length of ship}} = k \\[1em] \Rightarrow \dfrac{2}{\text{Length of ship}} = \dfrac{1}{300} \\[1em] \Rightarrow \text{Length of ship} = 2 \times 300 = 600 \text{ m}.$

Hence, length of ship = 600 m.

(ii)

$\phantom{\Rightarrow} \dfrac{\text{Area of deck of model}}{\text{Area of deck of ship}} = k^2 \\[1em] \Rightarrow \dfrac{\text{Area of deck of model}}{180000} = \dfrac{1}{300} \times \dfrac{1}{300} \\[1em] \Rightarrow \text{Area of deck of model} = 180000 \times \dfrac{1}{90000} = 2 \text{ m}^2.$

Hence, area of deck of model = 2 m².

(iii)

$\Rightarrow \dfrac{\text{Volume of model of ship}}{\text{Volume of ship}} = k^3 \\[1em] \Rightarrow \dfrac{6.5}{\text{Volume of ship}} = \Big(\dfrac{1}{300}\Big)^3 \\[1em] \Rightarrow \text{Volume of ship} = 6.5 \times (300)^3 = 6.5 \times 27000000 \text{ m}^3 \\[1em] = 175500000 \text{ m}^3.$

Hence, volume of ship = 175500000 m³.

Test Yourself

Question 1(a)

Triangles ABC and A'B'C' are similar to each other, the corresponding vertices of the two triangles are :

A and B'
C and A'
B and B'
C' and A

Answer

Given,

Triangles ABC and A'B'C' are similar to each other.

So, the corresponding vertices are A and A', B and B', C and C'.

Hence, Option 3 is the correct option.

Question 1(b)

Triangles ABC and RSP are similar to each other, the corresponding sides of the two triangles are :

AB and RS
BC and RP
AC and SP
AB and RP

Answer

Given,

Triangles ABC and RSP are similar to each other.

We know that,

Corresponding sides of similar triangle are proportional.

$\therefore \dfrac{AB}{RS} = \dfrac{BC}{SP} = \dfrac{CA}{PR}$

Hence, Option 1 is the correct option.

Question 1(c)

A : Two similar triangles are congruent.

B : Two congruent triangles are similar, then :

A is true, B is false
A is false, B is true
A is false, B is false
A is true, B is true

Answer

We know that,

Congruent triangles have both the same shape and the same size but it is not necessary that similar triangle are equal in size.

Hence, Option 2 is the correct option.

Question 1(d)

Triangles ABC and PQR are similar to each other, then :

$\dfrac{\text{Ar.(△ABC)}}{\text{Ar.(△PQR)}} = \dfrac{BC^2}{PQ^2}$
$\dfrac{AB^2}{PQ^2} = \dfrac{AC^2}{PR^2}$
$\dfrac{\text{Ar.(△BAC)}}{\text{Ar.(△QPR)}} \ne \dfrac{AB^2}{QP^2}$
$\dfrac{AC^2}{PR^2} = \dfrac{BC^2}{PQ^2}$

Answer

We know that,

The areas of two similar triangles are proportional to the squares on their corresponding sides.

$\Rightarrow \dfrac{\text{Ar.(△ABC)}}{\text{Ar.(△PQR)}} = \dfrac{AB^2}{PQ^2}$ .......(1)

$\Rightarrow \dfrac{\text{Ar.(△ABC)}}{\text{Ar.(△PQR)}} = \dfrac{AC^2}{PR^2}$ .........(2)

From equation (1) and (2), we get :

$\Rightarrow \dfrac{AB^2}{PQ^2} = \dfrac{AC^2}{PR^2}$

Hence, Option 2 is the correct option.

Question 1(e)

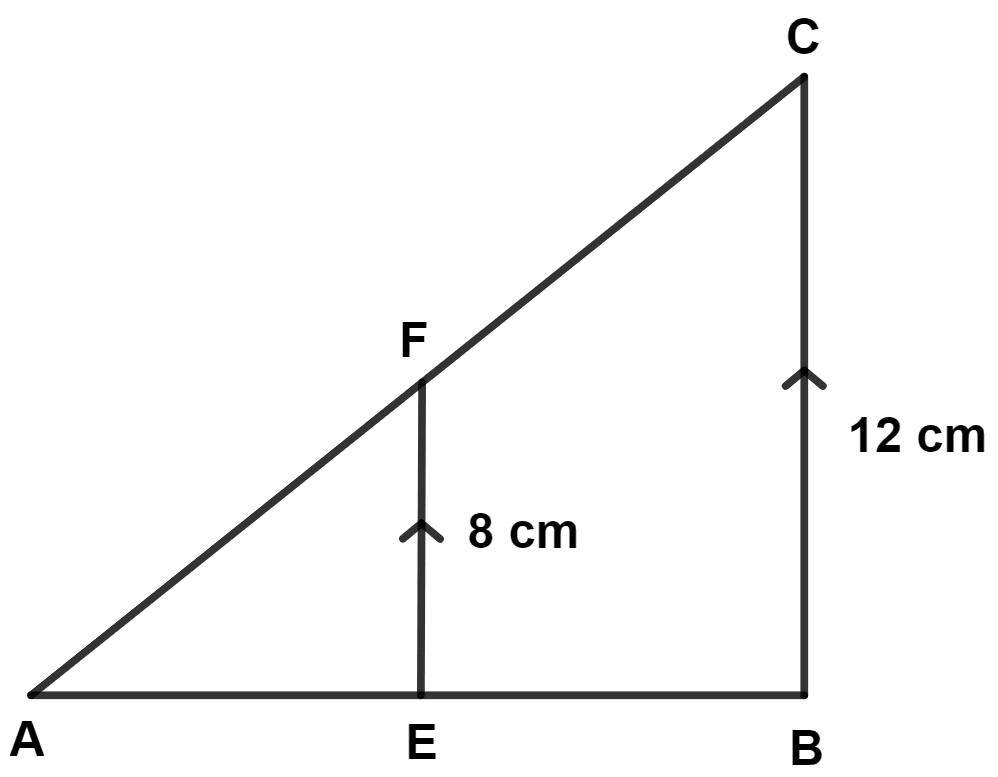
In the given figure, EF is parallel to BC. If area of triangle ABC is 576 cm², the area of triangle AEF is :

128 cm²
288 cm²
256 cm²
768 cm²

In the given figure, EF is parallel to BC. If area of triangle ABC is 576 cm^2, the area of triangle AEF is : Similarity, Concise Mathematics Solutions ICSE Class 10.

Answer

From figure,

In △ AEF and △ ABC,

⇒ ∠EAF = ∠BAC (Common angle)

⇒ ∠AEF = ∠ABC (Corresponding angle)

∴ △ AEF ~ △ ABC (By A.A. axiom)

We know that,

The areas of two similar triangles are proportional to the squares of their corresponding sides.

$\therefore \dfrac{\text{Area of △ AEF}}{\text{Area of △ ABC}} = \dfrac{EF^2}{BC^2} \\[1em] \Rightarrow \dfrac{\text{Area of △ AEF}}{576} = \dfrac{8^2}{12^2} \\[1em] \Rightarrow \dfrac{\text{Area of △ AEF}}{576} = \dfrac{64}{144} \\[1em] \Rightarrow \text{Area of △ AEF} = \dfrac{64}{144} \times 576 \\[1em] \Rightarrow \text{Area of △ AEF} = 64 \times 4 = 256 \text{ cm}^2.$

Hence, Option 3 is the correct option.

Question 1(f)

In △ABD, C is a point on side BD such that ∠ACD = ∠BAD. Is △BAD similar to triangle ACD? If yes, then which axiom is satisfied :

Yes, ASA
Yes, SAS
Yes, AA
No

Answer

From figure,

In △ BAD and △ ACD,

⇒ ∠BAD = ∠ACD (Given)

⇒ ∠ADB = ∠ADC (Common angle)

∴ △ BAD ~ △ ACD (By A.A. axiom)

Hence, Option 3 is the correct option.

Question 1(g)

The model of a ship is made to a scale of 3 : 500. If the length of the model is 1.5 m, the length of ship is :

750 m
1000 m
450 m
250 m

Answer

Given,

Scale factor (k) = 3 : 500

By formula,

⇒ Length of model = Scale factor × Length of ship

Substituting values we get :

$\Rightarrow 1.5 = \dfrac{3}{500} \times \text{ Length of ship} \\[1em] \Rightarrow \text{Length of ship} = \dfrac{1.5 \times 500}{3} \\[1em] \Rightarrow \text{Length of ship} = 0.5 \times 500 = 250 \text{ m}.$

Hence, Option 4 is the correct option.

Question 1(h)

The perpendicular BD drawn from the vertex of a right triangle ABC.

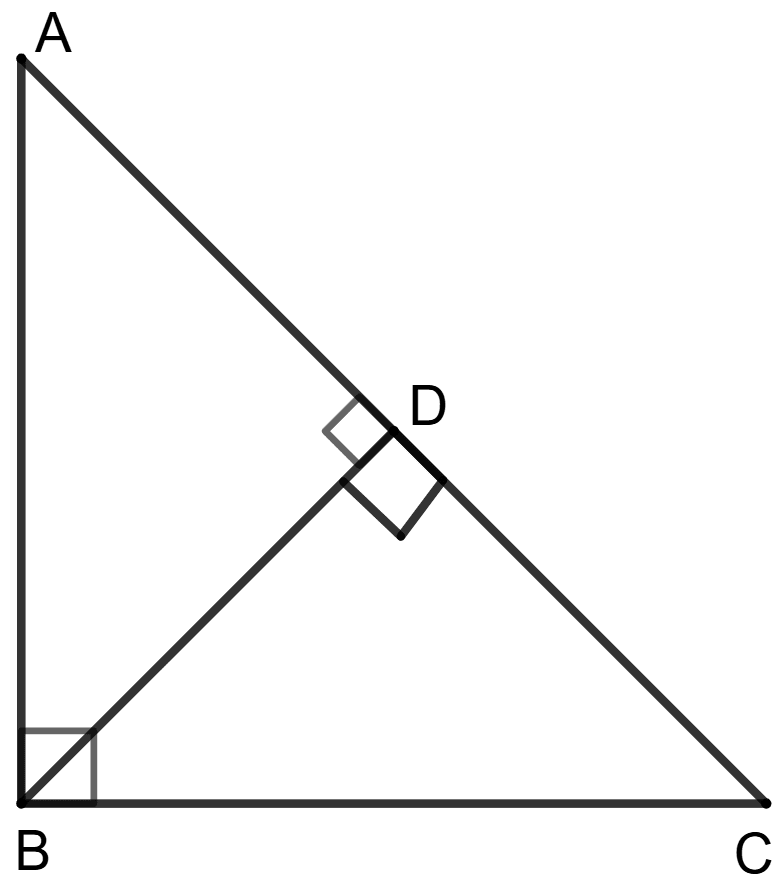
Assertion (A) : Triangles ABD and BCD are similar to each other.

Reason (R) : Triangles, which are similar to the same triangle, are similar to each other.

A is true, R is false.
A is false, R is true.
Both A and R are true and R is correct reason for A.
Both A and R are true and R is incorrect reason for A.

Answer

In Δ ABC and Δ ABD,

⇒ ∠ABC = ∠ADB (Both are 90°)

⇒ ∠BAC = ∠BAD (Common angle)

∴ Δ ABC ∼ Δ ADB (By AA postulate) .......... (1)

Similarly, in Δ ABC and Δ BDC,

⇒ ∠ABC = ∠BDC (Both are 90°)

⇒ ∠BCA = ∠BCD (Common angles)

∴ Δ ABC ∼ Δ BDC (By AA postulate) .......... (2)

As,

Triangles, which are similar to the same triangle, are similar to each other.

From equation (1) and (2), we get :

Δ ADB ∼ Δ BDC

∴ Both A and R are true and R is correct reason for A.

Hence, option 3 is the correct option.

Question 1(i)

Δ ABC and Δ PQR are congruent to each other.

Assertion (A) : Triangles ABC and PQR are similar to each other.

Reason (R) : Two similar triangles are congruent to each other.

A is true, R is false.
A is false, R is true.
Both A and R are true and R is correct reason for A.
Both A and R are true and R is incorrect reason for A.

Answer

Given, Δ ABC and Δ PQR are two congruent triangles.

Corresponding angles and sides are equal.

⇒ ∠A = ∠P, ∠B = ∠Q and ∠C = ∠R

∴ Δ ABC ∼ Δ PQR (By AAA postulate)

So, assertion (A) is true.

Similar triangles have the same shape but not necessarily the same size.

Congruent triangles have the same shape and size.

Size can be different in similar triangles but it has to be same in congruent triangles.

So, reason (R) is false.

Hence, option 1 is the correct option.

Question 1(j)

Δ ABC is reflected in origin to get Δ A'B'C'.

Statement (1) : Δ ABC is congruent to Δ A'B'C'.

Statement (2) : The two triangles are similar to each other.

Both the statement are true.
Both the statement are false.
Statement 1 is true, and statement 2 is false.
Statement 1 is false, and statement 2 is true.

Answer

Reflection in the origin means each point (x, y) becomes (-x, -y). Shape, size, angles and size length remains same in reflection.

So, Δ ABC is reflected in origin to get Δ A'B'C'.

Hence, Δ ABC is congruent to Δ A'B'C'.

So, statement 1 is true.

As we know that all congruent triangles are similar.

Hence, Δ ABC is similar to Δ A'B'C'.

So, statement 2 is true.

Hence, option 1 is the correct option.

Question 1(k)

Two similar triangles ABC and DEF such that area of Δ ABC = 64 sq. unit and area of Δ DEF = 121 sq. unit.

Statement (1) : $\dfrac{\text{Perimeter of Δ DEF}}{\text{Perimeter of Δ ABC}} = \dfrac{8}{11}$ .

Statement (2) : The ratio of perimeters of two similar triangles is equal to the ratio of their areas.

Both the statement are true.
Both the statement are false.
Statement 1 is true, and statement 2 is false.
Statement 1 is false, and statement 2 is true.

Answer

Given, △ ABC ∼ △ DEF.

We know that,

The ratio of the areas of two similar triangles is equal to the square of the ratio of their corresponding sides.

$\therefore \dfrac{\text{Area of Δ DEF}}{\text{Area of Δ ABC}} = \dfrac{DE^2}{AB^2}\\[1em] \Rightarrow\dfrac{121}{64} = \dfrac{DE^2} {AB^2}\\[1em] \Rightarrow \dfrac{AB^2}{DE^2} = \dfrac{64}{121} \\[1em] \Rightarrow \dfrac{AB}{DE} = \sqrt{\dfrac{64}{121}}\\[1em] \Rightarrow \dfrac{AB}{DE} = \dfrac{8}{11}$

Since, corresponding sides of similar triangle are proportional.

$\Rightarrow \dfrac{AB}{DE} = \dfrac{BC}{EF} = \dfrac{AC}{DF}$

We know that,

For any two or more equal ratios, each ratio is equal to the ratio between sum of their antecedents and sum of their consequents.

$\Rightarrow \dfrac{AB}{DE} = \dfrac{AB + BC + AC}{DE + EF + DF} \\[1em] \Rightarrow \dfrac{\text{Perimeter of Δ ABC}}{\text{Perimeter of Δ DEF}} = \dfrac{AB}{DE} \\[1em] \Rightarrow \dfrac{\text{Perimeter of Δ DEF}}{\text{Perimeter of Δ ABC}} = \dfrac{DE}{AB} = \dfrac{11}{8}\\[1em]$

So, statement 1 is false.

The ratio of perimeters of two similar triangles is equal to the ratio of their corresponding sides.

So, statement 2 is false.

Hence, option 2 is the correct option.

Question 1(l)

In triangle ABC, AD : DB = 2 : 3, DE is parallel to BC.

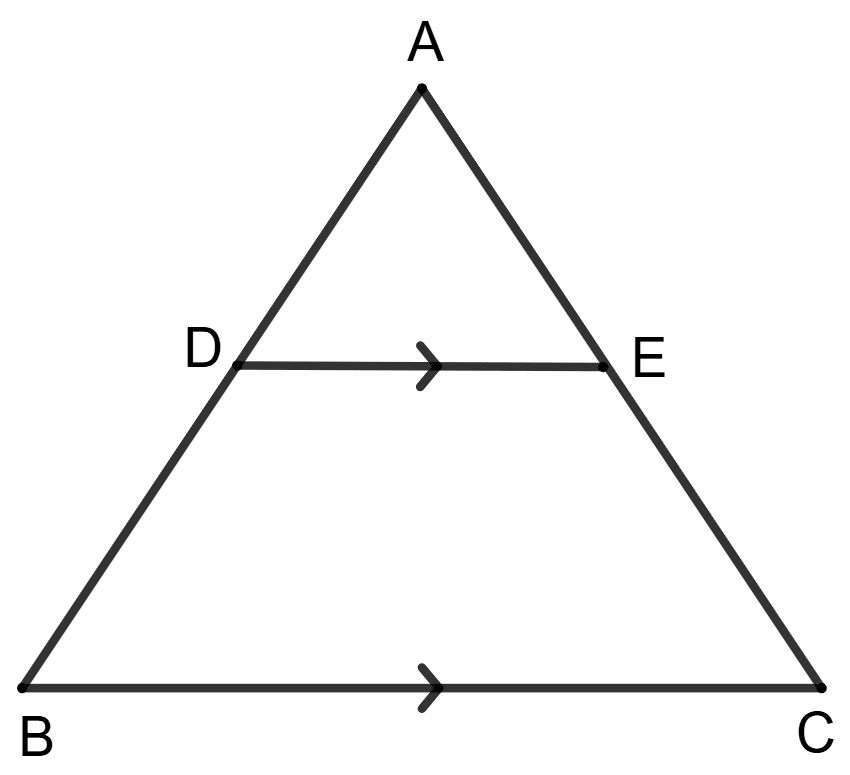
Assertion (A) : $\dfrac{\text{DE}}{\text{BC}} = \dfrac{\text{AD}}{\text{BD}} = \dfrac{2}{3}$ .

Reason (R) : $\dfrac{\text{DE}}{\text{BC}} = \dfrac{\text{AD}}{\text{AB}} = \dfrac{2}{5}$ .

A is true, R is false.
A is false, R is true.
Both A and R are true and R is correct reason for A.
Both A and R are true and R is incorrect reason for A.

Answer

In Δ ADE and Δ ABC

⇒ ∠DAE = ∠BAC (Common angle)

⇒ ∠ADE = ∠ABC (Corresponding angles are equal)

⇒ ∠AED = ∠ACB (Corresponding angles are equal)

∴ Δ ADE ∼ Δ ABC (By AAA postulate)

According to basic proportionality theorem, if a line is drawn parallel to one side of a triangle to intersect the other two sides in distinct points, then the other two sides are divided in the same ratio.

$\therefore \dfrac{DE}{BC} = \dfrac{AD}{DB} \\[1em] \Rightarrow \dfrac{DE}{BC} = \dfrac{2}{3}$

So, assertion is true but reason is false.

Hence, option 1 is the correct option.

Question 1(m)

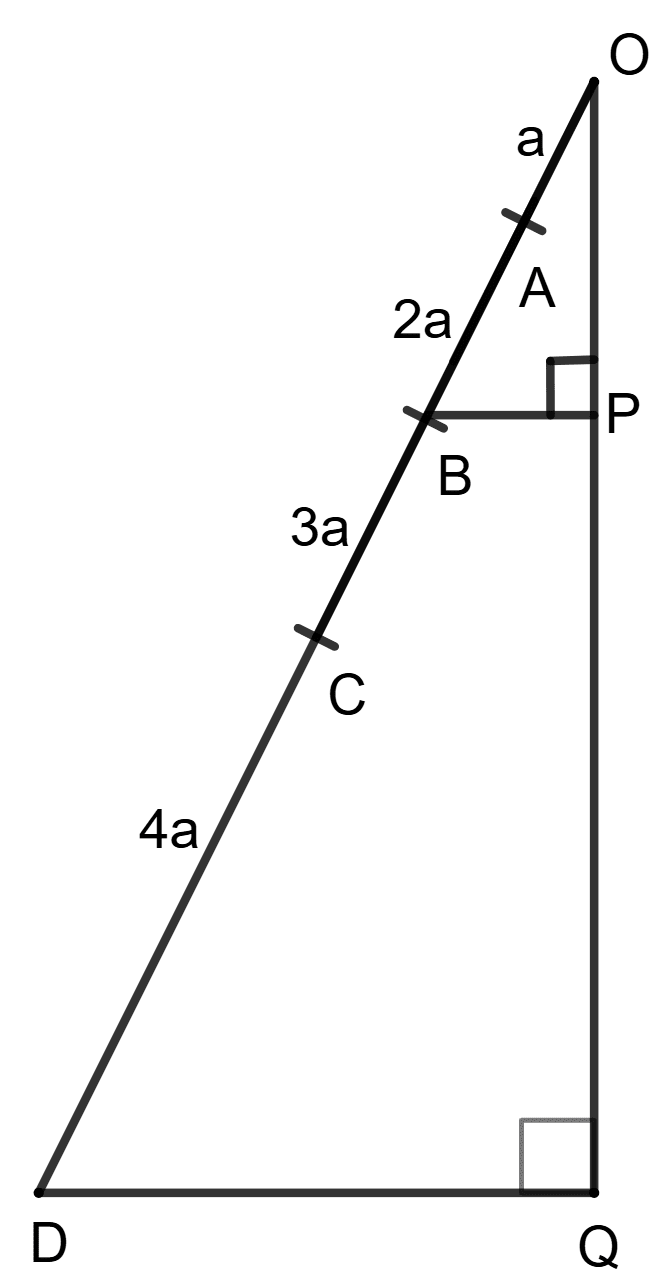
In triangle ODQ, ∠Q = ∠BPO = 90° AB = 2 x OA, BC = 3 x OA and CD = 4 x OA.

Assertion (A) : $\dfrac{\text{Δ OBP}}{\text{Trapezium BDQP}} = \dfrac{9}{100 - 9}$ .

Reason (R) : Δ OBP - ODQ and $\dfrac{\text{Δ OBP}}{\text{Δ ODQ}} = \dfrac{(3a)^2}{(10a)^2}$ .

A is true, R is false.
A is false, R is true.
Both A and R are true and R is correct reason for A.
Both A and R are true and R is incorrect reason for A.

Answer

In Δ ODQ and Δ OBP

⇒ ∠DOQ = ∠BOP (Common angle)

⇒ ∠OQD = ∠OPB (Both equal to 90°)

∴ Δ ODQ ∼ Δ OBP (By A.A. postulate)

From figure,

OB = a + 2a = 3a

OD = a + 2a + 3a + 4a = 10a

We know that,

The ratio of the areas of two similar triangles is equal to the square of the ratio of their corresponding sides.

$\therefore \dfrac{\text{Area of Δ ODQ}}{\text{Area of Δ OBP}} = \dfrac{OD^2}{OB^2}\\[1em] = \dfrac{(10a)^2}{(3a)^2}\\[1em] = \dfrac{100a^2}{9a^2}\\[1em] = \dfrac{100}{9}.$

Let the area of Δ OBP be 9m and that of area of Δ ODQ be 100m.

From figure,

Area of trapezium BPQD = Area of Δ ODQ - Area of Δ OBP = 100m - 9m

Now,

$\Rightarrow \dfrac{\text{Δ OBP}}{\text{Trapezium BDQP}} = \dfrac{9m}{100m - 9m}\\[1em] = \dfrac{9m}{(100 - 9)m}\\[1em] = \dfrac{9}{100 - 9}$

∴ Both A and R are true and R is correct reason for A.

Hence, option 3 is the correct option.

Question 1(n)

In triangle ABC, ∠B = 90° and in triangle ADE, ∠D = 90°.

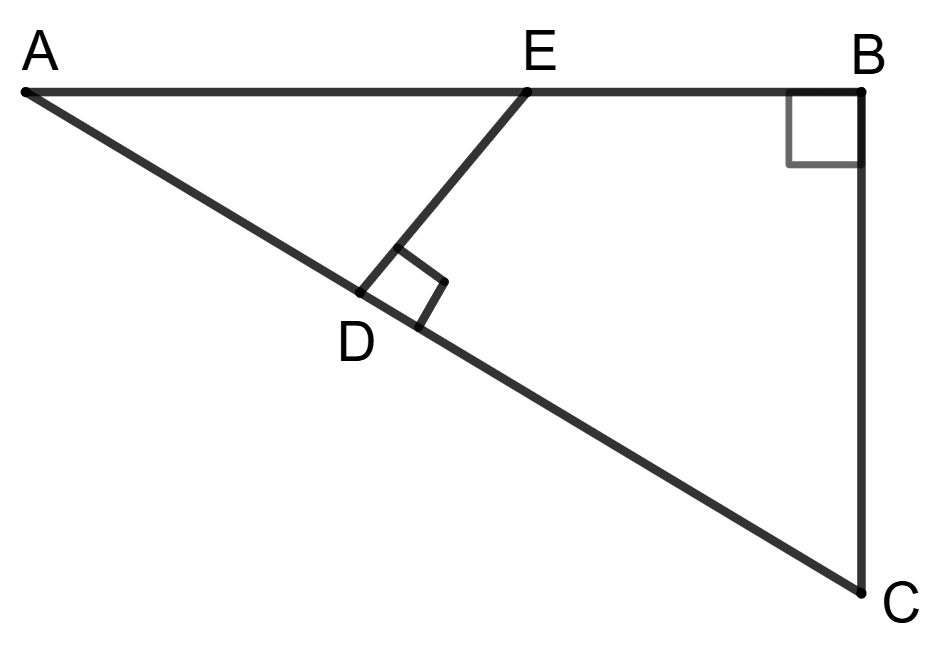
Statement (1) : $\dfrac{\text{AB}}{\text{AD}} = \dfrac{\text{AC}}{\text{AE}}$ .

Statement (2) : Triangle AED and ACB are similar.

Both the statement are true.
Both the statement are false.
Statement 1 is true, and statement 2 is false.
Statement 1 is false, and statement 2 is true.

Answer

In Δ ADE and Δ ABC,

⇒ ∠DAE = ∠BAC (Common angle)

⇒ ∠ADE = ∠ABC (Both are 90°)

∴ Δ ADE ∼ Δ ABC (By AA postulate)

We know that,

Corresponding sides of similar triangles are proportional.

$\Rightarrow \dfrac{AD}{AB} = \dfrac{AE}{AC}\\[1em] \Rightarrow \dfrac{AB}{AD} = \dfrac{AC}{AE}\\[1em]$

So, both the statements are true.

Hence, option 1 is the correct option.

Question 1(o)

Area of triangle ADE = 9 cm² and area of trapezium DBCE = 16 cm².

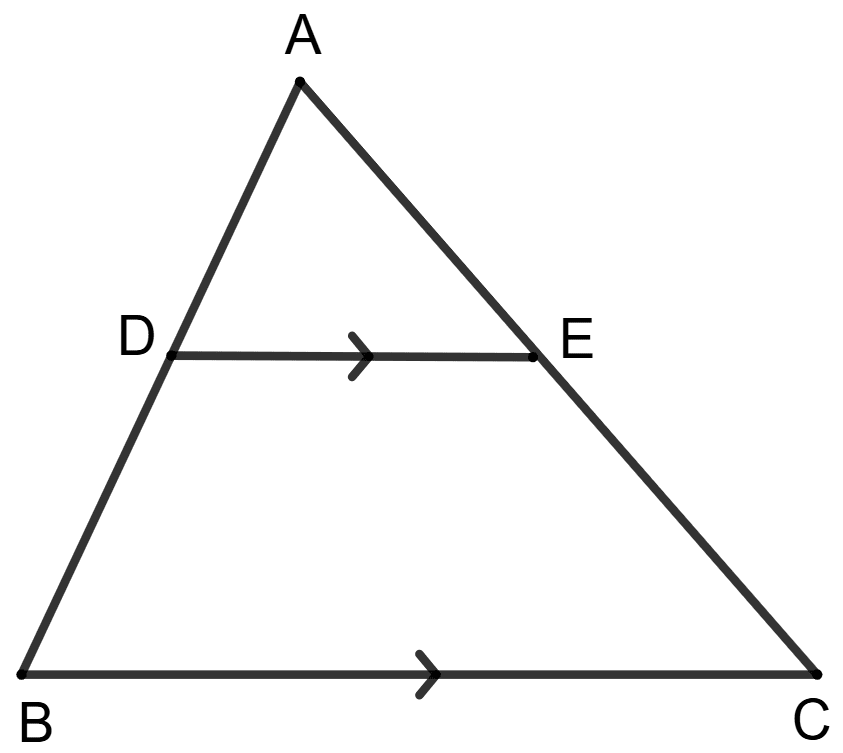
Area of triangle ADE = 9 cm2 and area of trapezium DBCE = 16 cm2. Concise Mathematics Solutions ICSE Class 10.

Statement (1) : $\dfrac{\text{DE}}{\text{BC}} = \dfrac{3}{4}$ .

Statement (2) : $\dfrac{\text{ΔADE}}{\text{ΔABC}} = \dfrac{9}{25} \Rightarrow \dfrac{\text{DE}}{\text{BC}} = \dfrac{3}{5}$ .

Both the statement are true.
Both the statement are false.
Statement 1 is true, and statement 2 is false.
Statement 1 is false, and statement 2 is true.

Answer

Given,

Area of triangle ADE = 9 cm² and area of trapezium DBCE = 16 cm².

In Δ ABC and Δ ADE,

⇒ ∠BAC = ∠DAE (Common angle)

⇒ ∠ABC = ∠ADE (Corresponding angles are equal)

⇒ ∠ACB = ∠AED (Corresponding angles are equal)

∴ Δ ABC ∼ Δ ADE (By A.A.A. postulate)

From figure,

⇒ Area of triangle ABC = Area of triangle ADE + Area of trapezium DBCE = 9 + 16 = 25 cm²

We know that,

The ratio of the areas of two similar triangles is equal to the square of the ratio of their corresponding sides.

$\therefore \dfrac{\text{Area of Δ ADE}}{\text{Area of Δ ABC}} = \dfrac{DE^2}{BC^2}\\[1em] \Rightarrow\dfrac{9}{25} = \dfrac{DE^2}{BC^2}\\[1em] \Rightarrow \dfrac{DE}{BC} = \sqrt{\dfrac{9}{25}} = \dfrac{3}{5}$

So, statement 1 is false but statement 2 is true.

Hence, option 4 is the correct option.

Question 2

In the following figure, XY is parallel to BC, AX = 9 cm, XB = 4.5 cm and BC = 18 cm.

Find:

(i) $\dfrac{AY}{YC}$

(ii) $\dfrac{YC}{AC}$

(iii) XY

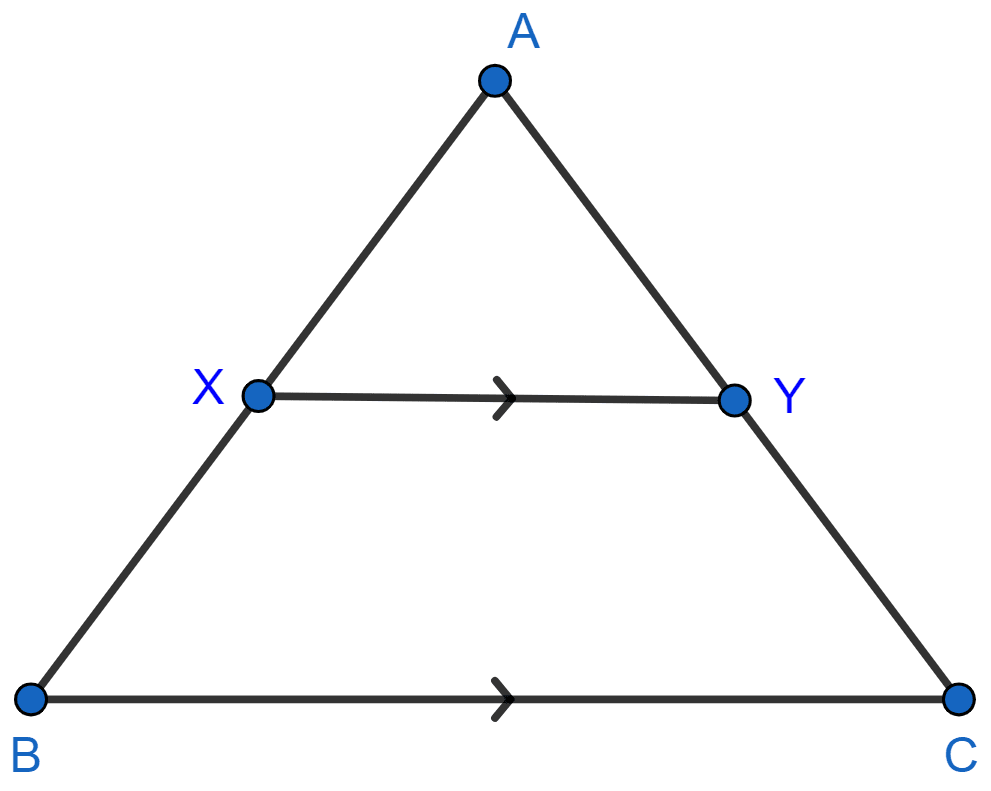
In the figure, XY is parallel to BC, AX = 9 cm, XB = 4.5 cm and BC = 18 cm. Find AY/YC, YC/AC. Similarity, Concise Mathematics Solutions ICSE Class 10.

Answer

(i) By basic proportionality theorem,

A line drawn parallel to a side of triangle divides the other two sides proportionally.

$\therefore \dfrac{AY}{YC} = \dfrac{AX}{XB} \\[1em] = \dfrac{9}{4.5} \\[1em] = \dfrac{2}{1}.$

Hence, $\dfrac{AY}{YC} = 2.$

(ii) Given,

$\Rightarrow \dfrac{AY}{YC} = \dfrac{2}{1}$

Let AY = 2x and YC = x.

From figure,

AC = AY + YC = 2x + x = 3x.

$\therefore \dfrac{YC}{AC} = \dfrac{x}{3x} = \dfrac{1}{3}$ .

Hence, $\dfrac{YC}{AC} = \dfrac{1}{3}$ .

(iii) In △AXY and △ABC,

∠AXY = ∠ABC [Corresponding angles are equal]

∠A = ∠A [Common]

∴ △AXY ~ △ABC.

Since, corresponding sides of similar triangle are proportional to each other.

$\Rightarrow \dfrac{AX}{AB} = \dfrac{XY}{BC} \\[1em] \Rightarrow \dfrac{AX}{AX + XB} = \dfrac{XY}{BC} \\[1em] \Rightarrow \dfrac{9}{9 + 4.5} = \dfrac{XY}{18} \\[1em] \Rightarrow \dfrac{9}{13.5} = \dfrac{XY}{18} \\[1em] \Rightarrow XY = \dfrac{9}{13.5} \times 18 \\[1em] \Rightarrow XY = 12 \text{ cm}. \\[1em]$

Hence, XY = 12 cm.

Question 3

In the following figure, ABCD is a trapezium with AB || DC. If AB = 9 cm, DC = 18 cm, CF = 13.5 cm, AP = 6 cm and BE = 15 cm,

Calculate :

(i) EC (ii) AF (iii) PE

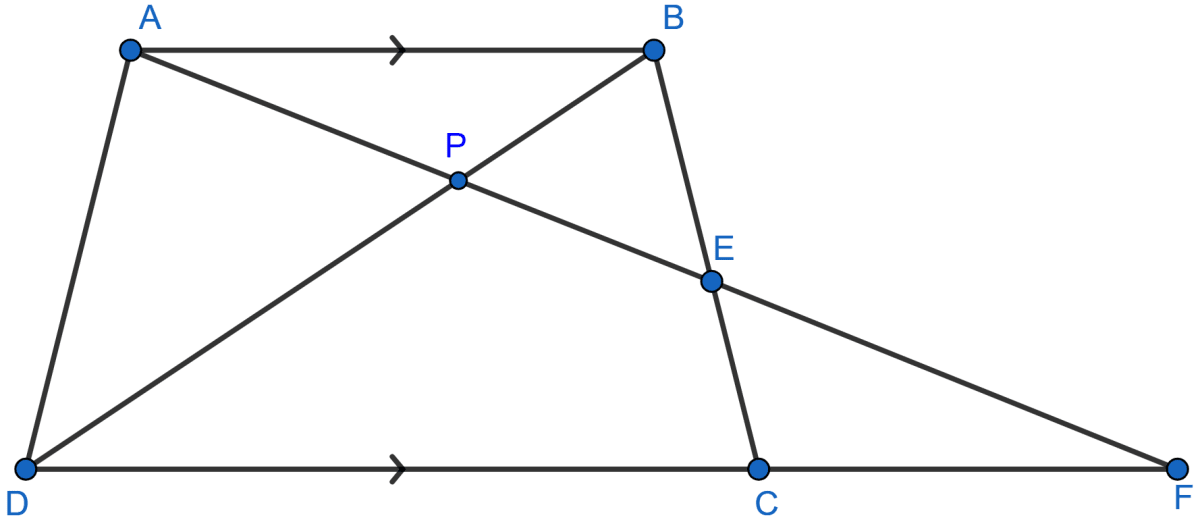
Answer

(i) In ΔAEB and ΔFEC,

∠AEB = ∠FEC [Vertically opposite angles are equal]

∠BAE = ∠CFE [Alternate angles are equal]

∴ ∆AEB ~ ∆FEC [By AA]

Since, corresponding sides of similar triangles are proportional.

$\Rightarrow \dfrac{BE}{EC} = \dfrac{AB}{FC} \\[1em] \Rightarrow \dfrac{15}{EC} = \dfrac{9}{13.5} \\[1em] \Rightarrow EC = \dfrac{15 \times 13.5}{9} = 22.5\text{ cm}$

Hence, EC = 22.5 cm.

(ii) In ΔAPB and ΔFPD,

∠APB = ∠FPD [Vertically opposite angles are equal]

∠BAP = ∠DFP [Alternate angles are equal]

∴ ∆APB ~ ∆FPD [By AA]

Since, corresponding sides of similar triangles are proportional.

$\Rightarrow \dfrac{AP}{FP} = \dfrac{AB}{FD} \\[1em] \Rightarrow \dfrac{AP}{FP} = \dfrac{AB}{DC + CF} \\[1em] \Rightarrow \dfrac{6}{FP} = \dfrac{9}{18 + 13.5} \\[1em] \Rightarrow \dfrac{6}{FP} = \dfrac{9}{31.5} \\[1em] \Rightarrow FP = \dfrac{6 \times 31.5}{9} \\[1em] \Rightarrow FP = \dfrac{63}{3} = 21\text{ cm}.$

From figure,

AF = AP + FP = 6 + 21 = 27 cm.

Hence, AF = 27 cm.

(iii) We already have, ∆AEB ~ ∆FEC

So,

$\Rightarrow \dfrac{AE}{FE} = \dfrac{AB}{FC} \\[1em] \Rightarrow \dfrac{AE}{FE} = \dfrac{9}{13.5} \\[1em] \Rightarrow \dfrac{(AF – EF)}{ FE} = \dfrac{9}{13.5} \\[1em] \Rightarrow \dfrac{AF}{EF} – 1 = \dfrac{9}{13.5} \\[1em] \Rightarrow \dfrac{27}{EF} = \dfrac{9}{13.5} + 1 \\[1em] \Rightarrow \dfrac{27}{EF} = \dfrac{22.5}{13.5} \\[1em] \Rightarrow EF = \dfrac{(27 \times 13.5)}{22.5} = 16.2 \text{ cm}.$

From figure,

PE = PF – EF = 21 – 16.2 = 4.8 cm

Hence, PE = 4.8 cm

Question 4

In the following figure, AB, CD and EF are perpendicular to the straight line BDF.

If AB = x and, CD = z unit and EF = y unit, prove that:

$\dfrac{1}{x} + \dfrac{1}{y} = \dfrac{1}{z}$

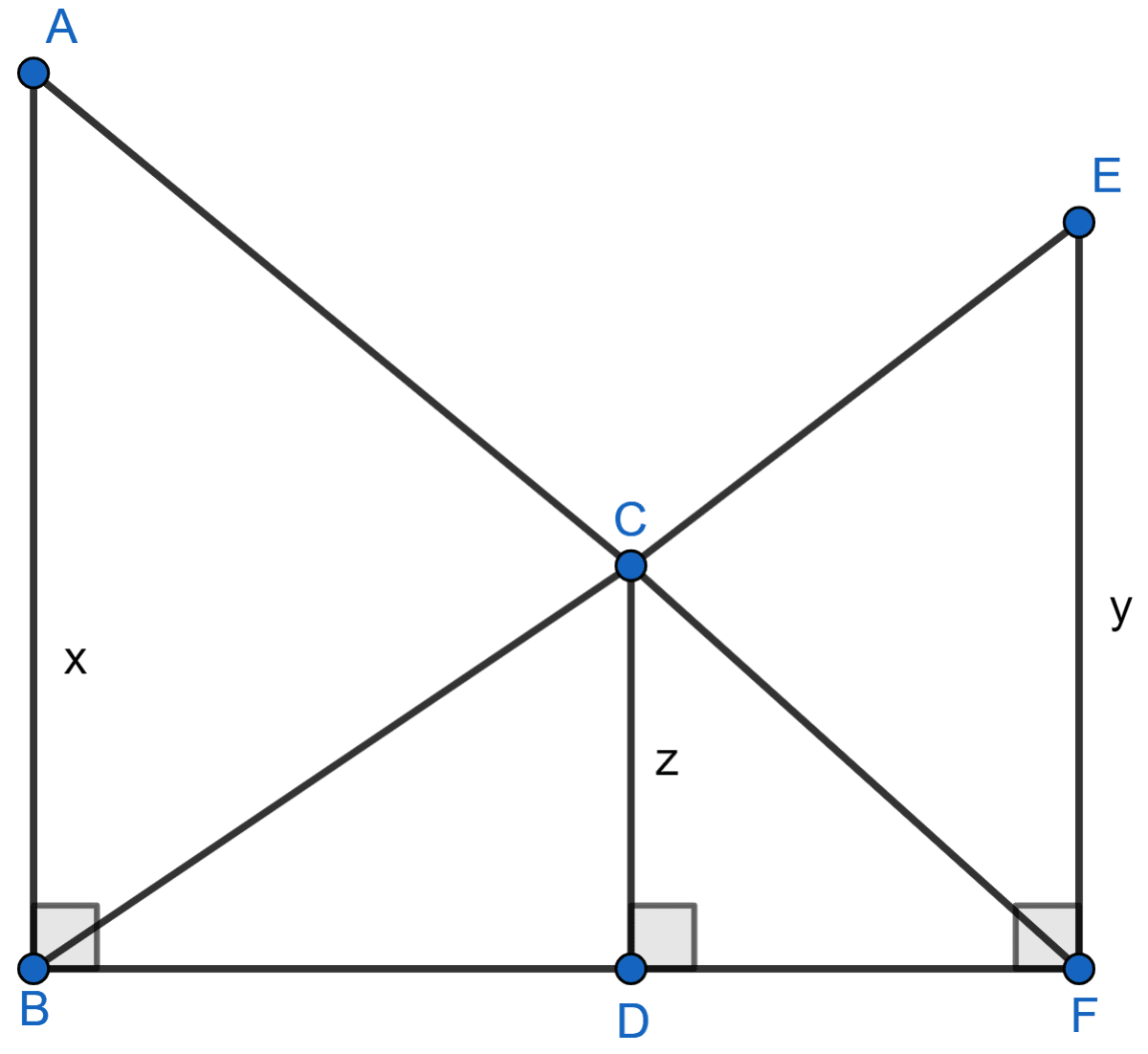
Answer

Let BD = a and DF = b.

In ΔFDC and ΔFBA,

∠FDC = ∠FBA [Both = 90°]

∠DFC = ∠BFA [Common angle]

∴ ∆FDC ~ ∆FBA [By AA]

Since, corresponding sides of similar triangle are proportional to each other.

$\Rightarrow \dfrac{DF}{BF} = \dfrac{DC}{AB} \\[1em] \Rightarrow \dfrac{DF}{BD + DF} = \dfrac{z}{x} \\[1em] \Rightarrow \dfrac{b}{a + b} = \dfrac{z}{x} ..... (1)$

In ΔBDC and ΔBFE,

∠BDC = ∠BFE [Both = 90°]

∠DBC = ∠FBE [Common angle]

∴ ∆BDC ~ ∆BFE [By AA]

Since, corresponding sides of similar triangle are proportional to each other.

$\Rightarrow \dfrac{BD}{BF} = \dfrac{CD}{EF} \\[1em] \Rightarrow \dfrac{BD}{BD + DF} = \dfrac{z}{y} \\[1em] \Rightarrow \dfrac{a}{a + b} = \dfrac{z}{y} ............ (2)$

Adding (1) and (2) we get :

$\Rightarrow \dfrac{b}{a + b} + \dfrac{a}{a + b} = \dfrac{z}{x} + \dfrac{z}{y} \\[1em] \Rightarrow \dfrac{a + b}{a + b} = z\Big(\dfrac{1}{x} + \dfrac{1}{y}\Big) \\[1em] \Rightarrow 1 = z\Big(\dfrac{1}{x} + \dfrac{1}{y}\Big) \\[1em] \Rightarrow \dfrac{1}{z} = \dfrac{1}{x} + \dfrac{1}{y}.$

Hence, proved that $\dfrac{1}{z} = \dfrac{1}{x} + \dfrac{1}{y}.$ .

Question 5

Triangle ABC is similar to triangle PQR. If AD and PM are corresponding medians of the two triangles, prove that: $\dfrac{\text{AB}}{\text{PQ}} = \dfrac{\text{AD}}{\text{PM}}$ .

Answer

Given, ∆ABC ~ ∆PQR

AD and PM are the medians, so BD = DC and QM = MR

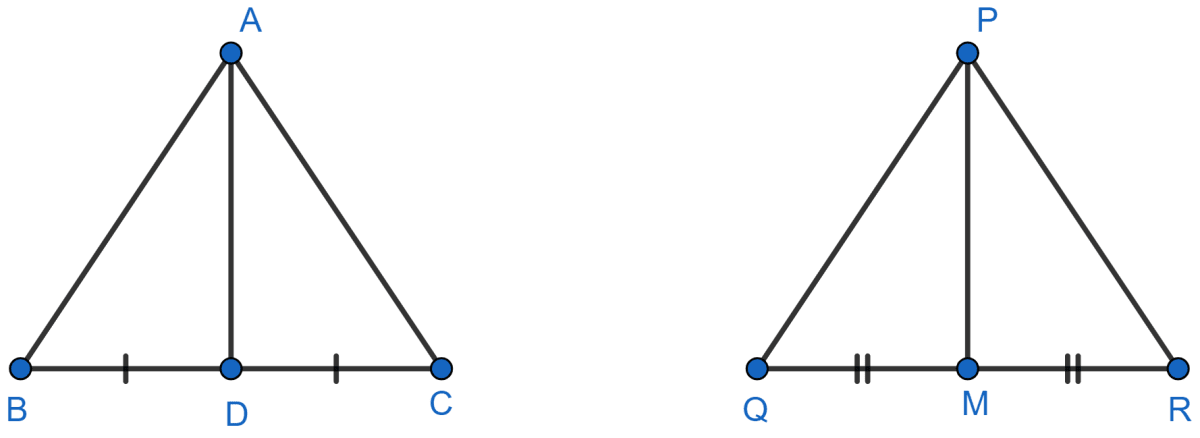
Triangle ABC is similar to triangle PQR. If AD and PM are corresponding medians of the two triangles, prove that: AB/PQ = AD/PM. Similarity, Concise Mathematics Solutions ICSE Class 10.

Since, corresponding sides of similar triangles are proportional.

$\dfrac{AB}{PQ} = \dfrac{BC}{QR}$

We can write,

$\dfrac{AB}{PQ} = \dfrac{\dfrac{BC}{2}}{\dfrac{QR}{2}} = \dfrac{BD}{QM}$

And, ∠ABC = ∠PQR i.e., ∠ABD = ∠PQM

∴ ∆ABD ~ ∆PQM [By SAS]

Since, corresponding sides of similar triangles are proportional.

$\dfrac{AB}{PQ} = \dfrac{AD}{PM}$ .

Hence, proved that $\dfrac{AB}{PQ} = \dfrac{AD}{PM}$ .

Question 6

Triangle ABC is similar to triangle PQR. If AD and PM are altitudes of the two triangles, prove that: $\dfrac{AB}{PQ} = \dfrac{AD}{PM}$ .

Answer

Given, ∆ABC ~ ∆PQR

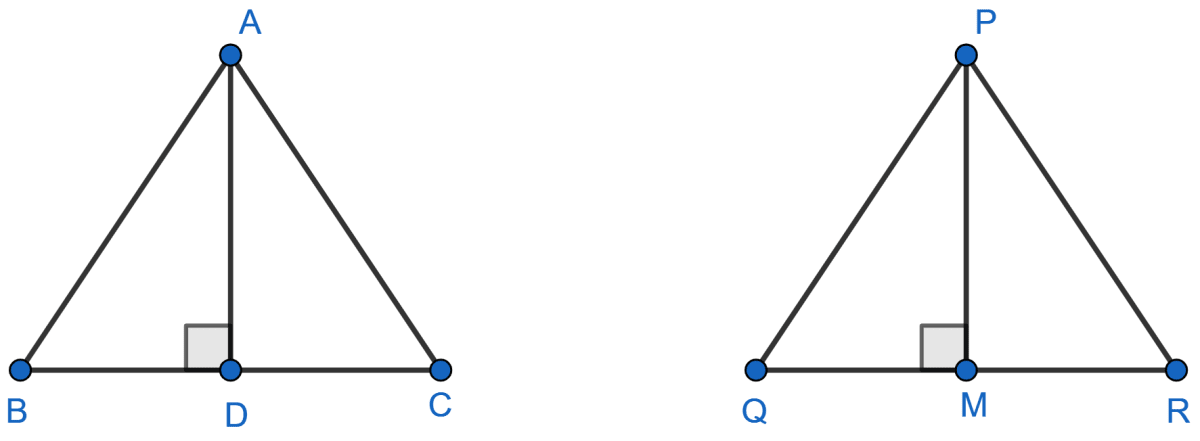
Triangle ABC is similar to triangle PQR. If AD and PM are altitudes of the two triangles, prove that: AB/PQ = AD/PM. Similarity, Concise Mathematics Solutions ICSE Class 10.

So,

∠ABC = ∠PQR i.e., ∠ABD = ∠PQM

Also, ∠ADB = ∠PMQ [Both are right angles]

∴ ∆ABD ~ ∆PQM [By AA]

Since, corresponding sides of similar triangles are proportional.

$\dfrac{AB}{PQ} = \dfrac{AD}{PM}$ .

Hence, proved that $\dfrac{AB}{PQ} = \dfrac{AD}{PM}$ .

Question 7

Triangle ABC is similar to triangle PQR. If bisector of angle BAC meets BC at point D and bisector of angle QPR meets QR at point M, prove that: $\dfrac{AB}{PQ} = \dfrac{AD}{PM}$ .

Answer

Given, ∆ABC ~ ∆PQR and AD and PM are the angle bisectors.

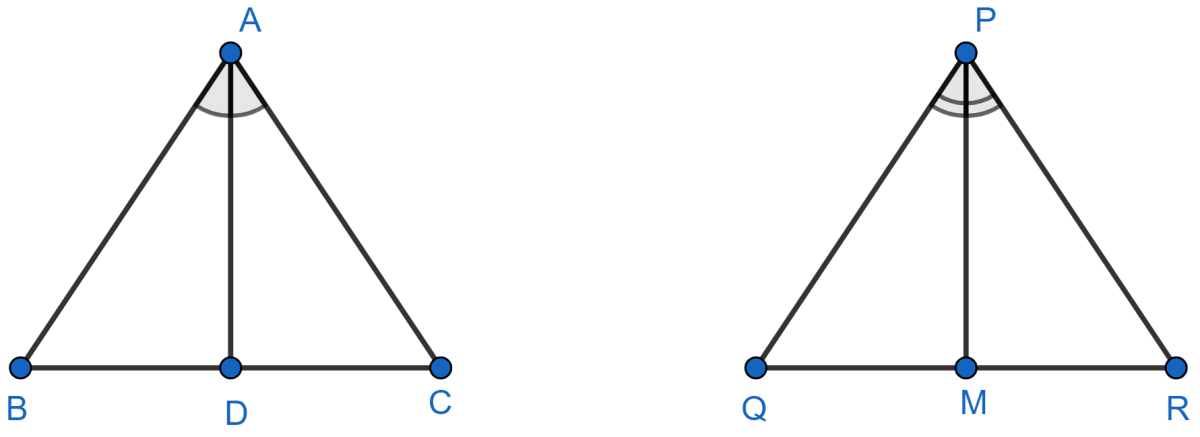
Triangle ABC is similar to triangle PQR. If bisector of angle BAC meets BC at point D and bisector of angle QPR meets QR at point M, prove that: AB/PQ = AD/PM. Similarity, Concise Mathematics Solutions ICSE Class 10.

So,

⇒ ∠A = ∠P

⇒ $\dfrac{∠\text{A}}{2} = \dfrac{∠\text{P}}{2}$

⇒ ∠BAD = ∠QPM

Also, ∠ABC = ∠PQR i.e., ∠ABD = ∠PQM.

∴ ∆ABD ~ ∆PQM [By AA]

Since, corresponding sides of similar triangles are proportional.

$\dfrac{AB}{PQ} = \dfrac{AD}{PM}$ .

Hence, proved that $\dfrac{AB}{PQ} = \dfrac{AD}{PM}$ .

Question 8

In the following figure, ∠AXY = ∠AYX.

If $\dfrac{BX}{AX} = \dfrac{CY}{AY}$ , show that triangle ABC is isosceles.

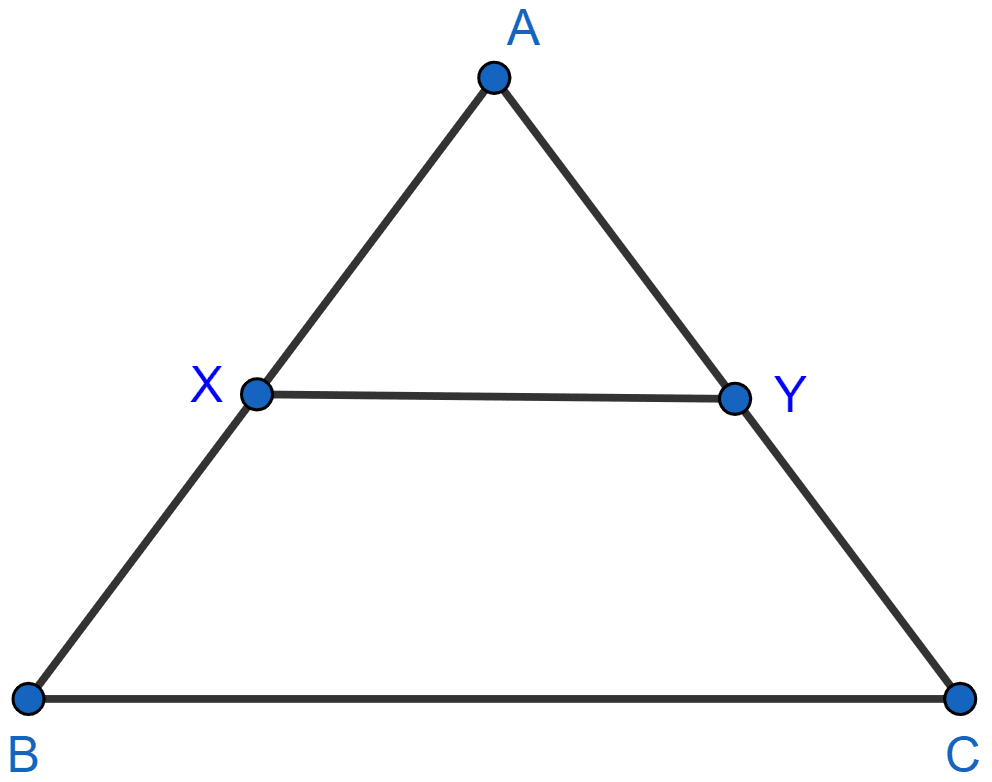
Answer

Given,

∠AXY = ∠AYX

So, AX = AY = a (let) [Sides opposite to equal angles are equal.]

Given,

$\Rightarrow \dfrac{BX}{AX} = \dfrac{CY}{AY} \\[1em] \Rightarrow \dfrac{BX}{a} = \dfrac{CY}{a} \\[1em] \Rightarrow BX = CY = b.$

From figure,

AB = AX + XB = a + b.

AC = AY + CY = a + b.

So, AB = AC.

Hence, proved that ∆ABC is an isosceles triangle.

Question 9

In the following figure, DE || AC and DC || AP. Prove that : $\dfrac{BE}{EC} = \dfrac{BC}{CP}$ .

In the following figure, DE || AC and DC || AP. Prove that : BE/EC = BC/CP. Similarity, Concise Mathematics Solutions ICSE Class 10.

Answer

Given, DE || AC

In △BAC,

By basic proportionality theorem,

$\dfrac{BE}{EC} = \dfrac{BD}{AD}$ .....(1)

Given, DC || AP

In △BPA,

By basic proportionality theorem,

$\dfrac{BC}{CP} = \dfrac{BD}{DA}$ .....(2)

$\dfrac{BE}{EC} = \dfrac{BC}{CP}$ .

Hence, proved that $\dfrac{BE}{EC} = \dfrac{BC}{CP}$ .

Question 10

In the figure given below, AB ‖ EF ‖ CD. If AB = 22.5 cm, EP = 7.5 cm, PC = 15 cm and DC = 27 cm.

Calculate: (i) EF (ii) AC

Answer

(i) In ∆PCD and ∆PEF,

∠CPD = ∠EPF [Vertically opposite angles are equal]

∠DCP = ∠FEP [Alternate angles are equal]

∴ ∆PCD ~ ∆PEF [By AA]

Since corresponding sides of similar triangle are proportional to each other.

$\Rightarrow \dfrac{CD}{EF} = \dfrac{PC}{EP} \\[1em] \Rightarrow \dfrac{27}{EF} = \dfrac{15}{7.5} \\[1em] \Rightarrow EF = \dfrac{27 \times 7.5}{15} \\[1em] \Rightarrow EF = 13.5 \text{ cm}.$

Hence, EF = 13.5 cm.

(ii) In ∆CEF and ∆CAB

∠FCE = ∠BCA [Common angles]

∠CFE = ∠CBA [As FE || BA, corresponding angles are equal]

∴ ∆CEF ~ ∆CAB [By AA]

Since corresponding sides of similar triangle are proportional to each other.

$\Rightarrow \dfrac{EC}{AC} = \dfrac{EF}{AB} \\[1em] \Rightarrow \dfrac{PC + PE}{AC} = \dfrac{13.5}{22.5} \\[1em] \Rightarrow \dfrac{15 + 7.5}{AC} = \dfrac{13.5}{22.5} \\[1em] \Rightarrow \dfrac{22.5}{AC} = \dfrac{13.5}{22.5} \\[1em] \Rightarrow AC = \dfrac{22.5 \times 22.5}{13.5} \\[1em] \Rightarrow AC = 37.5 \text{ cm}.$

Hence, AC = 37.5 cm.

Question 11

In ΔABC, ∠ABC = ∠DAC, AB = 8 cm, AC = 4 cm and AD = 5 cm.

(i) Prove that ΔACD is similar to ΔBCA.

(ii) Find BC and CD.

(iii) Find the area of ΔACD : area of ΔABC.

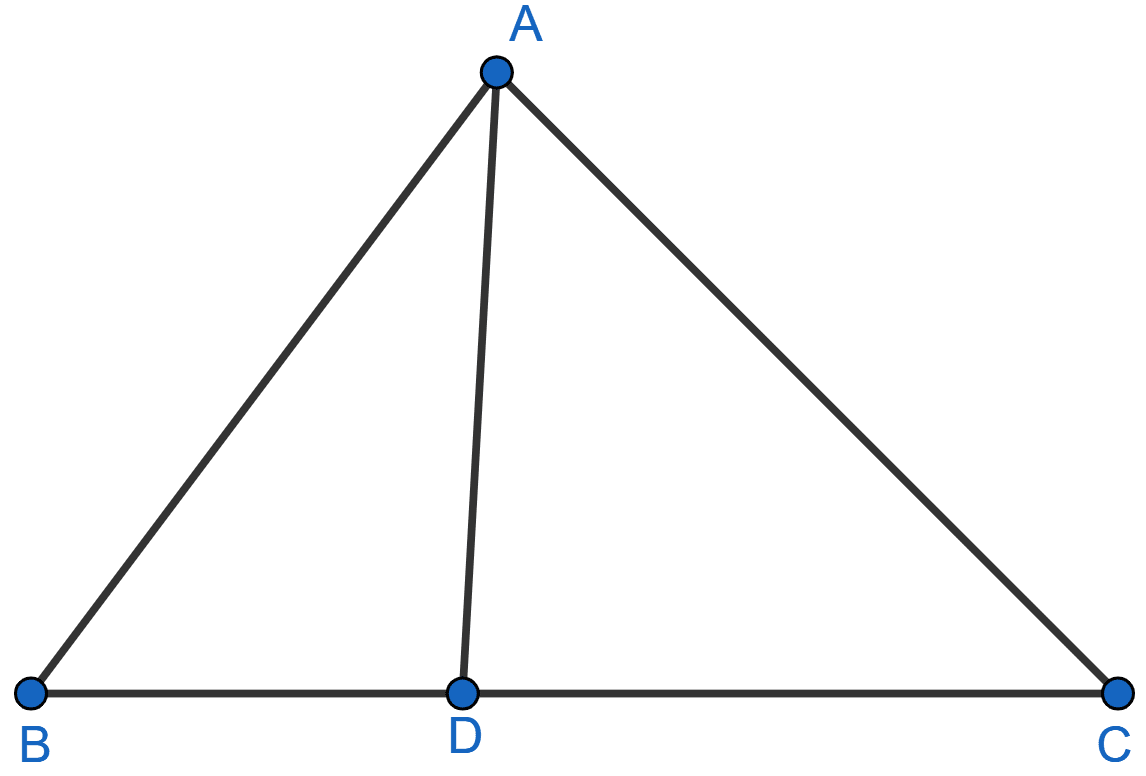
Answer

(i) In ∆ACD and ∆BCA,

∠DAC = ∠ABC [Given]

∠ACD = ∠BCA [Common angles]

∴ ∆ACD ~ ∆BCA [By AA]

Hence, proved that ∆ACD ~ ∆BCA.

(ii) Since, ∆ACD ~ ∆BCA

We know that,

Corresponding sides of similar triangle are proportional.

$\Rightarrow \dfrac{AC}{BC} = \dfrac{AD}{AB} \\[1em] \Rightarrow \dfrac{4}{BC} = \dfrac{5}{8} \\[1em] \Rightarrow BC = \dfrac{4 \times 8}{5} \\[1em] \Rightarrow BC = \dfrac{32}{5} = 6.4 \text{ cm}.$

Also,

$\Rightarrow \dfrac{CD}{AC} = \dfrac{AD}{AB} \\[1em] \Rightarrow \dfrac{CD}{4} = \dfrac{5}{8} \\[1em] \Rightarrow CD = \dfrac{4 \times 5}{8} \\[1em] \Rightarrow CD = \dfrac{5}{2} = 2.5 \text{ cm}.$

Hence, BC = 6.4 cm and CD = 2.5 cm.

(iii) As, ∆ACD ~ ∆BCA

We know that,

The areas of two similar triangles are proportional to the squares of their corresponding sides.

$\dfrac{\text{Area of ∆ACD}}{\text{Area of ∆ABC}} = \dfrac{AD^2}{AB^2} \\[1em] = \dfrac{5^2}{8^2} \\[1em] = \dfrac{25}{64}.$

Hence, area of ∆ACD : area of ∆ABC = 25 : 64.

Question 12

In the following figure, AD and CE are medians of ∆ABC. DF is drawn parallel to CE. Prove that:

(i) EF = FB,

(ii) AG : GD = 2 : 1

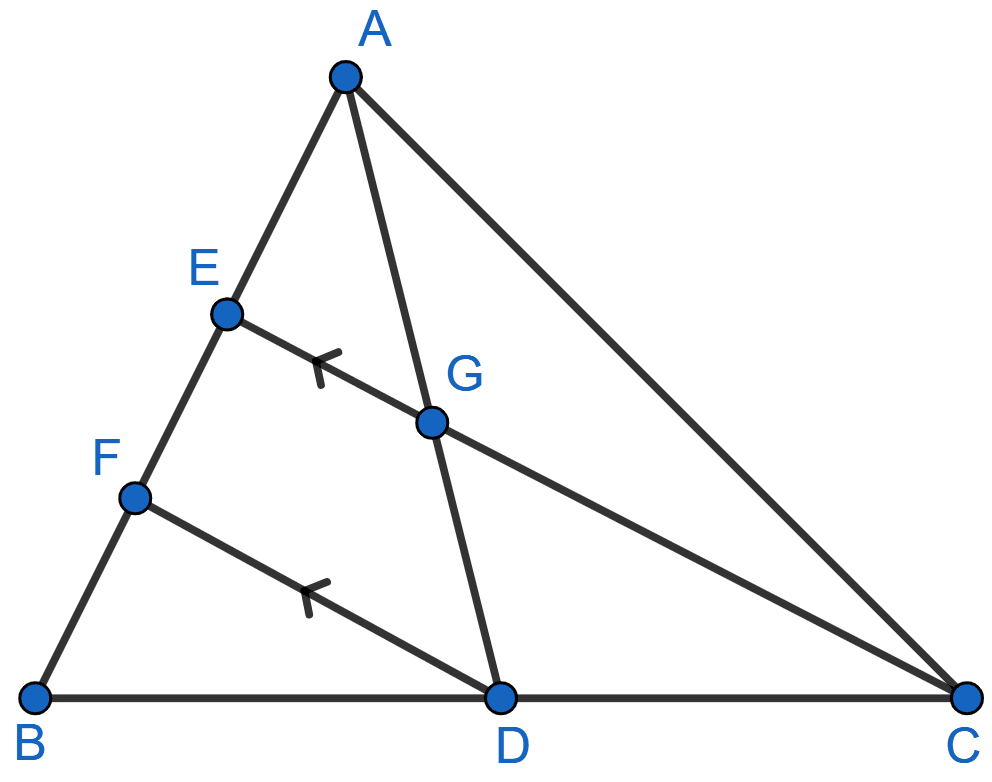
Answer

(i) In ∆BFD and ∆BEC,

∠BFD = ∠BEC [Corresponding angles are equal]

∠FBD = ∠EBC [Common]

∴ ∆BFD ~ ∆BEC [By AA].

Since, corresponding sides of similar triangles are proportional.

$\Rightarrow \dfrac{BF}{BE} = \dfrac{BD}{BC}$

$\Rightarrow \dfrac{BF}{BE} = \dfrac{1}{2}$ [∵ AD is median so D is the mid-point of BC]

$\Rightarrow BE = 2BF$

From figure,

⇒ BE = BF + FE

⇒ 2BF = BF + FE

⇒ BF = FE.

Hence, proved that EF = FB.

(ii) In ∆AFD, EG || FD.

By basic proportionality theorem we have,

$\dfrac{AE}{EF} = \dfrac{AG}{GD}$ .....(1)

Now, AE = EB [∵ CE is median so E is the mid-point of AB]

As, AE = EB = 2EF [As, EF = FB].

Substituting value of AE in (1) we get,

$\dfrac{AG}{GD} = \dfrac{2EF}{EF} = \dfrac{2}{1}$ .

Hence, AG : GD = 2 : 1.

Question 13

The two similar triangles are equal in area. Prove that the triangles are congruent.

Answer

Let's consider two similar triangles as ∆ABC ~ ∆PQR

We know that,

The areas of two similar triangles are proportional to the squares of their corresponding sides.

So,

$\dfrac{\text{Area of ∆ABC}}{\text{Area of ∆PQR}} = \Big(\dfrac{AB}{PQ}\Big)^2 = \Big(\dfrac{BC}{QR}\Big)^2 = \Big(\dfrac{AC}{PR}\Big)^2$

Since,

Area of ∆ABC = Area of ∆PQR [Given]

Hence,

AB = PQ

BC = QR

AC = PR

So, as the respective sides of two similar triangles are all of same length.

We can conclude that,

∆ABC ≅ ∆PQR [By SSS rule]

Hence proved that both triangles are congruent.

Question 14

The ratio between the altitudes of two similar triangles is 3 : 5; write the ratio between their:

(i) corresponding medians.

(ii) perimeters.

(iii) areas.

Answer

Let △ABC and △PQR be two similar triangles with AD and PS as perpendiculars.

The ratio between the altitudes of two similar triangles is 3 : 5; write the ratio between their: (i) corresponding medians, (ii) perimeters (iii) areas. Similarity, Concise Mathematics Solutions ICSE Class 10.

So,

∠ABD = ∠PQS [As ∠ABC = ∠PQR]

∠ADB = ∠PSQ [Both = 90°]

So, △ABD ~ △PQS.

$\therefore \dfrac{AB}{PQ} = \dfrac{AD}{PS} = \dfrac{3}{5}$ .

(i) The ratio between the medians of two similar triangles is same as the ratio between their sides.

Hence, the required ratio = 3 : 5.

(ii) The ratio between the perimeters of two similar triangles is same as the ratio between their sides.

Hence, the required ratio = 3 : 5.

(iii) The ratio between the areas of two similar triangles is same as the square of the ratio between their corresponding sides.

Ratio = (3)² : (5)² = 9 : 25.

Hence, the required ratio = 9 : 25.

Question 15

The ratio between the areas of two similar triangles is 16 : 25. State the ratio between their :

(i) perimeters

(ii) corresponding altitudes

(iii) corresponding medians.

Answer

We know that,

The ratio between the areas of two similar triangles is same as the square of the ratio between their corresponding sides.

Given,

Ratio between areas = 16 : 25.

So, ratio between sides = $\sqrt{16} : \sqrt{25}$ = 4 : 5.

(i) The ratio between the perimeters of two similar triangles is same as the ratio between their sides.

Hence, the required ratio = 4 : 5.

(ii) The ratio between the altitudes of two similar triangles is same as the ratio between their sides.

Hence, the required ratio = 4 : 5.

(iii) The ratio between the medians of two similar triangles is same as the ratio between their sides.

Hence, the required ratio = 4 : 5.

Question 16

On a map, drawn to a scale of 1 : 20000, a rectangular plot of land ABCD has AB = 24 cm and BC = 32 cm. Calculate :

(i) the diagonal distance of the plot in kilometre.

(ii) the area of the plot in sq. km.

Answer

The rectangular plot of land ABCD on the map is shown below:

On a map, drawn to a scale of 1 : 20000, a rectangular plot of land ABCD has AB = 24 cm and BC = 32 cm. Calculate (i) the diagonal distance of the plot in kilometre (ii) the area of the plot in sq. km. Similarity, Concise Mathematics Solutions ICSE Class 10.

(i) By pythagoras theorem,

⇒ AC² = AB² + BC²

⇒ AC² = 24² + 32²

⇒ AC² = 576 + 1024

⇒ AC² = 1600

⇒ AC = $\sqrt{1600}$ = 40 cm.

Given,

Scale (k) = $\dfrac{1}{20000}$

Length of diagonal distance in map = k × Length of diagonal of plot

40 = $\dfrac{1}{20000}$ × Length of diagonal of plot

Length of diagonal of plot = 40 × 20000 = 800000 cm = $\dfrac{800000}{100000}$ km = 8 km.

Hence, diagonal distance of plot = 8 km.

(ii) Area of plot on map = AB × BC = 24 × 32 = 768 cm².

Area of plot on map = k² × Area of actual plot

768 = $\Big(\dfrac{1}{20000}\Big)^2$ × Area of actual plot

Area of actual plot = 768 × 20000 × 20000 cm²

= $\dfrac{768 \times 20000 \times 20000}{100000 \times 100000}$ km²

= 30.72 km².

Hence, area of plot = 30.72 km².

Question 17

The dimensions of the model of a multistoreyed building are 1 m by 60 cm by 1.20 m. If the scale factor is 1 : 50, find the actual dimensions of the building.

Also, find :

(i) the floor area of a room of the building, if the floor area of the corresponding room in the model is 50 sq. cm.

(ii) the space (volume) inside a room of the model, if the space inside the corresponding room of the building is 90 m³.

Answer

Given,

Scale factor (k) = 1 : 50.

Dimensions of model = l × b × h = 1 m × 0.6 m × 1.2 m.

By formula,

$\phantom{\Rightarrow} \dfrac{\text{Length of building's model}}{\text{Length of building}} = k \\[1em] \Rightarrow \dfrac{1}{\text{Length of building}} = \dfrac{1}{50} \\[1em] \Rightarrow \text{Length of building} = 50 \text{ m}. \\[2em] \phantom{\Rightarrow} \dfrac{\text{Breadth of building's model}}{\text{Breadth of building}} = k \\[1em] \Rightarrow \dfrac{0.6}{\text{Breadth of building}} = \dfrac{1}{50} \\[1em] \Rightarrow \text{Breadth of building} = 50 \times 0.6 = 30 \text{ m}. \\[2em] \phantom{\Rightarrow} \dfrac{\text{Height of building's model}}{\text{Height of building}} = k \\[1em] \Rightarrow \dfrac{1.2}{\text{Height of building}} = \dfrac{1}{50} \\[1em] \Rightarrow \text{Height of building} = 50 \times 1.2 = 60 \text{ m}.$

Dimensions of building = 50 m × 30 m × 60 m.

(i) By formula,

Floor area of model room = k² × Floor area of building room

50 = $\dfrac{1}{50} \times \dfrac{1}{50}$ × Floor area of building room

Floor area of building room = 50 × 50 × 50 = 125000 cm² = $\dfrac{125000}{100 \times 100}$ m² = 12.5 m².

Hence, floor area of a room of the building = 12.5 m².

(ii) By formula,

Volume of a room of model = k³ × Volume of a room of building

Volume of a room of model = $\dfrac{1}{50} \times \dfrac{1}{50} \times \dfrac{1}{50} \times 90$ = 0.00072 m³ = 0.00072 x 100 x 100 x 100 cm³ = 720 cm³.

Hence, the space inside a room of the model = 720 cm³.

Question 18

In a triangle PQR, L and M are two points on the base QR, such that ∠LPQ = ∠QRP and ∠RPM = ∠RQP. Prove that :

(i) △PQL ~ △RPM

(ii) QL × RM = PL × PM

(iii) PQ² = QR × QL

Answer

(i) In △PQL and △RPM

∠LPQ = ∠MRP (Given ∠LPQ = ∠QRP)

∠LQP = ∠RPM (Given ∠RPM = ∠RQP)

∴ △PQL ~ △RPM [By AA]

Hence, proved that △PQL ~ △RPM.

(ii) Since, △PQL ~ △RPM and corresponding sides of similar triangle are proportional to each other.

$\therefore \dfrac{QL}{PM} = \dfrac{PL}{RM} \\[1em] \Rightarrow QL \times RM = PL \times PM.$

Hence, proved that QL × RM = PL × PM.

(iii) In △PQL and △RQP

∠LPQ = ∠QRP (Given)

∠Q = ∠Q [Common]

∴ △PQL ~ △RQP [By AA]

Since, corresponding sides of similar triangle are proportional to each other.

$\therefore \dfrac{PQ}{RQ} = \dfrac{QL}{QP} \\[1em] \Rightarrow PQ^2 = QR \times QL.$

Hence, proved that PQ² = QR x QL.

Question 19

A triangle ABC with AB = 3 cm, BC = 6 cm and AC = 4 cm is enlarged to △DEF such that the longest side of △DEF = 9 cm. Find the scale factor and hence, the lengths of the other sides of △DEF.

Answer

Longest side in △ABC = BC = 6 cm

Corresponding longest side in △DEF = EF = 9 cm.

Scale factor (k) = $\dfrac{EF}{BC} = \dfrac{9}{6} = \dfrac{3}{2}$ = 1.5

Triangle ABC is enlarged to DEF. So, the two triangles will be similar.

$\therefore \dfrac{AB}{DE} = \dfrac{BC}{EF} = \dfrac{AC}{DF} = \dfrac{2}{3}$ .

So,

$\phantom{\Rightarrow} \dfrac{AB}{DE} = \dfrac{2}{3} \\[1em] \Rightarrow DE = \dfrac{3}{2}AB \\[1em] = \dfrac{9}{2} \\[1em] = 4.5 \text{ cm}. \\[2em] \phantom{\Rightarrow} \dfrac{AC}{DF} = \dfrac{2}{3} \\[1em] \Rightarrow DF = \dfrac{3}{2}AC \\[1em] = \dfrac{12}{2} \\[1em] = 6 \text{ cm}. \\[1em]$

Hence, DE = 4.5 cm and DF = 6 cm.

Question 20

Two isosceles triangles have equal vertical angles. Show that the triangles are similar.

If the ratio between the areas of these two triangles is 16 : 25, find the ratio between their corresponding altitudes.

Answer

Let △ABC and △PQR be two isosceles triangles with AB = AC and PQ = PR.

Two isosceles triangles have equal vertical angles. Show that the triangles are similar. If the ratio between the areas of these two triangles is 16 : 25, find the ratio between their corresponding altitudes. Similarity, Concise Mathematics Solutions ICSE Class 10.

Then,

$\dfrac{AB}{AC} = \dfrac{PQ}{PR} = 1$ .

or,

$\dfrac{AB}{PQ} = \dfrac{AC}{QR}$

Also,

∠A = ∠P (Given)

∴ △ABC ~ △PQR (By SAS)

We know that,

Ratio of areas of two similar triangles is same as the square of the ratio between their corresponding sides.

$\therefore\dfrac{\text{Area of ∆ABC}}{\text{Area of ∆PQR}} = \Big(\dfrac{AB}{PQ}\Big)^2 \\[1em] \Rightarrow \dfrac{16}{25} = \Big(\dfrac{AB}{PQ}\Big)^2 \\[1em] \Rightarrow \dfrac{AB}{PQ} = \sqrt{\dfrac{16}{25}} = \dfrac{4}{5}.$

We know that,

The ratio between sides of similar triangle is equal to ratio of their altitudes.

Hence, ratio between altitudes = 4 : 5.

Question 21

In triangle ABC, AP : PB = 2 : 3. PO is parallel to BC and is extended to Q so that CQ is parallel to BA. Find :

(i) area △APO : area △ABC.

(ii) area △APO : area △CQO.

Answer

(i) In △APO and △ABC,

∠APO = ∠ABC [Corresponding angles are equal]

∠PAO = ∠BAC [Common angle]

∴ △APO ~ △ABC [By AA].

Given,

$\dfrac{AP}{PB} = \dfrac{2}{3}$

Let AP = 2x and PB = 3x.

From figure,

AB = AP + PB = 2x + 3x = 5x.

We know that,

Ratio of areas of two similar triangles is same as the square of the ratio between their corresponding sides.

$\therefore\dfrac{\text{Area of ∆APO}}{\text{Area of ∆ABC}} = \Big(\dfrac{AP}{AB}\Big)^2 \\[1em] = \Big(\dfrac{2x}{5x}\Big)^2 \\[1em] = \Big(\dfrac{2}{5}\Big)^2 \\[1em] = \dfrac{4}{25}.$

Hence, area △APO : area △ABC = 4 : 25.

(ii) Since, PO || BC.

In △ABC,

By basic proportionality theorem,

$\dfrac{AO}{OC} = \dfrac{AP}{PB} = \dfrac{2}{3}$ .

In △APO and △COQ,

∠AOP = ∠COQ [Vertical opposite angles are equal]

∠APO = ∠CQO [Alternate angles are equal]

∴ △APO ~ △COQ [By AA].

We know that,

Ratio of areas of two similar triangles is same as the square of the ratio between their corresponding sides.

$\therefore\dfrac{\text{Area of ∆APO}}{\text{Area of ∆COQ}} = \Big(\dfrac{AO}{OC}\Big)^2 \\[1em] = \Big(\dfrac{2}{3}\Big)^2 \\[1em] = \dfrac{4}{9}.$

Hence, area △APO : area △COQ = 4 : 9.

Question 22

In the given figure, ABC is a triangle with ∠EDB = ∠ACB. Prove that △ABC ~ △EBD. If BE = 6 cm, EC = 4 cm, BD = 5 cm and area of △BED = 9 cm². Calculate the :

(i) length of AB

(ii) area of △ABC

Answer

(i) In △ABC and △EBD,

⇒ ∠EDB = ∠ACB [Given]

⇒ ∠DBE = ∠ABC [Common]

∴ △ABC ~ △EBD

From figure,

⇒ BC = BE + EC = 6 + 4 = 10 cm.

Since, corresponding sides of similar triangles are proportional to each other.

$\Rightarrow \dfrac{AB}{BE} = \dfrac{BC}{BD} \\[1em] \Rightarrow AB = \dfrac{BC \times BE}{BD} \\[1em] \Rightarrow AB = \dfrac{10 \times 6}{5} \\[1em] \Rightarrow AB = 12 \text{ cm}.$

Hence, length of AB = 12 cm.

(ii) We know that,

Ratio of areas of two similar triangles is same as the square of the ratio between their corresponding sides.

$\therefore \dfrac{\text{Area of ∆ABC}}{\text{Area of ∆BED}} = \Big(\dfrac{AB}{BE}\Big)^2 \\[1em] \dfrac{\text{Area of ∆ABC}}{9} = \Big(\dfrac{12}{6}\Big)^2 \\[1em] \text{Area of ∆ABC} = \Big(\dfrac{12}{6}\Big)^2 \times 9 \\[1em] \text{Area of ∆ABC} = 36 \text{ cm}^2.$

Hence, area of ∆ABC = 36 cm².

Question 23

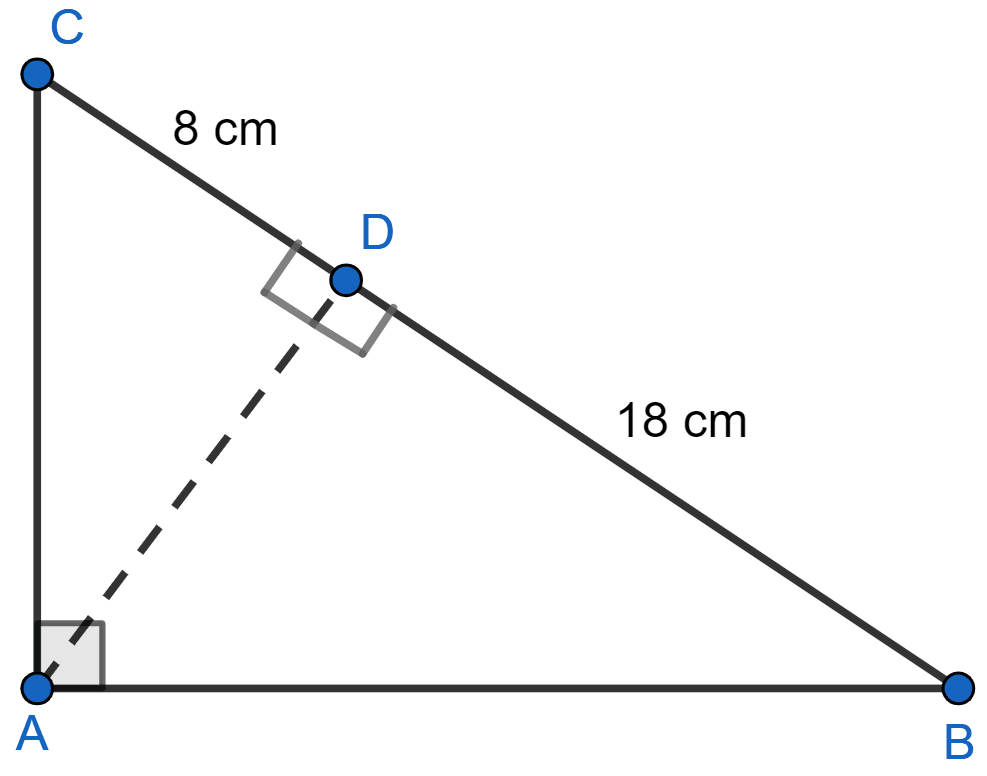
In the given figure, ABC is a right angled triangle with ∠BAC = 90°.

(i) Prove that : △ADB ~ △CDA.

(ii) If BD = 18 cm and CD = 8 cm, find AD.

(iii) Find the ratio of the area of △ADB is to area of △CDA.

Answer

(i) Let ∠CAD = x.

So, ∠DAB = 90° - x.

In △ABD,

⇒ ∠DAB + ∠ADB + ∠ABD = 180° [By angle sum property]

⇒ 90° - x + 90° + ∠ABD = 180°

⇒ 180° - x + ∠ABD = 180°

⇒ ∠ABD = x + 180° - 180°

⇒ ∠ABD = x.

In △ADB and △CDA,

⇒ ∠CAD = ∠ABD (Both = x)

⇒ ∠CDA = ∠ADB (Both = 90°)

∴ △ADB ~ △CDA [By AA]

Hence, proved that △ADB ~ △CDA.

(ii) Since, △ADB ~ △CDA and corresponding sides of similar triangles are proportional to each other.

$\dfrac{BD}{AD} = \dfrac{AD}{CD}$

⇒ AD² = BD × CD

⇒ AD² = 18 × 8

⇒ AD² = 144

⇒ AD = $\sqrt{144}$ = 12 cm.

Hence, AD = 12 cm.

(iii) We know that,

Ratio of areas of two similar triangles is same as the square of the ratio between their corresponding sides.

$\therefore\dfrac{\text{Area of ∆ADB}}{\text{Area of ∆CDA}} = \Big(\dfrac{AD}{CD}\Big)^2 \\[1em] = \Big(\dfrac{12}{8}\Big)^2 \\[1em] = \Big(\dfrac{3}{2}\Big)^2 \\[1em] = \dfrac{9}{4}.$

Hence, ratio of the area of △ADB to area of △CDA = 9 : 4.

Question 24

ABC is a right angled triangle with ∠ABC = 90°. D is any point on AB and DE is perpendicular to AC. Prove that :

(i) △ADE ~ △ACB

(ii) If AC = 13 cm, BC = 5 cm and AE = 4 cm. Find DE and AD.

(iii) Find, area of △ADE : area of quadrilateral BCED.

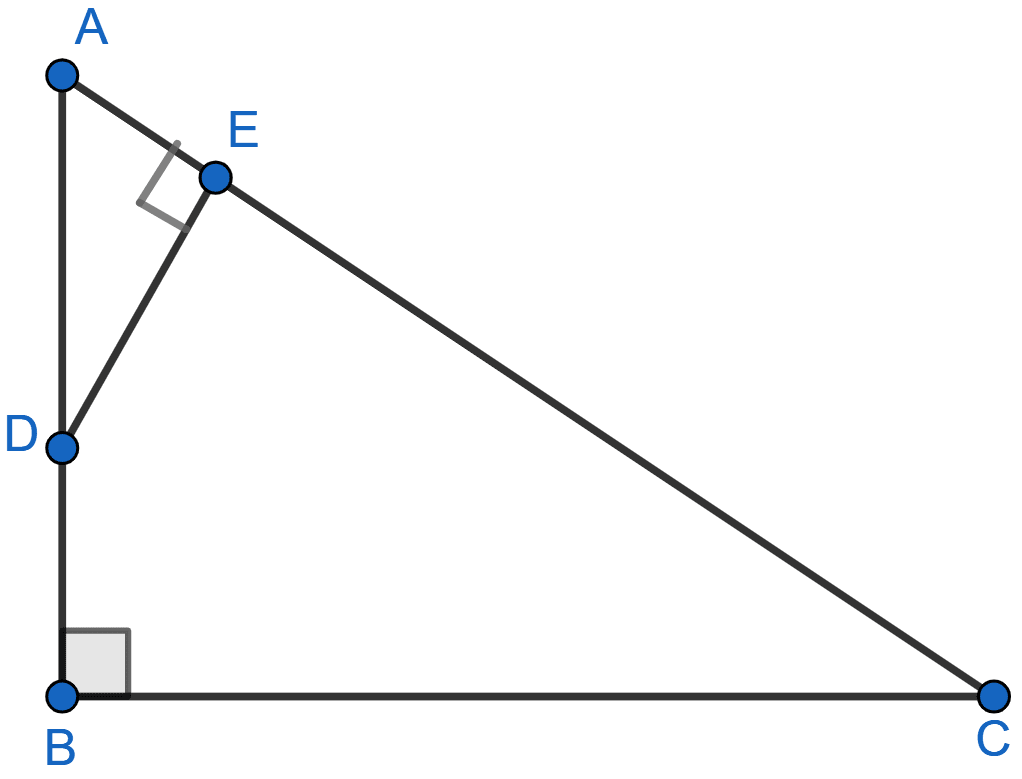
ABC is a right angled triangle with ∠ABC = 90°. D is any point on AB and DE is perpendicular to AC. Prove that (i) △ADE ~ △ACB (ii) If AC = 13 cm, BC = 5 cm and AE = 4 cm. Find DE and AD. (iii) Find, area of △ADE : area of quadrilateral BCED. Similarity, Concise Mathematics Solutions ICSE Class 10.

Answer

(i) In △ADE and △ACB,

⇒ ∠AED = ∠ABC [Both = 90°]

⇒ ∠EAD = ∠CAB [Common angle]

∴ △ADE ~ △ACB [By AA].

Hence, proved that △ADE ~ △ACB.

(ii) In right angle triangle ABC,

⇒ AC² = AB² + BC²

⇒ 13² = AB² + 5²

⇒ 169 = AB² + 25

⇒ AB² = 144

⇒ AB = $\sqrt{144}$ = 12 cm.

Since, △ADE ~ △ACB and corresponding sides of similar triangles are proportional to each other.

$\therefore \dfrac{AE}{AB} = \dfrac{DE}{BC} \\[1em] \Rightarrow \dfrac{DE}{5} = \dfrac{4}{12} \\[1em] \Rightarrow DE = \dfrac{20}{12} = \dfrac{5}{3} = 1\dfrac{2}{3} \text{ cm}. \\[1em] \Rightarrow \dfrac{AD}{AC} = \dfrac{AE}{AB} \\[1em] \Rightarrow \dfrac{AD}{13} = \dfrac{4}{12} \\[1em] \Rightarrow AD = \dfrac{52}{12} \\[1em] \Rightarrow AD = \dfrac{13}{3} = 4\dfrac{1}{3} \text{ cm}.$

Hence, DE = $1\dfrac{2}{3} \text{ cm and } AD = 4\dfrac{1}{3}$ cm.

(iii) From figure,

Area of △ADE = $\dfrac{1}{2} \times AE \times DE$

$= \dfrac{1}{2} \times 4 \times \dfrac{5}{3} \\[1em] = \dfrac{10}{3} \text{ cm}^2 \\[1em] \text{Area of △ABC} = \dfrac{1}{2} \times BC \times AB \\[1em] = \dfrac{1}{2} \times 5 \times 12 \\[1em] = 30 \text{ cm}^2.$

Area of quadrilateral BCED = Area of △ABC - Area of △ADE

$= 30 - \dfrac{10}{3} \\[1em] = \dfrac{90 - 10}{3} \\[1em] = \dfrac{80}{3} \text{ cm}^2. \\[1em] \dfrac{\text{Area of △ADE}}{\text{Area of quadrilateral BCED}} = \dfrac{\dfrac{10}{3}}{\dfrac{80}{3}} \\[1em] = \dfrac{10}{80} = \dfrac{1}{8}.$

Hence, area of △ADE : area of quadrilateral BCED = 1 : 8.

Question 25

Given : AB || DE and BC || EF. Prove that :

(i) $\dfrac{AD}{DG} = \dfrac{CF}{FG}$

(ii) △DFG ~ △ACG.

Given : AB || DE and BC || EF. Prove that AD/DG = CF/FG. Similarity, Concise Mathematics Solutions ICSE Class 10.

Answer

(i) In △ABG, DE || AB.

So, by basic proportionality theorem we get,

$\dfrac{DG}{AD} = \dfrac{GE}{BE}$ .....(1)

In △BCG, EF || BC.

So, by basic proportionality theorem we get,

$\dfrac{GE}{BE} = \dfrac{FG}{CF}$ .....(2)

From (1) and (2) we get,

$\Rightarrow \dfrac{DG}{AD} = \dfrac{FG}{CF} \\[1em] \Rightarrow \dfrac{AD}{DG} = \dfrac{CF}{FG}.$

Hence, proved that $\dfrac{AD}{DG} = \dfrac{CF}{FG}.$

(ii) In △DFG and △ACG,

⇒ $\dfrac{AD}{DG} = \dfrac{CF}{FG}$ [Proved above]

⇒ ∠DGF = ∠AGC [Common angle]

∴ △DFG ~ △ACG [By SAS]

Hence, proved that △DFG ~ △ACG.

Question 26

PQR is a triangle. S is a point on the side QR of △PQR such that ∠PSR = ∠QPR. Given QP = 8 cm, PR = 6 cm and SR = 3 cm.

(i) Prove △PQR ~ △SPR.

(ii) Find the lengths of QR and PS.

(iii) $\dfrac{\text{area of △PQR}}{\text{area of △SPR}}$

Answer

(i) In △PQR and △SPR,

⇒ ∠PSR = ∠QPR [Given]

⇒ ∠PRQ = ∠PRS [Common angle]

∴ △PQR ~ △SPR [By AA]

Hence, proved that △PQR ~ △SPR.

(ii) Since, △PQR ~ △SPR and corresponding sides of similar triangle are proportional to each other.

$\Rightarrow \dfrac{QR}{PR} = \dfrac{PR}{SR} \\[1em] \Rightarrow \dfrac{QR}{6} = \dfrac{6}{3} \\[1em] \Rightarrow QR = \dfrac{36}{3} = 12 \text{ cm}. \\[1em] \text{ Also}, \\[1em] \Rightarrow \dfrac{PQ}{SP} = \dfrac{PR}{SR} \\[1em] \Rightarrow \dfrac{8}{SP} = \dfrac{6}{3} \\[1em] \Rightarrow SP = \dfrac{24}{6} = 4 \text{ cm}.$

Hence, QR = 12 cm and PS = 4 cm.

(iii) We know that,

Ratio of areas of two similar triangles is same as the square of the ratio between their corresponding sides.

$\therefore\dfrac{\text{Area of ∆PQR}}{\text{Area of ∆SPR}} = \Big(\dfrac{PQ}{SP}\Big)^2 \\[1em] = \Big(\dfrac{8}{4}\Big)^2 \\[1em] = (2)^2 \\[1em] = 4.$

Hence, $\dfrac{\text{area of △PQR}}{\text{area of △SPR}}$ = 4 : 1.

Chapter 15

Similarity (With Applications to Maps and Modules)

Class - 10 Concise Mathematics Selina

Exercise 15(A)

Question 1(a)

Question 1(b)

Question 1(c)

Question 1(d)

Question 2

Question 3

Question 4

Question 5

Question 6

Exercise 15(B)

Question 1(a)

Question 1(b)

Question 1(c)

Question 1(d)

Question 2

Question 3

Question 4

Question 5

Question 6

Question 7

Question 8

Exercise 15(C)

Question 1(a)

Question 1(b)

Question 1(c)

Question 1(d)

Question 2

Question 3

Question 4

Question 5

Question 6

Question 7

Question 8

Question 9

Question 10

Question 11

Question 12

Question 13

Question 14

Question 15

Question 16

Question 17

Exercise 15(D)

Question 1(a)

Question 1(b)

Question 1(c)

Question 1(d)

Question 1(e)

Question 2

Question 3

Question 4

Question 5

Question 6

Question 7

Question 8

Question 9

Question 10

Question 11

Exercise 15(E)

Question 1(a)

Question 1(b)

Question 1(c)

Question 1(d)

Question 1(e)

Question 2

Question 3

Question 4

Question 5

Question 6

Question 7

Question 8

Question 9

Question 10

Exercise 15(F)

Question 1(a)

Question 1(b)