Loci (Locus and its Contructions)

P is a point on perpendicular bisector of side BC of △ABC, then :

1. PA = PB

2. PB = PC

3. PA = PC

4. none of these

Answer

We know that,

Locus of a point equidistant from two given points is the perpendicular bisector of the line joining the two points.

Given,

P is a point on perpendicular bisector of side BC of △ABC.

∴ PB = PC.

Hence, Option 2 is the correct option.

P is a point on bisector of angle A of △ABC. Then:

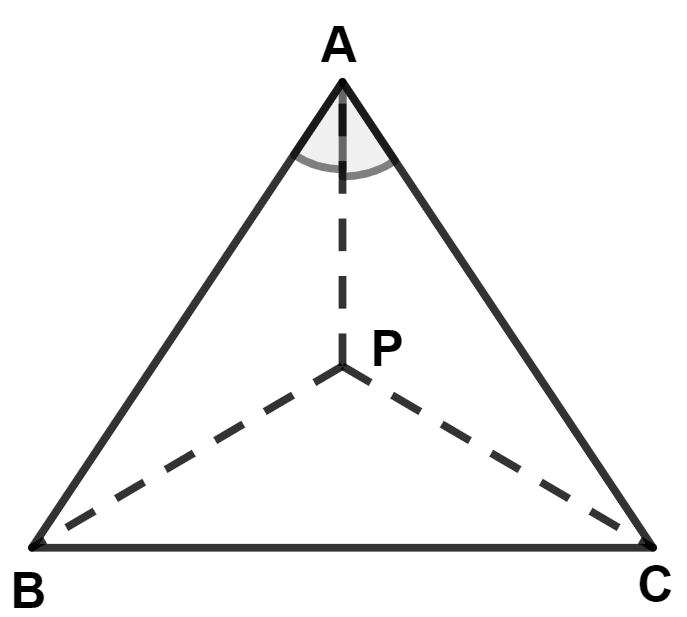
1. P is equidistant from the vertices B and C

2. PA = PC

3. PA = PB

4. P is equidistant from sides AB and AC of the △ABC.

Answer

We know that,

The locus of a point equidistant from two intersecting lines is the bisector of the angles between the lines.

Given,

P is a point on bisector of angle A of △ABC.

∴ P is equidistant from sides AB and AC of the △ABC.

Hence, Option 4 is the correct option.

The perpendicular bisector of side AB and bisector of angle A of △ABC meet at point P. Then :

1. PA = PB

2. PA = PC

3. PB = PC

4. PB bisects ∠ABC

Answer

We know that,

Locus of a point equidistant from two given points is the perpendicular bisector of the line joining the two points.

Since,

The perpendicular bisector of side AB and bisector of angle A of △ABC meet at point P.

∴ PA = PB.

Hence, Option 1 is the correct option.

Using the information in the given diagram, state if :

1. AD = DC

2. BD = DC

3. CD bisects angle ACB

4. angle CAD is greater than angle DAB

Answer

From figure,

AD = DB = AC = BC = x (let)

In △ ADC and △ BDC,

⇒ AD = DB (Both equal to x)

⇒ AC = BC (Both equal to x)

⇒ CD = CD (Common side)

∴ △ ADC ≅ △ BDC (By S.S.S. axiom)

We know that,

Corresponding parts of congruent triangle are equal.

∴ ∠ACD = ∠BCD

∴ CD bisects angle ACB.

Hence, Option 3 is the correct option.

Bisector of angle B of triangle ABC intersects side AC at point P, then point P is :

1. equidistant from vertices A and C

2. PA = PB

3. PB = PC

4. equidistant from sides AB and BC

Answer

We know that,

The locus of a point equidistant from two intersecting lines is the bisector of the angles between the lines.

Given,

Bisector of angle B of triangle ABC intersects side AC at point P.

∴ P is equidistant from sides AB and BC.

Hence, Option 4 is the correct option.

Given: PQ is a perpendicular bisector of side AB of the triangle ABC.

Prove: Q is equidistant from A and B.

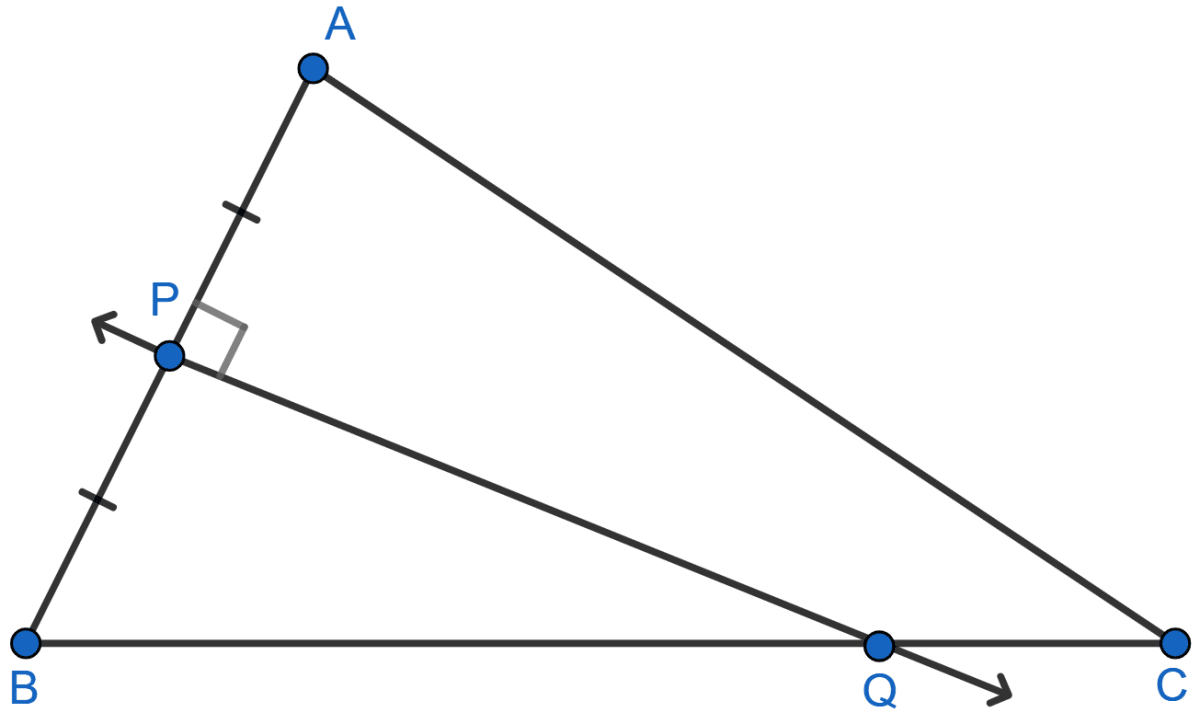
Answer

Join A and Q as shown in the figure below:

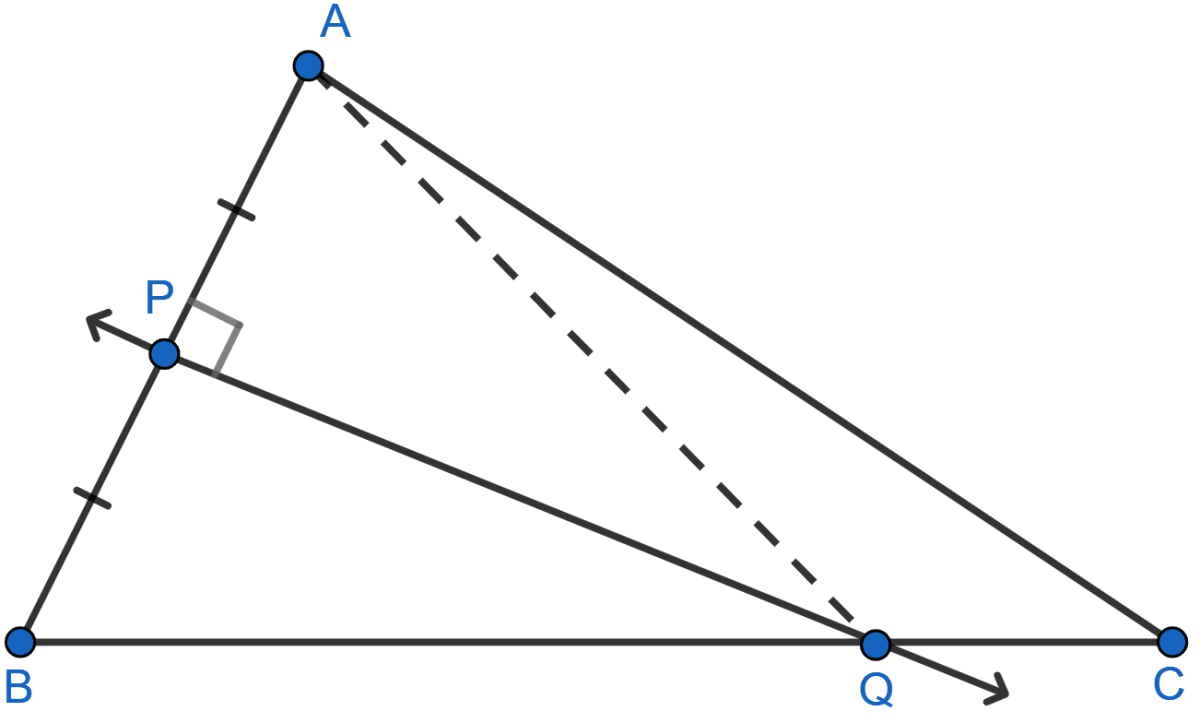
In ∆AQP and ∆BQP,

⇒ AP = BP [Given]

⇒ ∠QPA = ∠QPB [Each 90°]

⇒ PQ = PQ [Common]

∴ ∆AQP ≅ ∆BQP by SAS axiom.

∴ AQ = BQ [By C.P.C.T.]

Hence, proved that Q is equidistant from A and B.

Given: CP is the bisector of angle C of ∆ABC.

Prove: P is equidistant from AC and BC.

Answer

From P, draw PL ⊥ AC and PM ⊥ CB

In ∆LPC and ∆MPC,

⇒ ∠PLC = ∠PMC [Each 90°]

⇒ ∠PCL = ∠MCP [Since, CP is bisector of angle C]

⇒ PC = PC [Common]

∴ ∆LPC ≅ ∆MPC by AAS axiom.

∴ PL = PM [By C.P.C.T.]

Hence, proved that P is equidistant from AC and BC.

Given: AX bisects angle BAC and PQ is perpendicular bisector of AC which meets AX at point Y.

Prove :

(i) X is equidistant from AB and AC.

(ii) Y is equidistant from A and C.

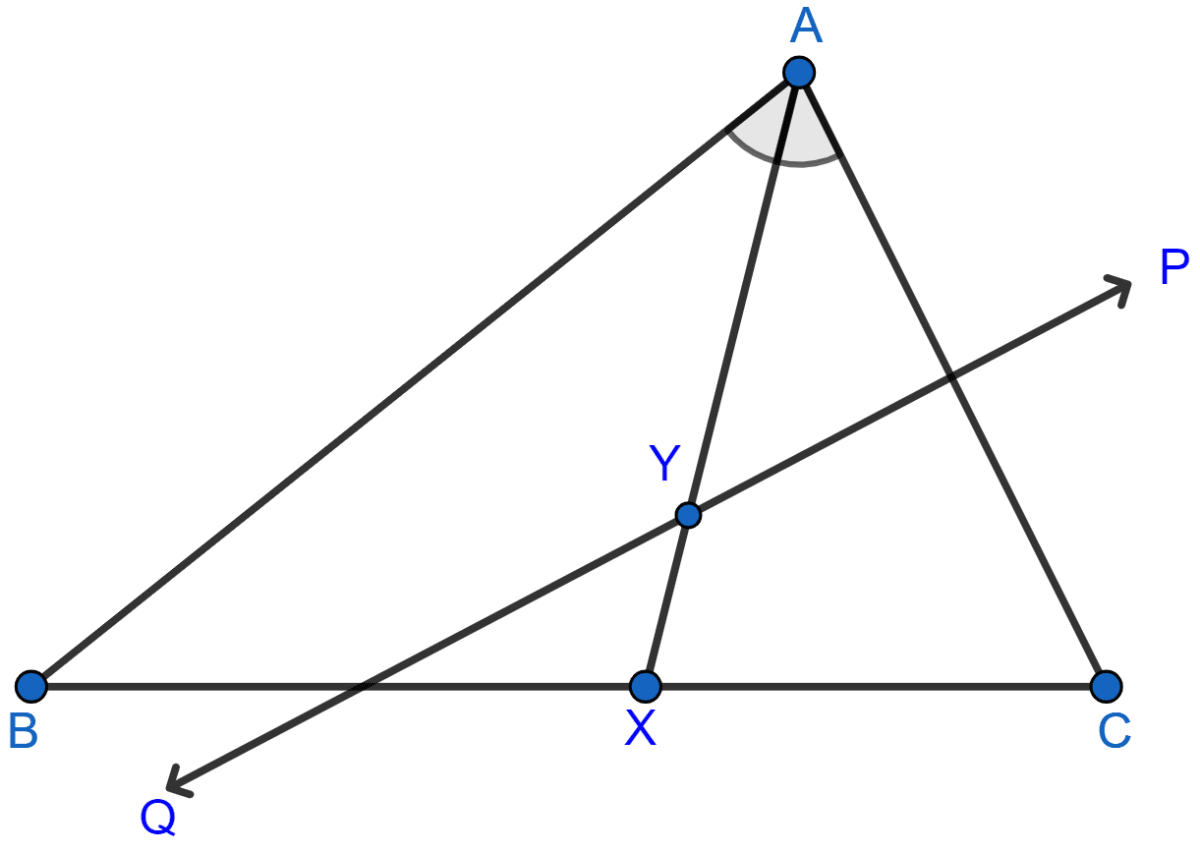
Answer

From X, draw XL ⊥ AC and XM ⊥ AB and join YC.

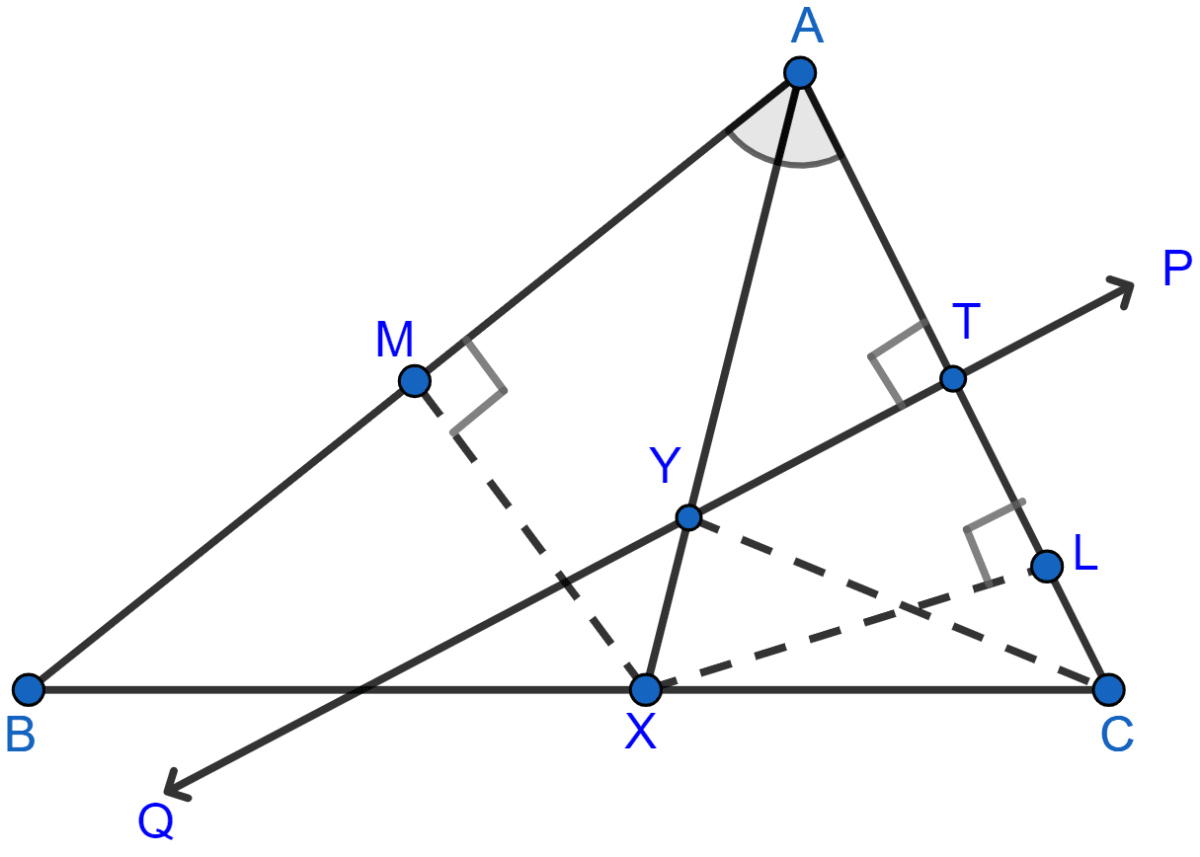
(i) In ∆AXL and ∆AXM,

⇒ ∠XAL = ∠XAM [Since, AX bisects angle BAC]

⇒ AX = AX [Common]

⇒ ∠XLA = ∠XMA [Each 90°]

∴ ∆AXL ≅ ∆AXM by AAS axiom.

∴ XL = XM [By C.P.C.T.]

Hence, proved that X is equidistant from AC and AB.

(ii) In ∆YTA and ∆YTC,

⇒ AT = CT [because PQ is perpendicular bisector of AC]

⇒ ∠YTA = ∠YTC [Each 90°]

⇒ YT = YT [Common]

∴ ∆YTA ≅ ∆YTC by SAS axiom.

∴ YA = YC [By C.P.C.T.]

Hence, proved that Y is equidistant from A and C.

Construct a triangle ABC, in which AB = 4.2 cm, BC = 6.3 cm and AC = 5 cm. Draw perpendicular bisector of BC which meets AC at point D. Prove that D is equidistant from B and C.

Answer

Steps of Construction:

1. Draw a line segment BC = 6.3 cm

2. With centre B and radius 4.2 cm, draw an arc.

3. With centre C and radius 5 cm, draw another arc which intersects the first arc at A.

4. Join AB and AC. Then, ∆ABC is the required triangle.

5. Draw LM, perpendicular bisector of BC.

6. Let LM intersect AC at D and BC at E.

7. Join DB.

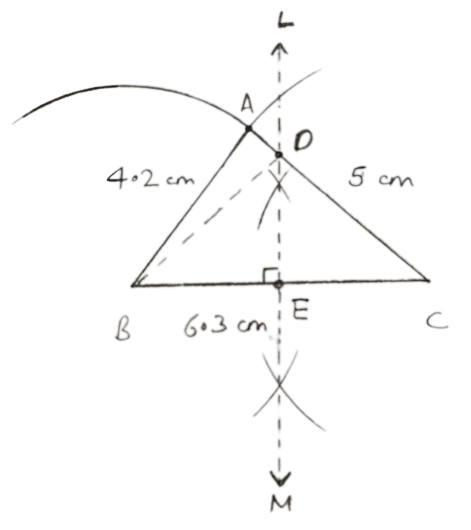
In ∆DBE and ∆DCE,

⇒ BE = EC [LM is the perpendicular bisector of BC]

⇒ ∠DEB = ∠DEC [Each 90°]

⇒ DE = DE [Common]

∴ ∆DBE ≅ ∆DCE [By SAS]

∴ DB = DC [By C.P.C.T.]

Hence, proved that D is equidistant from B and C.

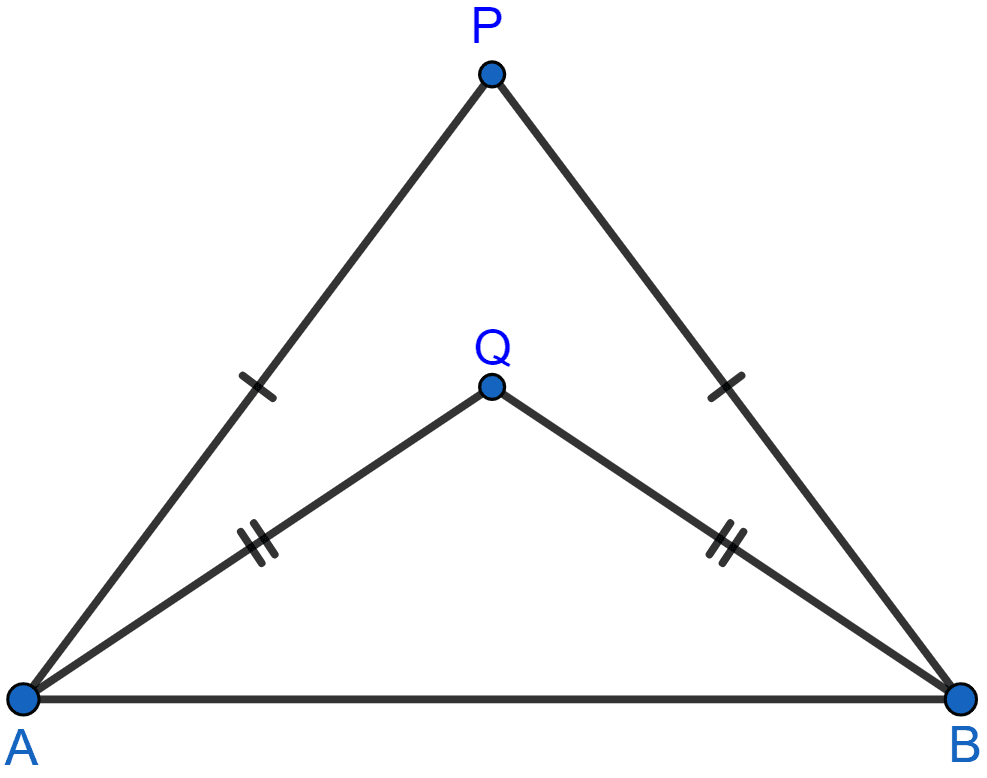
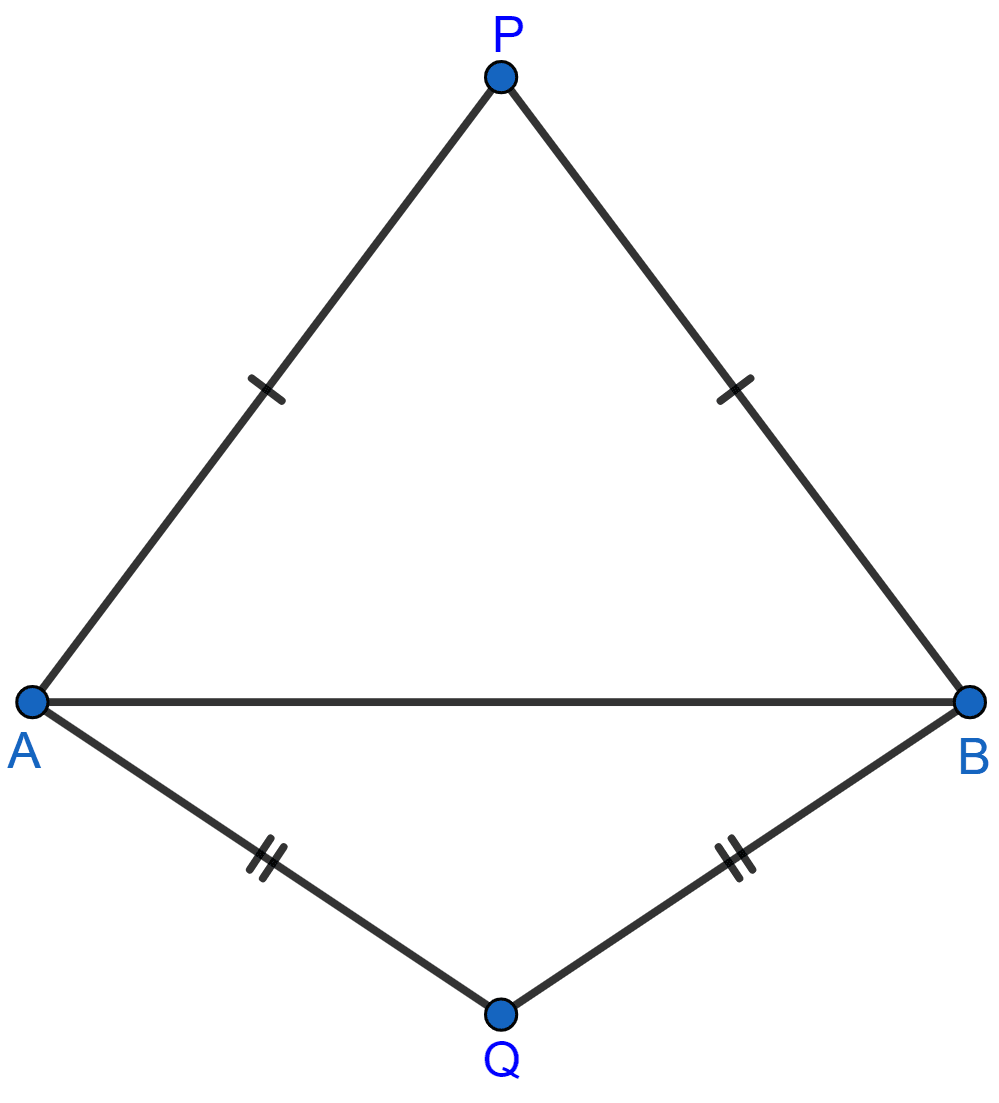
In each of the given figures; PA = PB and QA = QB.

(i)

(ii)

Prove in each case, that PQ (produce, if required) is perpendicular bisector of AB.

Hence, state the locus of the points equidistant from two given fixed points.

Answer

(i) Join PQ which meets AB in D.

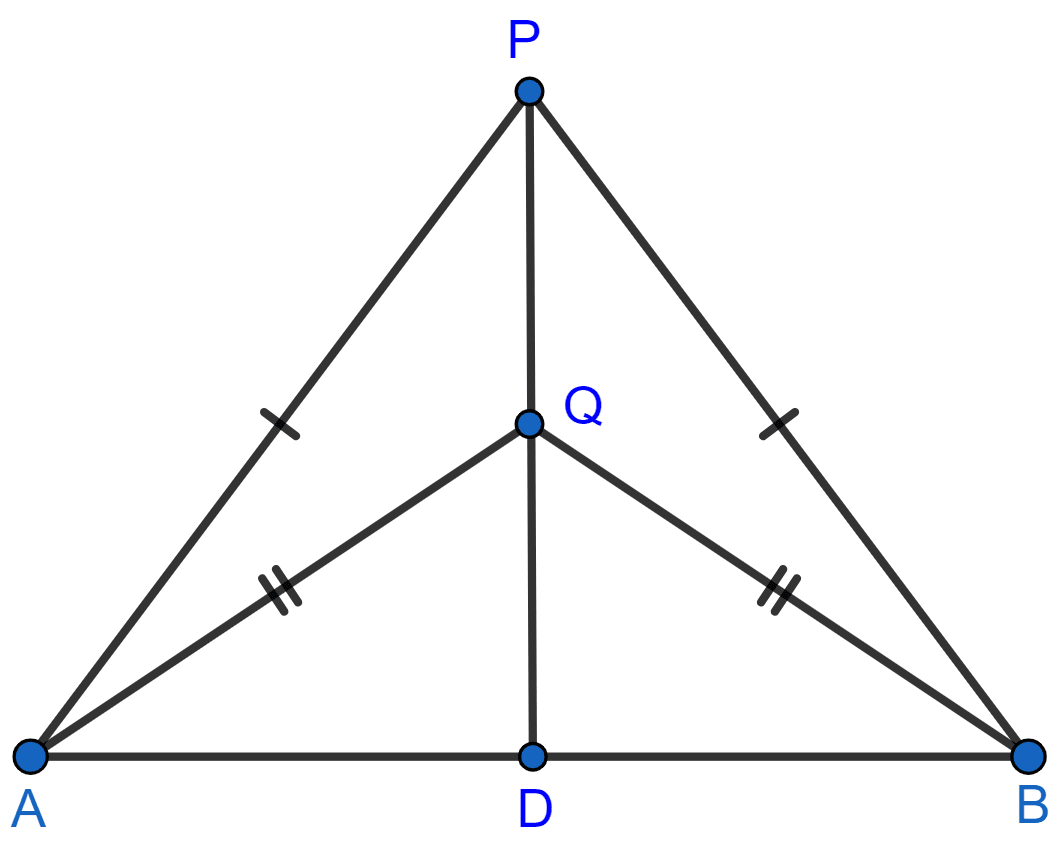
Given, PA = PB.

∴ P is equidistant from A and B. Thus, P lies on the perpendicular bisector of AB.

Given, QA = QB.

∴ Q is equidistant from A and B. Thus, Q lies on perpendicular bisector of AB.

Thus, both P and Q lie on the perpendicular bisector of AB.

Hence, proved that PQ is the perpendicular bisector of AB.

(ii) Join PQ which meets AB in D.

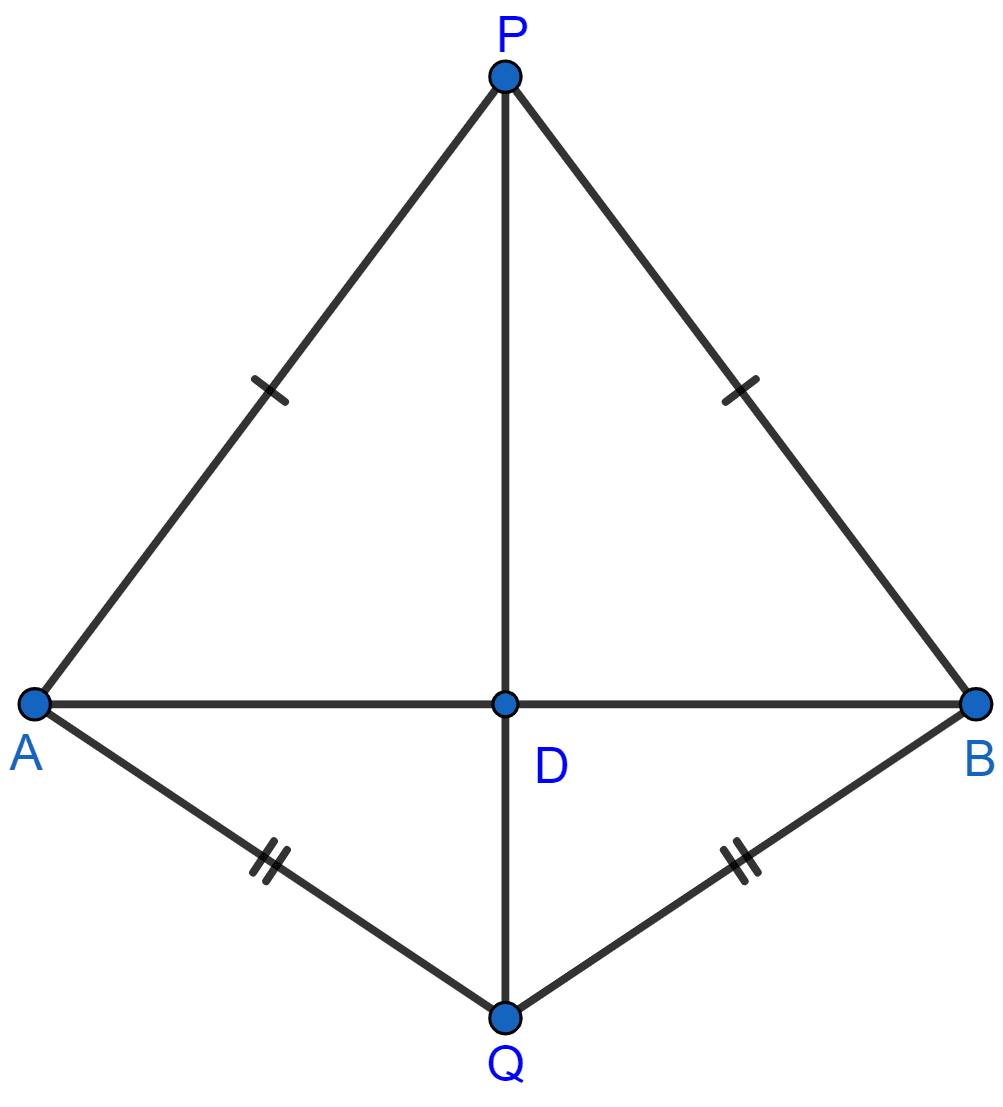
Given, PA = PB.

∴ P is equidistant from A and B. Thus, P lies on the perpendicular bisector of AB.

Given, QA = QB.

∴ Q is equidistant from A and B. Thus, Q lies on perpendicular bisector of AB.

Thus, both P and Q lie on the perpendicular bisector of AB.

Hence, proved that PQ is the perpendicular bisector of AB.

Hence, locus of the points which are equidistant from two fixed points, is the perpendicular bisector of the line joining the fixed points.

Construct a triangle ABC in which angle ABC = 75°, AB = 5 cm and BC = 6.4 cm. Draw perpendicular bisector of side BC and also the bisector of angle ACB. If these bisectors intersect each other at point P; prove that P is equidistant from B and C; and also from AC and BC.

Answer

Steps of Construction:

1. Draw a line segment BC = 6.4 cm

2. At B, draw a ray BX making an angle of 75° and cut off BA = 5 cm.

3. Join AC. ∆ABC is the required triangle.

4. Draw the perpendicular bisector of BC, intersecting BC at Q.

5. Draw CX, the angle bisector of angle ACB which intersects the perpendicular bisector of BC at P.

6. Join PB and draw PL ⊥ AC.

In ∆PBQ and ∆PCQ,

⇒ PQ = PQ [Common]

⇒ ∠PQB = ∠PQC [Each = 90°]

⇒ BQ = QC [As PQ is the perpendicular bisector of BC]

∴ ∆PBQ ≅ ∆PCQ [By SAS axiom]

∴ PB = PC [By C.P.C.T.]

∴ P is equidistant from B and C.

Also,

In ∆PQC and ∆PLC,

⇒ ∠PQC = ∠PLC [Each 90°]

⇒ ∠PCQ = ∠PCL [As CX is angle bisector of ∠ACB]

⇒ PC = PC [Common]

∴ ∆PQC ≅ ∆PLC by AAS axiom.

∴ PQ = PL [By C.P.C.T.]

∴ P is equidistant from AC and BC.

Hence, proved that P is equidistant from B and C and also from AC and BC.

In parallelogram ABCD, side AB is greater than side BC and P is a point in AC such that PB bisects angle B.

Prove that P is equidistant from AB and BC.

Answer

Steps of construction:

1. Draw a parallelogram such that AB > BC.

2. Join AC the diagonal of parallelogram.

3. Draw BX, the angle bisector of ∠ABC and let it intersect AC at P.

4. From P, draw PL ⊥ AB and PM ⊥ BC.

In ∆PLB and ∆PMB,

⇒ ∠PLB = ∠PMB [Each 90°]

⇒ ∠PBL = ∠PBM [As BX is angle bisector of ABC.]

⇒ PB = PB [Common]

∴ ∆PLB ≅ ∆PMB by AAS axiom.

∴ PL = PM

Hence, proved that P is equidistant from AB and BC.

In triangle LMN, bisectors of interior angles at L and N intersect each other at point A. Prove that:

(i) point A is equidistant from all the three sides of the triangle.

(ii) AM bisects angle LMN.

Answer

Steps of construction :

1. Construct a triangle LMN.

2. Draw angle bisectors of L and N. Let the angle bisectors meet at A.

3. Join AM.

(i) Since, A lies on bisector of ∠N

∴ A is equidistant from MN and LN.

Again, as A lies on the bisector of ∠L

∴ A is equidistant from LN and LM.

Hence, proved that A is equidistant from all three sides of the triangle LMN.

(ii) From above part we get,

A is equidistant from MN and LN and also from LN and LM.

We get,

A is equidistant from MN and LM.

∴ A lies on angle bisector of ∠LMN.

Hence, proved that AM bisects ∠LMN.

Use ruler and compasses only for this question.

(i) Construct ∆ABC, where AB = 3.5 cm, BC = 6 cm and ∠ABC = 60°.

(ii) Construct the locus of points inside the triangle which are equidistant from BA and BC.

(iii) Construct the locus of points inside the triangle which are equidistant from B and C.

(iv) Mark the point P which is equidistant from AB, BC and also equidistant from B and C. Measure and record the length of PB.

Answer

Steps of construction:

(i) Draw line BC = 6 cm and construct angle CBX = 60°. Cut off AB = 3.5 cm. Join AC, triangle ABC is the required triangle.

(ii) The locus of points which are equidistant from two sides is the angle bisector of angle between the lines. Construct BX, the bisector of angle B.

(iii) The locus of points inside the triangle which are equidistant from B and C is YZ, the perpendicular bisector of BC inside the triangle.

(iv) Let perpendicular bisector of BC meets BX at P.

Thus, P is the point which is equidistant from BA and BC, which is also equidistant from B and C. Measure PB.

Hence, PB = 3.5 cm

The locus of the centers of all circles, which are tangents to the arms AB and BC of angle ABC is :

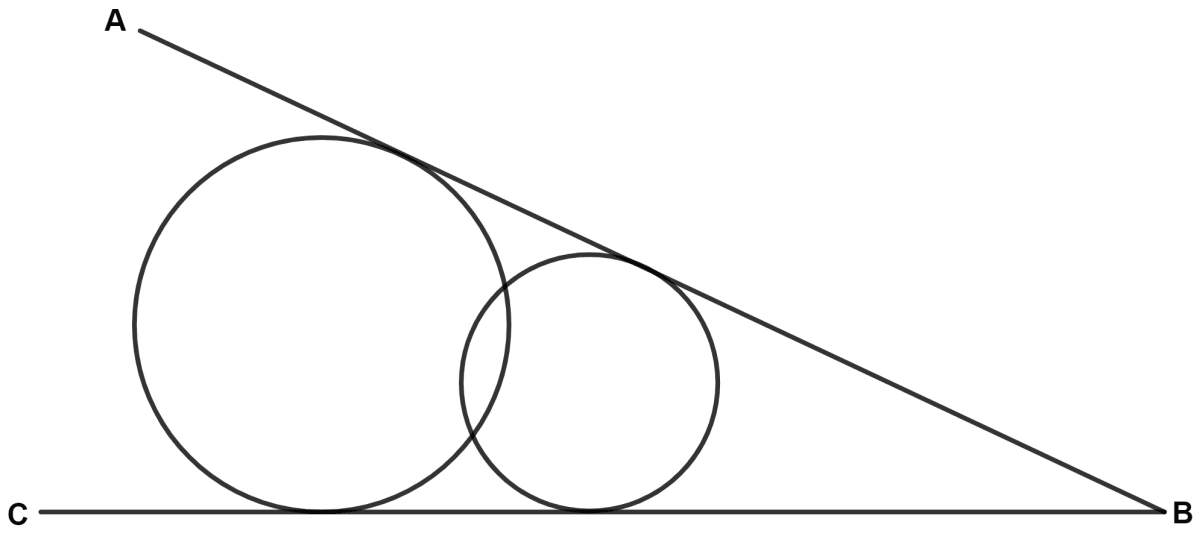
1. perpendicular bisector of arm AB

2. perpendicular bisector of arm BC

3. bisector of angle ABC

4. none of these

Answer

From figure,

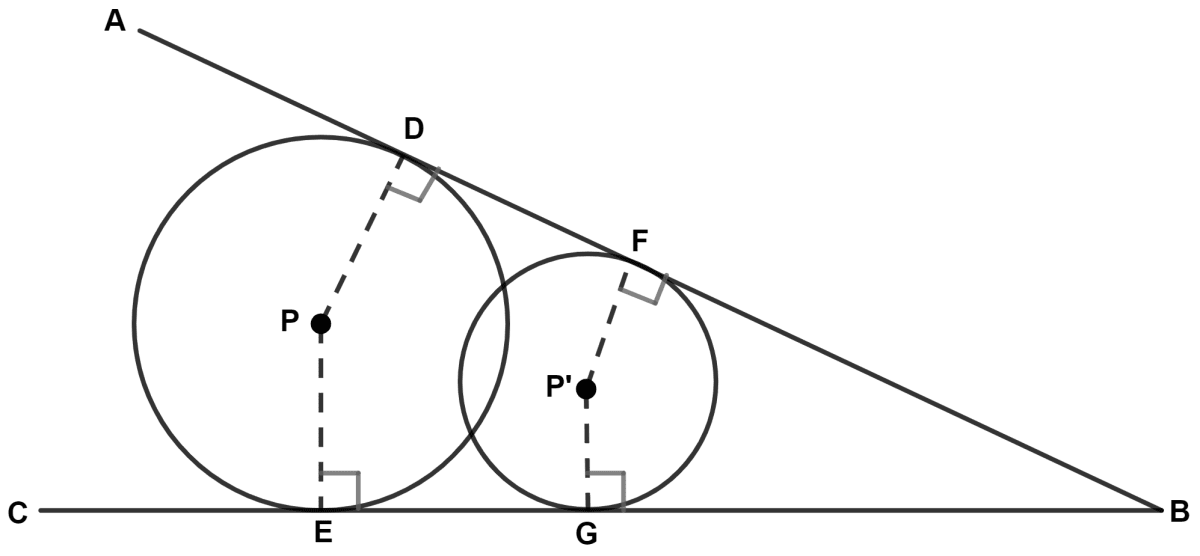
PD = PE (Radius of circle with center P)

P'F = P'G (Radius of circle with center P')

∴ The centers of circles are equidistant from the lines AB and BC.

We know that,

The locus of a point equidistant from two intersecting lines is the bisector of the angles between the lines.

∴ The locus of the centers of all circles, which are tangents to the arms AB and BC of angle ABC is the bisector of angle ABC.

Hence, Option 3 is the correct option.

P is a moving point and AB is a chord of a circle. If P moves, within this circle, in such a way that it is at equal distances from points A and B. The locus of P is :

1. a chord perpendicular to chord AB

2. a chord that bisects the chord AB

3. a diameter of the circle

4. the diameter of the circle which is perpendicular to chord AB

Answer

Let O be the center of the circle and AB be the chord.

Draw XY, perpendicular bisector of AB.

We know that,

Locus of a point equidistant from two given points is the perpendicular bisector of the line joining the two points.

∴ XY is the locus of point P.

We know that,

Perpendicular to a chord passes through center of the circle.

We know that,

Chord passing through the center is the diameter.

Locus of point P is the diameter of the circle which is perpendicular to chord AB.

Hence, Option 4 is the correct option.

AB is a line segment. A point P moves in such a way that the triangle APB is always an isosceles triangle with base AB. The locus of point P is the line which :

1. is parallel to AB

2. is perpendicular to AB

3. is perpendicular bisector of AB

4. passes through the mid-point of AB.

Answer

Steps of construction :

1. Draw a line segment AB.

2. Draw XY, the perpendicular bisector of AB.

We know that,

Locus of a point equidistant from two given points is the perpendicular bisector of the line joining the two points.

∴ Any point P on the line XY, will be such that PA = PB.

Hence, Option 3 is the correct option.

AB is a line segment and P is a moving point that moves in such a way that it is always equidistant from AB. The locus of point P is the line which :

1. is parallel to AB and through point P.

2. is perpendicular to AB through point P.

3. is perpendicular bisector of AB.

4. passes through the mid-point of AB.

Answer

Steps of construction :

1. Draw a line segment AB.

2. Draw lines l and m parallel to AB on either side.

We know that,

The locus of point which is equidistant from a particular line is a line parallel to it.

Hence, Option 1 is the correct option.

A point P moves in such a way that it is at a distance less than or equal to 5 cm from a fixed point O. The locus of point P is :

1. a circle with radius 5 cm.

2. a circle with OP as radius.

3. a circle with diameter of 10 cm.

4. a circle of radius 5 cm and the fixed point O as its center.

Answer

Steps of construction :

1. Draw a circle of radius 5 cm and center O.

From figure,

Any point on the circumference f the circle is at a distance 5 cm and any point inside the circle will be less than 5 cm.

Hence, Option 4 is the correct option.

Describe the locus of a point at a distant 3 cm from a fixed point.

Answer

Steps of construction :

Let fixed point be A and B be any point on circle.

1. Taking fixed point (A) as center draw a circle of radius (AB) = 3 cm.

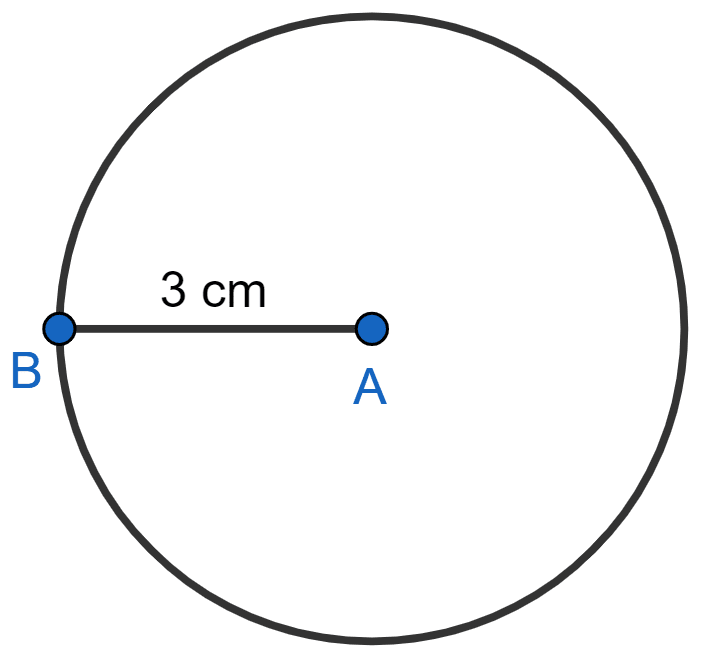
The locus of a point which is 3 cm away from a fixed point is circumference of a circle whose radius is 3 cm and the fixed point is the center of the circle.

Describe the locus of points at a distance 2 cm from a fixed line.

Answer

Steps of construction :

1. Let AB be the fixed line.

2. Draw a line l and m, parallel to AB on opposite sides at a distance of 2 cm from AB.

The locus of a point at a distance of 2 cm from a fixed line AB is a pair of straight lines (l and m) parallel to given fixed line and at a distance of 2 cm from it.

Describe the locus of the center of a wheel of a bicycle going straight along a level road.

Answer

Let radius of wheel be r units.

The locus of the center of a wheel, which is going straight along a level road will be a straight line parallel to the road at a distance equal to the radius of the wheel.

Describe the locus of the moving end of the minute hand of a clock.

Answer

Let radius of minute hand be r units.

The locus of the moving end of the minute hand of the clock will be the circumference of a circle with radius equal to the length of the minute hand.

Describe the locus of a stone dropped from the top of a tower.

Answer

The locus of a stone which is dropped from the top of a tower will be a line perpendicular to the ground through the point from which the stone is dropped.

Describe the locus of a runner, running round a circular track and always keeping a distance of 1.5 m from the inner edge.

Answer

Let the inner circular track be r meters.

The required locus will be the circumference of a circle concentric to the running circular track and whose radius will be equal to (r + 1.5) metres.

Describe the locus of the door handle, as the door opens.

Answer

The locus of the door handle will be the circumference of a circle with center at the axis of rotation of the door and radius equal to the distance between the door handle and the axis of rotation of the door.

Describe the locus of points inside a circle and equidistant from two fixed points on the circumference of the circle.

Answer

Steps of construction :

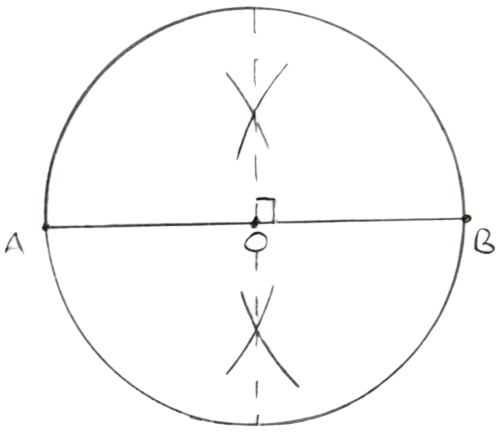
1. Draw a circle with O as center.

2. Mark two points A and B. Join AB.

3. Draw perpendicular bisector of AB. It should pass through center of the circle.

Since, O lies on perpendicular bisector of AB so OA = OB.

Hence, the locus of points inside the circle which are equidistant from the two fixed points on the circumference of a circle will be the diameter which is the perpendicular bisector of the chord joining the two fixed points on the circle.

Describe the locus of the centers of all circles passing through two fixed points.

Answer

Steps of construction :

1. Let two points be A and B.

2. Construct the circles passing through A and B.

3. Draw perpendicular bisector of AB.

From figure,

The centers lie on the perpendicular bisector of AB.

Hence, the locus of centers of all the circles which pass through two fixed points will be the perpendicular bisector of the line segment joining the two given fixed points.

Describe the locus of vertices of all isosceles triangles having a common base.

Answer

We know that,

The locus of point equidistant from two points is the perpendicular bisector of the line joining those points.

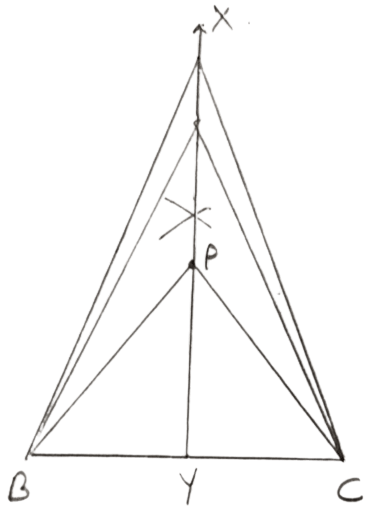
Steps of construction :

1. Draw a line segment BC (common base)

2. Draw XY, perpendicular bisector of BC.

3. Mark point P on XY.

So, PB = PC as P lies on perpendicular bisector of BC.

Hence, the locus of vertices of all isosceles triangles having a common base will be the perpendicular bisector of the common base of the triangles.

Describe the locus of a point P, so that :

AB² = AP² + BP²,

where A and B are two fixed points.

Answer

We know that,

Angle subtended by a diameter on any point of a circle is 90°.

From figure,

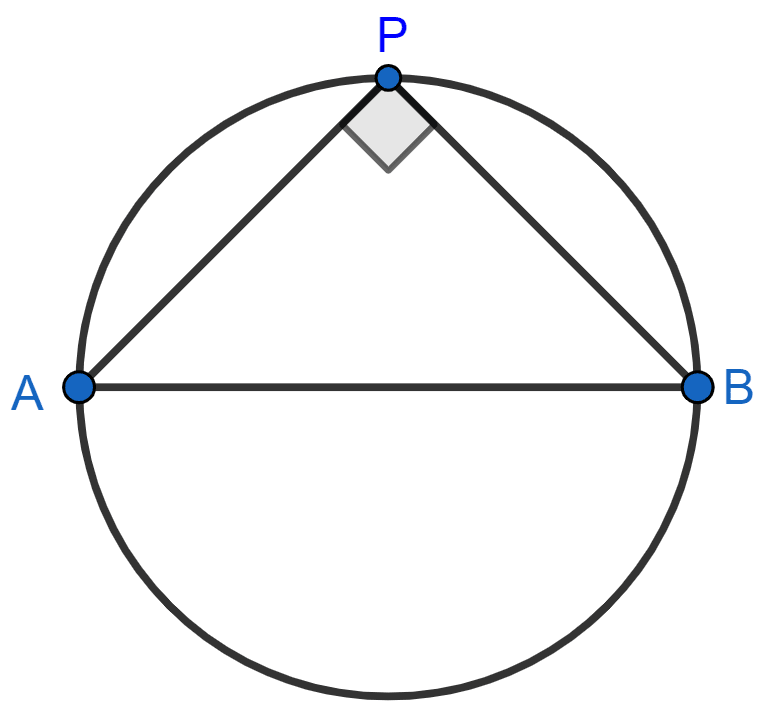
By pythagoras theorem,

⇒ Hypotenuse² = Perpendicular² + Base²

⇒ AB² = AP² + BP²

We know that,

Pythagoras theorem applies on right angle triangle.

∴ AP ⊥ BP.

Hence, the locus of the point P is the circumference of a circle with AB as diameter.

Describe the locus of a point in rhombus ABCD, so that it is equidistant from

(i) AB and BC.

(ii) B and D.

Answer

(i) We know that,

The locus of a point, which is equidistant from two intersecting straight lines, is a line which bisects the angle between the given lines.

In rhombus,

The diagonals bisect the interior angles.

Hence, the locus of point in a rhombus ABCD which is equidistant from AB and BC will be the diagonal BD.

(ii) We know that,

The locus of a point, which is equidistant from two points is the perpendicular bisector of the line joining those points.

In rhombus,

Diagonals bisect each other at right angles.

Hence, the locus of point in a rhombus ABCD which is equidistant from B and D is diagonal AC.

Describe :

(i) The locus of points at distances less than 3 cm from a given point.

(ii) The locus of points at distances greater than 4 cm from a given point.

(iii) The locus of points at distances less than or equal to 2.5 cm from a given point.

(iv) The locus of points at distances greater than or equal to 35 mm from a given point.

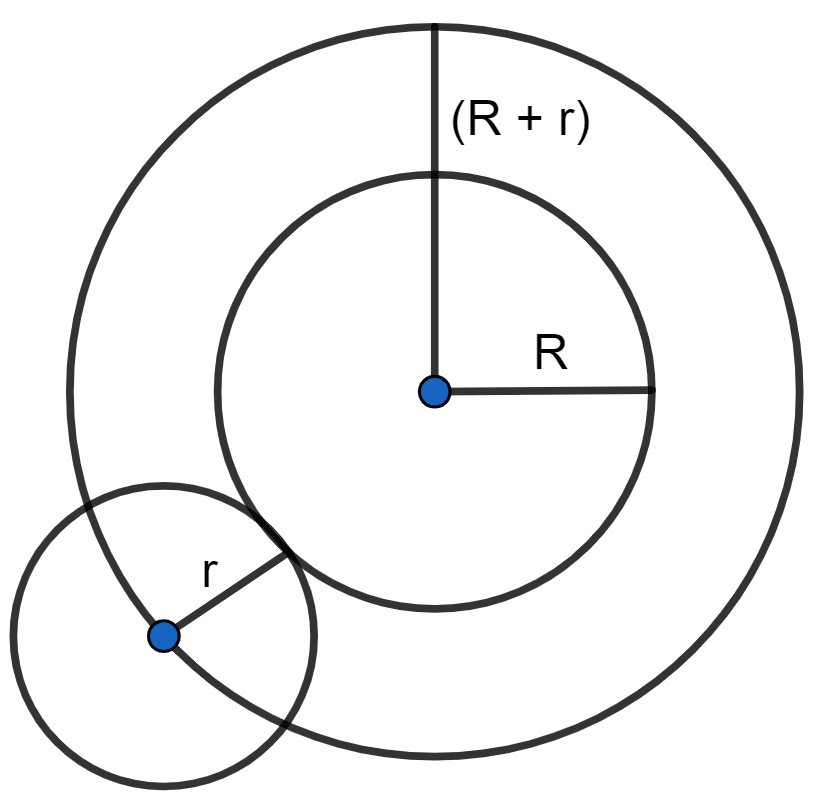
(v) The locus of the center of a given circle which rolls around the outside of a second circle and is always touching it.

(vi) The locus of the centers of all circles that are tangent to both the arms of a given angle.

(vii) The locus of the mid-points of all chords parallel to a given chord of a circle.

(viii) The locus of points within a circle that are equidistant from the end points of a given chord.

Answer

(i) The locus is the space inside the circumference of the circle with the given point as centre and radius equal to 3 cm.

(ii) The locus is the space outside the circumference of the circle with the given point as centre and radius equal to 4 cm.

(iii) The locus is the space inside and on the circumference of the circle with the given point as centre and radius equal to 2.5 cm.

(iv) The locus is the space outside and on the circumference of the circle with the given point as centre and radius equal to 35 mm.

(v) The locus is the circumference of the circle concentric with the second circle whose radius is equal to the sum of the radii of the two given circles.

(vi) The locus of the centers of all circles that are tangent to both the arms of a given angle is the bisector of that angle.

(vii) The locus of the mid-points of all chords parallel to a given chord of a circle is the diameter perpendicular to the given chords.

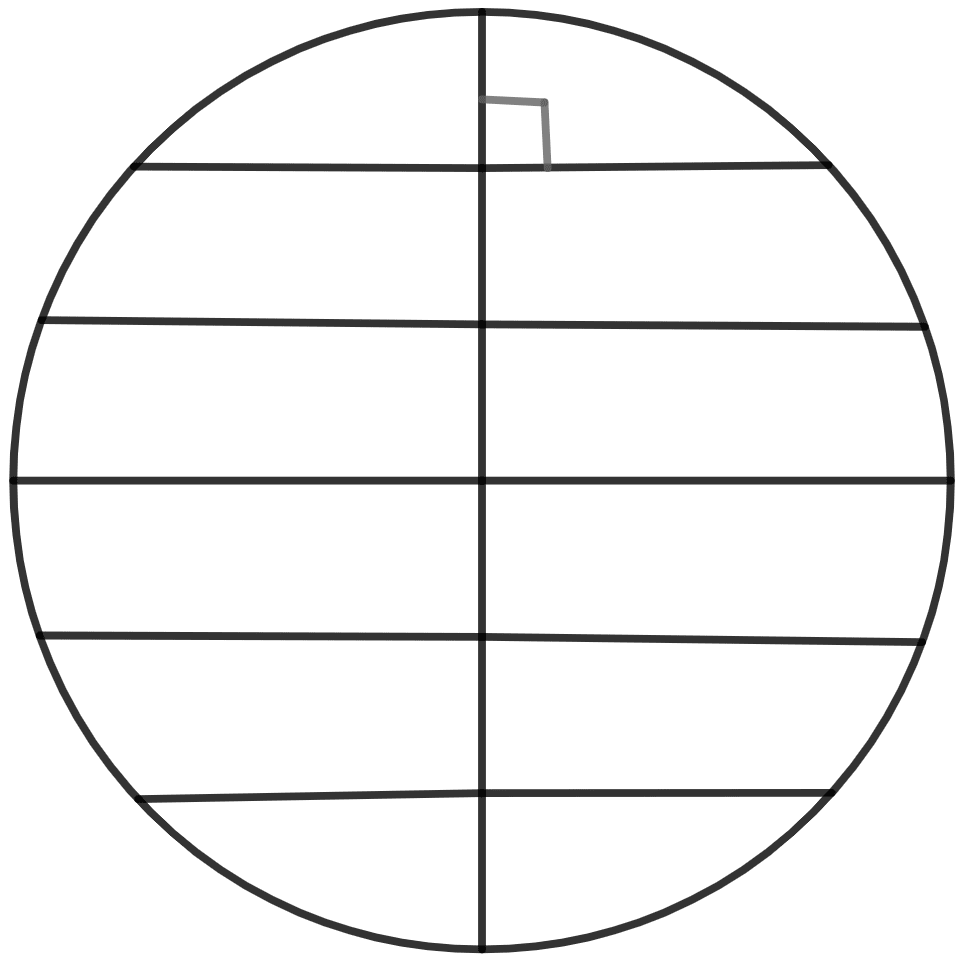
(viii) The locus of points within a circle that are equidistant from the end points of a given chord is the diameter which is perpendicular bisector of the given chord.

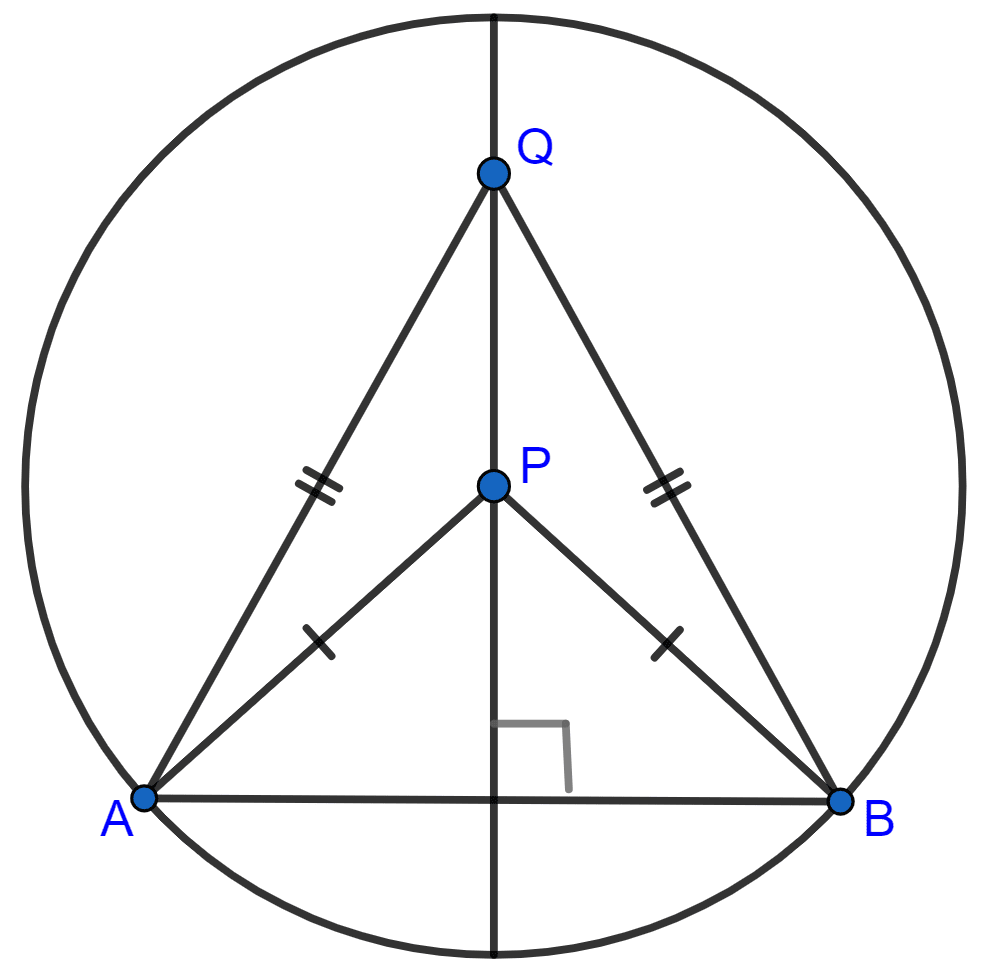
In the given figure, obtain all the points equidistant from lines m and n; and 2.5 cm from O.

Answer

Steps of construction :

1. Draw an angle bisector PQ and XY of angles formed by the lines m and n.

2. From O, draw arcs with radius 2.5 cm, which intersect the angle bisectors at a, b, c and d respectively.

Hence, a, b, c and d are the required four points.

Sketch and describe the locus of the vertices of all triangles with a given base and a given altitude.

Answer

Steps of construction :

1. Draw a line segment BC.

2. Draw XY, perpendicular bisector of BC intersecting BC at D and cut off DA, such that DA = altitude.

3. Draw a line segment EF parallel to BC at a distance = altitude and passing through A.

Hence, the line EF is the locus of the vertices of all triangles with a given base and a given altitude.

A straight line AB is 8 cm long. Draw and describe the locus of a point which is :

(i) always 4 cm from the line AB.

(ii) equidistant from A and B.

Mark the two points X and Y, which are 4 cm from AB and equidistant from A and B. Describe the figure AXBY.

Answer

Steps of construction :

1. Draw a line segment AB = 8 cm.

2. Draw two parallel lines l and m to AB at a distance of 4 cm.

3. Draw CD, the perpendicular bisector of AB which intersects parallel lines l and m at X and Y.

4. Join AX, AY, BX and BY.

Since, diagonals of AXBY are equal and intersect at right angles.

Hence, AXBY is a square.

(i) Hence, locus of point at a distance of 4 cm from AB will be a pair of lines, each parallel to AB.

(ii) Hence, locus of point equidistant from A and B will be perpendicular bisector of AB.

Draw a triangle ABC in which AB = 6 cm, BC = 4.5 cm and AC = 5 cm. Draw and label :

(i) the locus of the centers of all circles which touch AB and AC,

(ii) the locus of the centers of all the circles of radius 2 cm which touch AB.

Hence, construct the circle of radius 2 cm which touches AB and AC.

Answer

Steps of construction :

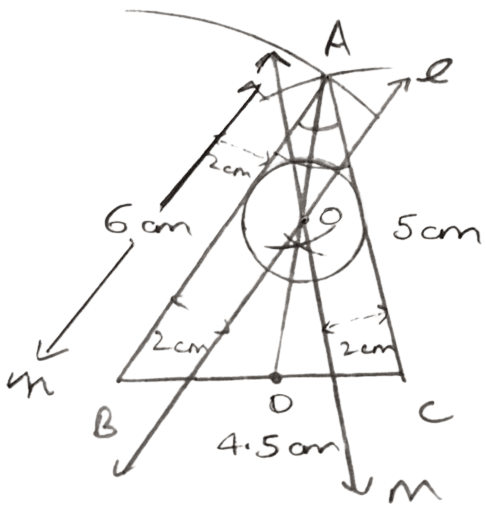
1. Draw a line segment BC = 4.5 cm

2. With B as center and radius = 6 cm and C as center and radius = 5 cm, draw arcs which intersect each other at A.

3. Join AB and AC. ABC is the required triangle.

4. Draw AD, the angle bisector of ∠BAC.

5. Draw lines l and n parallel to AB and m parallel to AC at a distance of 2 cm, which intersect each other and AD at O.

6. With center O and radius 2 cm, draw a circle which touches AB and AC.

(i) The locus of the centers of all circles which touch AB and AC is AD, the angle bisector of angle A.

(ii) The locus of the centers of all the circles of radius 2 cm which touch AB is line l and n.

Draw an angle ABC = 75°. Find a point P such that P is at a distance of 2 cm from AB and 1.5 cm from BC.

Answer

Steps of construction :

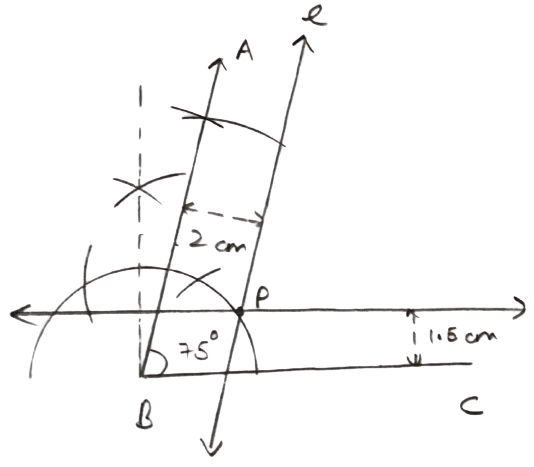
1. Draw a ray BC.

2. At B, draw a ray BA making an angle of 75° with BC.

3. Draw a line l parallel to AB at a distance of 2 cm.

4. Draw another line m parallel to BC at a distance of 1.5 cm which intersects line l at P.

Hence, P is the required point.

Construct a triangle ABC, with AB = 5.6 cm, AC = BC = 9.2 cm. Find the points equidistant from AB and AC; and also 2 cm from BC. Measure the distance between the two points obtained.

Answer

Steps of construction :

1. Draw a line segment AB = 5.6 cm

2. From A and B as centers and radius 9.2 cm, make two arcs which intersect each other at C.

3. Join CA and CB.

4. Draw two lines n and m parallel to BC at a distance of 2 cm.

5. Draw the angle bisector of ∠BAC which intersects n and m at points P and Q respectively.

On measuring PQ = 4.3 cm

Hence, P and Q are the required points which are equidistant from AB and AC; and also 2 cm from BC; PQ = 4.3 cm.

Construct a triangle ABC, with AB = 6 cm, AC = BC = 9 cm. Find a point 4 cm from A and equidistant from B and C.

Answer

Steps of construction :

1. Draw a line segment AB = 6 cm

2. From A and B as centers and radius 9 cm, make two arcs which intersect each other at C.

3. Join CA and CB.

4. Draw the perpendicular bisector of BC.

5. With A as center and radius 4 cm, draw an arc which intersects the perpendicular bisector of BC at P.

Hence, P is the required point which is equidistant from B and C and at a distance of 4 cm from A.

The locus of point which is equidistant from two non-parallel lines AB and CD is :

1. perpendicular to AB.

2. perpendicular to CD.

3. bisector of angle between AB and CD.

4. perpendicular bisector of CD.

Answer

Since, AB and CD are two non-parallel lines so they will intersect at a point.

We know that,

The locus of a point equidistant from two intersecting lines is the bisector of angles between the lines.

Hence, Option 3 is the correct option.

Three isosceles triangles PBC, QBC and RBC are on the same base, then :

1. P, Q and R are collinear.

2. △PQR is isosceles triangle.

3. Q lies on the circumference of a circle with BC as diameter.

4. Q is mid-point of line segment PR.

Answer

Steps of construction :

1. Draw a line segment BC.

2. Draw XY, perpendicular bisector of BC.

We know that,

Locus of a point equidistant from two given points is the perpendicular bisector of the line joining the two points.

Thus, any point on the line XY is at equal distance from B and C.

∴ P, Q and R lies on the line XY.

Hence, Option 1 is the correct option.

Locus of the centers of the circles passing through two fixed points A and B is :

1. a line parallel to line segment AB.

2. the bisector of the line segment AB.

3. perpendicular to line segment AB.

4. perpendicular bisector of line segment AB.

Answer

Let O and O' be the center of the circles, passing through points AB.

Steps of construction :

1. Join AB.

2. Draw a perpendicular from O to AB and O' to AB.

We know that,

Perpendicular from center to chord bisects it.

Since, both perpendiculars bisects AB.

∴ OO' is a straight line perpendicular to AB and bisecting it.

Hence, Option 4 is the correct option.

A point is equidistant from the sides of an obtuse angle triangle. The point is called :

1. circumcenter of the triangle.

2. incenter of the triangle.

3. centroid of the triangle.

4. orthocenter of the triangle.

Answer

Let ABC be the obtuse triangle.

Steps of construction :

1. Draw angle bisectors AX, BY and CZ of the interior angles A, B and C of a triangle.

2. Let the angle bisectors meet at point I.

We know that,

Locus of a point equidistant from two intersecting lines is the bisector of the angles between the lines.

∴ BY is equidistant from AB and BC

∴ AX is equidistant from AB and AC

∴ CZ is equidistant from AC and BC

∴ The point (incenter) joining AX, BY and CZ will be equidistant from all the three sides of the triangle.

Hence, Option 2 is the correct option.

ABC is a triangle. Point P moves with vertex B as center and radius 2.8 cm. The locus of point P is :

1. bisector of angle ABC.

2. a line parallel to BC and at a distance of 2.8 cm from it.

3. circle with center at point B and radius = 2.8 cm.

4. perpendicular bisector of BC.

Answer

We know that,

Locus of a point, in a plane and at a fixed distance from a given fixed point, is the circumference of the circle with the given fixed point as center and given fixed distance as radius.

∴ The locus of point P is a circle with center at point B and radius = 2.8 cm.

Hence, Option 3 is the correct option.

Draw an ∠ABC = 60°, having AB = 4.6 cm and BC = 5 cm. Find a point P equidistant from AB and BC; and also equidistant from A and B.

Answer

Steps of construction :

1. Draw a line segment BC = 5 cm.

2. At B, draw a ray BX making an angle of 60° and cut off BA = 4.6 cm.

3. Draw BY, the angle bisector of ∠ABC.

4. Draw MN, the perpendicular bisector of AB.

5. Let MN and BY meet at point P.

Hence, P is the point which is equidistant from AB and BC, as well as from A and B.

On a graph paper, draw the lines x = 3 and y = -5. Now, on the same graph paper, draw the locus of the point which is equidistant from the given lines.

Answer

Steps of construction :

1. Draw a line l with equation x = 3 and m having equation y = -5.

2. Let these lines intersect at point P.

3. Draw a line n, which is the angle bisector of ∠P.

Since, n is the angle bisector of ∠P so any point on n is equidistant from l and m.

Hence, locus of the point which is equidistant from the given lines is line n..

On a graph paper, draw the line x = 6. Now on the same graph paper, draw the locus of the point which moves in such a way that its distance from the given line is always equal to 3 units.

Answer

Steps of construction :

1. Draw a line l, x = 6 which is parallel to y-axis.

2. At a distance of 3 units on both sides from x = 6 mark points P and Q.

3. Draw line m and n parallel to l and through P and Q respectively.

From figure,

Equation of m : x = 3 and Equation of n : x = 9.

Hence, locus of the point which moves in such a way that its distance from the given line is always equal to 3 units are lines x = 3 and x = 9.

Ruler and compasses may be used in this question. All construction lines and arcs must be clearly shown and be of sufficient length and clarity to permit assessment.

(i) Construct a △ABC, in which BC = 6 cm, AB = 9 cm and angle ABC = 60°.

(ii) Construct the locus of all points inside triangle ABC, which are equidistant from B and C.

(iii) Construct the locus of the vertices of the triangles with BC as base and which are equal in area to triangle ABC.

(iv) Mark the point Q, in your construction, which would make △QBC equal in area to △ABC, and isosceles.

(v) Measure and record the length of CQ

Answer

(i) Steps of construction :

1. Draw a line segment BC = 6 cm.

2. At B, draw a ray BX making an angle 60° and cut off BA = 9 cm.

3. Join AC.

Hence, ABC is the required triangle.

(ii) Steps of construction :

1. Draw perpendicular bisector of BC which intersects BA at M and BC at L, then any point on LM is equidistant from B and C.

Hence, LM is the required locus.

(iii) Steps of construction :

1. Through A, draw a line m || BC.

2. The perpendicular bisector of BC and the parallel line m intersect each other at Q.

3. Join QB and QC.

Hence, line m is the locus of the vertices of the triangles with BC as base and which are equal in area to triangle ABC.

(iv) The triangle QBC is equal in area to triangle ABC.

Also, QB = QC as Q lies on perpendicular bisector of BC.

Hence, QBC is an isosceles triangle.

(v) On measuring CQ = 8.4 cm.

Construct an isosceles triangle ABC such that AB = 6 cm, BC = AC = 4 cm. Bisect ∠C internally and mark a point P on this bisector such that CP = 5 cm. Find the points Q and R which are 5 cm from P and also 5 cm from the line AB.

Answer

Steps of construction :

1. Draw a line segment AB = 6 cm.

2. With centers A and B and radius = 4 cm, draw two arcs which intersect each other at C.

3. Join CA and CB.

4. Draw the angle bisector of angle C and cut off CP = 5 cm.

5. Draw a line m parallel to AB at a distance of 5 cm.

6. With P as center and radius = 5 cm, draw arcs which intersect the line m at Q and R.

7. Join PQ and QR.

Construct a triangle BCP given BC = 5 cm, BP = 4 cm and ∠PBC = 45°.

(i) Complete the rectangle ABCD such that :

(a) P is equidistant from AB and BC.

(b) P is equidistant from C and D.

(ii) Measure and record the length of AB.

Answer

(i) Steps of construction :

1. Draw a line segment BC = 5 cm.

2. With B as center draw an arc BX, at an angle of 45°.

3. From BX cut off BP = 4 cm.

4. Join PC. Hence, BPC is the required triangle.

5. Draw perpendicular on B and C.

6. With P as center and radius PC, cut an arc on the perpendicular on C at D.

7. D as center, draw a line parallel to BC which intersects the perpendicular on B at A.

Hence, ABCD is the required rectangle.

(ii) On measuring we get,

AB = 5.7 cm.

Use ruler and compasses only for the following question. All construction lines and arcs must be clearly shown.

(i) Construct a △ABC in which BC = 6.5 cm, ∠ABC = 60° and AB = 5 cm.

(ii) Construct the locus of points at a distance of 3.5 cm from A.

(iii) Construct the locus of points equidistant from AC and BC.

(iv) Mark 2 points X and Y which are at a distance of 3.5 cm from A and also equidistant from AC and BC. Measure XY.

Answer

(i) Steps of constrcution :

1. Draw a line segment BC = 6.5 cm.

2. With B as center draw an arc BX, at an angle of 60°.

3. From BX cut off BA = 5 cm.

4. Join AC. Hence, ABC is the required triangle.

5. With A as center draw a circle of radius = 3.5 cm.

6. Draw CZ, the angle bisector of ∠C.

7. Mark the points as X and Y where CZ intersects circle with center A.

(ii) The locus of points at a distance of 3.5 cm from A is a circle with radius = 3.5 cm and center A.

(iii) The locus of points equidistant from AC and BC is CZ, the angle bisector of ∠C.

(iv) On measuring, XY = 4.8 cm.