Circles

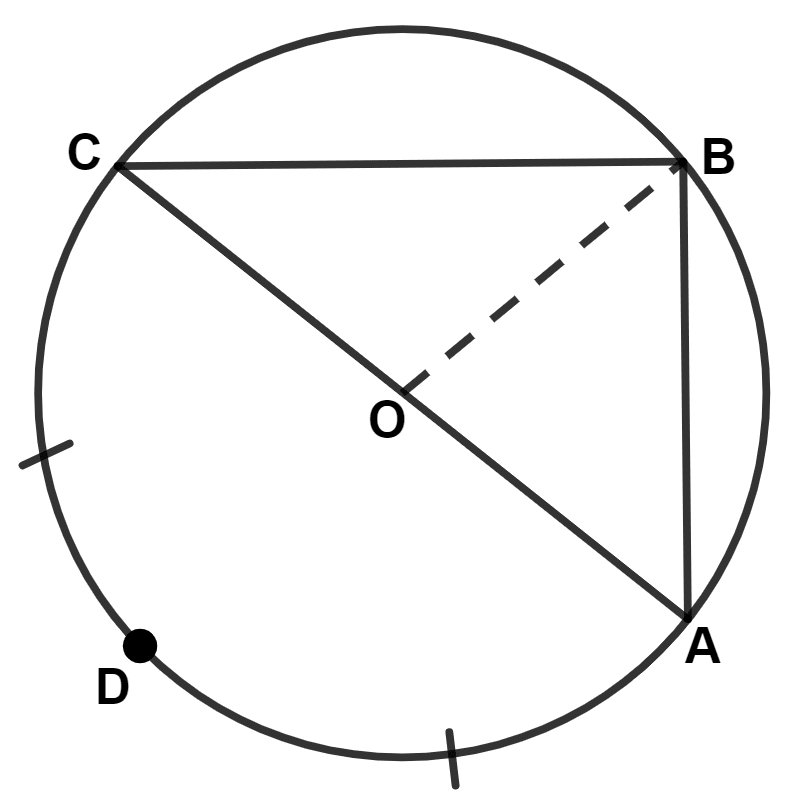
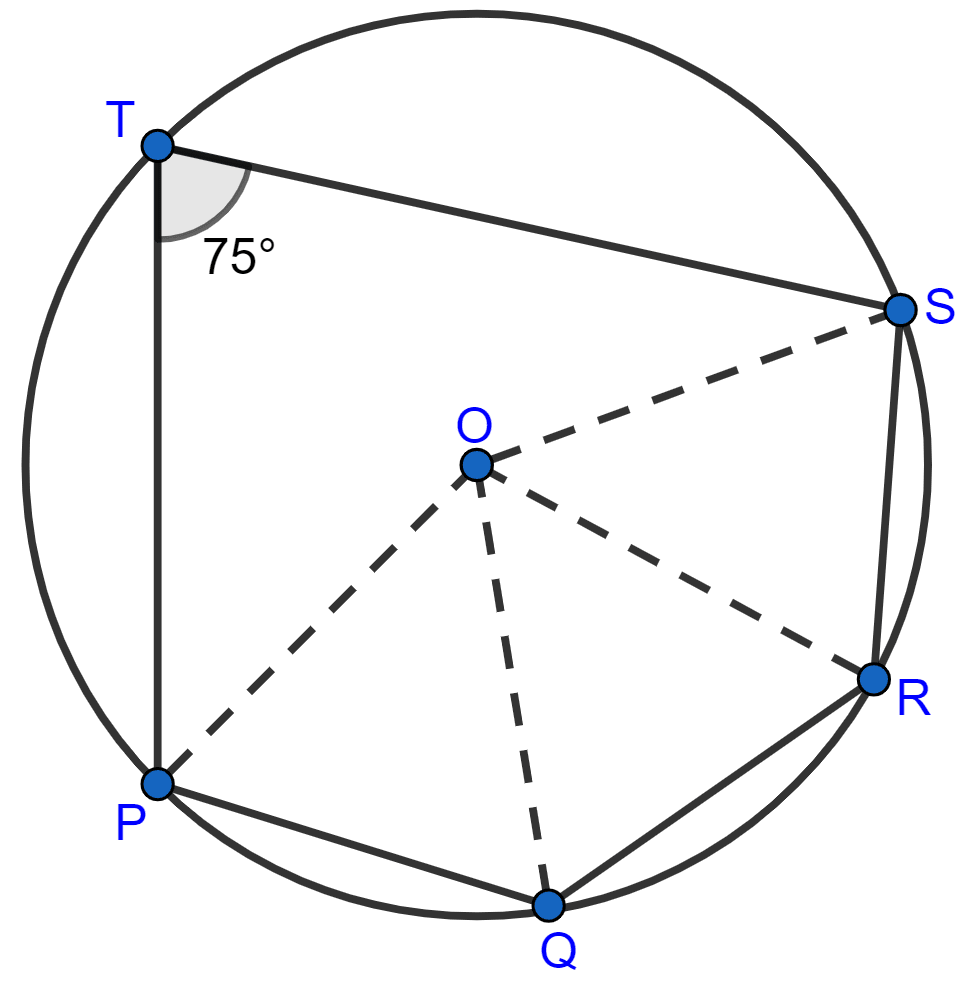
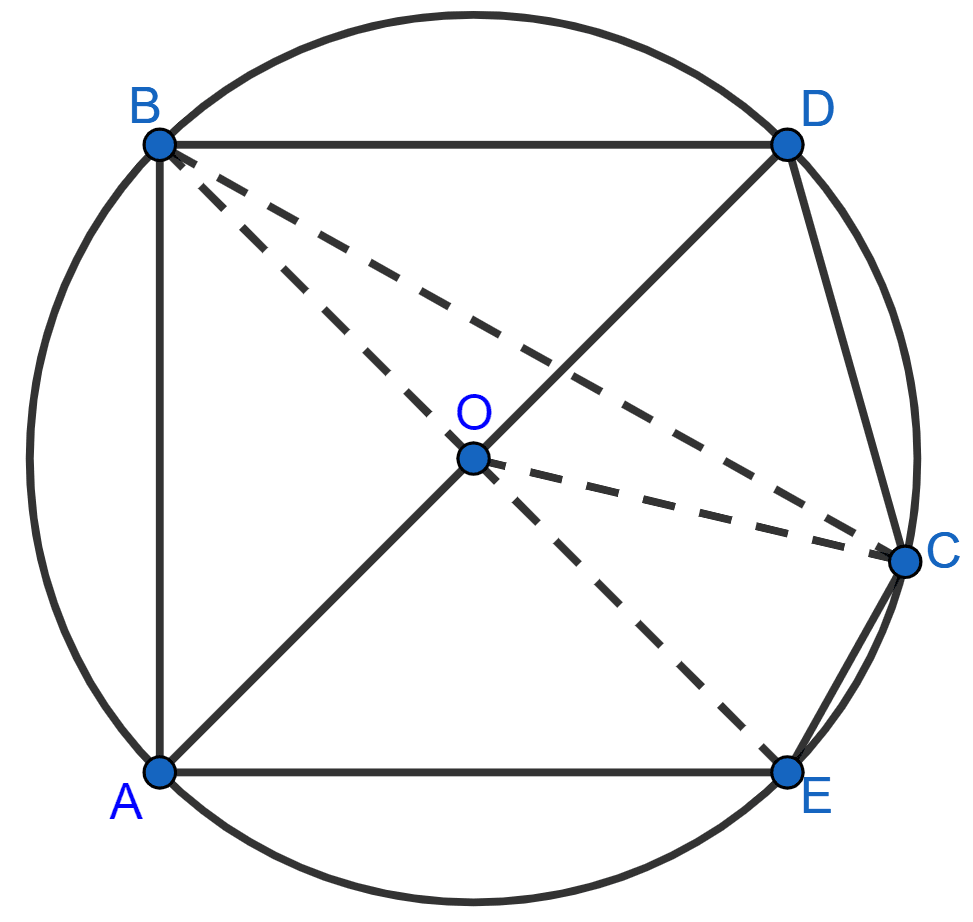
In the given figure, O is center of the circle and ∠B = 55°. The angle A is equal to :

1. 55°

2. 35°

3. 45°

4. 50°

Answer

From figure,

In △ OCB,

OB = OC (Radius of common circle)

We know that,

Angles opposite to equal sides of a triangle are equal.

∴ ∠C = ∠B = 55°

By angle sum property of triangle,

⇒ ∠C + ∠B + ∠O = 180°

⇒ 55° + 55° + ∠O = 180°

⇒ ∠O + 110° = 180°

⇒ ∠O = 180° - 110° = 70°.

We know that,

The angle which an arc subtends at the center is double that which it subtends at any point on the remaining part of the circumference.

⇒ ∠O = 2∠A

⇒ ∠A = $\dfrac{∠O}{2} = \dfrac{70°}{2}$ = 35°.

Hence, Option 2 is the correct option.

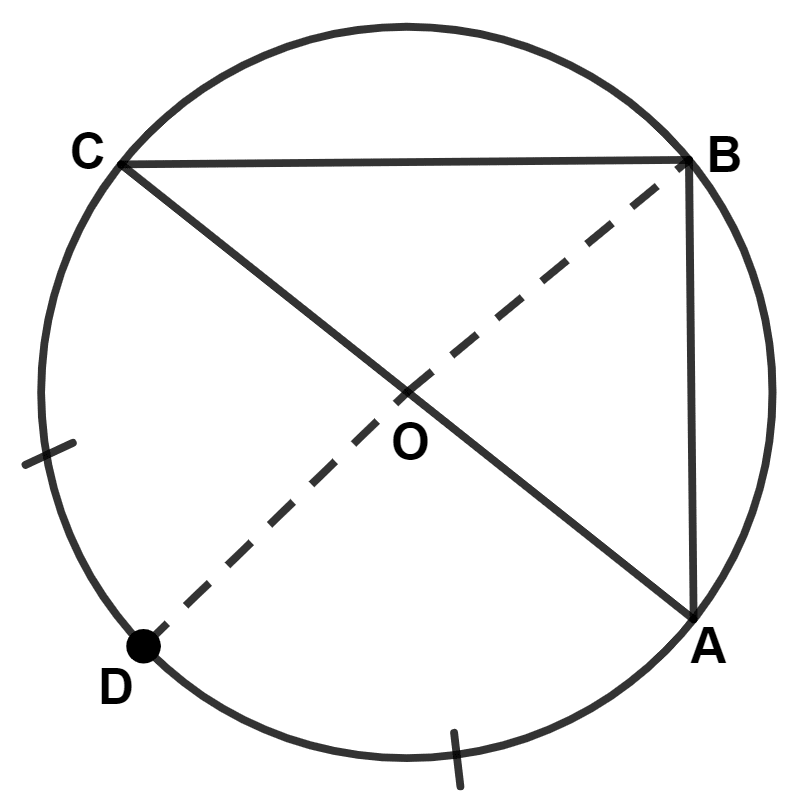
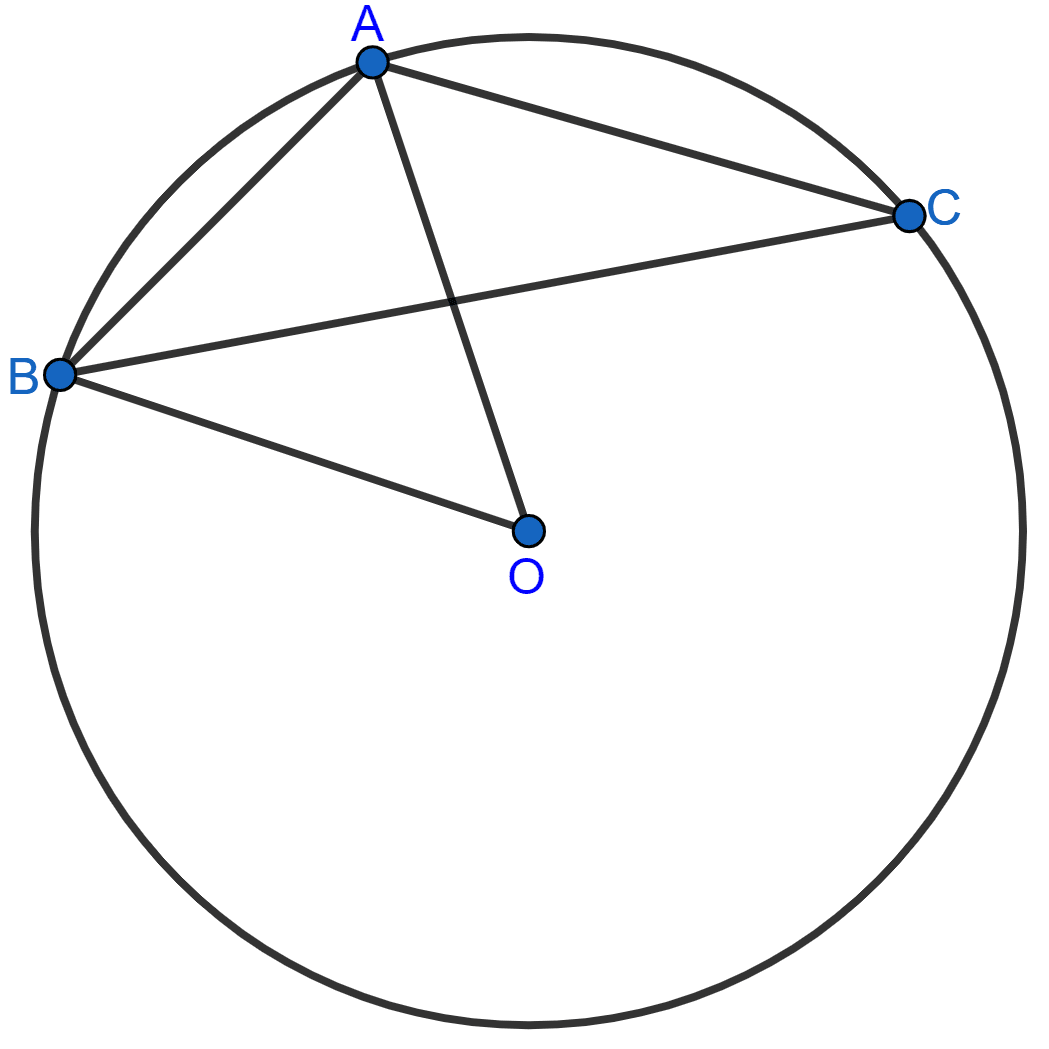
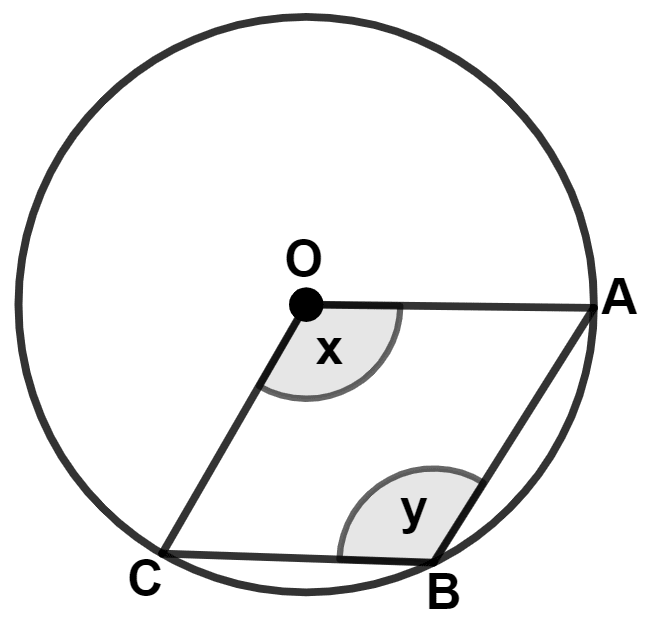
In the given figure, O is center of the circle and angle OBA = 50°. The angle P is :

1. 50°

2. 80°

3. 40°

4. 60°

Answer

From figure,

In △ OAB,

OA = OB (Radius of common circle)

We know that,

Angles opposite to equal sides of a triangle are equal.

∴ ∠A = ∠B = 50°

By angle sum property of triangle,

⇒ ∠A + ∠B + ∠O = 180°

⇒ 50° + 50° + ∠O = 180°

⇒ ∠O + 100° = 180°

⇒ ∠O = 180° - 100° = 80°.

We know that,

The angle which an arc subtends at the center is double that which it subtends at any point on the remaining part of the circumference.

⇒ ∠O = 2∠P

⇒ ∠P = $\dfrac{∠O}{2} = \dfrac{80°}{2}$ = 40°.

Hence, Option 3 is the correct option.

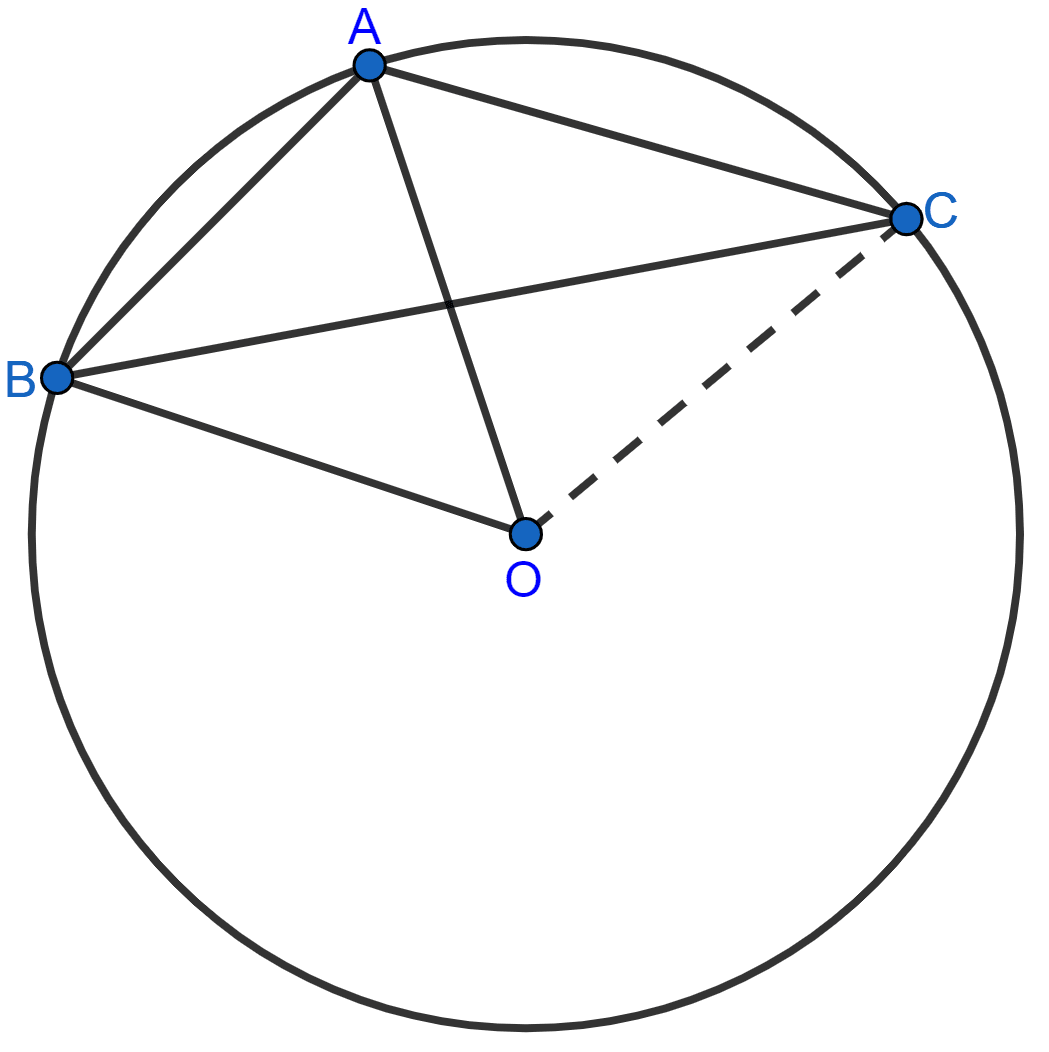
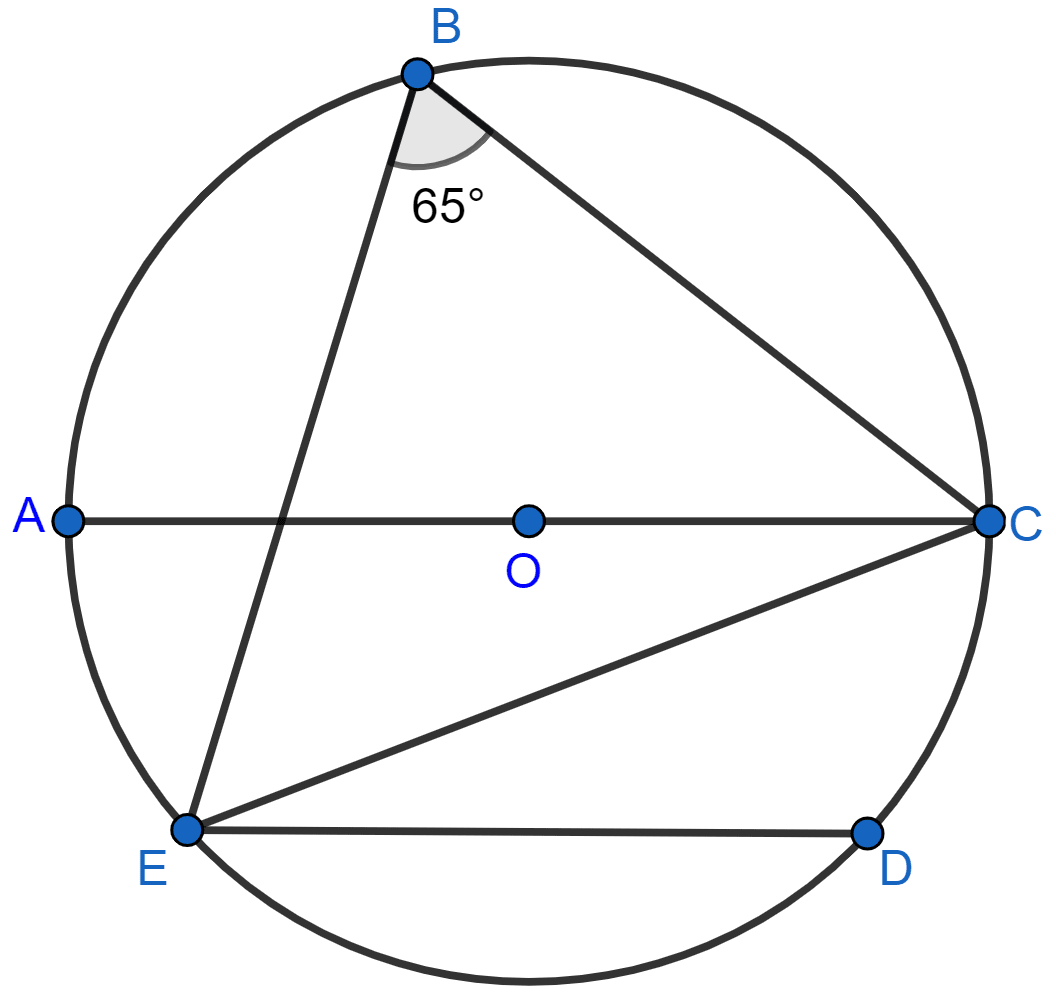
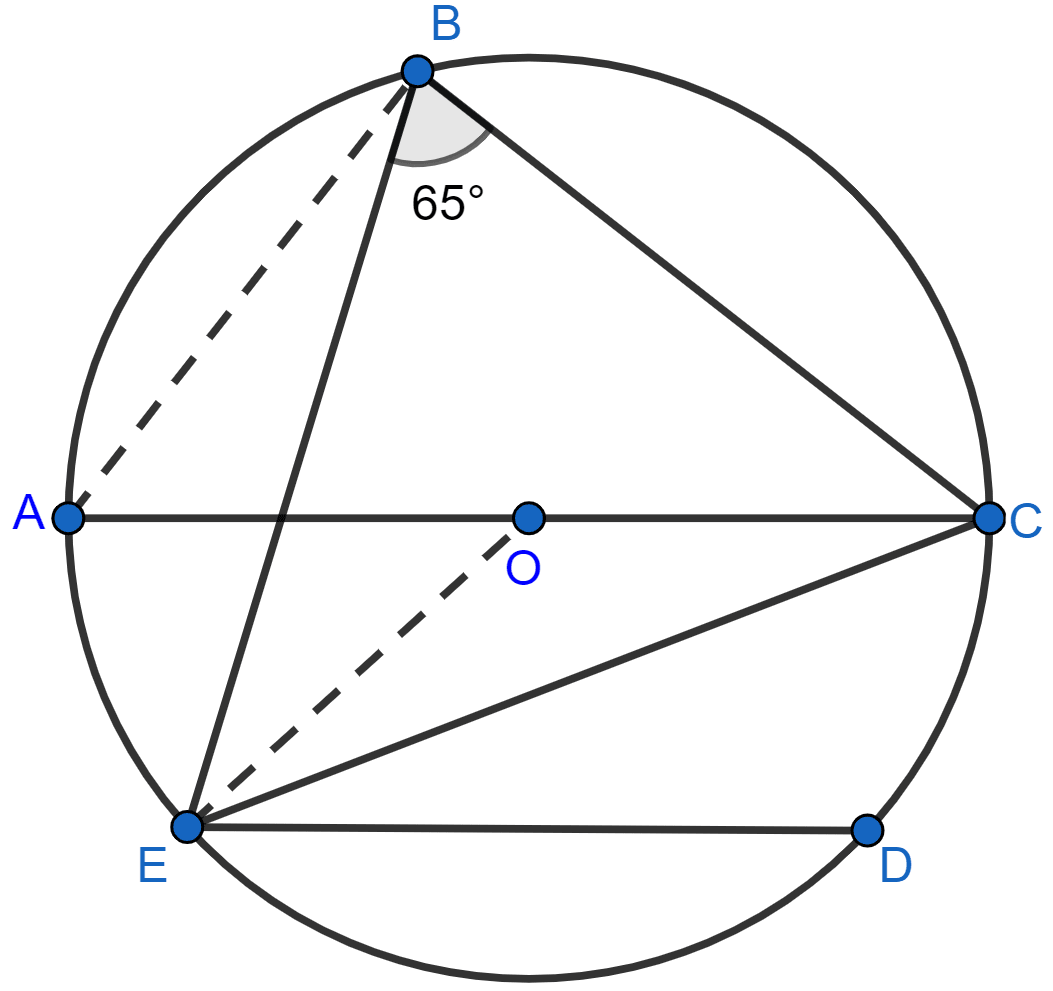
In the given figure, chord AB = chord PB and angle C = 50°. The angle PAB is equal to :

1. 65°

2. 50°

3. 75°

4. 60°

Answer

We know that,

Angle in same segment are equal.

∴ ∠APB = ∠ACB = 50°

In △ PAB,

PB = AB (Given)

We know that,

Angles opposite to equal sides of a triangle are equal.

∴ ∠PAB = ∠APB = 50°.

Hence, Option 2 is the correct option.

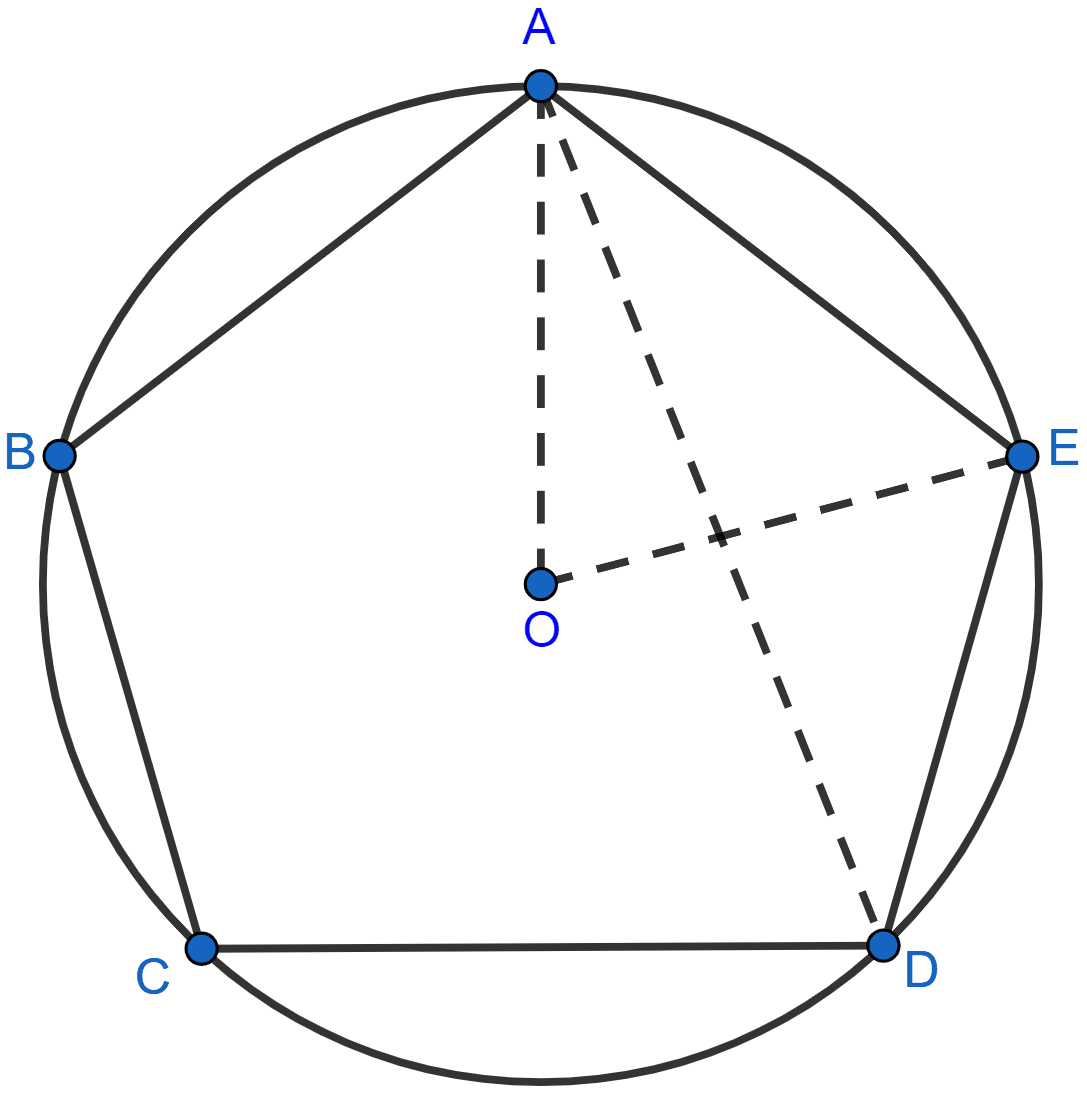
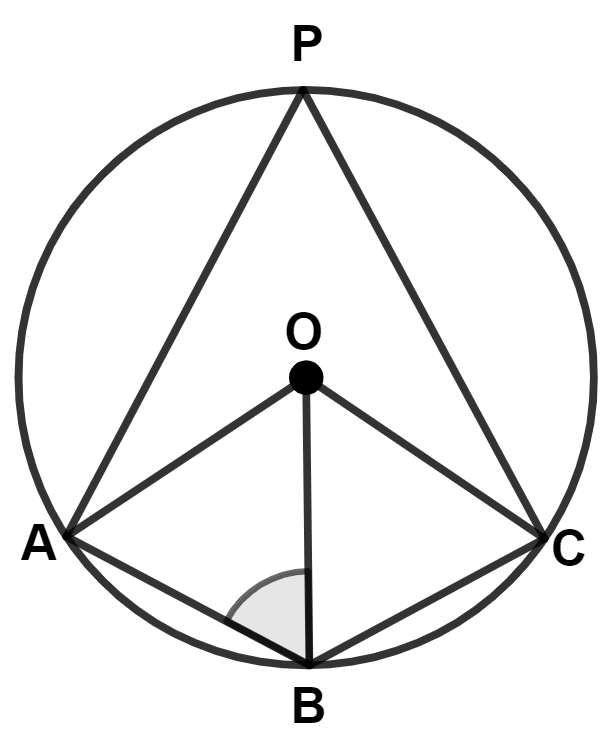
O' and O" are centers of two circles which intersect each other at points A and B. Then :

1. BC = BD

2. BC is larger than BD.

3. BC is smaller than BD.

4. C, B and D are collinear.

Answer

We know that,

Angle in semicircle is a right angle.

From figure,

AC and AD are diameter.

∴ ∠ABC = ∠ABD = 90°.

From figure,

⇒ ∠ABC + ∠ABD = 90° + 90° = 180°.

∴ CBD is a straight line, or points C, B and D are collinear.

Hence, Option 4 is the correct option.

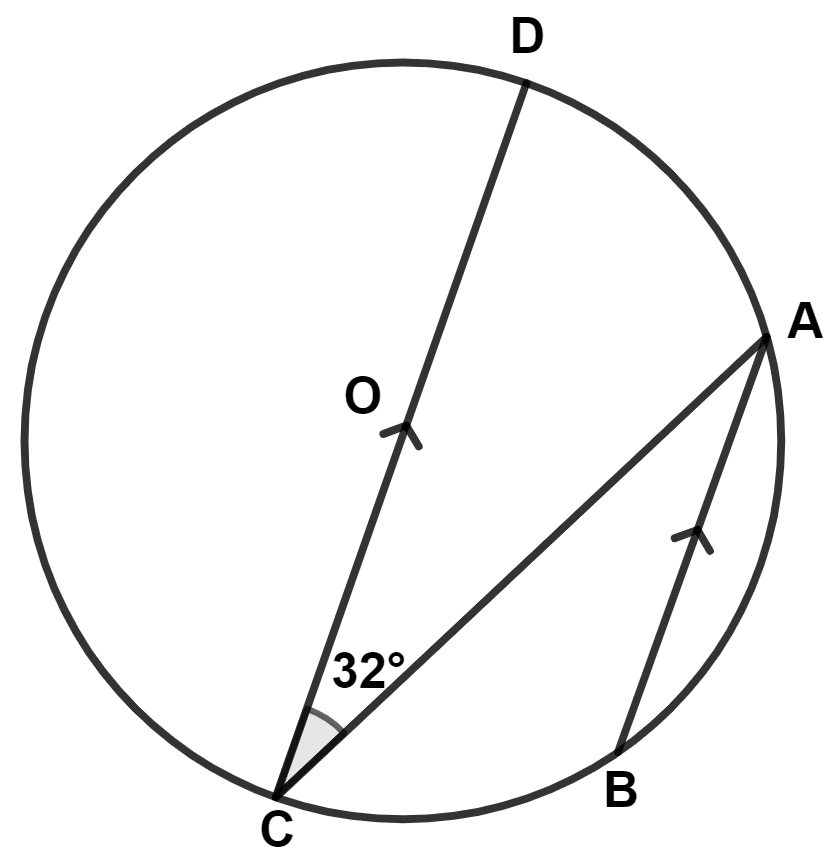
In the given figure, O is center of the circle, AB || DC and ∠ACD = 32°, ∠DAB is equal to :

1. 122°

2. 148°

3. 90°

4. none of the above

Answer

Join DA.

From figure,

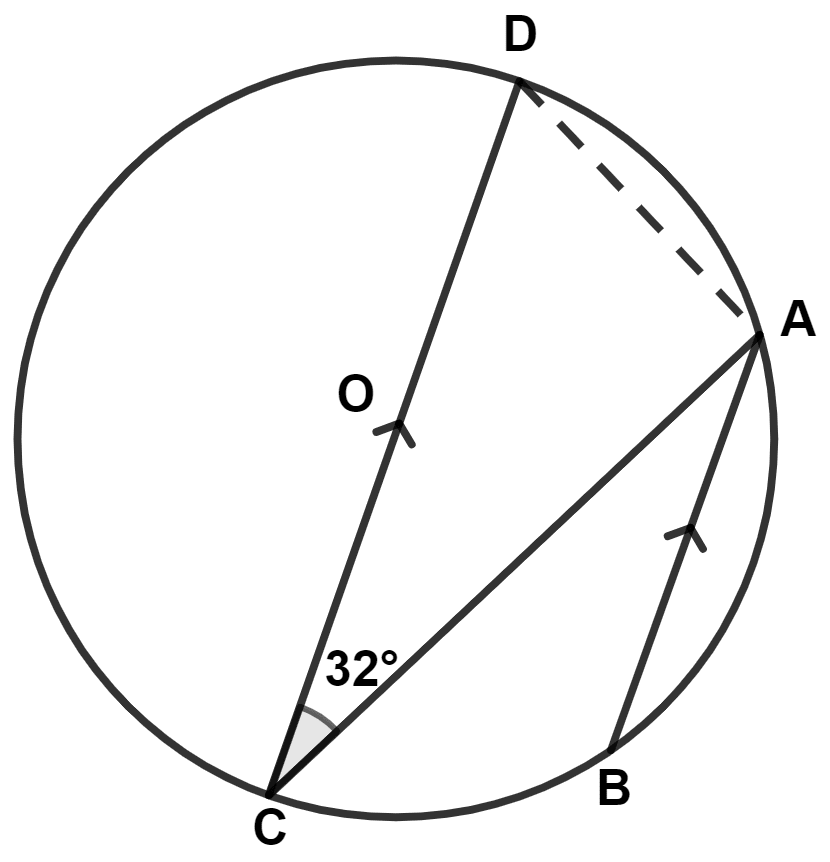
In △DAC,

∠DAC = 90° (Angle in semicircle is a right angle)

As, alternate angles are equal.

∴ ∠CAB = ∠ACD = 32°

From figure,

∠DAB = ∠DAC + ∠CAB = 90° + 32° = 122°.

Hence, Option 1 is the correct option.

In the given figure, ∠BAD = 65°, ∠ABD = 70°, ∠BDC = 45°

(i) Prove that AC is a diameter of the circle.

(ii) Find ∠ACB

Answer

(i) In ∆ABD,

⇒ ∠DAB + ∠ABD + ∠ADB = 180° [Angle sum property of a triangle]

⇒ 65° + 70° + ∠ADB = 180°

⇒ 135° + ∠ADB = 180°

⇒ ∠ADB = 180° - 135° = 45°

From figure,

⇒ ∠ADC = ∠ADB + ∠BDC = 45° + 45° = 90°.

As the angle in a semicircle is a right angle,

∴ Arc ADC is semi-circle and AC is the diameter.

Hence, proved that AC is the diameter.

(ii) We know that,

Angles in the same segment of a circle are equal.

∴ ∠ACB = ∠ADB = 45°.

Hence, ∠ACB = 45°.

In the following figure, O is the center of the circle. Find the value of a.

Answer

We know that,

Angle in semi-circle is a right angle.

∴ ∠BAD = 90°

From figure,

⇒ ∠BAD + ∠ADB + ∠DBA = 180°

⇒ 90° + ∠ADB + 35° = 180°

⇒ ∠ADB + 125° = 180°

⇒ ∠ADB = 180° - 125° = 55°.

We know that,

Angles subtended by the same chord on the circle are equal.

∴ a = ∠ADB = 55°.

Hence, a = 55°.

In the following figure, O is the center of the circle. Find the value of b.

Answer

Mark the point of intersection of AC and BD as E:

Since, AC is a straight line.

∴ ∠AEB + ∠BEC = 180°

⇒ 120° + ∠BEC = 180°

⇒ ∠BEC = 180° - 120° = 60°.

In △BEC,

⇒ ∠BEC + ∠ECB + ∠CBE = 180°

⇒ 60° + ∠ECB + 25° = 180°

⇒ ∠ECB + 85° = 180°

⇒ ∠ECB = 180° - 85° = 95°.

We know that,

Angles subtended by the same chord on the circle are equal.

∴ b = ∠ACB

From figure,

∠ACB = ∠ECB = 95°.

Hence, b = 95°.

In the following figure, O is the center of the circle. Find the value of c.

Answer

We know that,

Angle which an arc subtends at the center is double that which it subtends at any point on the remaining part of the circumference.

∠AOB = 2∠ACB = 2 x 50° = 100°.

Also, OA = OB = radius of circle.

∴ ∠OBA = ∠OAB = c [As angles opposite to equal sides are equal]

In △OAB,

⇒ ∠OAB + ∠AOB + ∠OBA = 180°

⇒ 2∠OAB + 100° = 180° [∵ ∠OBA = ∠OAB and ∠AOB = 100°]

⇒ 2c + 100° = 180°

⇒ 2c = 180° - 100°

⇒ 2c = 80°

⇒ c = $\dfrac{80}{2}$ = 40°.

Hence, c = 40°.

In the following figure, O is the center of the circle. Find the value of d.

Answer

We know that,

Angle in semi-circle is a right angle.

∴ ∠APB = 90°

In △APB,

⇒ ∠APB + ∠PBA + ∠PAB = 180°

⇒ 90° + 45° + ∠PAB = 180°

⇒ ∠PAB = 180° - 135° = 45°.

We know that,

Angles subtended by the same chord on the circle are equal.

∴ d = ∠PAB = 45°.

Hence, d = 45°.

Calculate:

(i) ∠CDB,

(ii) ∠ABC,

(iii) ∠ACB.

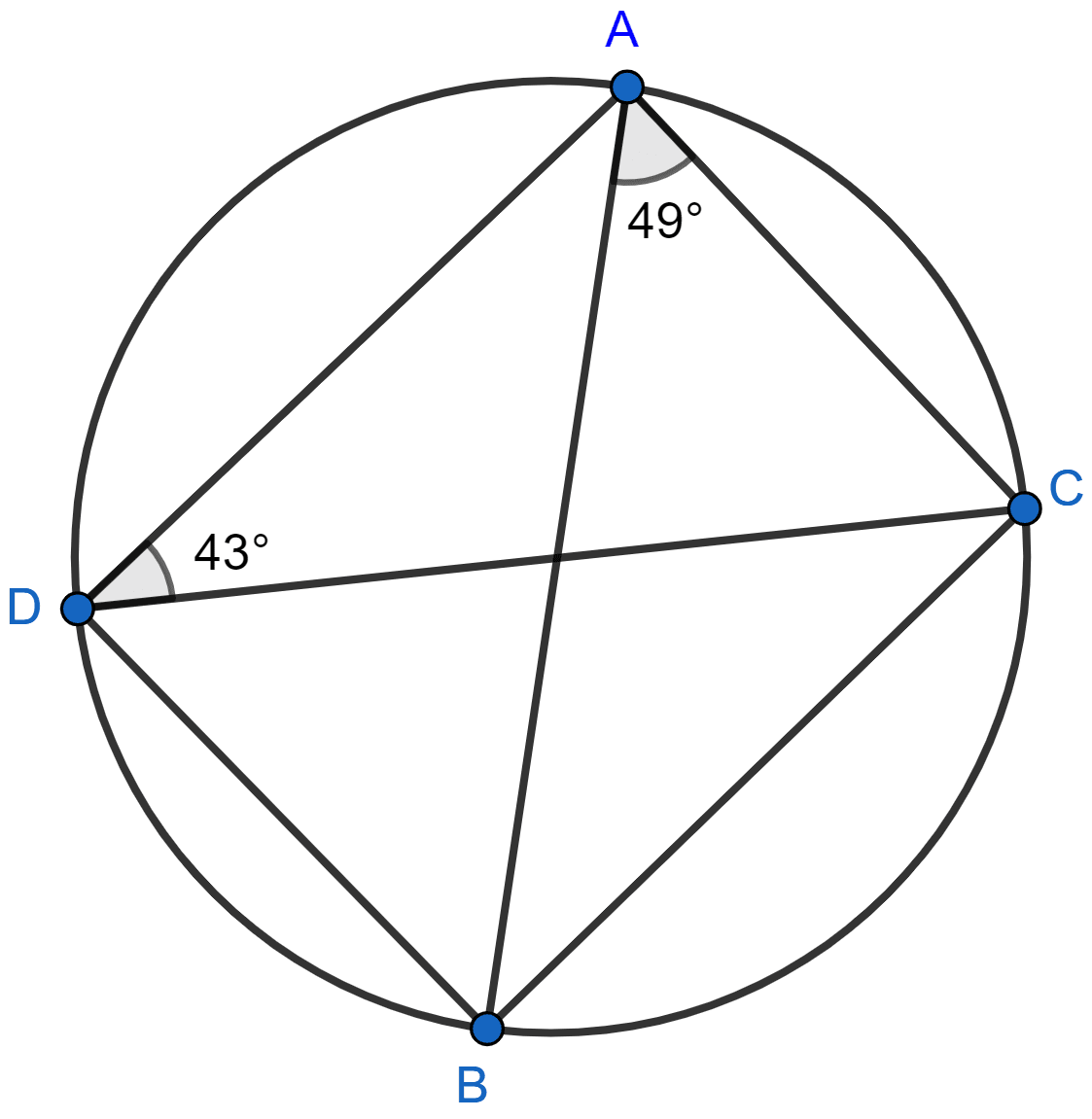
Answer

(i) We know that,

Angles subtended by the same chord on the circle are equal.

∴ ∠CDB = ∠BAC = 49°.

Hence, ∠CDB = 49°.

(ii) We know that,

Angles subtended by the same chord on the circle are equal.

∠ABC = ∠ADC = 43°.

Hence, ∠ABC = 43°.

(iii) In △ABC,

⇒ ∠ABC + ∠ACB + ∠BAC = 180°

⇒ 43° + ∠ACB + 49° = 180°

⇒ ∠ACB + 92° = 180°

⇒ ∠ACB = 180° - 92° = 88°.

Hence, ∠ACB = 88°.

Given: ∠CAB = 75° and ∠CBA = 50°. Find the value of ∠DAB + ∠ABD.

Answer

In ∆ABC, by angle sum property we have

⇒ ∠ACB + ∠CBA + ∠CAB = 180°

⇒ ∠ACB + 50° + 75° = 180°

⇒ ∠ACB + 125° = 180°

⇒ ∠ACB = 180° - 125° = 55°.

We know that,

Angles subtended by the same chord on the circle are equal.

⇒ ∠ADB = ∠ACB = 55°.

Now, taking ∆ABD

⇒ ∠DAB + ∠ABD + ∠ADB = 180° [Angle sum property]

⇒ ∠DAB + ∠ABD + 55° = 180°

⇒ ∠DAB + ∠ABD = 180° - 55°

⇒ ∠DAB + ∠ABD = 125°

Hence, ∠DAB + ∠ABD = 125°.

In the figure given alongside, AOB is a diameter of the circle and ∠AOC = 110°, find ∠BDC.

Answer

Join AD.

We know that,

Angle at the center is double the angle at the circumference subtended by the same chord.

∠ADC = $\dfrac{1}{2}$∠AOC = $\dfrac{1}{2}$ x 110° = 55°.

Also, we know that

Angle in the semi-circle is a right angle.

∠ADB = 90°

From figure,

∠BDC = ∠BDA - ∠ADC = 90° - 55° = 35°.

Hence, ∠BDC = 35°.

In the following figure, O is the centre of the circle, ∠AOB = 60° and ∠BDC = 100°. Find ∠OBC.

Answer

We know that,

Angle at the centre is double the angle at the circumference subtended by the same chord.

∠ACB = $\dfrac{1}{2}$∠AOB = $\dfrac{1}{2} \times 60°$ = 30°.

In △BDC,

⇒ ∠BDC + ∠DCB + ∠CBD = 180° [Angle sum property]

⇒ 100° + 30° + ∠CBD = 180° [From figure, ∠DCB = ∠ACB]

⇒ ∠CBD + 130° = 180°

⇒ ∠CBD = 180° - 130° = 50°.

From figure,

⇒ ∠OBC = ∠CBD = 50°.

Hence, ∠OBC = 50°.

In cyclic quadrilateral ABCD, ∠DAC = 27°; ∠DBA = 50° and ∠ADB = 33°. Calculate :

(i) ∠DBC,

(ii) ∠DCB,

(iii) ∠CAB.

Answer

(i) We know that,

Angles in same segment are equal.

∠DBC = ∠DAC = 27°.

Hence, ∠DBC = 27°.

(ii) We know that,

Angles in same segment are equal.

∠ACB = ∠ADB = 33°.

and,

∠ACD = ∠ABD = 50°.

From figure,

⇒ ∠DCB = ∠ACD + ∠ACB = 50° + 33° = 83°.

Hence, ∠DCB = 83°.

(iii) In quad. ABCD,

⇒ ∠DAB + ∠DCB = 180° [As sum of opposite angles in a cyclic quadrilateral = 180°]

⇒ ∠DAC + ∠CAB + ∠DCB = 180°

⇒ 27° + 83° + ∠CAB = 180°

⇒ ∠CAB + 110° = 180°

⇒ ∠CAB = 180° - 110° = 70°.

Hence, ∠CAB = 70°.

In the figure given alongside, AB and CD are straight lines through the centre O of a circle. If ∠AOC = 80° and ∠CDE = 40°, find the number of degrees in :

(i) ∠DCE,

(ii) ∠ABC.

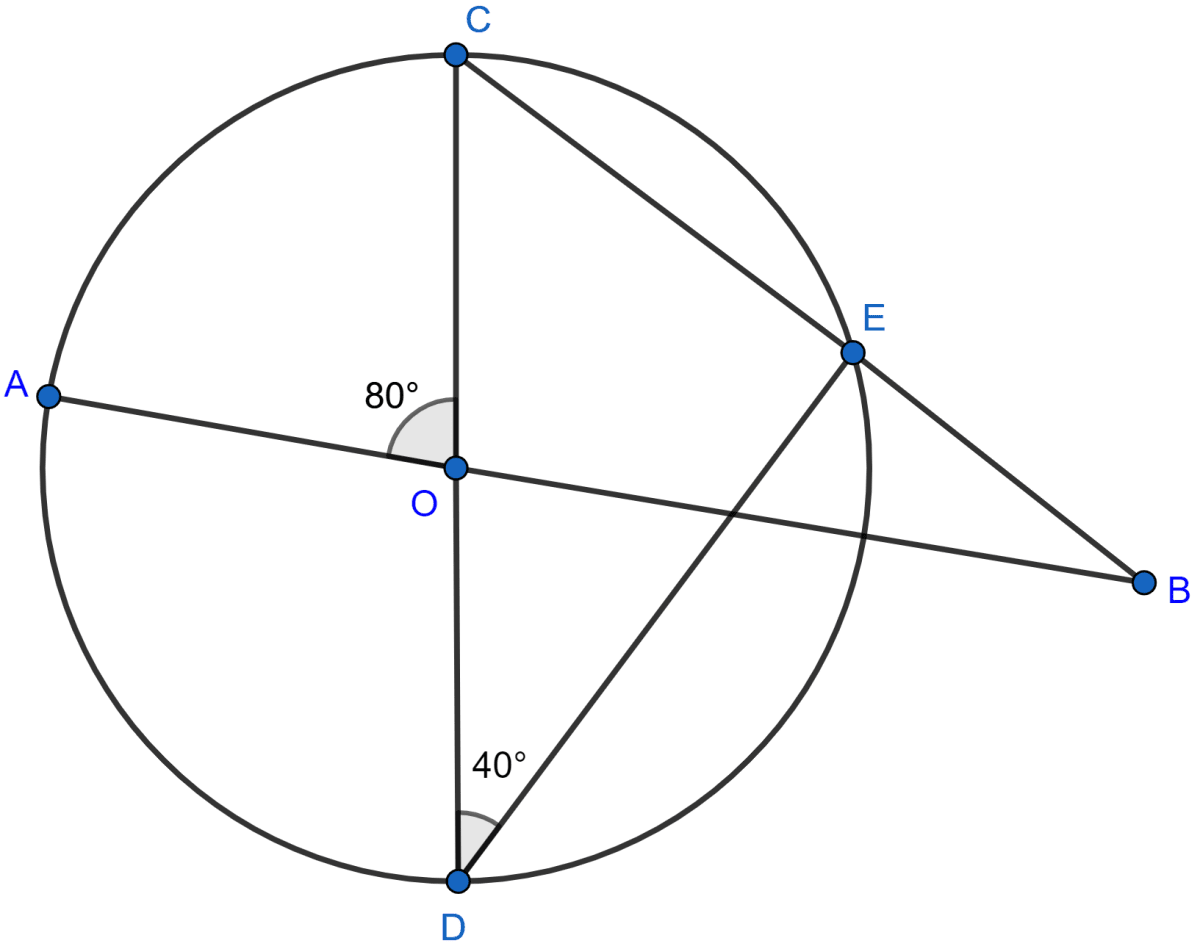
Answer

(i) From figure,

∠CED = 90° [As angle in semi-circle = 90°]

In △CED,

⇒ ∠CED + ∠CDE + ∠DCE = 180° [By angle sum property of triangle]

⇒ 90° + 40° + ∠DCE = 180°

⇒ ∠DCE + 130° = 180°

⇒ ∠DCE = 180° - 130° = 50°.

Hence, ∠DCE = 50°.

(ii) We know that,

An exterior angle is equal to sum of two opposite interior angles.

In ∆BOC,

⇒ ∠AOC = ∠OCB + ∠OBC

⇒ ∠OBC = ∠AOC - ∠OCB

⇒ ∠OBC = ∠AOC - ∠DCE

⇒ ∠OBC = 80° - 50° = 30°.

From figure,

∠ABC = ∠OBC = 30°.

Hence, ∠ABC = 30°.

In the figure given alongside, AB || CD and O is the center of the circle. If ∠ADC = 25°; find the angle AEB. Give reasons in support of your answer.

Answer

Join AC, BD and CB.

As angle is a semicircle is a right angle.

∴ ∠CAD = 90° and ∠CBD = 90°

Given, AB || CD

So, ∠BAD = ∠ADC = 25° [Alternate angles are equal]

From figure,

∠BAC = ∠BAD + ∠CAD = 25° + 90° = 115°.

Sum of opposite angles in a cyclic quadrilateral = 180°.

In quadrilateral ACDB,

⇒ ∠CDB + ∠BAC = 180°

⇒ ∠CDA + ∠ADB + ∠BAC = 180°

⇒ 25° + ∠ADB + 115° = 180°

⇒ ∠ADB = 180° - 115° - 25° = 40°.

As angles in same segment are equal.

∴ ∠AEB = ∠ADB = 40°.

Hence, ∠AEB = 40°.

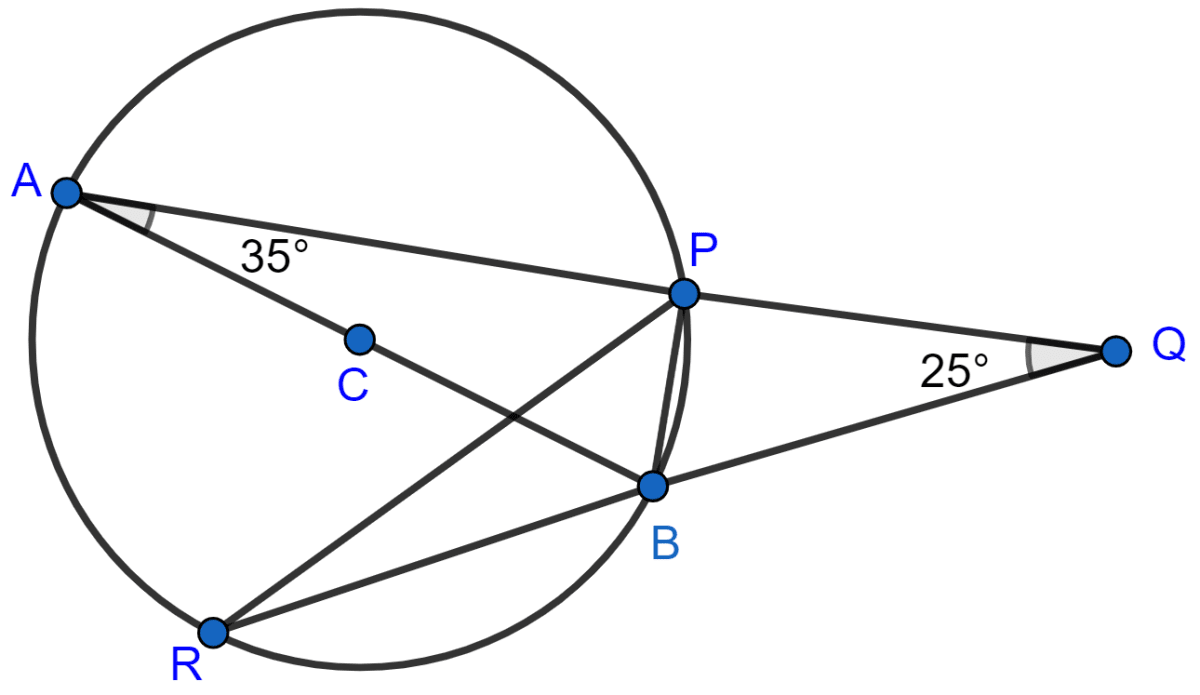
AB is a diameter of the circle APBR as shown in the figure. APQ and RBQ are straight lines. Find :

(i) ∠PRB,

(ii) ∠PBR,

(iii) ∠BPR.

Answer

(i) We know that,

Angles in same segment are equal.

∠PRB = ∠PAB = 35°.

Hence, ∠PRB = 35°.

(ii) From figure,

∠BPA = 90° [Angle in semi-circle is a right angle.]

⇒ ∠BPA + ∠BPQ = 180° [Linear pairs]

⇒ 90° + ∠BPQ = 180°

⇒ ∠BPQ = 180° - 90° = 90°.

Exterior angle of a triangle is equal to the sum of two opposite interior angles.

⇒ ∠PBR = ∠BPQ + ∠BQP = 90° + 25° = 115°.

Hence, ∠PBR = 115°.

(iii) In △ABP,

⇒ ∠BPA + ∠PAB + ∠ABP = 180°

⇒ 90° + 35° + ∠ABP = 180°

⇒ 125° + ∠ABP = 180°

⇒ ∠ABP = 180° - 125° = 55°.

From figure,

∠ABR = ∠PBR - ∠ABP = 115° - 55° = 60°.

∠APR = ∠ABR = 60°. [Angles in same segment are equal]

In △BPR,

⇒ ∠BPR + ∠PRB + ∠PBR = 180°

⇒ ∠BPR + 35° + 115° = 180°

⇒ 150° + ∠BPR = 180°

⇒ ∠BPR = 180° - 150° = 30°.

Hence, ∠BPR = 30°.

In the given figure, A is the center of the circle, ABCD is a parallelogram and CDE is a straight line. Prove that : ∠BCD = 2∠ABE.

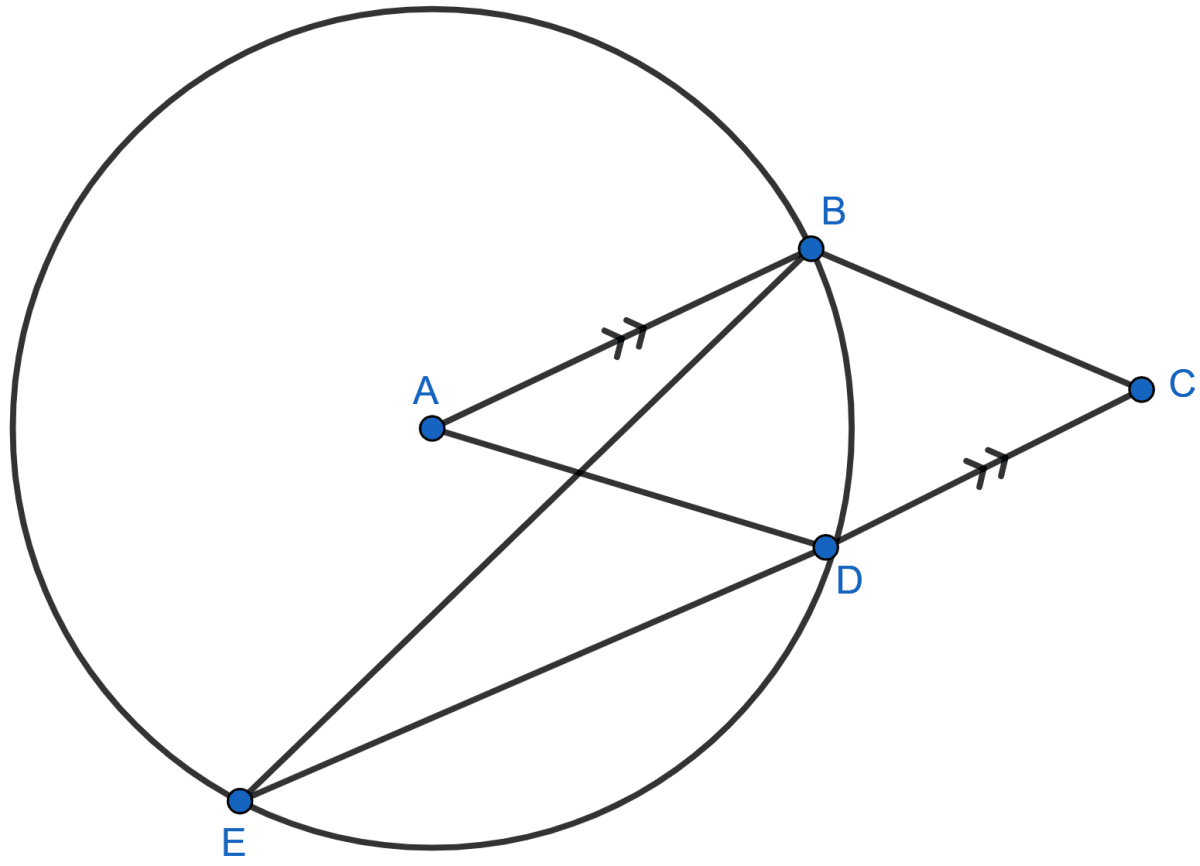
Answer

∠BAD = 2∠BED [Angle at the center is double the angle at the circumference subtended by the same chord.]

Since, CDE is a straight line and CD || AB.

∴ AB || ED.

⇒ ∠BED = ∠ABE [Alternate angles are equal]

Multiplying above equation by 2 we get,

⇒ 2∠BED = 2∠ABE

⇒ ∠BAD = 2∠ABE ...............(1)

ABCD is a parallelogram.

⇒ ∠BAD = ∠BCD [Opposite angles of a paralellogram are equal] ..........(2)

From (1) and (2) we get,

⇒ ∠BCD = 2∠ABE.

Hence, proved that ∠BCD = 2∠ABE.

In the given figure, I is the incenter of △ABC, BI when produced meets the circumcircle of △ABC at D. Given, ∠BAC = 55° and ∠ACB = 65°; calculate :

(i) ∠DCA,

(ii) ∠DAC,

(iii) ∠DCI,

(iv) ∠AIC.

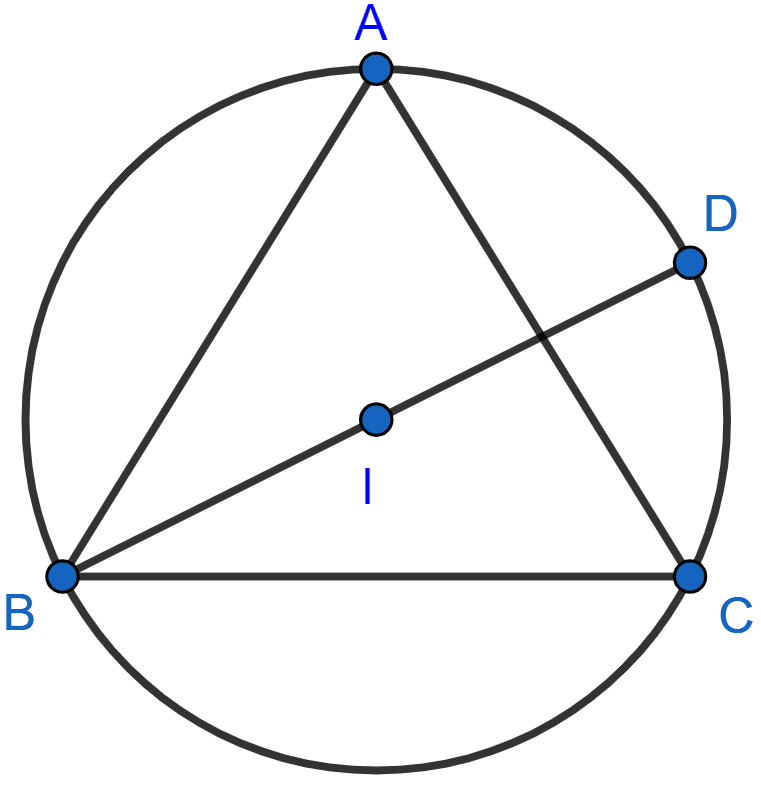
Answer

(i) Join IA, IC and CD.

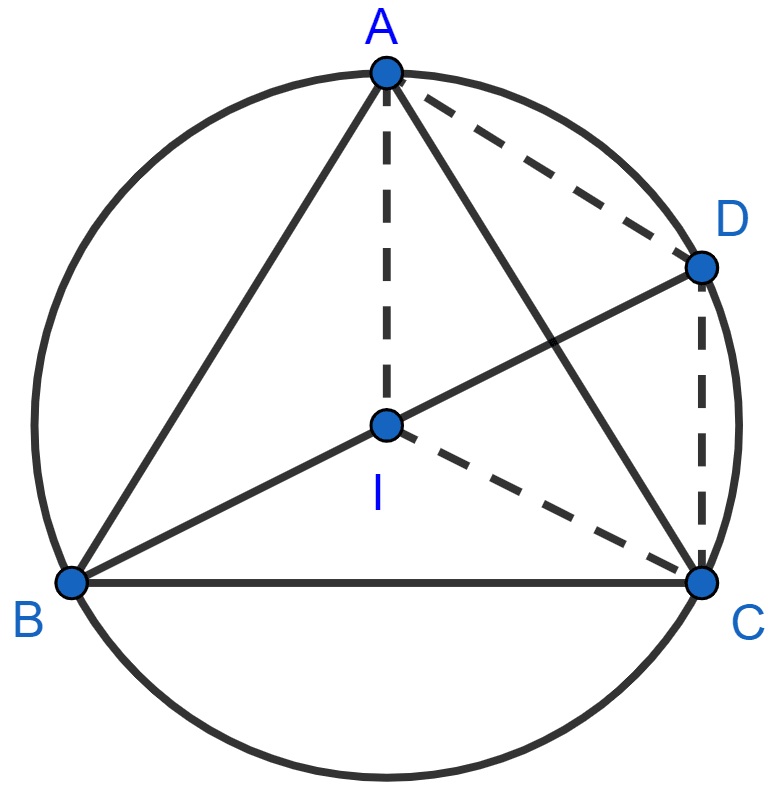
In △ABC,

⇒ ∠ABC + ∠BAC + ∠ACB = 180°

⇒ ∠ABC + 55° + 65° = 180°

⇒ ∠ABC + 120° = 180°

⇒ ∠ABC = 180° - 120° = 60°.

IB is the bisector of ∠ABC [As I is the incenter].

∠ABD = $\dfrac{1}{2}$∠ABC = $\dfrac{1}{2}$ x 60° = 30°.

We know that,

Angle in same segment are equal.

∴ ∠DCA = ∠ABD = 30°.

Hence, ∠DCA = 30°.

(ii) ∠CBD = ∠ABD = 30° [As IB is bisector of ∠ABC]

We know that,

Angle in same segment are equal.

∴ ∠DAC = ∠CBD = 30°.

Hence, ∠DAC = 30°.

(iii) As CI is the angle bisector of ∠ACB.

∠ACI = $\dfrac{1}{2}$∠ACB = $\dfrac{1}{2} \times 65°$ = 32.5°

From figure,

∠DCI = ∠DCA + ∠ACI = 30° + 32.5° = 62.5°

Hence, ∠DCI = 62.5°.

(iv) As AI is the angle bisector of ∠BAC.

∠IAC = $\dfrac{1}{2}$∠BAC = $\dfrac{1}{2} \times 55°$ = 27.5°

In △AIC,

⇒ ∠IAC + ∠ACI + ∠AIC = 180°

⇒ 27.5° + 32.5° + ∠AIC = 180°

⇒ 60° + ∠AIC = 180°

⇒ ∠AIC = 180° - 60° = 120°.

Hence, ∠AIC = 120°.

In the given figure, AB = AC = CD and ∠ADC = 38°. Calculate :

(i) Angle ABC

(ii) Angle BEC

Answer

Join BE.

(i) AC = CD

∠DAC = ∠ADC = 38° [Angles opposite to equal sides are equal]

In △ACD,

⇒ ∠DAC + ∠ADC + ∠ACD = 180°

⇒ 38° + 38° + ∠ACD = 180°

⇒ 76° + ∠ACD = 180°

⇒ ∠ACD = 180° - 76° = 104°

From figure,

⇒ ∠ACB + ∠ACD = 180° [BCD is a straight line]

⇒ ∠ACB + 104° = 180°

⇒ ∠ACB = 180° - 104° = 76°.

Given,

AB = AC

∴ ∠ABC = ∠ACB = 76°. [As angles opposite to equal sides are equal]

Hence, ∠ABC = 76°.

(ii) In △ABC,

⇒ ∠BAC + ∠ACB + ∠ABC = 180° [Angle sum property of triangle]

⇒ ∠BAC + 76° + 76° = 180°

⇒ ∠BAC + 152° = 180°

⇒ ∠BAC = 180° - 152° = 28°.

We know that,

Angles in same segment are equal.

⇒ ∠BEC = ∠BAC = 28°.

Hence, ∠BEC = 28°.

In the given figure, AC is the diameter of circle, centre O. Chord BD is perpendicular to AC. Write down the angles p, q and r in terms of x.

Answer

We know that,

Angle at the centre is double the angle at the circumference subtended by the same chord.

⇒ ∠AOB = 2∠ACB

⇒ x = 2q

⇒ q = $\dfrac{x}{2}$.

Angles in the same segment are equal.

∴ ∠ADB = ∠ACB = q = $\dfrac{x}{2}$

From figure,

∠ADC = 90° [Angle in semi-circle is a right angle.]

∠BDC = ∠ADC - ∠ADB = 90° - $\dfrac{x}{2}$.

∴ r = 90° - $\dfrac{x}{2}$.

In △EBC,

⇒ ∠EBC + ∠CEB + ∠ECB = 180° [Angle sum property of triangle]

⇒ ∠EBC + 90° + q = 180°

⇒ ∠EBC = 90° - q

From figure,

∠DBC = ∠EBC = 90° - q = 90° - $\dfrac{x}{2}$.

Angles in the same segment are equal.

∴ ∠DAC = ∠DBC

⇒ p = 90° - $\dfrac{x}{2}$.

Hence, p = 90° - $\dfrac{x}{2}$, q = $\dfrac{x}{2}$ and r = 90° - $\dfrac{x}{2}$.

In the given figure, AOB is a diameter and DC is parallel to AB. If ∠CAB = x°; find (in terms of x) the values of :

(i) ∠COB,

(ii) ∠DOC,

(iii) ∠DAC,

(iv) ∠ADC.

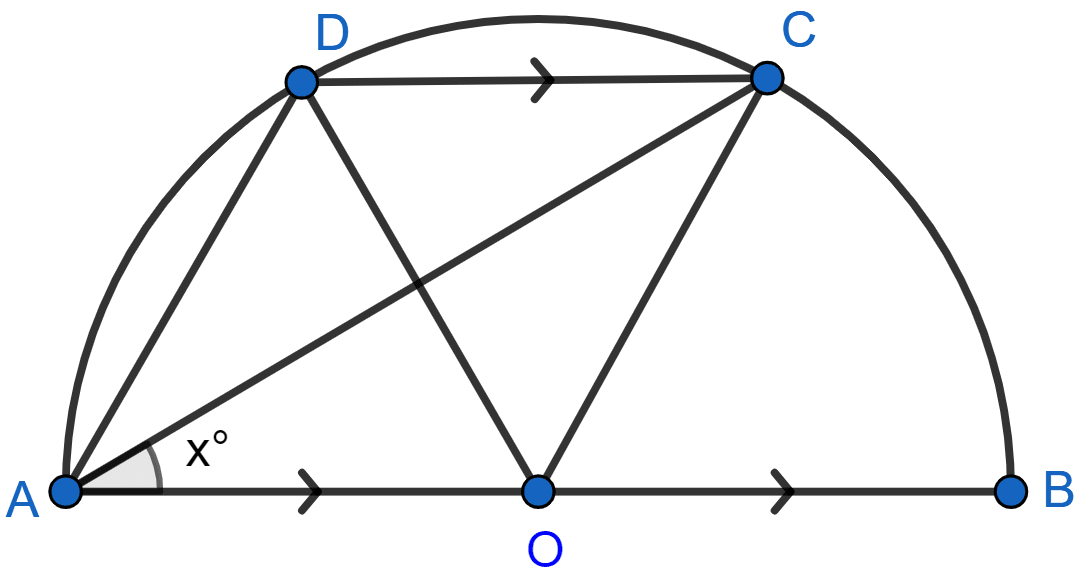
Answer

(i) We know that,

Angle at the centre is double the angle at the circumference subtended by the same chord.

⇒ ∠COB = 2∠CAB = 2x

Hence, ∠COB = 2x.

(ii) As DC || OB

⇒ ∠OCD = ∠COB = 2x [Alternate angles]

In △OCD,

OC = OD [Radius of same circle]

∠ODC = ∠OCD = 2x [Angles opposite to equal sides are equal]

⇒ ∠ODC + ∠OCD + ∠DOC = 180°

⇒ 2x + 2x + ∠DOC = 180°

⇒ ∠DOC = 180° - 4x.

Hence, ∠DOC = 180° - 4x.

(iii) We know that,

Angle at the centre is double the angle at the circumference subtended by the same chord.

⇒ ∠DOC = 2∠DAC

⇒ ∠DAC = $\dfrac{1}{2}$∠DOC = $\dfrac{1}{2}$ x (180° - 4x) = 90° - 2x.

Hence, ∠DAC = 90° - 2x.

(iv) DC || AO

∴ ∠ACD = ∠OAC = x (Alternate angles are equal)

In △ADC,

⇒ ∠ADC + ∠DAC + ∠ACD = 180° [Angle sum property of triangle]

⇒ ∠ADC + 90° - 2x° + x = 180°

⇒ ∠ADC + 90° - x = 180°

⇒ ∠ADC = 180° - 90° + x

⇒ ∠ADC = 90° + x

Hence, ∠ADC = 90° + x.

In the given figure, PQ is the diameter of the circle whose center is O. Given, ∠ROS = 42°, calculate ∠RTS.

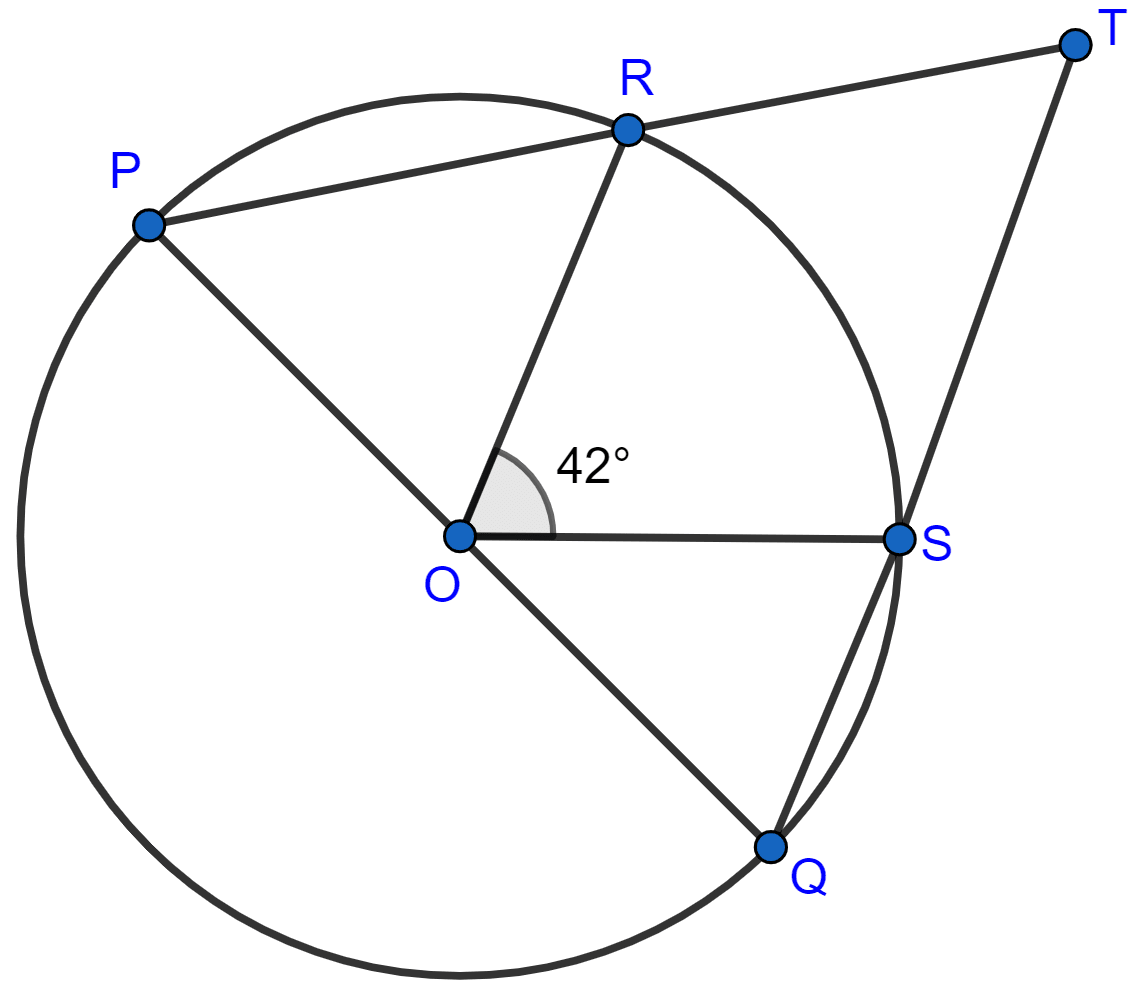
Answer

Join PS.

∠PSQ = 90° [Angle in semi-circle is a right angle.]

We know that,

Angle at the centre is double the angle at the circumference subtended by the same chord.

⇒ ∠ROS = 2∠SPR

⇒ ∠SPR = $\dfrac{1}{2}$∠ROS = $\dfrac{42}{2}$ = 21°

From figure,

⇒ ∠SPT = ∠SPR = 21°.

From figure,

⇒ ∠PSQ = 90° [Angle in a semi-circle is a right angle.]

Since, QST is a straight line.

⇒ ∠PSQ + ∠PST = 180°

⇒ 90° + ∠PST = 180°

⇒ ∠PST = 90°.

In △PST,

⇒ ∠PTS + ∠PST + ∠SPT = 180° [Angle sum property of triangle]

⇒ ∠PTS + 90° + 21° = 180°

⇒ ∠PTS + 111° = 180°

⇒ ∠PTS = 180° - 111° = 69°.

From figure,

∠RTS = ∠PTS = 69°.

Hence, ∠RTS = 69°.

The given figure shows a circle with center O and ∠ABP = 42°. Calculate the measure of :

(i) ∠PQB

(ii) ∠QPB + ∠PBQ

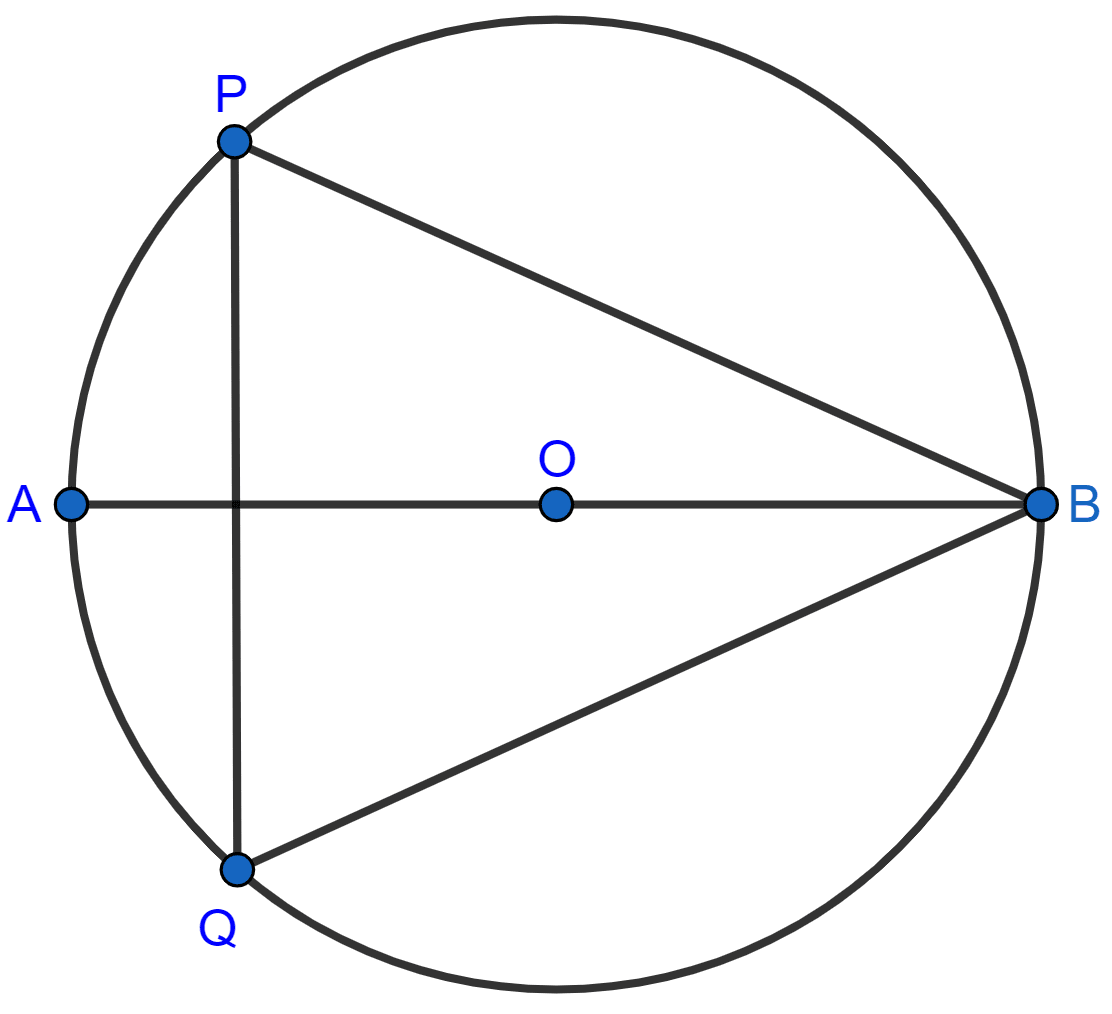
Answer

Join AP.

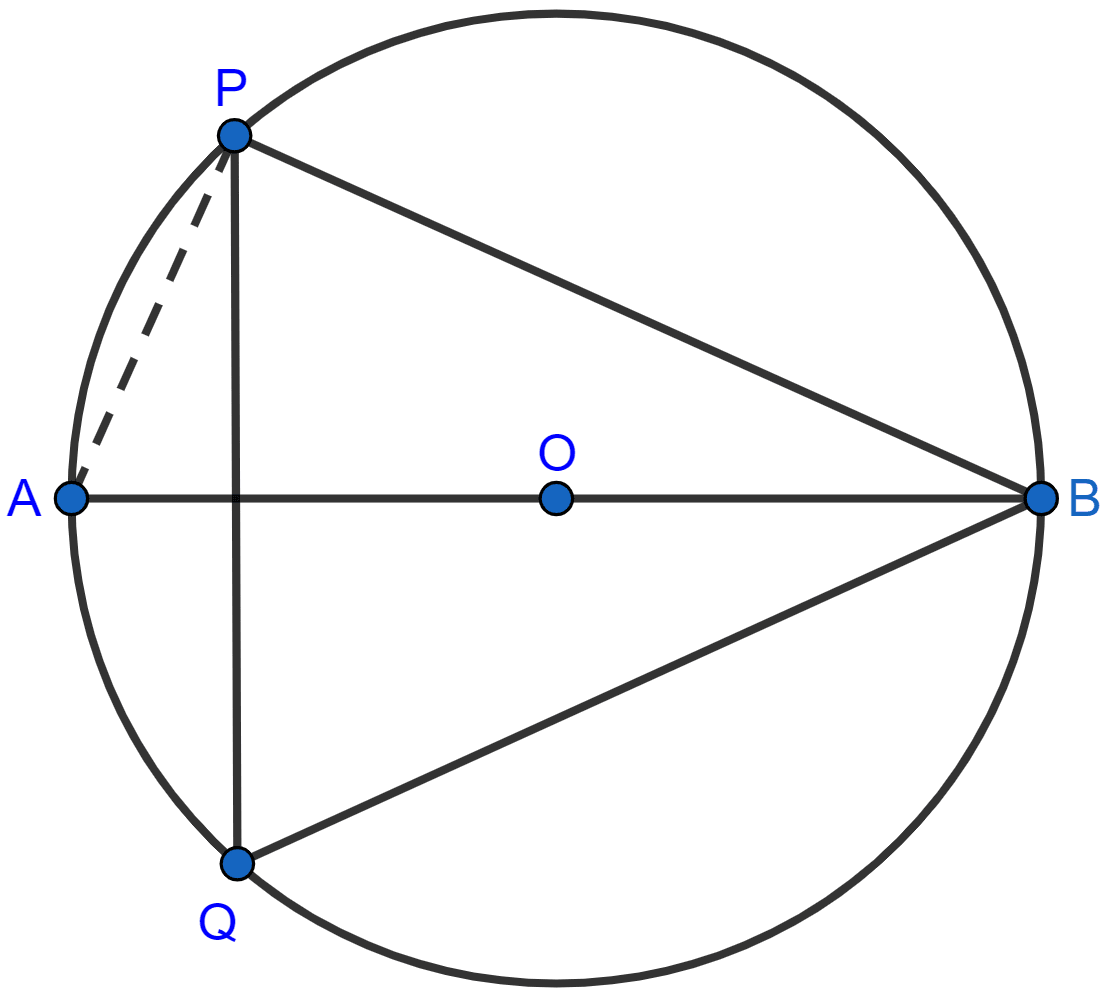
(i) We know that,

Angle in a semi-circle is a right angle.

∠APB = 90°.

In △APB,

⇒ ∠APB + ∠ABP + ∠BAP = 180° [Angle sum property of triangle]

⇒ 90° + 42° + ∠BAP = 180°

⇒ ∠BAP + 132° = 180°

⇒ ∠BAP = 180° - 132° = 48°.

From figure,

∠PQB = ∠BAP = 48° [Angles in same segment are equal]

Hence, ∠PQB = 48°.

(ii) In △BQP,

⇒ ∠QPB + ∠PBQ + ∠PQB = 180° [Angle sum property of triangle]

⇒ ∠QPB + ∠PBQ + 48° = 180°

⇒ ∠QPB + ∠PBQ = 180° - 48°

⇒ ∠QPB + ∠PBQ = 132°.

Hence, ∠QPB + ∠PBQ = 132°.

In the given figure, M is the centre of the circle. Chords AB and CD are perpendicular to each other. If ∠MAD = x and ∠BAC = y :

(i) express ∠AMD in terms of x.

(ii) express ∠ABD in terms of y.

(iii) prove that : x = y.

Answer

Mark the point of intersection of AB and CD as L.

(i) In △AMD,

MA = MD [Radius of circle]

∴ ∠MAD = ∠MDA = x.

In △AMD,

⇒ ∠MAD + ∠MDA + ∠AMD = 180° [Angle sum property of triangle]

⇒ x + x + ∠AMD = 180°

⇒ ∠AMD = 180° - 2x.

Hence, ∠AMD = 180° - 2x.

(ii) Let the perpendicular chords AB and CD intersect each other at L.

From figure,

∠ALC = 90°.

In △ALC,

⇒ ∠LAC + ∠LCA + ∠ALC = 180° [Angle sum property of triangle]

⇒ y + ∠DCA + 90° = 180°

⇒ ∠DCA = 180° - 90° - y

⇒ ∠DCA = 90° - y

From figure,

∠ABD = ∠DCA [Angles in same segment are equal]

∴ ∠ABD = 90° - y.

Hence, ∠ABD = 90° - y.

(iii) We know that,

Angle which an arc subtends at the center is double that which it subtends at any point on the remaining part of the circumference.

∴ ∠AMD = 2∠ABD

∠ABD = $\dfrac{1}{2}$ ∠AMD = $\dfrac{1}{2} \times (180° - 2x)$ = 90° - x.

We have,

∠ABD = 90° - y and ∠ABD = 90° - x

⇒ 90° - y = 90° - x

⇒ x = y.

Hence, proved that x = y.

ABCD is a trapezium with AD parallel to BC. Side BC is produced to point E and angle DCE = 95°. Angle B is equal to :

1. 85°

2. 105°

3. 95°

4. 175°

Answer

Given,

AD || BC

Since,

Side BC is produced to point E.

We can say that,

AD || BE

From figure,

∠ADC = ∠DCE = 95° (Alternate angles are equal)

We know that,

The opposite angles of a cyclic quadrilateral are supplementary.

∴ ∠ADC + ∠CBA = 180°

⇒ ∠CBA = 180° - ∠ADC = 180° - 95° = 85°.

Hence, Option 1 is the correct option.

In the given figure, ABC is an equilateral triangle. Angle ADC is :

1. 60°

2. 100°

3. 80°

4. 120°

Answer

Since, ABC is an equilateral triangle.

∴ ∠ABC = 60°.

We know that,

The opposite angles of a cyclic quadrilateral are supplementary.

∴ ∠ABC + ∠ADC = 180°

⇒ 60° + ∠ADC = 180°

⇒ ∠ADC = 180° - 60° = 120°.

Hence, Option 4 is the correct option.

In the given figure, O is the center of the circle. ∠OAB and ∠OCB are 30° and 40° respectively. ∠AOC is equal to :

1. 70°

2. 80°

3. 150°

4. 140°

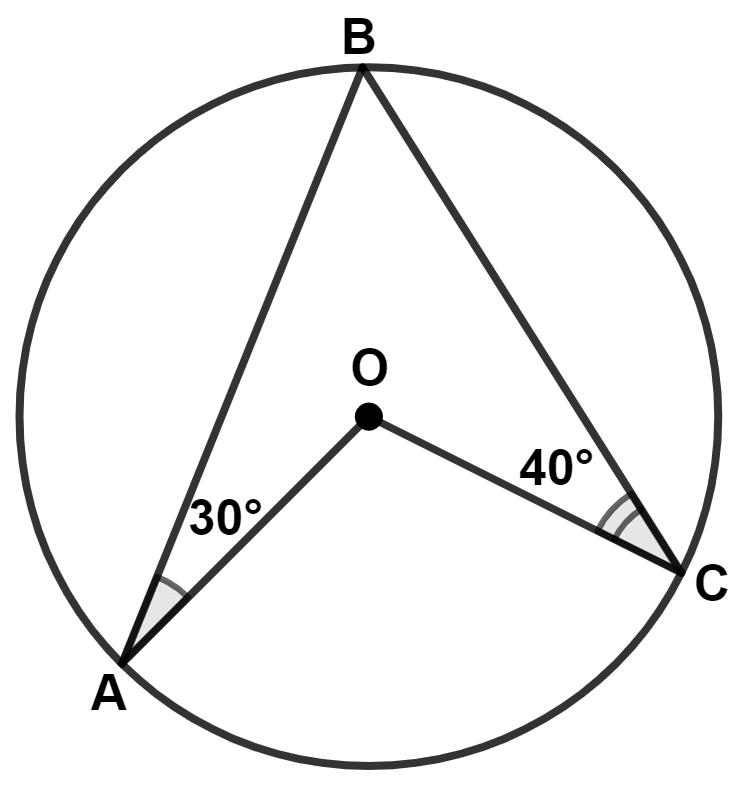
Answer

Join AC.

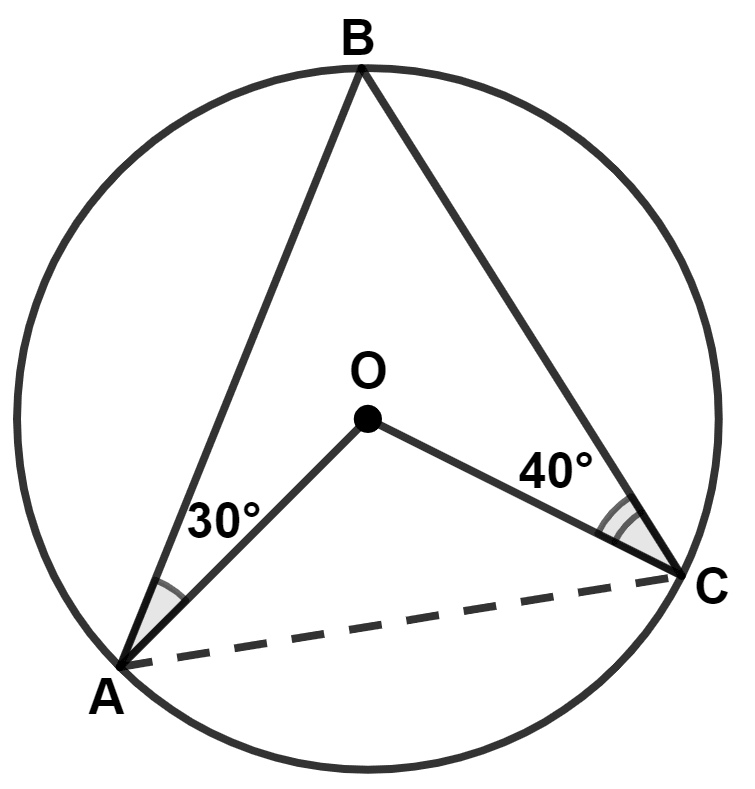
In △AOC,

Since,

OA = OC (Radius of same circle)

∴ ∠OAC = ∠OCA = x (let)

By angle sum property of triangle,

⇒ ∠OAC + ∠OCA + ∠AOC = 180°

⇒ x + x + ∠AOC = 180°

⇒ ∠AOC = 180° - 2x

In △AOC,

By angle sum property of triangle,

⇒ ∠BAC + ∠ACB + ∠CBA = 180°

⇒ (30° + x) + (40° + x) + ∠CBA = 180°

⇒ ∠CBA + 70° + 2x = 180°

⇒ ∠CBA = 180° - 70° - 2x

⇒ ∠CBA = 110° - 2x

We know that,

The angle which an arc subtends at the center is double that which it subtends at any point on the remaining part of the circumference.

∴ ∠AOC = 2∠CBA

⇒ 180° - 2x = 2(110° - 2x)

⇒ 180° - 2x = 220° - 4x

⇒ 4x - 2x = 220° - 180°

⇒ 2x = 40°

⇒ x = $\dfrac{40°}{2}$ = 20°.

⇒ ∠AOC = 180° - 2x

⇒ ∠AOC = 180° - 2(20°) = 180° - 40° = 140°.

Hence, Option 4 is the correct option.

In the given figure APB and CQD are two straight lines, then :

1. AB || CD

2. AC || PQ

3. PQ || BD

4. AC || BD

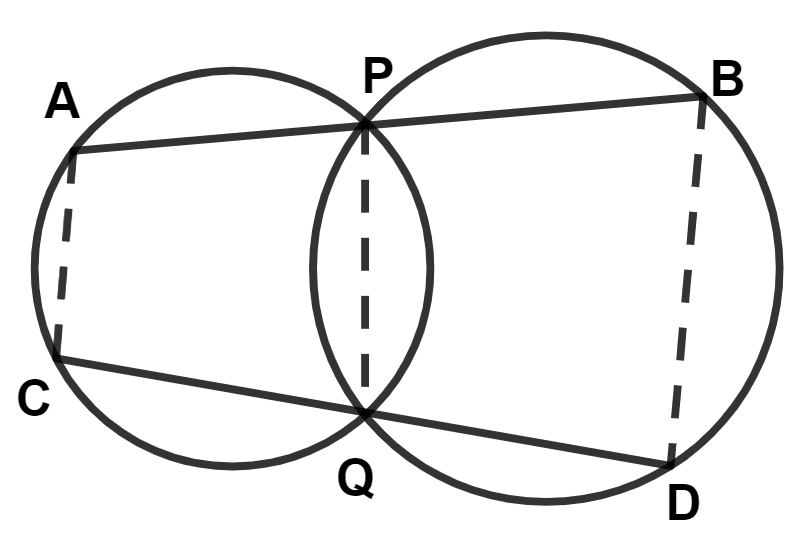
Answer

Let ∠BPQ = x and ∠DQP = y

We know that,

The exterior angle of a cyclic quadrilateral is equal to the opposite interior angle.

From figure,

In cyclic quadrilateral APQC,

∠A = ∠DQP = y and ∠C = ∠BPQ = x

From figure,

APB is a straight line.

∴ ∠APQ + ∠BPQ = 180°

⇒ ∠APQ + x = 180°

⇒ ∠APQ = 180° - x

CQD is a straight line.

∴ ∠CQP + ∠DQP = 180°

⇒ ∠CQP + y = 180°

⇒ ∠CQP = 180° - y

In cyclic quadrilateral PQDB,

∠B = ∠CQP = 180° - y and ∠D = ∠APQ = 180° - x

⇒ ∠A + ∠B = y + (180° - y) = 180°

⇒ ∠C + ∠D = x + (180° - x) = 180°

We know that,

Sum of adjacent angles in a trapezium is 180°.

∴ ABDC is a trapezium.

∴ AC || BD.

Hence, Option 4 is the correct option.

In the figure, given below, ∠ABC is equal to :

1. 105°

2. 75°

3. 90°

4. 45°

Answer

We know that,

Sum of co-interior angles in a trapezium is equal to 180°.

⇒ ∠A + ∠D = 180°

⇒ 105° + ∠D = 180°

⇒ ∠D = 180° - 105° = 75°

We know that,

The opposite angles of a cyclic quadrilateral is 180°.

In cyclic quadrilateral ABCD,

⇒ ∠D + ∠B = 180°

⇒ 75° + ∠B = 180°

⇒ ∠B = 180° - 75° = 105°.

Hence, Option 1 is the correct option.

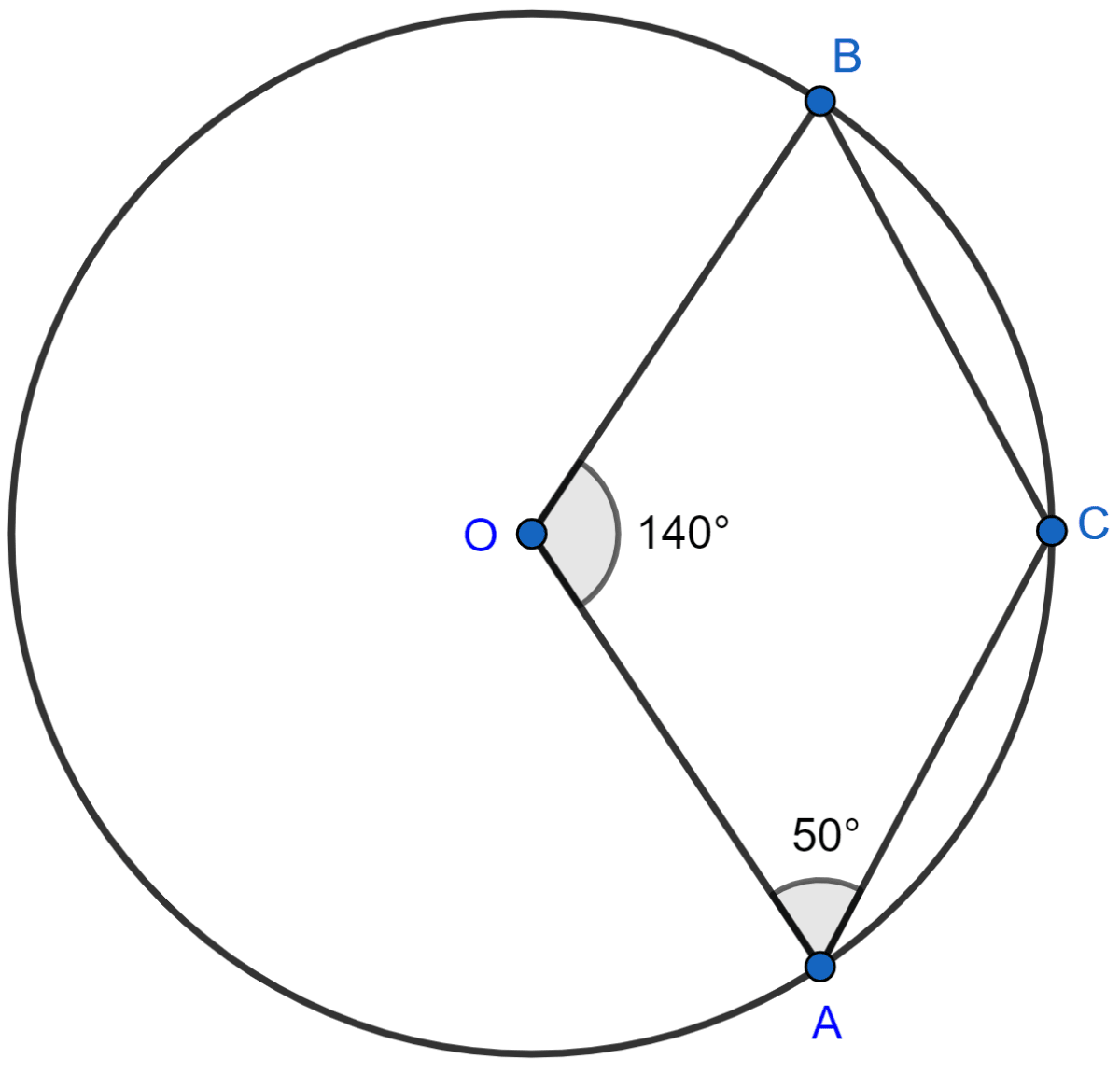
In the given figure, O is the centre of the circle. If ∠AOB = 140° and ∠OAC = 50°; find :

(i) ∠ACB,

(ii) ∠OBC,

(iii) ∠OAB,

(iv) ∠CBA.

Answer

Given, ∠AOB = 140° and ∠OAC = 50°

(i) We know that,

Angle at the center is double the angle at the circumference subtended by the same chord.

∠ACB = $\dfrac{1}{2}$Reflex ∠AOB

= $\dfrac{1}{2}$ (360° - 140°)

= $\dfrac{1}{2} \times 220°$ = 110°.

Hence, ∠ACB = 110°.

(ii) We know that,

The sum of angles in a quadrilateral is 360°

In quadrilateral OBCA,

∠OBC + ∠ACB + ∠OAC + ∠AOB = 360°

⇒ ∠OBC + 110° + 50° + 140° = 360°

⇒ ∠OBC + 300° = 360°

⇒ ∠OBC = 360° - 300° = 60°.

Hence, ∠OBC = 60°.

(iii) Join AB.

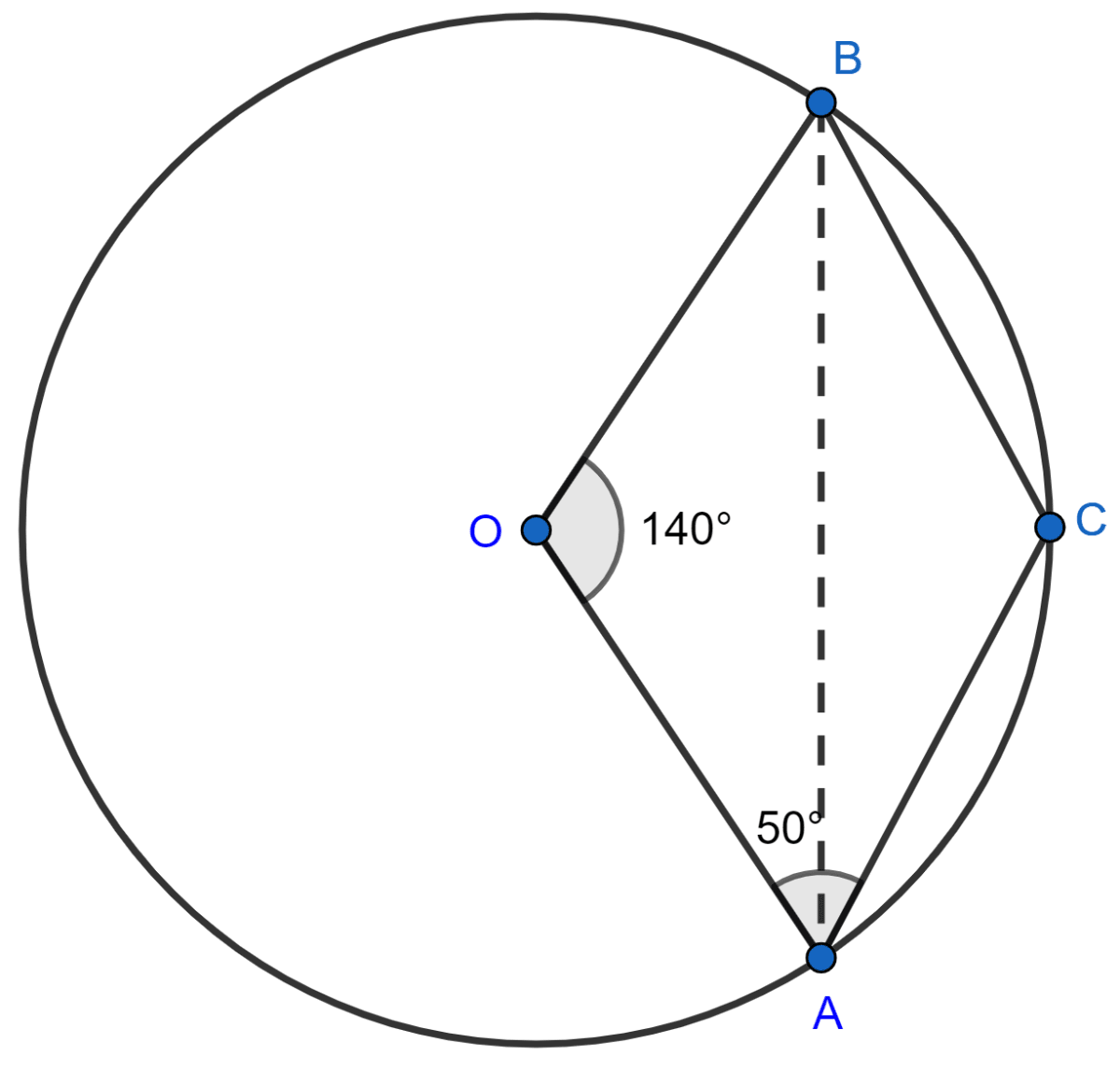
In ∆AOB, we have

OA = OB (radius of circle)

So, ∠OBA = ∠OAB (As angles opposite to equal sides are equal)

By angle sum property of a triangle we get,

⇒ ∠OBA + ∠OAB + ∠AOB = 180°

⇒ 2∠OAB + 140° = 180°

⇒ 2∠OAB = 40°

⇒ ∠OAB = $\dfrac{40}{2}$ = 20°

Hence, ∠OAB = 20°.

(iv) We already found, ∠OBC = 60°.

⇒ ∠OBC = ∠CBA + ∠OBA

⇒ 60° = ∠CBA + 20°

⇒ ∠CBA = 60° - 20° = 40°

Hence, ∠CBA = 40°.

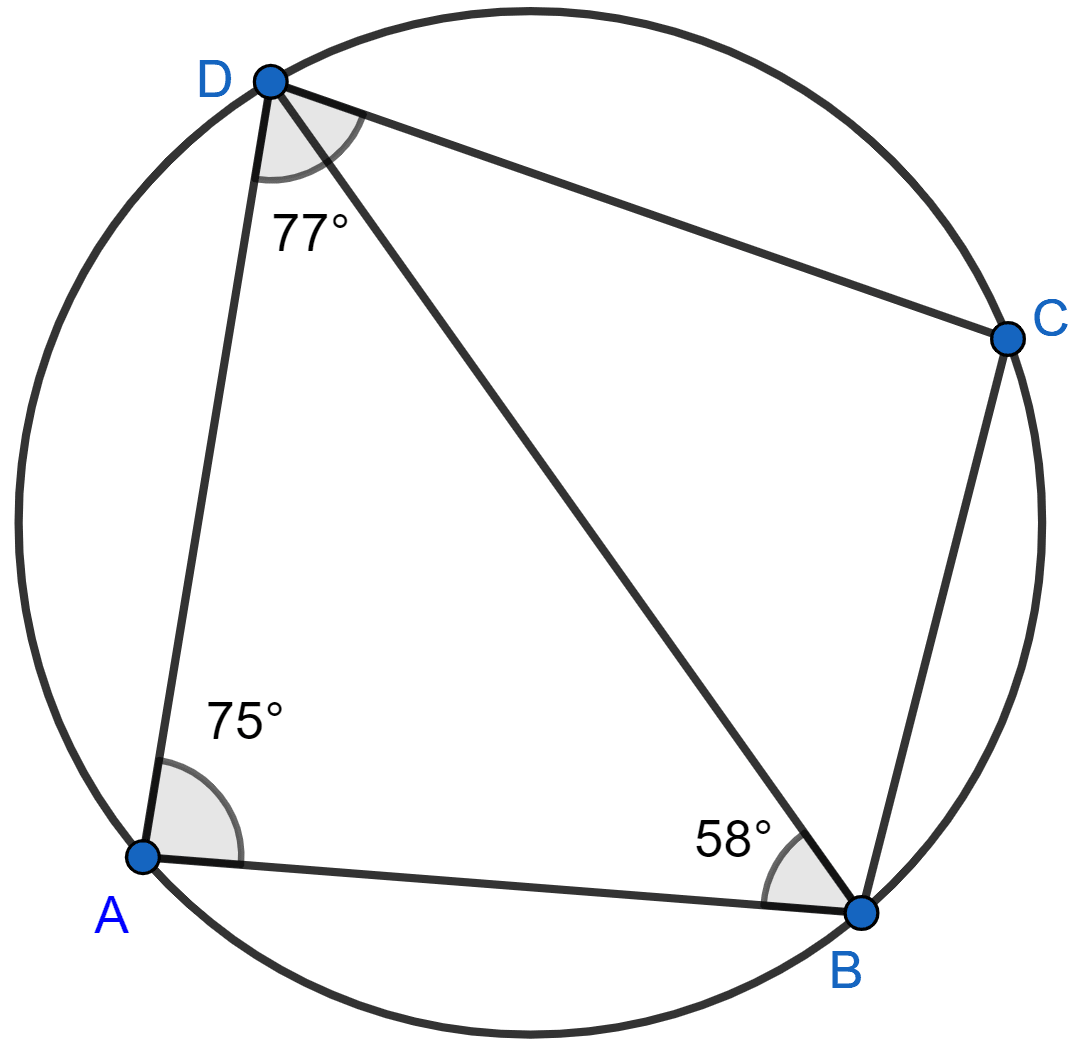
In the figure, given below, ABCD is a cyclic quadrilateral in which ∠BAD = 75°; ∠ABD = 58° and ∠ADC = 77°. Find :

(i) ∠BDC,

(ii) ∠BCD,

(iii) ∠BCA.

Answer

(i) We know,

Sum of angles in a triangle = 180°.

In △ABD,

⇒ ∠ADB + ∠ABD + ∠DAB = 180°

⇒ ∠ADB + 58° + 75° = 180°

⇒ ∠ADB + 133° = 180°

⇒ ∠ADB = 180° - 133° = 47°

From figure,

∠BDC = ∠ADC - ∠ADB = 77° - 47° = 30°.

Hence, ∠BDC = 30°.

(ii) We know that,

Sum of opposite angles of a cyclic quadrilateral is 180°.

⇒ ∠BAD + ∠BCD = 180°

⇒ ∠BCD = 180° - 75° = 105°.

Hence, ∠BCD = 105°.

(iii) Join AC.

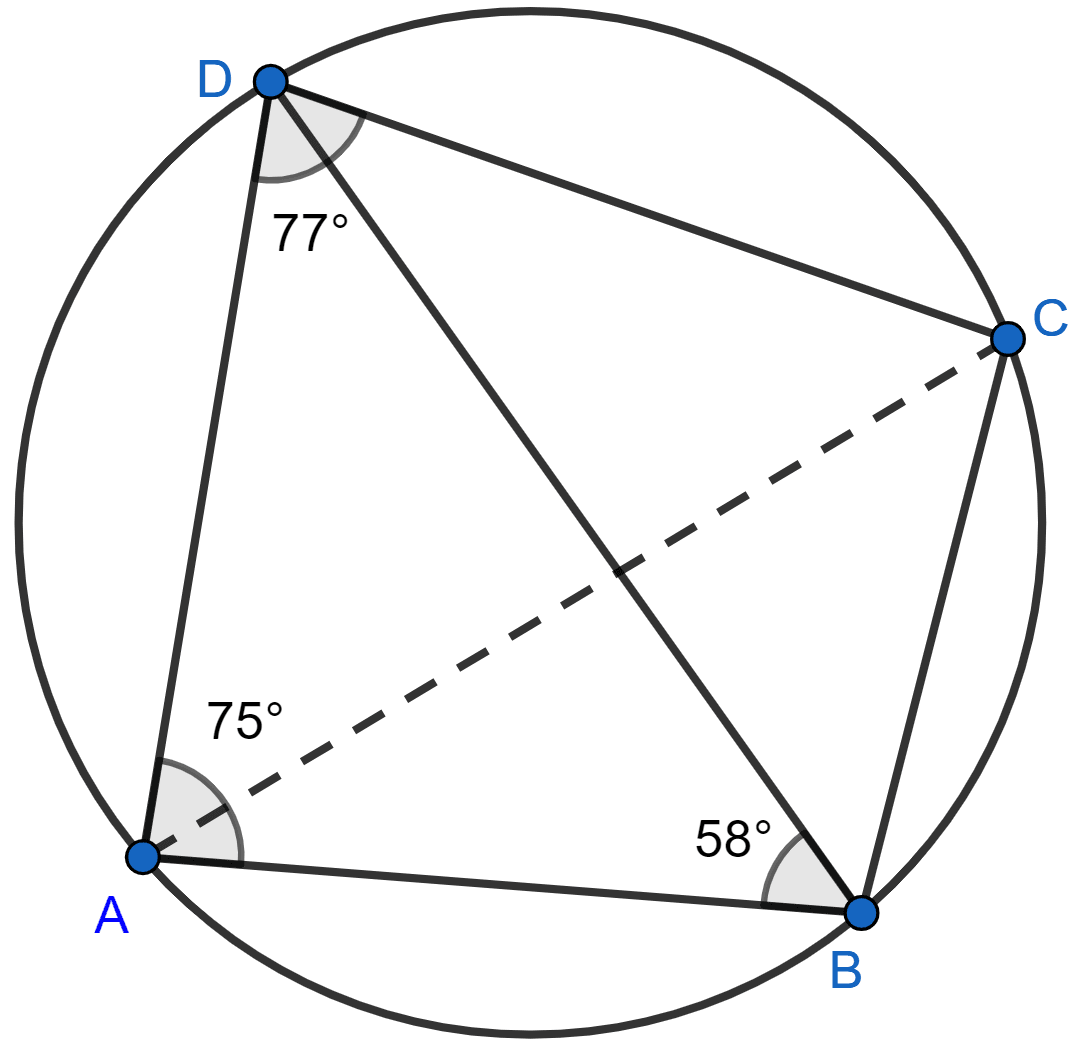
We know that,

Angles subtended by the same chord on the circle are equal.

∠BCA = ∠ADB = 47°

Hence, ∠BCA = 47°.

In the following figure, O is the centre of the circle and ΔABC is equilateral.

Find:

(i) ∠ADB, (ii) ∠AEB.

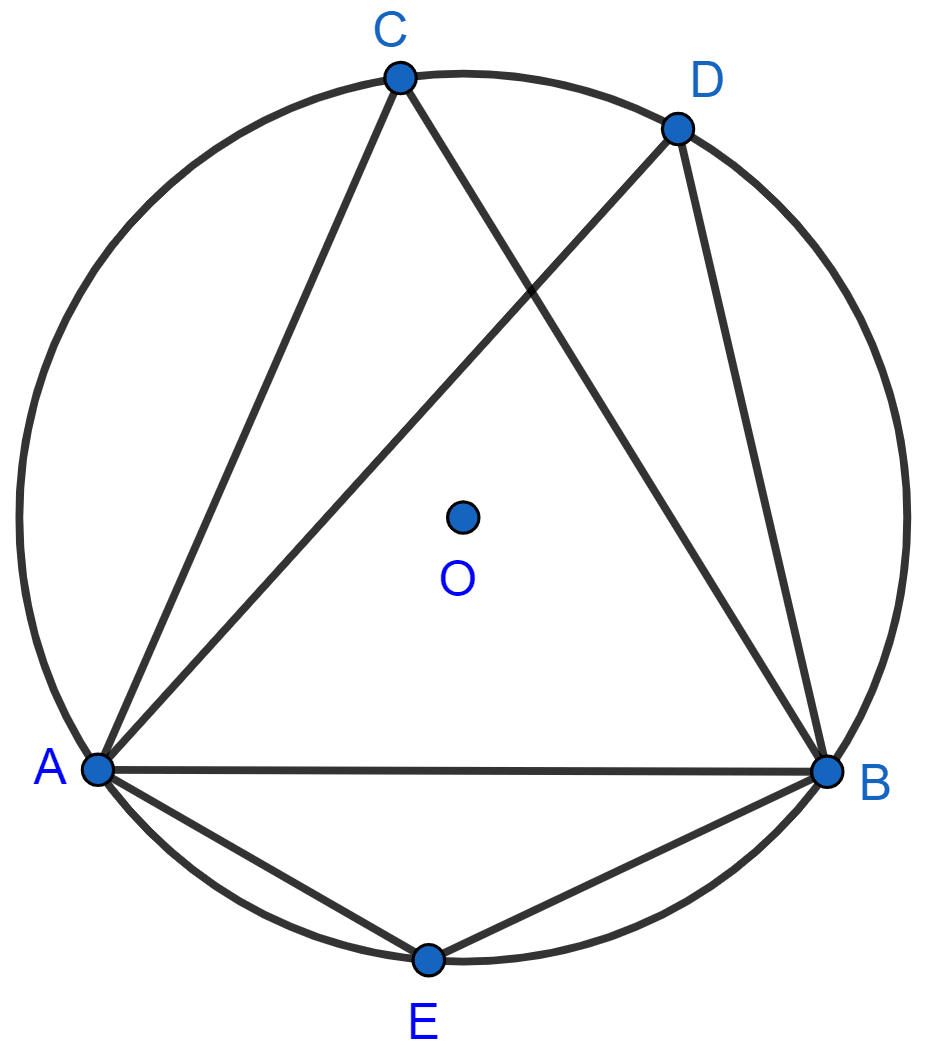
Answer

(i) We know that each angle in an equilateral triangle = 60°.

∴ ∠ACB = 60°

As angles in same segment are equal.

∴ ∠ADB = ∠ACB = 60°.

Hence, ∠ADB = 60°.

(ii) Join OA and OB.

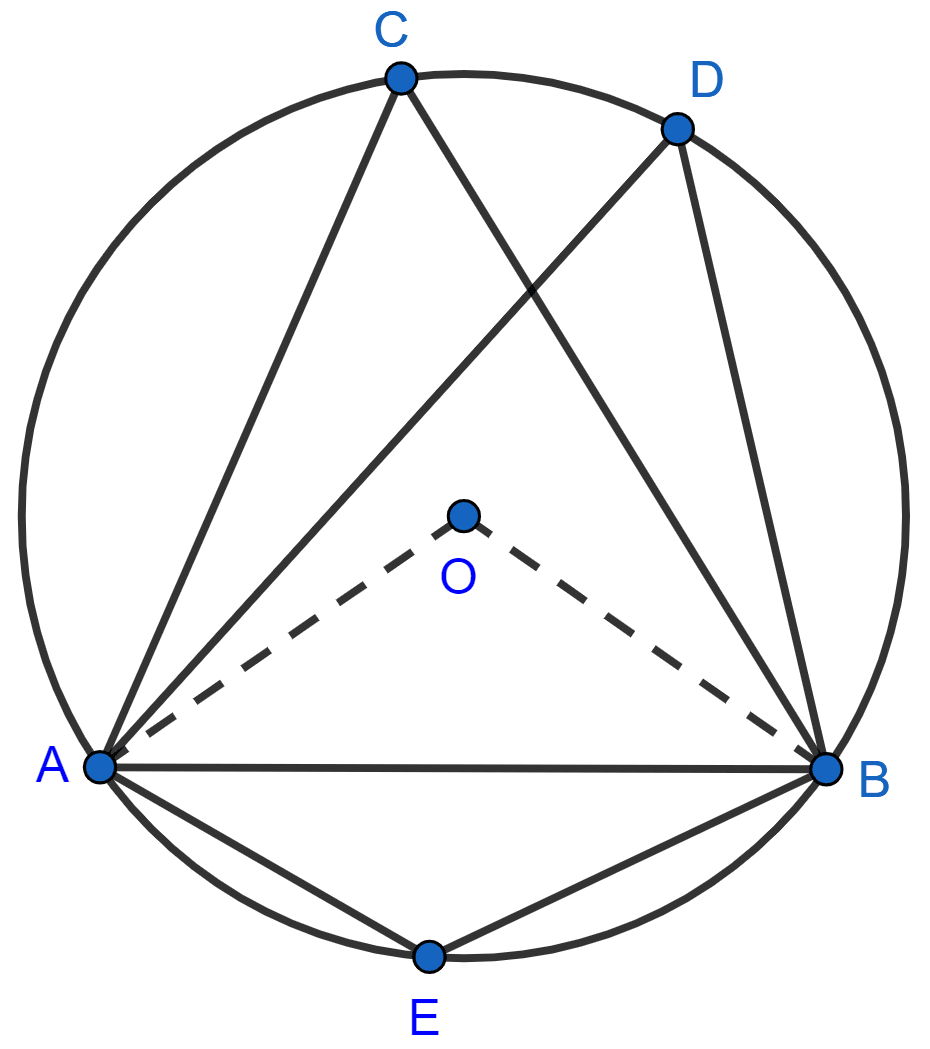
We know that,

Angle at the center is double the angle at the circumference subtended by the same chord.

∴ ∠AOB = 2∠ACB = 2 x 60° = 120°.

∴ ∠AEB = $\dfrac{1}{2}$ Reflex ∠AOB

= $\dfrac{1}{2}$(360° - 120°) = $\dfrac{1}{2} \times 240°$

= 120°.

Hence, ∠AEB = 120°.

ABCD is a cyclic quadrilateral in a circle with centre O. If ∠ADC = 130°, find ∠BAC.

Answer

We know that,

Angle in a semi-circle is 90°.

∠ACB = 90°.

We know that,

Sum of opposite angles of a cyclic quadrilateral = 180°.

⇒ ∠ABC = 180° - ∠ADC = 180° - 130° = 50°.

In △ACB,

⇒ ∠ACB + ∠CBA + ∠BAC = 180° [Angle sum property]

⇒ 90° + 50° + ∠BAC = 180°

⇒ ∠BAC + 140° = 180°

⇒ ∠BAC = 180° - 140° = 40°.

Hence, ∠BAC = 40°.

In the following figure,

(i) if ∠BAD = 96°, find ∠BCD and ∠BFE.

(ii) Prove that AD is parallel to FE.

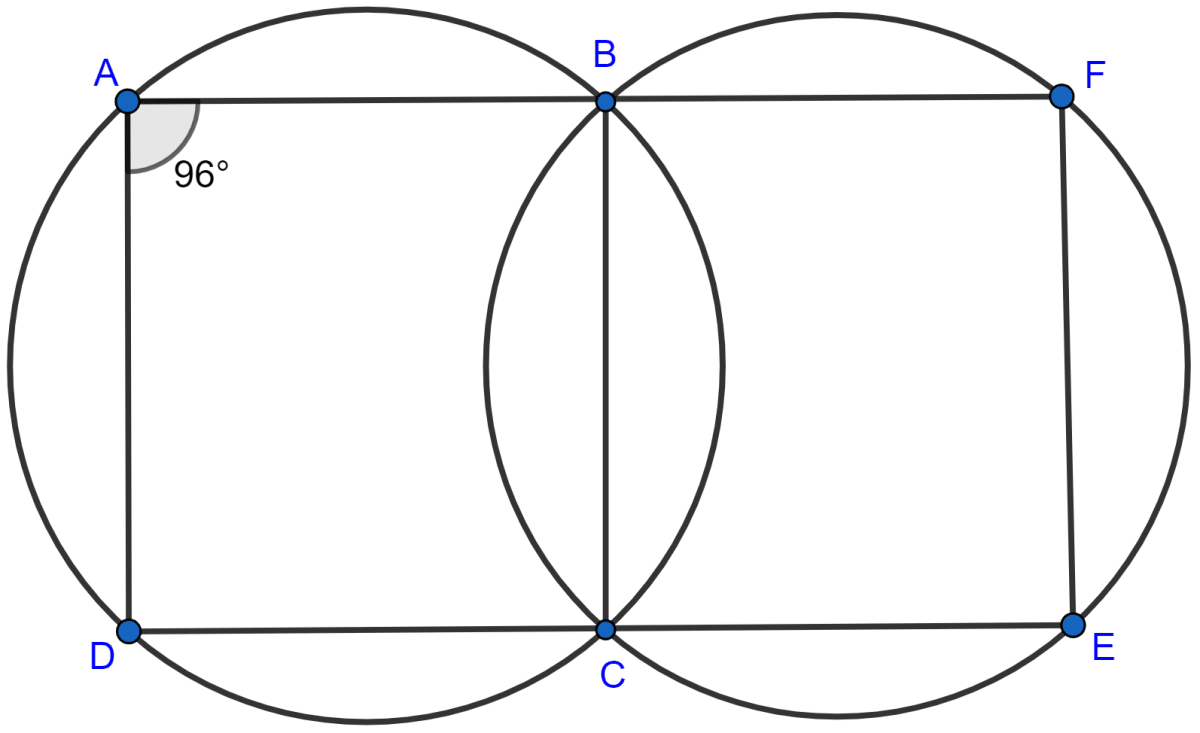
Answer

(i) ABCD is a cyclic quadrilateral.

So, ∠BAD + ∠BCD = 180° [As sum of opposite angles in a cyclic quadrilateral = 180°]

⇒ ∠BCD = 180° - ∠BAD

= 180° - 96°

= 84°.

As DCE is a straight line.

∴ ∠BCE = 180° - ∠BCD

= 180° - 84° = 96°.

BCEF is a cyclic quadrilateral,

So, ∠BCE + ∠BFE = 180°

⇒ ∠BFE = 180° - ∠BCE

= 180° - 96°

= 84°.

Hence, ∠BCD = 84° and ∠BFE = 84°.

(ii) Now, ∠BAD + ∠BFE = 96° + 84° = 180°.

But these two are interior angles on the same side of a pair of lines AD and FE.

Hence, proved that AD || FE.

ABCD is a parallelogram. A circle through vertices A and B meets side BC at point P and side AD at point Q. Show that quadrilateral PCDQ is cyclic.

Answer

The figure of the parallelogram ABCD with a circle through its vertices A and B meeting side BC at point P and side AD at point Q is shown below:

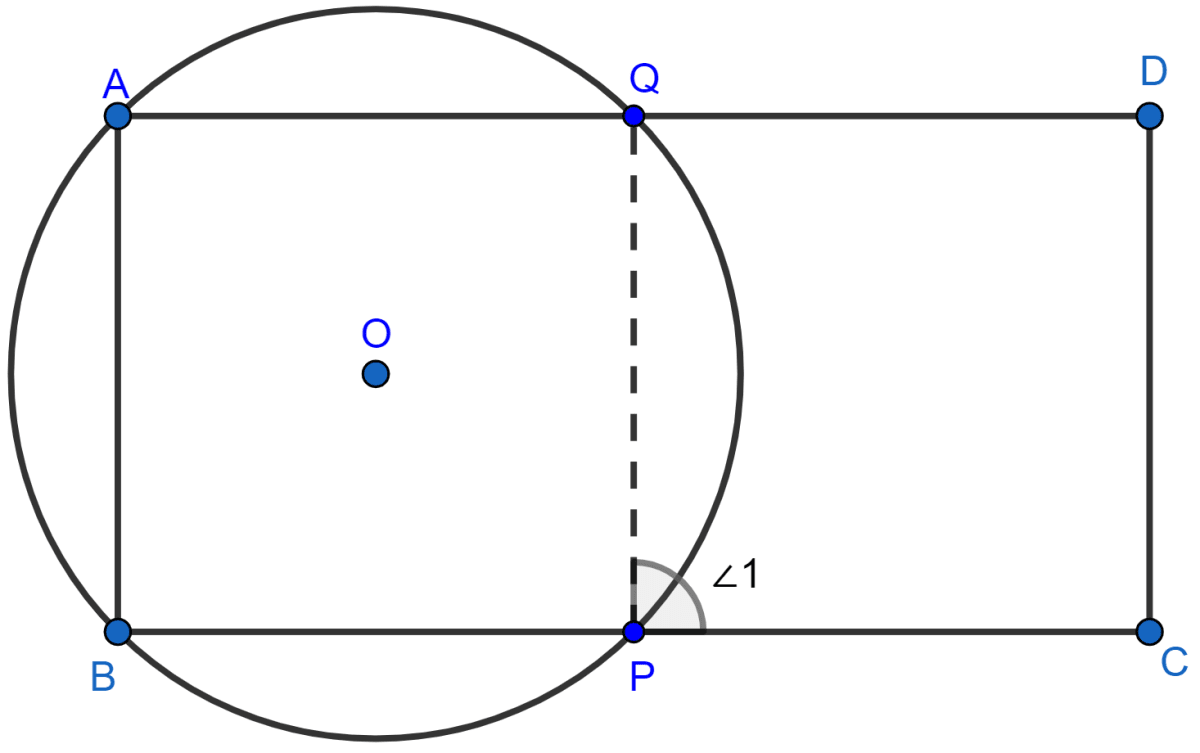
We know that,

An exterior angle of a cyclic quadrilateral is equal to its opposite interior angle.

∴ ∠1 = ∠A ....... (i)

Also,

∠A = ∠C ...........(ii) [Opposite angles of a parallelogram are equal.]

From (i) and (ii) we get,

∠1 = ∠C .........(iii)

Also,

⇒ ∠C + ∠D = 180° [Sum of co-interior angles of a parallelogram = 180°]

⇒ ∠1 + ∠D = 180°

Hence, proved that PCDQ is cyclic.

Prove that:

(i) the parallelogram, inscribed in a circle, is a rectangle.

(ii) the rhombus, inscribed in a circle, is a square.

Answer

(i) Let's assume that ABCD is a parallelogram which is inscribed in a circle.

⇒ ∠A = ∠C and ∠B = ∠D [Opposite angles of a parallelogram are equal]

⇒ ∠A + ∠C = 180° and ∠B + ∠D = 180° [Pair of opposite angles in a cyclic quadrilateral are supplementary]

⇒ 2∠A = 180° and 2∠B = 180°

⇒ ∠A = 90° and ∠B = 90°

⇒ ∠A = ∠C = 90° and ∠B = ∠D = 90°.

Also,

AB = CD and AD = BC [Opposite sides of parallelogram are equal]

Hence, proved that ABCD is a rectangle.

(ii) Let's assume that ABCD is a rhombus which is inscribed in a circle.

So, we have

∠BAD = ∠BCD [Opposite angles of a rhombus are equal]

From figure,

∠BAD + ∠BCD = 180° [Pair of opposite angles in a cyclic quadrilateral are supplementary]

⇒ 2∠BAD = 180°

Thus, ∠BAD = ∠BCD = 90°.

Also,

∠ABC = ∠ADC [Opposite angles of a rhombus are equal]

From figure,

∠ABC + ∠ADC = 180° [Pair of opposite angles in a cyclic quadrilateral are supplementary]

⇒ 2∠ABC = 180°

Thus, ∠ABC = ∠ADC = 90°.

Since, each side of rhombus are equal.

Thus,

Each angle of quadrilateral = 90° and all sides are equal.

Hence, proved that ABCD is a square.

In the given figure, AB = AC. Prove that DECB is an isosceles trapezium.

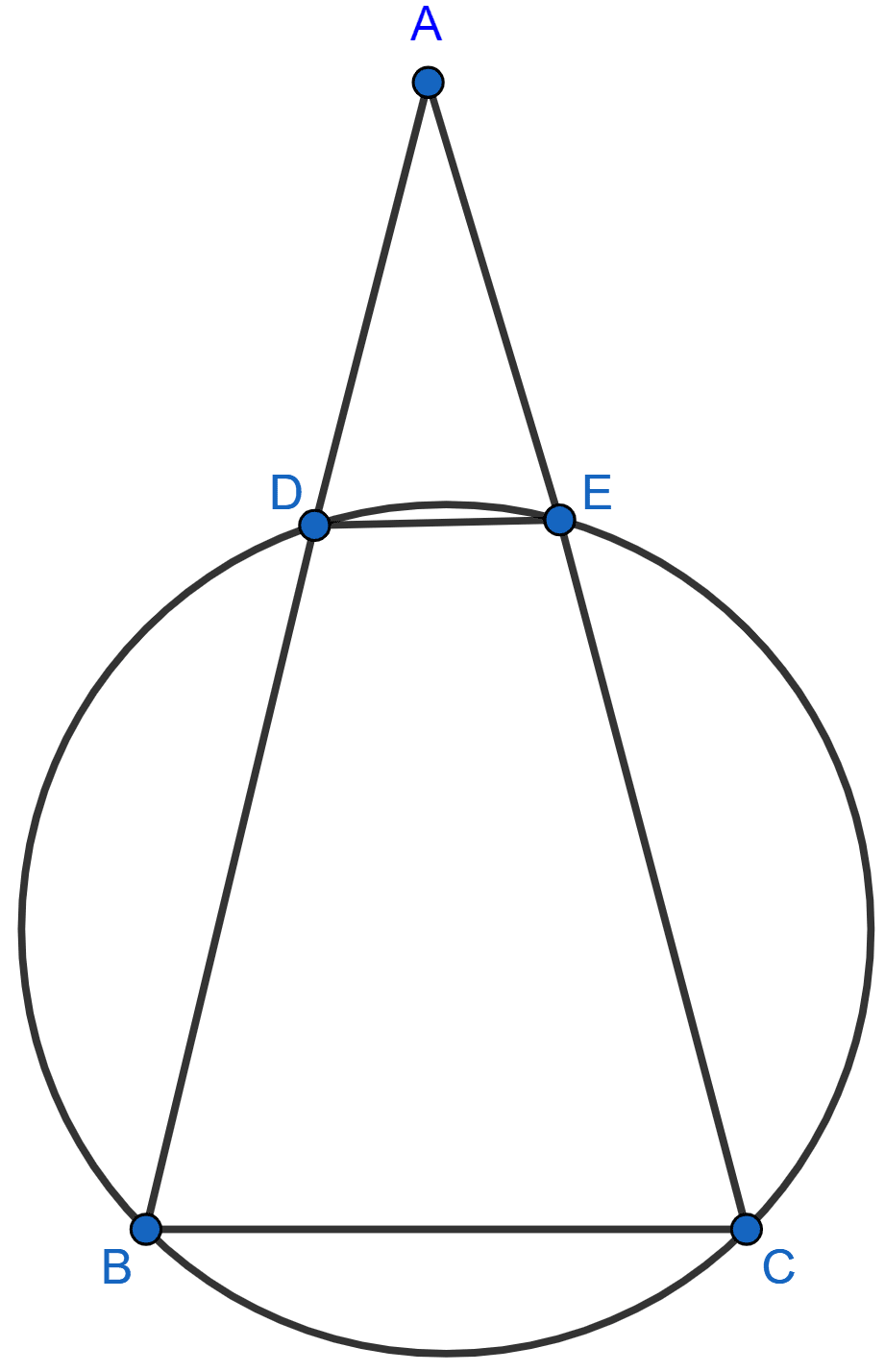
Answer

Given, AB = AC

So, ∠B = ∠C ........(1) [As Angles opposite to equal sides are equal]

From figure,

DECB is a cyclic quadrilateral.

∴ ∠B + ∠DEC = 180° [Sum of opposite angles in cyclic quadrilateral = 180°]

⇒ ∠C + ∠DEC = 180° (Using 1)

But this is the sum of interior angles on one side of a transversal.

∴ DE || BC.

∴ ∠ADE = ∠B and ∠AED = ∠C [Corresponding angles]

Thus, ∠ADE = ∠AED

∴ AD = AE

⇒ AB - AD = AC - AE [As AB = AC]

⇒ BD = CE

Hence, we have DE || BC and BD = CE.

Hence, proved that DECB is an isosceles trapezium.

The figure given below, shows a circle with centre O.

Given : ∠AOC = a and ∠ABC = b.

(i) Find the relationship between a and b.

(ii) Find the measure of angle OAB, if OABC is a parallelogram.

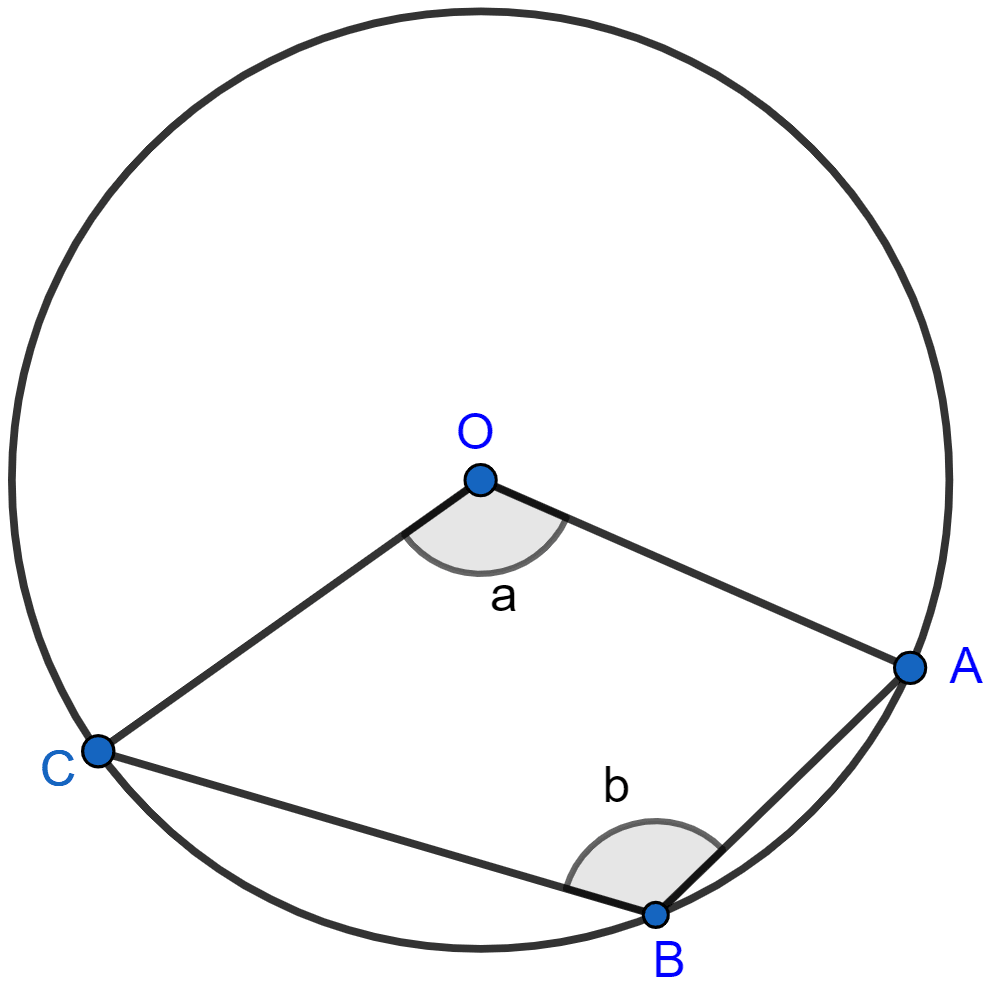
Answer

(i) We know that,

Angle at the centre is double the angle at the circumference subtended by the same chord

∴ ∠ABC = $\dfrac{1}{2}$ Reflex ∠COA

⇒ b = $\dfrac{1}{2}$ (360° - a)

⇒ 2b = 360° - a

⇒ a + 2b = 360° .....(1)

Hence, relationship between a and b is given by the equation : a + 2b = 360°.

(ii) From equation 1, we get :

⇒ a + 2b = 360°

⇒ a = 360° - 2b

As OABC is a parallelogram, the opposite angles are equal.

So, a = b

⇒ 360° - 2b = b

⇒ 3b = 360°

⇒ b = $\dfrac{360°}{3}$ = 120°

Let ∠OAB = x and ∠OCB = x.

⇒ ∠OAB + ∠OCB + ∠AOC + ∠ABC = 360°

⇒ x + x + a + b = 360°

⇒ 2x + 120° + 120° = 360°

⇒ 2x + 240° = 360°

⇒ 2x = 120°

⇒ x = $\dfrac{120°}{2}$ = 60°.

Hence, ∠OAB = 60°.

In the figure given, RS is a diameter of the circle. NM is parallel to RS and ∠MRS = 29°.

Calculate :

(i) ∠RNM,

(ii) ∠NRM.

Answer

(i) Join RN and MS.

∠RMS = 90° [Angle in a semi-circle is a right angle]

In ∆RMS

⇒ ∠RMS + ∠RSM + ∠MRS = 180° [Angle sum property of triangle]

⇒ 90° + ∠RSM + 29° = 180°

⇒ ∠RSM + 119° = 180°

⇒ ∠RSM = 180° - 119° = 61°.

Sum of opposite angles in a cyclic quadrilateral = 180°.

⇒ ∠RNM + ∠RSM = 180°

⇒ ∠RNM + 61° = 180°

⇒ ∠RNM = 180° - 61° = 119°.

Hence, ∠RNM = 119°.

(ii) Now as RS || NM,

∠NMR = ∠MRS = 29° [Alternate angles are equal]

From figure,

∠NMS = ∠NMR + ∠RMS = 29° + 90° = 119°.

Sum of opposite angles in a cyclic quadrilateral = 180°.

In quadrilateral NMSR,

⇒ ∠NRS + ∠NMS = 180°

⇒ ∠NRM + ∠MRS + ∠NMS = 180°

⇒ ∠NRM + 29° + 119° = 180°

⇒ ∠NRM = 180° - 119° - 29°

⇒ ∠NRM = 32°.

Hence, ∠NRM = 32°.

In the given figure, SP is the bisector of ∠RPT and PQRS is a cyclic quadrilateral. Prove that :

SQ = SR.

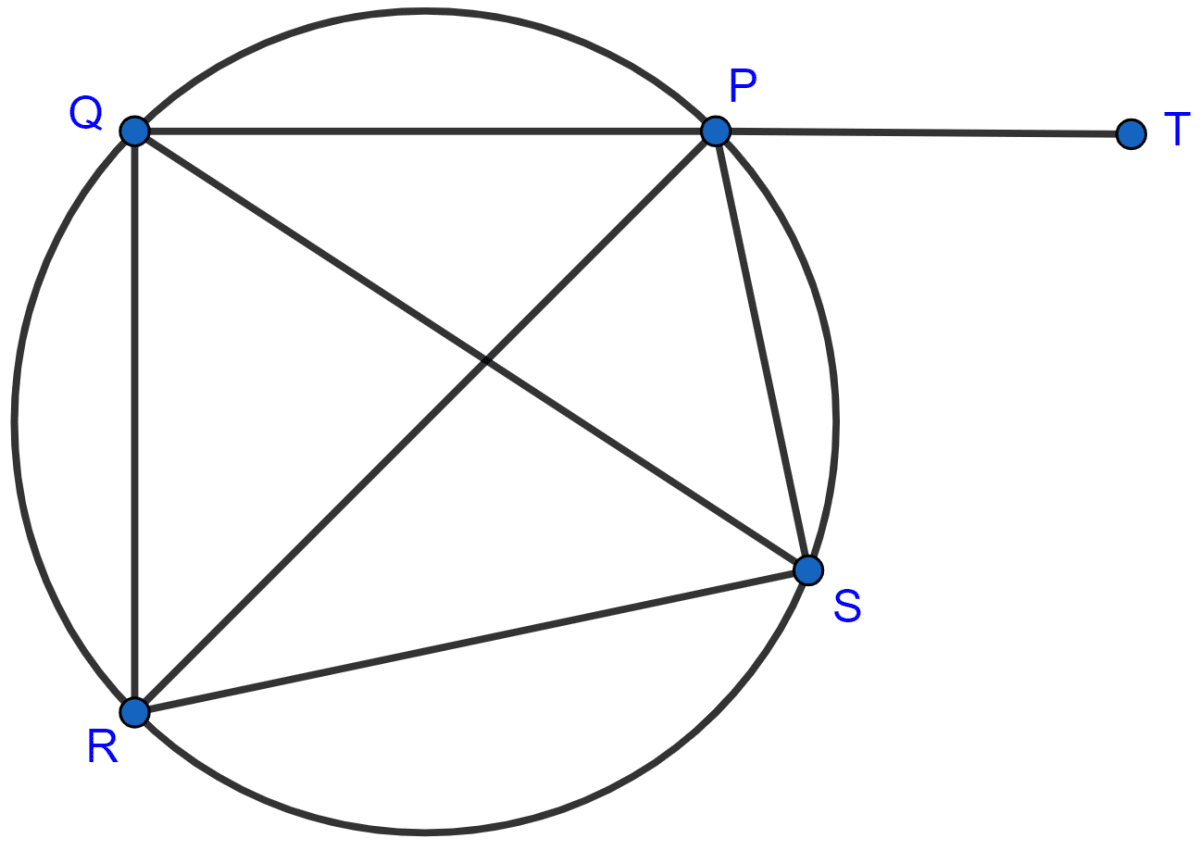
Answer

PQRS is a cyclic quadrilateral.

Sum of opposite angles in a cyclic quadrilateral = 180°.

∴ ∠QRS + ∠QPS = 180° ...........(1)

Also,

∠QPS + ∠SPT = 180° [As QPT is a straight line] ........(2)

Subtracting equation (2) from (1) we get,

⇒ ∠QRS + ∠QPS - (∠QPS + ∠SPT) = 180° - 180°

⇒ ∠QRS - ∠SPT = 0

⇒ ∠QRS = ∠SPT ..........(3)

∠RQS = ∠RPS [Angles in same segment are equal] ........(4)

∠RPS = ∠SPT [As PS bisects ∠RPT] .......(5)

From (3), (4) and (5) we get :

⇒ ∠QRS = ∠RQS.

∴ SQ = SR [As sides opposite to equal angles are also equal]

Hence, proved that SQ = SR.

In the figure, O is the center of the circle, ∠AOE = 150°, ∠DAO = 51°. Calculate the sizes of the angles CEB and OCE.

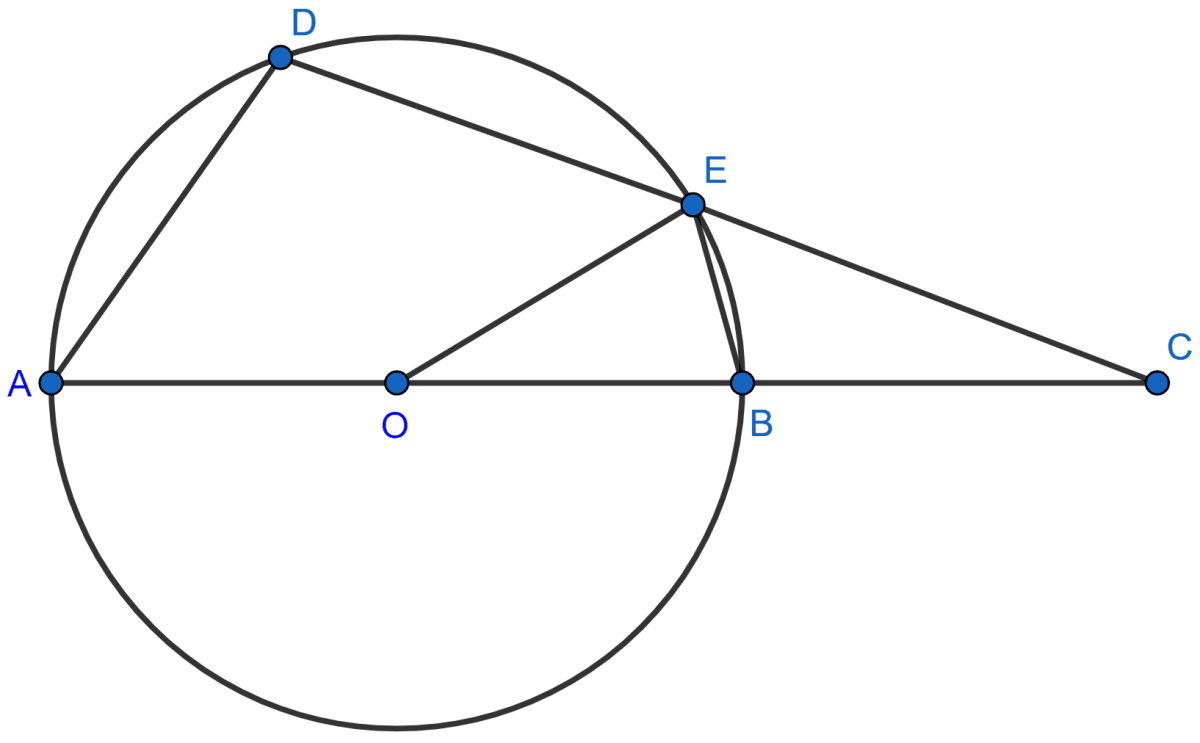
Answer

We know that,

Angle at the center is double the angle at the circumference subtended by the same chord.

⇒ Reflex ∠AOE = 2∠ADE

⇒ ∠ADE = $\dfrac{1}{2}$ Reflex ∠AOE

⇒ ∠ADE = $\dfrac{1}{2}$ (360° - 150°)

⇒ ∠ADE = $\dfrac{1}{2} \times 210°$ = 105°.

From figure,

⇒ ∠DAB + ∠BED = 180° [Sum of opposite angles in a cyclic quadrilateral = 180°.]

⇒ ∠BED = 180° - ∠DAB = 180° - 51° = 129°.

Also,

⇒ ∠CEB + ∠BED = 180° [As CED is a straight line]

⇒ ∠CEB = 180° - ∠BED = 180° - 129° = 51°.

In △ADC,

⇒ ∠ADC + ∠ACD + ∠DAC = 180°

⇒ ∠ADE + ∠ACD + ∠DAO = 180° [From figure, ∠ADC = ∠ADE and ∠DAC = ∠DAO]

⇒ 105° + ∠ACD + 51° = 180°

⇒ ∠ACD = 180° - 105° - 51° = 24°.

From figure,

∠OCE = ∠ACD = 24°.

Hence, ∠CEB = 51° and ∠OCE = 24°.

In the figure, given below, P and Q are the centers of two circles intersecting at B and C. ACD is a straight line. Calculate the numerical value of x.

Answer

We know that,

Angle at the center is double the angle at the circumference subtended by the same chord.

⇒ ∠APB = 2∠ACB

⇒ ∠ACB = $\dfrac{1}{2}$ ∠APB

⇒ ∠ACB = $\dfrac{1}{2} \times$ 150° = 75°.

From figure,

⇒ ∠ACB + ∠BCD = 180° [As ACD is a straight line]

⇒ 75° + ∠BCD = 180°

⇒ ∠BCD = 180° - 75° = 105°.

Also,

⇒ Reflex ∠BQD = 2∠BCD [Angle at the center is double the angle at the circumference subtended by the same chord.]

⇒ (360° - x) = 2 x 105°

⇒ x = 360° - 210° = 150°.

Hence, x = 150°.

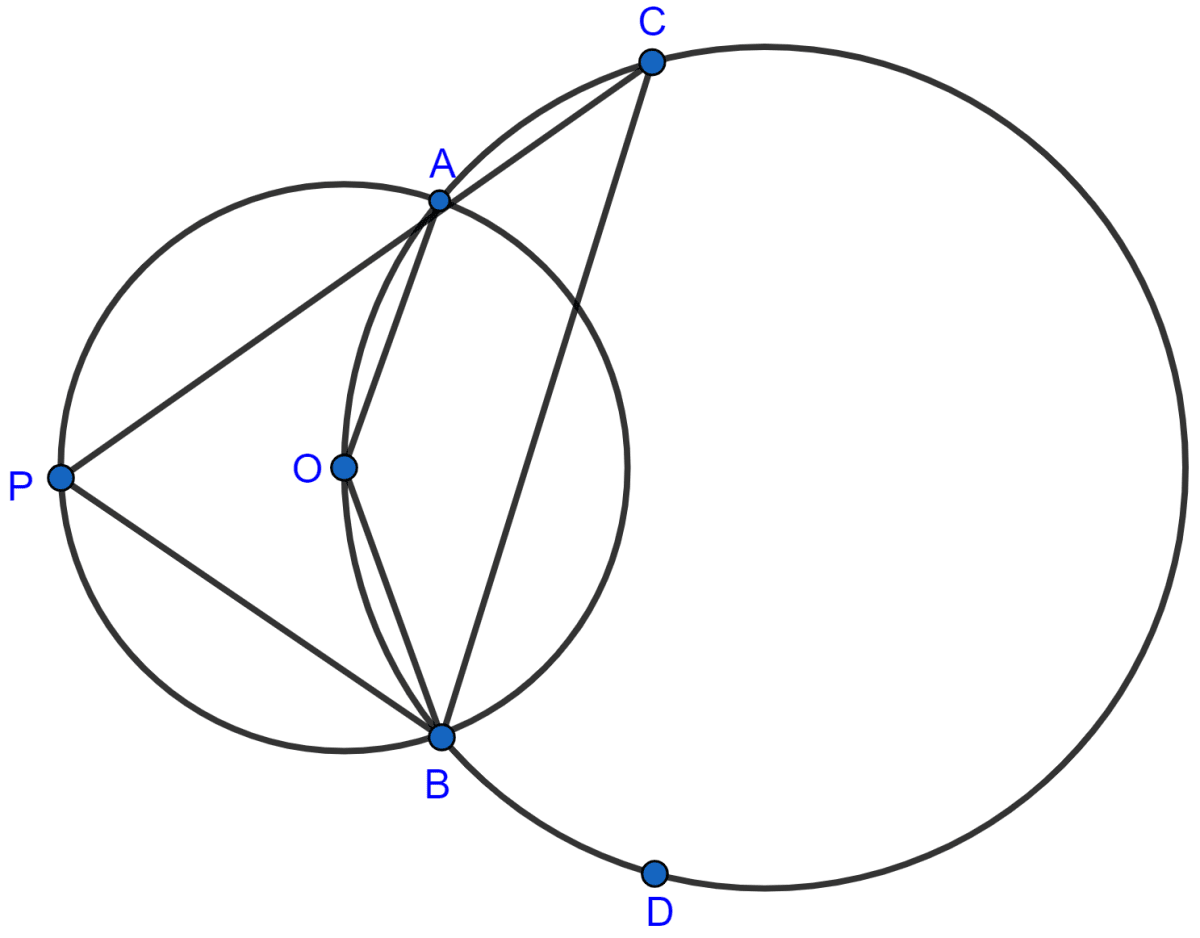
The figure shows two circles which intersect at A and B. The center of the smaller circle is O and lies on the circumference of the larger circle. Given ∠APB = a°.

Calculate, in terms of a°, the value of :

(i) obtuse ∠AOB,

(ii) ∠ACB,

(iii) ∠ADB.

Give reasons for your answers clearly.

Answer

(i) We know that,

Angle at the center is double the angle at the circumference subtended by the same chord.

obtuse ∠AOB = 2∠APB = 2a°.

Hence, obtuse ∠AOB = 2a°.

(ii) OACB is a cyclic quadrilateral.

⇒ ∠AOB + ∠ACB = 180° [Sum of opposite angles in a cyclic quadrilateral = 180°.]

⇒ ∠ACB + 2a° = 180°

⇒ ∠ACB = 180° - 2a°.

Hence, ∠ACB = 180° - 2a°.

(iii) Join AD and BD.

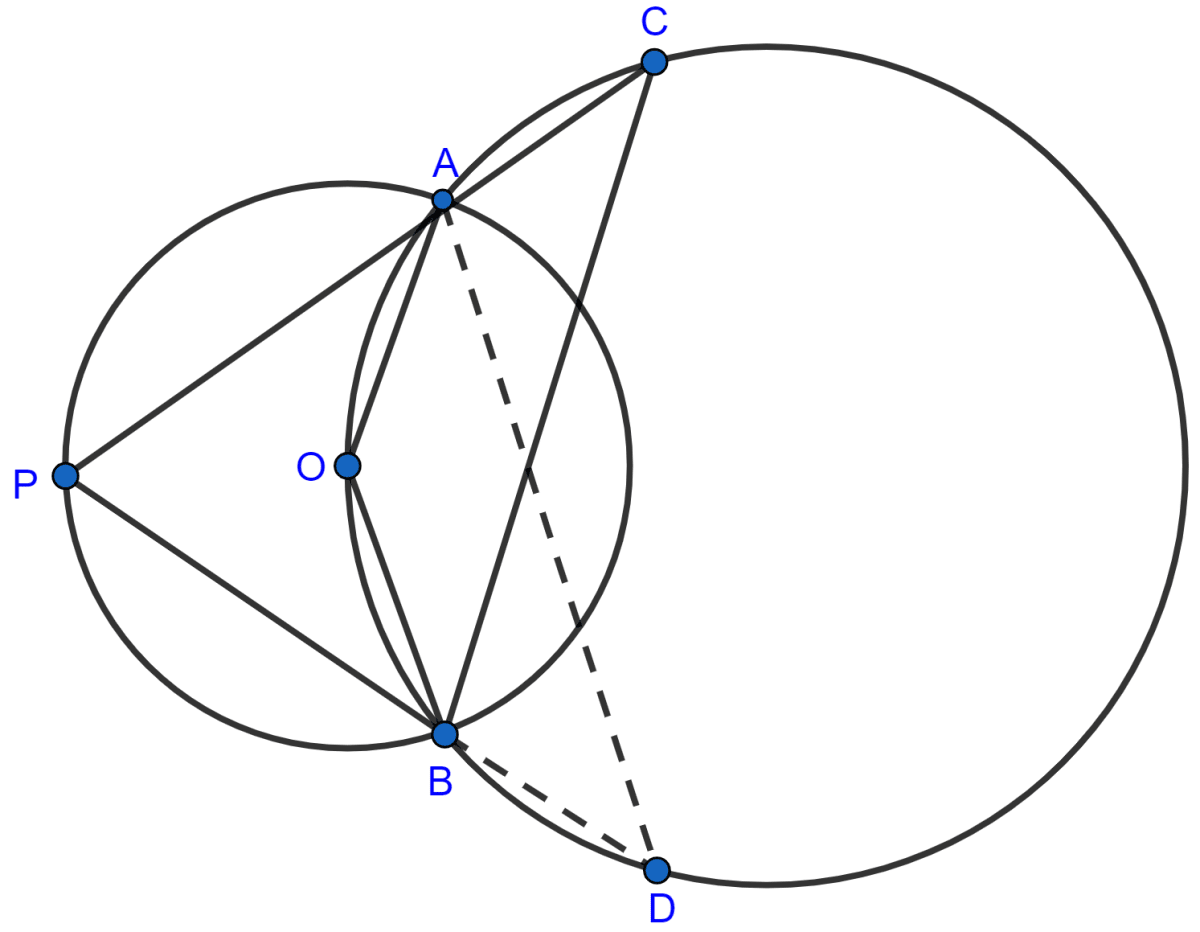
As, angles in same segment are equal.

∴ ∠ADB = ∠ACB = 180° - 2a°.

Hence, ∠ADB = 180° - 2a°.

In the given figure, O is the centre of the circle and ∠ABC = 55°. Calculate the values of x and y.

Answer

We know that,

Angle at the center is double the angle at the circumference subtended by the same chord.

∠AOC = 2∠ABC = 2 × 55° = 110°.

∴ x = 110°.

ABCD is a cyclic quadrilateral.

∴ ∠ADC + ∠ABC = 180°

⇒ y + 55° = 180°

⇒ y = 180° - 55° = 125°.

Hence, x = 110° and y = 125°.

In the given figure, ∠BAD = 65°, ∠ABD = 70°, ∠BDC = 45°

(i) Prove that AC is a diameter of the circle.

(ii) Find ∠ACB

Answer

(i) In ∆ABD,

⇒ ∠DAB + ∠ABD + ∠ADB = 180° [Angle sum property of a triangle]

⇒ 65° + 70° + ∠ADB = 180°

⇒ 135° + ∠ADB = 180°

⇒ ∠ADB = 180° - 135° = 45°

From figure,

⇒ ∠ADC = ∠ADB + ∠BDC = 45° + 45° = 90°.

As the angle in a semicircle is a right angle,

∴ Arc ADC is semi-circle and AC is the diameter.

Hence, proved that AC is the diameter.

(ii) We know that,

Angles in the same segment of a circle are equal.

∴ ∠ACB = ∠ADB = 45°.

Hence, ∠ACB = 45°.

In the given figure, AB is a diameter of the circle. Chord ED is parallel to AB and ∠EAB = 63°. Calculate :

(i) ∠EBA,

(ii) ∠BCD.

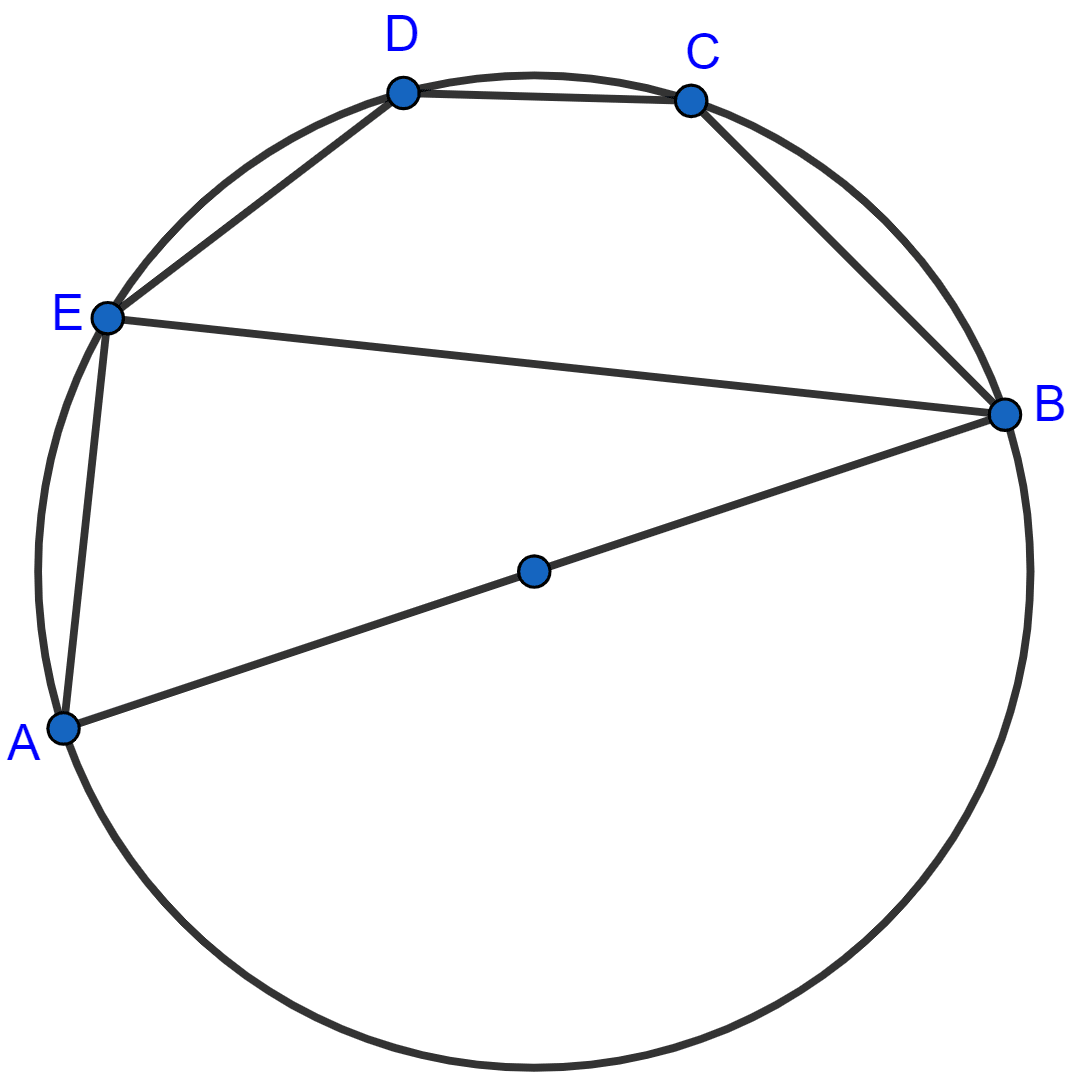
Answer

(i) We know that,

Angle in semi-circle is a right angle.

∴ ∠AEB = 90°.

In △AEB,

⇒ ∠AEB + ∠EBA + ∠EAB = 180°

⇒ 90° + ∠EBA + 63° = 180°

⇒ 153° + ∠EBA = 180°

⇒ ∠EBA = 180° - 153° = 27°.

Hence, ∠EBA = 27°.

(ii) As, AB || ED

∴ ∠DEB = ∠EBA = 27° [Alternate angles]

BCDE is a cyclic quadrilateral.

∴ ∠DEB + ∠BCD = 180° [Sum of opposite angles in a cyclic quadrilateral = 180°.]

⇒ 27° + ∠BCD = 180°

⇒ ∠BCD = 180° - 27° = 153°.

Hence, ∠BCD = 153°.

In the given figure, AB is a diameter of the circle with center O. DO is parallel to CB and ∠DCB = 120°. Calculate :

(i) ∠DAB,

(ii) ∠DBA,

(iii) ∠DBC,

(iv) ∠ADC.

Also, show that the △AOD is an equilateral triangle.

Answer

(i) ABCD is a cyclic quadrilateral.

∴ ∠DCB + ∠DAB = 180° [Sum of opposite angles in a cyclic quadrilateral = 180°.]

⇒ ∠DAB = 180° - ∠DCB

⇒ ∠DAB = 180° - 120° = 60°.

Hence, ∠DAB = 60°.

(ii) We know that,

Angle in a semi-circle is a right angle.

∠ADB = 90°.

In △DAB,

⇒ ∠ADB + ∠DAB + ∠DBA = 180°

⇒ 90° + 60° + ∠DBA = 180°

⇒ 150° + ∠DBA = 180°

⇒ ∠DBA = 180° - 150° = 30°.

Hence, ∠DBA = 30°.

(iii) OD = OB (Radius of circle)

∴ ∠ODB = ∠OBD [Angles opposite to equal sides are equal]

From figure,

∠OBD = ∠DBA = 30°.

∴ ∠ODB = 30°.

As, DO || BC

∴ ∠DBC = ∠ODB = 30° [Alternate angles are equal.]

Hence, ∠DBC = 30°.

(iv) From figure,

∠ABC = ∠ABD + ∠DBC = 30° + 30° = 60°.

In cyclic quadrilateral ABCD,

∴ ∠ADC + ∠ABC = 180° [Sum of opposite angles in a cyclic quadrilateral = 180°.]

⇒ ∠ADC = 180° - ∠ABC

⇒ ∠ADC = 180° - 60° = 120°.

Hence, ∠ADC = 120°.

In △AOD,

OA = OD [Radius of same circle]

∠AOD = ∠DAO [Angles opposite to equal sides are equal]

From figure,

⇒ ∠DAO = ∠DAB = 60°.

∴ ∠AOD = ∠DAO = ∠ADO = 60°

Hence, proved that △AOD is an equilateral triangle.

Calculate the angles x, y and z if :

$\dfrac{x}{3} = \dfrac{y}{4} = \dfrac{z}{5}$

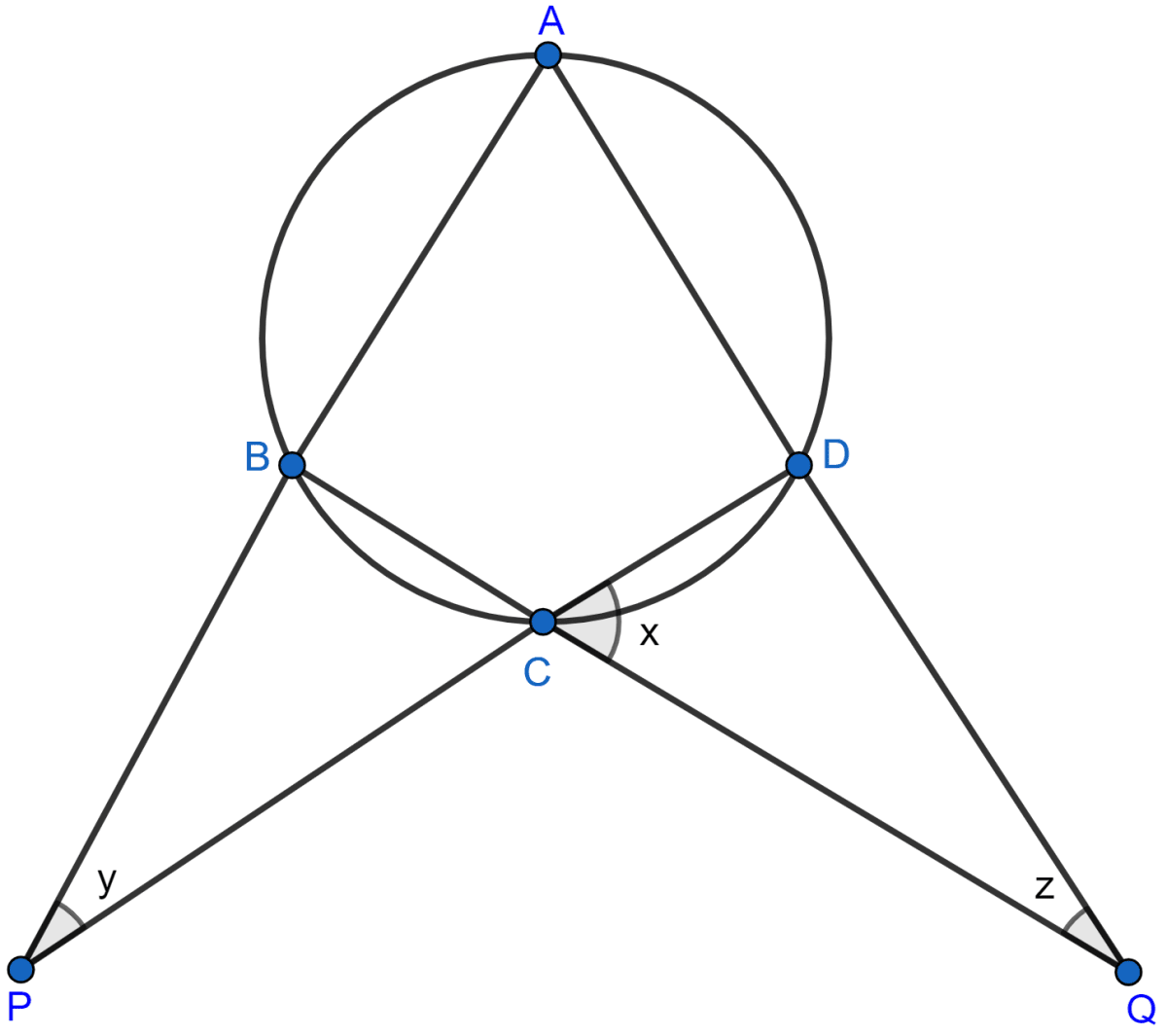
Answer

Let $\dfrac{x}{3} = \dfrac{y}{4} = \dfrac{z}{5}$ = k.

∴ x = 3k, y = 4k and z = 5k.

From figure,

∠BCP = ∠DCQ [Vertically opposite angles are equal.]

Exterior angle of a triangle is equal to the sum of two opposite interior angles.

∠ABC = ∠BCP + ∠BPC = x + y = 3k + 4k = 7k

∠ADC = ∠DCQ + ∠DQC = x + z = 3k + 5k = 8k.

ABCD is a cyclic quadrilateral.

We know that,

⇒ ∠ABC + ∠ADC = 180° [Sum of opposite angles in a cyclic quadrilateral = 180°]

⇒ 8k + 7k = 180°

⇒ 15k = 180°

⇒ k = $\dfrac{180}{15}$ = 12°.

x = 3k = 3 x 12° = 36°

y = 4k = 4 x 12° = 48°

z = 5k = 5 x 12° = 60°.

Hence, x = 36°, y = 48° and z = 60°.

In the given figure, AC is the diameter of the circle with center O. CD and BE are parallel. Angle ∠AOB = 80° and ∠ACE = 10°. Calculate :

(i) Angle BEC,

(ii) Angle BCD,

(iii) Angle CED.

Answer

(i) From figure,

⇒ ∠BOC + ∠BOA = 180° [As AOC is a straight line.]

⇒ ∠BOC + 80° = 180°

⇒ ∠BOC = 180° - 80° = 100°.

We know that,

Angle at the centre is double the angle at the circumference subtended by the same chord.

⇒ ∠BOC = 2∠BEC

⇒ ∠BEC = $\dfrac{1}{2}$∠BOC = $\dfrac{100°}{2}$ = 50°.

Hence, ∠BEC = 50°.

(ii) Given,

DC || EB

∴ ∠DCE = ∠BEC = 50° [Alternate angles are equal]

We know that,

Angle at the centre is double the angle at the circumference subtended by the same chord.

⇒ ∠AOB = 2∠ACB

⇒ ∠ACB = $\dfrac{1}{2}$∠AOB = $\dfrac{80°}{2}$ = 40°.

From figure,

∠BCD = ∠ACB + ∠ACE + ∠DCE = 40° + 10° + 50° = 100°.

Hence, ∠BCD = 100°.

(iii) As sum of opposite angles of cyclic quadrilateral = 180°.

⇒ ∠BED + ∠BCD = 180°

⇒ ∠BED = 180° - ∠BCD = 180° - 100° = 80°.

From figure,

⇒ ∠BED = ∠BEC + ∠CED

⇒ 80° = 50° + ∠CED

⇒ ∠CED = 80° - 50° = 30°.

Hence, ∠CED = 30°.

In the given figure, AE is the diameter of the circle. Write down the numerical value of ∠ABC + ∠CDE. Give reasons for your answer.

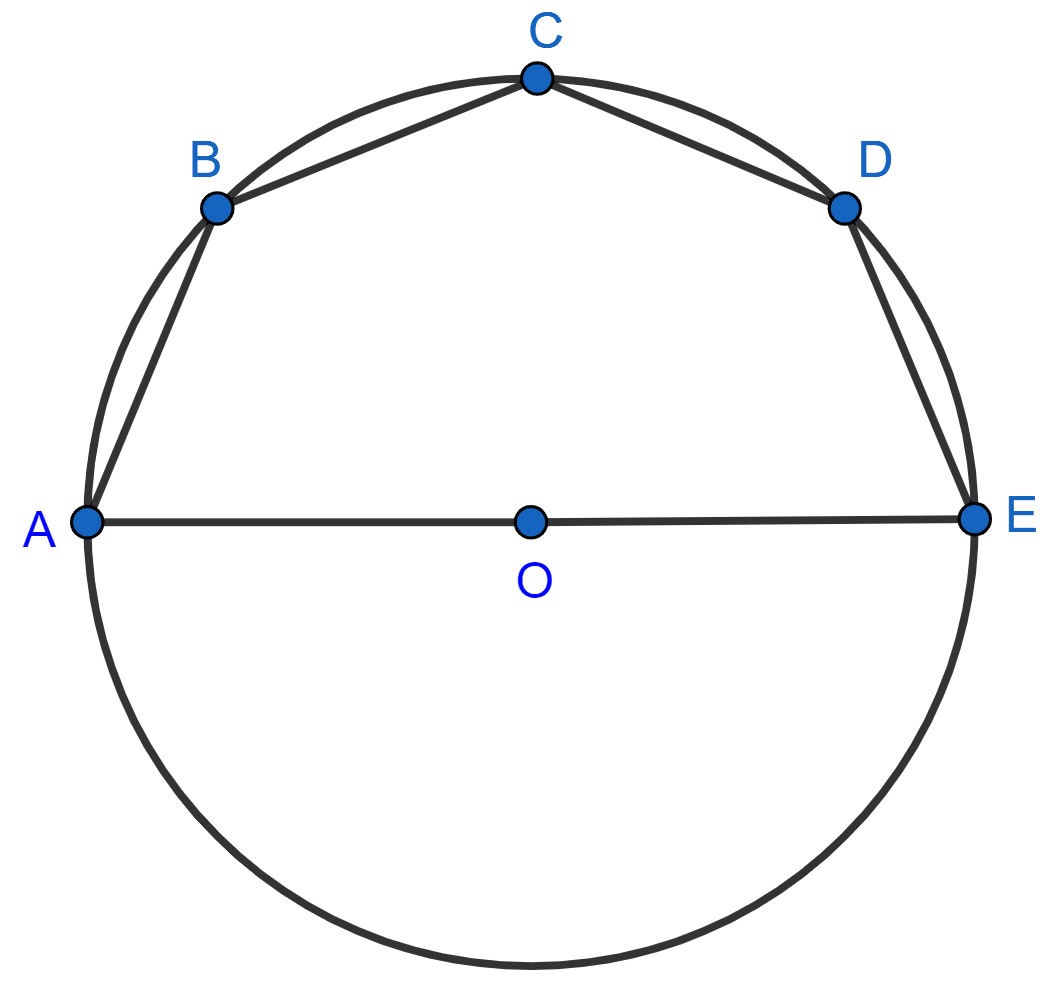
Answer

Join OA, OB, OC, OD.

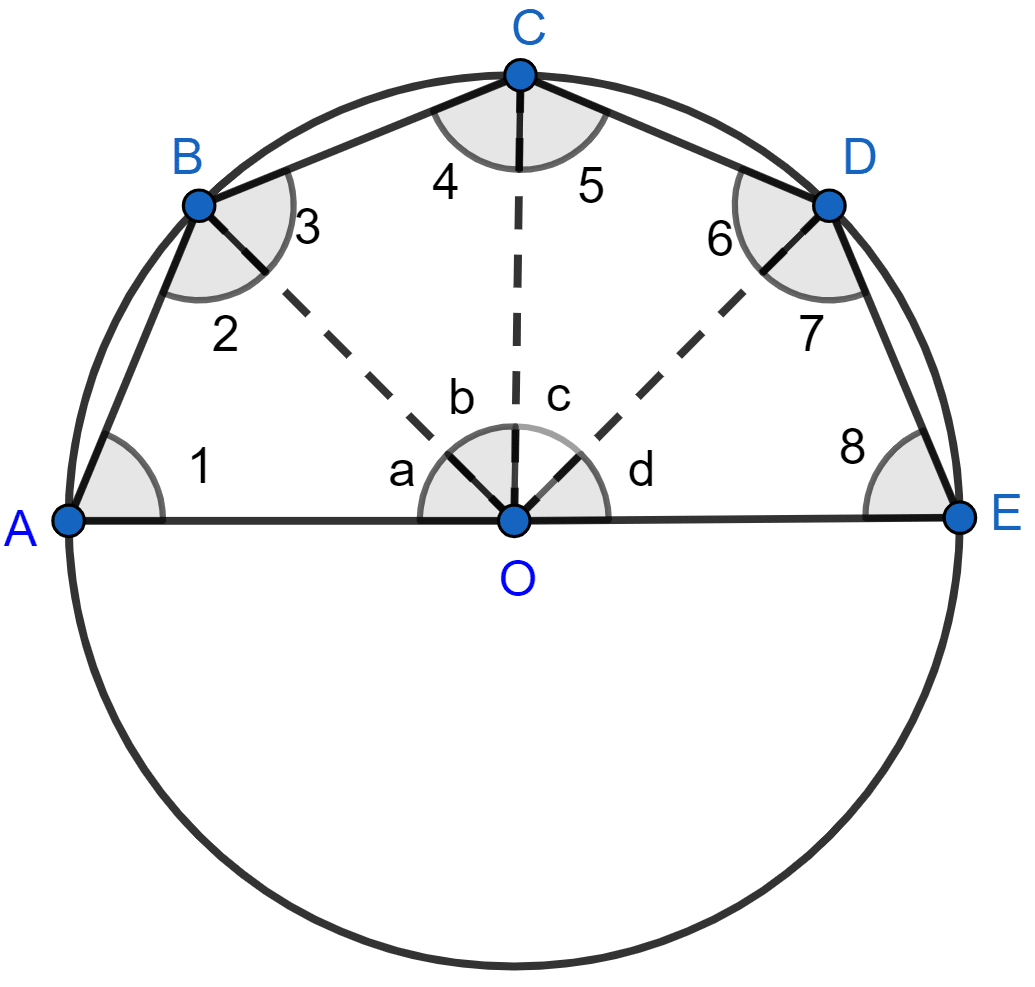
In △OAB,

OA = OB [Radius of same circle]

∠1 = ∠2.

In △OBC,

OB = OC [Radius of same circle]

∠3 = ∠4.

In △OCD,

OC = OD [Radius of same circle]

∠5 = ∠6.

In △ODE,

OD = OE [Radius of same circle]

∠7 = ∠8.

In △OAB,

⇒ ∠1 + ∠2 + ∠a = 180° [By angle sum property of triangle] ..........(1)

In △OBC,

⇒ ∠3 + ∠4 + ∠b = 180° [By angle sum property of triangle] ..........(2)

In △OCD,

⇒ ∠5 + ∠6 + ∠c = 180° [By angle sum property of triangle] ..........(3)

In △ODE,

⇒ ∠7 + ∠8 + ∠d = 180° [By angle sum property of triangle] .........(4)

Adding (1), (2), (3) and (4) we get,

⇒ ∠1 + ∠2 + ∠a + ∠3 + ∠4 + ∠b + ∠5 + ∠6 + ∠c + ∠7 + ∠8 + ∠d + = 180° + 180° + 180° + 180°

⇒ ∠2 + ∠2 + ∠a + ∠3 + ∠3 + ∠b + ∠6 + ∠6 + ∠c + ∠7 + ∠7 + ∠d + = 720°

⇒ 2∠2 + 2∠3 + 2∠6 + 2∠7 + ∠a + ∠b + ∠c + ∠d = 720°

⇒ 2[∠2 + ∠3] + 2[∠6 + ∠7] + 180° = 720° [As ∠a + ∠b + ∠c + ∠d = 180°]

⇒ 2∠ABC + 2∠CDE = 540°

⇒ ∠ABC + ∠CDE = 270°.

Hence, ∠ABC + ∠CDE = 270°.

In the given figure, AOC is a diameter and AC is parallel to ED. If ∠CBE = 64°, calculate ∠DEC.

Answer

Join AB.

∠ABC = 90° [As angle in a semi-circle is a right angle.]

From figure,

∠ABE = ∠ABC - ∠CBE = 90° - 64° = 26°.

As angles in same segment are equal.

∠ACE = ∠ABE = 26°.

Given,

AC || ED

∴ ∠DEC = ∠ACE = 26° [Alternate angles are equal]

Hence, ∠DEC = 26°.

Use the given figure to find :

(i) ∠BAD

(ii) ∠DQB.

Answer

(i) In △ADP,

⇒ ∠PAD + ∠ADP + ∠DPA = 180° [Angle sum property of triangle]

⇒ ∠PAD + 85° + 40° = 180°

⇒ ∠PAD + 125° = 180°

⇒ ∠PAD = 180° - 125° = 55°.

From figure,

⇒ ∠BAD = ∠PAD = 55°.

Hence, ∠BAD = 55°.

(ii) We know that,

Sum of opposite angles in a cyclic quadrilateral = 180°.

⇒ ∠ABC + ∠ADC = 180°

⇒ ∠ABC + 85° = 180°

⇒ ∠ABC = 180° - 85° = 95°.

In △AQB,

⇒ ∠AQB + ∠QAB + ∠ABQ = 180° [Angle sum property of triangle]

⇒ ∠AQB + ∠BAD + ∠ABC = 180° [From figure, ∠QAB = ∠BAD and ∠ABQ = ∠ABC]

⇒ ∠AQB + 55° + 95° = 180°

⇒ ∠AQB + 150° = 180°

⇒ ∠AQB = 180° - 150° = 30°.

From figure,

⇒ ∠DQB = ∠AQB = 30°.

Hence, ∠DQB = 30°.

In the given figure, PQ is a diameter. Chord SR is parallel to PQ. Given that ∠PQR = 58°, Calculate :

(i) ∠RPQ

(ii) ∠STP.

Answer

Join PR.

(i) ∠PRQ = 90° [Angle in semi-circle is a right angle.]

In △PQR,

⇒ ∠RPQ + ∠PRQ + ∠PQR = 180° [Angle sum property of triangle]

⇒ ∠RPQ + 90° + 58° = 180°

⇒ ∠RPQ + 148° = 180°

⇒ ∠RPQ = 180° - 148° = 32°.

Hence, ∠RPQ = 32°.

(ii) As, SR || PQ,

∠PRS = ∠RPQ = 32° [Alternate angles are equal]

In cyclic quadrilateral PRST,

⇒ ∠STP + ∠PRS = 180° [As sum of opposite angles in a cyclic quadrilateral = 180°]

⇒ ∠STP = 180° - ∠PRS = 180° - 32° = 148°.

Hence, ∠STP = 148°.

AB is the diameter of the circle with center O. OD is parallel to BC and ∠AOD = 60°. Calculate the numerical values of :

(i) ∠ABD,

(ii) ∠DBC,

(iii) ∠ADC.

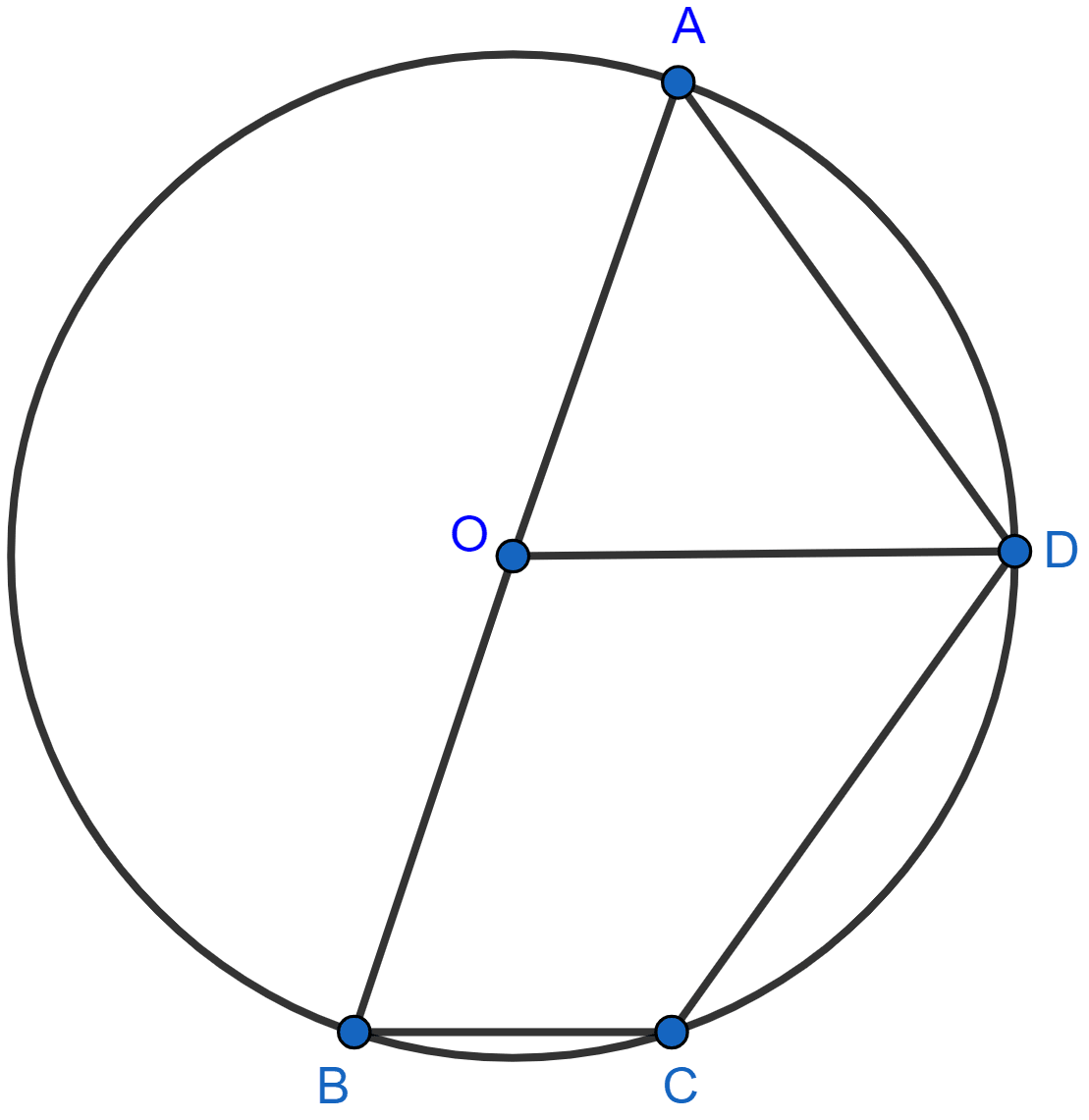
Answer

Join BD.

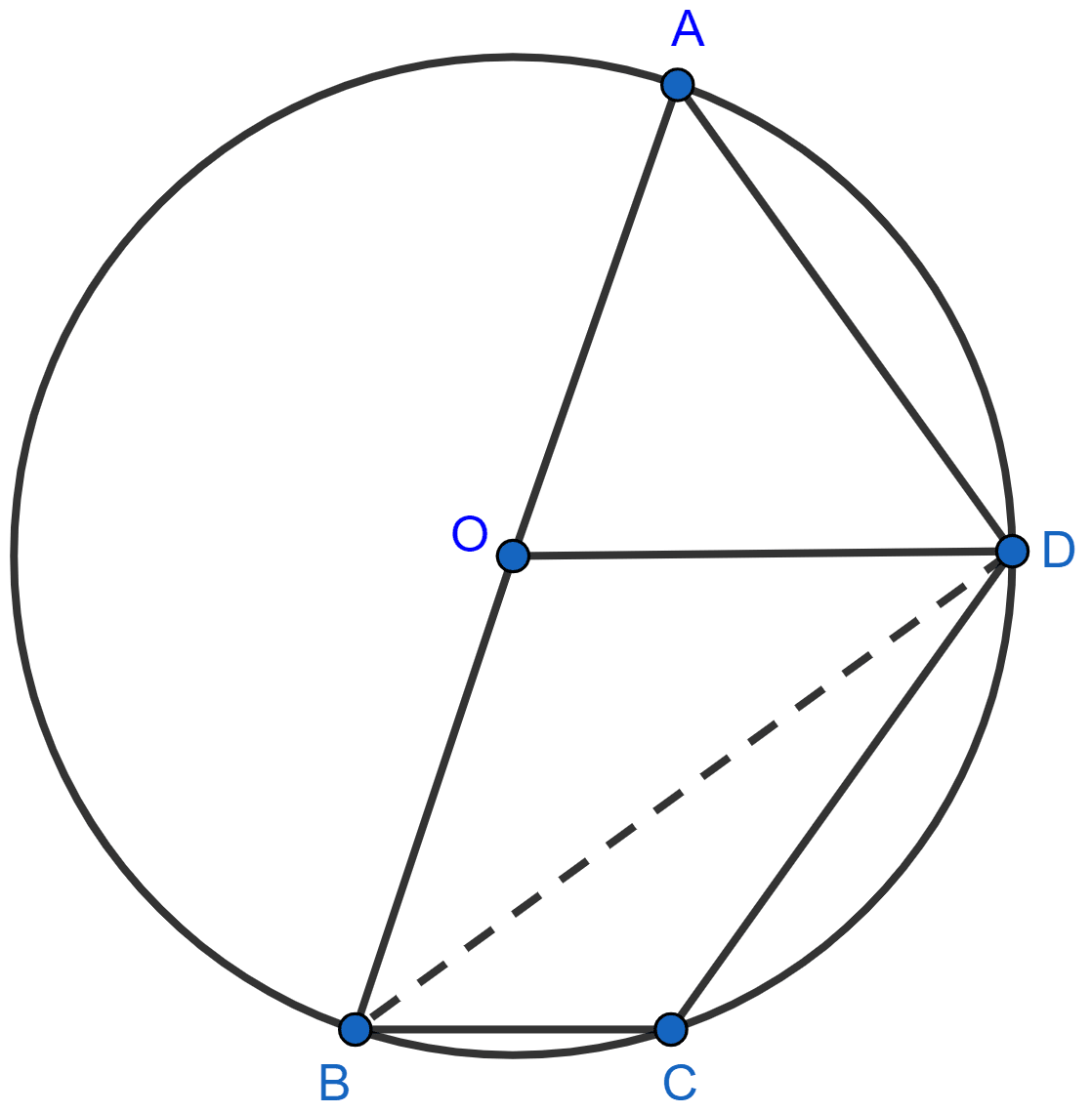
(i) From figure,

⇒ ∠BDA = 90° [Angle in semi-circle is a right angle.]

In △OAD,

OA = OD [Radius of same circle]

∠OAD = ∠ODA = x (let) [As angles opposite to equal side are equal]

In △OAD,

⇒ ∠OAD + ∠ODA + ∠AOD = 180° [Angle sum property of triangle]

⇒ x + x + 60° = 180°

⇒ 2x = 180° - 60°

⇒ 2x = 120°

⇒ x = $\dfrac{120°}{2}$ = 60°.

From figure,

∠ODB = ∠BDA - ∠ADO = 90° - 60° = 30°.

Given, OD || BC

∠DBC = ∠ODB = 30° [Alternate angles are equal]

Hence, ∠DBC = 30°.

(ii) We know that,

Angle in a semi-circle is a right angle.

∴ ∠BDA = 90°.

Since,

∠OAD = ∠ODA = ∠AOD = 60°.

From figure,

⇒ ∠BDA = ∠ODA + ∠ODB

⇒ 90° = 60° + ∠ODB

⇒ ∠ODB = 90° - 60° = 30°.

Given,

OD || BC

∴ ∠DBC = ∠ODB = 30° [Alternate angles are equal].

Hence, ∠DBC = 30°.

(iii) From figure,

∠ABC = ∠ABD + ∠DBC = 30° + 30° = 60°.

Since, sum of opposite nagles in a cyclic quadrilateral = 180°.

∴ ∠ABC + ∠ADC = 180°

⇒ 60° + ∠ADC = 180°

⇒ ∠ADC = 120°.

Hence, ∠ADC = 120°.

In the given figure, the center O of the small circle lies on the circumference of the bigger circle. If ∠APB = 75° and ∠BCD = 40°, find :

(i) ∠AOB,

(ii) ∠ACB,

(iii) ∠ABD,

(iv) ∠ADB.

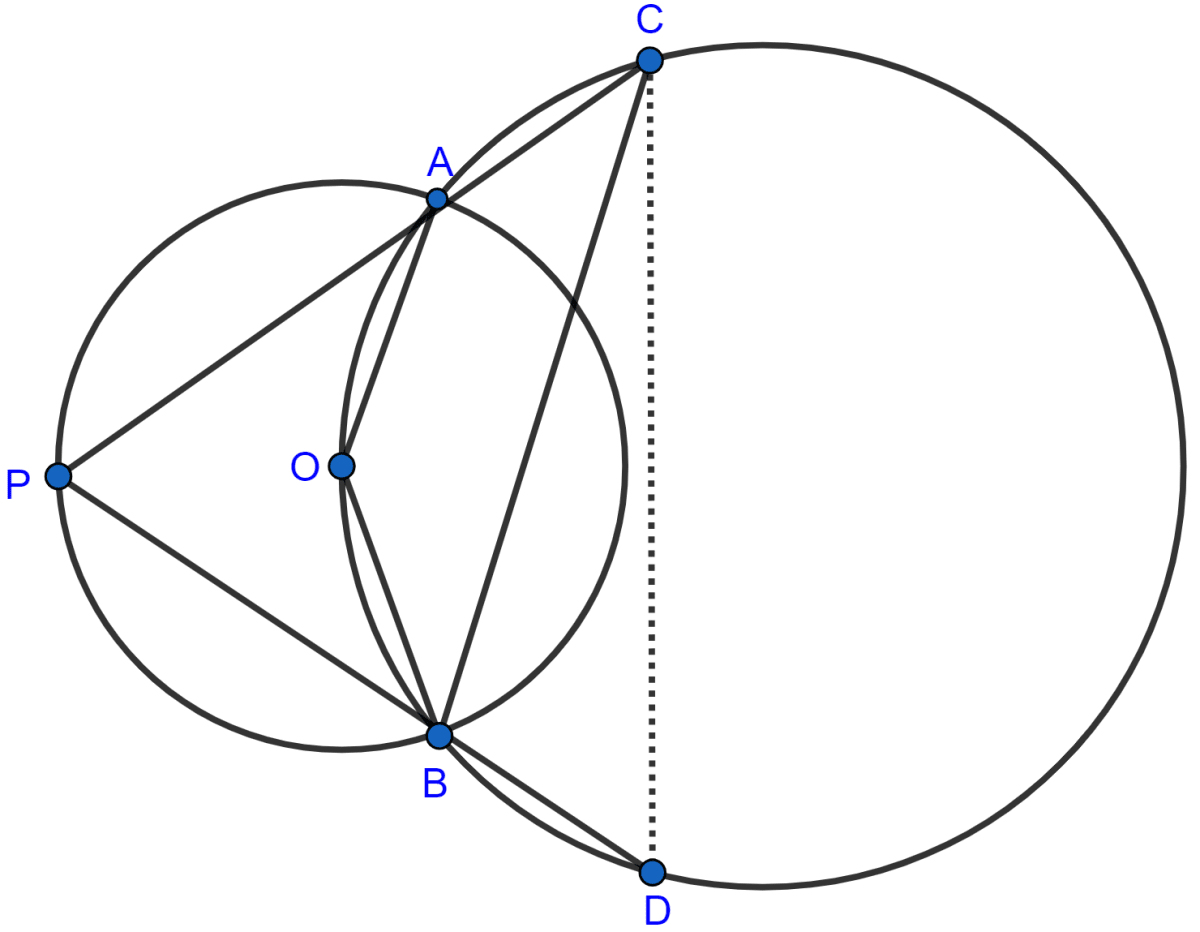
Answer

Join AB and AD.

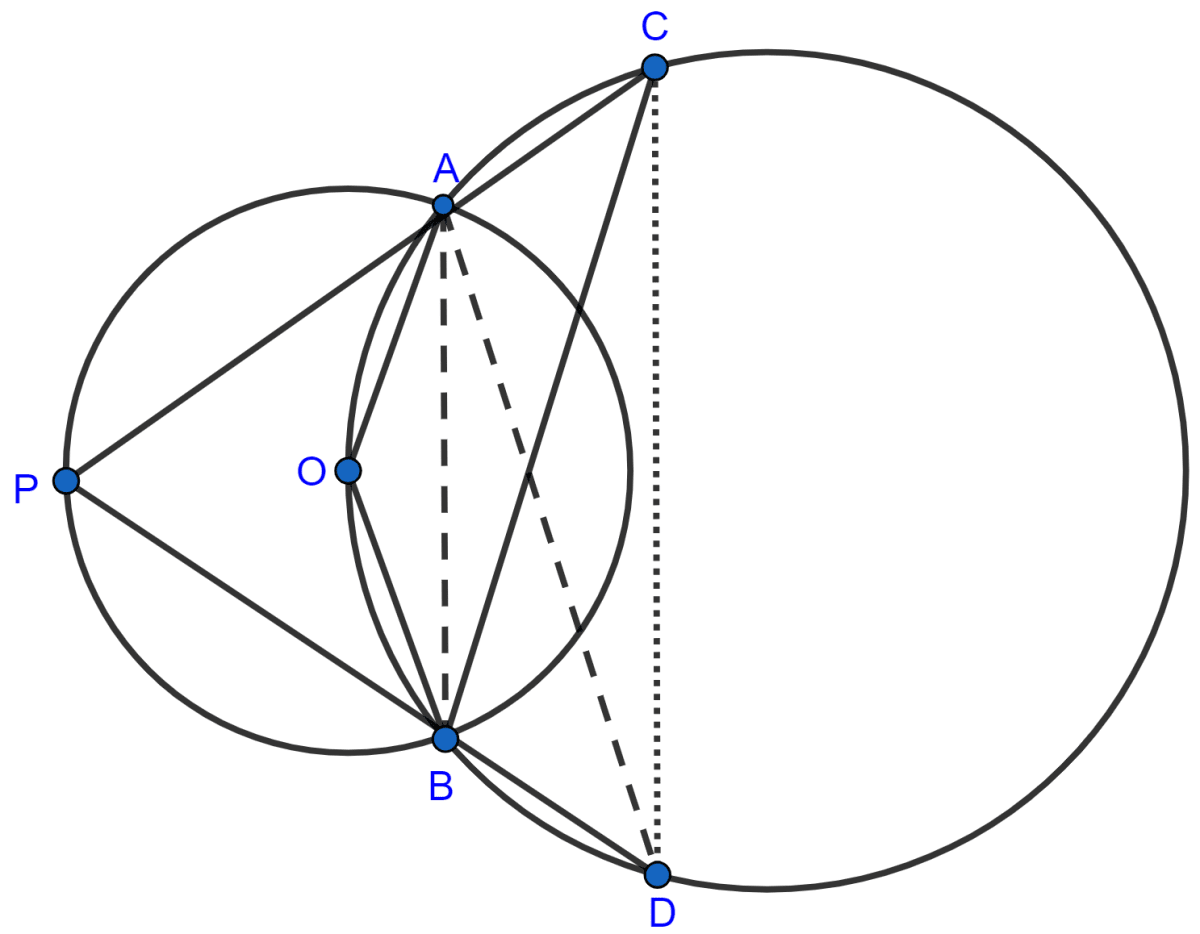
(i) We know that,

Angle which an arc subtends at the center is double that which it subtends at any point on the remaining part of the circumference.

∴ ∠AOB = 2∠APB = 2 × 75° = 150°.

Hence, ∠AOB = 150°.

(ii) We know that,

Sum of opposite angles in a cyclic quadrilateral = 180°.

∴ ∠ACB + ∠AOB = 180°

⇒ ∠ACB + 150° = 180°

⇒ ∠ACB = 180° - 150° = 30°.

Hence, ∠ACB = 30°.

(iii) From figure,

∠ACD = ∠ACB + ∠BCD = 30° + 40° = 70°.

We know that,

Sum of opposite angles in a cyclic quadrilateral = 180°.

In cyclic quadrilateral ABDC,

∴ ∠ABD + ∠ACD = 180°

⇒ ∠ABD + 70° = 180°

⇒ ∠ABD = 180° - 70° = 110°.

Hence, ∠ABD = 110°.

(iv) We know that,

Sum of opposite angles in a cyclic quadrilateral = 180°.

In cyclic quadrilateral AOBD,

∴ ∠ADB + ∠AOB = 180°

⇒ ∠ADB + 150° = 180°

⇒ ∠ADB = 180° - 150° = 30°.

Hence, ∠ADB = 30°.

In the given figure, ∠BAD = 65°, ∠ABD = 70° and ∠BDC = 45°. Find :

(i) ∠BCD

(ii) ∠ACB

Hence, show that AC is a diameter.

Answer

(i) We know that,

Sum of opposite angles in a cyclic quadrilateral = 180°.

In cyclic quadrilateral ABCD,

∴ ∠BCD + ∠BAD = 180°

⇒ ∠BCD + 65° = 180°

⇒ ∠BCD = 180° - 65° = 115°.

Hence, ∠BCD = 115°.

(ii) In △ABD,

⇒ ∠ADB + ∠BAD + ∠DBA = 180° [Angle sum property of triangle]

⇒ ∠ADB + 65° + 70° = 180°

⇒ ∠ADB + 135° = 180°

⇒ ∠ADB = 180° - 135° = 45°.

We know that,

Angles in same segment are equal.

∴ ∠ACB = ∠ADB = 45°.

Hence, ∠ADB = 45°.

From figure,

∠ADC = ∠ADB + ∠BDC = 45° + 45° = 90°.

Since, angle in a semi-circle is a right angle.

Hence, proved that AC is a diameter.

In a cyclic quadrilateral ABCD, ∠A : ∠C = 3 : 1 and ∠B : ∠D = 1 : 5; find each angle of the quadrilateral.

Answer

Let ∠A = 3x and ∠C = x.

In cyclic quadrilateral ABCD,

⇒ ∠A + ∠C = 180° [Sum of opposite angles in a cyclic quadrilateral = 180°]

⇒ 3x + x = 180°

⇒ 4x = 180°

⇒ x = $\dfrac{180°}{4}$ = 45°.

∠A = 3x = 3 x 45 = 135°

∠C = x = 45°.

Let ∠B = y and ∠D = 5y.

In cyclic quadrilateral ABCD,

⇒ ∠B + ∠D = 180° [Sum of opposite angles in a cyclic quadrilateral = 180°]

⇒ y + 5y = 180°

⇒ 6y = 180°

⇒ y = $\dfrac{180°}{6}$ = 30°.

∠B = y = 30°

∠D = 5y = 5 x 30° = 150°.

Hence, ∠A = 135°, ∠B = 30°, ∠C = 45° and ∠D = 150°.

In the given figure, O is the center of the circle and chord AB : chord CD = 3 : 5. If angle AOB = 60°, angle COD is equal to :

1. 60°

2. 120°

3. 90°

4. 100°

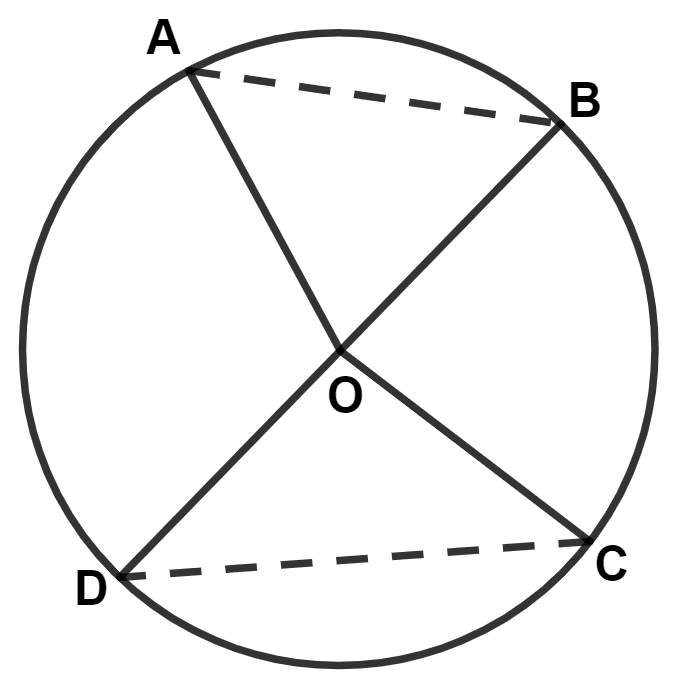
Answer

Given,

Chord AB : Chord CD = 3 : 5

∴ ∠AOB : ∠COD = 3 : 5

⇒ 60° : ∠COD = 3 : 5

⇒ $\dfrac{60°}{∠COD} = \dfrac{3}{5}$

⇒ ∠COD = $\dfrac{60° \times 5}{3} = \dfrac{300°}{3}$ = 100°.

Hence, Option 4 is the correct option.

In the given figure, O is the center of the circle and angle OAB = 55°, then angle ACB is equal to :

1. 55°

2. 35°

3. 70°

4. 30°

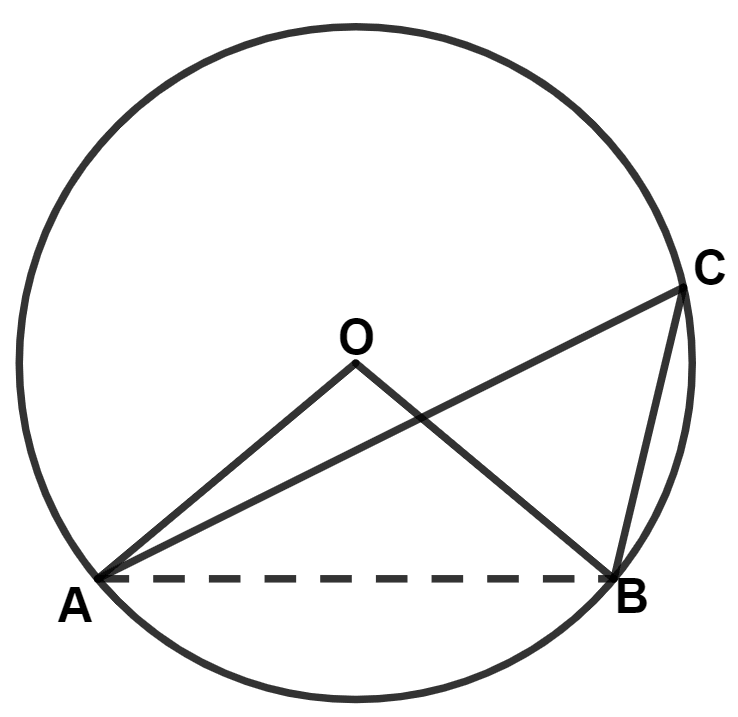
Answer

From figure,

In △OAB,

OA = OB (Radius of same circle)

We know that,

Angles opposite to equal sides are equal.

∴ ∠OBA = ∠OAB = 55°

By angle sum property of triangle,

⇒ ∠OBA + ∠OAB + ∠AOB = 180°

⇒ 55° + 55° + ∠AOB = 180°

⇒ ∠AOB + 110° = 180°

⇒ ∠AOB = 180° - 110° = 70°.

We know that,

The angle which an arc of a circle subtends at the center is double that which it subtends at any point on the remaining part of the circumference.

∴ ∠AOB = 2∠ACB

∠ACB = $\dfrac{∠AOB}{2} = \dfrac{70°}{2}$ = 35°.

Hence, Option 2 is the correct option.

In the given figure, O is the center of a circle. AB is the side of a square and BC is side of a regular hexagon. Also arc AD = arc CD. Angle DOC is equal to :

1. 150°

2. 105°

3. 130°

4. 210°

Answer

Join OD.

Since, AB is the side of square.

∴ ∠AOB = $\dfrac{360°}{4}$ = 90°.

Since, BC is the side of regular hexagon.

∴ ∠BOC = $\dfrac{360°}{6}$ = 60°.

We know that,

Equal arcs subtends equal angles at the center.

Since, arc AD = arc CD

∴ ∠AOD = ∠COD = x (let)

From figure,

⇒ ∠AOD + ∠COD + ∠AOB + ∠BOC = 360°

⇒ x + x + 90° + 60° = 360°

⇒ 2x + 150° = 360°

⇒ 2x = 360° - 150°

⇒ 2x = 210°

⇒ x = $\dfrac{210°}{2}$ = 105°.

Hence, Option 2 is the correct option.

In the given figure, O is the center of the circle, AB is side of a regular pentagon, then angle ACB is equal to :

1. 36°

2. 72°

3. 50°

4. 40°

Answer

Join OA and OB.

Given,

AB is side of a regular pentagon.

∴ ∠AOB = $\dfrac{360°}{5}$ = 72°.

We know that,

The angle which an arc of a circle subtends at the center is double that which it subtends at any point on the remaining part of the circumference.

∴ ∠AOB = 2∠ACB

∠ACB = $\dfrac{∠AOB}{2} = \dfrac{72°}{2}$ = 36°.

Hence, Option 1 is the correct option.

In the given figure, O is the center of the circle, chords AB, CD and EF are equal whereas chords BC, DE and FA are separately equal. The angle AOC is equal to :

1. 80°

2. 100°

3. 90°

4. 120°

Answer

Given,

Chords AB, CD and EF are equal.

∴ ∠AOB = ∠COD = ∠EOF = x (let)

Chords BC, DE and FA are equal.

∴ ∠BOC = ∠DOE = ∠AOF = y (let)

From figure,

⇒ ∠AOB + ∠COD + ∠EOF + ∠BOC + ∠DOE + ∠AOF = 360°

⇒ x + x + x + y + y + y = 360°

⇒ 3x + 3y = 360°

⇒ 3(x + y) = 360°

⇒ x + y = $\dfrac{360°}{3}$

⇒ x + y = 120°

From figure,

∠AOC = ∠AOB + ∠BOC = x + y = 120°.

Hence, Option 4 is the correct option.

In a cyclic-trapezium, the non-parallel sides are equal and the diagonals are also equal. Prove it.

Answer

Let ABCD be the cyclic trapezium in which AB || DC, AC and BD are the diagonals.

It's seen that chord AD subtends ∠ABD and chord BC subtends ∠BDC at the circumference of the circle.

But, ∠ABD = ∠BDC [Alternate angles, as AB || DC with BD as the transversal]

∴ Chord AD must be equal to chord BC [As equal chord subtends equal angles at circumference]

From figure,

⇒ ∠B + ∠D = 180° [As, sum of opposite angles in a cyclic quadrilateral = 180°]

Also,

⇒ ∠B + ∠C = 180° [Sum of co-interior angles = 180° (As, AB || CD)]

∴ ∠B + ∠C = ∠B + ∠D

⇒ ∠C = ∠D

Now, in ∆ADC and ∆BCD

⇒ DC = DC [Common]

⇒ ∠C = ∠D [Proved above]

⇒ AD = BC [Proved above]

Hence, by SAS criterion of congruence

∆ADC ≅ ∆BCD

∴ AC = BD [By C.P.C.T.]

Hence, proved above AC = BD and AD = BC.

In the following figure, AD is the diameter of the circle with centre O. Chords AB, BC and CD are equal. If ∠DEF = 110°, calculate :

(i) ∠AEF, (ii) ∠FAB.

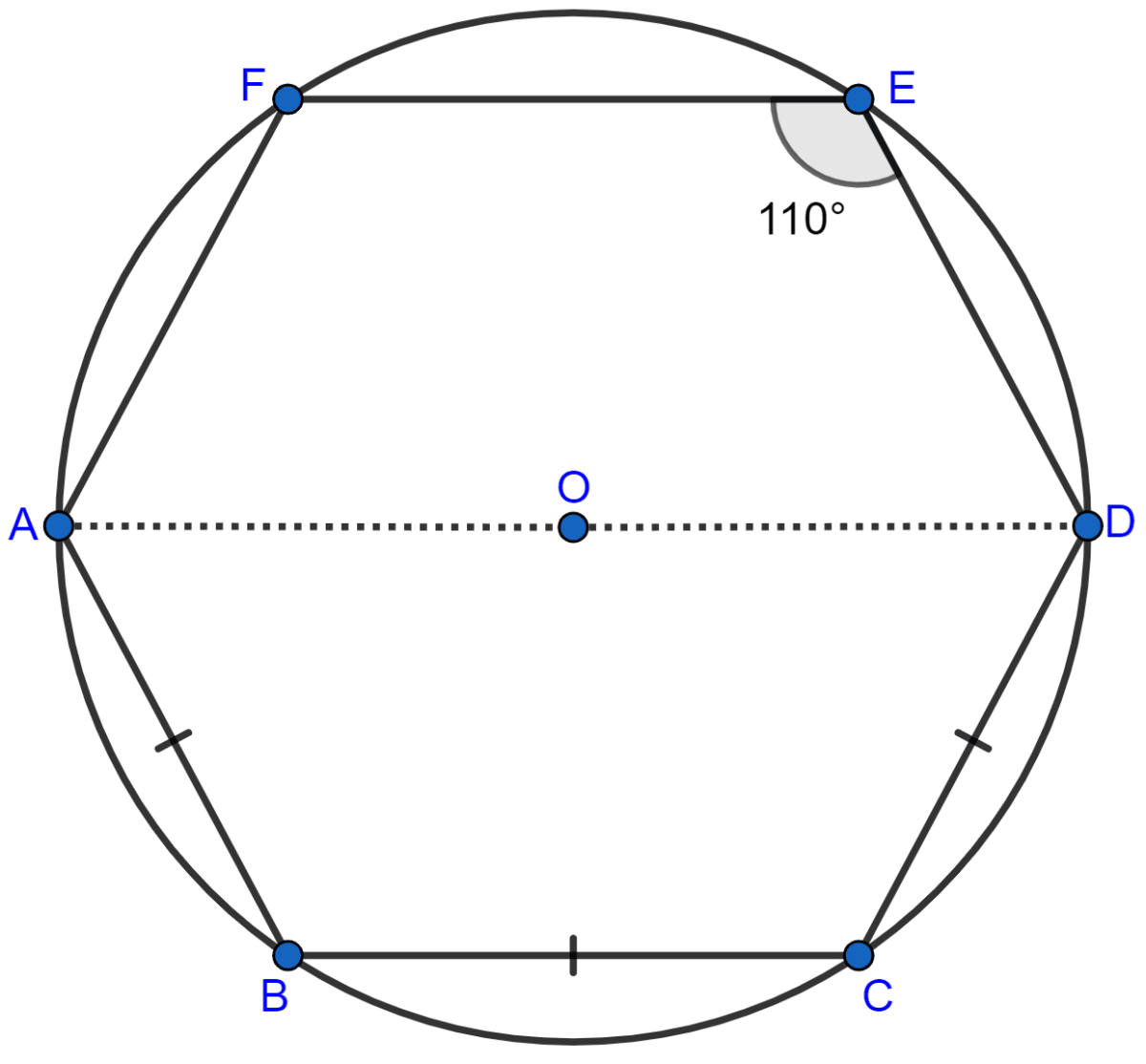
Answer

Join AE, OB and OC.

(i) As AOD is the diameter

∠AED = 90° [Angle in a semi-circle is a right angle]

But, given ∠DEF = 110°

So,

∠AEF = ∠DEF - ∠AED = 110° - 90° = 20°.

Hence, ∠AEF = 20°.

(ii) Also given, Chord AB = Chord BC = Chord CD

So,

∠AOB = ∠BOC = ∠COD [Equal chords subtends equal angles at the centre]

From figure,

⇒ ∠AOB + ∠BOC + ∠COD = 180° [AOD is a straight line]

⇒ ∠AOB = ∠BOC = ∠COD = $\dfrac{180°}{3}$ = 60°

Now, in ∆OAB we have

OA = OB [Radii of same circle]

So, ∠OAB = ∠OBA [Angles opposite to equal sides are equal]

In ∆OAB,

⇒ ∠OAB + ∠OBA + ∠AOB = 180° [By angle sum property of triangle]

⇒ ∠OAB + ∠OBA + 60° = 180°

⇒ ∠OAB + ∠OBA = 180° - 60° = 120°.

Since, ∠OAB = ∠OBA

∴ ∠OAB = ∠OBA = $\dfrac{120°}{2}$ = 60°.

Now, in cyclic quadrilateral ADEF

⇒ ∠DEF + ∠DAF = 180° [As sum of opposite angles in cyclic quadrilateral = 180°]

⇒ ∠DAF = 180° - ∠DEF

⇒ ∠DAF = 180° - 110° = 70°.

From figure,

∠FAB = ∠DAF + ∠OAB = 70° + 60° = 130°.

Hence, ∠FAB = 130°.

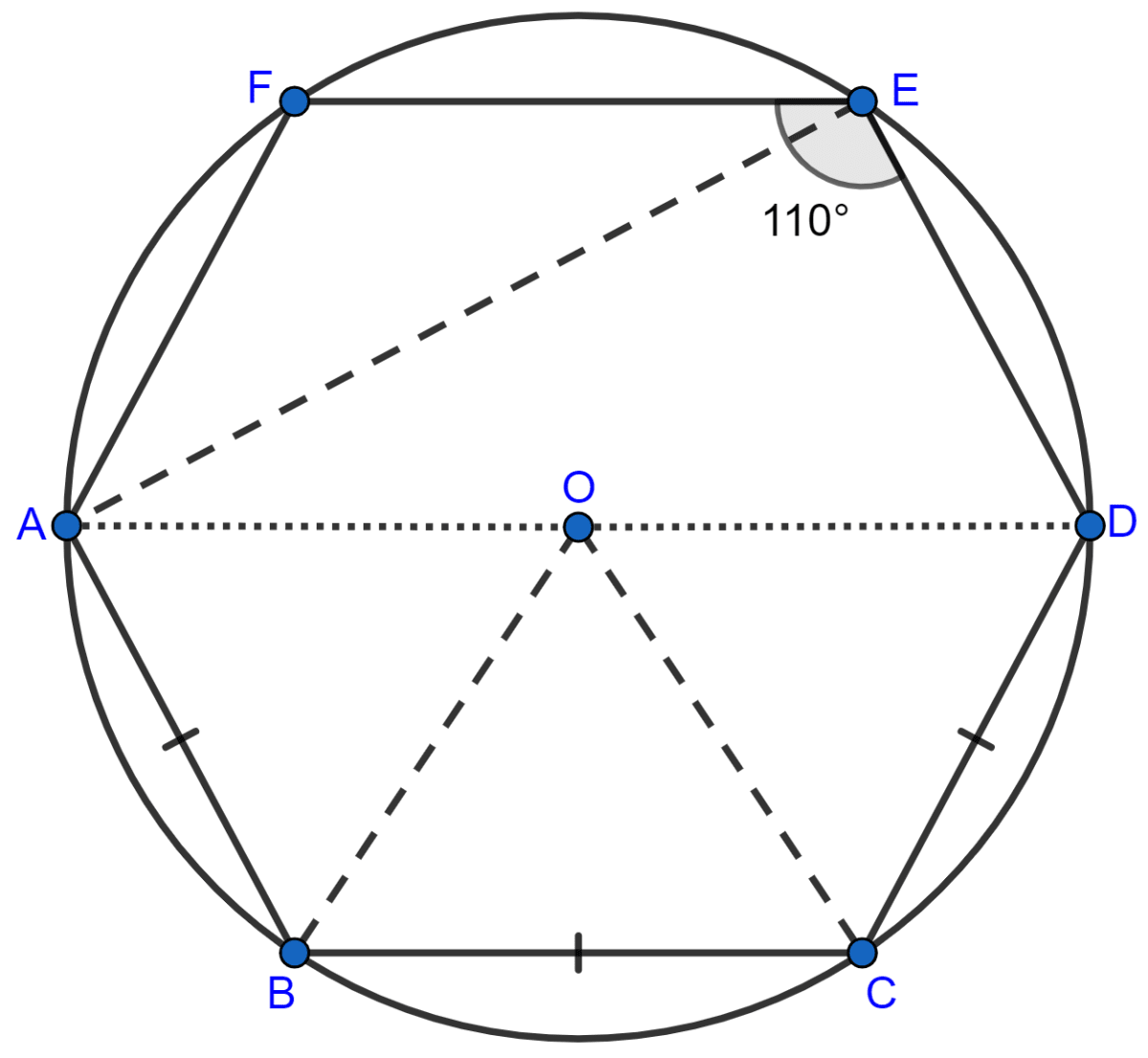
If two sides of a cyclic-quadrilateral are parallel; prove that :

(i) its other two sides are equal.

(ii) its diagonals are equal.

Answer

Let ABCD is a cyclic quadrilateral in which AB || DC. AC and BD are its diagonals.

As AB || DC (given)

∠DCA = ∠CAB [Alternate angles are equal]

Chord AD subtends ∠DCA and chord BC subtends ∠CAB at the circumference of the circle.

and

∠DCA = ∠CAB

We know that,

If the angles subtended by 2 chords on the circumference of the circle are equal, then the lengths of the chords are also equal.

∴ chord AD = chord BC or AD = BC.

Hence, proved that AD = BC.

(ii) From figure,

⇒ ∠A + ∠C = 180° [As, sum of opposite angles in a cyclic quadrilateral = 180°]

Also,

⇒ ∠B + ∠C = 180° [Sum of co-interior angles = 180° (As, AB || CD)]

∴ ∠B + ∠C = ∠A + ∠C

⇒ ∠B = ∠A

In ∆ABC and ∆ADB

⇒ AB = AB [Common]

⇒ ∠B = ∠A [Proved above]

⇒ BC = AD [Proved above]

Hence, by SAS criterion of congruence

∆ACB ≅ ∆ADB

∴ AC = BD [By C.P.C.T.]

Hence, proved that AC = BC.

The given figure show a circle with centre O. Also, PQ = QR = RS and ∠PTS = 75°.

Calculate:

(i) ∠POS,

(ii) ∠QOR,

(iii) ∠PQR.

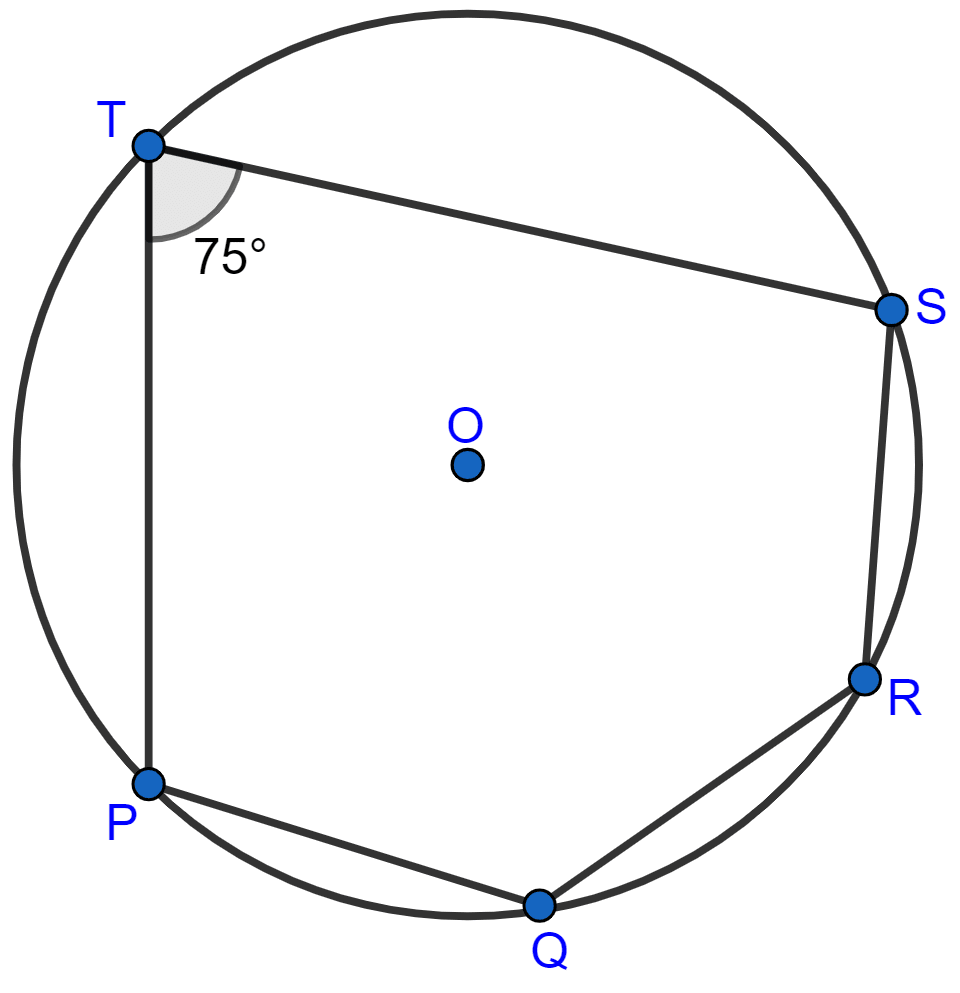
Answer

Join OP, OQ, OR and OS.

Given, PQ = QR = RS

∴ ∠POQ = ∠QOR = ∠ROS = x (let) [Equal chords subtends equal angles at the centre]

Arc PQRS subtends ∠POS at the centre and ∠PTS at the circumference of the circle.

Thus,

∠POS = 2 x ∠PTS = 2 x 75° = 150° [As angle subtended at the centre by the arc is double that it subtends at any point on the circumference of the circle.]

⇒ ∠POQ + ∠QOR + ∠ROS = 150°

⇒ x + x + x = 150°

⇒ 3x = 150°

⇒ x = $\dfrac{150°}{3}$ = 50°.

In ∆OPQ we have,

⇒ OP = OQ [Radii of the same circle]

⇒ ∠OPQ = ∠OQP = y (let) [Angles opposite to equal sides are equal]

In ∆OPQ,

⇒ ∠OPQ + ∠OQP + ∠POQ = 180°

⇒ ∠OPQ + ∠OQP + 50° = 180°

⇒ ∠OPQ + ∠OQP = 180° - 50°

⇒ ∠OPQ + ∠OQP = 130°

⇒ 2y = 130°

⇒ y = $\dfrac{130°}{2}$ = 65°

⇒ ∠OPQ = ∠OQP = y = 65°.

In ∆OQR we have,

⇒ OQ = OR [Radii of the same circle]

⇒ ∠OQR = ∠ORQ = z (let) [Angles opposite to equal sides are equal]

In ∆OQR

⇒ ∠OQR + ∠ORQ + ∠QOR = 180°

⇒ z + z + 50° = 180°

⇒ 2z = 180° - 50°

⇒ 2z = 130°

⇒ z = $\dfrac{130°}{2}$ = 65°

⇒ ∠OQR = ∠ORQ = z = 65°.

(i) Hence, ∠POS = 150°.

(ii) Hence, ∠QOR = 50°.

(iii) From figure,

∠PQR = ∠PQO + ∠OQR = 65° + 65° = 130°.

Hence, ∠PQR = 130°.

In the given figure, AB is a side of a regular six-sided polygon and AC is a side of a regular eight-sided polygon inscribed in the circle with centre O. Calculate the sizes of :

(i) ∠AOB,

(ii) ∠ACB,

(iii) ∠ABC.

Answer

Join OC.

(i) We know that,

Each side of a regular hexagon, inscribed in a circle subtends an angle of 60° at the centre.

⇒ ∠AOB = 60°.

Hence, ∠AOB = 60°.

(ii) We know that,

Angle at the centre is twice the angle at remaining circumference.

∴ ∠AOB = 2∠ACB

⇒ ∠ACB = $\dfrac{1}{2}$∠AOB = $\dfrac{1}{2} \times 60°$ = 30°.

Hence, ∠ACB = 30°.

(iii) Since AC is the side of a regular octagon,

∠AOC = $\dfrac{360°}{8}$ = 45°.

Again, arc AC subtends ∠AOC at the centre and ∠ABC at the remaining part of the circle.

∴ ∠AOC = 2∠ABC

∴ ∠ABC = $\dfrac{1}{2}$ x ∠AOC = $\dfrac{1}{2}$ x 45° = 22.5°

Hence, ∠ABC = 22.5°.

In a regular pentagon ABCDE, inscribed in a circle; find the ratio between angle EDA and angle ADC.

Answer

Regular pentagon ABCDE inscribed in a circle is shown in the figure below:

We know that,

Angle at the centre is twice the angle at remaining circumference.

∴ ∠AOE = 2∠ADE

⇒ ∠ADE = $\dfrac{1}{2}$∠AOE

As ∠AOE is subtended by AE which is a side of a regular pentagon inscribed in a circle,

∴ ∠AOE = $\dfrac{360°}{5}$ = 72°

⇒ ∠ADE = $\dfrac{1}{2}$∠AOE = $\dfrac{1}{2} \times 72°$ = 36°.

We know that,

Each side of interior angle of a regular pentagon = 108°.

From figure,

⇒ ∠ADC = ∠EDC - ∠ADE = 108° - 36° = 72°.

∴ ∠ADE : ∠ADC = 36° : 72° = 1 : 2.

Hence, the ratio between angle EDA and angle ADC = 1 : 2.

In the given figure, AB = BC = CD and ∠ABC = 132°. Calculate :

(i) ∠AEB,

(ii) ∠AED,

(iii) ∠COD.

Answer

(i) Join EB and EC.

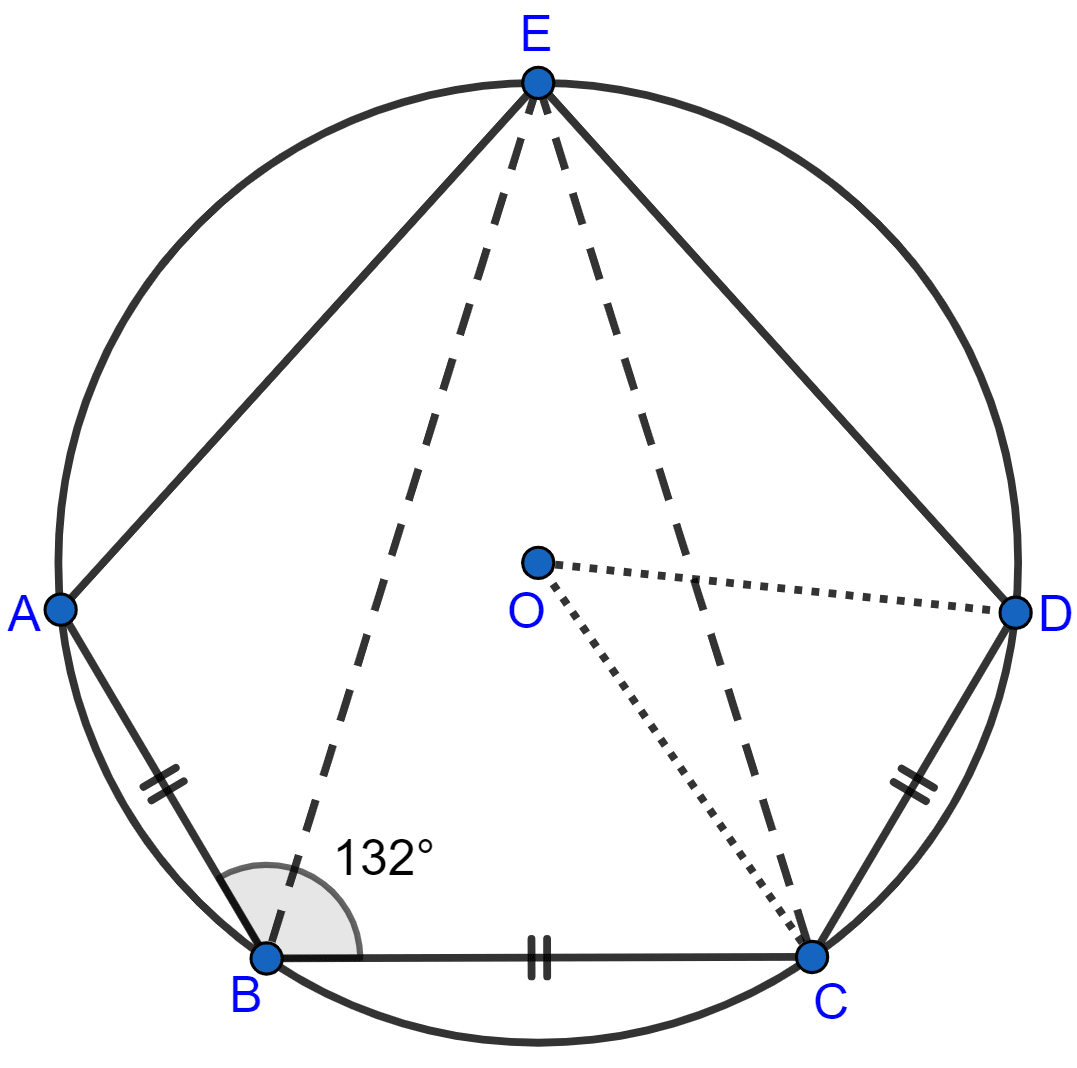
In cyclic quadrilateral ABCE,

⇒ ∠ABC + ∠AEC = 180° [Sum of opposite angles in cyclic quadrilateral = 180°]

⇒ 132° + ∠AEC = 180°

⇒ ∠AEC = 180° - 132° = 48°.

Since, AB = BC.

We know that,

Angle which an arc subtends at the center is double that which it subtends at any point on the remaining part of the circumference.

∴ ∠AEB = $\dfrac{1}{2}$∠AEC

= $\dfrac{1}{2} \times 48°$ = 24°.

Hence, ∠AEB = 24°.

(ii) We know that,

Equal chords subtend equal angles at the circumference of the circle.

∠AEB = ∠BEC = ∠CED = 24°

∠AED = ∠AEB + ∠BEC + ∠CED = 24° + 24° + 24° = 72°.

Hence, ∠AED = 72°.

(iii) We know that,

Angle which an arc subtends at the center is double that which it subtends at any point on the remaining part of the circumference.

∴ ∠COD = 2∠CED = 2 × 24° = 48°.

Hence, ∠COD = 48°.

In the figure, O is the centre of the circle and the length of arc AB is twice the length of arc BC. If angle AOB = 108°, find :

(i) ∠CAB,

(ii) ∠ADB.

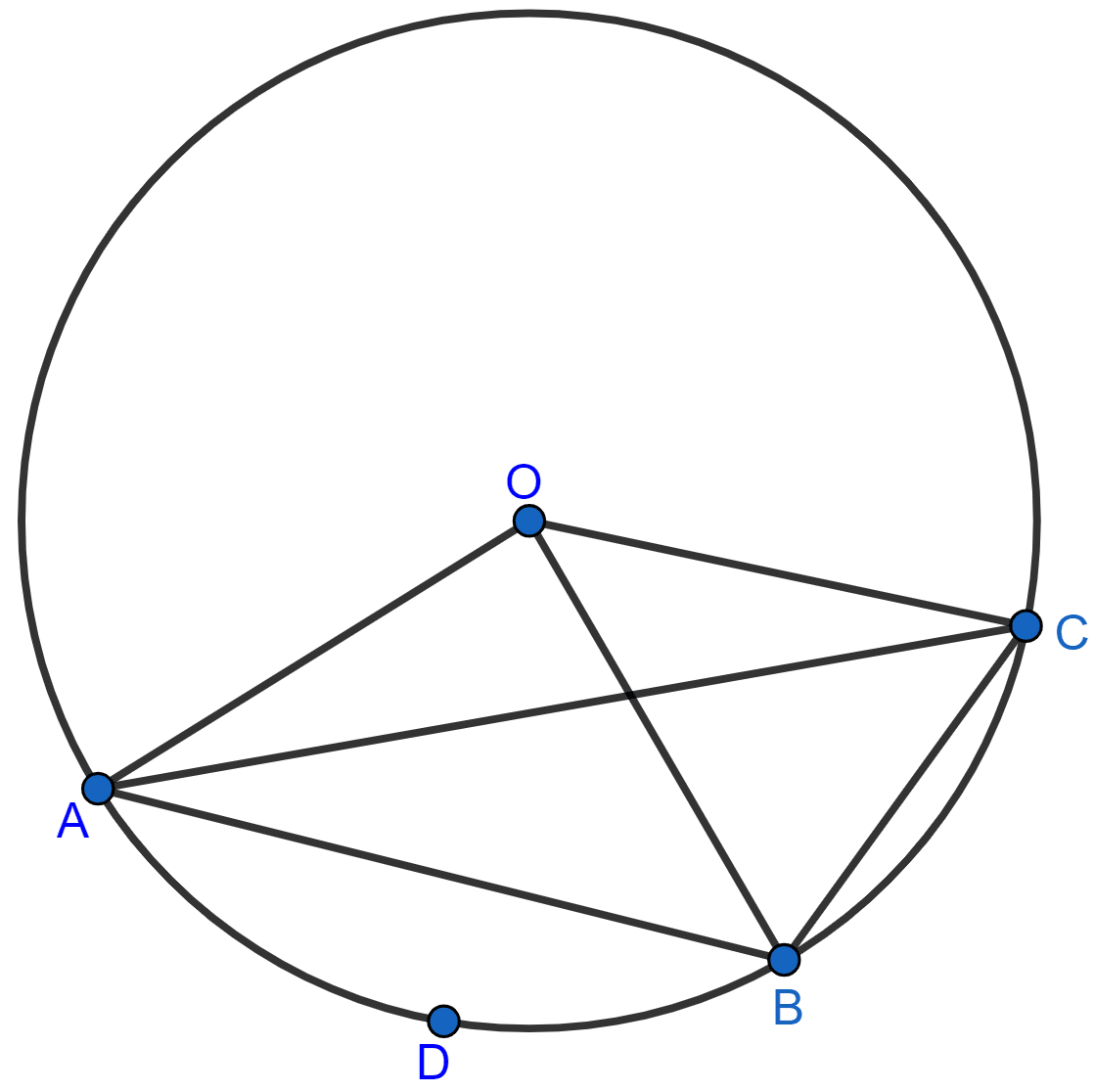
Answer

Join AD and BD.

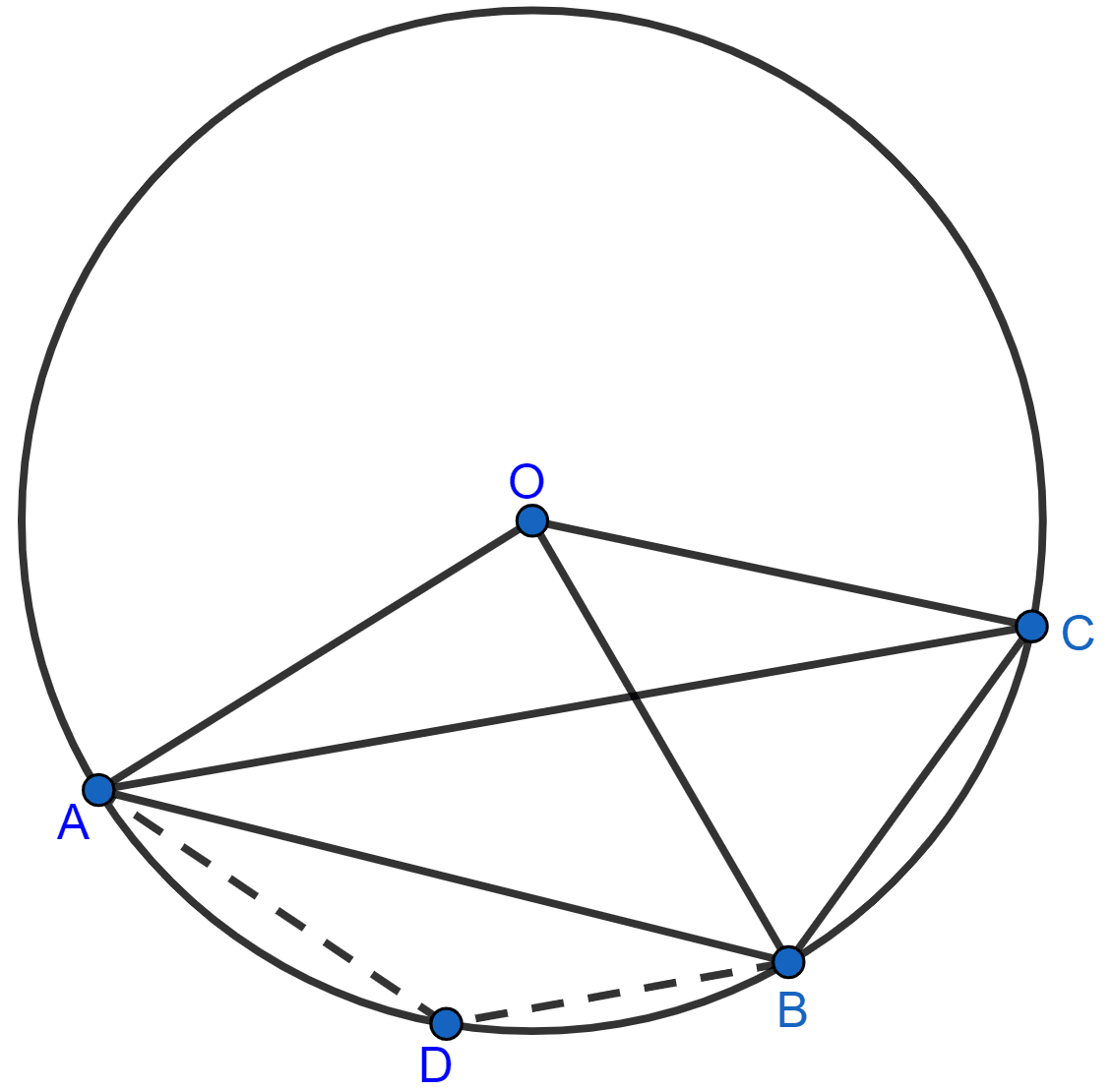
(i) Given,

⇒ arc AB = 2 arc BC

⇒ ∠AOB = 2∠BOC

⇒ ∠BOC = $\dfrac{1}{2}$∠AOB = $\dfrac{1}{2} \times 108°$ = 54°.

We know that,

Angle which an arc subtends at the center is double that which it subtends at any point on the remaining part of the circumference.

∴ ∠BOC = 2∠CAB

⇒ ∠CAB = $\dfrac{1}{2}$∠BOC = $\dfrac{1}{2} \times 54°$ = 27°.

Hence, ∠CAB = 27°.

(ii) Arc AB subtends ∠AOB at the centre and ∠ACB at the remaining part of the circle.

∴ ∠AOB = 2∠ACB

∠ACB = $\dfrac{1}{2}$∠AOB = $\dfrac{1}{2} \times 108°$ = 54°.

In cyclic quadrilateral ADBC,

⇒ ∠ADB + ∠ACB = 180° [As sum of opposite angles in cyclic quadrilateral = 180°]

⇒ ∠ADB + 54° = 180°

⇒ ∠ADB = 180° - 54° = 126°.

Hence, ∠ADB = 126°.

The figure shows a circle with centre O. AB is the side of regular pentagon and AC is the side of regular hexagon.

Find the angles of triangle ABC.

Answer

Join OA, OB and OC.

Since, AB is the side of regular pentagon,

∠AOB = $\dfrac{360°}{5}$ = 72°.

Since, AC is the side of regular hexagon,

∠AOC = $\dfrac{360°}{6}$ = 60°.

From figure,

⇒ ∠AOB + ∠AOC + reflex∠BOC = 360°

⇒ 72° + 60° + reflex∠BOC = 360°

⇒ reflex∠BOC + 132° = 360°

⇒ reflex∠BOC = 360° - 132° = 228°.

We know that,

Angle which an arc subtends at the center is double that which it subtends at any point on the remaining part of the circumference.

Arc BC subtends ∠BOC at the centre and ∠BAC at the remaining part of the circle.

∴ ∠BOC = 2∠BAC

⇒ ∠BAC = $\dfrac{1}{2}∠BOC = \dfrac{1}{2} \times 228°$ = 114°.

Arc AC subtends ∠AOC at the centre and ∠ABC at the remaining part of the circle.

∴ ∠AOC = 2∠ABC

⇒ ∠ABC = $\dfrac{1}{2} \times ∠AOC = \dfrac{1}{2} \times 60°$ = 30°.

Arc AB subtends ∠AOB at the centre and ∠ACB at the remaining part of the circle.

∴ ∠AOB = 2∠ACB

⇒ ∠ACB = $\dfrac{1}{2} \times ∠AOB = \dfrac{1}{2} \times 72°$ = 36°.

Hence, angles of triangle are ∠ABC = 30°, ∠ACB = 36° and ∠BAC = 114°.

In the given figure, BD is a side of regular hexagon, DC is a side of a regular pentagon and AD is a diameter. Calculate :

(i) ∠ADC,

(ii) ∠BDA,

(iii) ∠ABC,

(iv) ∠AEC.

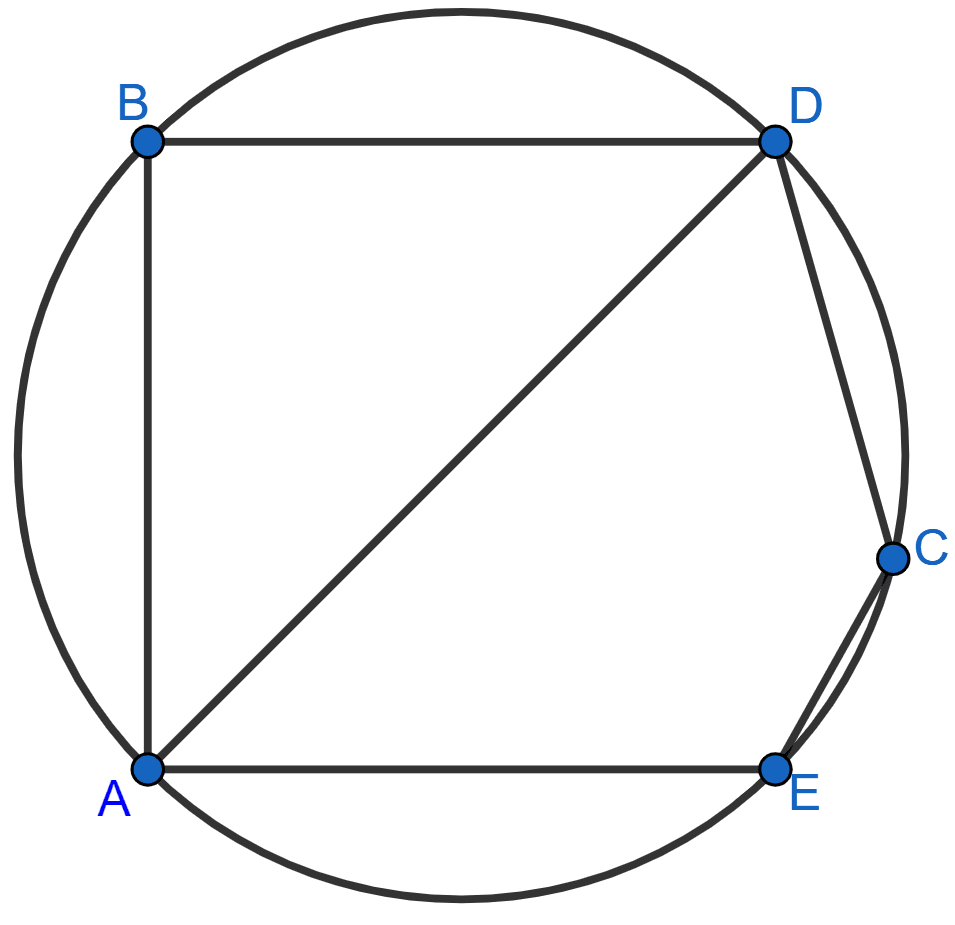
Answer

Let O be the center of the circle.

Join BC, BO, CO and EO.

Since, BD is the side of a regular hexagon,

∴ ∠BOD = $\dfrac{360°}{6}$ = 60°.

Since, DC is the side of a regular pentagon,

∴ ∠COD = $\dfrac{360°}{5}$ = 72°.

In △BOD,

OB = OD [Radii of same circle]

∴ ∠OBD = ∠ODB = x (let) [Angles opposite to equal sides are equal]

⇒ ∠OBD + ∠ODB + ∠BOD = 180°

⇒ x + x + 60° = 180°

⇒ 2x = 180° - 60°

⇒ 2x = 120°

⇒ x = $\dfrac{120°}{2}$ = 60°.

(i) In △OCD,

⇒ OD = OC [Radii of same circle]

⇒ ∠ODC = ∠OCD = y (let) [Angles opposite to equal sides are equal]

⇒ ∠OCD + ∠ODC + ∠COD = 180°

⇒ y + y + 72° = 180°

⇒ 2y = 180° - 72°

⇒ 2y = 108°

⇒ y = $\dfrac{108°}{2}$ = 54°.

From figure,

∠ADC = ∠ODC = y = 54°.

Hence, ∠ADC = 54°.

(ii) From figure,

∠BDA = ∠BDO = 60°.

Hence, ∠BDA = 60°.

(iii) We know that,

Angle at the centre is twice the angle at remaining circumference.

Arc AC subtends ∠AOC at the centre and ∠ABC at the remaining part of the circle.

∴ ∠AOC = 2∠ABC

⇒ ∠ABC = $\dfrac{1}{2}$∠AOC

⇒ ∠ABC = $\dfrac{1}{2}$[∠AOD - ∠COD]

⇒ ∠ABC = $\dfrac{1}{2}$[180° - 72°]

⇒ ∠ABC = $\dfrac{1}{2} \times 108°$

⇒ ∠ABC = 54°.

Hence, ∠ABC = 54°.

(iv) In cyclic quadrilateral AECD,

⇒ ∠AEC + ∠ADC = 180°

⇒ ∠AEC + 54° = 180°

⇒ ∠AEC = 180° - 54°

⇒ ∠AEC = 126°.

Hence, ∠AEC = 126°.

In the given figure x°, y°, z° and p° are exterior angles of cyclic quadrilateral ABCD, then x° + y° + z° + p° is :

1. 180°

2. 270°

3. 360°

4. 720°

Answer

We know that,

The exterior angle of a cyclic quadrilateral is equal to the interior opposite angle.

In cyclic quadrilateral ABCD,

∠C = x°, ∠B = p°, ∠D = y° and ∠A = z°.

∴ x° + y° + z° + p° = ∠C + ∠D + ∠A + ∠B

We know that,

Sum of angles in a cyclic quadrilateral is 360°.

∴ ∠A + ∠B + ∠C + ∠D = 360°.

Hence, Option 3 is the correct option.

In the given figure, O is center of the circle and OABC is a rhombus, then :

1. x° + y° = 180°

2. x° = y° = 90°

3. x° + 2y° = 360°

4. x° = y° = 45°

Answer

Join OB.

From figure,

OB = OA (Radius of same circle) ........(1)

We know that,

Sides of rhombus are equal.

∴ OA = AB .............(2)

From (1) and (2), we get :

⇒ OA = OB = AB

∴ OAB is an equilateral triangle.

Since, diagonals of rhombus bisect the interior angles.

In △OAB,

∠AOB = $\dfrac{x}{2}$

∠OBA = $\dfrac{y}{2}$

Since, each angle of equilateral triangle is 60°.

∴ ∠AOB = 60°

⇒ $\dfrac{x}{2} = 60°$

⇒ x = 120°.

∴ ∠OBA = 60°

⇒ $\dfrac{y}{2} = 60°$

⇒ y = 120°.

Substituting value of x and y in L.H.S. of equation x° + 2y° = 360°, we get :

⇒ 120° + 2(120°)

⇒ 120° + 240°

⇒ 360°.

Since, L.H.S. = R.H.S.

Hence, Option 3 is the correct option.

Arcs AB and BC are of lengths in the ratio 11 : 4 and O is center of the circle. If angle BOC = 32°, the angle AOB is :

1. 64°

2. 88°

3. 128°

4. 132°

Answer

Given,

Arcs AB and BC are of lengths in the ratio 11 : 4.

∴ ∠AOB : ∠BOC = 11 : 4

⇒ ∠AOB : 32° = 11 : 4

$\Rightarrow \dfrac{∠AOB}{32°} = \dfrac{11}{4}$

⇒ ∠AOB = $\dfrac{11}{4} \times 32°$ = 88°.

Hence, Option 2 is the correct option.

In the given figure, AB is the side of regular pentagon and BC is the side of regular hexagon. Angle BAC is :

1. 132°

2. 66°

3. 90°

4. 120°

Answer

Since,

AB is the side of regular pentagon.

∴ ∠AOB = $\dfrac{360°}{5}$ = 72°.

BC is the side of regular hexagon.

∴ ∠BOC = $\dfrac{360°}{6}$ = 60°.

From figure,

∠AOC = ∠AOB + ∠BOC = 72° + 60° = 132°.

We know that,

The angle which an arc of a circle subtends at the center is double that which it subtends at any point on the remaining part of the circumference.

⇒ ∠AOC = 2∠APC

⇒ ∠APC = $\dfrac{∠AOC}{2} = \dfrac{132°}{2}$ = 66°.

Hence, Option 2 is the correct option.

In the given figure, O is center of the circle. Chord BC = chord CD and angle A = 80°. Angle BOC is :

1. 120°

2. 80°

3. 100°

4. 160°

Answer

Given,

Chord BC = chord CD

∴ ∠BOC = ∠COD = x (let)

From figure,

∠BOD = ∠BOC + ∠COD = x + x = 2x

We know that,

The angle which an arc subtends at the center is double that which it subtends at any point on the remaining part of the circumference.

⇒ ∠BOD = 2∠BAD

⇒ 2x = 2 × 80°

⇒ x = 80°.

Hence, Option 2 is the correct option.

In the given circle, ∠BAD = 95°, ∠ABD = 40° and ∠BDC = 45°.

Assertion (A) : To show that AC is a diameter, the angle ADC or angle ABC need to be proved to be 90°.

Reason (R) : In △ADB,

∠ADB = 180° - 95° - 40° = 45°

∴ Angle ADC = 45° + 45° = 90°

(i) A is true, R is false

(ii) A is true, R is true

(iii) A is false, R is false

(iv) A is false, R is true

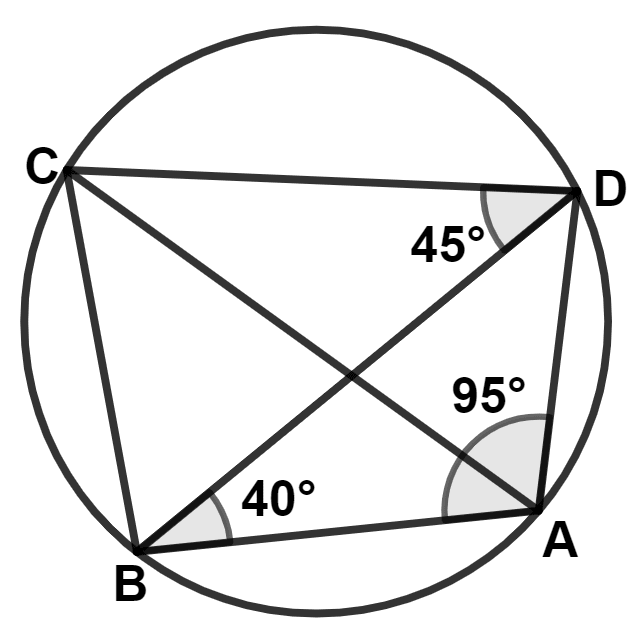
Answer

We know that,

Angle in semicircle is a right angle.

If AC is the diameter, then ∠ADC = ∠ABC = 90°.

∴ Assertion (A) is true.

From figure,

In △ADB,

By angle sum property of triangle,

∴ ∠ADB + ∠DBA + ∠BAD = 180°

⇒ ∠ADB + 40° + 95° = 180°

⇒ ∠ADB + 135° = 180°

⇒ ∠ADB = 180° - 135° = 45°.

From figure,

⇒ ∠ADC = ∠ADB + ∠BDC = 45° + 45° = 90°.

∴ Reason (R) is true.

Hence, Option 2 is the correct option.

ABCD is a cyclic quadrilateral, BD and AC are its diameters. Also, ∠DBC = 50°.

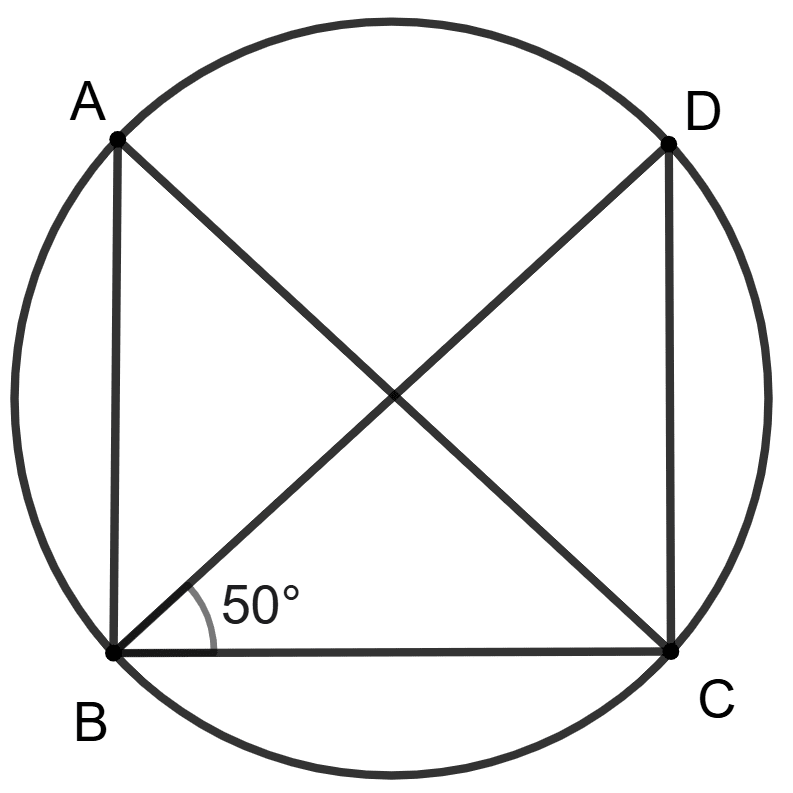
Assertion (A) : ∠BAC = 40°.

Reason (R) : ∠BAC = ∠BDC = 180° - (50° + 90°) = 40°.

1. A is true, R is false.

2. A is false, R is true.

3. Both A and R are true and R is correct reason for A.

4. Both A and R are true and R is incorrect reason for A.

Answer

Since BD and AC are diameters, that means:

∠ABC and ∠BCD are right angles (Angles in a semicircle is a right angle)

In △ DBC, using angle sum property,

⇒ ∠DBC + ∠BCD + ∠BDC = 180°

⇒ 50° + 90° + ∠BDC = 180°

⇒ 140° + ∠BDC = 180°

⇒ ∠BDC = 180° - 140°

⇒ ∠BDC = 40°

We know that, angles in the same segment of a circle are equal.

⇒ ∠BAC = ∠BDC

⇒ ∠BAC = 40°

So, assertion and reason are true and reason clearly explains assertion.

Hence, option 3 is the correct option.

Points A, C, B and D are concyclic, AB is diameter and ∠ABC = 60°.

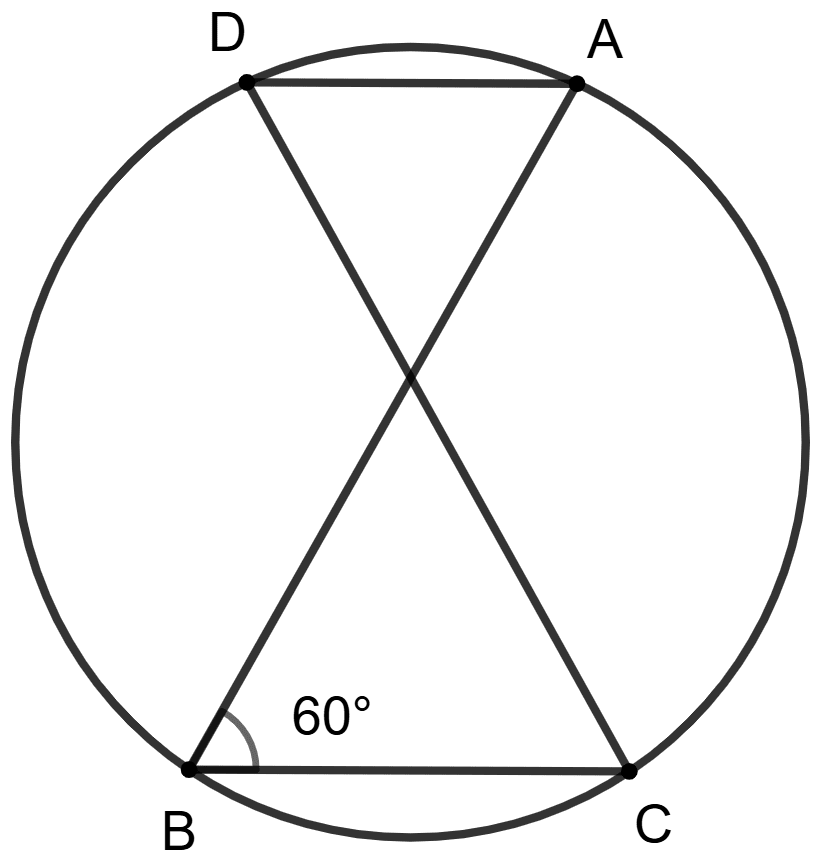
Assertion (A) : ∠BAC = 60°.

Reason (R) : AB is diameter so ∠ACB = 90° and ∠ABC + ∠BAC = 90°.

1. A is true, R is false.

2. A is false, R is true.

3. Both A and R are true and R is correct reason for A.

4. Both A and R are true and R is incorrect reason for A.

Answer

Join AC.

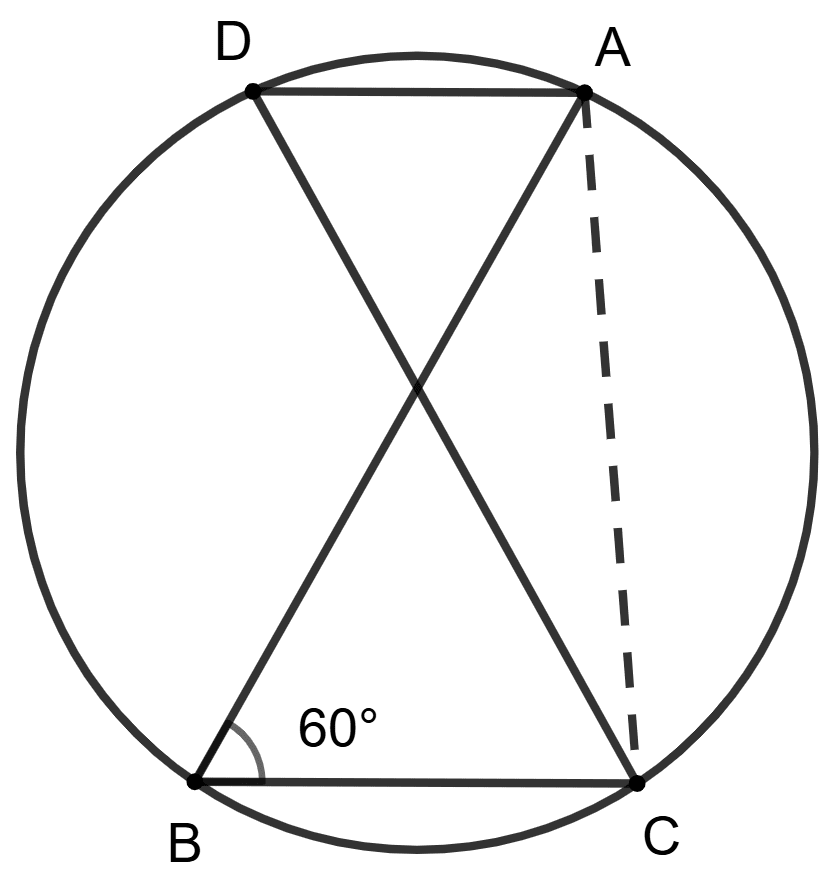
Since AB is diameter, that means :

∠ACB = 90° (Angles in a semicircle is a right angle)

In △ ABC, using angle sum property,

⇒ ∠ABC + ∠ACB + ∠BAC = 180° ....................(1)

⇒ 60° + 90° + ∠BAC = 180°

⇒ 150° + ∠BAC = 180°

⇒ ∠BAC = 180° - 150°

⇒ ∠BAC = 30°

So, assertion (A) is false.

From equation (1),

⇒ ∠ABC + 90° + ∠BAC = 180°

⇒ ∠ABC + ∠BAC = 180° - 90°

⇒ ∠ABC + ∠BAC = 90°

So, reason (R) is true.

Hence, option 2 is the correct option.

AB is diameter of the circle and ∠ACD = 38°.

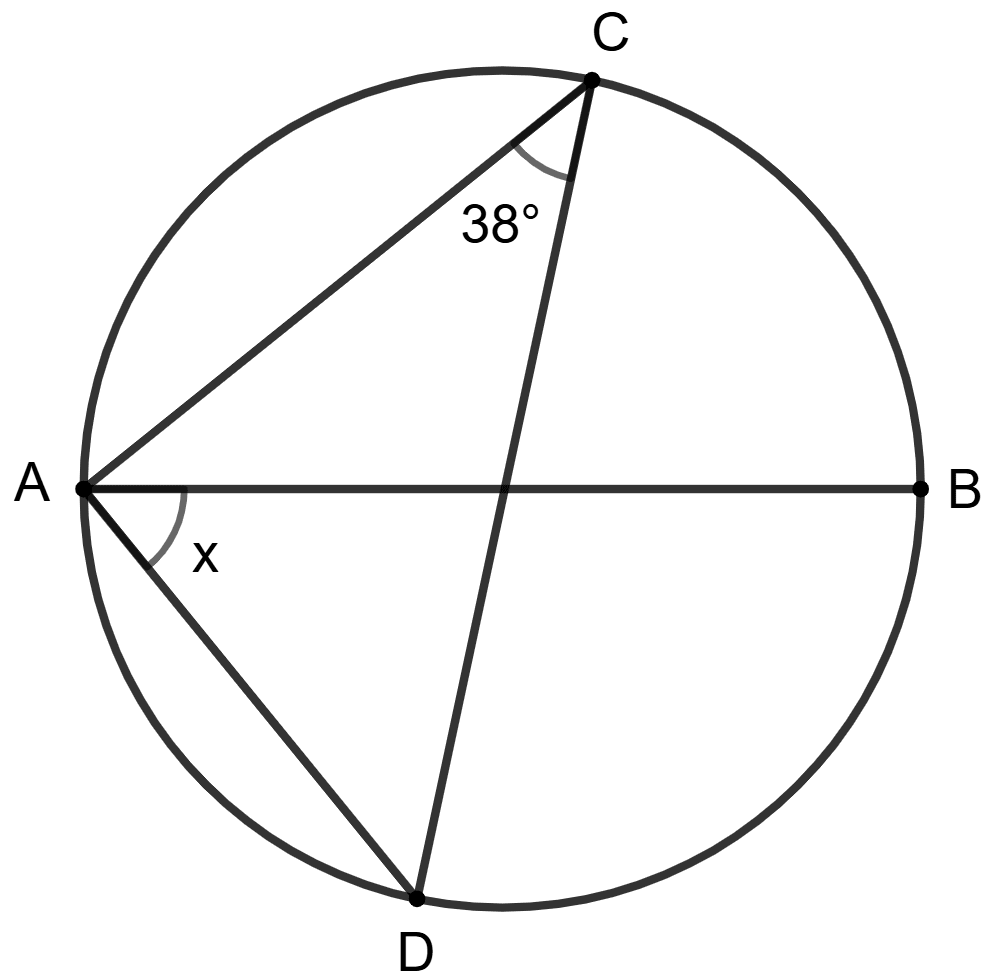
Assertion (A) : x = 38°.

Reason (R) : ∠ACB = 90°, x = ∠DCB = 90° - 38° = 52°.

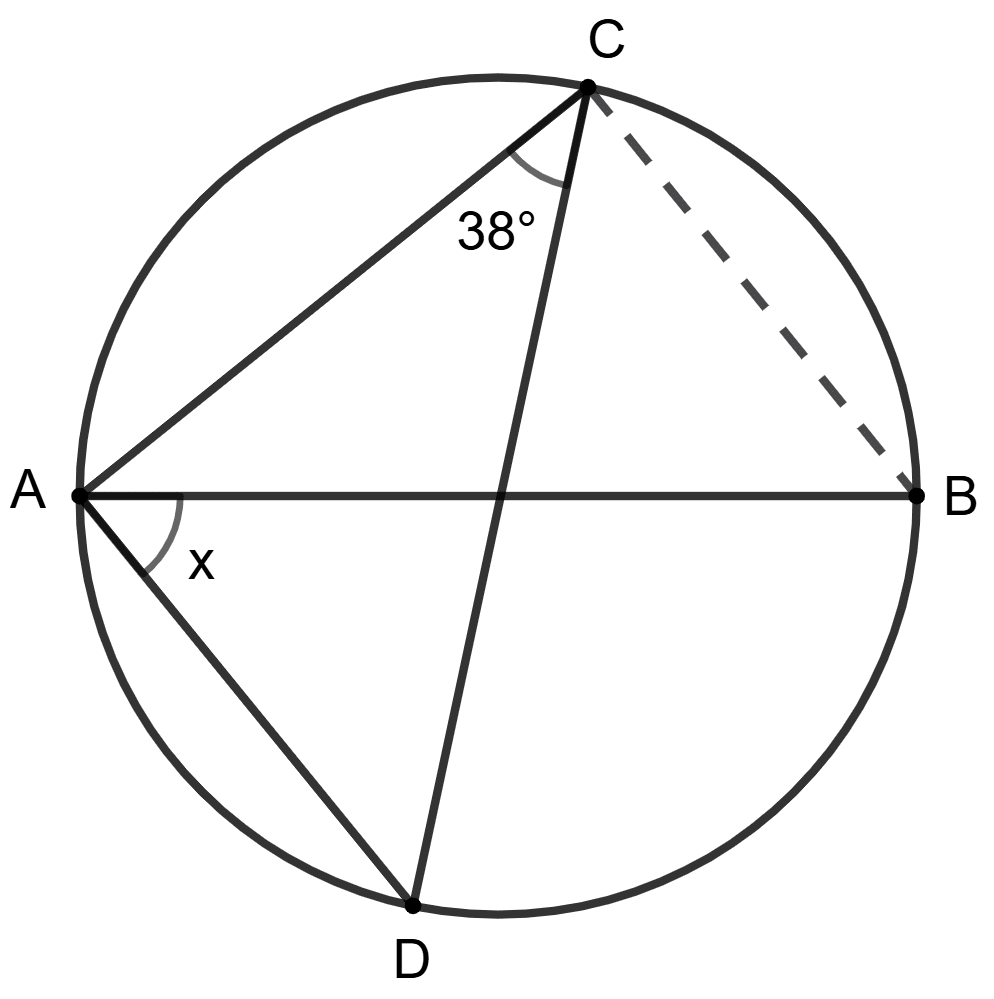
1. A is true, R is false.

2. A is false, R is true.

3. Both A and R are true and R is correct reason for A.

4. Both A and R are true and R is incorrect reason for A.

Answer

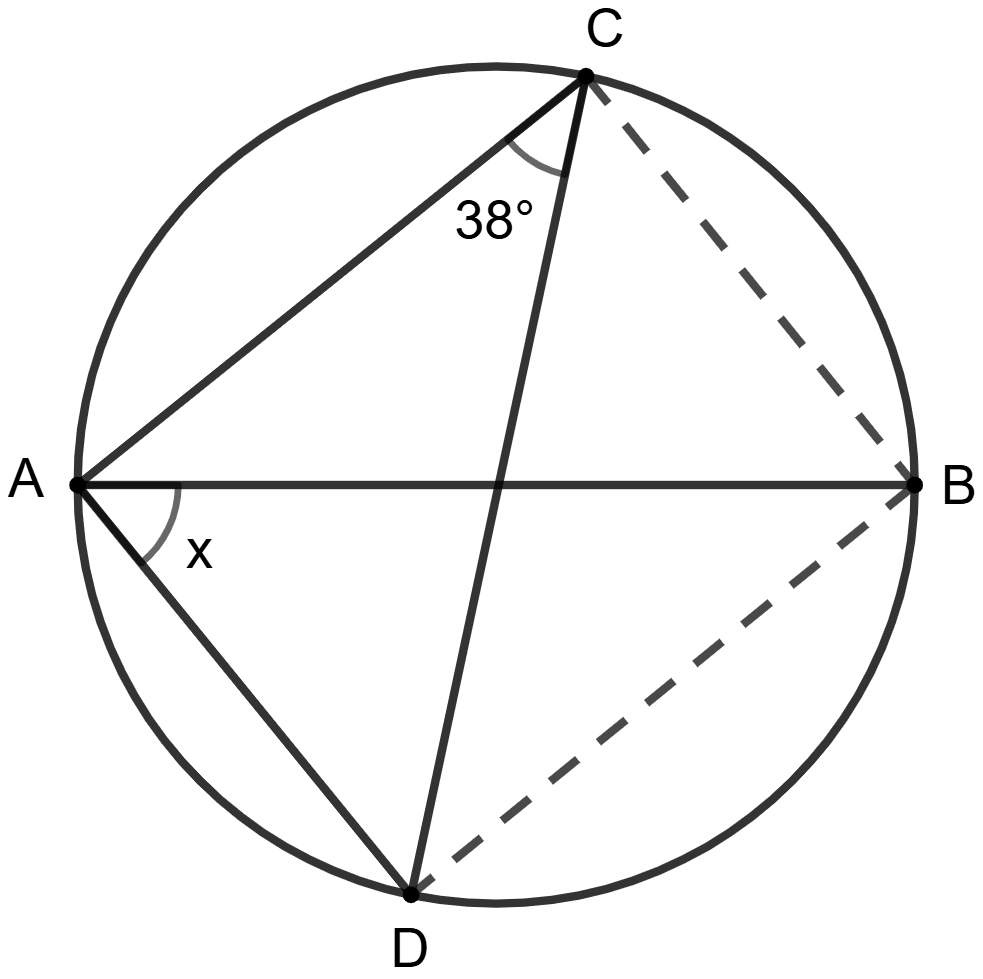
Join DB and CB.

It is given AB is diameter of the circle and angles in a semicircle is a right angle.

⇒ ∠ACB = 90°

⇒ ∠ACD + ∠DCB = 90°

⇒ 38° + ∠DCB = 90°

⇒ ∠DCB = 90° - 38°

⇒ ∠DCB = 52°

We know that, angles subtended by the same chord in the same segment of a circle are equal.

⇒ ∠BAD (x) = ∠BCD = 52°

So, assertion (A) is false but reason (R) is true.

Hence, option 2 is the correct option.

Chords AC and BD intersect each other at point P.

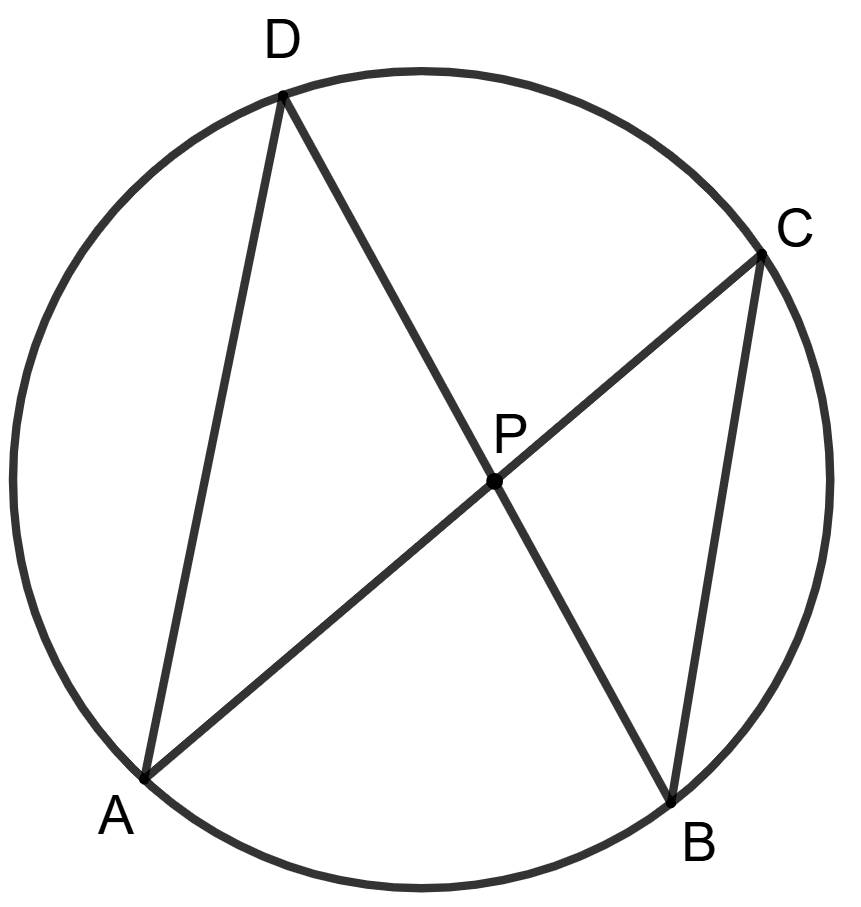
Assertion (A) : PA x PC = PB x PD.

Reason (R) : Δ APD ∼ Δ BPC

$\Rightarrow \dfrac{PA}{PB} = \dfrac{PD}{PC}$

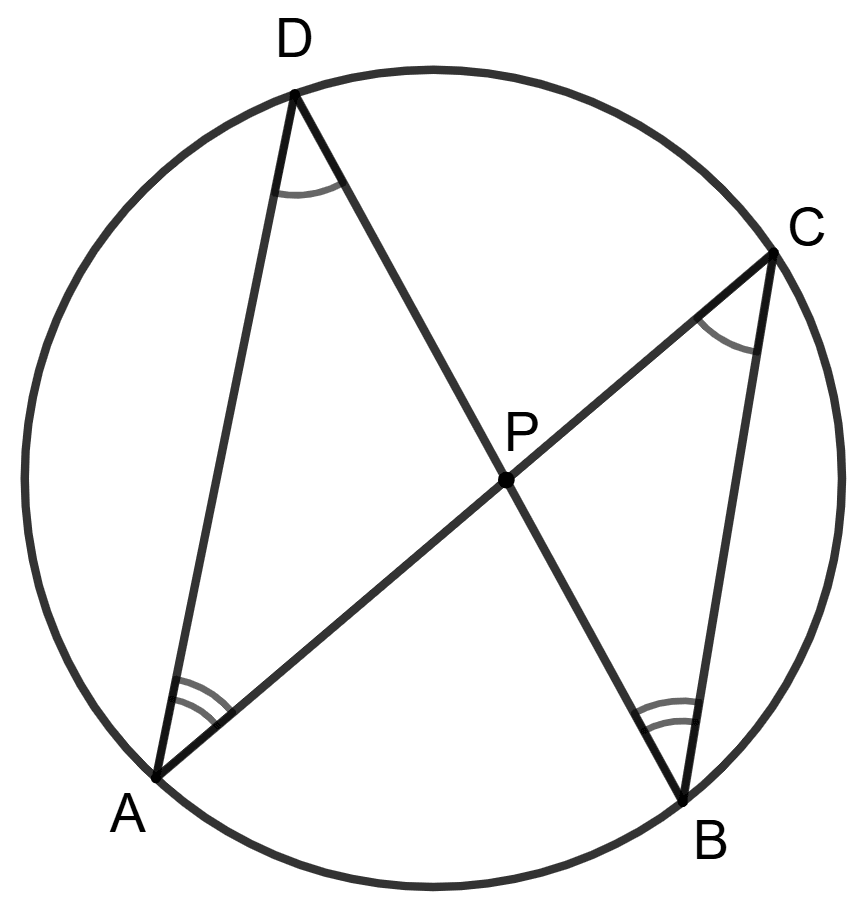
1. A is true, R is false.

2. A is false, R is true.

3. Both A and R are true and R is correct reason for A.

4. Both A and R are true and R is incorrect reason for A.

Answer

In Δ APD and Δ BPC,

⇒ ∠APD = ∠BPC (Vertically opposite angles are equal)

⇒ ∠ADP = ∠BCP (Angles in same segment are equal)

∴ Δ APD ∼ Δ BPC (By A.A. similarity)

Corresponding sides of similar triangles are proportional.

$\Rightarrow \dfrac{AP}{PB} = \dfrac{PD}{PC}$ ........(1)

So, reason (R) is true.

Solving (1),

⇒ AP x PC = PD x PB

So, assertion (A) is true and R is the correct reason for A.

Hence, option 3 is the correct option.

A circle with center at point O and ∠AOC = 160°.

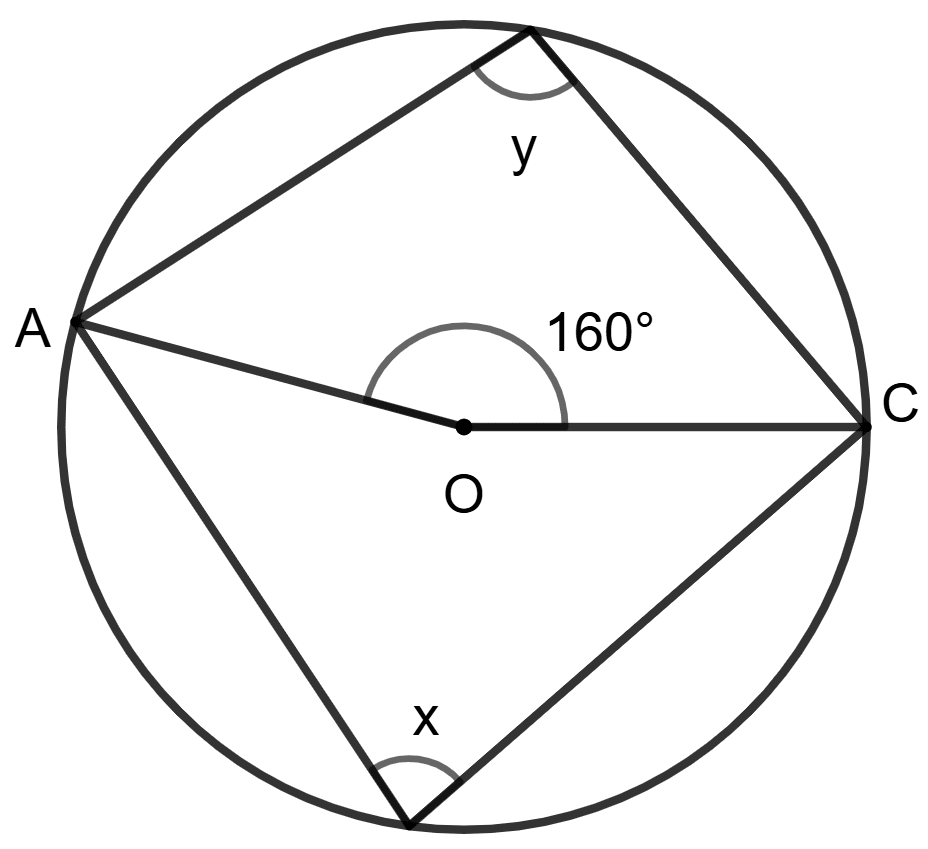
Statement (1) : Angle x = 100° and angle y = 80°.

Statement (2) : The angle, which an arc of a circle subtends at the center of the circle is double the angle which it subtends at any point on the remaining part of the circumference.

1. Both statements are true.

2. Both statements are false.

3. Statement 1 is true, and statement 2 is false.

4. Statement 1 is false, and statement 2 is true.

Answer

We know that, the angle, subtended by an arc of a circle is double the angle subtended by it at any point on the remaining part of the circle.

So, statement 2 is true.

⇒ ∠AOC = 2x

⇒ 160° = 2x

⇒ x = $\dfrac{160°}{2}$ = 80°

We know that, sum of either pair of opposite angles of a cyclic quadrilateral is 180°.

⇒ x + y = 180°

⇒ 80° + y = 180°

⇒ y = 180° - 80° = 100°

So, statement 1 is false.

Hence, option 4 is the correct option.

AC is diameter, AE is parallel to BC and ∠BAC = 50°.

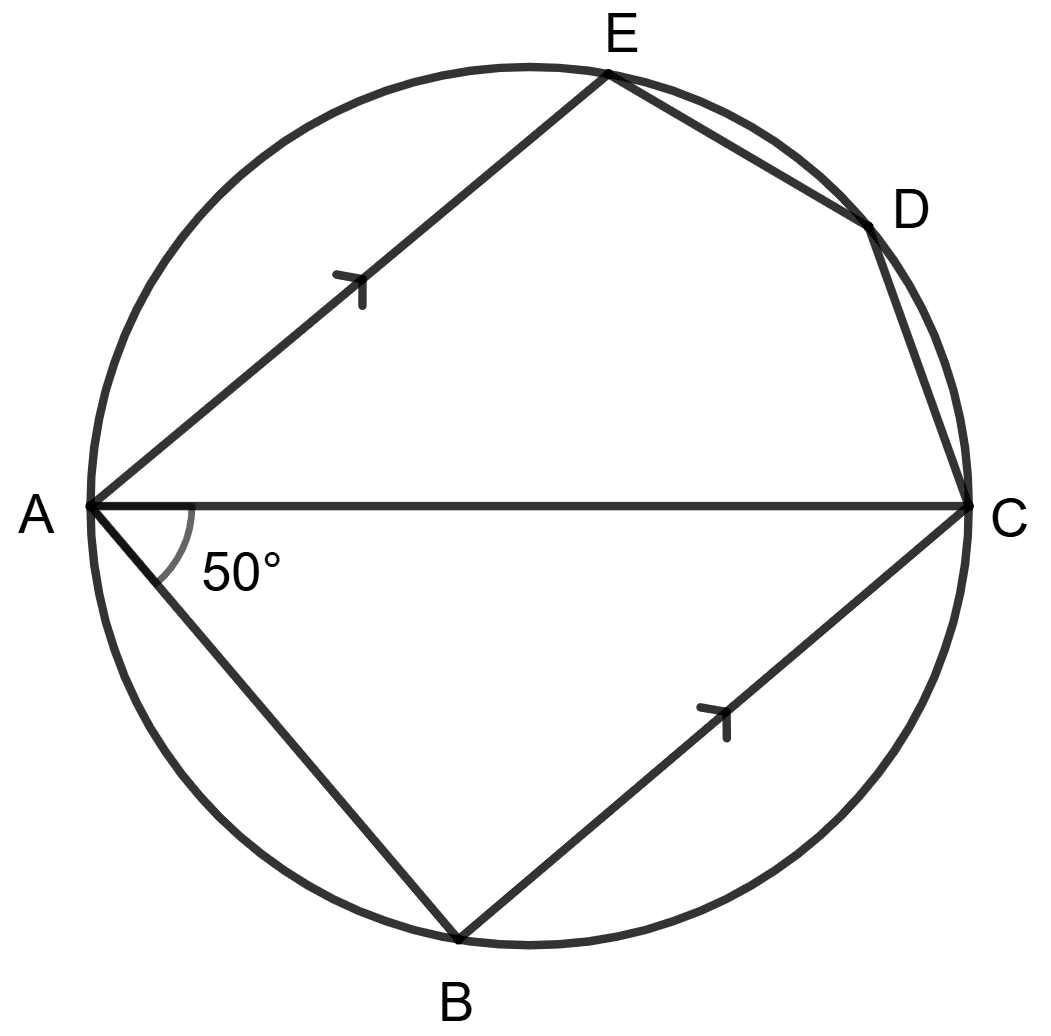
Statement (1) : ∠EDC + 50° = 180°.

Statement (2) : ∠EDC + ∠EAC = 180°.

1. Both statements are true.

2. Both statements are false.

3. Statement 1 is true, and statement 2 is false.

4. Statement 1 is false, and statement 2 is true.

Answer

It is given that AC is diameter and angles in a semicircle is a right angle.

⇒ ∠ABC = 90°

Since, AE is parallel to BC and AB is transversal.

⇒ ∠ABC + ∠BAE = 180° [The sum of co-interior angles formed when a transversal intersects two parallel lines is always 180°]

⇒ 90° + ∠BAE = 180°

⇒ ∠BAE = 180° - 90°

⇒ ∠BAE = 90°

⇒ ∠BAC + ∠EAC = 90°

⇒ 50° + ∠EAC = 90°

⇒ ∠EAC = 90° - 50°

⇒ ∠EAC = 40°

AEDC form a cyclic quadrilateral and sum of either pair of opposite angles of a cyclic quadrilateral is 180°.

⇒ ∠EDC + ∠EAC = 180°

⇒ ∠EDC + 40° = 180°

So, statement 1 is false but statement 2 is true.

Hence, option 4 is the correct option.

O is the center of the circle, OB = BC and ∠BOC = 20°.

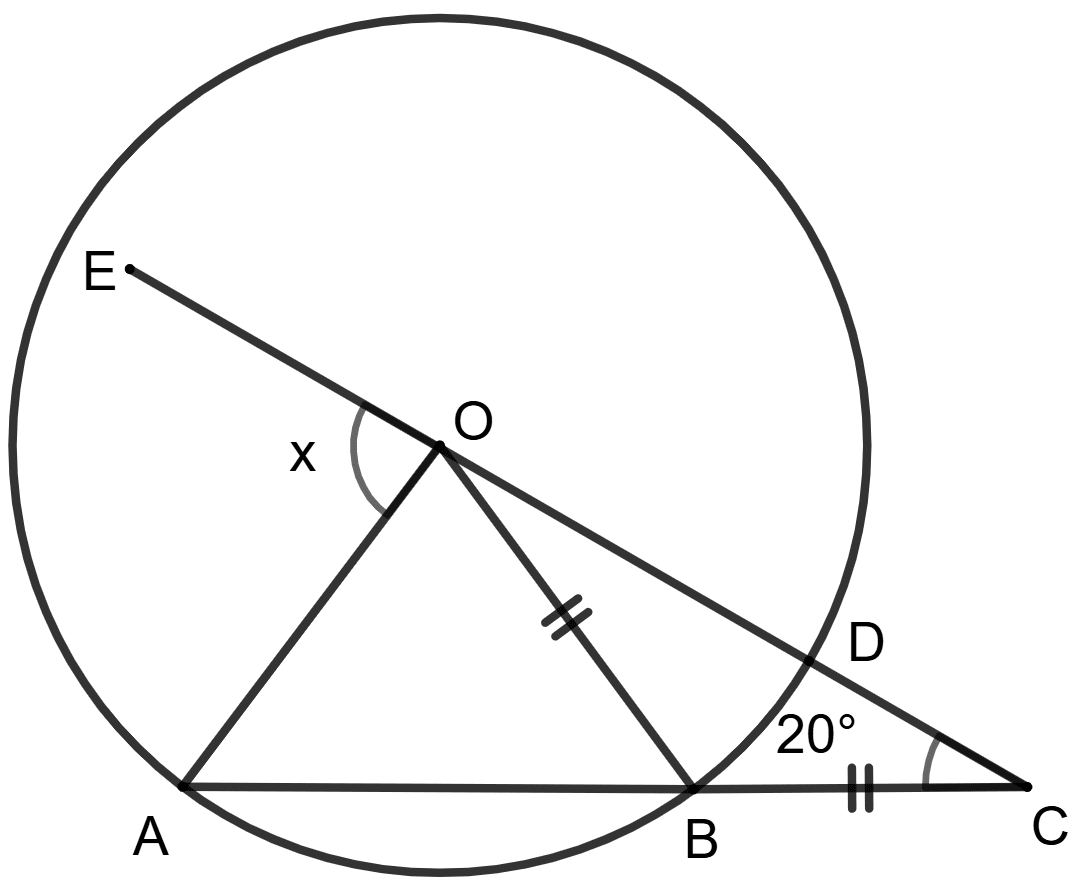
Statement (1) : x = 2 x 20° = 40°

Statement (2) : ∠BOC = 20°.

x = ∠OAB + 20° = ∠OBA + 20° = 40° + 20° = 60°

1. Both statements are true.

2. Both statements are false.

3. Statement 1 is true, and statement 2 is false.

4. Statement 1 is false, and statement 2 is true.

Answer

Given,

⇒ OB = OC

⇒ ∠BOC = ∠BCO = 20° (Angles opposite to equal sides of a triangle are always equal)

In △ OBC, using angle sum property,

⇒ ∠OBC + ∠BCO + ∠BOC = 180°

⇒ ∠OBC + 20° + 20° = 180°

⇒ ∠OBC + 40° = 180°

⇒ ∠OBC = 180° - 40°

⇒ ∠OBC = 140°

∠OBC and ∠OBA forms linear pairs of angle.

⇒ ∠OBC + ∠OBA = 180°

⇒ 140° + ∠OBA = 180°

⇒ ∠OBA = 180° - 140°

⇒ ∠OBA = 40°

Since OB = OA (Radii of same circle)

⇒ ∠OBA = ∠OAB = 40° (Angles opposite to equal sides of a triangle are always equal)

Using exterior angle property, the exterior angle of a triangle is equal to the sum of the two opposite interior angles.

In triangle OAC,

⇒ ∠EOA = ∠OAC + ∠OCA

⇒ x = ∠OAB + 20°

⇒ x = ∠OBA + 20° = 40° + 20° = 60°

So, statement 1 is false and statement 2 is true.

Hence, option 4 is the correct option.

O is the center of the circle and ∠AOC = 120°.

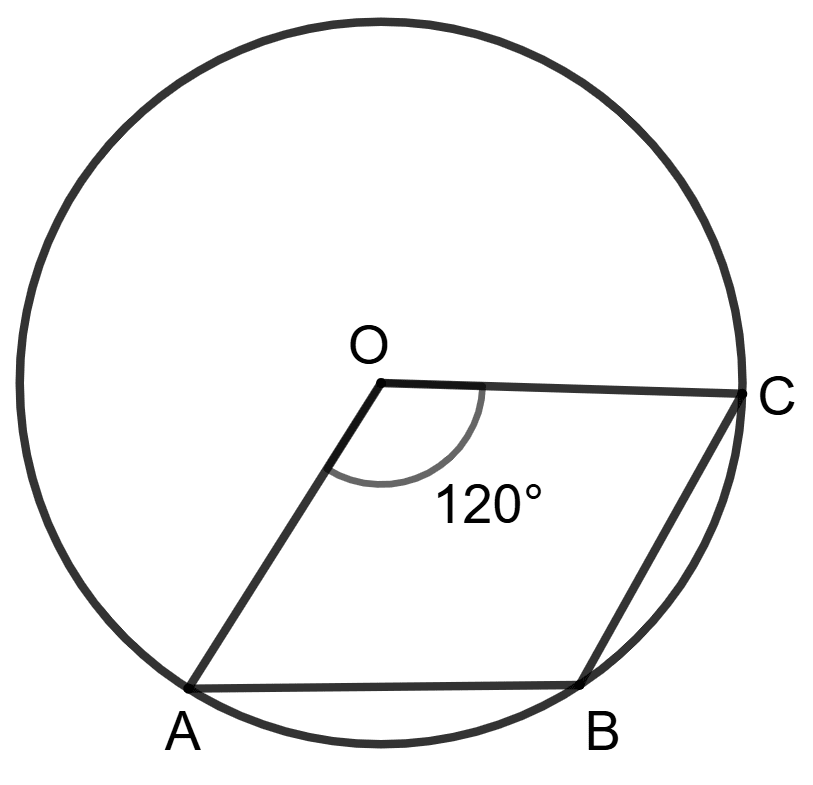
Statement (1) : ∠ABC = 120°

Statement (2) : ∠ABC + ∠ADC = 180° ⇒ ∠ABC + 60° = 180°.

1. Both statements are true.

2. Both statements are false.

3. Statement 1 is true, and statement 2 is false.

4. Statement 1 is false, and statement 2 is true.

Answer

Since, the angle, which an arc of a circle subtends at the center of the circle is double the angle which it subtends at any point on the remaining part of the circumference.

⇒ ∠AOC = 2 x ∠ADC

⇒ 120° = 2 x ∠ADC

⇒ ∠ADC = $\dfrac{120°}{2}$ = 60°

ABCD form a cyclic quadrilateral and sum of opposite angles of cyclic quadrilateral is 180°.

⇒ ∠ADC + ∠ABC = 180°

⇒ 60° + ∠ABC = 180°

⇒ ∠ABC = 180° - 60°

⇒ ∠ABC = 120°

So, both statement are true.

Hence, option 1 is the correct option.

In the given circle with diameter AB, find the value of x.

Answer

As angles in same segment are equal.

∴ ∠ABD = ∠ACD = 30°.

From figure,

∠ADB = 90° [As angle in semi-circle is a right angle.]

In △ADB,

⇒ ∠ABD + ∠ADB + ∠BAD = 180° [By angle sum property of triangle]

⇒ 30° + 90° + x = 180°

⇒ 120° + x = 180°

⇒ x = 180° - 120° = 60°.

Hence, the value of x = 60°.

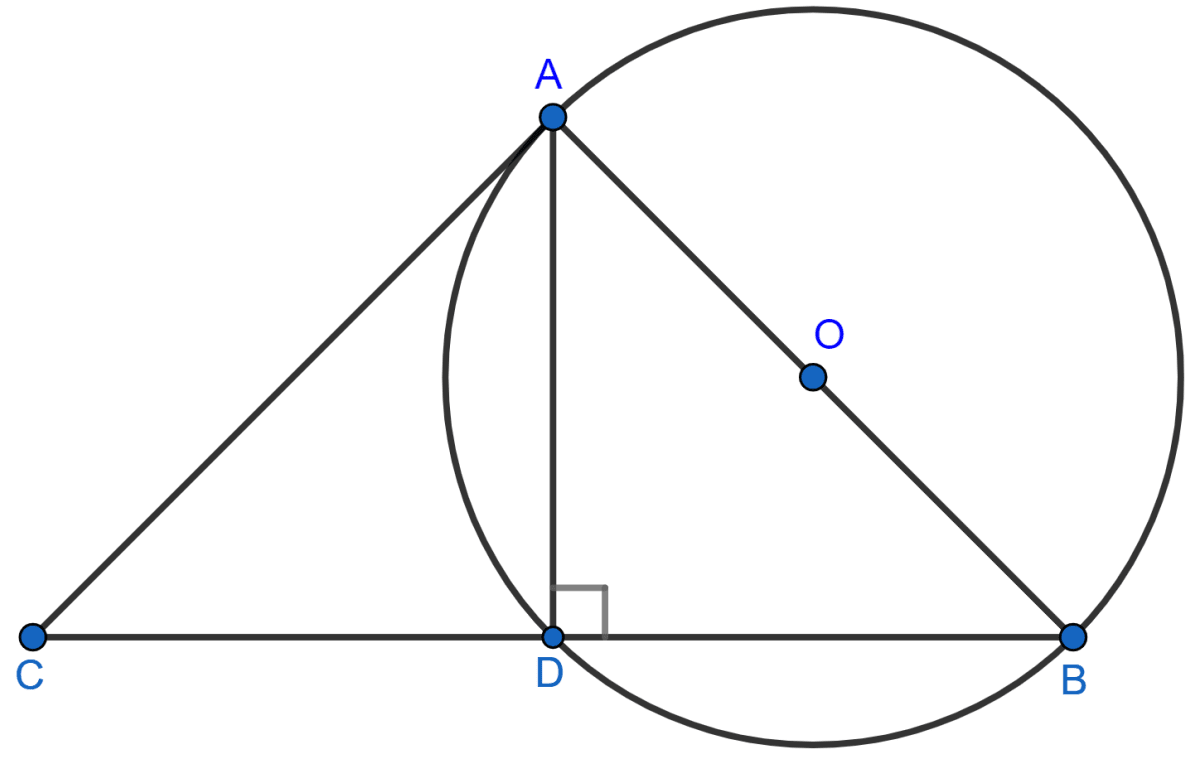
In the given figure, ABC is a triangle in which ∠BAC = 30°. Show that BC is equal to the radius of the circumcircle of the triangle ABC, whose centre is O.

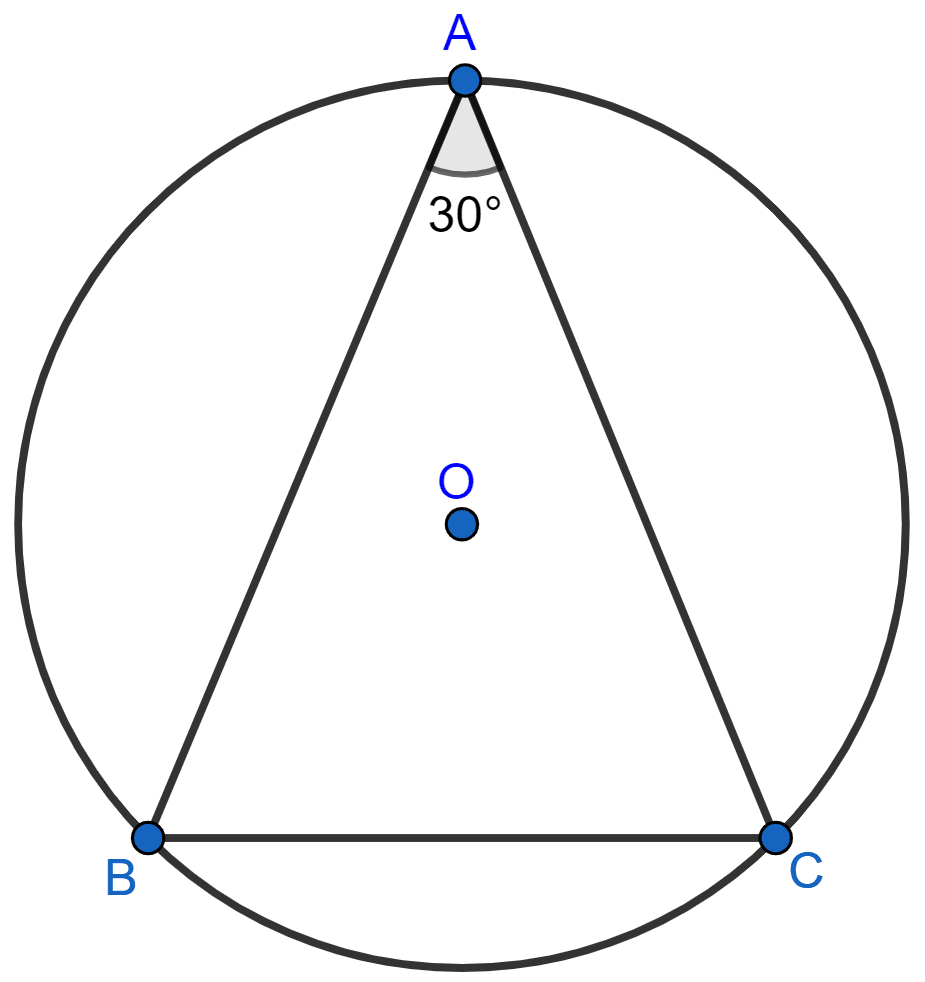
Answer

Join OB and OC.

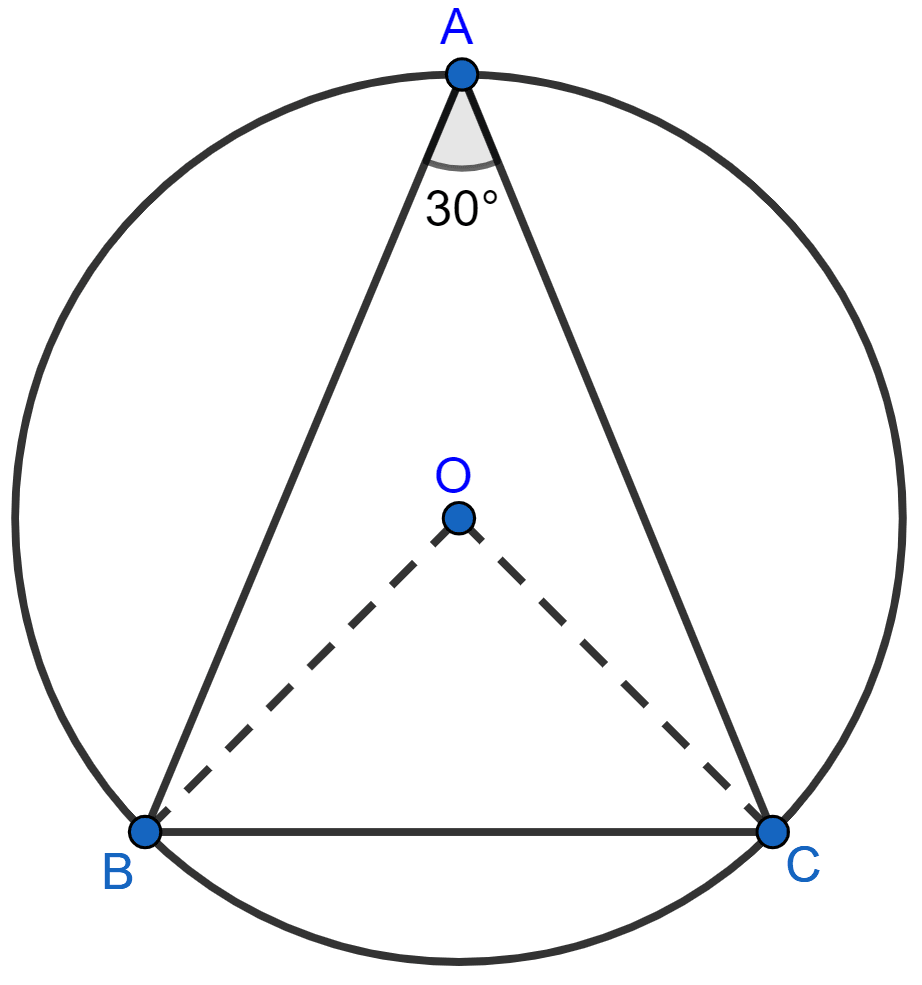
We know that,

Angle at the centre is twice the angle at remaining circumference.

∴ ∠BOC = 2∠BAC = 2 × 30° = 60°

In △OBC,

⇒ OB = OC [Radii of same circle]

⇒ ∠OBC = ∠OCB = x (let) [As angles opposite to equal sides are equal]

⇒ ∠BOC + ∠OBC + ∠OCB = 180°

⇒ 60° + x + x = 180°

⇒ 2x + 60° = 180°

⇒ 2x = 180° - 60°

⇒ 2x = 120°

⇒ x = $\dfrac{120°}{2}$ = 60°.

∴ ∠OBC = ∠OCB = ∠BOC = 60°.

Hence, △OBC is an equilateral triangle.

∴ OB = OC = BC.

Hence, proved that BC is equal to the radius of the circumcircle of the triangle ABC.

Prove that the circle drawn on any one of the equal sides of an isosceles triangle as diameter bisects the base.

Answer

In △ABC, AB = AC and a circle with AB as diameter is drawn which intersects the side BC at D.

From figure,

∠ADB = 90° [Angle in semi-circle is a right angle.]

Also,

⇒ ∠ADB + ∠ADC = 180° [Linear pair]

⇒ ∠ADC = 180° - ∠ADB

⇒ ∠ADC = 180° - 90° = 90°.

In △ABD and △ACD,

⇒ AB = AC [Given]

⇒ ∠ADB = ∠ADC = 90°

⇒ AD = AD [Common]

∴ △ABD ≅ △ACD by RHS axiom of congruency

∴ BD = CD [By C.P.C.T.]

∴ D is mid-point of BC.

Hence, proved that the circle drawn on any one of the equal sides of an isosceles triangle as diameter bisects the base.

In the given figure, chord ED is parallel to diameter AC of the circle. Given ∠CBE = 65°, calculate ∠DEC.

Answer

Join OE and AB.

Arc EC subtends ∠EOC at the centre and ∠EBC at the remaining part of the circle.

We know that,

Angle at the centre is twice the angle at remaining circumference.

∴ ∠EOC = 2∠EBC = 2 x 65° = 130°.

Now, in ∆OEC

OE = OC [Radii of the same circle]

So, ∠OEC = ∠OCE [Angle opposite to equal sides are equal.]

In ∆OCE by angle sum property,

⇒ ∠OEC + ∠OCE + ∠EOC = 180°

⇒ 2∠OCE + 130° = 180°

⇒ 2∠OCE = 180° - 130°

⇒ 2∠OCE = 50°

⇒ ∠OCE = $\dfrac{50°}{2}$ = 25°.

Given, AC || ED

∴ ∠DEC = ∠OCE [Alternate angles are equal]

⇒ ∠DEC = 25°.

Hence, ∠DEC = 25°.

In the figure, ∠DBC = 58°. BD is a diameter of the circle. Calculate :

(i) ∠BDC

(ii) ∠BEC

(iii) ∠BAC

Answer

(i) Given that BD is a diameter of the circle.

We know that,

Angle in a semicircle is a right angle.

So, ∠BCD = 90°

Also given that,

∠DBC = 58°

In ∆BDC,

⇒ ∠DBC + ∠BCD + ∠BDC = 180° [Angle sum property of triangle]

⇒ 58° + 90° + ∠BDC = 180°

⇒ 148° + ∠BDC = 180°

⇒ ∠BDC = 180° - 148° = 32°.

Hence, ∠BDC = 32°.

(ii) We know that, the opposite angles of a cyclic quadrilateral are supplementary.

So, in cyclic quadrilateral BECD

⇒ ∠BEC + ∠BDC = 180°

⇒ ∠BEC + 32° = 180°

⇒ ∠BEC = 180° - 32° = 148°

Hence, ∠BEC = 148°.

(iii) In cyclic quadrilateral ABEC,

⇒ ∠BAC + ∠BEC = 180° [Sum of opposite angles of a cyclic quadrilateral = 180°]

⇒ ∠BAC + 148° = 180°

⇒ ∠BAC = 180° - 148°= 32°.

Hence, ∠BAC = 32°.

D and E are points on equal sides AB and AC of an isosceles triangle ABC such that AD = AE. Prove that the points B, C, E and D are concyclic.

Answer

Join DE.

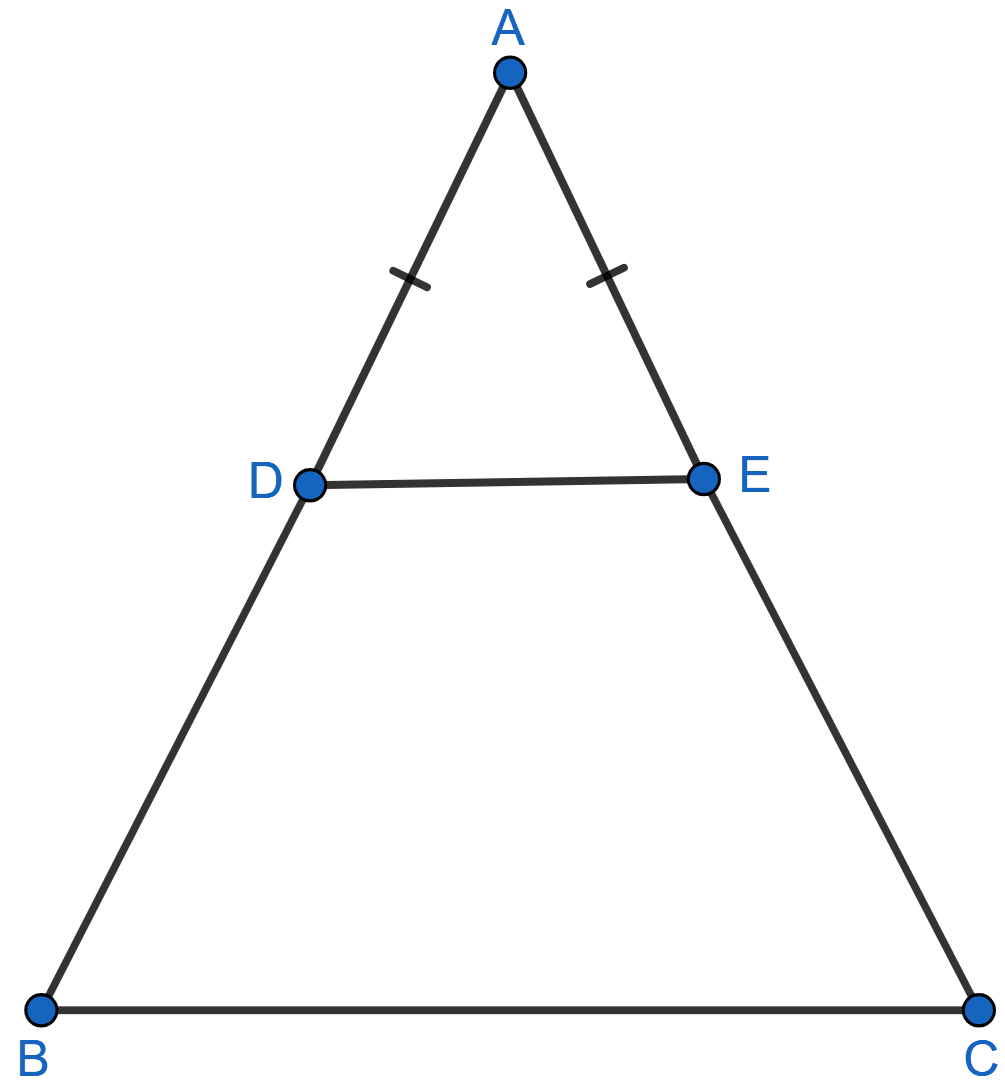
In ∆ABC,

AB = AC = x (let) [Given]

So, ∠B = ∠C [Angles opposite to equal sides are equal]

Similarly,

In ∆ADE,

AD = AE = y (let) [Given]

So, ∠ADE = ∠AED [Angles opposite to equal sides are equal]

Now, in ∆ABC we have

$\dfrac{AD}{AB} = \dfrac{AE}{AC} = \dfrac{y}{x}$.

Hence, DE || BC [By converse of BPT]

So,

⇒ ∠ADE = ∠B [Corresponding angles are equal]

⇒ (180° - ∠EDB) = ∠B

⇒ ∠B + ∠EDB = 180°

∠B = ∠C [Proved above]

So,

⇒ ∠C + ∠EDB = 180°

Thus, opposite angles are supplementary.

Similarly,

⇒ ∠B + ∠CED = 180°

Since, sum of opposite angles of cyclic quadrilateral = 180°.

Hence, proved that B, C, E and D are concyclic.

In the given figure, ABCD is a cyclic quadrilateral. AF is drawn parallel to CB and DA is produced to point E. If ∠ADC = 92°, ∠FAE = 20°; determine ∠BCD. Given reason in support of your answer.

Answer

Given,

In cyclic quad. ABCD

AF || CB and DA is produced to E such that ∠ADC = 92° and ∠FAE = 20°.

From figure,

⇒ ∠B + ∠D = 180° [As sum of opposite angles in a cyclic quadrilateral = 180°]

⇒ ∠B + 92° = 180°

⇒ ∠B = 180° - 92° = 88°

As AF || CB,

∠FAB = ∠B = 88° [Alternate angles are equal]

But, ∠FAE = 20° [Given]

From figure,

∠BAE = ∠BAF + ∠FAE = 88° + 20° = 108°.

∠BAD = 180° - ∠BAE = 180° - 108° = 72°.

∠BCD + ∠BAD = 180° [As sum of opposite angles in a cyclic quadrilateral = 180°]

⇒ ∠BCD + 72° = 180°

⇒ ∠BCD = 180° - 72° = 108°.

Hence, ∠BCD = 108°.

If I is the incentre of triangle ABC and AI when produced meets the circumcircle of triangle ABC in point D. If ∠BAC = 66° and ∠ABC = 80°. Calculate :

(i) ∠DBC,

(ii) ∠IBC,

(iii) ∠BIC.

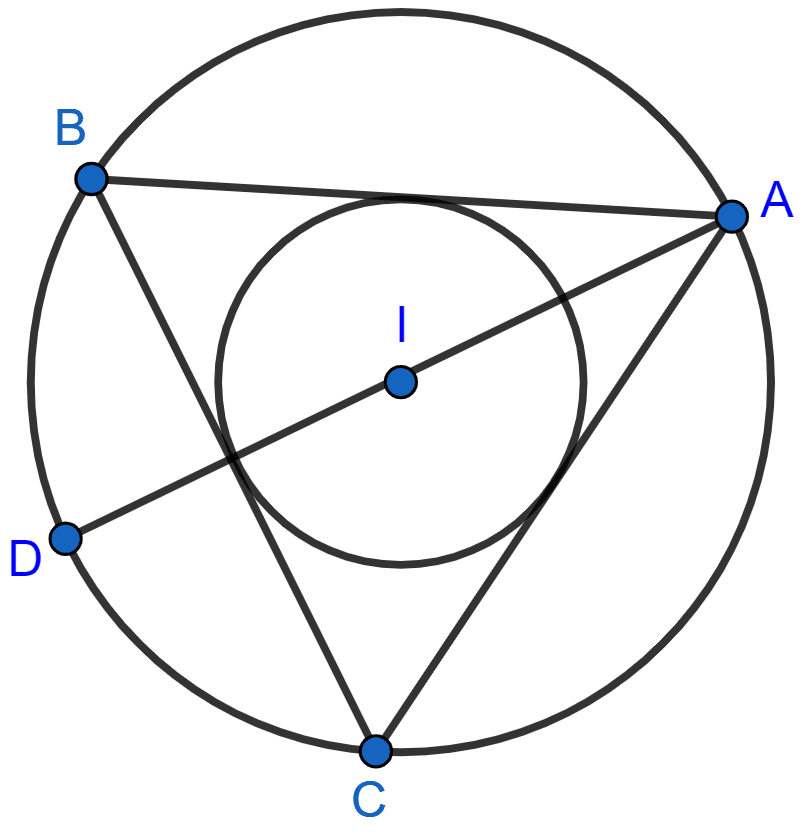
Answer

Join DB and DC, IB and IC.

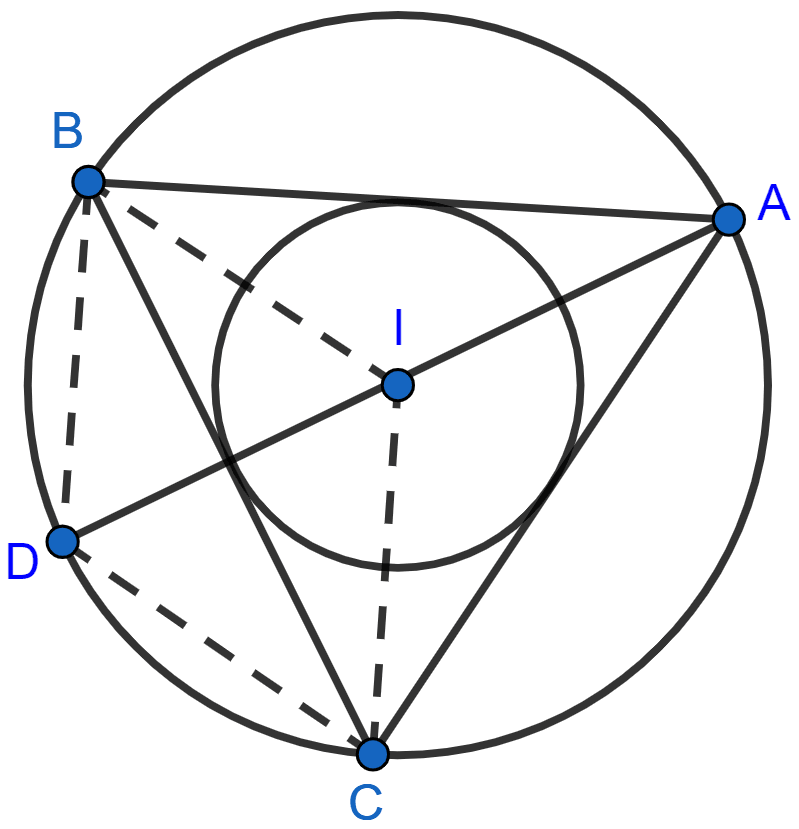
(i) From figure,

∠DAC = $\dfrac{1}{2}$∠BAC [As I is the incenter]

∠DAC = $\dfrac{1}{2}$ x 66° = 33°.

As angle in same segment are equal.

∴ ∠DBC = ∠DAC = 33°.

Hence, ∠DBC = 33°.

(ii) Since, I is the incentre of ∆ABC, IB bisects ∠ABC.

∴ ∠IBC = $\dfrac{1}{2}$∠ABC

= $\dfrac{1}{2} \times 80°$ = 40°.

Hence, ∠IBC = 40°.

(iii) In ∆ABC,

⇒ ∠ACB + ∠ABC + ∠BAC = 180° [By angle sum property]

⇒ ∠ACB = 180° - ∠ABC - ∠BAC

⇒ ∠ACB = 180° - 80° - 66°

⇒ ∠ACB = 180° - 146°

⇒ ∠ACB = 34°.

As I is incenter so, IC bisects ∠C

∴ ∠ICB = $\dfrac{1}{2}$∠ACB = $\dfrac{1}{2} \times 34°$ = 17°.

In ∆IBC

⇒ ∠IBC + ∠ICB + ∠BIC = 180° [By angle sum property of triangle]

⇒ 40° + 17° + ∠BIC = 180°

⇒ 57° + ∠BIC = 180°

⇒ ∠BIC = 180° - 57° = 123°.

Hence, ∠BIC = 123°.

In the given Figure, AB = AD = DC = PB and ∠DBC = x°. Determine, in terms of x :

(i) ∠ABD, (ii) ∠APB.

Hence or otherwise, prove that AP is parallel to DB.

Answer

(i) Join AC and BD.

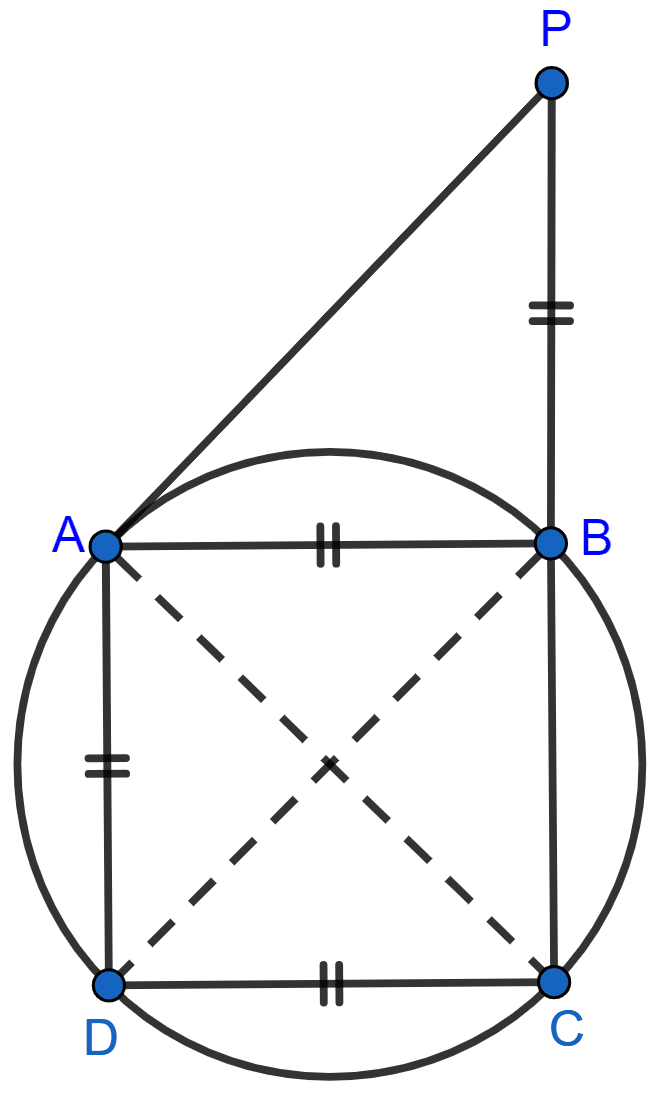
∠DAC = ∠DBC = x° [Angles in the same segment are equal]

∠DCA = ∠DAC = x° [As angles opposite to equal sides are equal]

Also, we have

∠ABD = ∠DCA = x° [Angles in the same segment are equal]

Hence, ∠ABD = x°.

(ii) In ∆ABP

⇒ Ext. ∠ABC = ∠BAP + ∠APB

But, ∠BAP = ∠APB [As angles opposite to equal sides are equal]

⇒ 2x° = ∠APB + ∠APB = 2∠APB

⇒ 2∠APB = 2x°

⇒ ∠APB = x°

Hence, ∠APB = x°.

Thus, ∠APB = ∠DBC = x° [These are corresponding angles]

Hence, proved that AP || DB.

In the given figure; ABC, AEQ and CEP are straight lines. Show that ∠APE and ∠CQE are supplementary.

Answer

Join EB.

We know that,

In cyclic quadrilateral sum of opposite angles = 180°.

In cyclic quad. ABEP

⇒ ∠APE + ∠ABE = 180° .....(1) [Opposite angles of a cyclic quad. are supplementary]

Similarly, in cyclic quad. BCQE

⇒ ∠CQE + ∠CBE = 180° .....(2)

Adding (1) and (2), we have

⇒ ∠APE + ∠ABE + ∠CQE + ∠CBE = 180° + 180°

⇒ ∠APE + ∠ABE + ∠CQE + ∠CBE = 360° .....(3)

From figure,

∠ABE + ∠CBE = 180° [Linear pair]

Putting this value of ∠ABE + ∠CBE in Eq 3 we get,

∠APE + ∠CQE + 180° = 360°

⇒ ∠APE + ∠CQE = 360° - 180°

⇒ ∠APE + ∠CQE = 180°

Hence, proved that ∠APE and ∠CQE are supplementary.

In the given figure, AB is the diameter of the circle with centre O.

If ∠ADC = 32°, find angle BOC.

Answer

We know that,

Angle at the centre is twice the angle at remaining circumference.

Arc AC subtends ∠AOC at the centre and ∠ADC at the remaining part of the circle.

⇒ ∠AOC = 2∠ADC

⇒ ∠AOC = 2 x 32° = 64°

From figure,

∠AOC and ∠BOC are linear pair,

∴ ∠AOC + ∠BOC = 180°

⇒ 64° + ∠BOC = 180°

⇒ ∠BOC = 180° - 64° = 116°.

Hence, ∠BOC = 116°.

In a cyclic quadrilateral PQRS, angle PQR = 135°. Sides SP and RQ produced meet at point A whereas sides PQ and SR produced meet at point B.

If ∠A : ∠B = 2 : 1, find angles A and B.

Answer

Let ∠A = 2x and ∠B = x.

In cyclic quadrilateral PQRS,

⇒ ∠PSR + ∠PQR = 180° [As sum of opposite angles in a cyclic quadrilateral = 180°]

⇒ ∠PSR + 135° = 180°

⇒ ∠PSR = 180° - 135° = 45°.

From figure,

⇒ ∠PQR + ∠PQA = 180° [Linear pairs]

⇒ ∠PQA + 135° = 180°

⇒ ∠PQA = 180° - 135° = 45°.

In △PBS,

⇒ ∠BSP + ∠BPS + ∠PBS = 180°

⇒ ∠PSR + ∠BPS + ∠B = 180°

⇒ ∠BPS + 45° + x = 180°

⇒ ∠BPS = 180° - 45° - x

⇒ ∠BPS = 135° - x ............(1)

We know that,

An exterior angle is equal to the sum of two opposite interior angles.

In △PQA,

⇒ ∠BPS = ∠PQA + ∠A

⇒ ∠BPS = 45° + 2x ...........(2)

From 1 and 2 we get,

⇒ 135° - x = 45° + 2x

⇒ 2x + x = 135° - 45°

⇒ 3x = 90°

⇒ x = $\dfrac{90°}{3}$ = 30°.

∠A = 2x = 2 x 30° = 60°

∠B = x = 30°.

Hence, ∠A = 60° and ∠B = 30°.

In the following figure, ABCD is a cyclic quadrilateral in which AD is parallel to BC. If the bisector of angle A meets BC at point E and the given circle at point F, prove that :

(i) EF = FC

(ii) BF = DF

Answer

AF is the angle bisector of ∠A,

∴ ∠BAF = ∠DAF

Also,

∠DAE = ∠BAE .......(1)

and

∠DAE = ∠AEB ........(2) [Alternate angles are equal]

From (1) and (2) we get,

∠BAE = ∠AEB

(i) In △ABE,

⇒ ∠BAE + ∠AEB + ∠ABE = 180°

⇒ ∠AEB + ∠AEB + ∠ABE = 180°

⇒ 2∠AEB + ∠ABE = 180°

⇒ ∠ABE = 180° - 2∠AEB

Since, ABCD is a cyclic quadrilateral and sum of opposite angles in a cyclic quadrilateral = 180°.

∴ ∠ABC + ∠ADC = 180°

⇒ ∠ABE + ∠ADC = 180°

⇒ 180° - 2∠AEB + ∠ADC = 180°

⇒ ∠ADC = 180° - 180° + 2∠AEB

⇒ ∠ADC = 2∠AEB .........(3)

Since, ADCF is also a cyclic quadrilateral,

∴ ∠AFC + ∠ADC = 180°

⇒ ∠AFC = 180° - ∠ADC

⇒ ∠AFC = 180° - 2∠AEB [From (3)]

In △ECF,

⇒ ∠EFC + ∠ECF + ∠FEC = 180°

⇒ ∠AFC + ∠ECF + ∠FEC = 180° [From figure, ∠EFC = ∠AFC]

⇒ ∠AFC + ∠ECF + ∠AEB = 180° [∠FEC = ∠AEB (Vertically opposite angles are equal)]

⇒ ∠ECF = 180° - (∠AFC + ∠AEB)

⇒ ∠ECF = 180° - (180° - 2∠AEB + ∠AEB)

⇒ ∠ECF = ∠AEB

⇒ ∠ECF = ∠FEC

∴ EF = FC [As sides opposite to equal angles are equal.]

Hence, proved that EF = FC.

(ii) AF is the angle bisector of ∠A,

∴ ∠BAF = ∠DAF

∴ arc BF = arc DF [As equal arcs subtends equal angles]

∴ BF = DF [Equal arcs have equal chords]

Hence, proved that BF = DF.

ABCD is a cyclic quadrilateral. Sides AB and DC produced meet at point E; whereas sides BC and AD produced meet at point F. If ∠DCF : ∠F : ∠E = 3 : 5 : 4, find the angles of the cyclic quadrilateral ABCD.

Answer

Let ∠DCF = 3x, ∠F = 5x and ∠E = 4x.

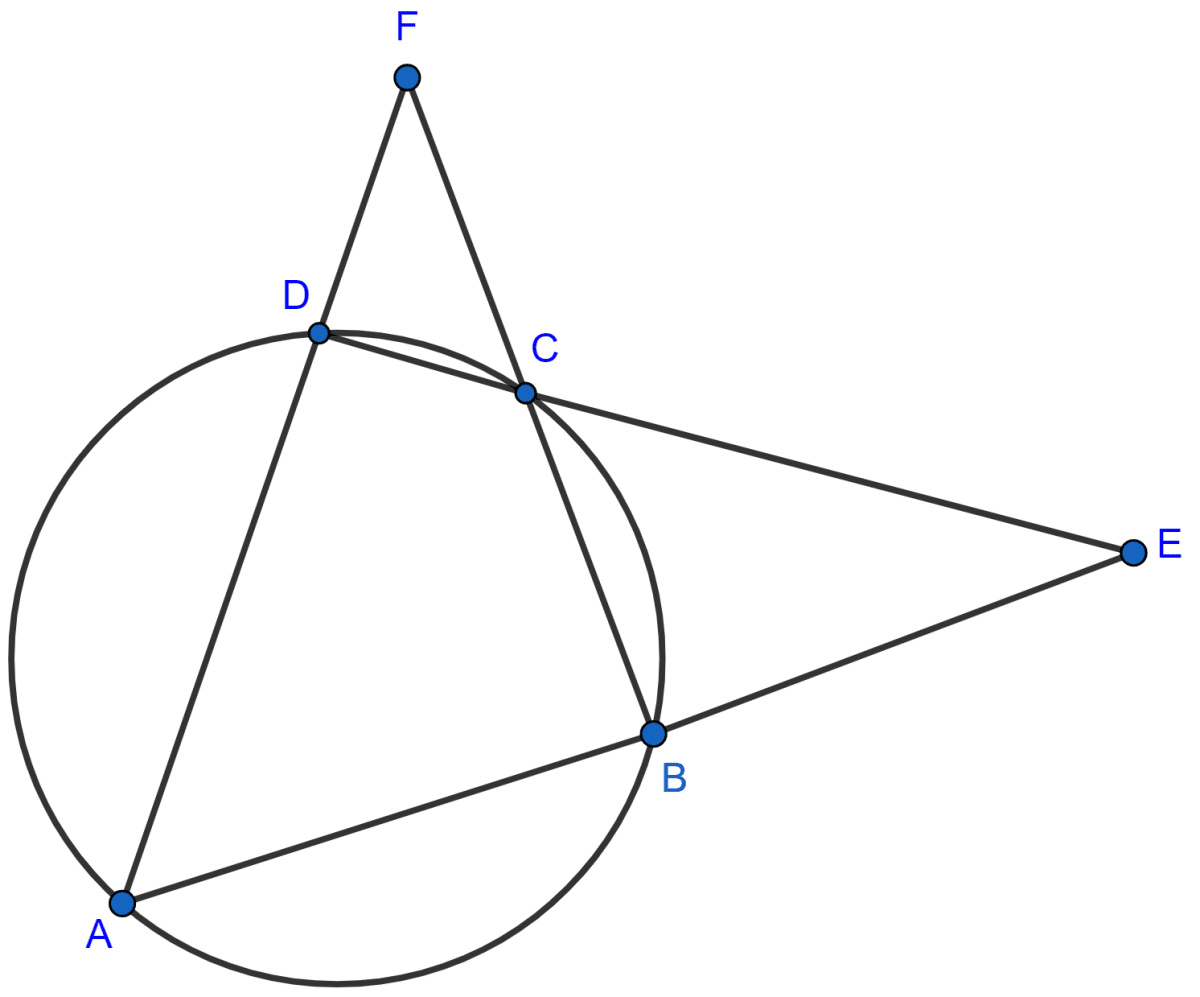
From figure,

⇒ ∠A + ∠DCB = 180° [As sum of opposite angles in a cyclic quadrilateral = 180°]

⇒ ∠A = 180° - ∠DCB

⇒ ∠A = 180° - (180° - ∠DCF) [As ∠DCF and DCB form a linear pair]

⇒ ∠A = ∠DCF = 3x.

In △CDF,

∠CDA = ∠F + ∠DCF [As exterior angle in a triangle is equal to sum of two opposite interior angles.]

= 5x + 3x = 8x

In △BCE,

⇒ ∠ABC = ∠BCE + ∠E [As exterior angle in a triangle is equal to sum of two opposite interior angles.]

⇒ ∠ABC = ∠DCF + ∠E [∠BCE = ∠DCF, Vertically opposite angles are equal]

⇒ ∠ABC = 3x + 4x = 7x.

In cyclic quadrilateral ABCD,

⇒ ∠ABC + ∠CDA = 180°

⇒ 7x + 8x = 180°

⇒ 15x = 180°

⇒ x = $\dfrac{180°}{15}$ = 12°.

∠A = 3x = 3 x 12° = 36°,

∠B = 7x = 7 x 12° = 84°,

∠C = 180° - ∠A = 180° - 36° = 144°,

∠D = 8x = 8 x 12° = 96°.

Hence, ∠A = 36°, ∠B = 84°, ∠C = 144°, ∠D = 96°.

In the given figure, AB is the diameter of a circle with center O. If chord AC = chord AD, prove that :

(i) arc BC = arc DB

(ii) AB is the bisector of ∠CAD.

Further, if the length of arc AC is twice the length of arc BC, find :

(a) ∠BAC

(b) ∠ABC

Answer

Join BC and BD.

In △ABC and △ABD,

⇒ AC = AD [Given]

⇒ AB = AB [Common]

⇒ ∠ACB = ∠ADB [Both = 90°, Angle in semi-circle is a right angle.]

∴ △ ABC ≅ △ ABD [By RHS axiom of congruency]

(i) Since,

△ABC ≅ △ABD

∴ BC = BD [By C.P.C.T.]

∴ Arc BC = Arc BD [Equal chords have equal arcs].

Hence, proved that arc BC = arc BD.

(ii) Since,

△ABC ≅ △ABD

∴ ∠BAC = ∠BAD [By C.P.C.T.]

∴ AB is the bisector of ∠CAD.

Hence, proved that AB is the bisector of ∠CAD.

(a) Given,

arc AC = 2 arc BC

∴ ∠ABC = 2∠BAC

But,

⇒ ∠ABC + ∠BAC = 90° [ΔABC is right angled at C]

⇒ 2∠BAC + ∠BAC = 90°

⇒ 3∠BAC = 90°

⇒ ∠BAC = $\dfrac{90°}{3}$ = 30°.

Hence, ∠BAC = 30°.

(b) ∠ABC = 2∠BAC = 2 x 30° = 60°.

Hence, ∠ABC = 60°.

In cyclic quadrilateral ABCD; AD = BC, ∠BAC = 30° and ∠CBD = 70°; find :

(i) ∠BCD

(ii) ∠BCA

(iii) ∠ABC

(iv) ∠ADC

Answer

(i) From figure,

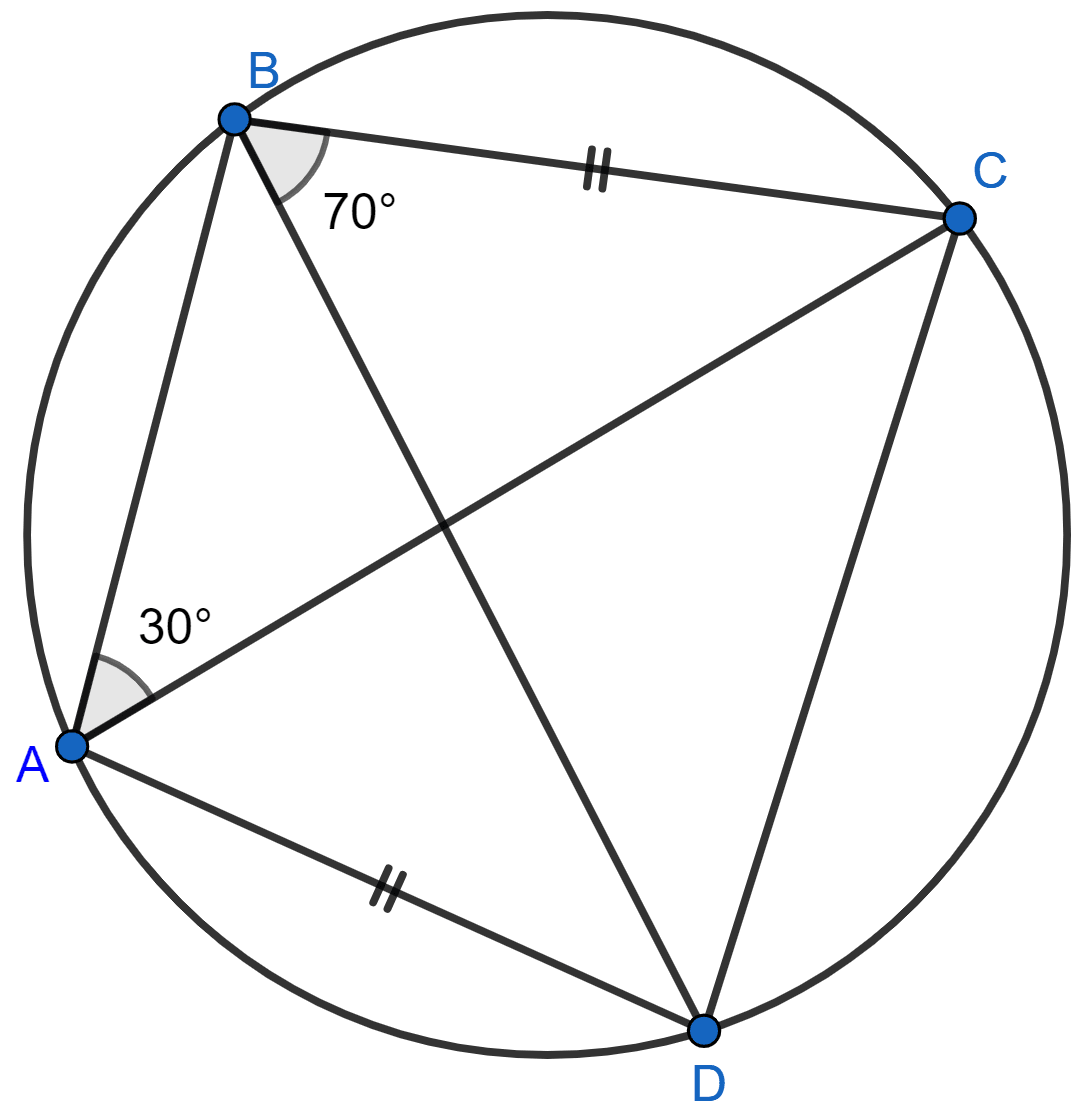
∠DAC = ∠CBD = 70° [Angles in same segment are equal]

∠BAD = ∠BAC + ∠DAC = 30° + 70° = 100°.

Since, sum of opposite angles of cyclic quadrilateral = 180°.

⇒ ∠BAD + ∠BCD = 180°

⇒ 100° + ∠BCD = 180°

⇒ ∠BCD = 180° - 100° = 80°.

Hence, ∠BCD = 80°.

(ii) Since, AD = BC

∠ACD = ∠BDC ............(1) [Equal chords subtends equal angles]

As,

Angles in same segment are equal.

∠ACB = ∠ADB ...........(2)

Adding (1) and (2) we get,

⇒ ∠ACD + ∠ACB = ∠BDC + ∠ADB

⇒ ∠BCD = ∠ADC = 80°.

In △BCD,

⇒ ∠CBD + ∠BCD + ∠BDC = 180°

⇒ 70° + 80° + ∠BDC = 180°

⇒ 150° + ∠BDC = 180°

⇒ ∠BDC = 180° - 150° = 30°.

∠ACD = ∠BDC = 30° [As equal chords subtends equal angles.]

From figure,

⇒ ∠BCA = ∠BCD - ∠ACD = 80° - 30° = 50°.

Hence, ∠BCA = 50°.

(iii) As sum of opposite angles in a cyclic quadrilateral = 180°.

⇒ ∠ADC + ∠ABC = 180°

⇒ 80° + ∠ABC = 180°

⇒ ∠ABC = 180° - 80° = 100°.

Hence, ∠ABC = 100°.

(iv) From part (ii) we get,

Hence, ∠ADC = 80°.

In the given figure, ∠ACE = 43° and ∠CAF = 62°; find the values of a, b and c.

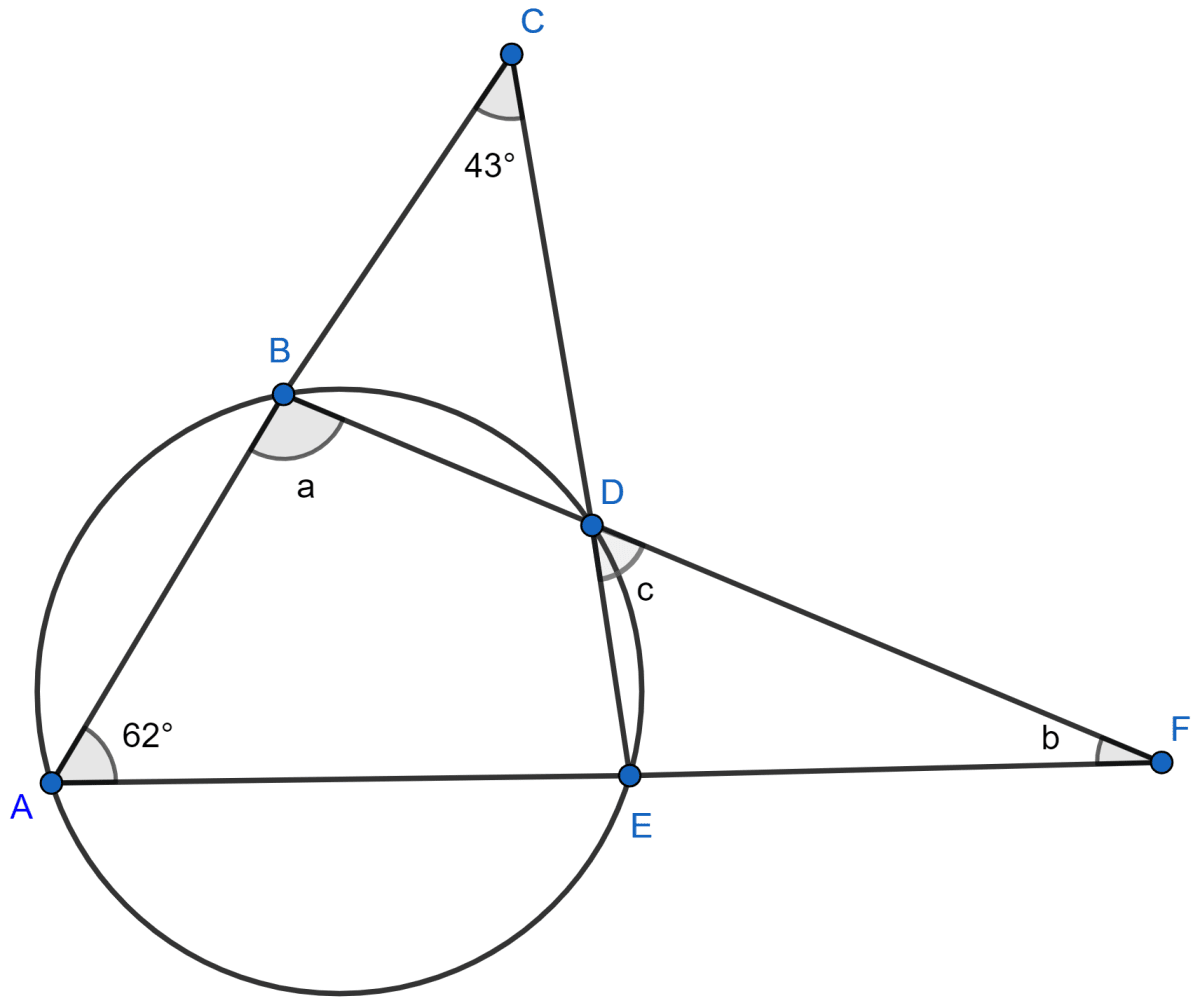
Answer

In △AEC,

⇒ ∠ACE + ∠CAE + ∠AEC = 180°

⇒ 43° + 62° + ∠AEC = 180°

⇒ ∠AEC = 180° - 105° = 75°.

From figure,

⇒ ∠ABD + ∠AED = 180° [As sum of opposite angles in a cyclic quadrilateral = 180°]

⇒ a + ∠AEC = 180° [From figure, ∠AED = ∠AEC]

⇒ a + 75° = 180°

⇒ a = 180° - 75° = 105°.

∠BDC = c [Vertically opposite angles are equal]

∠DBC = 180° - a [Linear pairs]
= 180° - 105°
= 75°.

In △DBC,

⇒ ∠DBC + ∠BCD + ∠BDC = 180° [Angle sum property of triangle]

⇒ 75° + 43° + c = 180°

⇒ 118° + c = 180°

⇒ c = 180° - 118° = 62°.

In △BAF,

⇒ ∠ABF + ∠BAF + ∠AFB = 180° [Angle sum property of triangle]

⇒ a + 62° + b = 180°

⇒ 105° + 62° + b = 180°

⇒ b + 167° = 180°

⇒ b = 180° - 167° = 13°.

Hence, a = 105°, b = 13° and c = 62°.

In the given figure, AB is parallel to DC, ∠BCE = 80° and ∠BAC = 25°.

Find :

(i) ∠CAD

(ii) ∠CBD

(iii) ∠ADC

Answer

(i) We know that,

Exterior angle of a cyclic quadrilateral is equal to interior opposite angle.

∠BAD = Exterior ∠BCE = 80°.

From figure,

∠CAD = ∠BAD - ∠BAC = 80° - 25° = 55°.

Hence, ∠CAD = 55°.

(ii) We know that,

Angles in same segment are equal.

∴ ∠CBD = ∠CAD = 55°.

Hence, ∠CBD = 55°.

(iii) We know that,

Angles in same segment are equal.

∴ ∠BDC = ∠BAC = 25°.

AB || DC and BD is transversal.

So, ∠ABD = ∠BDC = 25°. [Alternate angles are equal]

From figure,

∠ABC = ∠ABD + ∠CBD = 25° + 55° = 80°.

In cyclic quadrilateral ABCD,

⇒ ∠ABC + ∠ADC = 180° [Sum of opposite angles in a cyclic quadrilateral = 180°]

⇒ 80° + ∠ADC = 180°

⇒ ∠ADC = 180° - 80° = 100°.

Hence, ∠ADC = 100°.

In the figure, given below, CP bisects angle ACB. Show that DP bisects angle ADB.

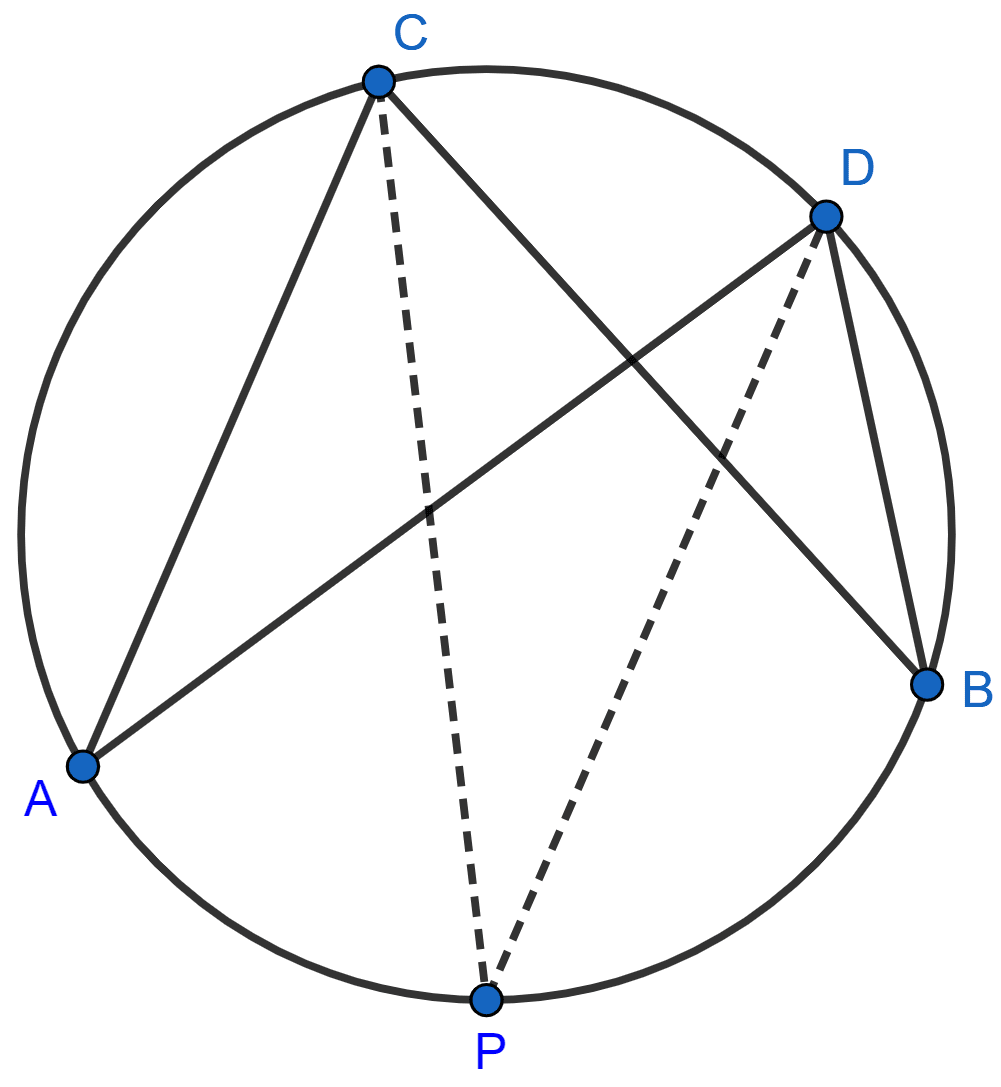
Answer

Since, CP is the bisector of ∠ACB,

∴ ∠ACP = ∠BCP .........(1)

We know that,

Angles in same segment are equal.

∴ ∠ACP = ∠ADP ..........(2)

∠BCP = ∠BDP ...........(3)

From (1) and (2) we get,

∠BCP = ∠ADP ...........(4)

From (3) and (4) we get,

∠ADP = ∠BDP.

∴ DP is the bisector of ∠ADB.

Hence, proved that DP is the bisector of ∠ADB.

In the figure, given below, AD = BC, ∠BAC = 30° and ∠CBD = 70°. Find :

(i) ∠BCD

(ii) ∠BCA

(iii) ∠ABC

(iv) ∠ADB

Answer

We know that,

Angles in same segment are equal.

∴ ∠CAD = ∠CBD = 70°.

From figure,

∠BAD = ∠BAC + ∠CAD = 30° + 70° = 100°.

(i) As sum of opposite angles in cyclic quadrilateral = 180°.

In cyclic quadrilateral ABCD,

⇒ ∠BCD + ∠BAD = 180°

⇒ ∠BCD + 100° = 180°

⇒ ∠BCD = 180° - 100° = 80°.

Hence, ∠BCD = 80°.

(ii) Since, AD = BC.

∴ ABCD is an isosceles trapezium and AB || DC.

∠DCA = ∠BAC = 30° [Alternate angles]

From figure,

∠BCA = ∠BCD - ∠DCA = 80° - 30° = 50°.

Hence, ∠BCA = 50°.

(iii) As angles in same segment are equal.

∠ABD = ∠DCA = 30°

From figure,

∠ABC = ∠ABD + ∠CBD = 30° + 70° = 100°.

Hence, ∠ABC = 100°.

(iv) As angles in same segment are equal.

∠ADB = ∠BCA = 50°.

Hence, ∠ADB = 50°.

In the given figure, AD is a diameter. O is the centre of the circle. AD is parallel to BC and ∠CBD = 32°. Find :

(i) ∠OBD

(ii) ∠AOB

(iii) ∠BED

Answer

(i) Given,

AD || BC

∴ OD || BC and BD is transversal.

∠ODB = ∠CBD = 32° [Alternate angles are equal]

In △OBD,

OB = OD [Radius of same circle]

∠OBD = ∠ODB = 32°.

Hence, ∠OBD = 32°.

(ii) Given,

AD || BC

∴ AO || BC and OB is transversal.

∠AOB = ∠OBC [Alternate angles are equal]

From figure,

∠OBC = ∠OBD + ∠DBC = 32° + 32° = 64°.

∴ ∠AOB = 64°.

Hence, ∠AOB = 64°.

(iii) In △OAB,

OA = OB [Radius of same circle]

∠OAB = ∠OBA = x (let)

⇒ ∠OAB + ∠OBA + ∠AOB = 180°

⇒ x + x + 64° = 180°

⇒ 2x = 180° - 64°

⇒ 2x = 116°

⇒ x = $\dfrac{116°}{2}$ = 58°

i.e., ∠OAB = 58°.

From figure,

∠DAB = ∠OAB = 58°.

We know that,

Angle in same segment are equal.

∠BED = ∠DAB = 58°.

Hence, ∠BED = 58°.

In the figure given, O is the centre of the circle. ∠DAE = 70°. Find giving suitable reasons, the measure of

(i) ∠BCD

(ii) ∠BOD

(iii) ∠OBD

Answer

(i) Given,

∠DAE = 70°

⇒ ∠DAE + ∠BAD = 180° [Linear pairs]

⇒ 70° + ∠BAD = 180°

⇒ ∠BAD = 180° - 70° = 110°.

We know that,

Sum of opposite angles in a cyclic quadrilateral = 180°

⇒ ∠BCD + ∠BAD = 180°

⇒ ∠BCD + 110° = 180°

⇒ ∠BCD = 180° - 110° = 70°.

Hence, ∠BCD = 70°.

(ii) We know that,

Angle which an arc subtends at the centre is double that which it subtends at any point on the remaining part of the circumference.

⇒ ∠BOD = 2∠BCD = 2 × 70° = 140°.

Hence, ∠BOD = 140°.

(iii) In △OBD,

OB = OD [Radius of same circle]

∠OBD = ∠ODB = x.

⇒ ∠OBD + ∠ODB + ∠BOD = 180°

⇒ x + x + 140° = 180°

⇒ 2x = 180° - 140°

⇒ 2x = 40°

⇒ x = $\dfrac{40°}{2}$ = 20°.

∴ ∠OBD = 20°.

Hence, ∠OBD = 20°.