Tangents and Intersecting Chords

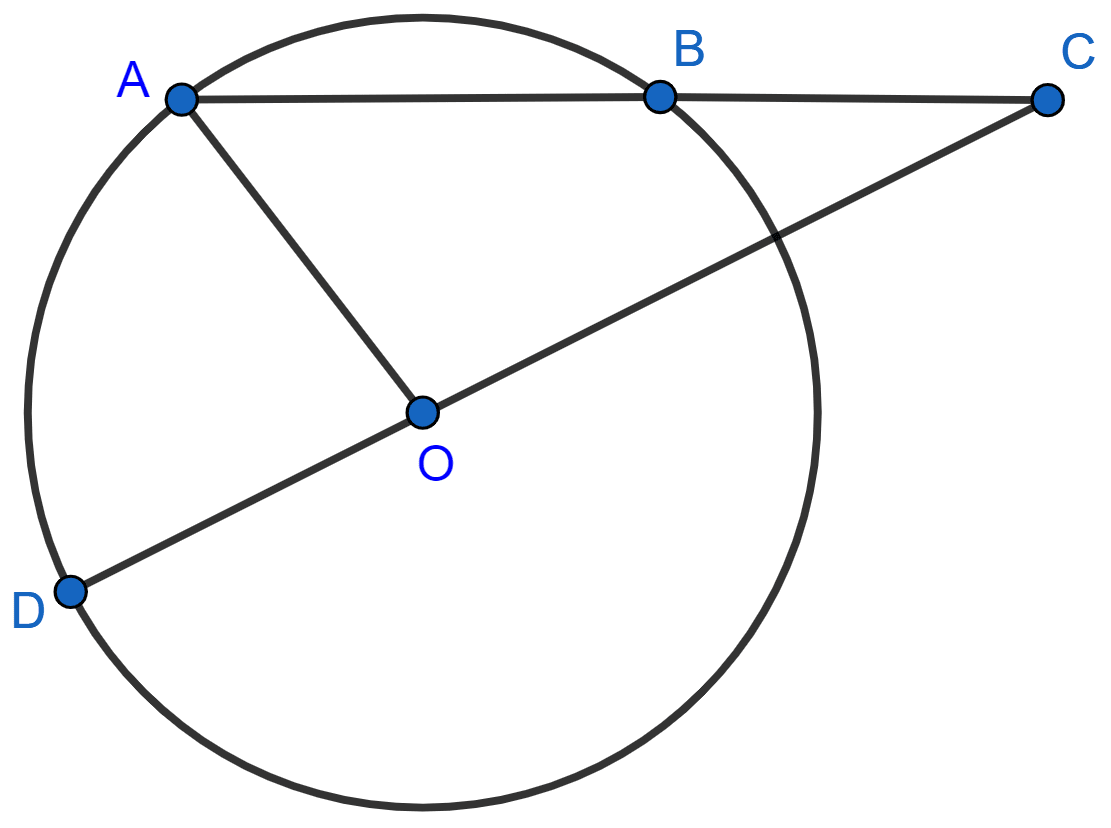
In the given figure, PA, PB and QR are tangents to a circle. If perimeter of the △PQR = 18 cm, the length of tangent PA is :

1. 18 cm

2. 27 cm

3. 9 cm

4. none of these

Answer

Let tangent QR intersect circle at point D.

Given,

Perimeter of the △PQR = 18 cm.

⇒ PQ + QD + RD + PR = 18 .............(1)

We know that,

Two tangents drawn to a circle form an exterior point are equal in length.

∴ PA = PB = x (let), RD = RA and QD = QB.

Substituting above values in equation (1), we get :

⇒ PQ + QB + RA + PR = 18

⇒ PB + PA = 18

⇒ x + x = 18

⇒ 2x = 18

⇒ x = 9 cm.

∴ PA = 9 cm.

Hence, Option 3 is the correct option.

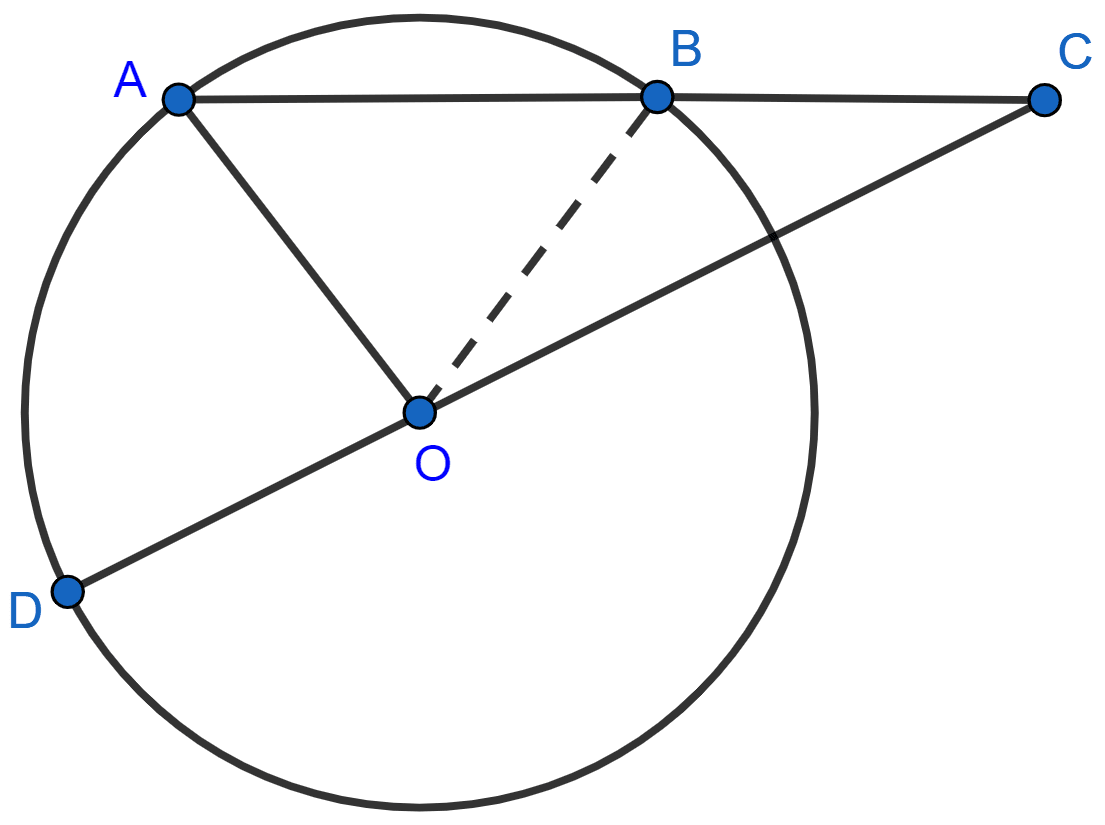
In the given figure, APB is tangent to the inner circle and also a chord of outer circle. Both the circles are concentric. If OA = 10 cm and OP = 6 cm, the length of AB is :

1. 16 cm

2. 10 cm

3. 14 cm

4. 20 cm

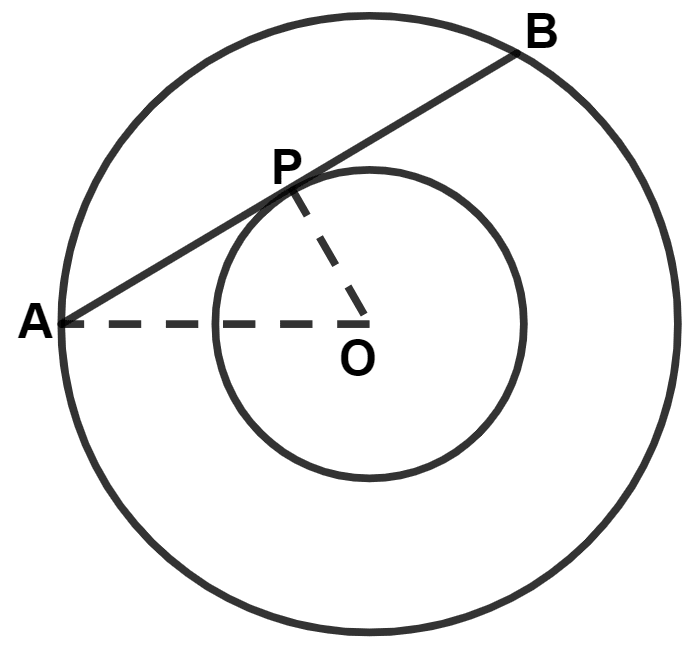
Answer

We know that,

Tangent at any point of a circle and the radius through this point are perpendicular to each other.

∴ OP ⊥ AP

In right angle triangle OAP,

By pythagoras theorem,

⇒ OA² = OP² + AP²

⇒ 10² = 6² + AP²

⇒ 100 = 36 + AP²

⇒ AP² = 100 - 36

⇒ AP² = 64

⇒ AP = $\sqrt{64}$ = 8 cm.

Since, AB is the chord to the bigger circle, with center O.

We know that,

Perpendicular from center to the chord, bisects it.

∴ PB = AP = 8 cm.

AB = AP + PB = 8 + 8 = 16 cm.

Hence, Option 1 is the correct option.

A, B and C are three circles which touch each other as shown. Using the information, given in the diagram, we find the length AB as :

1. 6 cm

2. 17 cm

3. (289 - 9 - 2) cm

4. 11 cm

Answer

From figure,

AC = 9 + 6 = 15 cm

BC = 2 + 6 = 8 cm

In right angle triangle ACB,

⇒ AB² = AC² + BC²

⇒ AB² = 15² + 8²

⇒ AB² = 225 + 64

⇒ AB² = 289

⇒ AB = $\sqrt{289}$ = 17 cm.

Hence, Option 2 is the correct option.

BC is a tangent to the circle with center O. OD is radius of the circle. If ∠DOC = 100°, ∠B is equal to :

1. 50°

2. 60°

3. 40°

4. 70°

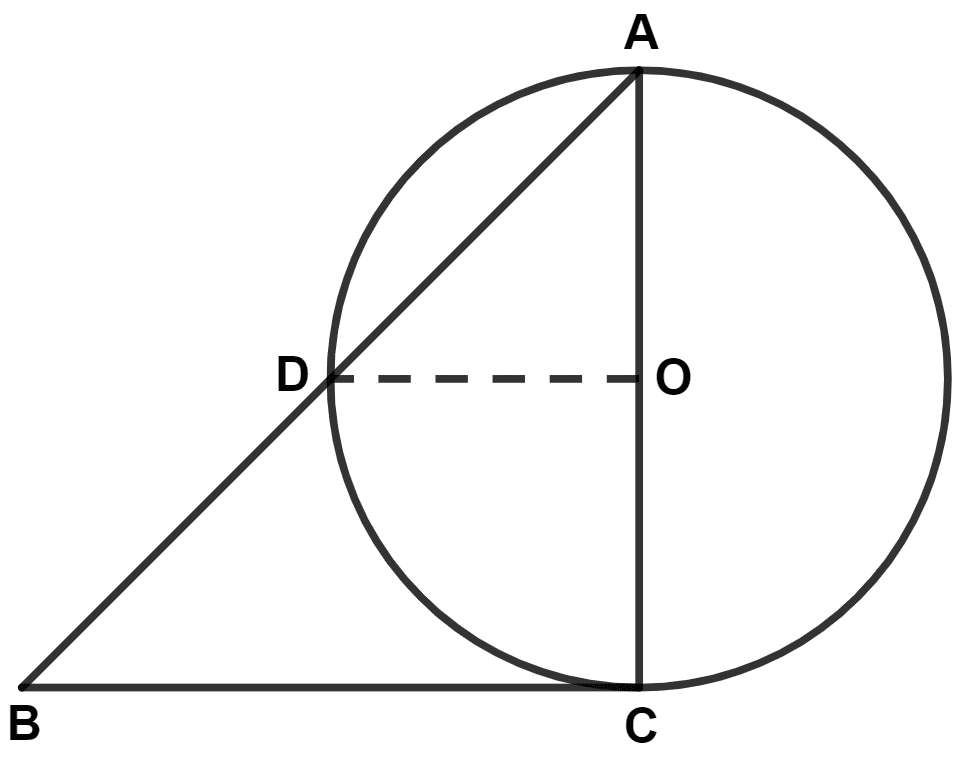
Answer

From figure,

OD = OA (Radius of same circle)

In △OAD,

∠ODA = ∠OAD = x (let) (As angles opposite to equal sides are equal)

Since, exterior angle in a triangle is equal to the sum of two opposite interior angles.

∴ ∠DOC = ∠ODA + ∠OAD

⇒ 100° = 2x

⇒ x = $\dfrac{100°}{2}$

⇒ x = 50°.

⇒ ∠OAD = 50°.

We know that,

Tangent at any point of a circle and the radius through this point are perpendicular to each other.

∴ ∠BCA = 90°.

In △ABC,

By angle sum property of triangle,

⇒ ∠ABC + ∠BCA + ∠CAB = 180°

⇒ ∠ABC + ∠BCA + ∠OAD = 180° [∵ From figure, ∠CAB = ∠OAD]

⇒ ∠ABC + 90° + 50° = 180°

⇒ ∠ABC + 140° = 180°

⇒ ∠ABC = 180° - 140° = 40°.

Hence, Option 3 is the correct option.

PA and PB are tangents to a circle with center O. If angle BPA = 70°, the angle ACB is :

1. 70°

2. 105°

3. 140°

4. 55°

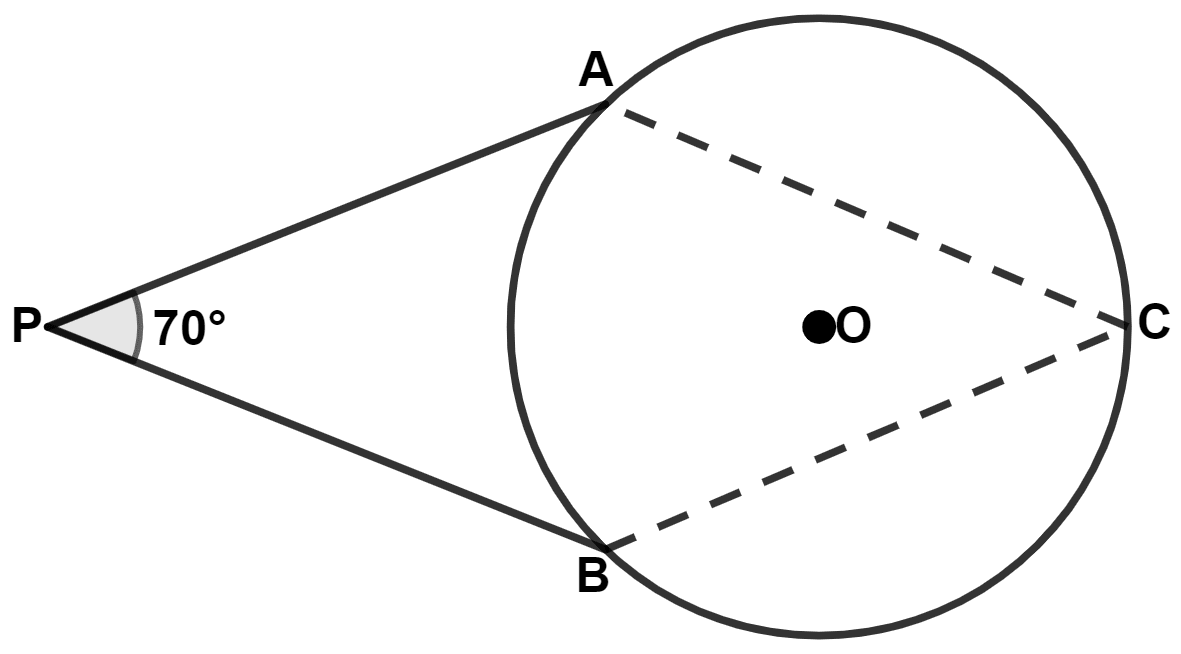
Answer

Join OA and OB.

We know that,

Tangent at any point of a circle and the radius through this point are perpendicular to each other.

∴ ∠OAP = 90° and ∠OBP = 90°

In quadrilateral OAPB,

⇒ ∠OAP + ∠APB + ∠PBO + ∠BOA = 360°

⇒ 90° + 70° + 90° + ∠BOA = 360°

⇒ ∠BOA + 250° = 360°

⇒ ∠BOA = 360° - 250° = 110°.

We know that,

The angle which an arc of a circle subtends at the center is double that which it subtends at any point on the remaining part of the circumference.

∴ ∠AOB = 2∠ACB

⇒ ∠ACB = $\dfrac{1}{2}$ ∠AOB

⇒ ∠ACB = $\dfrac{1}{2} \times 110°$ = 55°.

Hence, Option 4 is the correct option.

The radius of a circle is 8 cm. Calculate the length of a tangent drawn to this circle from a point at a distance of 10 cm from its centre.

Answer

Let a circle be with centre O and radius 8 cm.

Let P be an external point from where a tangent is drawn to meet the circle at T.

∴ OP = 10 cm and OT = 8 cm

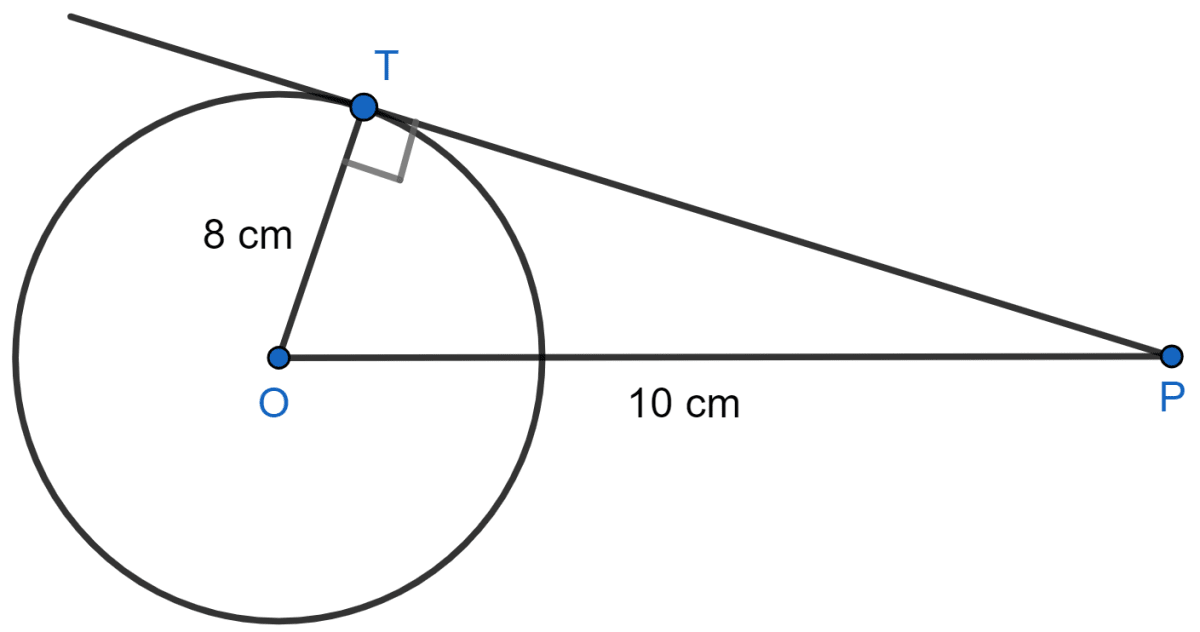
We know that,

The tangent at any point of a circle and the radius through this point are perpendicular to each other.

In right ∆OTP, we have

⇒ OP² = OT² + PT² [By Pythagoras Theorem]

⇒ 10² = 8² + PT²

⇒ PT² = 100 - 64 = 36

⇒ PT = 6 cm.

Hence, the length of tangent = 6 cm.

In the given figure, O is the centre of the circle and AB is a tangent to the circle at B. If AB = 15 cm and AC = 7.5 cm, calculate the radius of the circle.

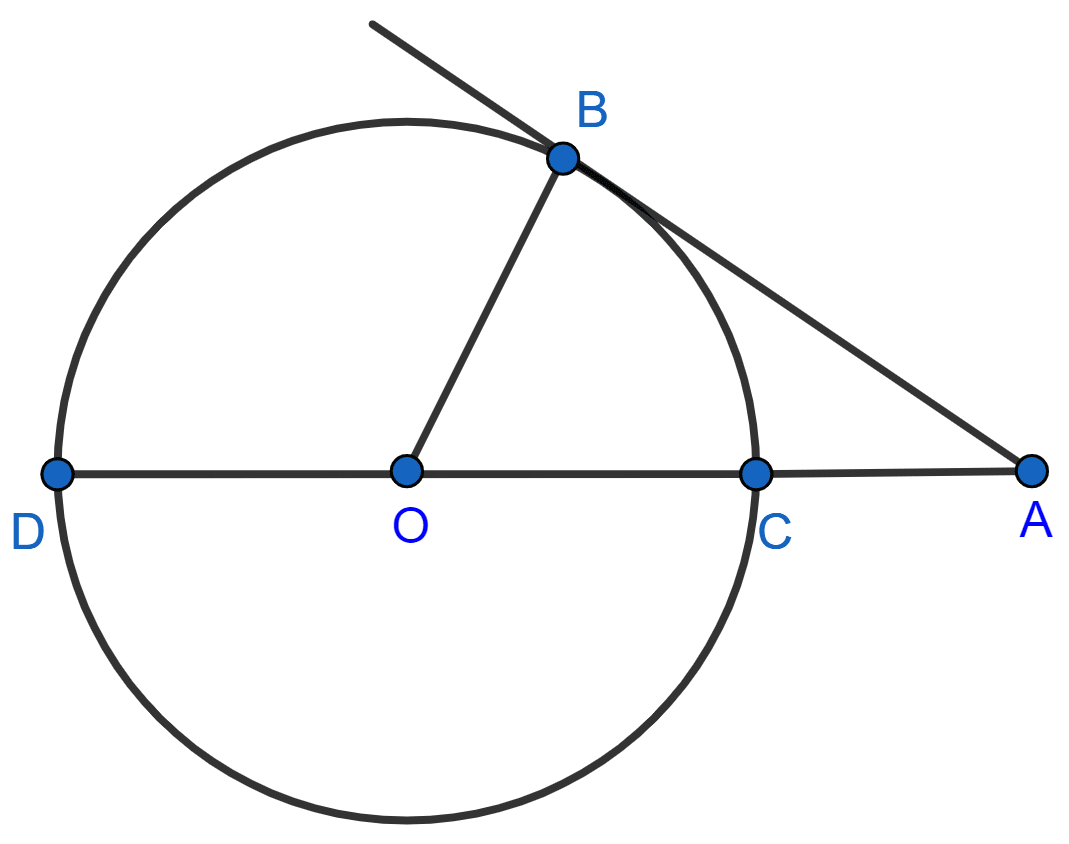
Answer

Let the radius of the circle to be r cm.

So, AO = AC + OC = (7.5 + r) cm.

In right ∆AOB, we have

⇒ AO² = AB² + OB² [By Pythagoras Theorem]

⇒ (7.5 + r)² = 15² + r²

⇒ 56.25 + r² + 15r = 225 + r²

⇒ 15r = 225 - 56.25

⇒ 15r = 168.75

⇒ r = $\dfrac{168.75}{15}$ = 11.25 cm.

Hence, radius of circle = 11.25 cm.

Two circles of radii 5 cm and 3 cm are concentric. Calculate the length of a chord of the outer circle which touches the inner.

Answer

We know that,

The tangent at any point of a circle and the radius through this point are perpendicular to each other.

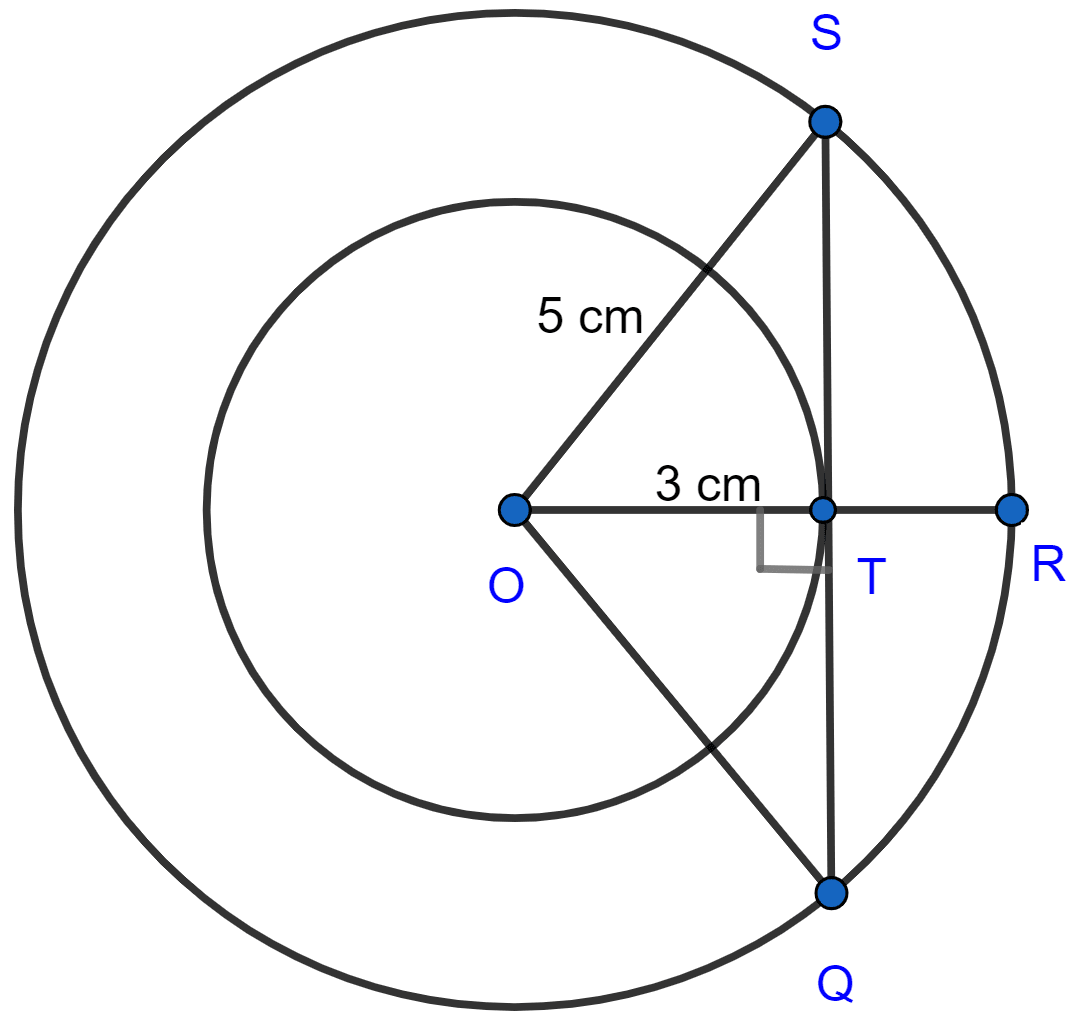
In right triangle OST, we have

⇒ OS² = OT² + ST²

⇒ 5² = 3² + ST²

⇒ ST² = 25 - 9

⇒ ST² = 16

⇒ ST = $\sqrt{16}$

⇒ ST = 4 cm.

Similarly, in right triangle OQT, we have

⇒ OQ² = OT² + QT²

⇒ 5² = 3² + QT²

⇒ QT² = 25 - 9

⇒ QT² = 16

⇒ QT = $\sqrt{16}$

⇒ QT = 4 cm.

From figure,

QS = ST + QT = 4 + 4 = 8 cm.

Hence, the length of a chord of the outer circle which touches the inner = 8 cm.

Three circles touch each other externally. A triangle is formed when the centers of these circles are joined together. Find the radii of the circles, if the sides of the triangle formed are 6 cm, 8 cm and 9 cm.

Answer

Let there be three circles with center A, B and C and ABC be the triangle formed when centres of 3 circles are joined.

Let,

AB = 6 cm, AC = 8 cm and BC = 9 cm.

Let the radii of the circles having centres A, B and C be r₁, r₂ and r₃ respectively.

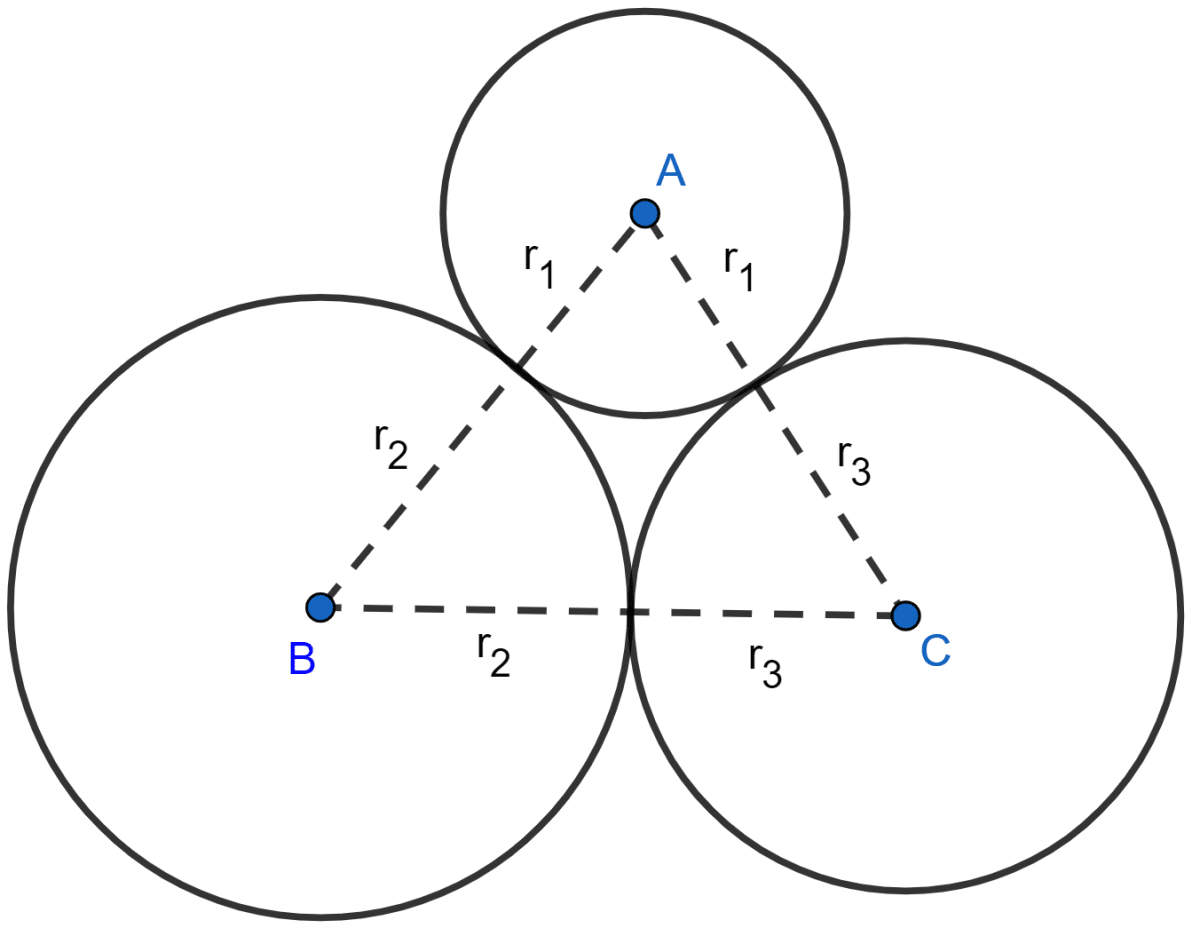
As,

⇒ AB = r₁ + r₂ = 6 ............(1)

⇒ AC = r₁ + r₃ = 8 ............(2)

⇒ BC = r₂ + r₃ = 9 .............(3)

Adding all the above equations, we get

⇒ r₁ + r₂ + r₁ + r₃ + r₂ + r₃ = 6 + 8 + 9

⇒ 2(r₁ + r₂ + r₃) = 23

⇒ r₁ + r₂ + r₃ = $\dfrac{23}{2}$

⇒ r₁ + r₂ + r₃ = 11.5 cm ...........(4)

Substituting value of r₂ + r₃ = 9 in equation (4) we get :

⇒ r₁ + 9 = 11.5

⇒ r₁ = 11.5 - 9

⇒ r₁ = 2.5 cm.

Substituting value of r₁ + r₂ = 6 in equation (4) we get :

⇒ 6 + r₃ = 11.5

⇒ r₃ = 11.5 - 6

⇒ r₃ = 5.5 cm.

Substituting value of r₁ + r₃ = 8 in equation (4) we get :

⇒ 8 + r₂ = 11.5

⇒ r₂ = 11.5 - 8

⇒ r₂ = 3.5 cm.

Hence, the radii of the circles are 2.5 cm, 3.5 cm and 5.5 cm.

If the sides of a quadrilateral ABCD touch a circle, prove that AB + CD = BC + AD.

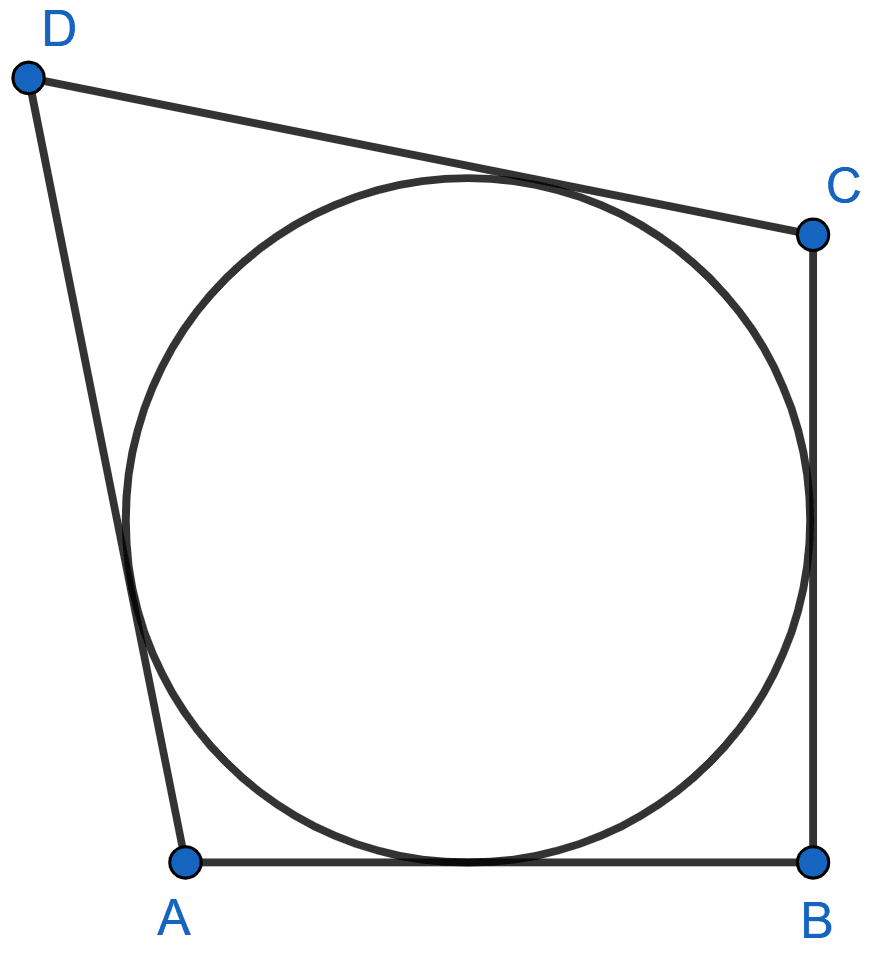
Answer

Let a circle touch the sides AB, BC, CD and DA of quadrilateral ABCD at P, Q, R and S respectively.

We know that,

If two tangents are drawn to a circle from an exterior point, the tangents are equal in length.

As, AP and AS are tangents to the circle from an external point A, we have

AP = AS ......... (1)

Similarly, we also get

BP = BQ ......... (2)

CR = CQ ......... (3)

DR = DS ......... (4)

Adding (1), (2), (3) and (4), we get

⇒ AP + BP + CR + DR = AS + DS + BQ + CQ

From figure,

AP + BP = AB, CR + DR = CD, AS + DS = AD and BQ + CQ = BC

⇒ AB + CD = AD + BC

Hence, proved that AB + CD = AD + BC.

If the sides of a parallelogram touch a circle, prove that the parallelogram is a rhombus.

Answer

Let a circle touch the sides AB, BC, CD and DA of parallelogram ABCD at P, Q, R and S respectively.

We know that,

If two tangents are drawn to a circle from an exterior point, the tangents are equal in length.

Now, from point A, AP and AS are tangents to the circle.

So, AP = AS .......... (1)

Similarly, we also have

BP = BQ .......... (2)

CR = CQ .......... (3)

DR = DS .......... (4)

Adding (1), (2), (3) and (4), we get :

AP + BP + CR + DR = AS + BQ + CQ + DS

From figure,

⇒ AP + BP = AB, BQ + CQ = BC, CR + DR = CD and AS + DS = AD.

∴ AB + CD = AD + BC ..........(5)

As,

AB = CD and BC = AD [Opposite sides of a parallelogram]

Substituting values in equation 5, we get :

⇒ AB + AB = BC + BC

⇒ 2AB = 2 BC

⇒ AB = BC

∴ AB = BC = CD = DA.

Hence, proved that ABCD is a rhombus.

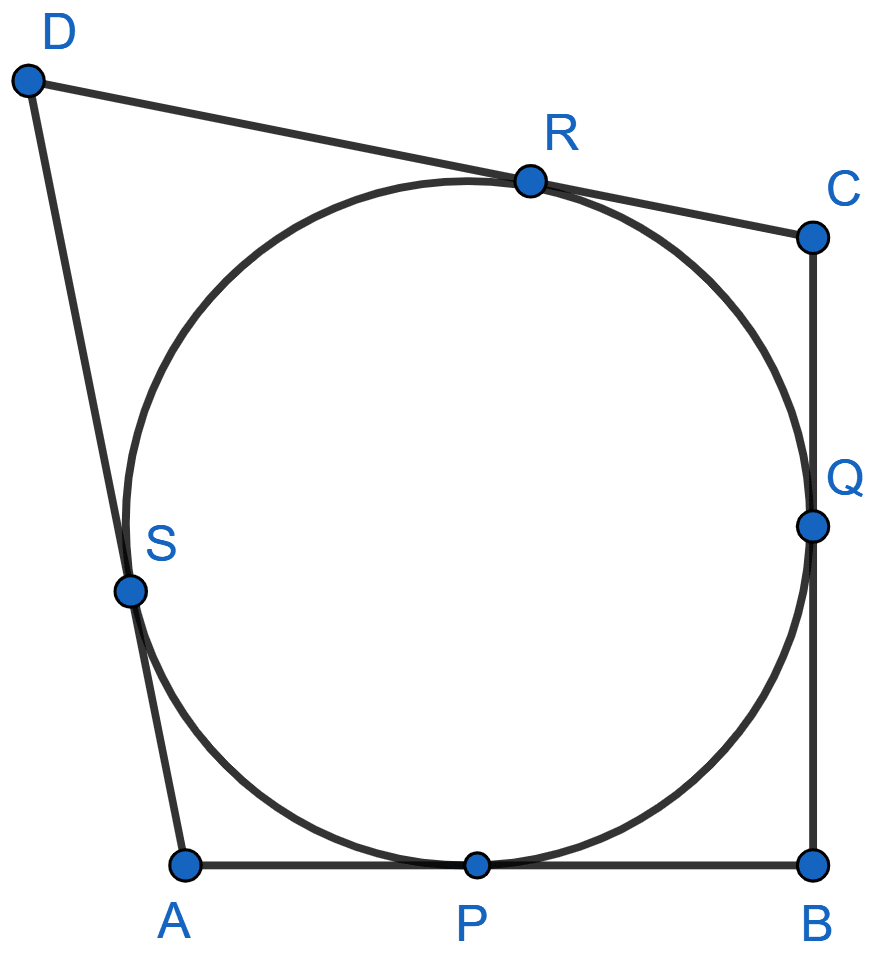
From the given figure, prove that :

AP + BQ + CR = BP + CQ + AR.

Also, show that :

AP + BQ + CR = $\dfrac{1}{2}$ x Perimeter of triangle ABC.

Answer

We know that,

If two tangents are drawn to a circle from an exterior point, the tangents are equal in length.

From point B, BQ and BP are the tangents to the circle

BQ = BP ........ (1)

From point A, AP and AR are the tangents to the circle

AP = AR ........ (2)

From point C, CR and CQ are the tangents to the circle

CR = CQ ........ (3)

Adding (1), (2) and (3) we get,

AP + BQ + CR = BP + CQ + AR ......... (4)

Hence, proved that AP + BQ + CR = BP + CQ + AR.

Now, adding AP + BQ + CR to both sides in (4), we get

2(AP + BQ + CR) = AP + BP + CQ + BQ + AR + CR ..........(5)

From figure,

AP + BP = AB, BQ + CQ = BC and AR + CR = AC.

Substituting above value in equation (5), we get :

⇒ 2(AP + BQ + CR) = AB + BC + CA

⇒ AP + BQ + CR = $\dfrac{1}{2}$(AB + BC + CA).

⇒ AP + BQ + CR = $\dfrac{1}{2}$ (Perimeter of △ABC). [∵ Perimeter = AB + BC + CA]

Hence, proved that AP + BQ + CR = $\dfrac{1}{2}$ (Perimeter of △ABC).

In the given figure, if AB = AC then prove that BQ = CQ.

Answer

As, from point A, AP and AR are the tangents to the circle.

We know that,

If two tangents are drawn to a circle from an exterior point, the tangents are equal in length.

So, we have AP = AR ..........(1)

From point B, BP and BQ are the tangents to the circle.

∴ BP = BQ ..........(2)

From point C, CQ and CR are the tangents to the circle.

∴ CQ = CR ............(3)

Adding equations (1), (2) and (3), we get :

⇒ AP + BP + CQ = AR + BQ + CR

⇒ (AP + BP) + CQ = (AR + CR) + BQ

⇒ AB + CQ = AC + BQ

Given,

AB = AC

∴ BQ = CQ.

Hence, proved that BQ = CQ.

Radii of two circles are 6.3 cm and 3.6 cm. State the distance between their centers if :

(i) they touch each other externally,

(ii) they touch each other internally.

Answer

Let O be the center of the circle with radius = 6.3 cm and O' be the center of circle with radius = 3.6 cm.

(i) When the two circles touch each other at P externally. O' and O are the centers of the circles. Join O'P and OP.

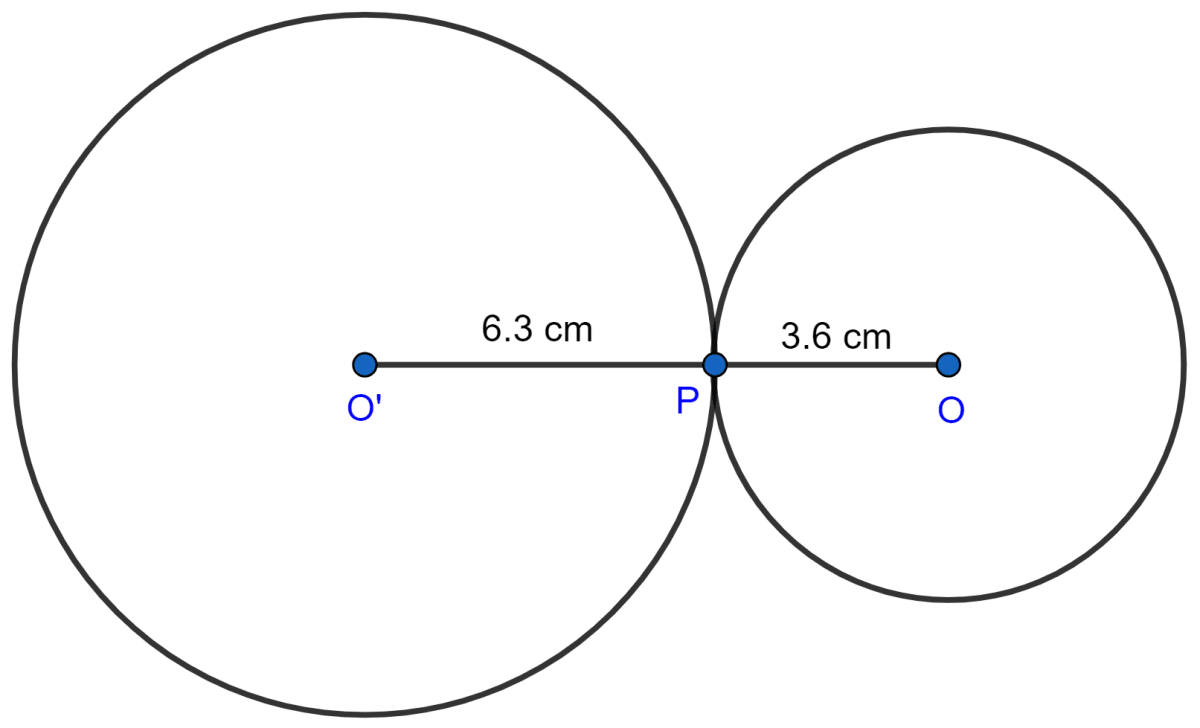
So, O'P = 6.3 cm, OP = 3.6 cm

Hence, the distance between their centres (O'O) is given by

O'O = O'P + OP = 6.3 + 3.6 = 9.9 cm.

Hence, distance between their centers if they touch each other externally is 9.9 cm.

(ii) When the two circles touch each other at P internally, O and O' are the centers of the circles. Join OP and O'P.

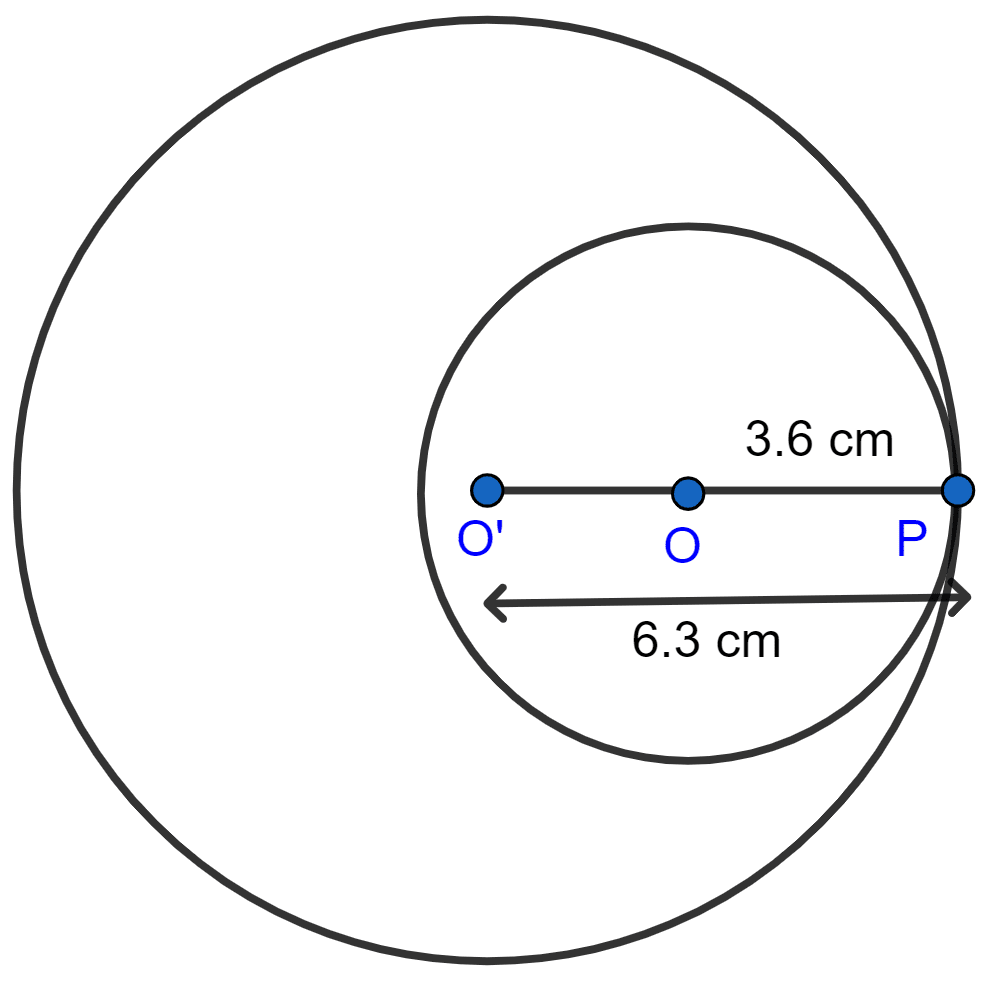
So, O'P = 6.3 cm, OP = 3.6 cm.

Hence, the distance between their centres (O'O) is given by

O'O = O'P - OP = 6.3 - 3.6 = 2.7 cm.

Hence, distance between their centers if they touch each other internally is 2.7 cm.

From a point P outside the circle, with centre O, tangents PA and PB are drawn. Prove that:

(i) ∠AOP = ∠BOP

(ii) OP is the ⊥ bisector of chord AB.

Answer

The circle with centre O and tangents PA and PB drawn from point P outside the circle is shown in the below figure:

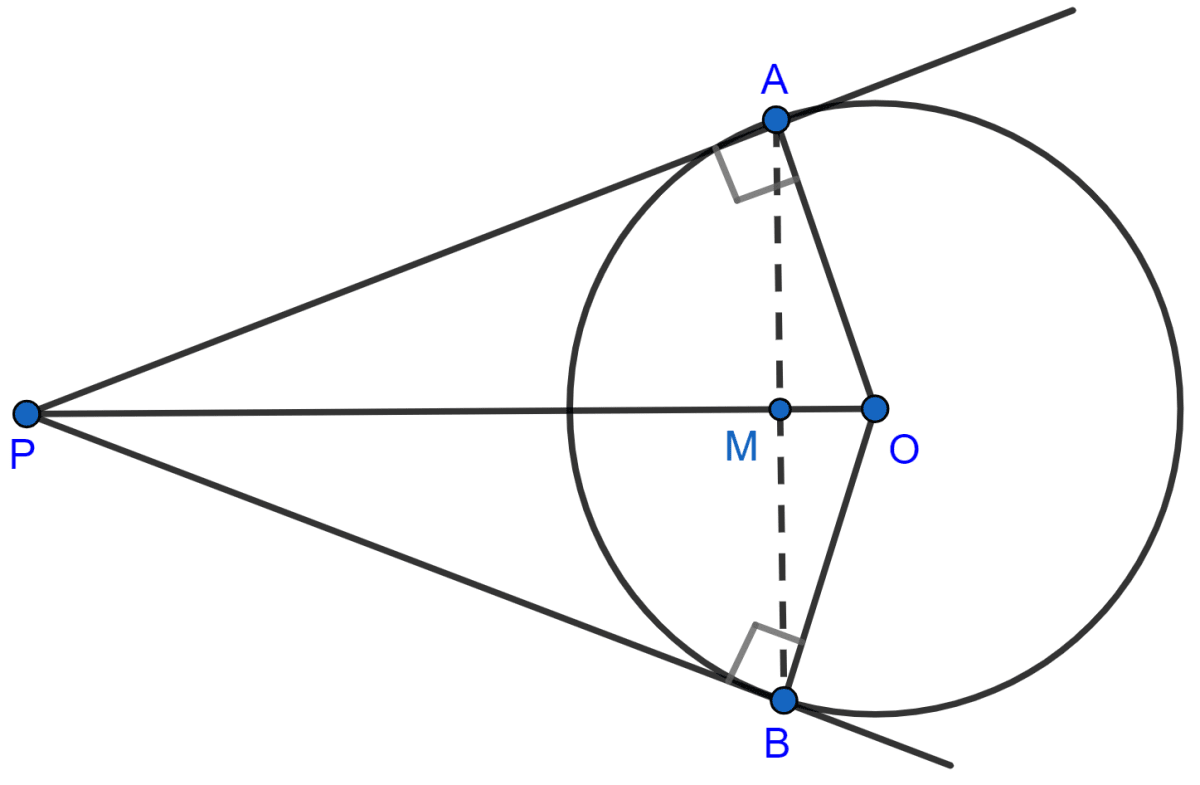
(i) In ∆AOP and ∆BOP, we have

⇒ AP = BP [Tangents from an exterior point P, are equal in length.]

⇒ OA = OB [Radius of circle]

⇒ OP = OP [Common]

∴ ΔAOP ≅ ΔBOP by SSS axiom.

∴ ∠AOP = ∠BOP [By C.P.C.T.]

Hence, proved that ∠AOP = ∠BOP.

(ii) In ∆OAM and ∆OBM, we have

OA = OB [Radii of the same circle]

∠AOM = ∠BOM [Proved ∠AOP = ∠BOP]

OM = OM [Common]

∴ ΔOAM ≅ ΔOBM [By SAS axiom]

By C.P.C.T.

⇒ AM = MB and ∠OMA = ∠OMB = x

From figure,

⇒ ∠OMA + ∠OMB = 180° [As, AB is a straight line]

⇒ x + x = 180°

⇒ 2x = 180°

⇒ x = $\dfrac{180°}{2}$

⇒ x = 90°.

Thus, ∠OMA = ∠OMB = 90°.

Hence proved, that OP is the ⊥ bisector of chord AB.

In the given Figure, two circles touch each other externally at point P. AB is the direct common tangent of these circles. Prove that :

(i) tangent at point P bisects AB.

(ii) angle APB = 90°.

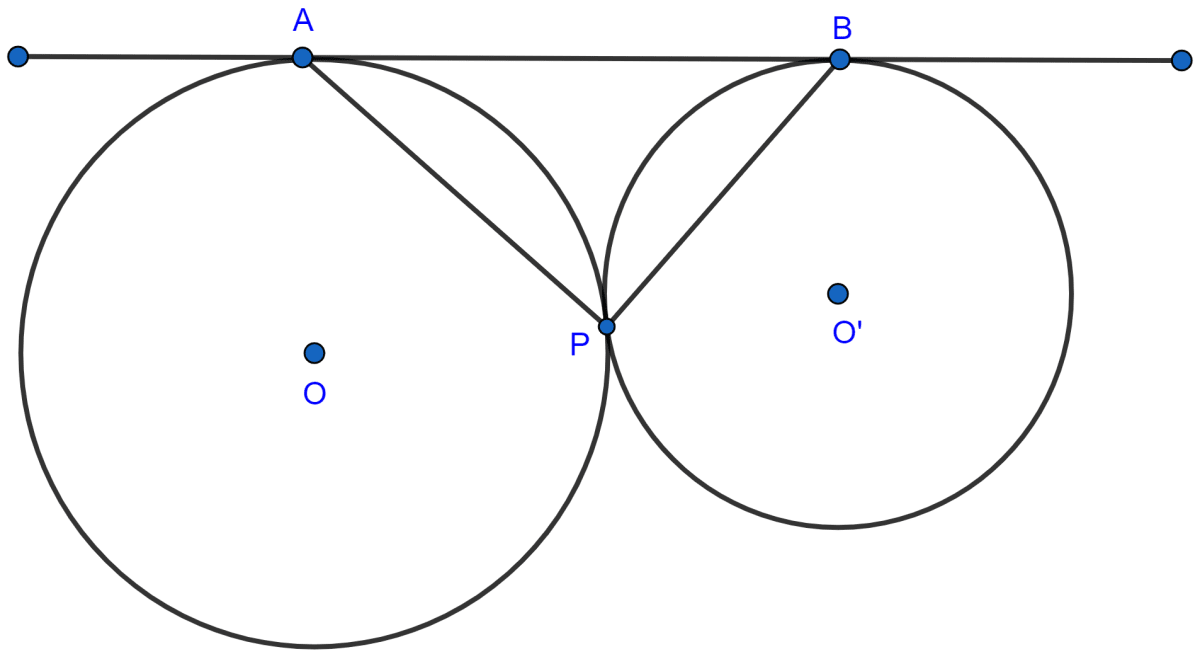
Answer

(i) We know that,

If two tangents are drawn to a circle from an exterior point, the tangents are equal in length.

From figure,

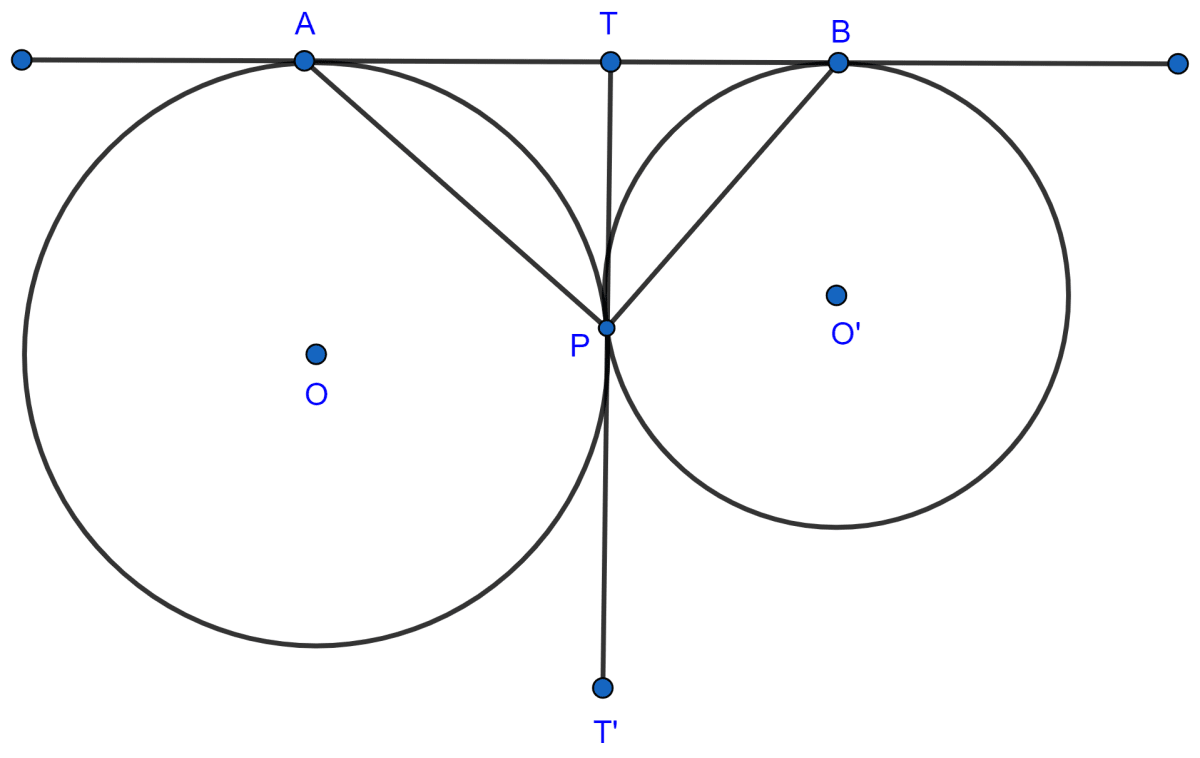
TA and TP are the tangents to the circle with center O.

∴ TA = TP ...........(1)

TB and TP are the tangents to the circle with center O'.

∴ TB = TP ...........(2)

From (1) and (2) we get :

TA = TB.

Hence, proved that tangent at point P bisects AB.

(ii) In △ATP,

TA = TP [Proved above]

∴ ∠TAP = ∠TPA .........(1) [∵ angles opposite to equal sides are equal.]

In △BTP,

TB = TP [Proved above]

∴ ∠TBP = ∠TPB ..........(2) [∵ angles opposite to equal sides are equal.]

Adding (1) and (2), we get :

∠TAP + ∠TBP = ∠TPA + ∠TPB

∠TAP + ∠TBP = ∠APB ...........(3)

In △ABP,

⇒ ∠APB + ∠BAP + ∠ABP = 180° [Angle sum property of triangle]

⇒ ∠APB + ∠TAP + ∠TBP = 180° [From figure, ∠TAP = ∠BAP and ∠TBP = ∠ABP.]

⇒ ∠APB + ∠APB = 180°

⇒ 2∠APB = 180°

⇒ ∠APB = 90°.

Hence, proved that ∠APB = 90°.

Tangents AP and AQ are drawn to a circle, with center O, from an exterior point A. Prove that :

∠PAQ = 2∠OPQ

Answer

We know that,

The tangent at any point of a circle and the radius through this point are perpendicular to each other.

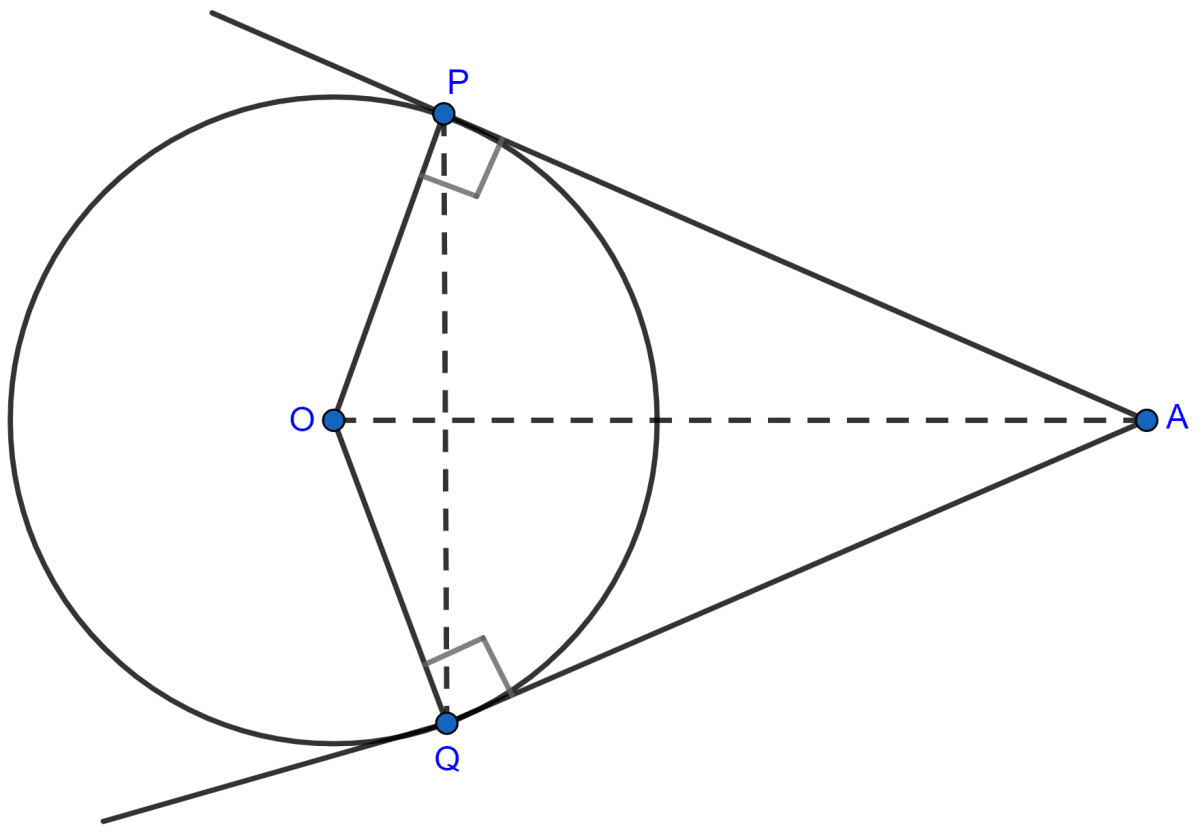
In quadrilateral OPAQ,

∠OPA = ∠OQA = 90°.

∠OPA + ∠OQA + ∠POQ + ∠PAQ = 360° [∵ Sum of angles in quadrilateral = 360°]

90° + 90° + ∠POQ + ∠PAQ = 360°

∠POQ + ∠PAQ = 360° - 180°

∠POQ + ∠PAQ = 180° ..........(1)

In △OPQ,

OP = OQ [Radius of same circle]

∴ ∠OPQ = ∠OQP [Angles opposite to equal sides are equal]

By angle sum property of triangle,

⇒ ∠OPQ + ∠OQP + ∠POQ = 180°

⇒ ∠OPQ + ∠OPQ + ∠POQ = 180°

⇒ 2∠OPQ + ∠POQ = 180° .........(2)

From (1) and (2) we get,

∠POQ + ∠PAQ = 2∠OPQ + ∠POQ

⇒ ∠PAQ = 2∠OPQ.

Hence, proved that ∠PAQ = 2∠OPQ.

ABC is a right angled triangle with AB = 12 cm and AC = 13 cm. A circle, with center O, has been inscribed inside the triangle. Calculate the value of x, the radius of the inscribed circle.

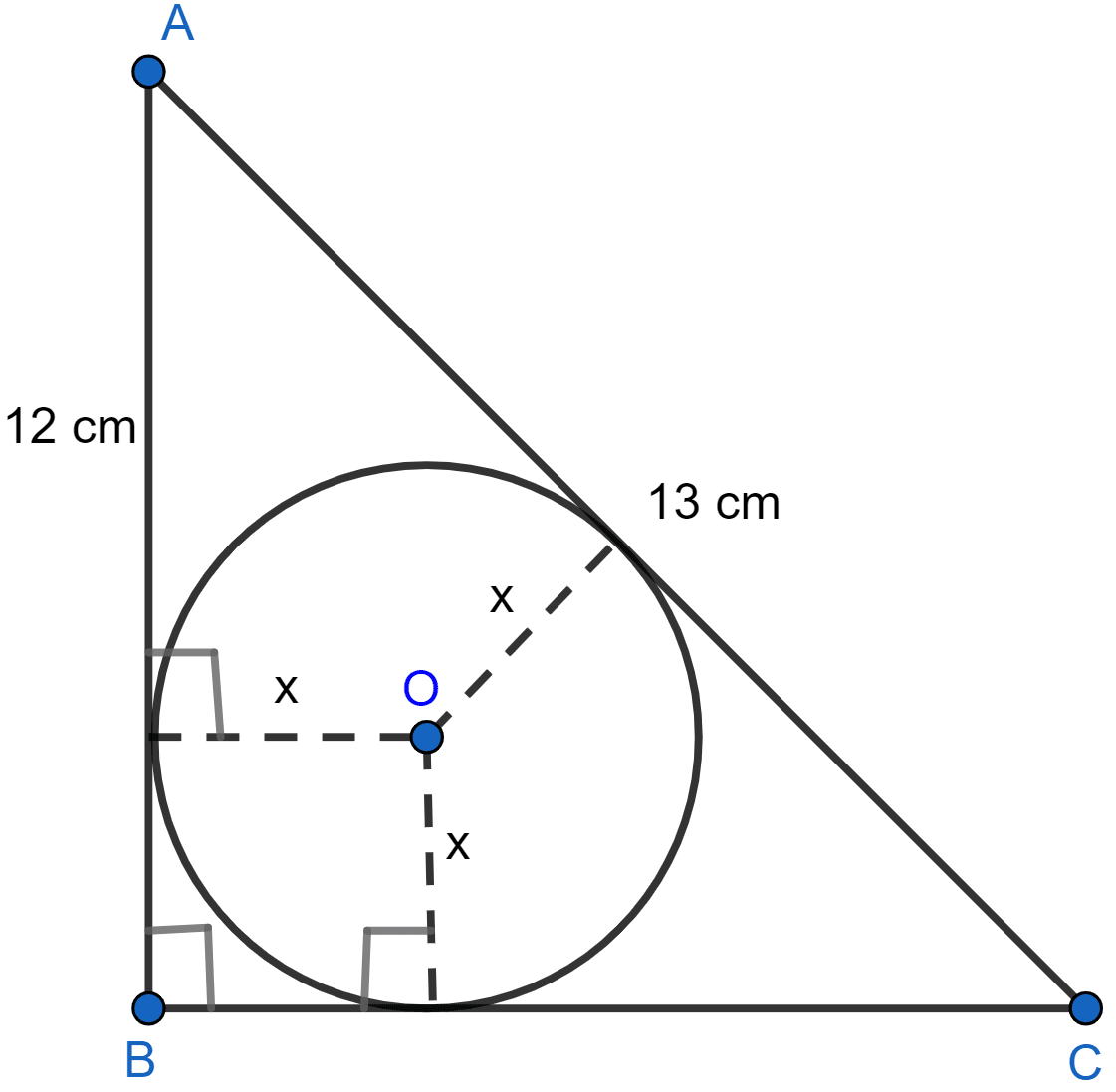
Answer

Let AB touches the circle at L, AC at N and BC at M.

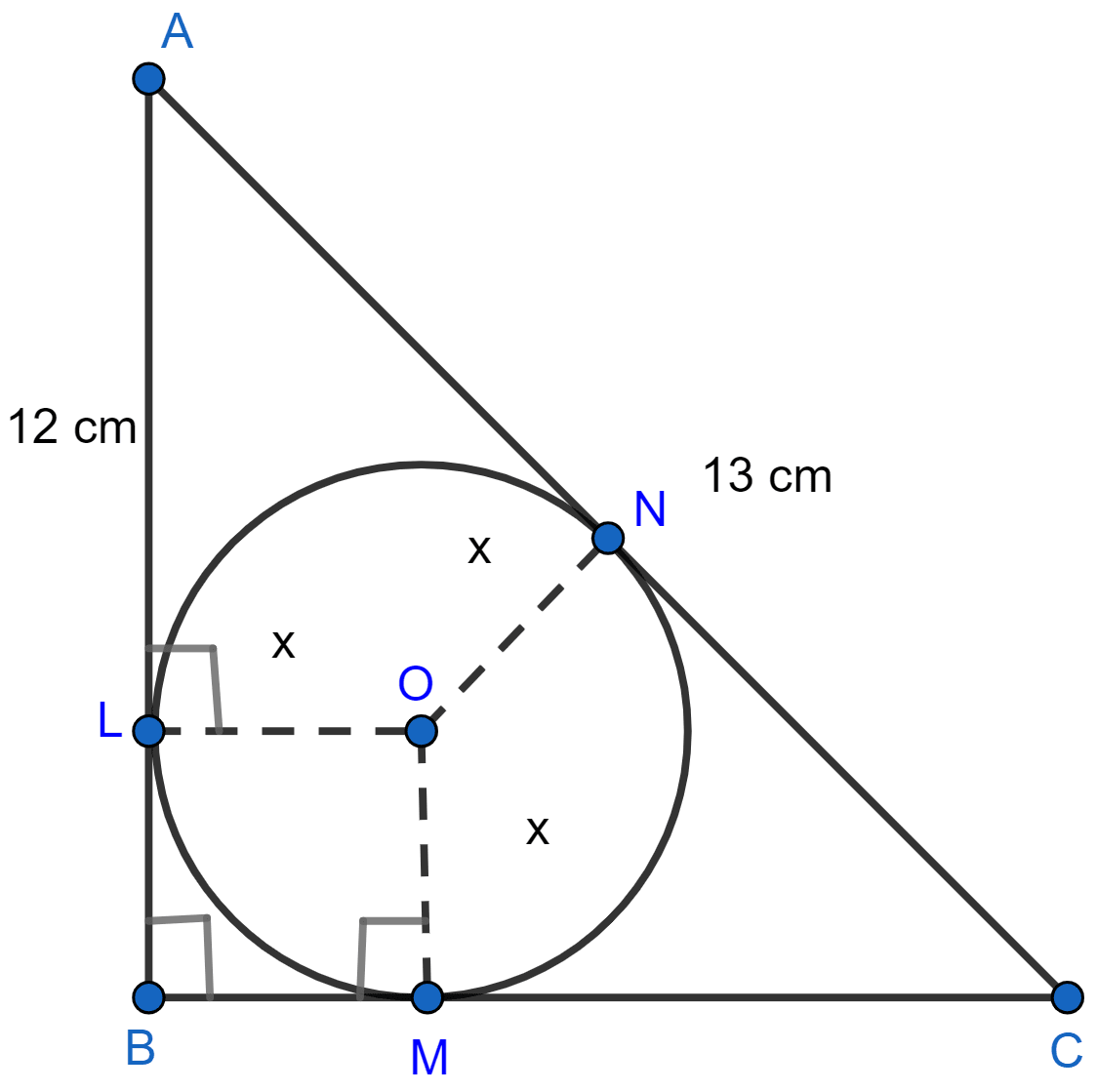
From figure,

LBMO is a square.

LB = BM = OM = OL = x.

AL = AB - LB = (12 - x) cm.

AL = AN = (12 - x) cm. [∵ Tangents from exterior point are equal in length.]

Since, ABC is a right angled triangle,

∴ AC² = AB² + BC² [By pythagoras theorem]

⇒ 13² = 12² + BC²

⇒ BC² = 13² - 12²

⇒ BC² = 169 - 144

⇒ BC² = 25

⇒ BC = $\sqrt{25}$

⇒ BC = 5 cm.

From figure,

MC = BC - BM = (5 - x) cm.

Also,

CN = CM = (5 - x) cm. [∵ Tangents from exterior point are equal in length.]

Also,

⇒ AC = AN + CN

⇒ 13 = (12 - x) + (5 - x)

⇒ 13 = 17 - 2x

⇒ 2x = 17 - 13

⇒ 2x = 4

⇒ x = $\dfrac{4}{2}$

⇒ x = 2 cm.

Hence, x = 2.

In a triangle ABC, the incircle (center O) touches BC, CA and AB at points P, Q and R respectively. Calculate :

(i) ∠QOR

(ii) ∠QPR;

given that ∠A = 60°.

Answer

ΔABC with its incircle having center O and touching BC, CA and AB at points P, Q and R, respectively is shown in the below figure:

(i) We know that,

The tangent at any point of a circle and the radius through this point are perpendicular to each other.

∴ ∠ORA = ∠OQA = 90°.

In quadrilateral AROQ,

∠ORA + ∠OQA + ∠QOR + ∠A = 360° [∵ Sum of interior angles in a quadrilateral = 360°]

⇒ 90° + 90° + ∠QOR + 60° = 360°

⇒ 240° + ∠QOR = 360°

⇒ ∠QOR = 360° - 240°

⇒ ∠QOR = 120°.

Hence, ∠QOR = 120°.

(ii) From figure,

Arc RQ subtends ∠ROQ at center and ∠QPR at the remaining part of the circle.

∴ ∠QPR = $\dfrac{1}{2}$∠QOR

⇒ ∠QPR = $\dfrac{1}{2} \times 120°$ = 60°.

Hence, ∠QPR = 60°.

In the given figure, PT touches the circle with center O at point R. Diameter SQ is produced to meet the tangent TR at P.

Given ∠SPR = x° and ∠QRP = y°;

prove that :

(i) ∠ORS = y°

(ii) write an expression connecting x and y.

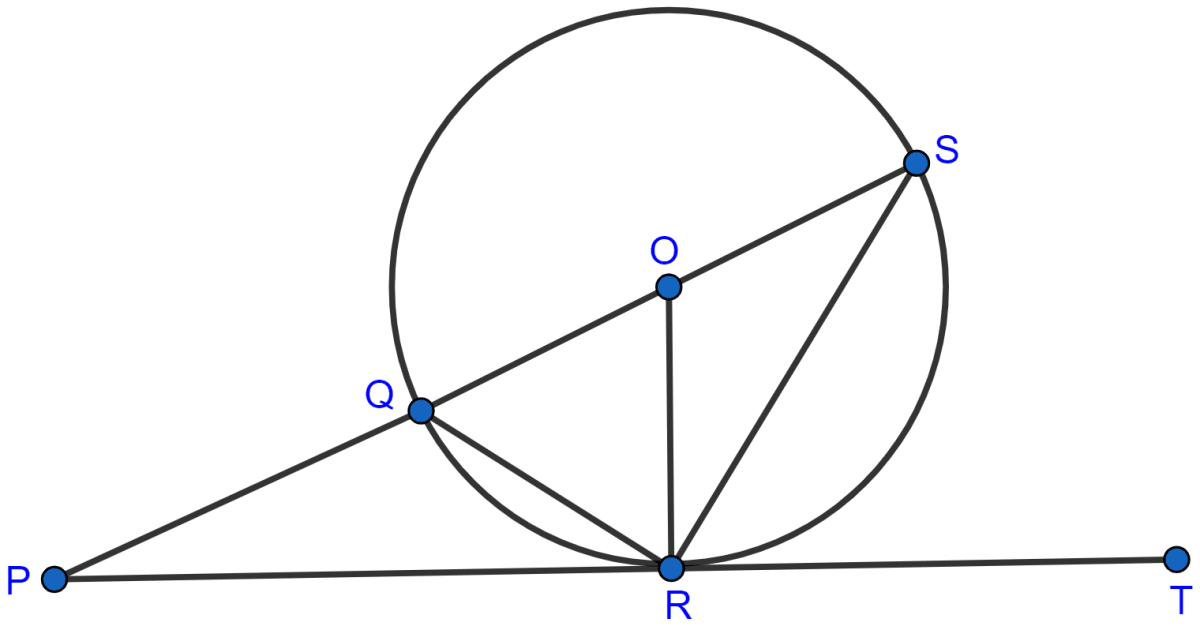
Answer

(i) From figure,

⇒ ∠QRP = ∠OSR = y° [Angles in alternate segment are equal]

⇒ OS = OR (Radius of same circle)

As, angles opposite to equal sides are equal,

∴ ∠ORS = ∠OSR = y°.

Hence, proved that ∠ORS = y°.

(ii) From figure,

∠ORP = 90° [As, tangent to a point and radius from that point are perpendicular to each other.]

⇒ ∠ORQ = ∠ORP - ∠QRP = 90° - y° ...........(1)

OQ = OR (Radius of same circle)

As, angles opposite to equal sides are equal,

∴ ∠OQR = ∠ORQ = 90° - y°

In △PQR,

⇒ ∠OQR = ∠QPR + ∠QRP (As exterior angle in a trinagle is equal to the sum of two opposite interior angles.)

⇒ 90° - y° = x° + y°

⇒ x° + 2y° = 90°.

Hence, x + 2y = 90°.

PT is a tangent to the circle at T. If ∠ABC = 70° and ∠ACB = 50°; calculate :

(i) ∠CBT

(ii) ∠BAT

(iii) ∠APT

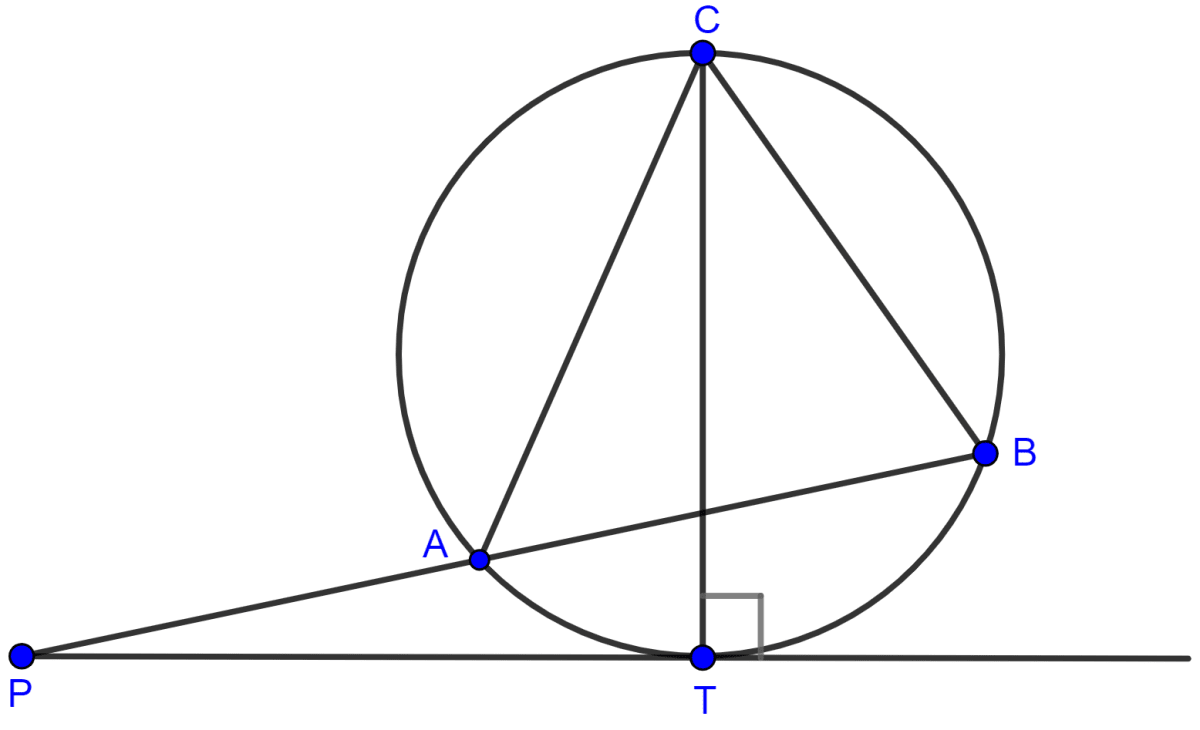
Answer

Join AT and BT.

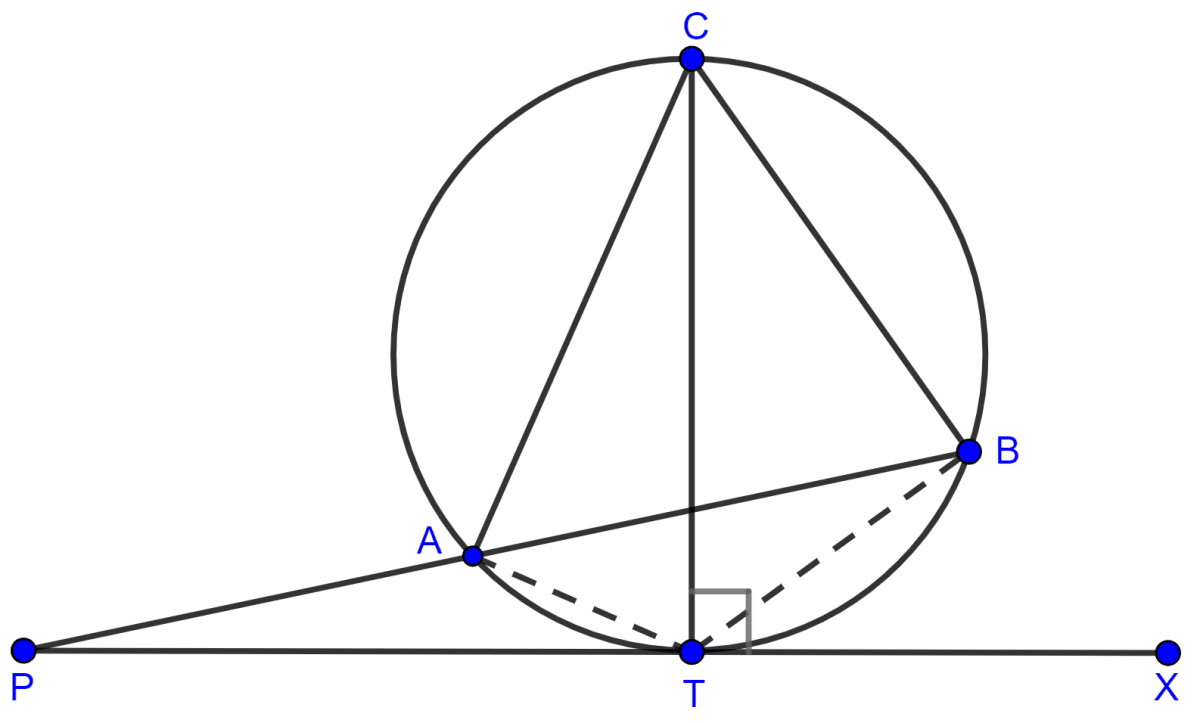
(i) TC is the diameter of the circle.

Since, angle in a semi-circle is a right angle.

∴ ∠CBT = 90°.

Hence, ∠CBT = 90°.

(ii) In cyclic quadrilateral ATBC,

⇒ ∠CBT + ∠CAT = 180° (∵ Sum of opposite angles of a cyclic quadrilateral = 180°)

⇒ 90° + ∠CAT = 180°

⇒ ∠CAT = 180° - 90°

⇒ ∠CAT = 90°.

In △ABC,

⇒ ∠CBA + ∠CAB + ∠ACB = 180° [By angle sum property of triangle]

⇒ 70° + ∠CAB + 50° = 180°

⇒ ∠CAB + 120° = 180°

⇒ ∠CAB = 180° - 120°

⇒ ∠CAB = 60°.

From figure,

∠BAT = ∠CAT - ∠CAB = 90° - 60° = 30°.

Hence, ∠BAT = 30°.

(iii) From figure,

∠BTX = ∠BAT = 30° [Angle in same segment are equal]

∠PBT = ∠CBT - ∠CBA = 90° - 70° = 20°.

⇒ ∠PTB = 180° - ∠BTX = 180° - 30° = 150°.

In △PBT,

⇒ ∠PBT + ∠PTB + ∠APT = 180° [By angle sum property of triangle]

⇒ 20° + 150° + ∠APT = 180°

⇒ ∠APT + 170° = 180°

⇒ ∠APT = 180° - 170°

⇒ ∠APT = 10°.

Hence, ∠APT = 10°.

In the given figure, O is the center of the circumcircle ABC. Tangents A and C intersect at P. Given angle AOB = 140° and angle APC = 80°; find the angle BAC.

Answer

Join OC

∴ PA and PC are the tangents

∴ OA ⊥ PA and OC ⊥ PC

In quadrilateral APCO,

⇒ ∠APC + ∠AOC = 180°

⇒ 80° + ∠AOC = 180°

⇒ ∠AOC = 180° - 80°

⇒ ∠AOC = 100°

From figure,

∠BOC = 360° - (∠AOB + ∠AOC)

= 360° - (140° + 100°)

= 360° - 240° = 120°.

We know that,

The angle at the centre of a circle is twice the angle at the circumference, subtended by the same arc.

Now arc BC subtends ∠BOC at the centre and ∠BAC at the remaining part of the circle.

∴ ∠BAC = $\dfrac{1}{2}$∠BOC = $\dfrac{1}{2} \times 120°$ = 60°.

Hence, ∠BAC = 60°.

In the given figure, PQ is a tangent to the circle at A. AB and AD are bisectors of ∠CAQ and ∠PAC. If ∠BAQ = 30°, prove that : BD is diameter of the circle.

Answer

From figure,

∠CAB = ∠BAQ = 30° (AB is angle bisector of ∠CAQ)

⇒ ∠CAQ = 2∠BAQ = 60°.

From figure,

⇒ ∠CAQ + ∠PAC = 180° [Linear pair]

⇒ 60° + ∠PAC = 180°

⇒ ∠PAC = 180° - 60°

⇒ ∠PAC = 120°.

⇒ ∠PAC = 2∠CAD (AD is angle bisector of ∠PAC)

⇒ 120° = 2∠CAD

⇒ ∠CAD = $\dfrac{120°}{2}$

⇒ ∠CAD = 60°.

From figure,

∠DAB = ∠CAD + ∠CAB = 60° + 30° = 90°.

Thus BD, subtends 90° on the circle. Since, angle in semi-circle is a right angle.

Hence, BD is the diameter of the circle.

Chords AB and CD of a circle intersect each other at point O such that OA : OC = 4 : 7. Then OB : OD is equal to :

1. 4 : 7

2. 5 : 4

3. 7 : 4

4. 4 : 5

Answer

Given,

OA : OC = 4 : 7

We know that,

If two chords of a circle intersect internally or externally then the product of the lengths of their segments is equal.

From figure,

⇒ OA × OB = OC × OD

⇒ $\dfrac{OD}{OB} = \dfrac{OA}{OC}$

⇒ $\dfrac{OD}{OB} = \dfrac{4}{7}$

⇒ $\dfrac{OB}{OD} = \dfrac{7}{4}$.

⇒ OB : OD = 7 : 4.

Hence, Option 3 is the correct option.

If ∠PAC : ∠PCA = 4 : 5, ∠P is :

1. 40°

2. 60°

3. 105°

4. 45°

Answer

We know that,

Sum of co-interior angles in a trapezium is 180°.

In trapezium ABDC,

⇒ ∠B + ∠BAC = 180°

⇒ 60° + ∠BAC = 180°

⇒ ∠BAC = 180° - 60° = 120°.

From figure,

⇒ ∠PAC + ∠BAC = 180°

⇒ ∠PAC + 120° = 180°

⇒ ∠PAC = 180° - 120° = 60°.

Given,

⇒ ∠PAC : ∠PCA = 4 : 5

$\Rightarrow \dfrac{∠\text{PAC}}{∠\text{PCA}} = \dfrac{4}{5} \\[1em] \Rightarrow \dfrac{60°}{∠\text{PCA}} = \dfrac{4}{5} \\[1em] \Rightarrow ∠\text{PCA} = \dfrac{60° \times 5}{4} \\[1em] \Rightarrow ∠\text{PCA} = \dfrac{300°}{4} = 75°.$

In △PCA,

By angle sum property of triangle,

⇒ ∠APC + ∠PAC + ∠PCA = 180°

⇒ ∠APC + 60° + 75° = 180°

⇒ ∠APC + 135° = 180°

⇒ ∠APC = 180° - 135° = 45°.

Hence, Option 4 is the correct option.

AC is a tangent to the given circle which touches the circle at point B. If ∠EBC = 45°; angle EDB is equal to :

1. 45°

2. 90°

3. 125°

4. 135°

Answer

From figure,

⇒ ∠ABE + ∠EBC = 180° [Linear pair]

⇒ ∠ABE + 45° = 180°

⇒ ∠ABE = 180° - 45° = 135°.

We know that,

The angle between a tangent and a chord through the point of contact is equal to an angle in the alternate segment.

⇒ ∠EDB = ∠ABE = 135°.

Hence, Option 4 is the correct option.

In the given circle, PA is tangent and PBC is secant, PA = 8 cm and PB = 4 cm. The length of BC is :

1. 8 cm

2. 12 cm

3. 16 cm

4. 2 cm

Answer

We know that,

If a chord and a tangent intersect externally, then the product of the lengths of the segments of the chord is equal to the square of the length of the tangent from the point of contact to the point of intersection.

⇒ PB × PC = PA²

⇒ 4 × PC = 8²

⇒ 4 × PC = 64

⇒ PC = $\dfrac{64}{4}$ = 16 cm.

From figure,

BC = PC - PB = 16 - 4 = 12 cm.

Hence, Option 2 is the correct option.

In the given figure, O is the center of the circle, PA is tangent and PBC is secant. If ∠ABC = 60°; ∠P is :

1. 30°

2. 60°

3. 120°

4. 90°

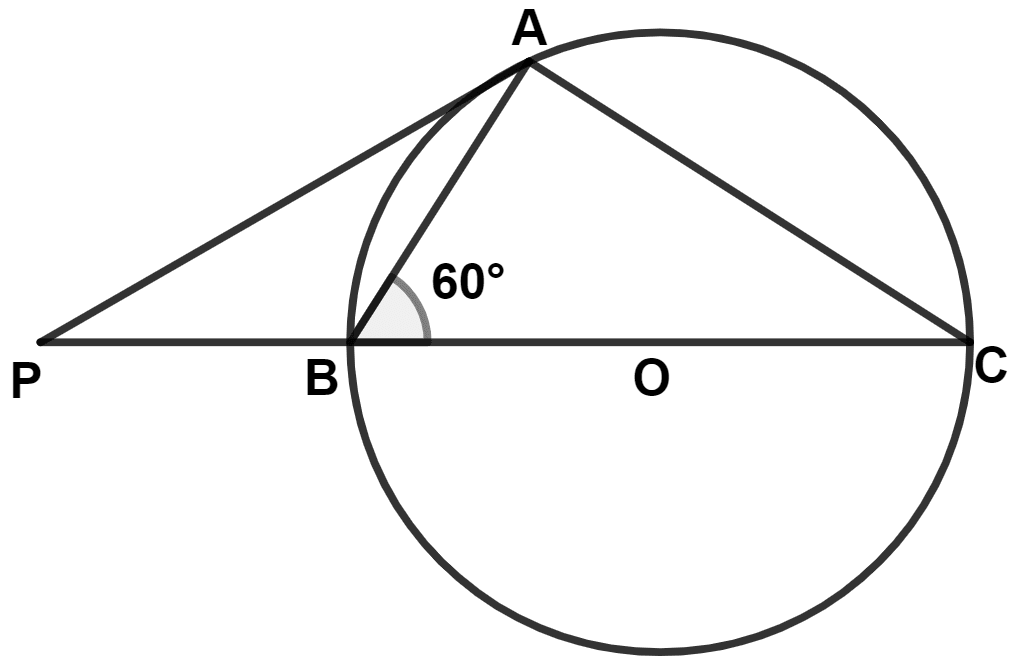
Answer

In △ABC,

∠BAC = 90° (Angle in semi-circle is a right angle)

⇒ ∠ABC + ∠BAC + ∠ACB = 180° (By angle sum property of triangle)

⇒ 60° + 90° + ∠ACB = 180°

⇒ 150° + ∠ACB = 180°

⇒ ∠ACB = 180° - 150° = 30°.

We know that,

The angle between a tangent and a chord through the point of contact is equal to an angle in the alternate segment.

⇒ ∠BAP = ∠ACB = 30°.

From figure,

⇒ ∠PBA + ∠ABC = 180° [Linear pairs]

⇒ ∠PBA + 60° = 180°

⇒ ∠PBA = 180° - 60° = 120°.

In △PBA,

⇒ ∠PBA + ∠BAP + ∠APB = 180° (By angle sum property of triangle)

⇒ 120° + 30° + ∠APB = 180°

⇒ 150° + ∠APB = 180°

⇒ ∠APB = 180° - 150° = 30°.

∴ ∠P = 30°.

Hence, Option 1 is the correct option.

In the given figure, diameter AB and chord CD of a circle meet at P. PT is a tangent to the circle at T. CD = 7.8 cm, PD = 5 cm, PB = 4 cm. Find :

(i) AB

(ii) the length of tangent PT.

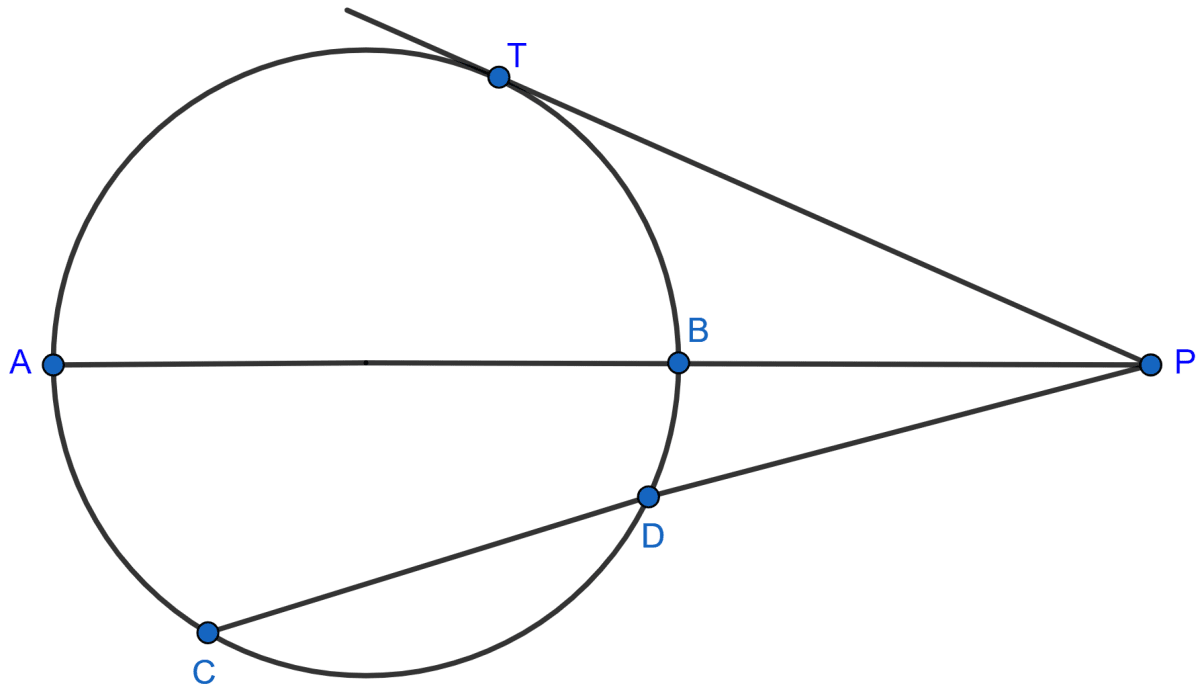
Answer

(i) From figure,

PC = PD + CD = 5 + 7.8 = 12.8 cm.

We know that,

If two chords of a circle intersect internally of externally then the product of the lengths of their segments is equal.

Since, here AB and CD intersect externally at P.

∴ AP x PB = CP x PD

⇒ AP x 4 = 12.8 x 5

⇒ AP = $\dfrac{12.8 \times 5}{4} = \dfrac{64}{4}$ = 16 cm.

From figure,

AB = PA - PB = 16 - 4 = 12 cm.

Hence, AB = 12 cm.

(ii) We know that,

If a chord and a tangent intersect externally, then the product of lengths of the segments of the chord is equal to the square of the length of the tangent from the point of contact to the point of intersection.

∴ PA x PB = PT²

⇒ 16 x 4 = PT²

⇒ PT = $\sqrt{64}$ = 8 cm.

Hence, PT = 8 cm.

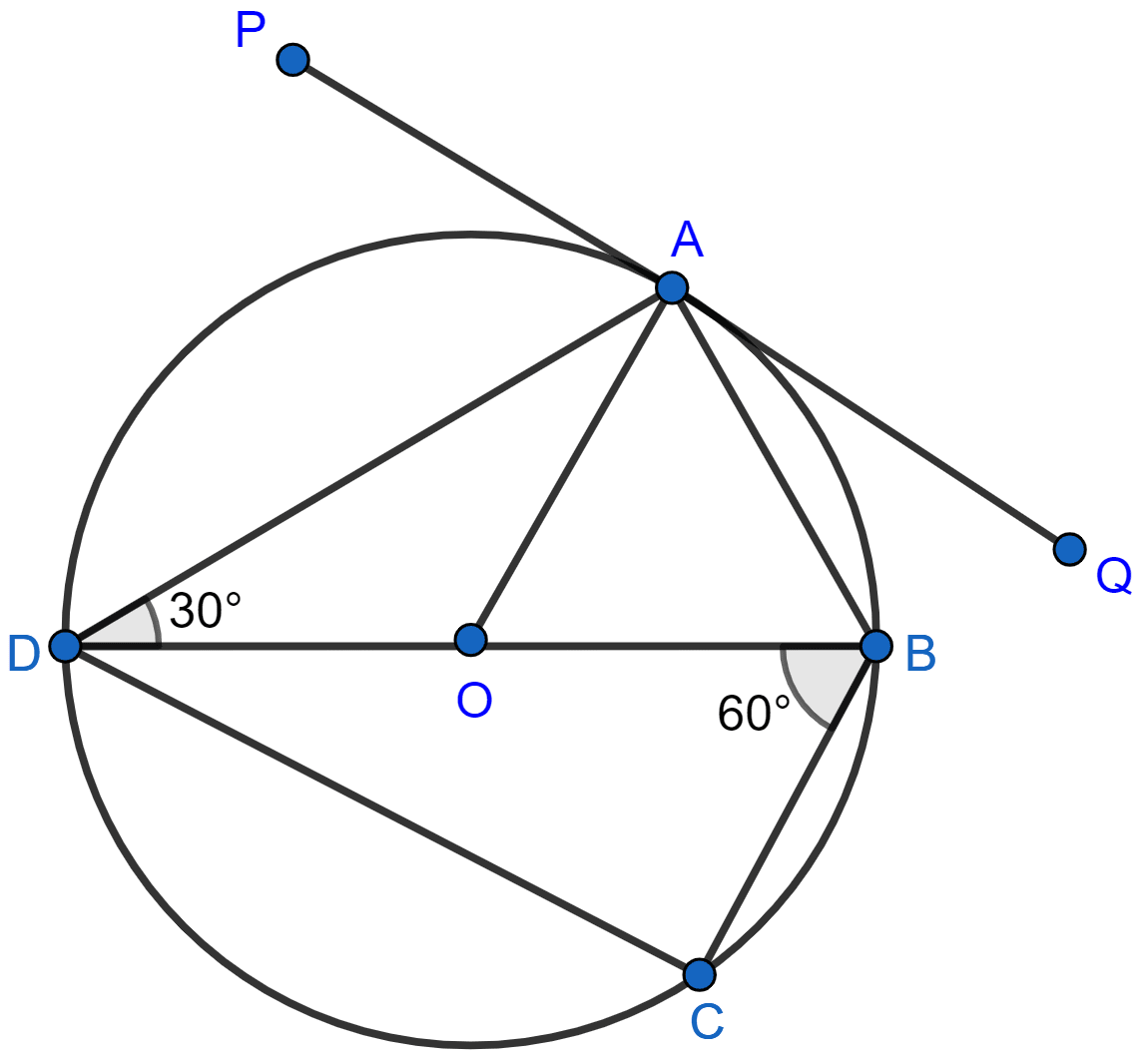
In the following figure, PQ is the tangent to the circle at A, DB is a diameter and O is the centre of the circle. If ∠ADB = 30° and ∠CBD = 60°, calculate:

(i) ∠QAB,

(ii) ∠PAD,

(iii) ∠CDB.

Answer

(i) ∠QAB = ∠ADB [∵ angles in alternate segment are equal.]

∴ ∠QAB = 30°.

Hence, the value of ∠QAB = 30°.

(ii) In △DAO,

OA = OD [∵ radii of the same circle]

So, ∠OAD = ∠ODA = 30° [∵ angles opposite to equal sides are equal.]

We know that,

The tangent at any point of a circle is perpendicular to the radius through the point of contact.

∴ ∠OAP = 90°.

From figure,

⇒ ∠PAD = ∠OAP - ∠OAD = 90° - 30° = 60°.

Hence, ∠PAD = 60°.

(iii) In △BCD,

∠BCD = 90° [∵ angle in a semi-circle is a right angle.]

∠CBD = 60°

∠CDB + ∠CBD + ∠BCD = 180° [By angle sum property of triangle]

⇒ ∠CDB + 60° + 90° = 180°

⇒ ∠CDB = 180° - 150° = 30°.

Hence, ∠CDB = 30°.

If PQ is a tangent to the circle at R; calculate :

(i) ∠PRS,

(ii) ∠ROT.

Given, O is the center of the circle and angle TRQ = 30°.

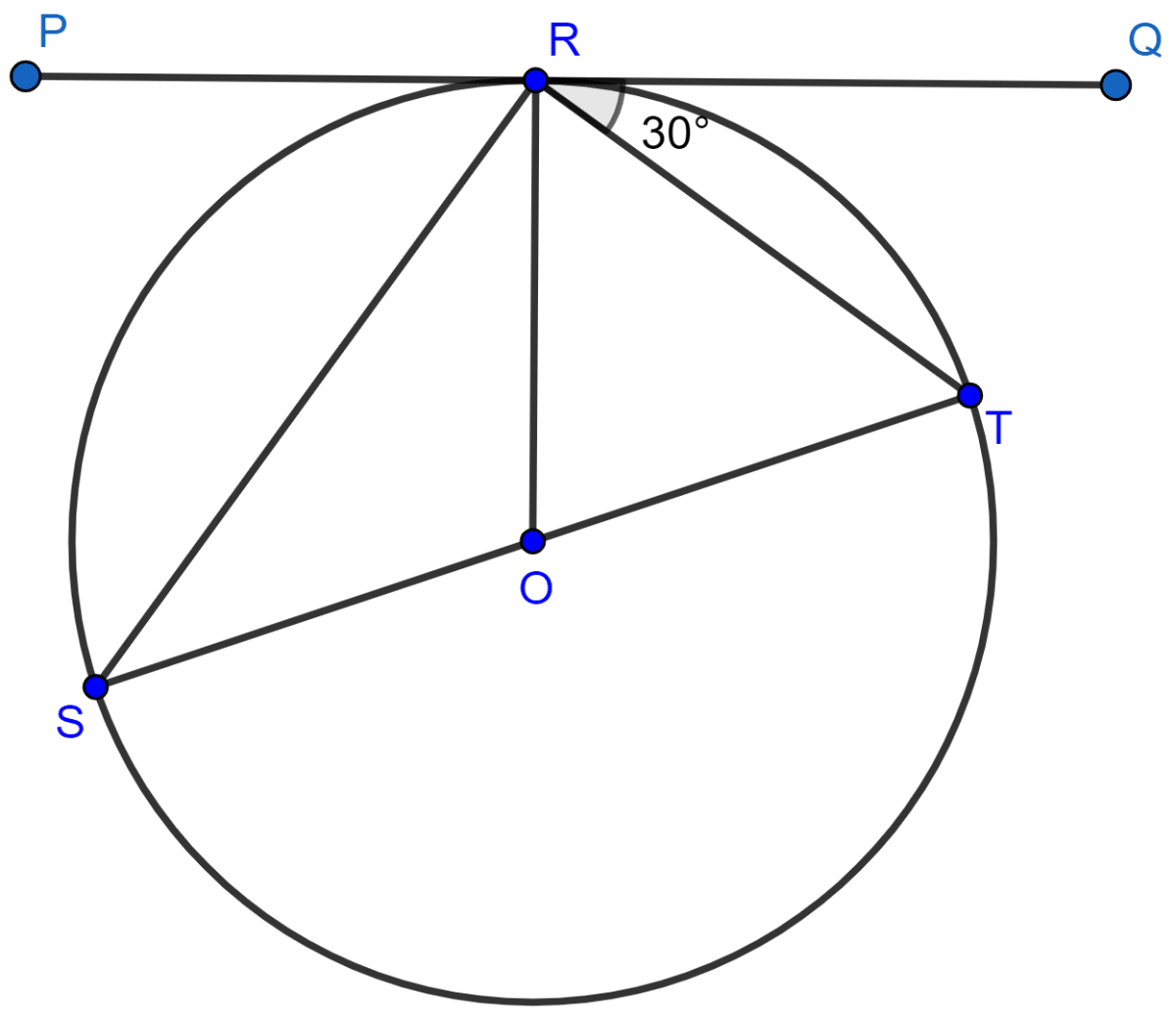
Answer

(i) Since, ST passes through O, so ST is the diameter of the circle.

We know that,

Angle in a semi-circle is a right angle.

∴ ∠SRT = 90°.

Since, PQ is a straight line.

∴ ∠PRS + ∠SRT + ∠TRQ = 180°

⇒ ∠PRS + 90° + 30° = 180°

⇒ ∠PRS + 120° = 180°

⇒ ∠PRS = 180° - 120°

⇒ ∠PRS = 60°.

Hence, ∠PRS = 60°.

(ii) We know that,

The angle between a tangent and chord through the point of contact is equal to an angle in the alternate segment.

∠TSR = ∠TRQ = 30°.

Since, angle subtended by a segment at the center is double the angle suspended at the circumference.

∠ROT = 2∠TSR = 2 × 30° = 60°.

Hence, ∠ROT = 60°.

Two circles with centers O and O' are drawn to intersect each other at points A and B. Center O of one circle lies on the circumference of the other circle and CD is drawn tangent to the circle with center O' at A. Prove that OA bisects angle BAC.

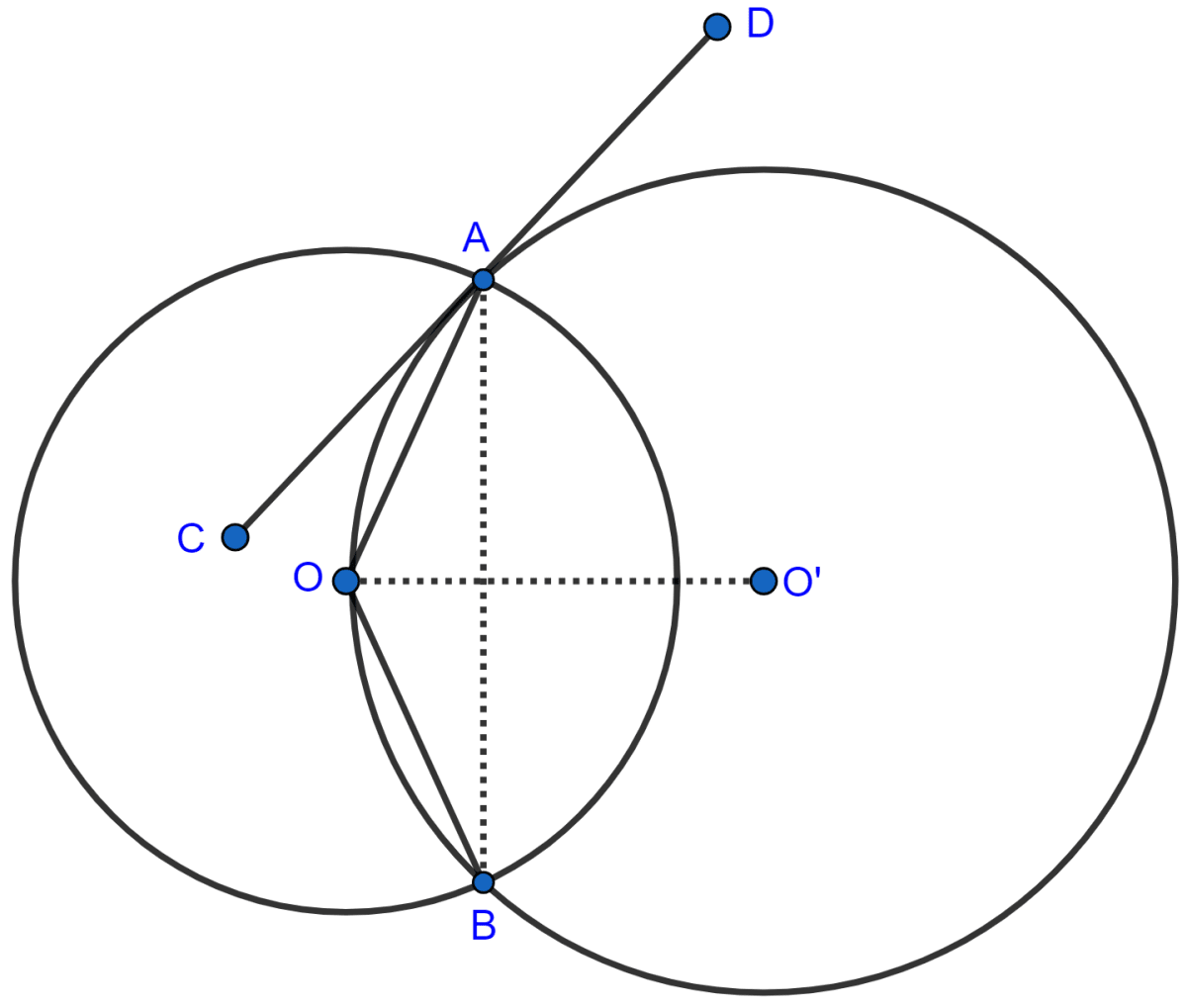
Answer

Join O'A and O'B.

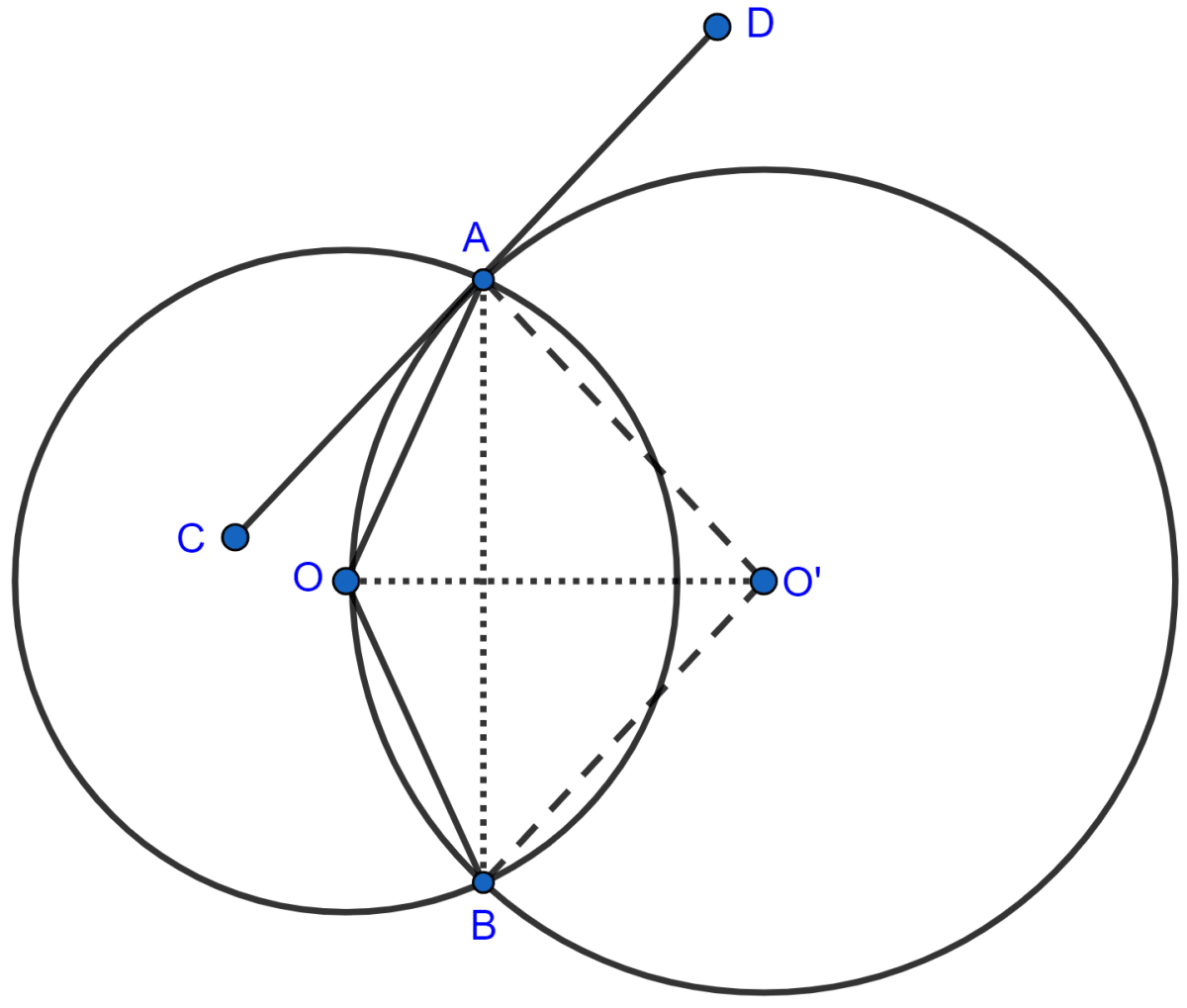
As, the angle between a tangent and a chord through the point of contact is equal to the angle in the alternate segment, we have :

CD is the tangent and AO is the chord.

∴ ∠OAC = ∠OBA ......... (1)

In ∆OAB,

OA = OB [Radius of the circle with center O.]

∠OAB = ∠OBA .......... (2) [Angles opposite to equal sides]

From (1) and (2), we have

∠OAC = ∠OAB

Hence, proved that OA is the bisector of ∠BAC.

In the figure, ABCD is a cyclic quadrilateral with BC = CD. TC is tangent to the circle at point C and DC is produced to point G. If ∠BCG = 108° and O is the center of the circle, find :

(i) angle BCT

(ii) angle DOC

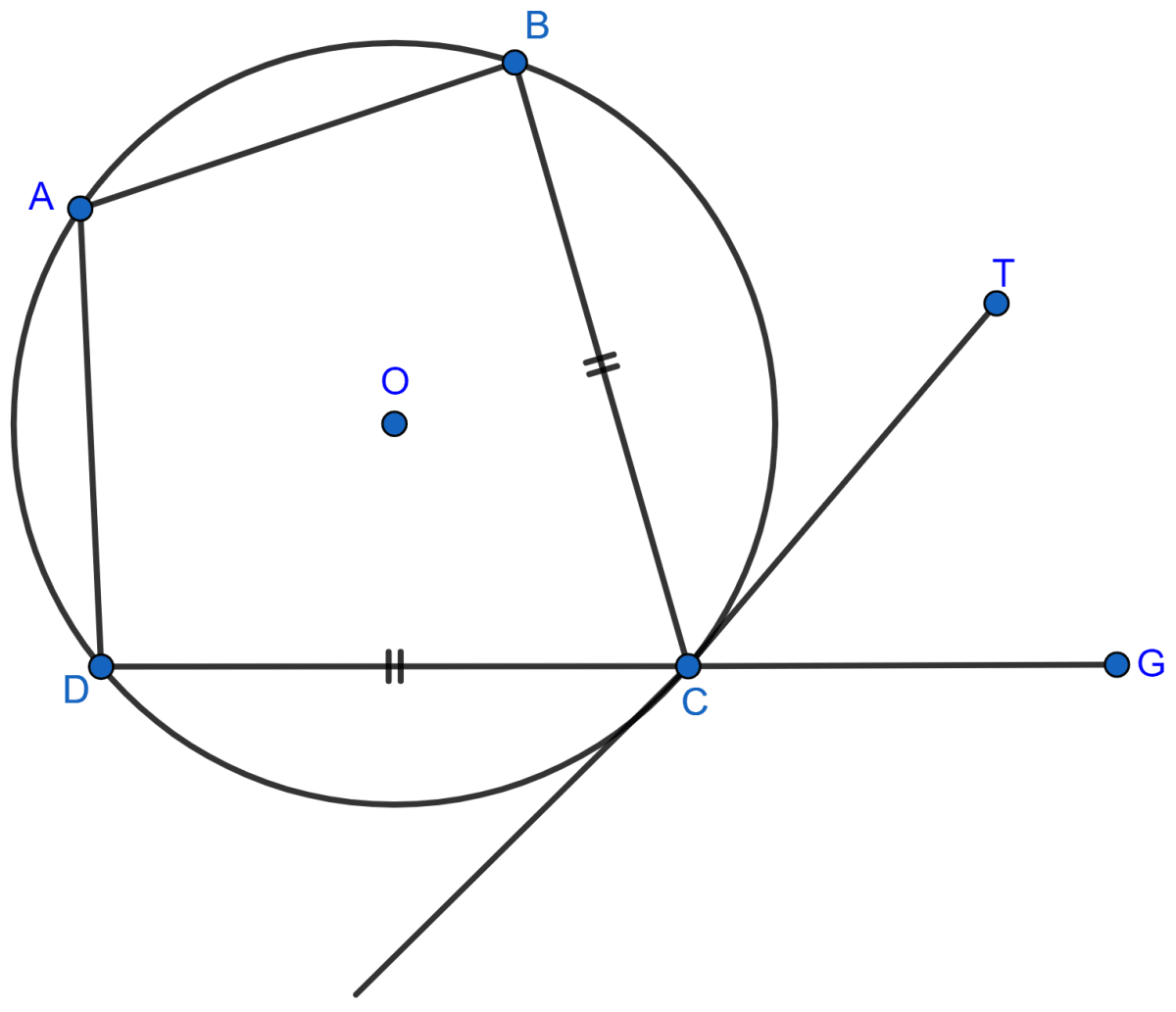
Answer

Join OC, OD and BD.

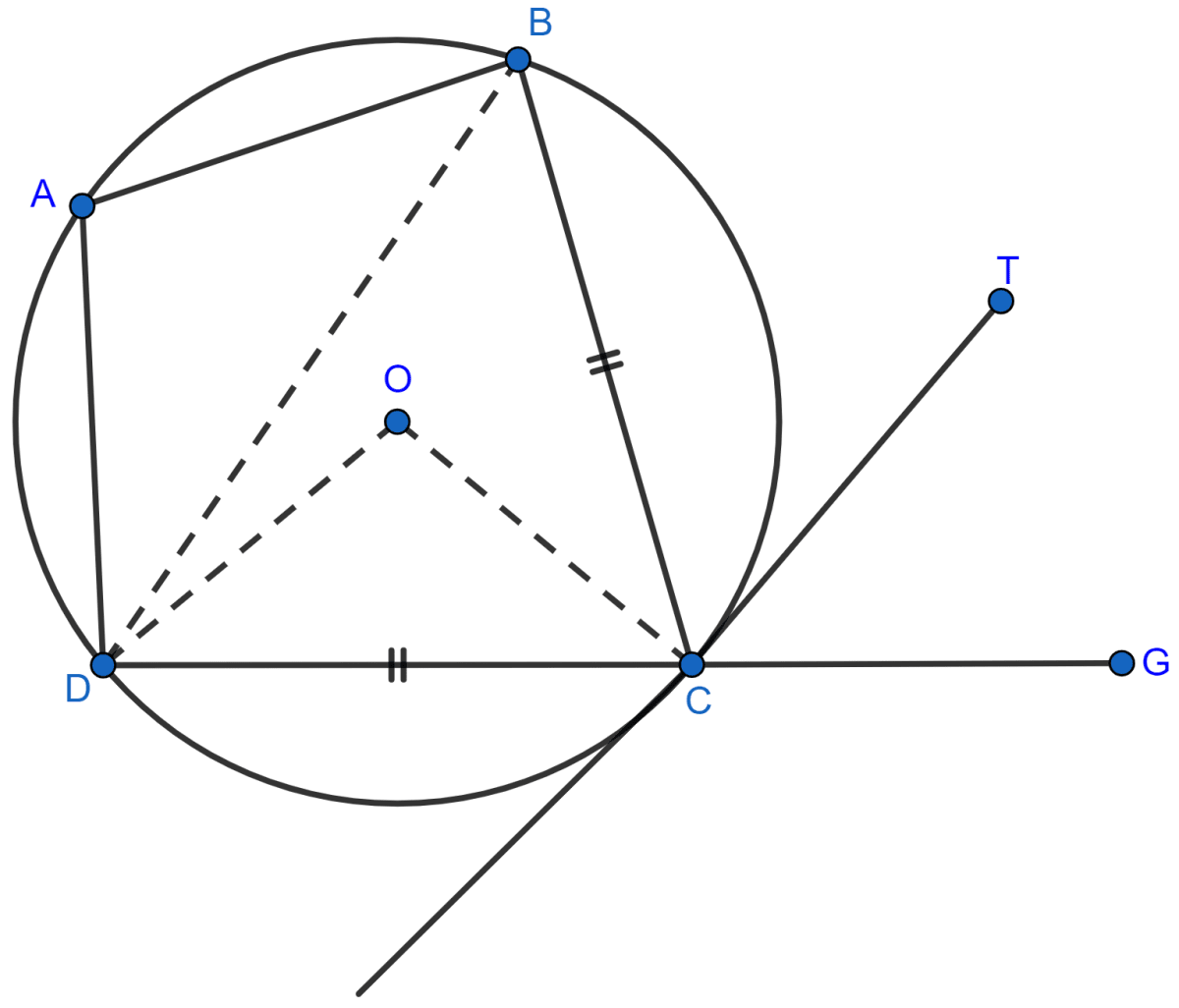
Given,

∠BCG = 108°

From figure,

⇒ ∠BCG + ∠BCD = 180° [Linear pairs]

⇒ 108° + ∠BCD = 180°

⇒ ∠BCD = 180° - 108°

⇒ ∠BCD = 72°.

From figure,

⇒ ∠BDC = ∠DBC = x(let) [As, angles opposite to equal sides are equal]

In triangle BDC,

⇒ ∠DBC + ∠BDC + ∠BCD = 180° [Angle sum property of triangle]

⇒ x + x + 72° = 180°

⇒ 2x + 72° = 180°

⇒ 2x = 180° - 72°

⇒ 2x = 108°

⇒ x = $\dfrac{108°}{2}$

⇒ x = 54°.

From figure.

∠BCT = ∠BDC (Angles in alternate segment are equal)

∠BCT = 54°.

Hence, ∠BCT = 54°.

(ii) As, angle subtended by a segment on center is twice the angle subtended by it on any other part of circumference.

⇒ ∠DOC = 2∠DBC

⇒ ∠DOC = 2(54°) = 108°.

Hence, ∠DOC = 108°.

In the figure; PA is a tangent to the circle, PBC is secant and AD bisects angle BAC. Show that triangle PAD is an isosceles triangle. Also, show that :

∠CAD = $\dfrac{1}{2}$ [∠PBA - ∠PAB]

Answer

As, the angle between a tangent and a chord through the point of contact is equal to the angle in the alternate segment, we have :

From figure,

PA is a tangent and AB is a chord.

∴ ∠PAB = ∠C [Angles in alternate segment are equal]...........(1)

Given,

AD is bisector of ∠BAC.

∴ ∠BAD = ∠DAC .......(2)

We know that,

An exterior angle is equal to sum of two opposite interior angles.

⇒ ∠ADP = ∠C + ∠DAC

⇒ ∠ADP = ∠PAB + ∠BAD [From (1) and (2)]

⇒ ∠ADP = ∠PAD

Since, sides opposite to equal sides are equal.

∴ PA = PD

∴ PAD is an isosceles triangle.

In △ABC,

⇒ ∠PBA = ∠C + ∠BAC [Exterior angle is equal to sum of two opposite interior angles]

⇒ ∠BAC = ∠PBA - ∠C

⇒ ∠BAC = ∠PBA - ∠PAB [As, ∠C = ∠PAB]

⇒ 2∠CAD = ∠PBA - ∠PAB [As, AD bisects ∠BAC]

⇒ ∠CAD = $\dfrac{1}{2}$(∠PBA - ∠PAB).

Hence, proved that ∠CAD = $\dfrac{1}{2}$(∠PBA - ∠PAB).

Two circles intersect each other at point A and B. Their common tangent touches the circles at points P and Q as shown in the figure. Show that the angles PAQ and PBQ are supplementary.

Answer

Join AB.

As, the angle between a tangent and a chord through the point of contact is equal to the angle in the alternate segment, we have :

From figure,

PQ is a tangent and AB is a chord.

∴ ∠QPA = ∠PBA [Angles in alternate segment are equal] .........(1)

Also,

∴ ∠PQA = ∠QBA [Angles in alternate segment are equal] ..........(2)

Adding (1) and (2) we get,

⇒ ∠QPA + ∠PQA = ∠PBA + ∠QBA ..........(3)

⇒ ∠PBA + ∠QBA = ∠PBQ ...........(4)

In △PAQ,

⇒ ∠QPA + ∠PQA + ∠PAQ = 180° [Angle sum property of triangle]

⇒ ∠QPA + ∠PQA = 180° - ∠PAQ

⇒ ∠PBA + ∠QBA = 180° - ∠PAQ [From (3)] ..........(5)

From (4) and (5), we get :

⇒ ∠PBQ = 180° - ∠PAQ

⇒ ∠PBQ + ∠PAQ = 180°.

Hence, proved that PAQ and PBQ are supplementary.

In the figure, chords AE and BC intersect each other at point D.

(i) If ∠CDE = 90°, AB = 5 cm, BD = 4 cm and CD = 9 cm; find DE.

(ii) If AD = BD, show that : AE = BC.

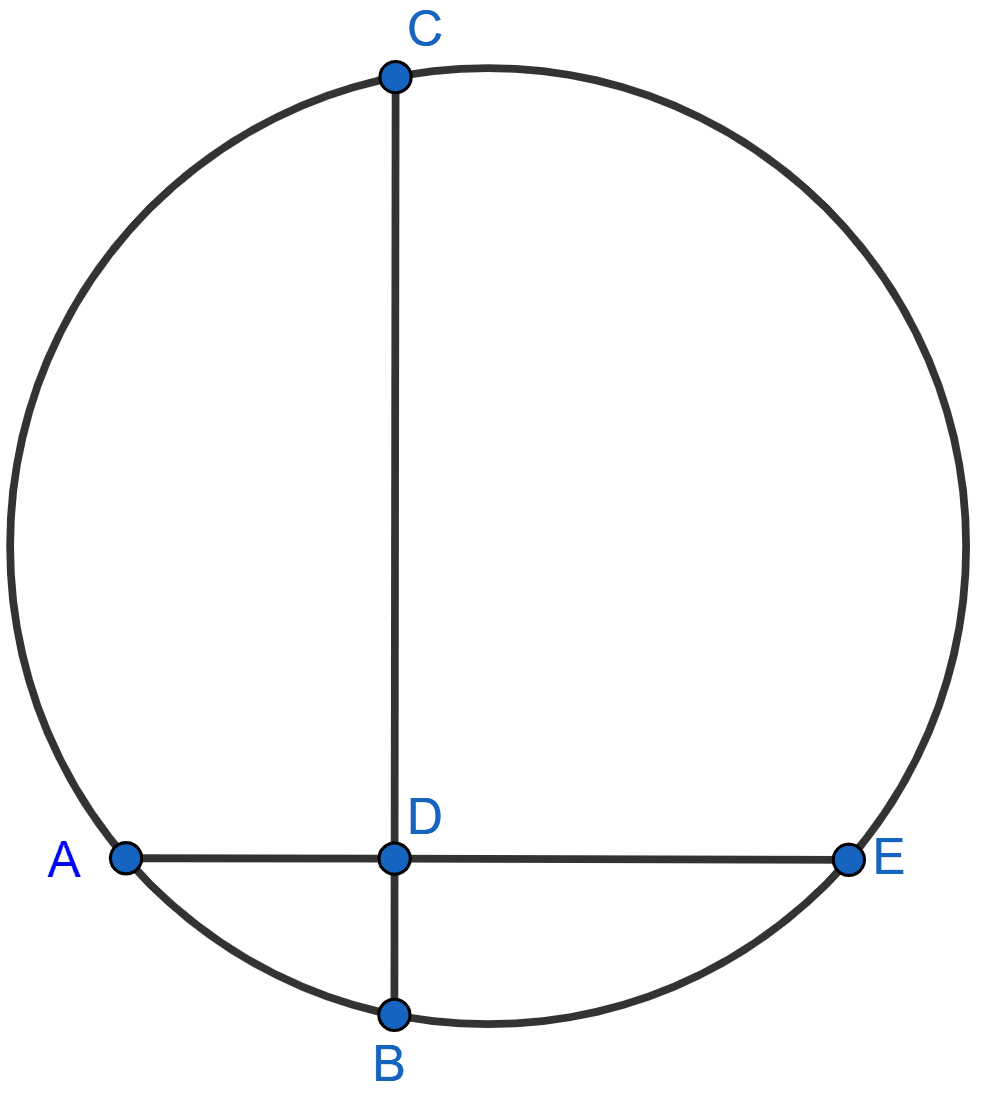
Answer

(i) Join AB.

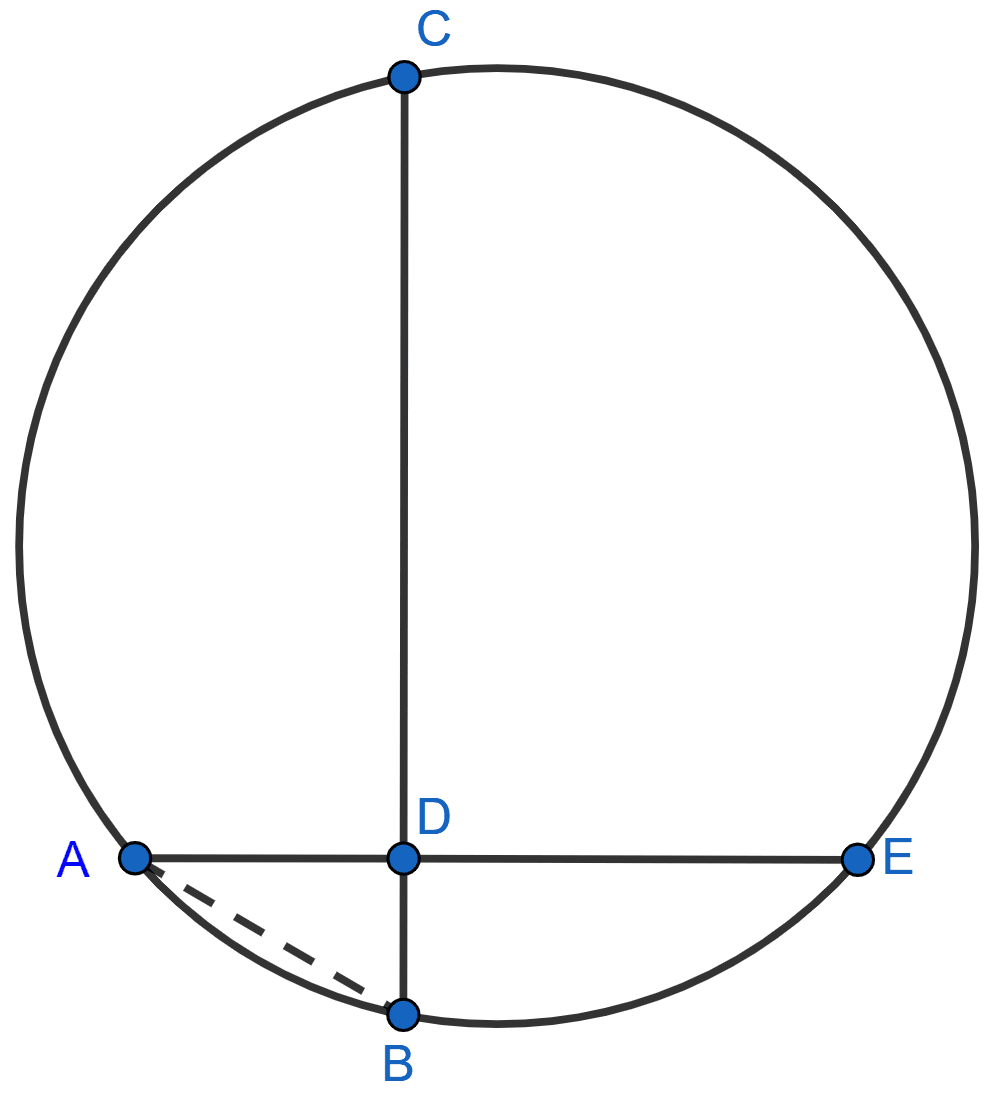
∠ADB = ∠CDE = 90° [Vertically opposite angles are equal.]

In right angle triangle ADB,

⇒ AB² = AD² + BD²

⇒ 5² = AD² + 4²

⇒ 25 = AD² + 16

⇒ AD² = 25 - 16

⇒ AD² = 9

⇒ AD = $\sqrt{9}$

⇒ AD = 3 cm.

We know that,

If two chords of a circle intersect internally or externally then the product of the lengths of their segment is equal.

From figure,

Chords AE and CB intersect internally at point D.

⇒ AD × DE = CD × BD

⇒ 3 × DE = 4 × 9

⇒ DE = $\dfrac{36}{3}$

⇒ DE = 12 cm.

Hence, DE = 12 cm.

(ii) Given,

AD = BD ........(1)

AD = BD = x (let)

We know that,

⇒ AD × DE = CD × BD

⇒ (x)DE = (x)CD

⇒ DE = CD ..........(2)

Adding (1) and (2), we get :

⇒ AD + DE = BD + CD

⇒ AE = BC.

Hence, proved that AE = BC.

In the adjoining figure, O is the center of the circle and AB is a tangent to it at point B. ∠BDC = 65°. Find ∠BAO.

Answer

From figure,

⇒ ∠ADE + ∠BDE = 180° [Linear pairs]

⇒ ∠ADE + 65° = 180°

⇒ ∠ADE = 180° - 65°

⇒ ∠ADE = 115° ..............(1)

∠DBO = 90° [As, DB is tangent and BC is diameter.]

In △BDC,

⇒ ∠BDC + ∠DBC + ∠DCB = 180° [Angle sum property of triangle]

⇒ 65° + 90° + ∠DCB = 180°

⇒ ∠DCB = 180° - 155° = 25°.

From figure,

OE = OC [Radius of same circle.]

⇒ ∠OCE = ∠OEC [As, angles opposite to equal sides are equal.]

⇒ ∠OEC = ∠DCB = 25°. [As, ∠OCE = ∠DCB]

In △ADE,

⇒ ∠ADE + ∠DEA + ∠DAE = 180° [Angle sum property of triangle]

⇒ 115° + 25° + ∠DAE = 180° [From figure, ∠DEA = ∠OEC [Vertically opposite angles are equal]]

⇒ ∠DAE = 180° - 140° = 40°.

From figure,

∠BAO = ∠DAE = 40°.

Hence, ∠BAO = 40°.

AP is a tangent to the given circle. If AB = 8 cm and BC = 10 cm, then AP is :

1. 8 cm

2. 16 cm

3. 12 cm

4. 24 cm

Answer

We know that,

If a chord and a tangent intersect externally, then the product of the lengths of the segments of the chord is equal to the square of the length of the tangent from the point of contact to the point of intersection.

From figure,

AC = AB + BC = 8 + 10 = 18 cm.

⇒ AB × AC = AP²

⇒ 8 × 18 = AP²

⇒ AP² = 144

⇒ AP = $\sqrt{144}$ = 12 cm.

Hence, Option 3 is the correct option.

In the given figure, O is center of the circle and PQ is a tangent. If angle OAB = x; the measure of angle ABP; in terms of x, is :

1. x

2. 180° - 2x

3. 90° + x

4. 90° - x

Answer

From figure,

In △OAB,

OA = OB (Radius of same circle)

We know that,

Angles opposite to equal sides are equal.

⇒ ∠OBA = ∠OAB = x

We know that,

Tangent at any point of a circle and the radius through this point are perpendicular to each other.

∴ OB ⊥ PQ

∴ ∠PBO = 90°

From figure,

∠ABP = ∠PBO - ∠OBA = 90° - x.

Hence, Option 4 is the correct option.

In the given figure, AB is tangent to the circle with center O. If OCB is a straight line segment, the angle BAC is :

1. 40°

2. 55°

3. 35°

4. 20°

Answer

We know that,

Tangent at any point of a circle and the radius through this point are perpendicular to each other.

∴ OA ⊥ AB

∴ ∠OAB = 90°.

Let, ∠BAC = x

From figure,

In △OAC,

∠A = ∠OAB - ∠BAC = 90° - x.

Also,

OA = OC (Radius of same circle)

We know that,

Angles opposite to equal sides are equal.

∴ ∠C = ∠A = 90° - x.

By angle sum property of triangle,

⇒ ∠A + ∠O + ∠C = 180°

⇒ 90° - x + ∠O + 90° - x = 180°

⇒ ∠O + 180° - 2x = 180°

⇒ ∠O = 180° - 180° + 2x = 2x.

In △OAB,

By angle sum property of triangle,

⇒ ∠O + ∠A + ∠B = 180°

⇒ ∠O + ∠OAB + ∠B = 180°

⇒ 2x + 90° + 20° = 180°

⇒ 2x + 110° = 180°

⇒ 2x = 180° - 110°

⇒ 2x = 70°

⇒ x = $\dfrac{70°}{2}$ = 35°.

⇒ ∠BAC = 35°.

Hence, Option 3 is the correct option.

In the given figure O is center, PQ is tangent at point A. BD is diameter and ∠AOD = 84° then angle QAD is :

1. 32°

2. 84°

3. 48°

4. 42°

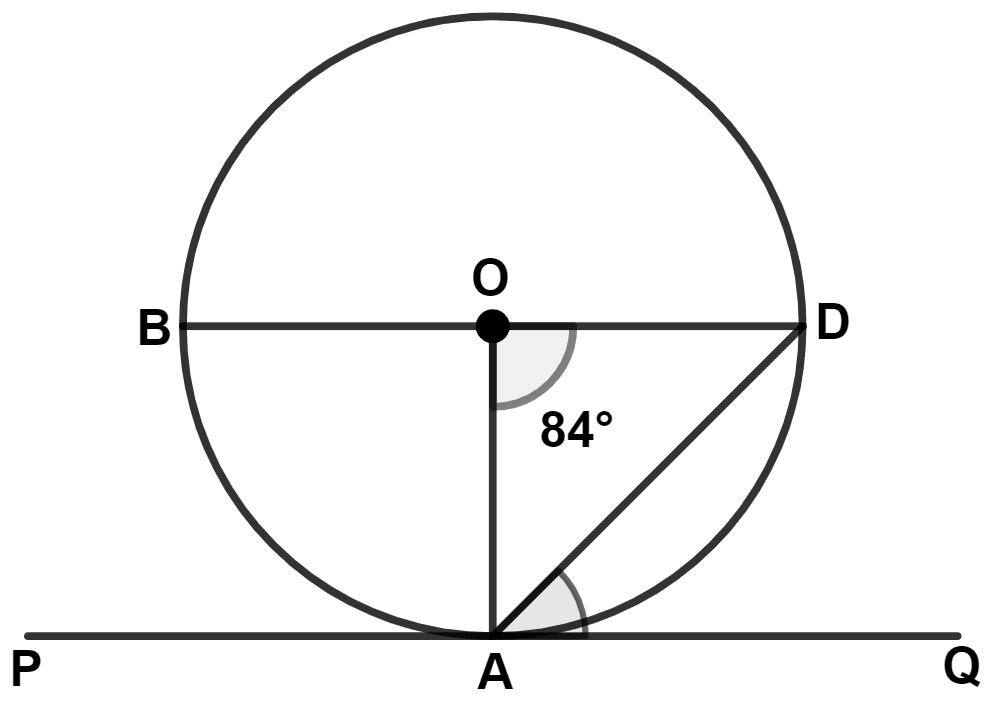
Answer

In △OAD,

OA = OD (Radius of same circle)

We know that,

Angles opposite to equal sides are equal.

∴ ∠A = ∠D = x (let)

⇒ ∠O + ∠A + ∠D = 180° (By angle sum property of triangle)

⇒ 84° + x + x = 180°

⇒ 2x = 180° - 84°

⇒ 2x = 96°

⇒ x = $\dfrac{96°}{2}$ = 48°.

From figure,

∠OAD = ∠A = 48°

We know that,

Tangent at any point of a circle and the radius through this point are perpendicular to each other.

∴ ∠OAQ = 90°

From figure,

∠DAQ = ∠OAQ - ∠OAD = 90° - 48° = 42°.

Hence, Option 4 is the correct option.

Two mutually perpendicular tangents are drawn to a circle with radius $R\sqrt{2}$ units. The shortest distance between the two points of contact is :

1. R units

2. $\dfrac{1}{2}R$ units

3. $R\sqrt{2}$ units

4. 2R units

Answer

Let two perpendicular tangents from external point A touch the circle at points B and C.

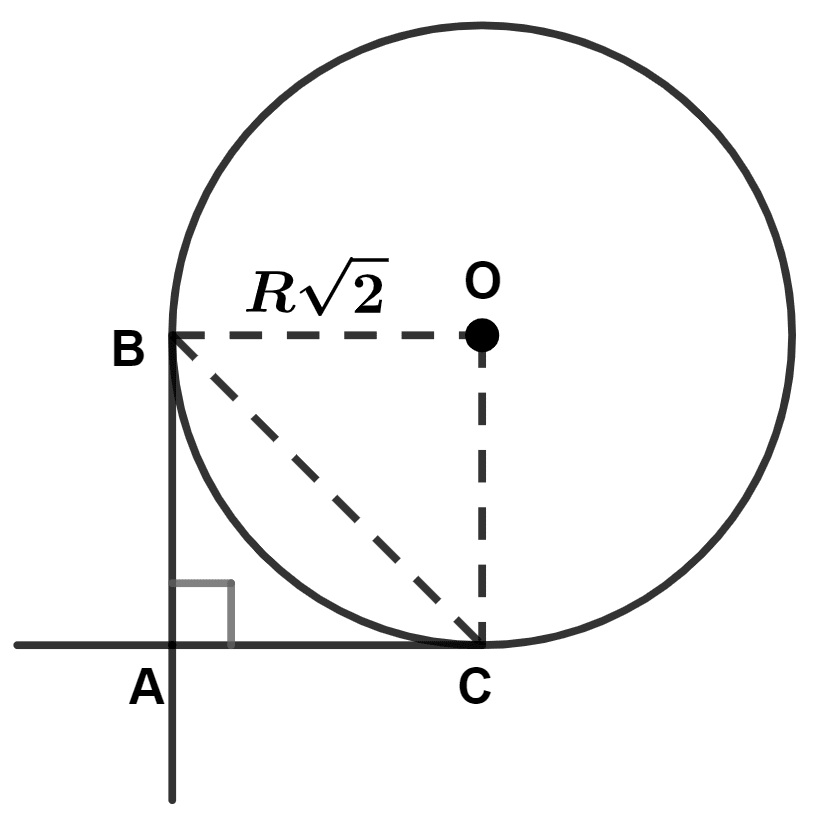
Given,

Radius = $R\sqrt{2}$ units

From figure,

AC = OB = $R\sqrt{2}$,

AB = OC = $R\sqrt{2}$.

In right angle triangle ABC,

⇒ BC² = AB² + AC²

⇒ BC² = $(R\sqrt{2})^2 + (R\sqrt{2})^2$

⇒ BC² = 2R² + 2R²

⇒ BC² = 4R²

⇒ BC = $\sqrt{4R^2}$

⇒ BC = 2R units.

Hence, Option 4 is the correct option.

For the three circles with centers A, B and C and radii 5 cm, 2 cm and 6 cm respectively.

Assertion (A) : To find the perimeter of the triangle ABC, add the radii of given three circles.

Reason (R) : The required perimeter is the product of sum of radii by 2.

1. A is true, R is true

2. A is true, R is false

3. A is false, R is true

4. A is false, R is false

Answer

Let the circles intersect at points D, E and F.

From figure,

Perimeter of triangle ABC = AB + BC + CA

= (AD + BD) + (BE + CE) + (CF + FA)

= 5 + 2 + 2 + 6 + 6 + 5

= 26 cm.

On adding radii of three circles, we get :

5 + 2 + 6 = 13 cm, which is not equal to perimeter.

Sum of radii × 2 = 13 × 2 = 26 cm, which is equal to perimeter.

∴ A is false, R is true

Hence, Option 3 is correct option.

AB is diameter of the circle. PA is tangent and ∠AOC = 60°.

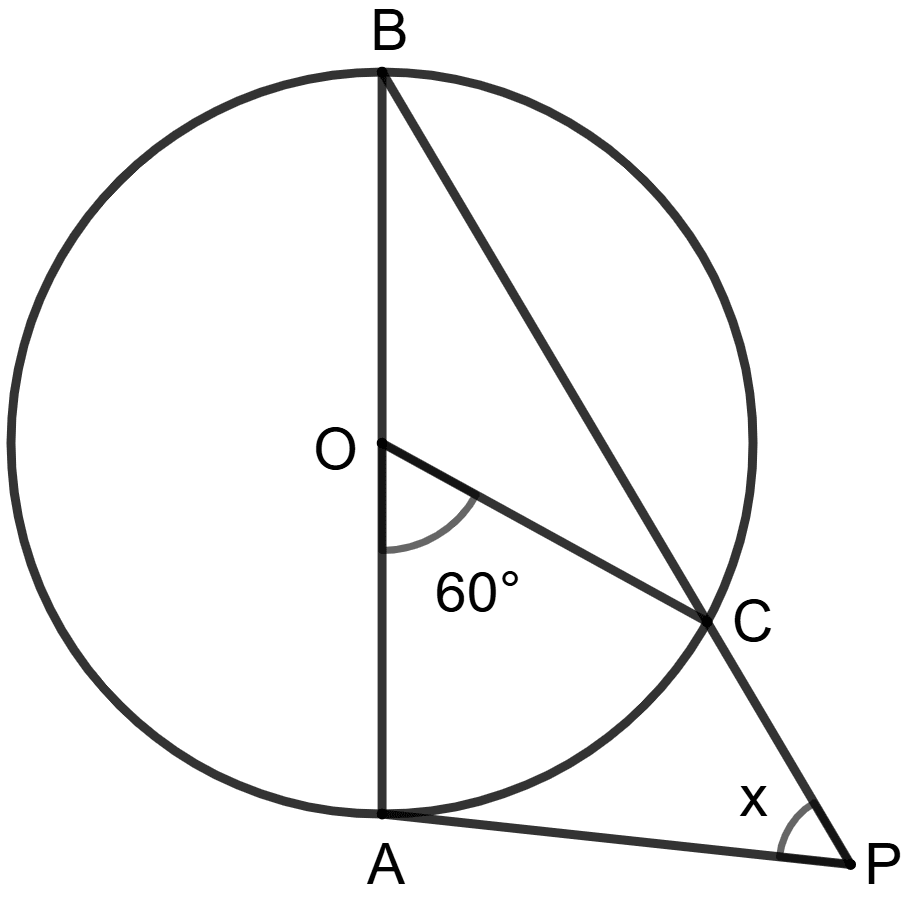
Assertion(A): x + 30° = 90°.

Reason(R): PA is tangent

⇒ ∠BAP = 90°

∴ x + 30° = 90°

1. A is true, R is false.

2. A is false, R is true.

3. Both A and R are true and R is correct reason for A.

4. Both A and R are true and R is incorrect reason for A.

Answer

We know that,

The angle subtended by an arc of a circle at the center is double the angle subtended by it at any point on the remaining part of the circle.

∴ ∠AOC = 2 x ∠ABC

⇒ 60° = 2 x ∠ABC

⇒ ∠ABC = $\dfrac{60°}{2}$ = 30°

The tangent at any point of a circle is perpendicular to the radius through the point of contact.

∴ AP ⊥ OA

⇒ ∠OAP = 90°

⇒ ∠OAP = ∠BAP = 90°

In ΔABP, according to angle sum property,

∴ ∠ABP + ∠APB + ∠BAP = 180°

⇒ 30° + x + 90° = 180°

⇒ 30° + x = 180° - 90°

⇒ 30° + x = 90°.

∴ Both A and R are true and R is correct reason for A.

Hence, option 3 is the correct option.

Chords AD and BC one produce meet at exterior point P.

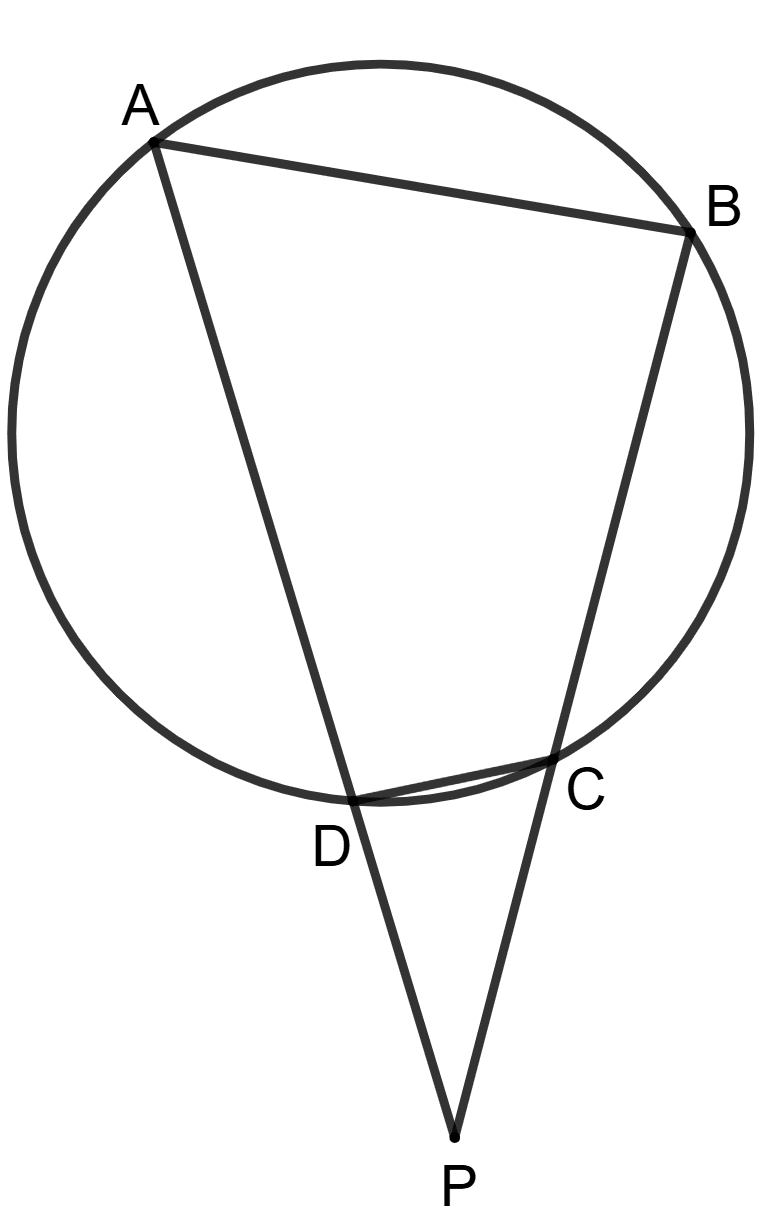
Assertion(A): PD x AD = PC x BC.

Reason(R): In triangles PAB and PCD.

∠PAB = ∠PCD ⇒ ΔPAB ∼ ΔPCD

$\Rightarrow \dfrac{PD}{PB} = \dfrac{PC}{PA}$

1. A is true, R is false.

2. A is false, R is true.

3. Both A and R are true and R is correct reason for A.

4. Both A and R are true and R is incorrect reason for A.

Answer

In ΔPAB and ΔPCD,

⇒ ∠PBA = ∠PDC (Exterior angles of a cyclic quadrilateral is always equal to interior opposite angle)

⇒ ∠PAB = ∠PCD ((Exterior angles of a cyclic quadrilateral is always equal to interior opposite angle))

ΔPAB ~ ΔPCD (By A.A. axiom of similarity)

We know that,

Corresponding sides of similar triangles are proportional.

$\Rightarrow \dfrac{PD}{PB} = \dfrac{PC}{PA}$

∴ Reason (R) is true.

⇒ PD x PA = PC x PB

∴ Assertion (A) is false.

∴ A is false, R is true.

Hence, option 2 is the correct option.

Two circles touch each other externally at point P. OA and OB are the tangent of the two circles (as shown) and OA = 10 cm.

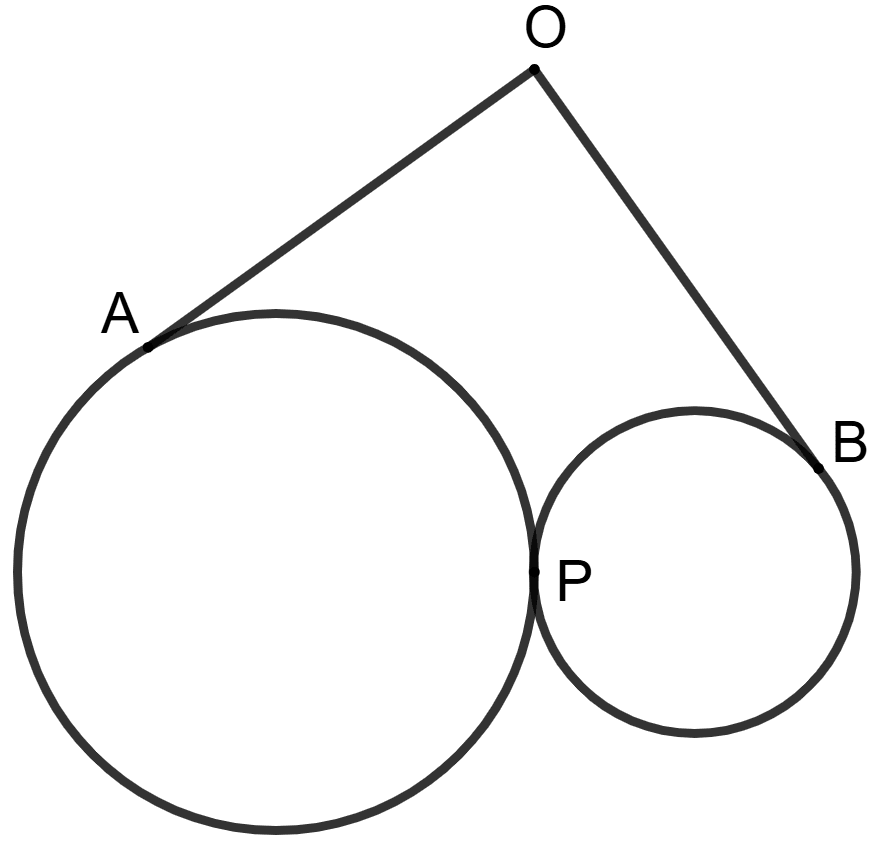
Statement (1): OB = 10 cm.

Statement (2): On joining O and P, tangent OP = tangent OA and tangent OP = tangent OB

1. Both the statement are true.

2. Both the statement are false.

3. Statement 1 is true, and statement 2 is false.

4. Statement 1 is false, and statement 2 is true.

Answer

Join OP.

We know that,

If two tangents are drawn to a circle from an exterior point, the tangents are equal in length.

From figure,

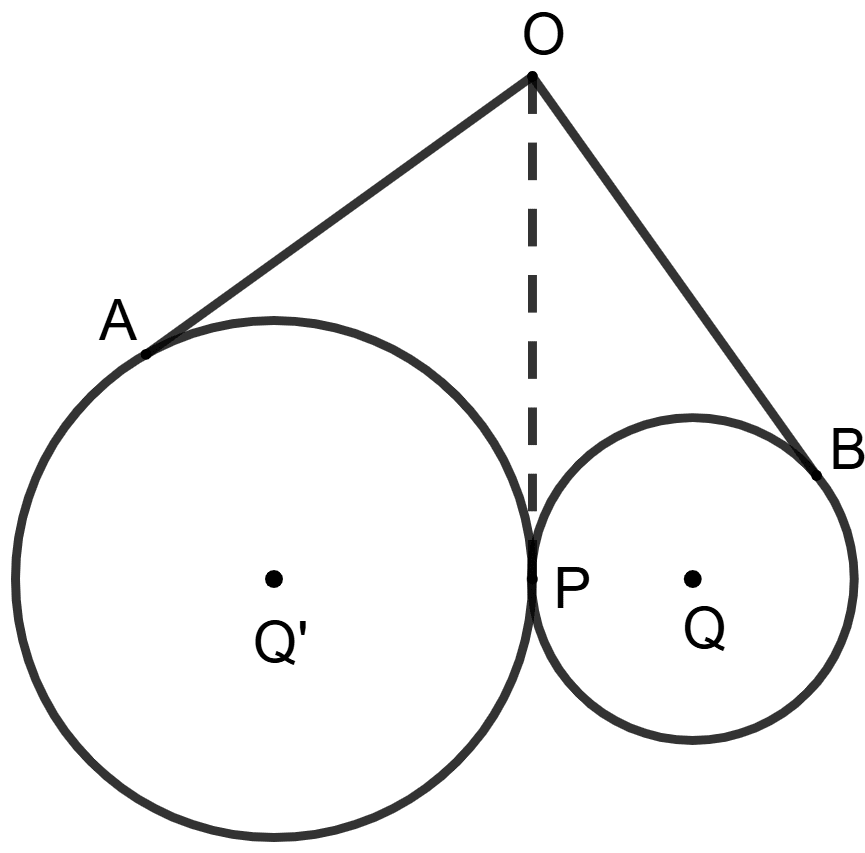
O is the point from which, OA and OP are two tangents to the circle with centre Q'.

So, OA = OP .......(1)

Similarly, from point O, OB and OP are two tangents to the circle with centre Q.

So, OB = OP ......(2)

From (1) and (2), we have

⇒ OA = OB

⇒ OB = 10 cm

∴ Both the statements are true.

Hence, option 1 is the correct option.

O is centre of the circle, PB and PC are tangents and ∠BPC = 50°.

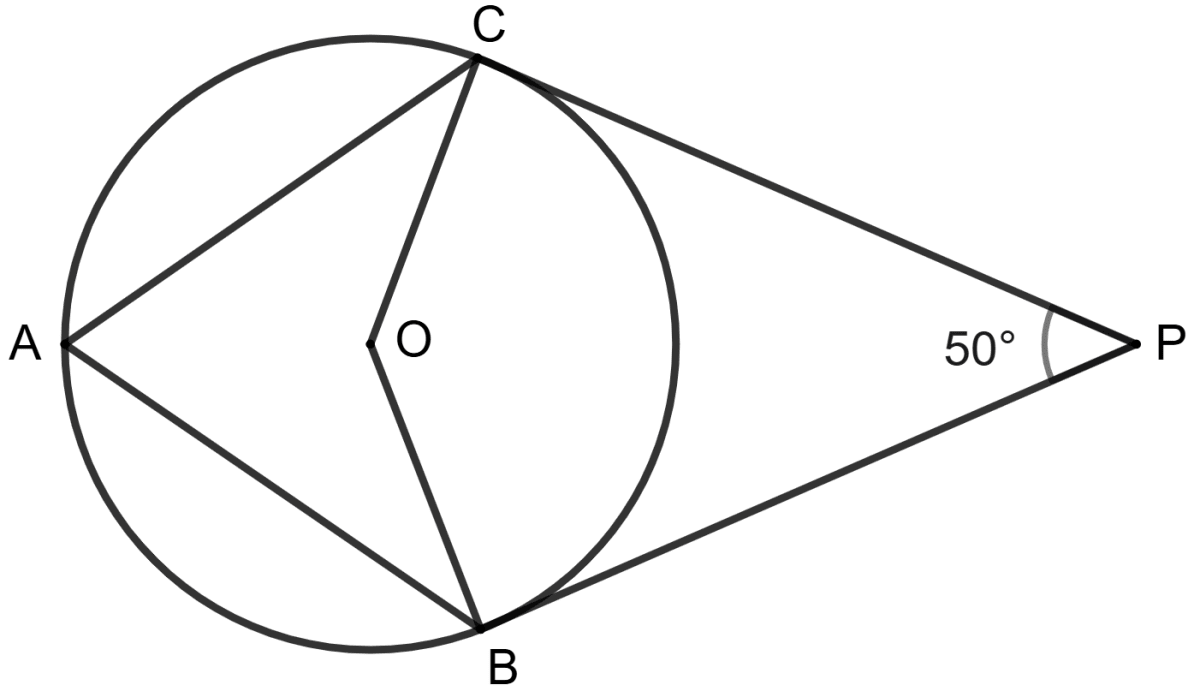
Statement (1): ∠BAC = ∠P = 50°

Statement (2): ∠BOC + 50° = 180°

⇒ ∠BOC = 130°

∴ ∠BAC = 65°

1. Both the statement are true.

2. Both the statement are false.

3. Statement 1 is true, and statement 2 is false.

4. Statement 1 is false, and statement 2 is true.

Answer

The tangent at any point of a circle is perpendicular to the radius through the point of contact.

∴ OB ⊥ BP and OC ⊥ CP

⇒ ∠OBP = 90° and ∠OCP = 90°

OCPB is a quadrilateral.

∴ ∠OBP + ∠BPC + ∠OCP + ∠BOC = 360°

⇒ 90° + 50° + 90° + ∠BOC = 360°

⇒ 230° + ∠BOC = 360°

⇒ ∠BOC = 360° - 230°

⇒ ∠BOC = 130°

We know that,

The angle subtended by an arc of a circle at the center is double the angle subtended by it at any point on the remaining part of the circle.

∴ ∠BOC = 2 x ∠BAC

⇒ 130° = 2 x ∠BAC

⇒ ∠BAC = $\dfrac{130°}{2}$ = 65°.

So, Statement 1 is false, and statement 2 is true.

Hence, option 4 is the correct option.

Prove that, of any two chords of a circle, the greater chord is nearer to the centre.

Answer

Let there be a circle with center O and radius r. AB and CD are two chords of this circle. OM < ON where OM ⊥ AB and ON ⊥ CD.

To prove: AB > CD

We know that,

The perpendicular from the centre of a circle to a chord bisects the chord.

∴ AM = $\dfrac{AB}{2}$ and CN = $\dfrac{CD}{2}$

Join OA and OC.

In right angle triangle OAM,

⇒ OA² = AM² + OM²

⇒ AM² = OA² - OM² ..... (1)

In right angle triangle ONC,

⇒ OC² = CN² + ON²

⇒ CN² = OC² - ON² ..... (2)

OM < ON

⇒ OM² < ON²

⇒ -OM² > -ON²

⇒ OA² - OM² > OC² - ON² [∵ OA = OC]

⇒ AM² > CN² [From (1) and (2)]

⇒ $\Big(\dfrac{\text{AB}}{2}\Big)^2$ > $\Big(\dfrac{\text{CD}}{2}\Big)^2$

⇒ $\dfrac{1}{4}$AB² > $\dfrac{1}{4}$CD²

⇒ AB² > CD²

⇒ AB > CD

Hence proved that, of any two chords of a circle, the greater chord is nearer to the centre.

ABCD is a cyclic quadrilateral in which BC is parallel to AD, angle ADC = 110° and angle BAC = 50°. Find angle DAC and angle DCA.

Answer

Given, ABCD is a cyclic quadrilateral in which AD || BC

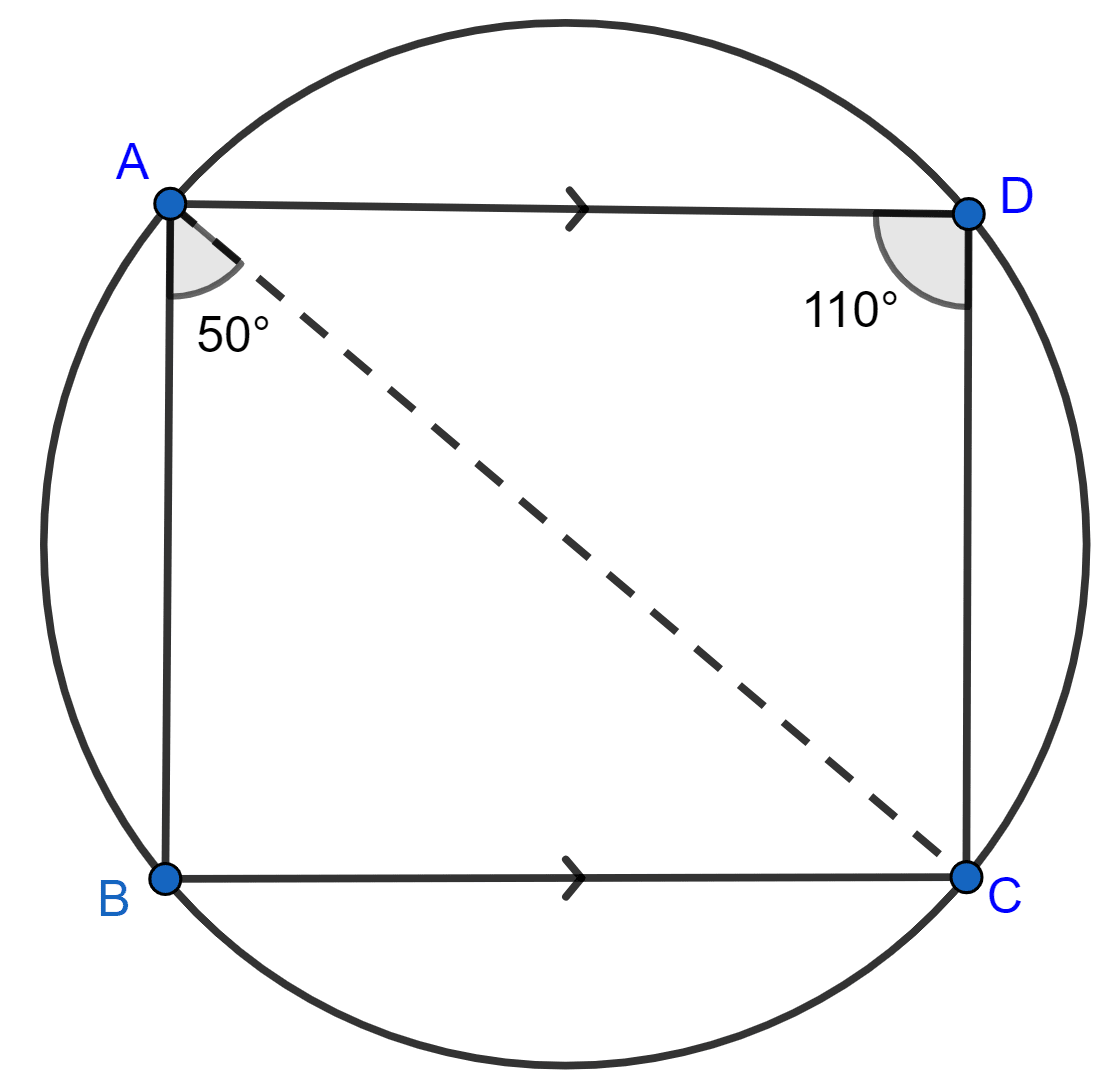
With, ∠ADC = 110°, ∠BAC = 50°.

We know that,

⇒ ∠B + ∠D = 180° [Sum of opposite angles of a cyclic quadrilateral = 180°]

⇒ ∠B + 110° = 180°

⇒ ∠B = 180° - 110°

⇒ ∠B = 70°.

Now in ∆ABC, we have

⇒ ∠BAC + ∠ABC + ∠ACB = 180° [By angle sum property of triangle]

⇒ 50° + 70° + ∠ACB = 180°

⇒ ∠ACB = 180° - 120° = 60°

As, AD || BC we have

∠DAC = ∠ACB = 60° [Alternate angles]

Now in ∆ADC,

⇒ ∠DAC + ∠ADC + ∠DCA = 180°

⇒ 60° + 110° + ∠DCA = 180°

⇒ ∠DCA = 180° - 170° = 10°

Hence, ∠DAC = 60° and ∠DCA = 10°.

In the given figure, C and D are points on the semi-circle described on AB as diameter.

Given angle BAD = 70° and angle DBC = 30°, calculate angle BDC.

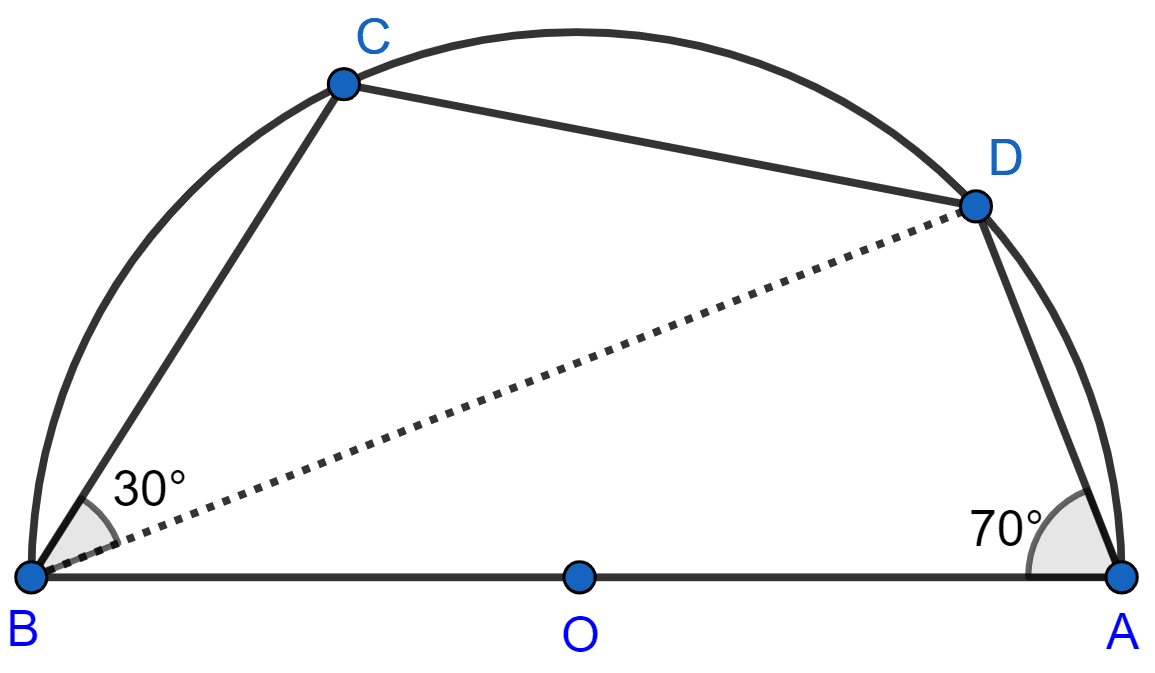
Answer

As ABCD is a cyclic quadrilateral, we have

⇒ ∠BCD + ∠BAD = 180° [Opposite angles of a cyclic quadrilateral are supplementary]

⇒ ∠BCD + 70° = 180°

⇒ ∠BCD = 180° - 70° = 110°

In ∆BCD,

⇒ ∠CBD + ∠BCD + ∠BDC = 180° [By angle sum property of triangle]

⇒ 30° + 110° + ∠BDC = 180°

⇒ ∠BDC = 180° - 140° = 40°.

Hence, ∠BDC = 40°.

In cyclic quadrilateral ABCD, ∠A = 3∠C and ∠D = 5∠B. Find the measure of each angle of the quadrilateral.

Answer

Given, cyclic quadrilateral ABCD

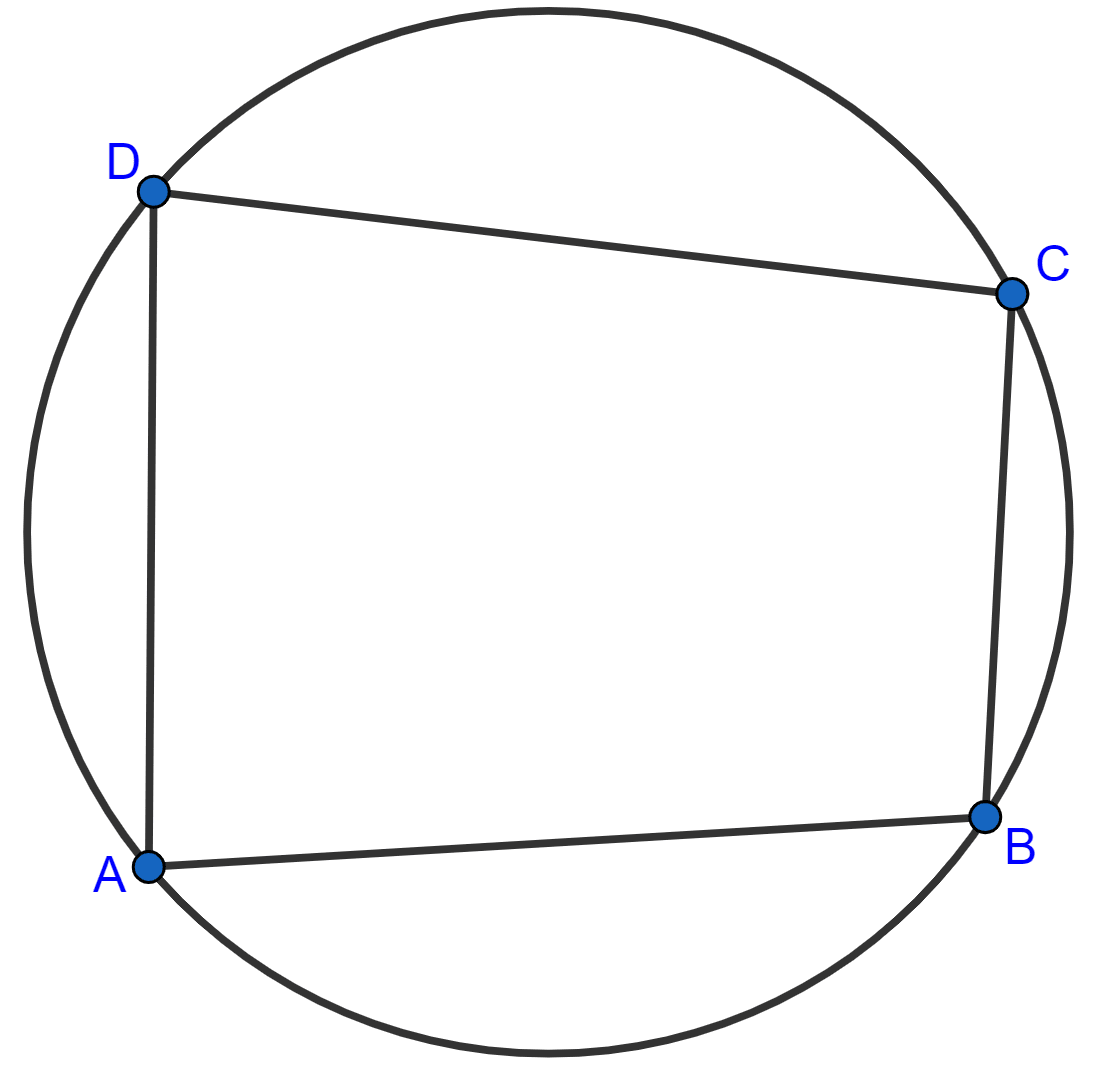
So, ∠A + ∠C = 180° [Opposite angles in a cyclic quadrilateral is supplementary]

⇒ 3∠C + ∠C = 180° [As ∠A = 3∠C]

⇒ 4∠C = 180°

⇒ ∠C = $\dfrac{180°}{4}$

⇒ ∠C = 45°.

Now,

⇒ ∠A = 3∠C = 3 x 45° = 135°.

Similarly,

⇒ ∠B + ∠D = 180°

⇒ ∠B + 5∠B = 180° [As, ∠D = 5∠B]

⇒ 6∠B = 180°

⇒ ∠B = $\dfrac{180°}{6}$

⇒ ∠B = 30°.

Now,

⇒ ∠D = 5∠B = 5 x 30° = 150°.

Hence, ∠A = 135°, ∠B = 30°, ∠C = 45° and ∠D = 150°.

Show that the circle drawn on any one of the equal sides of an isosceles triangle as diameter bisects the base.

Answer

Let circle be drawn on one of the equal sides AB of the isosceles triangle ABC as shown in the figure below:

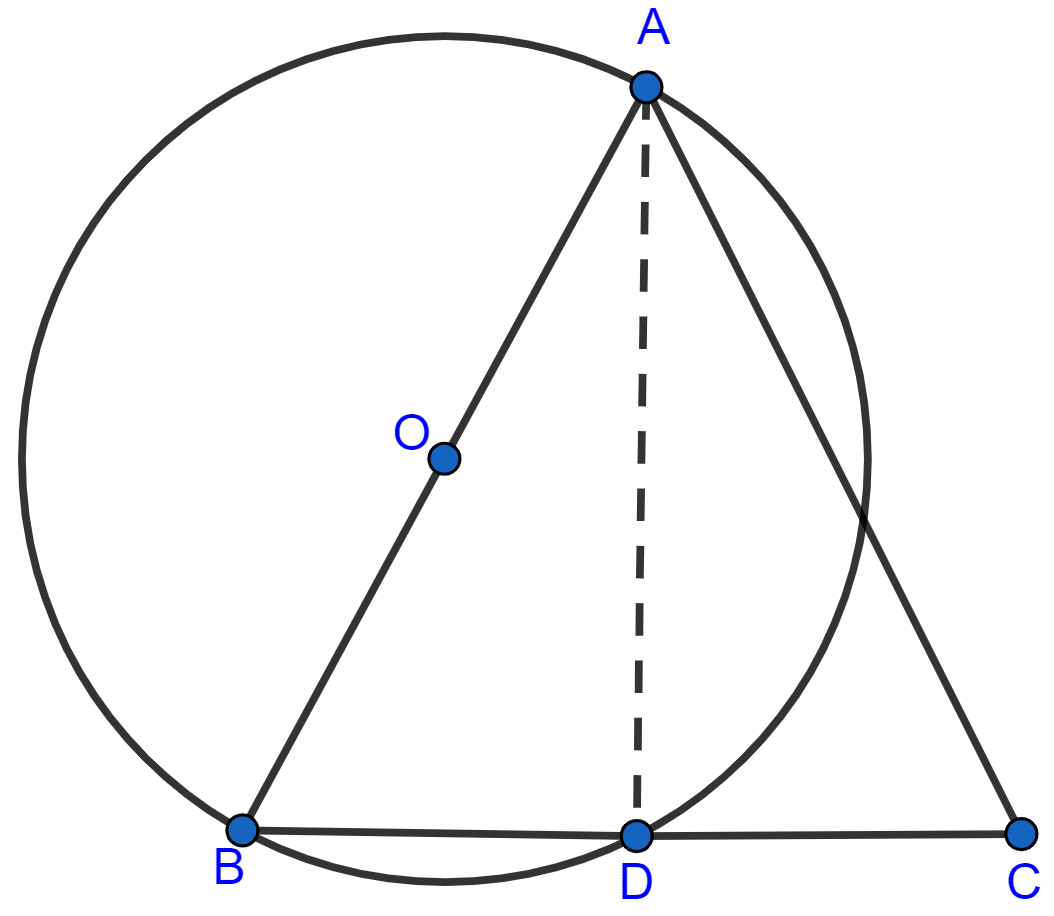
We have ∠ADB = 90° [Angle in a semi-circle is a right angle]

But,

⇒ ∠ADB + ∠ADC = 180° [Linear pair]

⇒ 90° + ∠ADC = 180°

⇒ ∠ADC = 180° - 90°

⇒ ∠ADC = 90°.

In ∆ABD and ∆ACD, we have

⇒ ∠ADB = ∠ADC [Each 90°]

⇒ AB = AC [Given]

⇒ AD = AD [Common]

Hence, ∆ABD ≅ ∆ACD by RHS congruence criterion.

By, C.P.C.T we get :

BD = DC

Hence, the circle bisects base BC at D.

Bisectors of vertex angles A, B and C of a triangle ABC intersect its circumcircle at points D, E and F respectively. Prove that angle EDF = 90° - $\dfrac{1}{2}$∠A.

Answer

BE is the bisector of ∠B.

⇒ ∠ABE = $\dfrac{∠B}{2}$

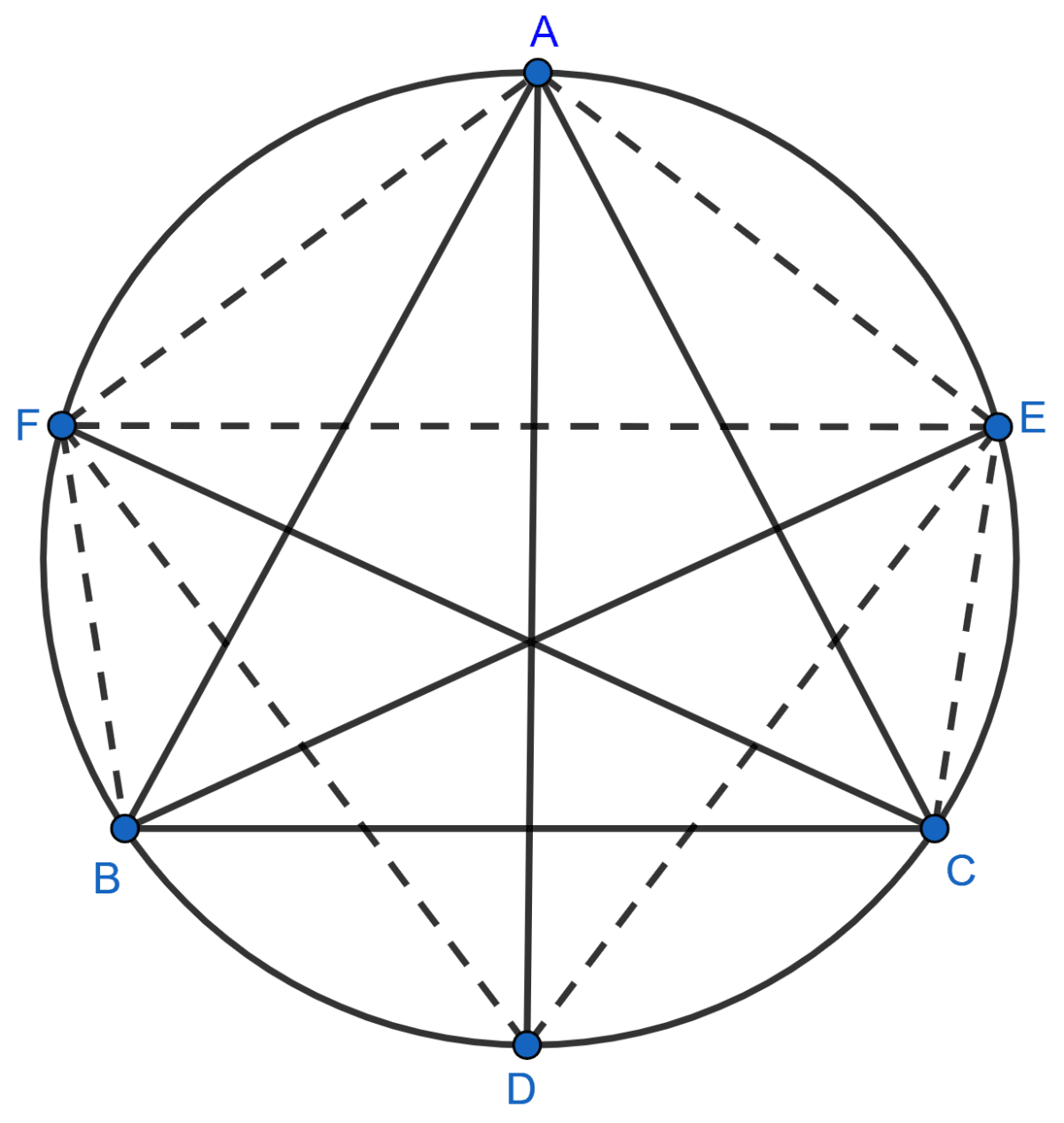
From figure,

⇒ ∠ADE = ∠ABE [Angles in same segment are equal]

⇒ ∠ADE = $\dfrac{∠B}{2}$ ...........(1)

Also,

FC is the bisector of ∠C.

⇒ ∠ACF = $\dfrac{∠C}{2}$

⇒ ∠ACF = ∠ADF [Angles in same segment are equal]

⇒ ∠ADF = $\dfrac{∠C}{2}$ .............(2)

From figure,

⇒ ∠D = ∠ADE + ∠ADF

⇒ ∠D = $\dfrac{∠B + ∠C}{2}$ ...........(3)

In triangle ABC,

⇒ ∠A + ∠B + ∠C = 180°

⇒ ∠B + ∠C = 180° - ∠A

Substituting above value in (3), we get :

⇒ ∠D = $\dfrac{180° - ∠A}{2}$

⇒ ∠D = 90° - $\dfrac{1}{2}$∠A.

From figure,

∠EDF = ∠D.

Hence, proved that ∠EDF = $90° - \dfrac{1}{2}∠A$.

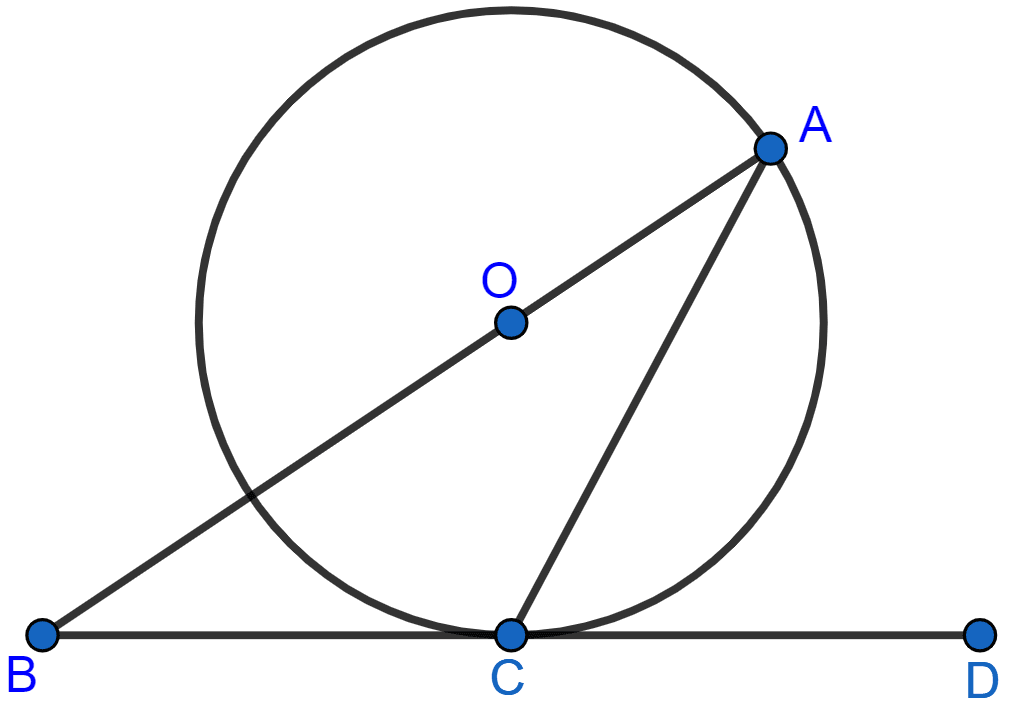
In the figure, AB is the chord of a circle with centre O and DOC is a line segment such that BC = DO. If ∠C = 20°, find angle AOD.

Answer

Join OB.

Given,

BC = OD = radius of circle

⇒ BC = OB.

As, angles opposite to equal sides are equal.

⇒ ∠BOC = ∠BCO = 20°.

An exterior angle is equal to the sum of two opposite interior angles.

∴ ∠ABO = ∠BCO + ∠BOC = 20° + 20° = 40° ............(1)

Now in ∆OAB,

OA = OB [Radii of the same circle]

As, angles opposite to equal sides are equal.

∠OAB = ∠ABO = 40° [from (1)]

By angle sum property of triangle,

⇒ ∠AOB + ∠OAB + ∠OBA = 180°

⇒ ∠AOB + 40° + 40° = 180°

⇒ ∠AOB + 80° = 180°

⇒ ∠AOB = 180° - 80°

⇒ ∠AOB = 100°

As DOC is a straight line,

⇒ ∠AOD + ∠AOB + ∠BOC = 180°

⇒ ∠AOD + 100° + 20° = 180°

⇒ ∠AOD = 180° - 120° = 60°.

Hence, ∠AOD = 60°.

P is the midpoint of an arc APB of a circle. Prove that the tangent drawn at P will be parallel to the chord AB.

Answer

We know that,

The angle between a tangent and a chord through the point of contact is equal to the angle in the alternate segment, we have :

From figure,

As, TPS is a tangent and PA is the chord of the circle.

∠BPT = ∠PAB [Angles in alternate segments are equal] ..........(1)

But,

∠PBA = ∠PAB [Since, PA = PB as P is mid-point of arc APB.] ........(2)

From (1) and (2), we get :

∠BPT = ∠PBA

The above angles are alternate angles,

∴ TPS || AB

Hence, proved that the tangent drawn at P will be parallel to the chord AB.

In the given figure, ABCD is a cyclic quadrilateral, PQ is tangent to the circle at point C and BD is its diameter. If ∠DCQ = 40° and ∠ABD = 60°, find:

(i) ∠DBC

(ii) ∠BCP

(iii) ∠ADB

Answer

(i) We know that,

The angle between a tangent and a chord through the point of contact is equal to the angle in the alternate segment, we have :

From figure,

PQ is a tangent and CD is a chord.

⇒ ∠DBC = ∠DCQ [Angles in the alternate segment are equal]

⇒ ∠DBC = 40°.

Hence, ∠DBC = 40°.

(ii) In △DCB

⇒ ∠DBC + ∠DCB + ∠CDB = 180° [By angle sum property of triangle]

⇒ 40° + 90° + ∠CDB = 180° [∠DCB = 90°, as angle in a semi-circle is a right angle]

⇒ ∠CDB = 180° - 130° = 50°.

From figure,

⇒ ∠BCP = ∠CDB = 50°. [Angles in the alternate segment are equal]

Hence, ∠BCP = 50°.

(iii) In ∆ABD,

∠BAD = 90° [Angle in a semi-circle is a right angle]

∠ABD = 60° [Given]

⇒ ∠ADB + ∠BAD + ∠ABD = 180° [By angle sum property of triangle]

⇒ ∠ADB + 90° + 60° = 180°

⇒ ∠ADB = 180° - 150° = 30°

Hence, ∠ADB = 30°.

The given figure shows a circle with centre O and BCD is a tangent to it at C. Show that : ∠ACD + ∠BAC = 90°.

Answer

Join OC.

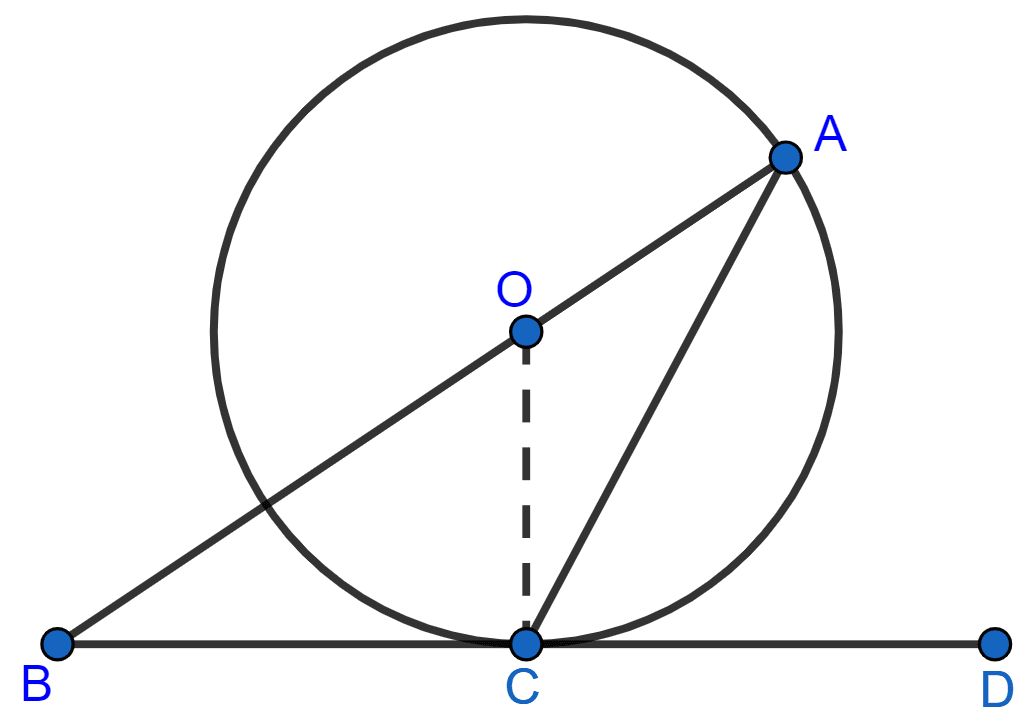
We know that,

The radius from the center of the circle to the point of tangent is perpendicular to the tangent line.

BCD is the tangent and OC is the radius.

As, OC ⊥ BD

∠OCD = 90°

∴ ∠OCA + ∠ACD = 90° ............. (1)

In ∆OCA,

⇒ OA = OC [Radius of the same circle]

∴ ∠OCA = ∠OAC [As, angles opposite to equal sides are equal]

Substituting in (1), we get

⇒ ∠OAC + ∠ACD = 90°

⇒ ∠BAC + ∠ACD = 90° [From figure, ∠BAC = ∠OAC]

Hence, proved that ∠ACD + ∠BAC = 90°.

ABC is a right triangle with angle B = 90°. A circle with BC as diameter meets hypotenuse AC at point D. Prove that:

(i) AC x AD = AB²

(ii) BD² = AD x DC.

Answer

(i) In ∆ABC, we have

∠B = 90° and BC is the diameter of the circle.

Hence, AB is the tangent to the circle at B.

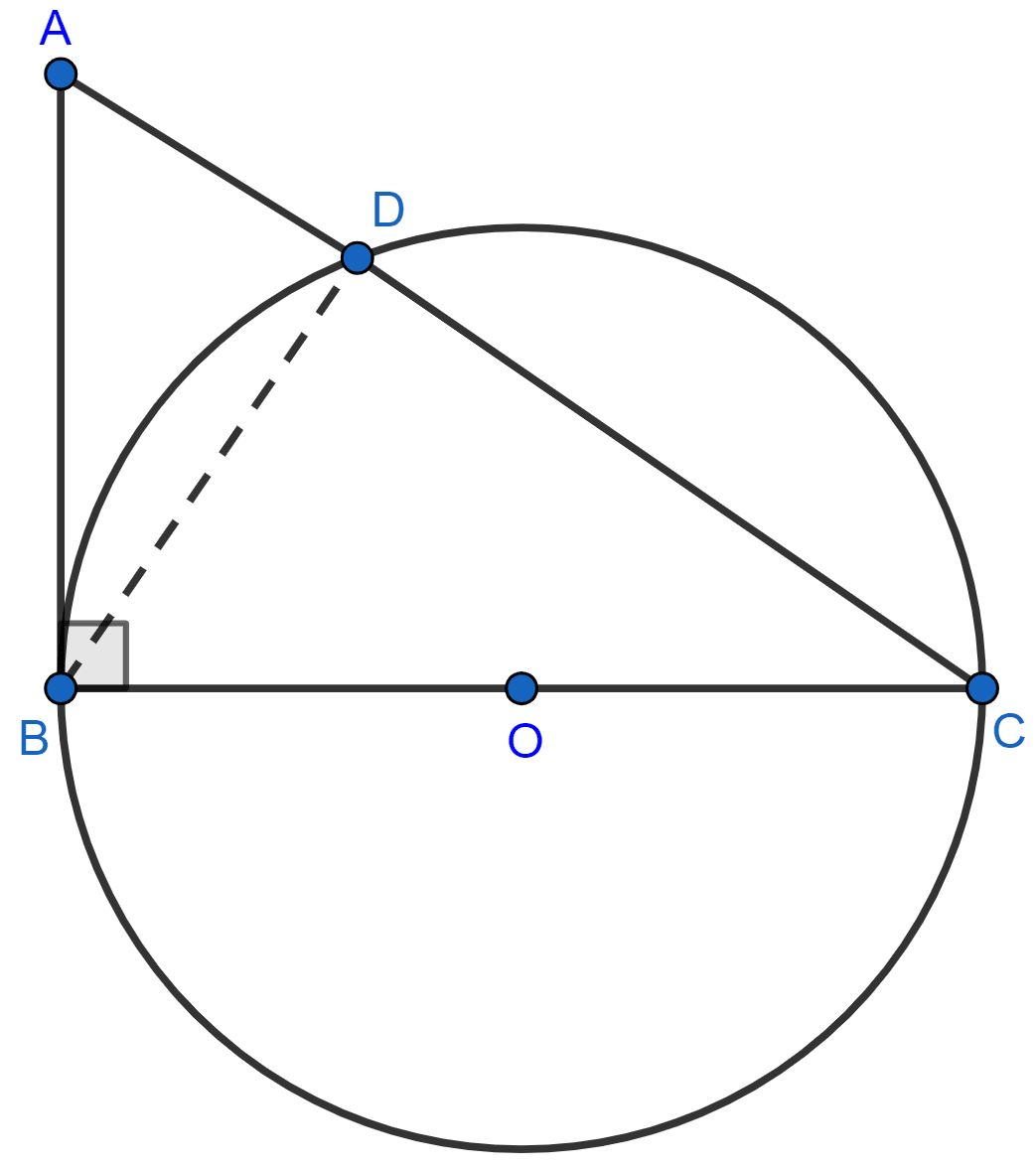
We know that,

If a chord and a tangent intersect externally, then the product of the lengths of the segments of the chord is equal to the square of the length of the tangent from the point of contact to the point of intersection.

∴ AB² = AD x AC.

Hence, proved that AB² = AD x AC.

(ii) From figure,

∠BDC = 90° [Angle in a semi-circle is a right angle.]

From figure,

⇒ ∠ADB + ∠BDC = 180° [Linear pairs]

⇒ ∠ADB + 90° = 180°

⇒ ∠ADB = 180° - 90°

⇒ ∠ADB = 90°

In ∆ADB,

⇒ ∠ADB + ∠A + ∠ABD = 180° [By angle sum property of triangle]

⇒ 90° + ∠A + ∠ABD = 180°

⇒ ∠A + ∠ABD = 90° ...............(1)

In ∆ABC, ∠ABC = 90°.

⇒ ∠ABC + ∠A + ∠ACB = 180° [By angle sum property of triangle]

⇒ 90° + ∠A + ∠ACB = 180°

⇒ ∠A + ∠ACB = 90° ...............(2)

From (1) and (2),

⇒ ∠A + ∠ABD = ∠A + ∠ACB

⇒ ∠ABD = ∠ACB.

From figure,

⇒ ∠ACB = ∠BCD

∴ ∠ABD = ∠BCD

Now in ∆ABD and ∆CBD, we have

∠BDA = ∠BDC [Both equal to 90°]

∠ABD = ∠BCD

Hence, ∆ABD ~ ∆CBD by AA postulate.

We know that,

Ratio of corresponding sides of similar triangles are same.

$\dfrac{BD}{DC} = \dfrac{AD}{BD}$

∴ BD² = AD x DC.

Hence, proved that BD² = AD x DC.

In the given figure, AC = AE.

Show that :

(i) CP = EP

(ii) BP = DP

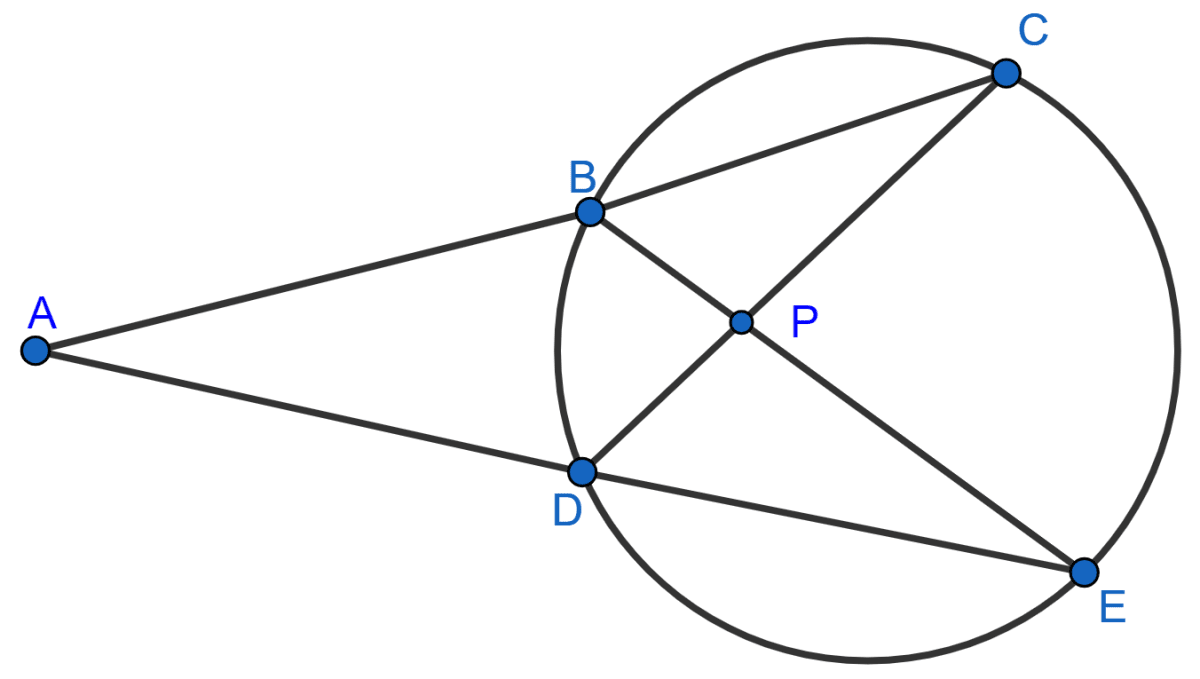
Answer

(i) In ∆ADC and ∆ABE,

⇒ ∠ACD = ∠AEB [Angles in the same segment are equal]

⇒ AC = AE [Given]

⇒ ∠A = ∠A [Common]

Hence, ∆ADC ≅ ∆ABE by ASA axiom.

So, by C.P.C.T we have

⇒ AD = AB ..............(1)

Given,

⇒ AE = AC .............(2)

Subtracting equation (1) from (2), we get :

⇒ AE - AD = AC - AB

⇒ DE = BC

In ∆BPC and ∆DPE,

⇒ ∠C = ∠E [Angles in the same segment are equal]

⇒ BC = DE [Proved above]

⇒ ∠CBP = ∠PDE [Angles in the same segment are equal]

Hence, ∆BPC ≅ ∆DPE by ASA axiom.

So, by C.P.C.T we have

⇒ CP = EP

Hence, proved that CP = EP.

(ii) Proved above,

∆BPC ≅ ∆DPE

∴ BP = DP [By C.P.C.T]

Hence, proved that BP = DP.

ABCDE is a cyclic pentagon with centre of its circumcircle at point O such that AB = BC = CD and angle ABC = 120°.

Calculate :

(i) ∠BEC

(ii) ∠BED

Answer

Cyclic pentagon ABCDE with its circumcircle with centre at point O is shown in the figure below:

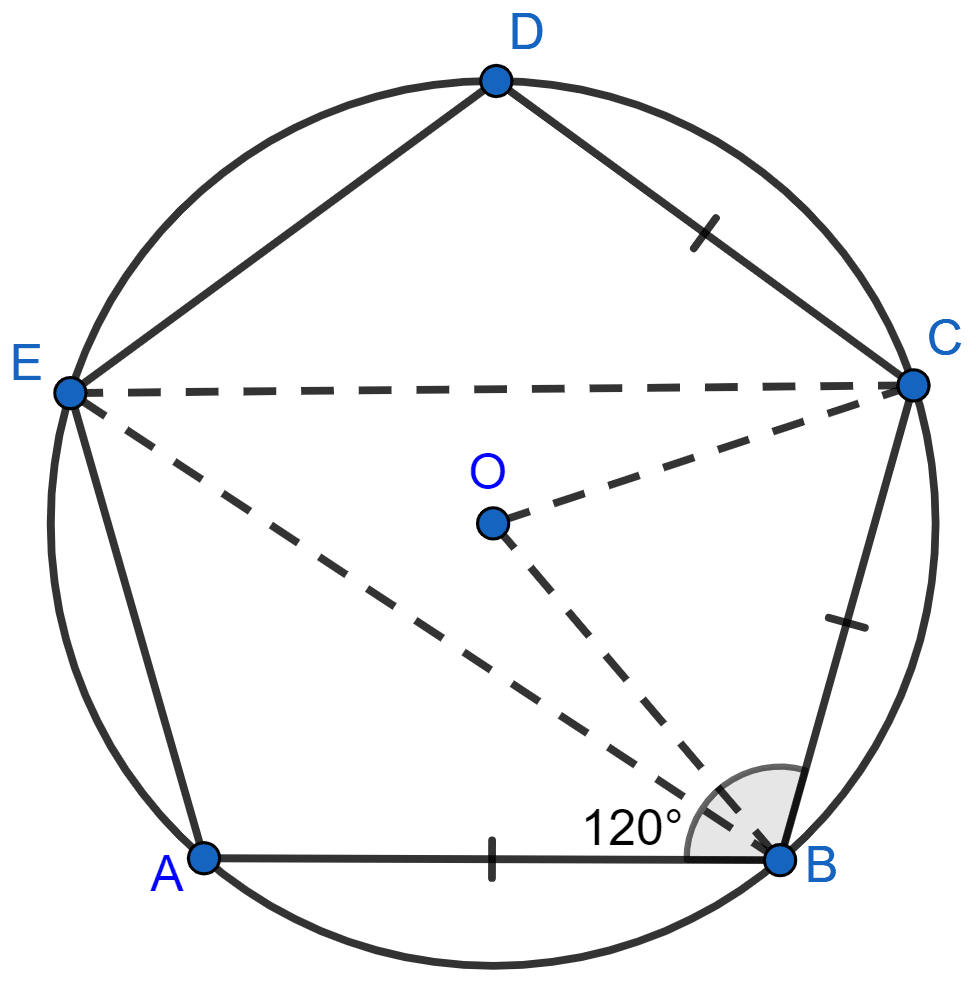
(i) Given,

AB = BC = CD and ∠ABC = 120°

So, ∠BCD = ∠ABC = 120°

OB and OC are the bisectors of ∠ABC and ∠BCD, respectively.

So, ∠OBC = ∠BCO = 60°

In ∆BOC,

⇒ ∠OBC + ∠BCO + ∠BOC = 180° [By angle sum property of triangle]

⇒ 60° + 60° + ∠BOC = 180°

⇒ ∠BOC = 180° - 120° = 60°.

Arc BC subtends ∠BOC at the centre and ∠BEC at the remaining part of the circle.

We know that.

Angle which an arc subtends at the center is double that which it subtends at any point on the remaining part of the circumference.

∠BEC = $\dfrac{1}{2}$∠BOC = $\dfrac{1}{2}$ x 60° = 30°.

Hence, ∠BEC = 30°.

(ii) In cyclic quadrilateral BCDE, we have

⇒ ∠BED + ∠BCD = 180° [Sum of opposite angles in cyclic quadrilateral = 180°]

⇒ ∠BED + 120° = 180°

⇒ ∠BED = 180° - 120°

⇒ ∠BED = 60°.

Hence, ∠BED = 60°.

In the given figure, O is the centre of the circle. Tangents at A and B meet at C. If ∠ACO = 30°, find:

(i) ∠BCO

(ii) ∠AOB

(iii) ∠APB

Answer

(i) In ∆OAC and ∆OBC, we have

⇒ OC = OC [Common]

⇒ OA = OB [Radii of the same circle]

⇒ CA = CB [Tangents to the circle from an exterior point are equal.]

Hence, ∆OAC ≅ ∆OBC by SSS congruence criterion.

∴ ∠ACO = ∠BCO = 30° [By C.P.C.T.]

Hence, ∠BCO = 30°.

(ii) From figure,

∠ACB = ∠ACO + ∠BCO = 30° + 30° = 60°.

Sum of opposite angles of cyclic quadrilateral = 180°.

⇒ ∠AOB + ∠ACB = 180°

⇒ ∠AOB = 180° - 60° = 120°.

Hence, ∠AOB = 120°.

(iii) Arc AB subtends ∠AOB at the center and ∠APB is the remaining part of the circle.

We know that.

When two angles are subtended by the same arc, the angle at the centre of a circle is twice the angle at the circumference.

⇒ ∠APB = $\dfrac{1}{2}$∠AOB = $\dfrac{1}{2}$ x 120° = 60°.

Hence, ∠APB = 60°.

The given figure shows a semi-circle with center O and diameter PQ. If PA = AB and ∠BCQ = 140°; find measures of angles PAB and AQB. Also, show that AO is parallel to BQ.

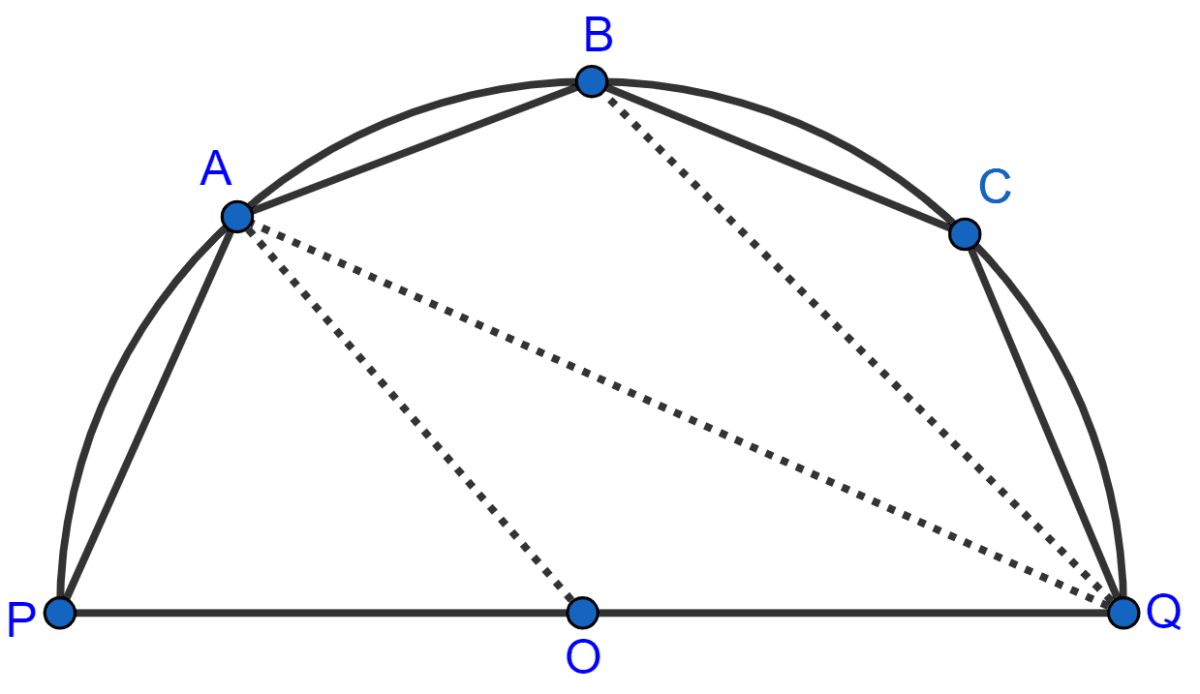
Answer

Join PB.

In cyclic quadrilateral PBCQ,

⇒ ∠BPQ + ∠BCQ = 180° [Sum of opposite angles of a cyclic quadrilateral = 180°]

⇒ ∠BPQ + 140° = 180°

⇒ ∠BPQ = 180° - 140°

⇒ ∠BPQ = 40° ............(1)

In △PBQ,

∠PBQ = 90° [Angle in a semi-circle is a right angle.]

⇒ ∠PBQ + ∠BPQ + ∠PQB = 180° [Angle sum property of triangle]

⇒ 90° + 40° + ∠PQB = 180°

⇒ 130° + ∠PQB = 180°

⇒ ∠PQB = 180° - 130°

⇒ ∠PQB = 50°.

In cyclic quadrilateral PQBA,

⇒ ∠PQB + ∠PAB = 180° [Sum of opposite angles of a cyclic quadrilateral = 180°]

⇒ 50° + ∠PAB = 180°

⇒ ∠PAB = 180° - 50°

⇒ ∠PAB = 130°.

In △PAB,

⇒ ∠PAB + ∠PBA + ∠BPA = 180° [Angle sum property of triangle]

⇒ 130° + ∠PBA + ∠BPA = 180°

⇒ ∠PBA + ∠BPA = 180° - 130°

⇒ ∠PBA + ∠BPA = 50° ................(2)

Given, PA = PB

Angles opposite to equal sides are equal.

∴ ∠PBA = ∠BPA = x (let)

Substituting above value in (2), we get :

⇒ x + x = 50°

⇒ 2x = 50°

⇒ x = $\dfrac{50°}{2}$

⇒ x = 25°.

From figure,

∠AQB = ∠APB = 25° [Angles in same segment are equal.]

∠APQ = ∠APB + ∠BPQ = 25° + 40° = 65.

We know that,

Angle subtended by an arc at the center is twice the angle subtended at any other point of circumference.

Arc AQ subtends ∠AOQ at the center and ∠APQ at the remaining part of the circle.

∠AOQ = 2∠APQ = 2 × 65° = 130°.

In △AOQ,

OA = OQ [Radii of same circle]

As, angles opposite to equal sides are equal.

∠OAQ = ∠OQA = y (let)

⇒ ∠OAQ + ∠OQA + ∠AOQ = 180° [Angle sum property of triangle]

⇒ y + y + 130° = 180°

⇒ 2y = 180° - 130°

⇒ 2y = 50°

⇒ y = $\dfrac{50°}{2}$

⇒ y = 25°.

∴ ∠OAQ = 25°.

Since, ∠OAQ = ∠AQB = 25°.

∠OAQ and ∠AQB are alternate angles.

Thus, AO and BQ are parallel.

Hence, ∠AQB = 25° and ∠PAB = 130°.

The given figure shows a circle with center O such that chord RS is parallel to chord QT, angle PRT = 20° and angle POQ = 100°. Calculate :

(i) angle QTR

(ii) angle QRP

(iii) angle QRS

(iv) angle STR

Answer

(i) From figure,

⇒ ∠POQ + ∠QOR = 180° [Linear pairs]

⇒ 100° + ∠QOR = 180°

⇒ ∠QOR = 180° - 100°

⇒ ∠QOR = 80°.

We know that,

Angle subtended by an arc at the center is twice the angle subtended at any other point of circumference.

Arc RQ subtends ∠QOR at the center and ∠QTR at the remaining part of the circle.

⇒ ∠QOR = 2∠QTR

⇒ ∠QTR = $\dfrac{1}{2}$∠QOR = $\dfrac{1}{2} \times 80° = 40°.$

Hence, ∠QTR = 40°.

(ii) We know that,

Angle subtended by an arc at the center is twice the angle subtended at any other point of circumference.

Arc QP subtends ∠QOP at the center and ∠QRP at the remaining part of the circle.

⇒ ∠QOP = 2∠QRP

⇒ ∠QRP = $\dfrac{1}{2}$∠QOP = $\dfrac{1}{2} \times 100° = 50°.$

Hence, ∠QRP = 50°.

(iii) Given,

RS || QT

⇒ ∠SRT = ∠QTR = 40° (Alternate angles are equal)

From figure,

∠QRS = ∠QRP + ∠PRT + ∠SRT = 50° + 20° + 40° = 110°.

Hence, ∠QRS = 110°.

(iv) Since, RSTQ is a cyclic quadrilateral and sum of opposite angles of cyclic quadrilateral = 180°.

⇒ ∠QRS + ∠QTS = 180°

⇒ ∠QRS + ∠QTR + ∠STR = 180°

⇒ 110° + 40° + ∠STR = 180°

⇒ ∠STR = 180° - 150°

⇒ ∠STR = 30°.

Hence, ∠STR = 30°.

TA and TB are tangents to a circle with center O from an external point T. OT intersects the circle at point P. Prove that AP bisects the angle TAB.

Answer

Given TA and TB are tangent to a circle with centre O from point T.

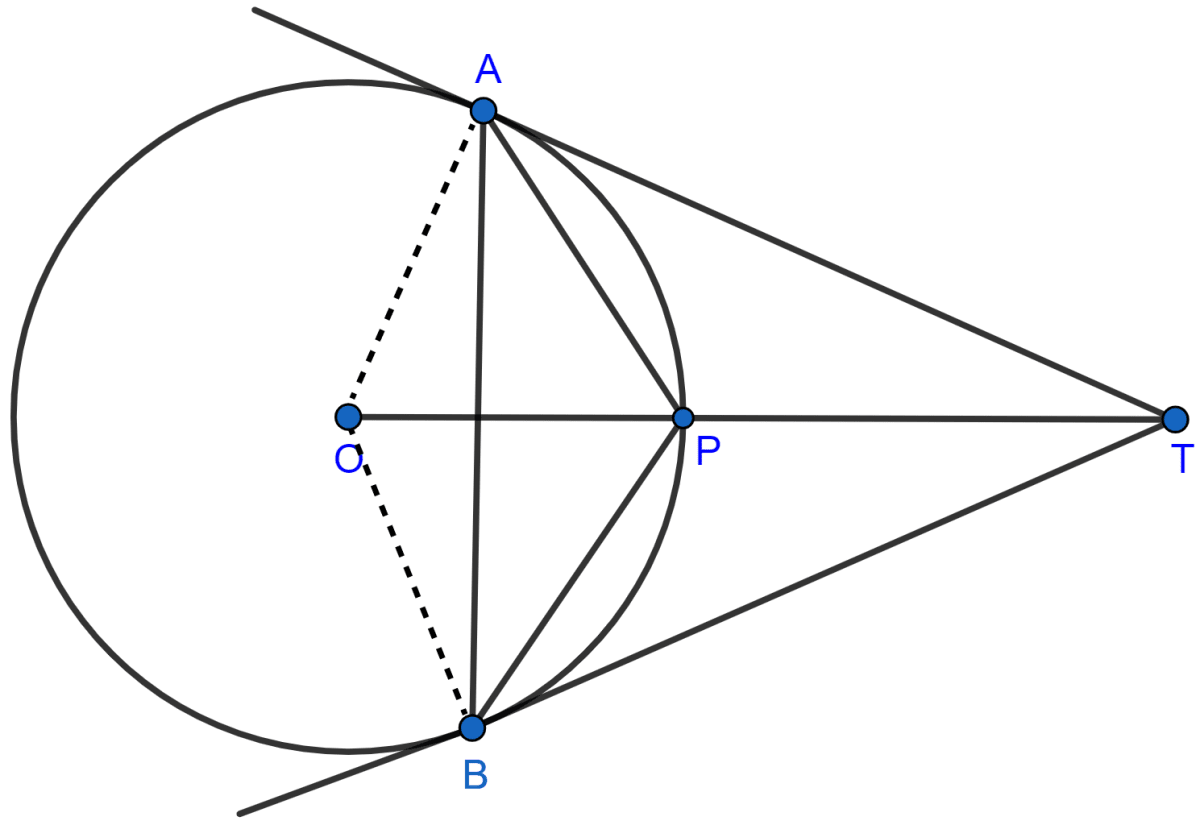
Consider, ΔOAT and ΔOBT

Here, OA = OB [Radii of circle]

OT = OT [Common side]

TA = TB [Tangents from an external point to a circle are equal in length]

∴ ΔOAT ≅ ΔOBT [By SSS congruence criterion]

∴ ∠ATO = ∠BTO [By C.P.C.T.]

⇒ ∠ATP = ∠BTP [From figure, ∠ATO = ∠ATP and ∠BTO = ∠BTP]

In ΔAPT and ΔBPT,

AT = BT [Tangents from an external point to a circle are equal in length]

PT = PT [Common side]

∠ATP = ∠BTP [Proved above]

∴ ΔAPT ≅ ΔBPT [By SAS congruence criterion]

∴ ∠PAT = ∠PBT [By C.P.C.T.]

and AP = BP [By C.P.C.T.]

In ΔPAB,

∠PAB = ∠PBA [Angles opposite to equal sides are equal]

∠PAT = ∠PBA [Angles in alternate segments are equal]

∴ ∠PAB = ∠PAT

∴ AP is the bisector of ∠TAB

Hence, proved that AP bisects ∠TAB.

Chords AB and CD of a circle when extended meet at point X. Given AB = 4 cm, BX = 6 cm and XD = 5 cm, calculate the length of CD.

Answer

Chords AB and CD of the circle meeting at point X are shown below:

We know that,

If two chords of a circle intersect internally or externally then the product of the lengths of their segments is equal.

⇒ XB.XA = XD.XC

⇒ 6.(6 + 4) = 5.(5 + CD)

⇒ 6 × 10 = 25 + 5CD

⇒ 5CD = 60 - 25

⇒ 5CD = 35

⇒ CD = $\dfrac{35}{5}$

⇒ CD = 7 cm.

Hence, CD = 7 cm.

In the following figure, a circle is inscribed in the quadrilateral ABCD. If BC = 38 cm, QB = 27 cm, DC = 25 cm and that AD is perpendicular to DC, find the radius of the circle.

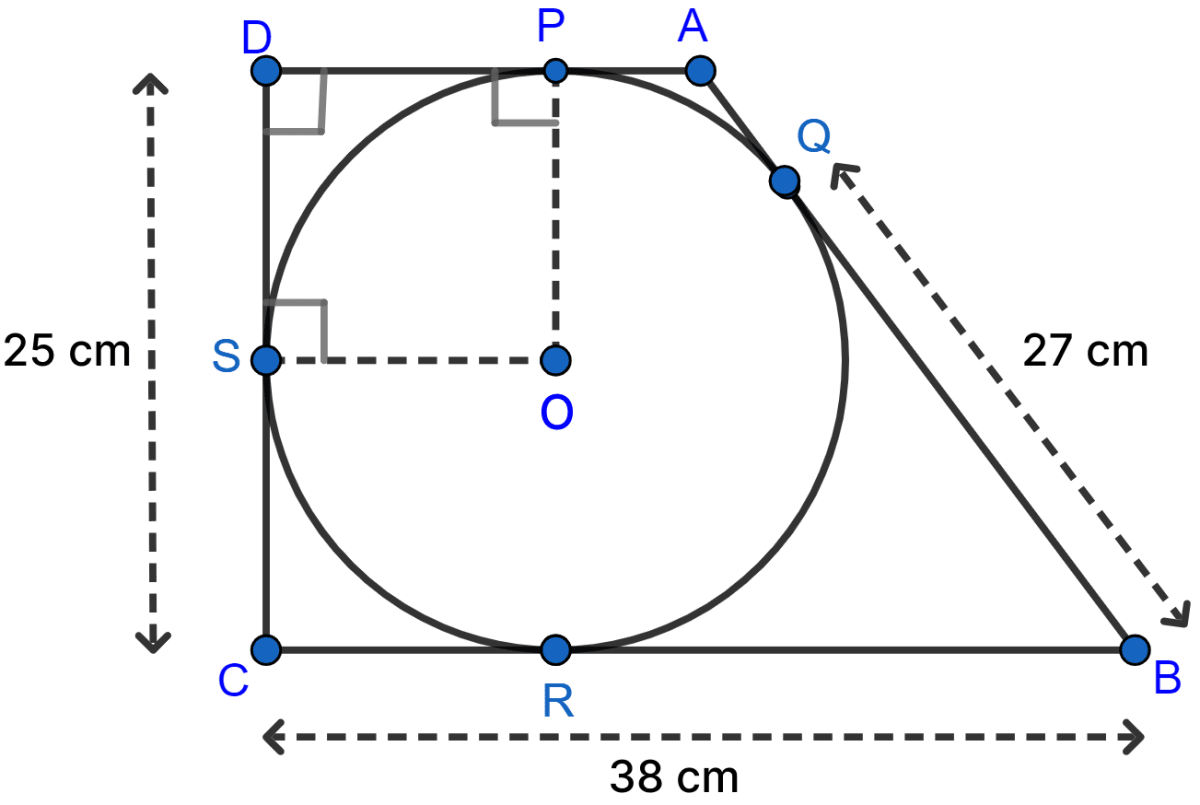
Answer

From figure,

⇒ BR = BQ = 27 cm [∵ Length of tangents form an external point to a circle are equal.]

⇒ CR = BC - BR = 38 - 27 = 11 cm.

⇒ CR = CS = 11 cm [∵ Length of tangents form an external point to a circle are equal.]

⇒ DS = DC - CS = 25 - 11 = 14 cm.

In quadrilateral DSOP,

⇒ ∠SDP + ∠DPO + ∠OSD + ∠POS = 360°

⇒ 90° + 90° + 90° + ∠POS = 360°

⇒ ∠POS = 360° - 270° = 90°.

Since, all angles are 90° and OS = OP [∵ Both equal to radius of same circle]

Hence, proved that DPOS is a square.

OP = DS = 14 cm.

Hence, radius of circle = 14 cm.

In the given figure, XY is the diameter of the circle and PQ is a tangent to the circle at Y.

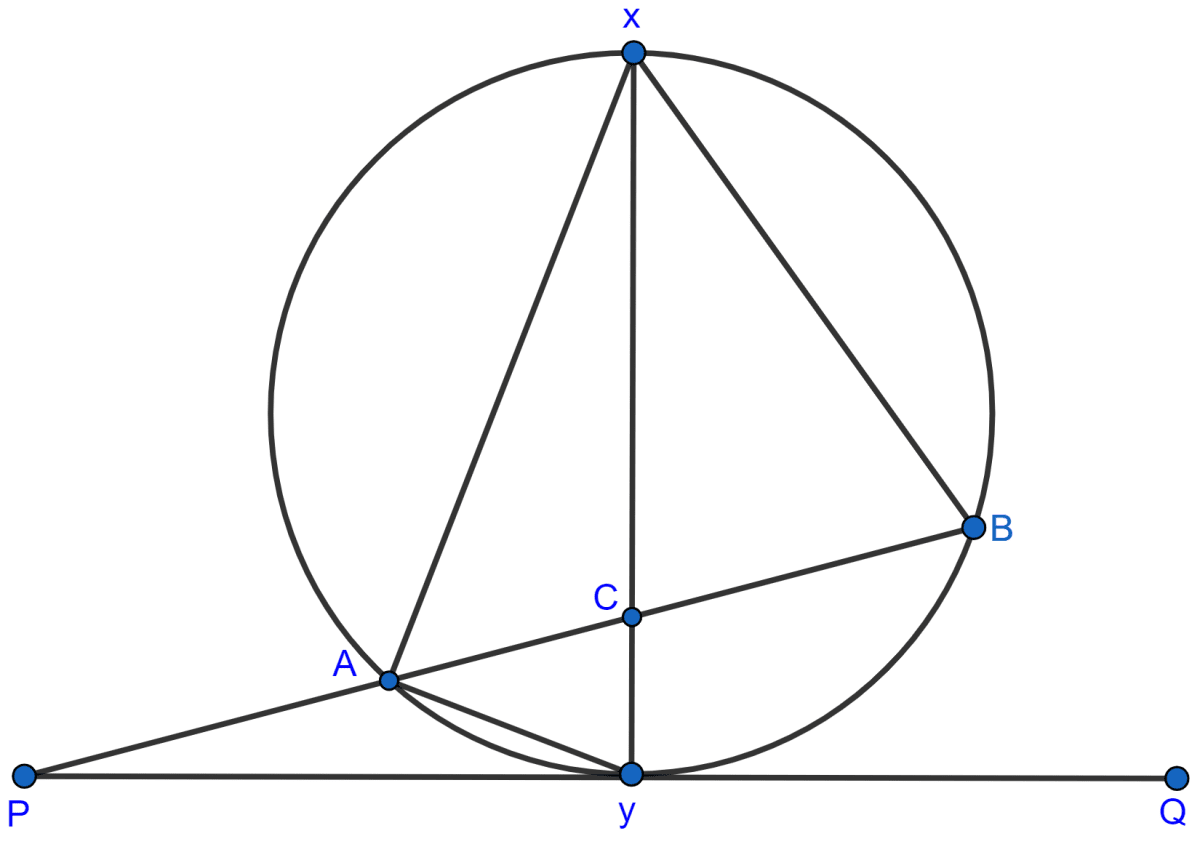
If ∠AXB = 50° and ∠ABX = 70°, find ∠BAY and ∠APY.

Answer

In △AXB,

⇒ ∠AXB + ∠XAB + ∠ABX = 180° [Angle sum property of triangle]

⇒ 50° + XAB + 70° = 180°

⇒ ∠XAB = 180° - 120° = 60°.

From figure,

∠XAY = 90° [Angle in a semi-circle is a right angle.]

∠BAY = ∠XAY - ∠XAB = 90° - 60 = 30°.

∠BXY = ∠BAY = 30° [Angles in same segment are equal]

We know that,

An exterior angle is equal to the sum of two opposite interior angles.

⇒ ∠ACX = ∠BXC + ∠CBX

⇒ ∠ACX = ∠BXY + ∠ABX [From figure, ∠BXC = ∠BXY and ∠CBX = ∠ABX]

⇒ ∠ACX = 30° + 70° = 100°.

We know that,

Diameter is perpendicular to tangent.

⇒ ∠XYP = 90°

An exterior angle in a triangle is equal to sum of two opposite interior angles.

⇒ ∠ACX = ∠APY + ∠CYP

⇒ ∠APY = ∠ACX - ∠CYP = 100° - 90° = 10°.

Hence, ∠APY = 10° and ∠BAY = 30°.

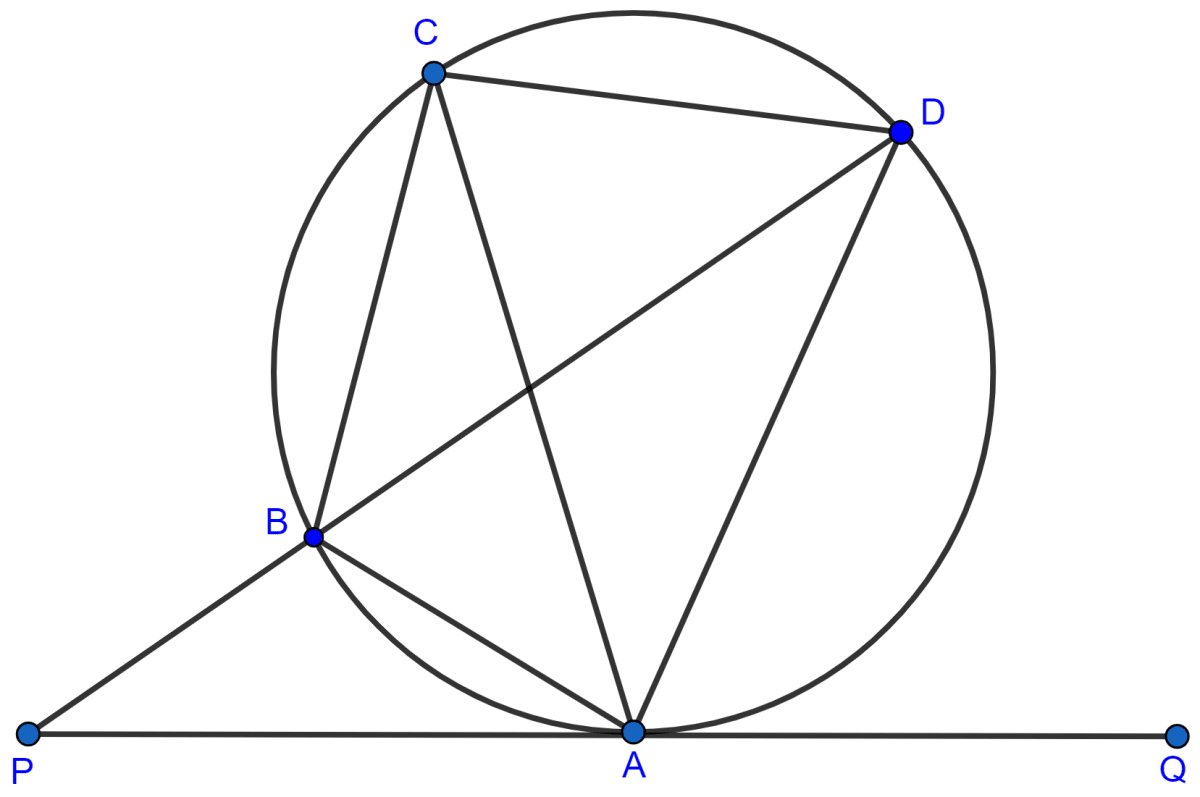
In the given figure, QAP is the tangent at point A and PBD is a straight line.

If ∠ACB = 36° and ∠APB = 42°, find :

(i) ∠BAP

(ii) ∠ABD

(iii) ∠QAD

(iv) ∠BCD

Answer

(i) We know that,

The angle between a tangent and a chord through the point of contact is equal to an angle in the alternate segment.

∴ ∠BAP = ∠ACB = 36°.

Hence, ∠BAP = 36°.

(ii) We know that,

An exterior angle in a triangle is equal to the sum of two opposite interior angles.

In △APB,

∠ABD = ∠APB + ∠BAP = 42° + 36° = 78°.

Hence, ∠ABD = 78°.

(iii) From figure,

∠ADB = ∠ACB = 36° (Angles in same segment are equal)

In △PAD,

∠QAD = ∠APB + ∠ADB = 42° + 36° = 78°. [Exterior angle is equal to sum of two opposite interior angles.]

Hence, ∠QAD = 78°.

(iv) We know that,

The angle between a tangent and a chord through the point of contact is equal to an angle in the alternate segment.

∴ ∠ACD = ∠QAD = 78°.

From figure,

∠BCD = ∠ACB + ∠ACD = 36° + 78° = 114°.

Hence, ∠BCD = 114°.

In the given figure, AB is the diameter. The tangent at C meets AB produced at Q.

If ∠CAB = 34°, find :

(i) ∠CBA

(ii) ∠CQB

Answer

(i) From figure,

∠ACB = 90° (Angle in a semi-circle is a right angle.)

In △ACB,

⇒ ∠ACB + ∠CAB + ∠CBA = 180° [By angle sum property of triangle]

⇒ 90° + 34° + ∠CBA = 180°

⇒ ∠CBA = 180° - 124° = 56°.

Hence, ∠CBA = 56°.

(ii) From figure,

∠QCB = ∠CAB = 34° [Angle in alternate segment are equal.]

⇒ ∠CBQ + ∠CBA = 180° [Linear pairs]

⇒ ∠CBQ + 56° = 180°

⇒ ∠CBQ = 124°.

In △CBQ,

⇒ ∠CBQ + ∠QCB + ∠CQB = 180° [By angle sum property of triangle]

⇒ 124° + 34° + ∠CQB = 180°

⇒ ∠CQB = 180° - 158° = 22°.

Hence, ∠CQB = 22°.

In the given figure, O is the center of the circle. The tangents at B and D intersect each other at point P. If AB is parallel to CD and ∠ABC = 55°, find :

(i) ∠BOD

(ii) ∠BPD

Answer

(i) From figure,

∠BCD = ∠ABC = 55° [Alternate angles are equal.]

We know that,

The angle subtended by an arc at the centre is double the angle subtended by it at any point on the remaining part of the circle.

∴ ∠BOD = 2∠BCD = 2 x 55° = 110°.

Hence, ∠BOD = 110°.

(ii) We know that,

A tangent line is always at a right angle to the radius of the circle at the point of tangency.

∴ ∠OBP = 90° and ∠ODP = 90°.

In quadrilateral ODPB,

⇒ ∠BOD + ∠OBP + ∠ODP + ∠BPD = 360° [Angle sum property of quadrilateral]

⇒ 110° + 90° + 90° + ∠BPD = 360°

⇒ ∠BPD = 360° - 290° = 70°.

Hence, ∠BPD = 70°.

In the following figure, PQ = QR, ∠RQP = 68°, PC and CQ are tangents to the circle with center O.

Calculate the values of :

(i) ∠QOP

(ii) ∠QCP

Answer

(i) Given,

PQ = QR

∴ ∠PRQ = ∠QPR [Angles opposite to equal sides are equal in a triangle.]

In △PQR,

⇒ ∠PRQ + ∠QPR + ∠RQP = 180°

⇒ ∠PRQ + ∠PRQ + 68° = 180°

⇒ 2∠PRQ = 180° - 68°

⇒ 2∠PRQ = 112°

⇒ ∠PRQ = $\dfrac{112°}{2}$

⇒ ∠PRQ = 56°.

We know that,

The angle subtended by an arc at the centre is double the angle subtended by it at any point on the remaining part of the circle.

∴ ∠QOP = 2∠PRQ = 2 x 56 = 112°.

Hence, ∠QOP = 112°.

(ii) We know that,

A tangent line is always at a right angle to the radius of the circle at the point of tangency.

∴ ∠OPC = 90° and ∠OQC = 90°.

In quadrilateral OQCP,

⇒ ∠QOP + ∠OPC + ∠OQC + ∠QCP = 360° [Angle sum property of quadrilateral]

⇒ 112° + 90° + 90° + ∠QCP = 360°

⇒ ∠QCP = 360° - 292° = 68°.

Hence, ∠QCP = 68°.

In the figure, given below, AC is a transverse common tangent to two circles with centers P and Q and of radii 6 cm and 3 cm respectively. Given that AB = 8 cm, calculate PQ.

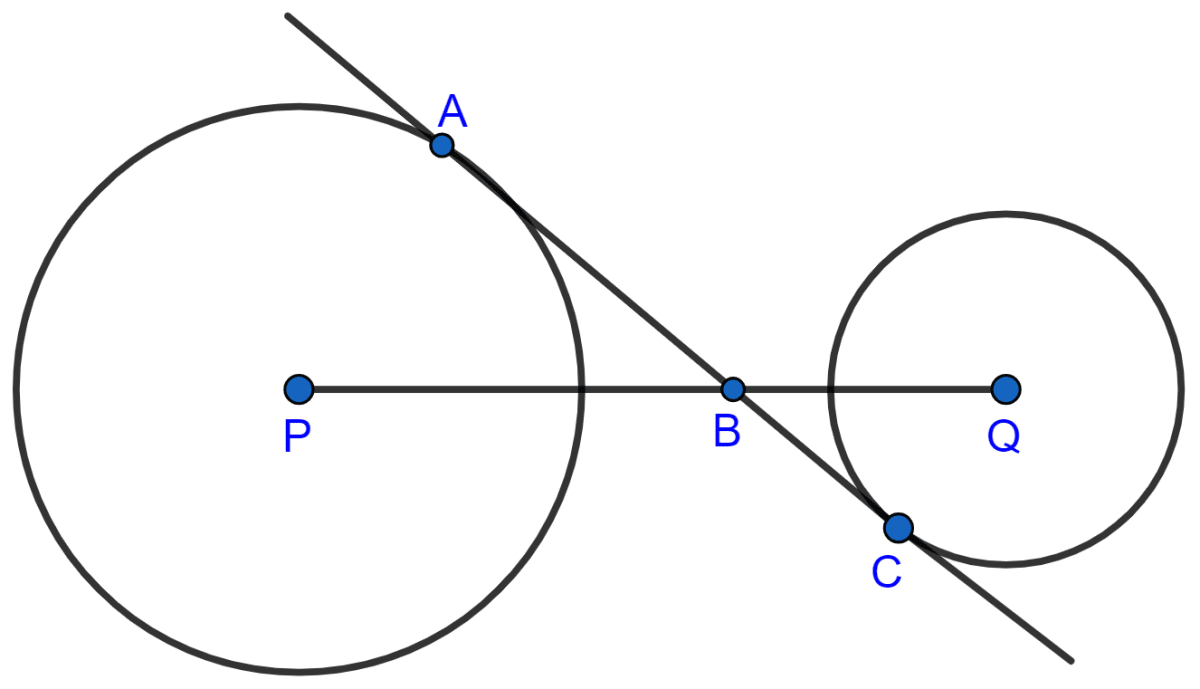
Answer

Since, AC is a tangent to the circle with center P at point A.

∴ ∠PAB = 90°.

Since, AC is a tangent to the circle with center Q at point C.

∴ ∠QCB = 90°.

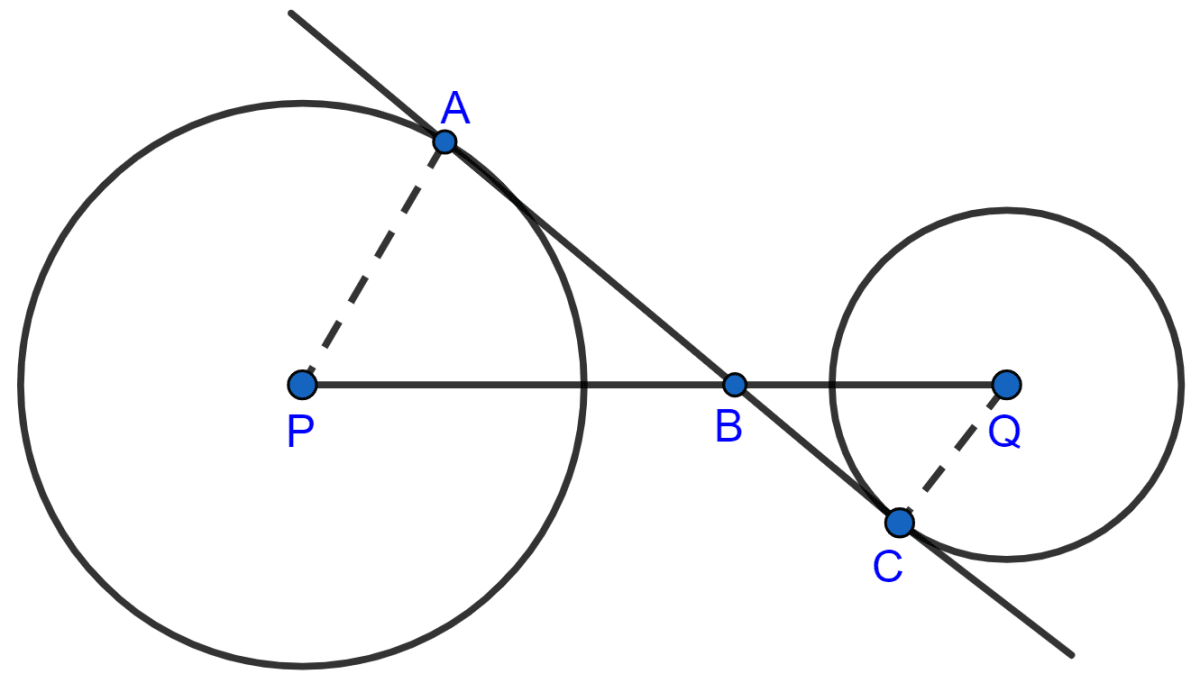
In △PAB and △QCB,

⇒ ∠PAB = ∠QCB (Both equal to 90°)

⇒ ∠PBA = ∠QBC (Vertically opposite angles are equal)

⇒ △PAB ~ △QCB.

In right angle △PAB,

$\phantom{\Rightarrow} \text{PB}^2 = \text{PA}^2 + \text{AB}^2 \\[1em] \Rightarrow \text{PB} = \sqrt{\text{PA}^2 + \text{AB}^2} \\[1em] \Rightarrow \text{PB} = \sqrt{6^2 + 8^2} \\[1em] \Rightarrow \text{PB} = \sqrt{36 + 64} \\[1em] \Rightarrow \text{PB} = \sqrt{100} \\[1em] \Rightarrow \text{PB} = 10 \text{ cm}$

We know that,

In similar triangles ratio of corresponding sides are equal.

$\Rightarrow \dfrac{PA}{QC} = \dfrac{PB}{QB} \\[1em] \Rightarrow \dfrac{6}{3} = \dfrac{10}{QB} \\[1em] \Rightarrow QB = \dfrac{3 \times 10}{6} \\[1em] \Rightarrow QB = \dfrac{30}{6} \\[1em] \Rightarrow QB = 5 \text{ cm}.$

From figure,

QP = QB + PB = 5 + 10 = 15 cm.

Hence, QP = 15 cm.

In the figure, given below, O is the center of the circumcircle of triangle XYZ. Tangents at X and Y intersect at point T. Given ∠XTY = 80° and ∠XOZ = 140°, calculate the value of ∠ZXY.

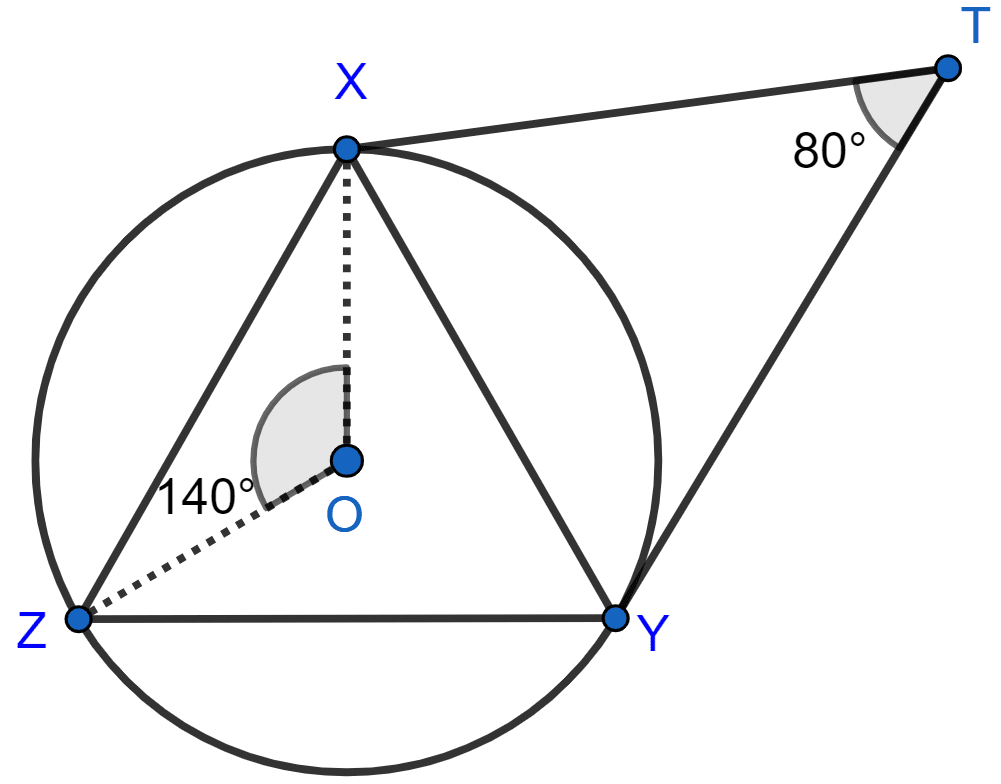
Answer

YT and XT are tangents to the circle.

∴ ∠OYT = 90° and ∠OXT = 90°.

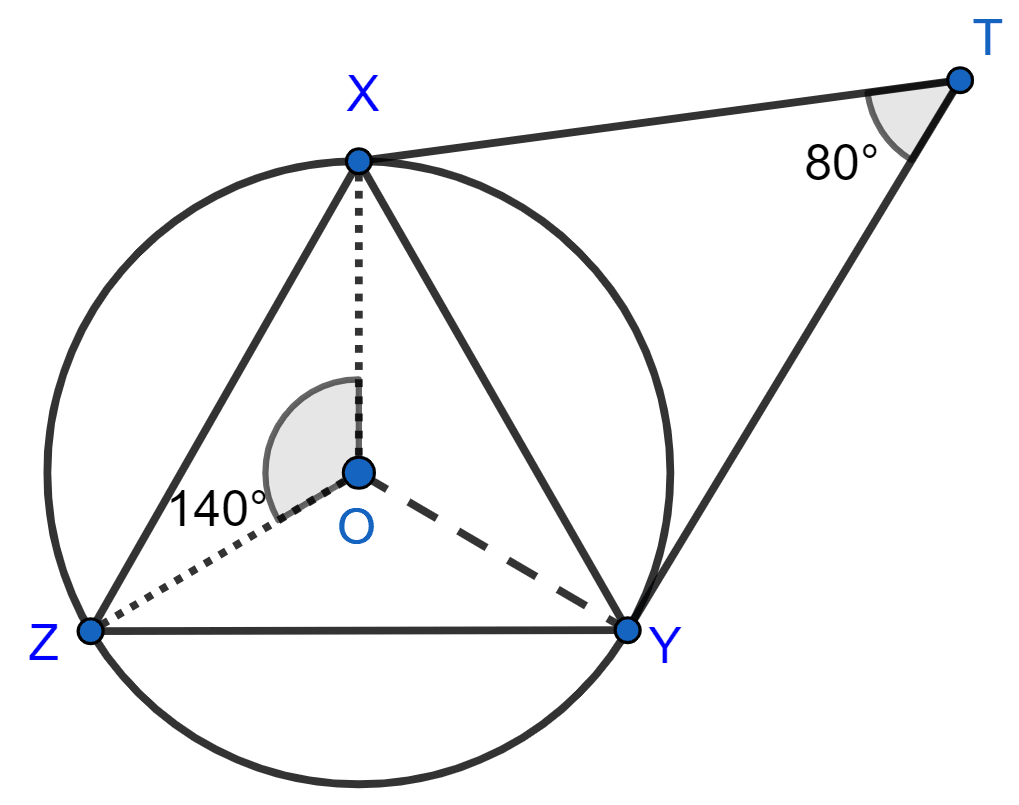
In quadrilateral OYTX,

⇒ ∠XOY + ∠OYT + ∠OXT + ∠XTY = 360°

⇒ ∠XOY + 90° + 90° + 80° = 360°

⇒ ∠XOY = 360° - 260° = 100°.

From figure,

⇒ ∠XOZ + ∠YOZ + ∠XOY = 360°

⇒ 140° + ∠YOZ + 100° = 360°

⇒ ∠YOZ = 360° - 240° = 120°.

We know that,

When two angles are subtended by the same arc, the angle at the centre of a circle is twice the angle at the circumference.

∴ ∠YOZ = 2∠ZXY

⇒ ∠ZXY = $\dfrac{1}{2}$∠YOZ = $\dfrac{1}{2} \times 120°$ = 60°.

Hence, ∠ZXY = 60°.

In the given figure, AE and BC intersect each other at point D. If ∠CDE = 90°, AB = 5 cm, BD = 4 cm and CD = 9 cm, find AE.

Answer

In right angle triangle ABD,

⇒ AB² = BD² + AD²

⇒ 5² = 4² + AD²

⇒ 25 = 16 + AD²

⇒ AD² = 25 - 16

⇒ AD² = 9

⇒ AD = $\sqrt{9}$

⇒ AD = 3 cm.

We know that,

If two chords of circle intersect internally or externally then the product of the lengths of their segment is equal.

⇒ AD × DE = CD × BD

⇒ 3 × DE = 9 × 4

⇒ DE = $\dfrac{9 \times 4}{3}$

⇒ DE = 12 cm.

From figure,

AE = AD + DE = 3 + 12 = 15 cm.

Hence, AE = 15 cm.

In the given circle with centre O, angle ABC = 100°, ∠ACD = 40° and CT is a tangent to the circle at C. Find ∠ADC and ∠DCT.

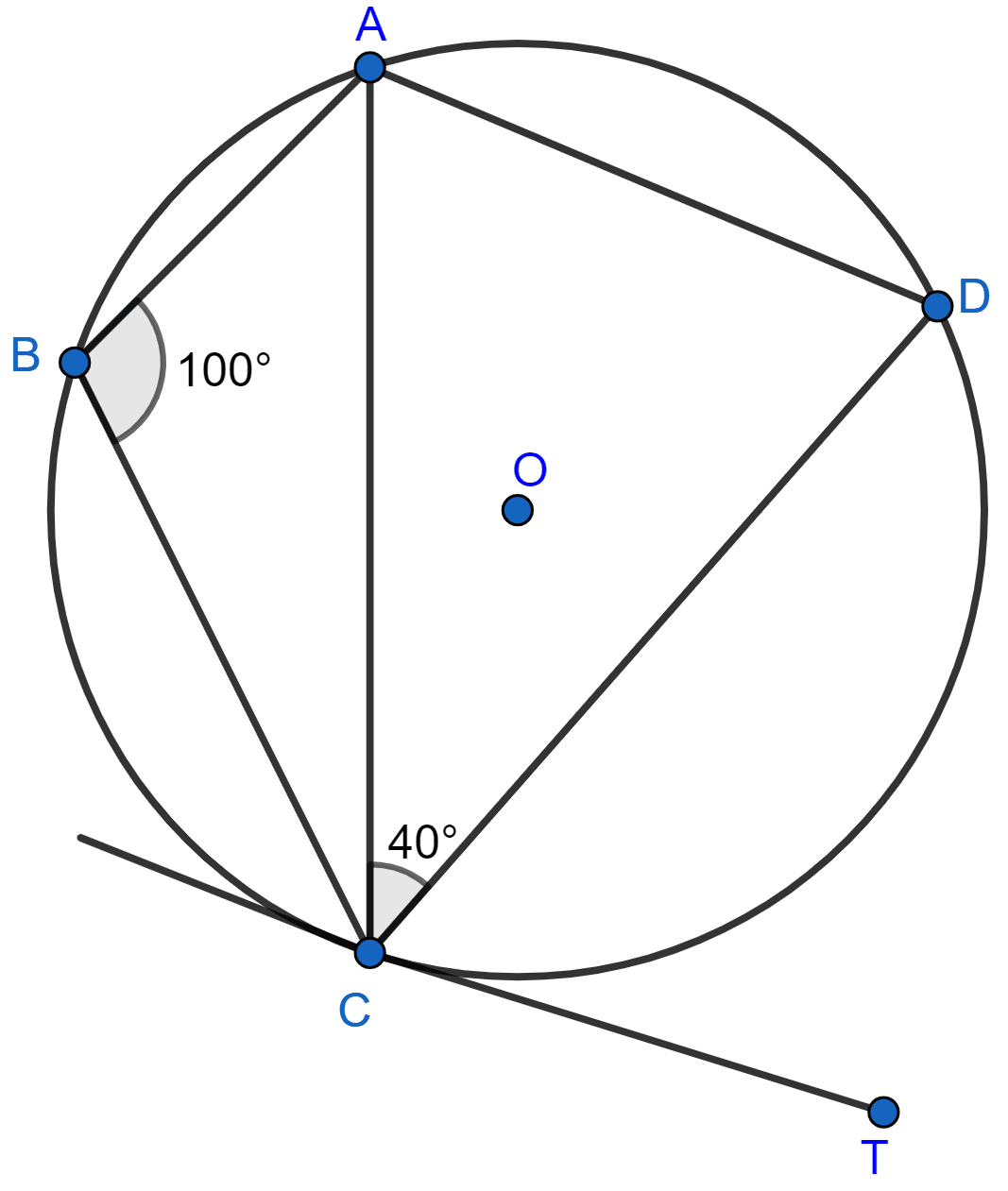
Answer

From figure,

⇒ ∠ADC + ∠ABC = 180° [Sum of opposite angles in a cyclic quadrilateral = 180°]

⇒ ∠ADC + 100° = 180°

⇒ ∠ADC = 180° - 100°

⇒ ∠ADC = 80°.

In △ADC,

⇒ ∠ADC + ∠CAD + ∠ACD = 180° [By angle sum property of triangle]

⇒ 80° + ∠CAD + 40° = 180°

⇒ ∠CAD = 180° - 120° = 60°.

From figure,

⇒ ∠DCT = ∠CAD = 60° [Angles in alternate segment are equal].

Hence, ∠DCT = 60° and ∠ADC = 80°.

In the figure given below, O is the center of the circle and SP is a tangent. If ∠SRT = 65°, find the values of x, y and z.

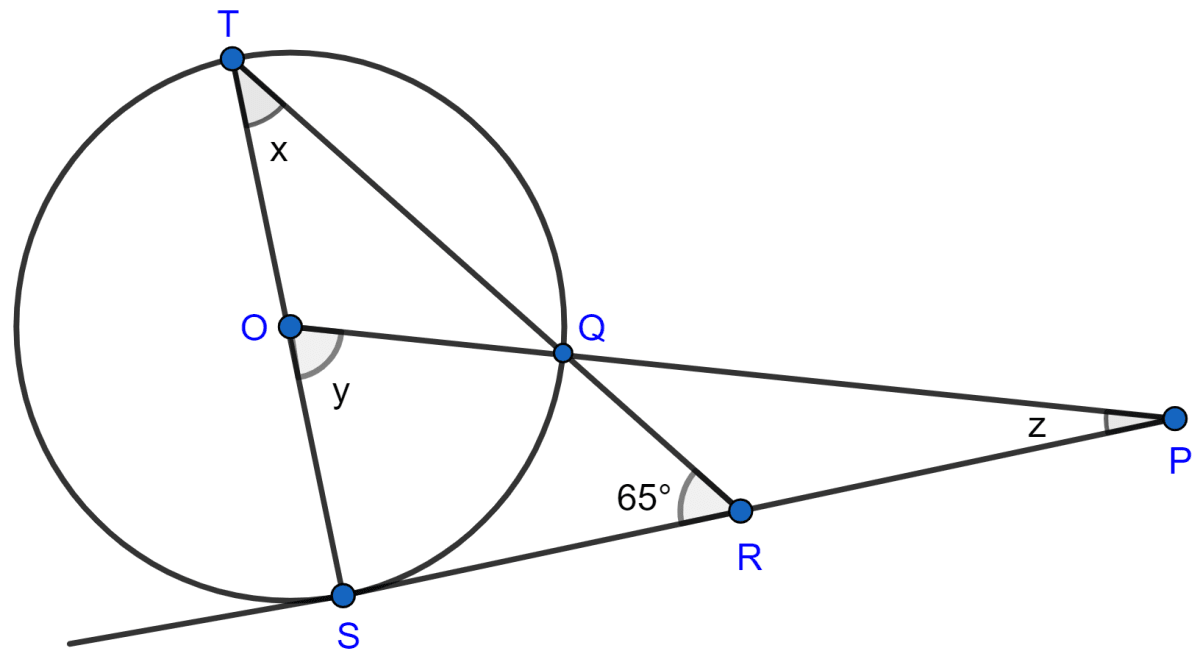
Answer

As, SP is tangent to the circle.

∴ ∠TSR = 90°.

In △TSR,

⇒ ∠TSR + ∠STR + ∠SRT = 180° [By angle sum property of triangle]

⇒ 90° + x + 65° = 180°

⇒ x = 180° - 155° = 25°.

We know that,

Angle which an arc subtends at the center is double that which it subtends at any point on the remaining part of the circumference.

∴ ∠SOQ = 2∠STQ

⇒ y = 2x = 2(25°) = 50°.

In △OSP,

⇒ ∠OSP + ∠SOP + ∠SPO = 180° [By angle sum property of triangle]

⇒ 90° + y + z = 180°

⇒ 90° + 50° + z = 180°

⇒ z = 180° - 140° = 40°.

Hence, x = 25°, y = 50° and z = 40°.