Constructions (Circles)

In the given figure, AP is bisector of angle A of △ ABC and DP is perpendicular bisector of side AB, then :

1. P is incenter of △ ABC

2. P is circumcenter of △ ABC

3. PB bisects angle B

4. none of these

Answer

The incenter of a triangle is the intersection point of all the three interior angle bisectors of the triangle.

The circumcenter of a triangle is defined as the point where the perpendicular bisectors of the sides of triangle intersect.

Since,

In the given figure, P is intersection of an angle bisector and perpendicular bisector of a side.

Hence, Option 4 is the correct option.

Incenter of a triangle is the point of intersection of the :

1. perpendicular bisector of its sides

2. bisectors of its angles

3. one perpendicular of its side and bisector of any one angle of it

4. none of these.

Answer

The incenter of a triangle is the intersection point of all the three interior angle bisectors of the triangle.

Hence, Option 2 is the correct option.

For a regular hexagon, inscribing a circle, the length of the side of the hexagon and the radius of the circle are :

1. equal

2. not equal

3. side of hexagon is bigger than the radius of the circle

4. side of hexagon is smaller than the radius of the circle.

Answer

We know that,

A regular hexagon comprises 6 equilateral triangles.

∴ BAC is an equilateral triangle.

∴ AB = BC = CA.

From figure,

⇒ AP < CA

⇒ AP < BC

⇒ Radius < Side of hexagon

Hence, Option 3 is the correct option.

For a regular hexagon inscribed in a circle, the radius of the circle and the length of a side of the hexagon are :

1. equal

2. not equal

3. equal, if hexagon is regular

4. not equal, if hexagon is regular.

Answer

We know that,

A regular hexagon comprises 6 equilateral triangles.

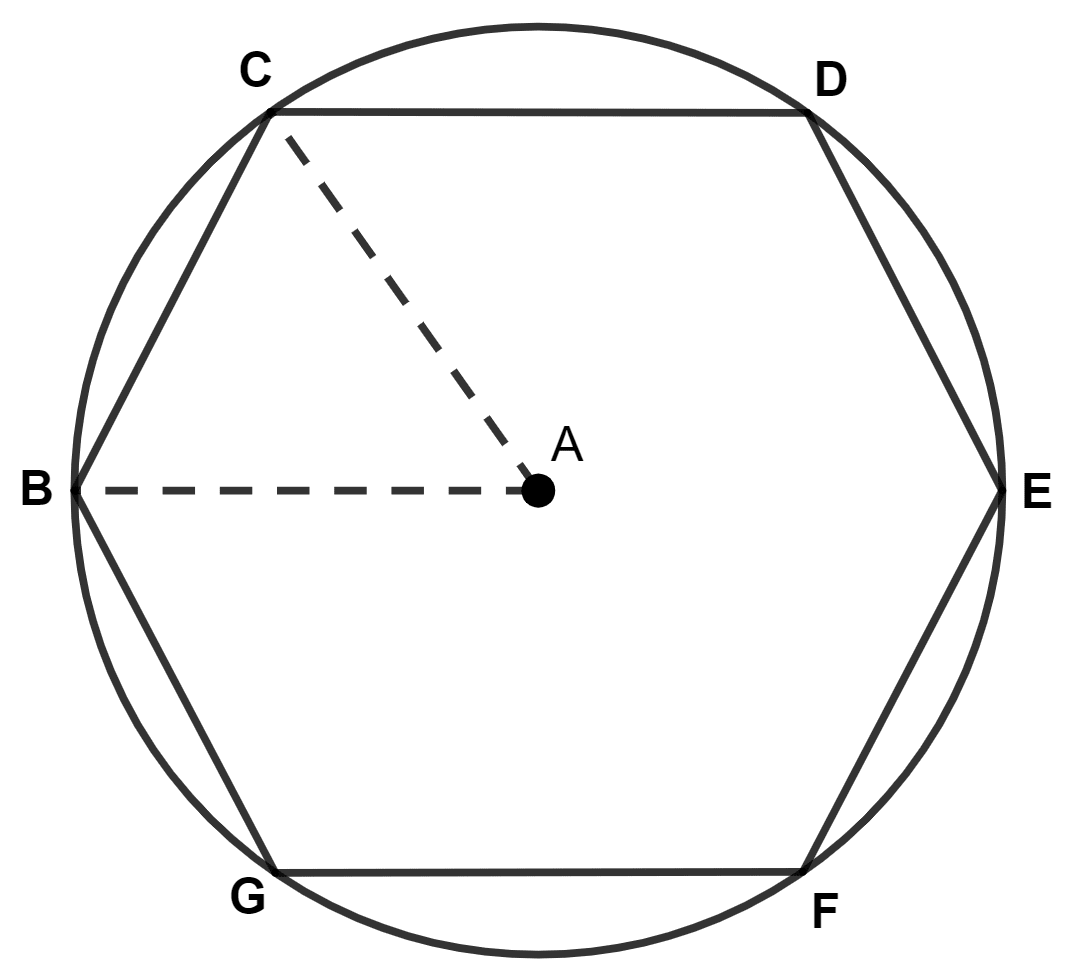
∴ BAC is an equilateral triangle.

∴ AB = BC = CA.

From figure,

AB and AC are radius of the circle.

⇒ AB = BC.

⇒ Radius = Side of hexagon

Hence, Option 1 is the correct option.

In triangle ABC, bisectors of angles A and B meet at point P.

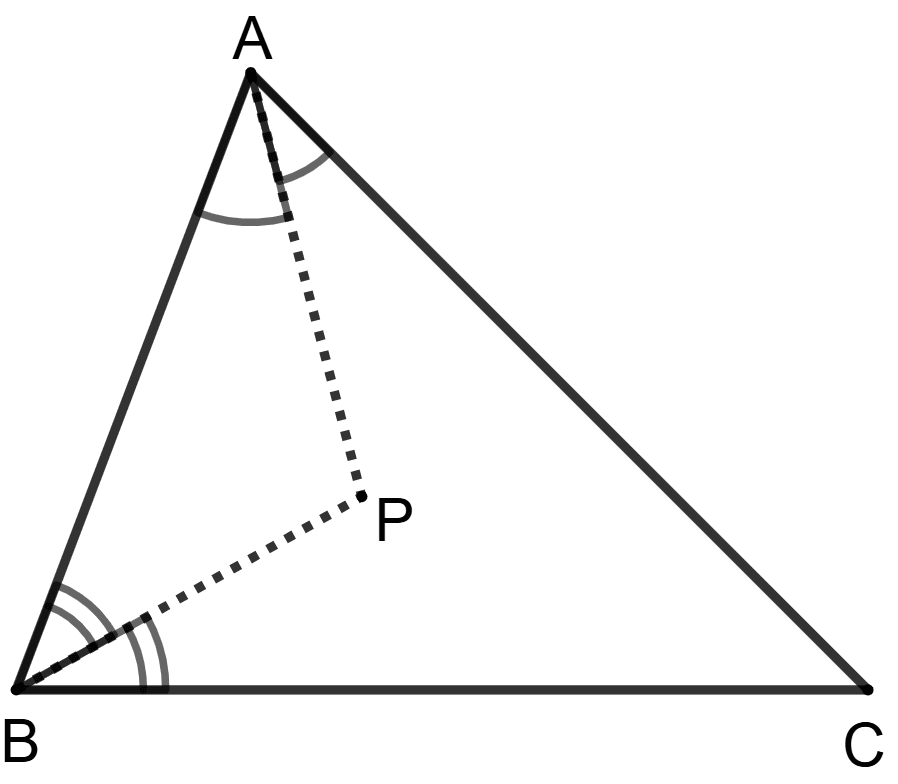
Assertion (A): PC bisects angle C.

Reason(R): Bisectors of angles of a triangle are concurrent.

1. A is true, R is false.

2. A is false, R is true.

3. Both A and R are true and R is correct reason for A.

4. Both A and R are true and R is incorrect reason for A.

Answer

The point of intersection of the bisectors of angles of a triangle is called the incenter of the triangle.

Thus, we can say that,

Bisectors of angles of a triangle are concurrent.

So, reason (R) is true.

Since, from figure, P is the incenter, so bisector of angle C will pass through it.

Thus, we can say that,

PC bisects angles C.

So, assertion (A) is true.

∴ Both A and R are true and R is correct reason for A.

Hence, option 3 is the correct option.

In triangle ABC, ∠A = 35° and ∠C = 55°.

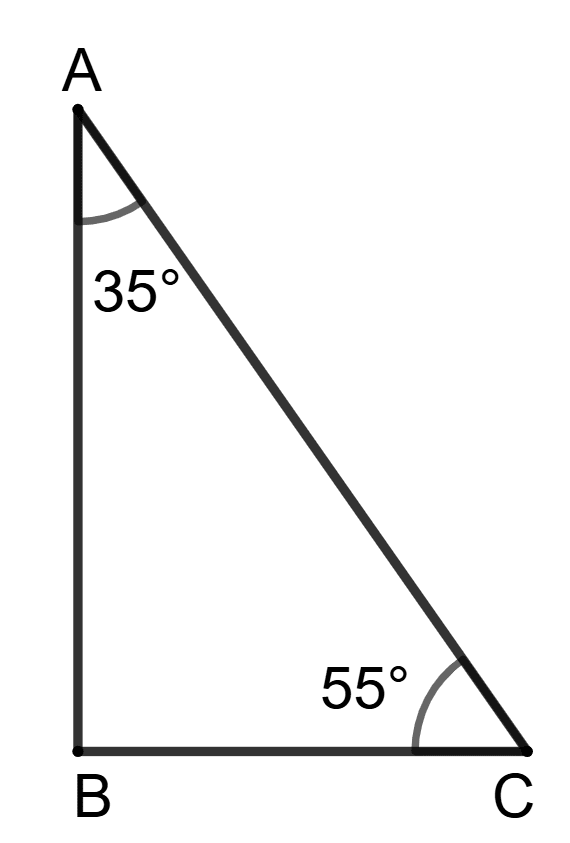
Assertion (A): Circle with AC as diameter will pass through the vertex B.

Reason(R): ∠ABC = 180° - (35° + 55°) = 90° = angle of semi-circle.

1. A is true, R is false.

2. A is false, R is true.

3. Both A and R are true and R is correct reason for A.

4. Both A and R are true and R is incorrect reason for A.

Answer

Given, in triangle ABC, ∠A = 35° and ∠C = 55°.

The sum of angles in a triangle is always 180°.

⇒ ∠A + ∠B + ∠C = 180°

⇒ 35° + ∠B + 55° = 180°

⇒ 90° + ∠B = 180°

⇒ ∠B = 180° - 90°

⇒ ∠B = 90°.

An angle inscribed in a semicircle is always a right angle (90°).

So, reason (R) is true.

Since ∠ABC is 90°, and AC is the diameter of the circle, the circle must pass through point B.

This is because the angle subtended by the diameter (AC) at any point on the circumference of the circle (in this case, point B) is always a right angle.

So, assertion (A) is true.

∴ Both A and R are true and R is correct reason for A.

Hence, option 3 is the correct option.

In ΔABC, PQ is perpendicular bisector of side AB and PR is perpendicular bisector of side BC.

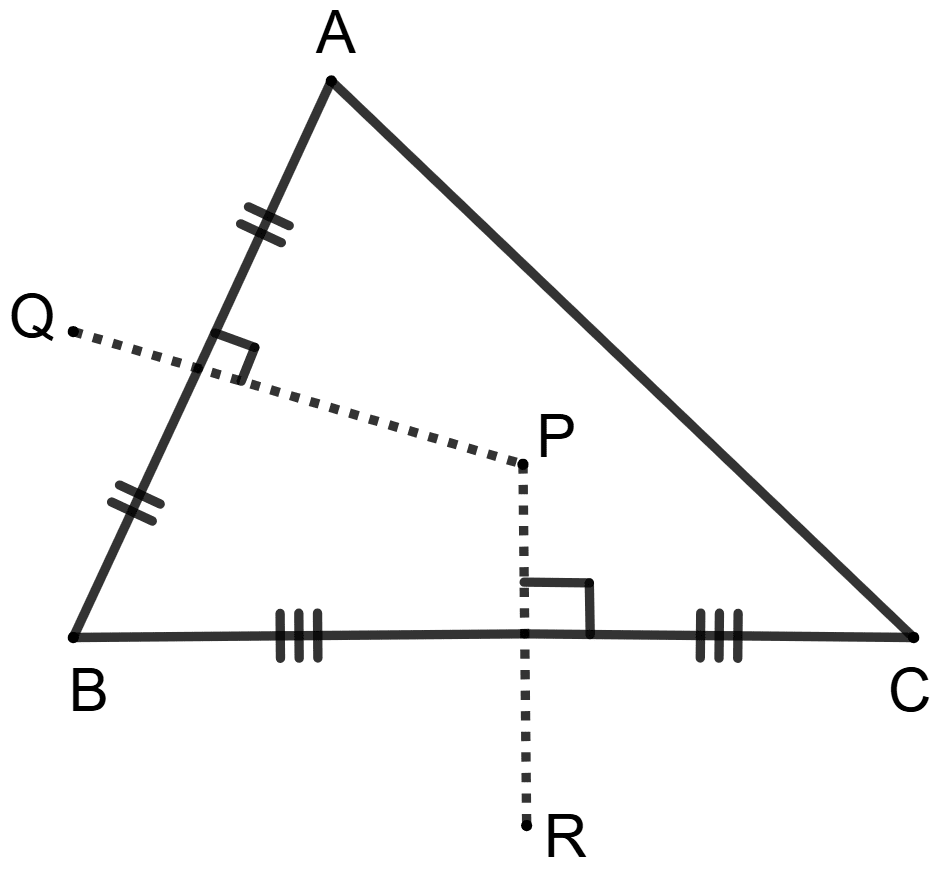
Statement (1): Perpendicular bisector of side AC will pass through point P.

Statement (2): Perpendicular bisectors of sides of a triangle are concurrent.

1. Both the statements are true.

2. Both the statements are false.

3. Statement 1 is true, and statement 2 is false.

4. Statement 1 is false, and statement 2 is true.

Answer

Since PQ is the perpendicular bisector of AB, any point on PQ is equidistant from A and B.

Similarly, since PR is the perpendicular bisector of BC, any point on PR is equidistant from B and C.

Therefore, point P, which lies on both PQ and PR, is equidistant from A, B and C.

This means that P is the center of a circle passing through A, B and C.

The perpendicular bisectors for sides AB, BC, and CA always meet at a single point called the circumcenter of ∆ ABC that is equidistant from all three vertices.

Thus, we can say that,

Perpendicular bisectors of sides of a triangle are concurrent.

So, statement 2 is true.

Consequently, the perpendicular bisector of AC must also pass through P, as P is equidistant from A and C.

So, statement 1 is true.

∴ Both the statements are true.

Hence, option 1 is the correct option.

Pentagon ABCDE is inscribed in a circle with center O.

Statement (1): ∠AOB = $\dfrac{360°}{5}$

Statement (2): If pentagon is regular, ∠AOB = $\dfrac{360°}{5}$

1. Both the statements are true.

2. Both the statements are false.

3. Statement 1 is true, and statement 2 is false.

4. Statement 1 is false, and statement 2 is true.

Answer

Given, pentagon ABCDE is inscribed in a circle with center O.

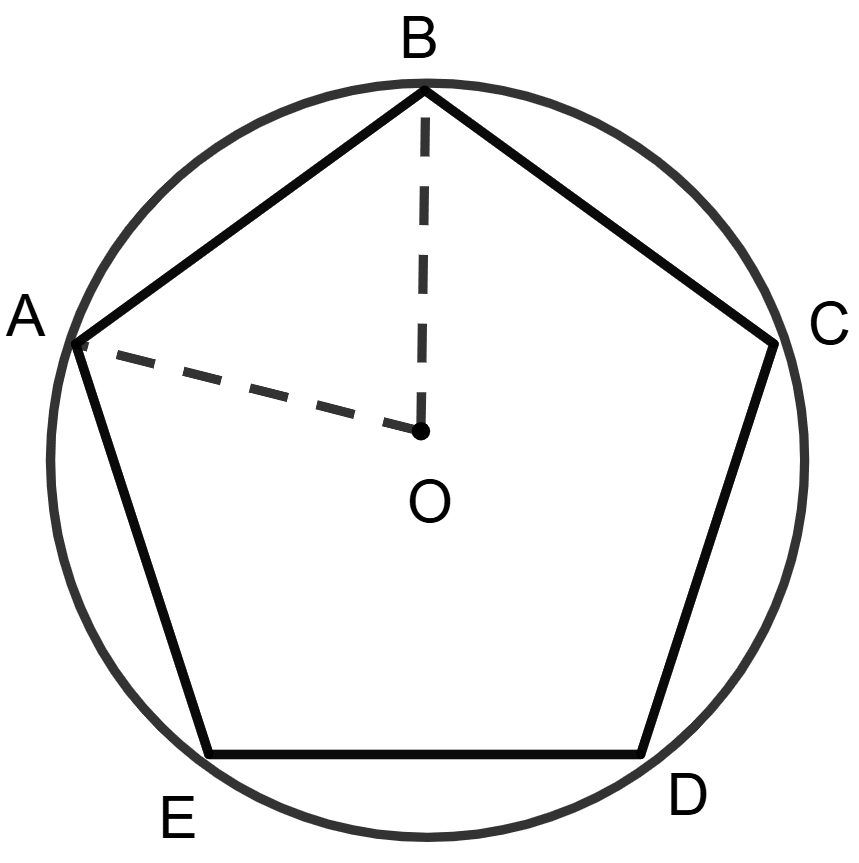
If a pentagon is regular then the sides subtends equal angles at the center.

If ABCDE is a regular pentagon, then ∠AOB = $\dfrac{360°}{5}$.

∴ Statement 1 is false, and statement 2 is true.

Hence, option 4 is the correct option.

Draw a circle of radius 3 cm. Mark a point P at a distance of 5 cm from the center of the circle drawn. Draw two tangents PA and PB to the given circle and measure the length of each tangent.

Answer

Steps of Construction :

1. Draw a circle with center O and radius 3 cm.

2. From O, take a point P such that OP = 5 cm.

3. Draw a perpendicular bisector of OP which intersects OP at M.

4. With center M and radius OM, draw a circle which intersects the circle with center O at A and B.

5. Join AP and BP. Measure AP and BP.

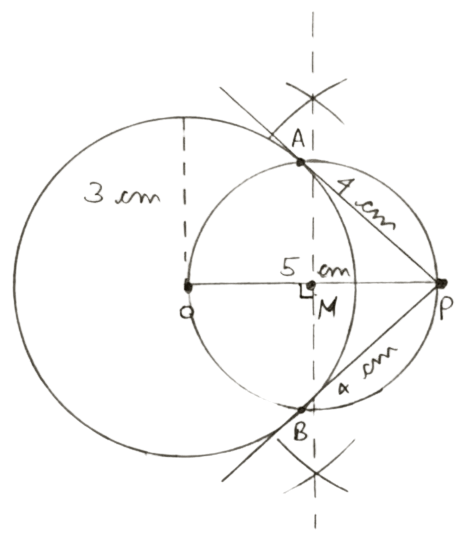
Hence, AP and BP are required tangents.

On measuring,

AP = BP = 4 cm.

Hence, length of each tangent = 4 cm.

Draw a circle of radius 5 cm. Draw two tangents to this circle so that the angle between tangents is 45°.

Answer

Steps of Construction :

1. Draw a circle with center O, radius = 5 cm and BC as diameter.

2. Draw arcs making an angle of 135° (180° - 45°) at O such that ∠AOB = 135°.

3. At A and B, draw two rays making an angle of 90° at each point which meet other at point P.

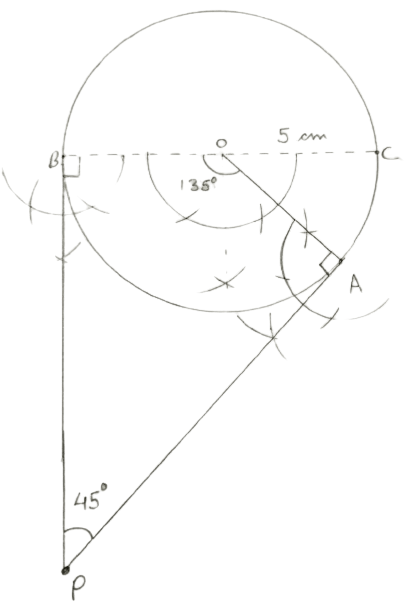
Hence, AP and BP are required tangents making an angle of 45° with each other.

Using ruler and compasses only, draw an equilateral triangle of side 4.5 cm and draw its circumscribed circle. Measure the radius of the circle.

Answer

Steps of Construction :

1. Draw a line segment BC = 4.5 cm.

2. With centers B and C, draw two arcs of radius 4.5 cm which intersect each other at A.

3. Join AC and AB.

4. Draw perpendicular bisectors of AC and BC intersecting each other at O.

5. With center O, and radius OA or OB or OC draw a circle which pass through A, B and C. Measure OC.

On measuring, OC = 2.6 cm.

Hence, above is the required circumcircle with radius 2.6 cm.

Using ruler and compasses only,

(i) Construct triangle ABC, having given BC = 7 cm, AB - AC = 1 cm and ∠ABC = 45°.

(ii) Inscribe a circle in the △ABC constructed in (i) above.

Answer

(i) Steps of construction :

1. Draw a line segment BC = 7 cm.

2. At B, draw a ray BX making an angle of 45° and cut off BE = AB - AC = 1 cm.

3. Join EC and draw the perpendicular bisector of EC intersecting BX at A.

4. Join AC.

Hence, ABC is the required triangle.

(ii) Steps of construction :

1. Draw angle bisectors of ∠ABC and ∠ACB intersecting each other at O.

2. From O, draw perpendicular OL to BC.

3. With O as center and OL as radius draw a circle, touching sides of △ABC. Measure OL.

On measuring,

OL = 1.8 cm.

Hence, above is the required incircle of △ABC with radius = 1.8 cm.

Using ruler and compasses only,

(i) Construct a triangle ABC with the following data :

Base AB = 6 cm, BC = 7.5 cm and angle CAB = 60°.

(ii) In same diagram, draw a circle which passes through the points A, B and C and mark its center O.

(iii) Draw a perpendicular from O to AB which meets AB in D.

(iv) Prove that : AD = BD.

Answer

Steps of construction :

1. Draw a line segment AB = 6 cm.

2. At A, draw a ray (AX) making an angle of 60° with AB.

3. With B as center and radius = 7.5 cm draw an arc which intersects AX ray at C.

4. Join BC. ABC is the required triangle.

5. Draw the perpendicular bisectors of AB and AC intersecting each other at O.

6. With center O and radius OA, OB or OC, draw a circle passing through A, B and C.

7. From O, draw OD ⊥ AB.

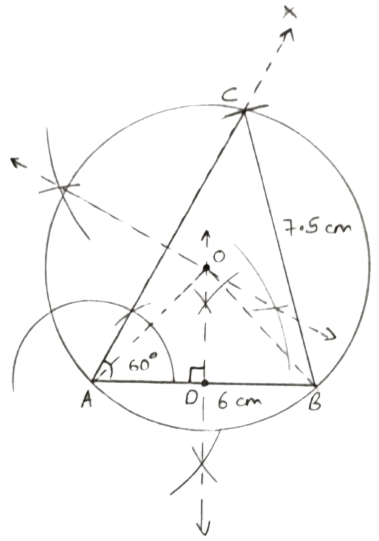
Proof :

In right △OAD and △OBD,

⇒ OA = OB (Radius of same circle)

⇒ OD = OD (Common)

⇒ ∠ODA = ∠ODB (Both = 90°)

∴ △OAD ≅ △OBD (By R.H.S. axiom)

By C.P.C.T.

⇒ AD = BD.

Hence, proved that AD = BD.

Using ruler and compasses only construct a triangle ABC in which BC = 4 cm, ∠ACB = 45° and perpendicular from A on BC is 2.5 cm. Draw a circle circumscribing the triangle ABC.

Answer

Steps of construction :

1. Draw a line segment BC = 4 cm.

2. At C, draw a perpendicular line CX and from it, cut off CE = 2.5 cm.

3. From E, draw EY, perpendicular to CX.

4. From C, draw a ray making an angle 45° with CB, which intersects EY at A.

5. Join AB. Hence, ABC is the required triangle.

6. Draw perpendicular bisectors of sides AB and BC intersecting each other at O.

7. With center O, and radius OA or OB or OC draw a circle passing through A, B and C. Measure OB.

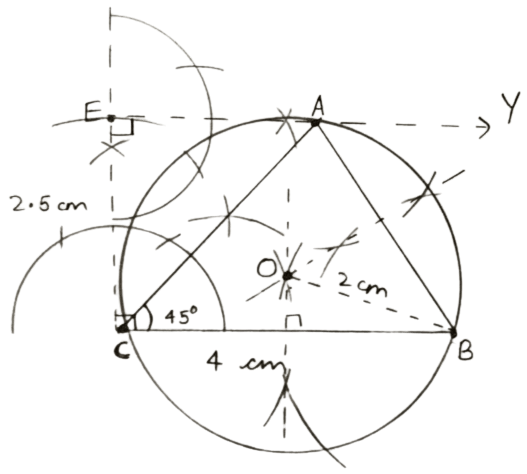
On measuring,

OB = 2 cm.

Hence, above is the required circumcircle of △ABC with radius = 2 cm.

Perpendicular bisectors of the sides AB and AC of a triangle ABC meet at O.

(i) What do you call the point O ?

(ii) What is the relation between the distances OA, OB and OC ?

(iii) Does the perpendicular bisector of BC pass through O ?

Answer

(i) O is called the circumcenter of the triangle.

(ii) Since, OA, OB and OC are radius of circumcircle.

Hence, OA = OB = OC.

(iii) From figure,

Yes, the perpendicular bisector of BC pass through O.

The bisectors of angles A and B of a scalene triangle ABC meet at O.

(i) What is the point O called ?

(ii) OR and OQ are perpendiculars drawn to AB and CA respectively. What is the relation between OR and OQ ?

(iii) What is relation between angle ACO and angle BCO ?

Answer

(i) O is called the incenter of △ABC.

(ii) From figure,

OR and OQ are radius of incircle.

Hence, OR = OQ.

(iii) OC is the bisector of angle C.

∴ ∠ACO = ∠BCO.

Hence, ∠ACO = ∠BCO.

(i) Using ruler and compasses only, construct a triangle ABC in which AB = 8 cm, BC = 6 cm and CA = 5 cm.

(ii) Find its incenter and mark it I.

(iii) With I as centre, draw a circle which will cut off 2 cm chords from each side of the triangle.

Answer

Steps of construction :

1. Draw a line segment BC = 6 cm.

2. With B as center and radius 8 cm draw an arc.

3. With C as center and radius 5 cm draw another arc which intersects first arc at A.

4. Join AB and AC. ABC is the required triangle.

5. Draw angle bisectors of B and A intersecting each other at I. I is the incenter.

6. Through I, draw ID ⊥ AB.

7. From D as center cut off DP = DQ = $\dfrac{2}{2}$ = 1 cm.

8. With I as center and radius IP or IQ, draw a circle cutting off 2 cm chords from each side of triangle.

Draw a circle circumscribing a regular hexagon with side = 5 cm.

Answer

Each interior angle of a regular hexagon = $\Big(\dfrac{2n - 5}{n}\Big) \times 90°$

$= \dfrac{2 \times 6 - 4}{6} \times 90° \\[1em] = 8 \times 15° \\[1em] = 120°.$

Steps of construction :

1. Draw a regular hexagon ABCDEF with each side equal to 5 cm and each interior angle = 120°.

2. Draw the perpendicular bisectors of AB and AF which intersect each other at O.

3. With O as center and OA as radius draw a circle which will pass through all the vertices of the regular hexagon.

Hence, above is the required circumcircle of regular hexagon.

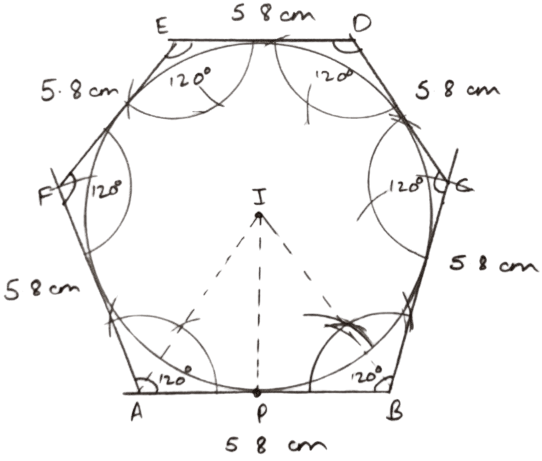
Draw an inscribing circle of regular hexagon of side 5.8 cm.

Answer

Each interior angle of a regular hexagon = $\Big(\dfrac{2n - 5}{n}\Big) \times 90°$

$= \dfrac{2 \times 6 - 4}{6} \times 90° \\[1em] = 8 \times 15° \\[1em] = 120°.$

Steps of construction :

1. Draw a regular hexagon ABCDEF with each side equal to 5.8 cm and each interior angle = 120°.

2. Draw the bisectors of interior angles at A and B which intersect each other at point I.

3. From point I , draw IP perpendicular to AB.

4. With I as center and IP as radius, draw a circle which will touch all the sides of the regular hexagon drawn.

Hence, above is the required incircle of regular hexagon.

Construct a triangle ABC in which base BC = 5.5 cm, AB = 6 cm and ∠ABC = 120°.

(i) Construct a circle circumscribing the triangle ABC.

(ii) Draw a cyclic quadrilateral ABCD so that D is equidistant from B and C.

Answer

(i) Steps of construction :

1. Draw a line segment BC = 5.5 cm

2. From B draw a ray BX such that ∠XBC = 120°.

3. From B draw an arc of 6 cm cutting BX at A.

4. Join AC. ABC is the required triangle.

5. Construct perpendicular bisectors of AB and BC, such that they intersect at O.

6. With O as center and OA as radius draw a circle passing through A, B and C.

Hence, above is the required circumcircle of triangle ABC.

(ii) Steps of construction :

1. Draw perpendicular bisector of BC, such that it intersects the circle at D.

2. Join CD and AD. ABCD is the cyclic quadrilateral.

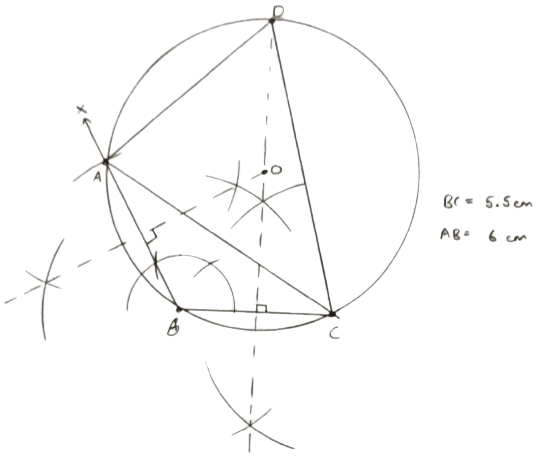
Hence, above is the required cyclic quadrilateral.

Using a ruler and compasses only :

(i) Construct a triangle ABC with the following data :

AB = 3.5 cm, BC = 6 cm and ∠ABC = 120°.

(ii) In same diagram, draw a circle with BC as diameter. Find a point P on the circumference of the circle which is equidistant from AB and BC.

(iii) Measure ∠BCP.

Answer

Steps of construction :

1. Draw a line BC = 6 cm.

2. At B, draw a ray BX making an angle of 120° with BC. With B as center and radius 3.5 cm, cut off AB = 3.5 cm.

3. Join AC. ABC is the required triangle.

4. Draw perpendicular bisector of BC which cuts BC at point O. With O as center and radius = OB, draw a circle.

5. Draw angle bisector of ∠ABC which meets the circle at point P. Thus, point P is equidistant from AB and BC.

Measure ∠BCP.

Hence, ∠BCP = 30°.

Draw a line AB = 5 cm. Mark a point C on AB such that AC = 3 cm. Using a ruler and a compass only, construct :

(i) a circle of radius 2.5 cm, passing through A and C.

(ii) construct two tangents to the circle from the external point B. Measure and record the length of the tangents.

Answer

(i) Steps of construction :

1. Draw a line segment AB = 5 cm.

2. With A as center cut an arc of 3 cm on AB to obtain C.

3. With A as center and radius = 2.5 cm draw an arc.

4. With C as center and radius = 2.5 cm draw an arc cutting the previous arc and mark the point O.

5. With O as center and radius = 2.5 cm draw a circle.

Hence, above is the required circle.

(ii) Steps of construction :

1. Join OB.

2. Draw the perpendicular bisector of OB, let it meet OB at point M.

3. With M as center and radius equal to OM, draw a circle to cut the previous circle at points P and Q.

4. Join PB and QB. Hence, PB and QB are required tangents. Measure PB and QB.

On measuring PB = QB = 3.2 cm.

Hence, length of each tangent = 3.2 cm.

Using a ruler and a compass, construct a triangle ABC in which AB = 7 cm, ∠CAB = 60° and AC = 5 cm. Construct the locus of :

(i) points equidistant from AB and AC.

(ii) points equidistant from BA and BC.

Hence construct a circle touching the three sides of the triangle internally.

Answer

Steps of construction :

1. Draw a line segment AB = 7 cm.

2. Construct AX such that ∠XAB = 60°.

3. With A as center and radius = 5 cm cut arc on AX and mark it as point C.

4. Join BC. ABC is the required triangle.

5. Draw AY and BZ, angle bisector of A and B.

6. Let AY and BZ meet at point O.

7. Draw OD ⊥ AB.

8. With O as center and OD as radius draw a circle.

(i) Hence, AY is the locus of points equidistant from AB and AC.

(ii) Hence, BZ is the locus of points equidistant from BA and BC.

Construct a triangle ABC in which AB = 5 cm, BC = 6.8 cm and median AD = 4.4 cm. Draw incircle of this triangle.

Answer

Steps of construction :

1. Draw a line segment BC = 6.8 cm.

2. Mark D as the mid-point of BC.

3. With B as center and radius = 5 cm draw an arc.

4. With D as center and radius = 4.4 cm draw an arc cutting another arc at A.

5. Join AC. Hence, ABC is the required triangle.

6. Draw angle bisectors of B and C. Let it meet at point I.

7. Draw IM ⊥ BC.

8. With I as center and IM as radius draw a circle.

Hence, above is the required incircle of the triangle.

Draw two concentric circles with radii 4 cm and 6 cm. Taking a point on the outer circle, construct a pair of tangents to inner circle. By measuring the lengths of both the tangents, show that they are equal to each other.

Answer

Steps of construction :

1. Draw two concentric circles of radius 4 cm and 6 cm with O as center.

2. Take a point P on the outer circle.

3. Join OP.

4. Draw perpendicular bisectors of OP, let it meet OP at point M.

5. With M as centre and OM as radius cut arcs at inner circle at point A and B.

6. Join PA and PB. Measure PA and PB.

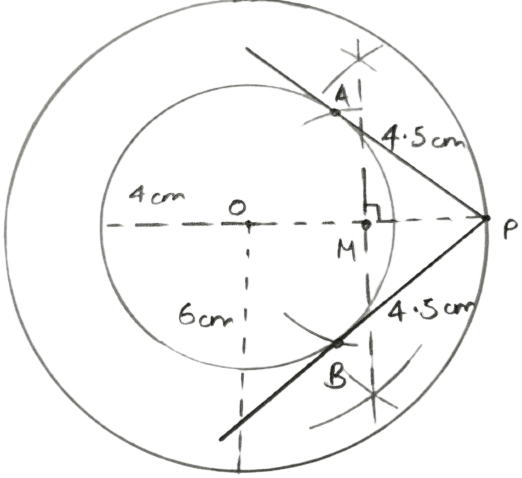
On measuring,

PA = PB = 4.5 cm.

Hence, PA and PB are tangents and length of each tangent = 4.5 cm.

In triangle ABC, ∠ABC = 90°, side AB = 6 cm, side BC = 7.2 cm and BD is perpendicular to side AC. Draw circumcircle of triangle BDC and then state the length of the radius of this circumcircle drawn.

Answer

Steps of construction :

1. Draw BC = 7.2 cm.

2. Draw a ray BX, such that ∠XBC = 90°.

3. With B as center and radius = 6 cm cut an arc on BX and mark point A.

4. Join AC.

5. Take a point D on AC such that BD ⊥ AC.

6. Draw perpendicular bisectors of BD and BC which intersect at I.

7. With I as center and IC as radius draw a circle passing through B, D and C. Measure IC.

Hence, above is the required circumcircle with radius = 3.6 cm.