An open hollow cylindrical container, made of very thin metal sheet, has radius r cm and height h cm, its total surface area (in cm2) is :
πr2h + 2πrh
4πrh + πr2
4πrh + 2πr2
2πrh + 2πr2
Answer
Given,
It is an open hollow cylindrical container.
∴ It will be open at one end and closed at the other end.
Since, hollow cylindrical container is made up of very thin metal sheet.
∴ External radius = Internal radius = r cm.
Given,
Height = h cm.
Total surface area of hollow cylinder = External curved surface area + Internal curved surface area + Area of cross section (lower end)
= 2πrh + 2πrh + πr2
= 4πrh + πr2.
Hence, Option 2 is the correct option.
The curved area of a solid cylinder is S cm2 and the circumference of its base is C cm; the height of the cylinder is :
C × S
C + S
S ÷ C
S - C
Answer
Let height of cylinder be h cm and radius be r cm.
Given,
The curved area of a solid cylinder is S cm2.
By formula,
Circumference of base = 2πr
Curved surface area = 2πrh
⇒ S = 2πrh
⇒ S = C.h
⇒ h = = S ÷ C.
Hence, Option 3 is the correct option.
A cylindrical container has sufficient water to submerge a solid cubical object of its each edge a cm. If the radius of the container is r cm, the rise in level (h cm) of water in the container is :

Answer
Suppose rise in level of water be h cm.
Increase in volume of cylinder = πr2h.
Given,
Edge of cubical solid submerged = a cm.
Volume of cubical solid submerged = a3
We know that,
Volume of cubical solid submerged = Increase in volume of cylinder
⇒ a3 = πr2h
⇒ h = .
Hence, Option 3 is the correct option.
A solid cylinder of radius R cm and height H cm is melted and recast into smaller identical solid cylinders of height h cm and radius r cm. The number of smaller solid cylinders obtained is :
R2H ÷ r2h2
Answer
Given,
A solid cylinder of radius R cm and height H cm is melted and recast into smaller identical solid cylinders of height h cm and radius r cm.
Let no. of smaller cylinders formed be n.
∴ Volume of larger cylinder = n × Volume of one smaller cylinder
⇒ πR2H = n × πr2h
⇒ n =
Hence, Option 2 is the correct option.
The total surface area of an open pipe of length H cm, external radius R cm and internal radius r cm, is :
πR2 - πr2 + 2π(R - r)H
2πR2 - 2πr2 + 2πRH
2πRH - 2πrh + πR2 - πr2
2(πR2 - πr2) + 2πRH + 2πrH
Answer
Given,
External radius = R cm,
Internal radius = r cm,
Height = H cm.
Total surface area of hollow cylinder = External curved surface area + Internal curved surface area + 2(Area of cross section)
= 2πRH + 2πrH + 2(πR2 - πr2).
Hence, Option 4 is the correct option.
The inner radius of a pipe is 2.1 cm. How much water can 12 m of this pipe hold ?
Answer
By formula,
Volume of cylinder = πr2h
Since, pipe is in the form of cylinder.
Given, radius (r) = 2.1 cm and height (h) = 12 m = 1200 cm.
Volume of water inside pipe =
= 22 × 0.3 × 2.1 × 1200
= 16632 cm3.
Hence, pipe can hold 16632 cm3 of water.
How many cubic meters of earth must be dug out to make a well 28 m deep and 2.8 m in diameter ? Also, find the cost of plastering its inner surface at ₹ 4.50 per sq meter.
Answer
Given,
Diameter of well = 2.8 m
Radius of the well = = 1.4 m
Depth of the well = 28 m.
Volume of earth dug out = Volume of well = πr2h
= x 1.4 x 1.4 x 28
= 172.48 m3.
Area of curved surface = 2πrh
= 2 x x 1.4 x 28
= 2 x 22 x 0.2 x 28
= 246.4 m2.
Given, the cost of plastering at the rate of ₹ 4.50 per sq meter.
∴ Cost of plastering inner surface = ₹ 246.40 x 4.50
= ₹ 1108.80.
Hence, volume of earth to be dug out = 172.48 m3 and cost of plastering inner surface = ₹ 1108.80.
What length of solid cylinder 2 cm in diameter must be taken to recast into a hollow cylinder of external diameter 20 cm, 0.25 cm thick and 15 cm long?
Answer
Given,
External diameter of hollow cylinder = 20 cm
So, external radius (R) = = 10 cm.
Thickness = 0.25 cm
Hence, the internal radius (r) = (10 - 0.25) = 9.75 cm.
Length of cylinder (h) = 15 cm
By formula,
Given,
Diameter of the solid cylinder = 2 cm
so, radius (a) = = 1 cm
Let h be the length of the solid cylinder,
Volume = πa2h = π(1)2h = πh cm3.
In order for recasting, volume of solid cylinder must be equal to volume of material of hollow cylinder .
∴ πh = 15 π x 4.9375
⇒ h = 15 x 4.9375
⇒ h = 74.0625 cm.
Hence, the length of solid cylinder = 74.06 cm.
A cylinder has a diameter of 20 cm. The area of curved surface is 100 cm2. Find :
(i) the height of the cylinder correct to one decimal place.
(ii) the volume of the cylinder correct to one decimal place.
Answer
Given,
The diameter of the cylinder = 20 cm
So, the radius (r) = = 10 cm
Given, the curved surface area = 100 cm2.
Let height = h cm
(i) By formula,
Curved surface area of cylinder = 2πrh
∴ 2πrh = 100
⇒ 2 x x 10 x h = 100
⇒ h =
⇒ h = = 1.6 cm.
Hence, the height of cylinder = 1.6 cm.
(ii) By formula,
Volume of the cylinder = πr2h
= x 10 x 10 x 1.6
= 502.9 cm3.
Hence, the volume of cylinder = 502.9 cm3.
A metal pipe has a bore (inner diameter) of 5 cm. The pipe is 5 mm thick all round. Find the weight, in kilogram, of 2 metres of the pipe if 1 cm3 of the metal weights 7.7 g.
Answer
Given,
Inner diameter = 5 cm and thickness of pipe = 5 mm = 0.5 cm.
Inner radius of the pipe (r) = = 2.5 cm.
External radius of the pipe (R) = Inner radius of the pipe + Thickness of the pipe
= 2.5 cm + 0.5 cm = 3 cm
Length of the pipe (h) = 2 m = 200 cm.
Volume of the pipe = External Volume - Internal Volume
= πR2h - πr2h
= π(R2 - r2)h
= π(R + r)(R - r) h
= (3 + 2.5)(3 - 2.5) x 200
= (5.5) x (0.5) x 200 = 1728.6 cm3.
Given, 1 cm3 of the metal weight 7.7 g,
∴ Weight of the pipe = (1728.6 x 7.7) g = kg = 13.31 kg.
Hence, weight of the pipe = 13.31 kg.
A cylindrical container with diameter of base 42 cm contains sufficient water to submerge a rectangular solid of iron with dimensions 22 cm x 14 cm x 10.5 cm. Find the rise in the level of the water when the solid is submerged.
Answer
Given,
Diameter of base = 42 cm and radius = = 21 cm.
Let rise in level of water be h cm.
Since, water rises on submerging of a rectangular solid.
So, the increase in volume of water = volume of rectangular solid.
∴ πr2h = 22 x 14 x 10.5
= 3234
h = cm
Hence, the water level will be raised to a level of cm when the solid is submerged.
A cylindrical container with internal radius of its base 10 cm, contains water up to a height of 7 cm. Find the area of wet surface of the cylinder.
Answer
Given,
Internal radius of the cylindrical container (r) = 10 cm
Height of water (h) = 7 cm
So, the surface area of the wet surface = 2πrh + πr2 = πr(2h + r)
= x 10 x (2 x 7 + 10)
= x 24
= 754.29 cm2.
Hence, the area of wet surface of cylinder = 754.29 cm2.
Find the total surface area of an open pipe of length 50 cm, external diameter 20 cm and internal diameter 6 cm.
Answer
Given,
Length of the open pipe = 50 cm
External diameter = 20 cm
External radius (R) = = 10 cm
Internal diameter = 6 cm
Internal radius (r) = = 3 cm
Surface area of pipe open from both sides = 2πRh + 2πrh = 2πh(R + r)
= 2 x x 50 x (10 + 3)
= 4085.71 cm2
Area of upper and lower part = 2πR2 - 2πr2
= 2 x x (102 - 32)
= 2 x x 91
= 572 cm2.
Total surface area = 4085.71 + 572 = 4657.71 cm2.
Hence, total surface area of open pipe = 4657.71 cm2.
The height and the radius of the base of a cylinder are in the ratio 3 : 1. If its volume is 1029 π cm3; find its total surface area.
Answer
Given,
The ratio between height and radius of a cylinder = 3 : 1
Volume = 1029π cm3 ..............(1)
Let the radius of the base = r
Then, it’s height will be = 3r.
By formula,
Volume = πr2h ............. (2)
From (1) and (2), we get
⇒ πr2h = 1029π
⇒ r2 × 3r = 1029
⇒ r3 =
⇒ r3 = 343
⇒ r =
⇒ r = 7 cm.
Thus, radius = r = 7 cm and height = 3r = 3 x 7 = 21 cm.
By formula,
Total surface area = 2πr(h + r)
= 2 x x 7 x (21 + 7)
= 2 x 22 x 28
= 1232 cm2.
Hence, total surface area of cylinder = 1232 cm2.
The radius of a solid right circular cylinder decreases by 20% and its height increases by 10%. Find the percentage change in its:
(i) volume (ii) curved surface area
Answer
Let the original dimensions of the solid right circular cylinder be
radius = r cm and height = h cm.
Volume = πr2h.
Curved surface area = 2πrh
Now, after the changes the new dimensions are:
Radius (r') = r - = r - 0.2r = 0.8r
Height (h') = h + = h + 0.1h = 1.1h
So,
New volume = πr'2h'
= π(0.8r)2(1.1h)
= 0.704 πr2h.
New curved surface area = 2πr'h' = 2π(0.8r)(1.1h)
= 1.76πrh
(i) Decrease in volume = Original volume - New volume
= πr2h - 0.704 πr2h
= 0.296 πr2h
Percentage change in its volume = x 100 %
= x 100 %
= 0.296 x 100 % = 29.6 %.
Hence, decrease in volume = 29.6 %.
(ii) Decrease in curved surface area = Original curved surface area - New curved surface area
= 2πrh - 1.76πrh
= 0.24πrh.
Percentage change in its curved surface area = x 100 %
= x 100 %
= 0.12 x 100 %
= 12 %.
Hence, decrease in volume = 12 %.
Find the minimum length in cm and correct to nearest whole number of the thin metal sheet required to make a hollow and closed cylindrical box of diameter 20 cm and height 35 cm. Given that the width of the metal sheet is 1 m. Also, find the cost of the sheet at the rate of Rs. 56 per m.
Find the area of metal sheet required, if 10% of it is wasted in cutting, overlapping, etc.
Answer
Given,
Height of the cylinder box (h) = 35 cm
Base radius of the cylinder box (r) = = 10 cm
Width of metal sheet = 1m = 100 cm
Area of metal sheet required = Total surface area of the box
⇒ Length x width = 2πr(r + h)
⇒ Length x 100 = 2 x x 10(10 + 35)
⇒ Length x 100 = 2 x x 10 x 45
⇒ Length = = 28.28 cm ≈ 28 cm (correcting to the nearest whole number)
Thus,
Area of metal sheet = length x width = 28 x 100 = 2800 cm2 = = 0.28 m2.
So, the cost of the sheet at the rate of ₹ 56 per m2 = ₹ (56 x 0.28) = ₹ 15.68
Let the total sheet required be x.
Then, x - 10 % of x = 2800 cm
⇒ = 2800
⇒ = 2800
⇒ = 2800
⇒ = 2800
⇒
⇒ x = 3111.11 cm2 ≈ 3111 cm2 (correcting to the nearest whole number)
Hence, length = 28 cm, cost of sheet = ₹15.68 and area of sheet required = 3111 cm2.
3080 cm3 of water is required to fill a cylindrical vessel completely and 2310 cm3 of water is required to fill it upto 5 cm below the top. Find :
(i) radius of the vessel.
(ii) height of the vessel.
(iii) wetted surface area of the vessel when it is half-filled with water.
Answer
Let radius of vessel be r cm and height be h cm.
Given,
Volume of cylindrical vessel = 3080 cm3
∴ πr2h = 3080 ...........(1)
Given,
It takes 2310 cm3 of water to fill cylinder upto 5 cm below the top.
∴ πr2(h - 5) = 2310 ...........(2)
Dividing (1) by (2) we get,
(i) Substituting value of h in equation (1), we get :
Hence, radius of vessel = 7 cm.
(ii) From above,
h = 20 cm.
Hence, height of vessel = 20 cm.
(iii) When vessel is half-filled, water will be filled upto = 10 cm.
Wetted surface area = 2πrh + πr2
= πr(2h + r)
=
=
= 594 cm2.
Hence, wetted surface area = 594 cm2.
Find the volume of the largest cylinder formed when a rectangular piece of paper 44 cm by 33 cm is rolled along its :
(i) shorter side
(ii) longer side.
Answer
(i) When paper is rolled along shorter side then height = 44 cm and circumference = 33 cm.
⇒ Circumference = 33 cm
⇒ 2πr = 33
⇒
⇒ r = = 5.25 cm.
Volume = πr2h
=
=
= = 3811.5 cm3.
Hence, volume of cylinder = 3811.5 cm3.
(ii) When paper is rolled along longer side then height = 33 cm and circumference = 44 cm.
⇒ Circumference = 44 cm
⇒ 2πr = 44
⇒
⇒ r = = 7 cm.
Volume = πr2h
=
=
= 5082 cm3.
Hence, volume of cylinder = 5082 cm3.
A metal cube of side 11 cm is completely submerged in water contained in a cylindrical vessel with diameter 28 cm. Find the rise in the level of water.
Answer
Given,
⇒ Diameter = 28 cm
⇒ Radius (r) = 14 cm
⇒ Side of cube (a) = 11 cm.
Let the rise in level of water be h cm.
So, the volume of water risen = volume of cube
∴ πr2h = a3
Hence, rise in level of water = 2.16 cm.
A circular tank of diameter 2 m is dug and the earth removed is spread uniformly all around the tank to form an embarkment 2 m in width and 1.6 m in height. Find the depth of the circular tank.
Answer
Given,
Tank's diameter = 2 m
Tank's radius (r) = = 1 m
Width of embarkment (w) = 2 m
External radius (R) = r + w = 1 + 2 = 3 m.
Height of embarkment (h) = 1.6 m
Let depth of tank be h' meters.
Volume of earth removed = Volume of embarkment formed
⇒ πr2h' = π(R2 - r2)h
⇒ 12h' = (32 - 12) × 1.6
⇒ h' = (9 - 1) × 1.6 m
⇒ h' = 12.8 m
Hence, depth of circular tank = 12.8 m.
The sum of the height and the radius of a solid cylinder is 35 cm and its total surface area is 3080 cm2; find the volume of the cylinder.
Answer
According to question,
h + r = 35 .........(1)
Total surface area = 3080
⇒ 2πr(h + r) = 3080
⇒ 2πr × 35 = 3080
⇒ = 3080
⇒ 220r = 3080
⇒ r =
⇒ r = 14 cm.
⇒ h + r = 35
⇒ h + 14 = 35
⇒ h = 35 - 14
⇒ h = 21 cm.
Volume of cylinder = πr2h
=
= 22 × 2 × 14 × 21
= 12936 cm3.
Hence, volume of cylinder = 12936 cm3.
The total surface area of a solid cylinder is 616 cm2. If the ratio between its curved surface area and total surface area is 1 : 2; find the volume of the cylinder.
Answer
Given,
Total surface area = 616 cm2
⇒ 2πr(h + r) = 616
⇒ πr(h + r) =
⇒ πr(h + r) = 308 ..........(1)
Ratio between its curved surface area and total surface area = 1 : 2
Substituting value of h in equation (1), we get :
⇒ πr(r + r) = 308
⇒ πr.2r = 308
⇒ 2πr2 = 308
⇒ πr2 = 154
⇒ = 154
⇒ r2 =
⇒ r2 = 49
⇒ r =
⇒ r = 7 cm
⇒ h = 7 cm.
Volume of cylinder = πr2h
=
= 22 × 49
= 1078 cm3.
Hence, volume of cylinder = 1078 cm3.
A cylindrical vessel of height 24 cm and diameter 40 cm is full of water. Find the exact number of small cylindrical bottles, each of height 10 cm and diameter 8 cm, which can be filled with this water.
Answer
Given,
Height of large cylindrical vessel (h1) = 24 cm
Diameter of large cylindrical vessel = 40 cm
Radius of large cylindrical vessel (r1) = = 20 cm.
Height of small cylindrical vessel (h2) = 10 cm
Diameter of small cylindrical vessel = 8 cm
Radius of small cylindrical vessel (r2) = = 4 cm.
Let no. of small cylindrical bottles which can be filled be n.
Volume of large cylindrical vessel = n × Volume of small cylindrical vessel
Hence, no. of small cylindrical bottles which an be filled = 60.
Two solid cylinders, one with diameter 60 cm and height 30 cm and the other with radius 30 cm and height 60 cm, are melted and recasted into a third solid cylinder of height 10 cm. Find the diameter of the cylinder formed.
Answer
For new cylinder formed,
Let Radius = r
and
Volume = V
Height (h) = 10 cm (Given)
For 1st cylinder melted,
Diameter (d) = 60 cm
Radius (r1) = 30 cm
Height (h1) = 30 cm
Volume = V1
For 2nd cylinder melted,
Radius (r2) = 30 cm
Height (h2) = 60 cm
Volume = V2
Volume of new cylinder formed will be equal to the sum of two cylinders melted,
V = V1 + V2
Diameter = 2r = 2 x 90 = 180 cm.
Hence, diameter of new cylinder = 180 cm.
The total surface area of a hollow cylinder, which is open from both the sides, is 3575 cm2; area of its base ring is 357.5 cm2 and its height is 14 cm. Find the thickness of the cylinder.
Answer
Let external radius be R cm and internal radius be r cm.
Given,
Area of base of ring = 357.5 cm2
∴ π(R2 - r2) = 357.5
Given,
Total surface area of hollow cylinder = 3575 cm2.
Dividing (1) by (2), we get :
Hence, thickness of hollow cylinder = 3.5 cm.
Two right circular solid cylinders have radii in the ratio 3 : 5 and heights in the ratio 2 : 3. Find the ratio between their :
(i) curved surface areas.
(ii) volumes.
Answer
(i) According to question,
r1 : r2 = 3 : 5
Let, r1 = 3x and r2 = 5x.
h1 : h2 = 2 : 3
Let, h1 = 2y and h2 = 3y.
Hence, ratio between curved surface area = 2 : 5.
(ii)
Hence, ratio between volume = 6 : 25.
A closed cylindrical tank, made of thin iron-sheet, has diameter = 8.4 m and height 5.4 m. How much metal sheet, to the nearest m2, is used in making this tank, if of the sheet actually used was wasted in making the tank ?
Answer
Radius of cylindrical tank = = 4.2 m.
Total surface area of cylindrical tank = 2πr(h + r)
= 2 × × 4.2 × (5.4 + 4.2)
= 2 × 22 × 0.6 × 9.6
= 253.44 m2.
Given,
of the sheet actually used was wasted in making the tank.
∴ Fraction of sheet used in making the tank =
Let metal sheet used be m2
of = TSA of Cylindrical tank
Area of metal sheet in nearest m2 = 272 m2
Hence, total metal (iron) sheet used in nearest m2 is 272 m2.
The radius and height of a solid metallic cone are r cm each. The volume of the cone is :
Answer
By formula,
Volume of cone = × (radius)2 × height
Given,
Radius and Height of a solid metallic cone are r cm each.
Volume of cone = .
Hence, Option 3 is the correct option.
The radius of the base of a solid cone is r cm and its height is h cm; its curved surface area is :
π × r ×
π × r ×
π × r × (h + r)
πr2(h + r)
Answer
By formula,
Curved surface area = πrl
= .
Hence, Option 2 is the correct option.
A conical toy tent-house, 28 cm in radius and 21 cm in height, is made from a rectangular sheet of paper 22 cm wide. The smallest length of the paper sheet required is :
70 cm
105 cm
140 cm
280 cm
Answer
Since, conical toy is made from the rectangular sheet.
∴ Surface area of cone = Area of rectangular sheet.
Let smallest length of the paper sheet required be a cm.
∴ πrl = length × breadth
Hence, Option 3 is the correct option.
For a cone, the ratio between the volume and area of its base is 11 : 6. The height of the cone is :
units
5.5 units
11 units
5 units
Answer
Let radius of cone be r cm and height be h cm.
Given,
For a cone, the ratio between the volume and area of its base is 11 : 6.
Hence, Option 2 is the correct option.
The radii of two solid cones are equal and their slant heights are in the ratio 7 : 4. The ratio between their curved surface areas is :
4 : 7
7 : 4
16 : 49
49 : 16
Answer
Let radii of both the cones be r units each.
Let slant height of two cones be l1 and l2.
Curved surface area of first cone = πrl1
Curved surface area of second cone = πrl2
= 7 : 4.
Hence, Option 2 is the correct option.
Find the volume of a cone whose slant height is 17 cm and radius of base is 8 cm.
Answer
Given,
Slant height (l) = 17 cm
Radius (r) = 8 cm
Let height of cone be h cm.
We know that,
⇒ l2 = h2 + r2
⇒ 172 = h2 + 82
⇒ 289 = h2 + 64
⇒ h2 = 225
⇒ h = = 15 cm.
By formula,
Volume of cone =
Hence, volume of cone = 1005.71 cm3.
The curved surface area of a cone is 12320 cm2. If the radius of its base is 56 cm, find its height.
Answer
By formula,
Curved surface area = πrl
We know that,
⇒ l2 = h2 + r2
⇒ 702 = h2 + 562
⇒ 4900 = h2 + 3136
⇒ h2 = 4900 - 3136
⇒ h2 = 1764
⇒ h = = 42 cm.
Hence, height of cone = 42 cm.
The circumference of the base of a 12 m high conical tent is 66 m. Find the volume of the air contained in it.
Answer
Given,
Circumference of base = 66 m
⇒ 2πr = 66
⇒
⇒ r = = 10.5 cm
By formula,
Volume of cone =
Hence, volume of air contained in cone = 1386 m3.
The radius and the height of a right circular cone are in the ratio 5 : 12 and its volume is 2512 cubic cm. Find the radius and slant height of the cone. (Take π = 3.14)
Answer
Given,
Radius : Height = 5 : 12
Let radius (r) = 5x and height (h) = 12x.

By formula,
Volume of cone =
Radius (r) = 5x = 5(2) = 10 cm and Height (h) = 12x = 12(2) = 24 cm.
By formula,
⇒ l2 = h2 + r2
⇒ l2 = (24)2 + (10)2
⇒ l2 = 576 + 100
⇒ l2 = 676
⇒ l = = 26 cm.
Hence, radius = 10 cm and slant height = 26 cm.
The diameters of two cones are equal. If their slant heights are in the ratio 5 : 4, find the ratio of their curved surface areas.
Answer
Given, ratio of slant height = 5 : 4
Let slant height of 1st cone be 5x cm and 2nd cone be 4x cm.
For 1st cone,
⇒ Diameter = d1
⇒ Radius = r1
⇒ Slant height (l1) = 5x
For 2nd cone,
⇒ Diameter = d2
⇒ Radius = r2
⇒ Slant height (l2) = 4x
Given,
⇒ d1 = d2
∴ r1 = r2.
Hence, ratio of curved surface areas = 5 : 4.
There are two cones. The curved surface area of one is twice that of the other. The slant height of the latter is twice that of the former. Find the ratio of their radii.
Answer
Let curved surface area of 1st cone be twice than that of 2nd cone.
For 1st cone,
⇒ Slant height (l1) = l
⇒ Radius = r1
⇒ Curved surface area (C1) = 2C .........(1)
For 2nd cone,
⇒ Slant height (l2) = 2l
⇒ Radius = r2
⇒ Curved surface area (C2) = C .........(2)
Dividing equation (1) by (2), we get :
⇒ r1 : r2 = 4 : 1.
Hence, ratio of radii = 4 : 1.
A heap of wheat is in the form of a cone of diameter 16.8 m and height 3.5 m. Find its volume. How much cloth is required to just cover the heap?
Answer
Given,
Diameter of heap of cone = 16.8 m
Radius of heap of cone (r) = = 8.4 m
Height (h) = 3.5 m
Volume of cone =
We know that,
⇒ l2 = r2 + h2
⇒ l2 = (8.4)2 + (3.5)2
⇒ l2 = 70.56 + 12.25
⇒ l2 = 82.81
⇒ l = = 9.1 cm.
Cloth required to cover the heap = Curved surface area of heap = πrl
=
= 240.24 m2.
Hence, volume = 258.72 m3 and cloth required to cover the heap = 240.24 m2.
If you are given a rectangular canvas of 1.5 m in width, what length of this canvas would you require to make a conical tent that is 48 m in diameter and 7 m in height? Note that 10% of the canvas is used (wasted) in folds and stitching.
Also, find the cost of the canvas at the rate of ₹ 24 per meter.
Answer
Given,
Diameter of conical tent = 48 m
Radius of conical tent (r) = = 24 m
Height of conical tent (h) = 7 m
Let l be the slant height of the conical tent.
By formula,
By formula,
Surface area of conical tent (S) = πrl
Given,
10% of the canvas is used in folds and stitching.
Thus, 90% of the total canvas area is used for making the tent.
Thus,
⇒ Total canvas area = Length of canvas × Width of canvas
⇒ = Length of canvas × 1.5
⇒ Length of canvas = = 1396.83 m
Cost of canvas = Rate per m × Length
= 24 × 1396.83
= ₹ 33,523.92
Hence, length of canvas required = 1396.83 m and cost of canvas = ₹ 33,523.92
A solid cone of height 8 cm and base radius 6 cm is melted and recast into identical cones, each of height 2 cm and diameter 1 cm. Find the number of cones formed.
Answer
For larger cone,
Height (h1) = 8 cm
Radius (r1) = 6 cm
For smaller cones,
Height (h2) = 2 cm
Radius (r2) = = 0.5 cm
Let no. of smaller cones be n.
Volume of larger cone = n × Volume of smaller cones
Hence, no. of cones formed = 576.
The total surface area of a right circular cone of slant height 13 cm is 90π cm2. Calculate :
(i) its radius in cm
(ii) its volume in cm3.
[Take π = 3.14]
Answer
(i) Given,
Total surface area = 90π
∴ πrl + πr2 = 90π
⇒ πr(l + r) = 90π
⇒ r(l + r) = 90
⇒ r(13 + r) = 90
⇒ r2 + 13r - 90 = 0
⇒ r2 + 18r - 5r - 90 = 0
⇒ r(r + 18) - 5(r + 18) = 0
⇒ (r - 5)(r + 18) = 0
⇒ (r - 5) = 0 or (r + 18) = 0
⇒ r = 5 or r = -18.
Since, radius cannot be negative.
∴ radius = 5 cm.
Hence, radius = 5 cm.
(ii) By formula,
⇒ l2 = r2 + h2
⇒ 132 = 52 + h2
⇒ h2 = 169 - 25
⇒ h2 = 144
⇒ h =
⇒ h = 12 cm.
Volume =
=
=
= 314 cm3.
Hence, volume of circular cone = 314 cm3.
The area of the base of a conical solid is 38.5 cm2 and its volume is 154 cm3. Find the curved surface area of the solid.
Answer
Given,
Area of the base of conical solid = 38.5 cm2
⇒ πr2 = 38.5 ............(1)
⇒ = 38.5
⇒ r2 = = 12.25
⇒ r = = 3.5 cm
Given,
By formula,
⇒ l2 = r2 + h2
⇒ l2 = (3.5)2 + (12)2
⇒ l2 = 12.25 + 144
⇒ l2 = 156.25
⇒ l = = 12.5 cm.
Curved surface area = πrl
=
= 137.5 cm2.
Hence, curved surface area = 137.5 cm2.
A vessel, in the form of an inverted cone, is filled with water to the brim. Its height is 32 cm and diameter of the base is 25.2 cm. Six equal solid cones are dropped in it, so that they are fully submerged. As a result one-fourth of water in the original cone overflows. What is the volume of each of the solid cones submerged?
Answer

Radius of vessel (R) = = 12.6 cm.
Total volume of water in vessel =
On submerging six equal cones in vessel, one-fourth of water in the original cone overflows.
Let radius of small cones be r and height be h,
Hence, volume of each cone = 221.76 cm3.
The volume of a conical tent is 1232 m3 and the area of the base floor is 154 m2. Calculate the :
(i) radius of the floor,
(ii) height of the tent,
(iii) length of the canvas required to cover this conical tent if its width is 2 m.
Answer
(i) Given,
Area of base floor = 154 m2
Hence, radius of the floor = 7 m.
(ii) Given,
Volume of tent = 1232 m3
Hence, height of tent = 24 m.
(iii) By formula,
⇒ l2 = r2 + h2
⇒ l2 = (7)2 + (24)2
⇒ l2 = 49 + 576
⇒ l2 = 625
⇒ l =
⇒ l = 25 m.
Curved surface area of cone = πrl
=
= 550 m2.
Let length of canvas be l.
Area of canvas = Curved surface area of cone
⇒ l × b = 550
⇒ l × 2 = 550
⇒ l =
⇒ l = 275 m.
Hence, length of canvas required = 275 m.
A solid metallic sphere of radius 16 cm is melted to form small identical spheres each of diameter 4 cm. The number of spheres formed is :
64
252
512
1024
Answer
Given,
A solid metallic sphere of radius 16 cm is melted to form small identical spheres each of diameter 4 cm.
Larger metallic ball sphere radius (R) = 16 cm
Radius of smaller metallic sphere (r) = = 2 cm
Let no. of smaller spheres formed be n.
∴ Volume of larger metallic ball = n × Volume of smaller metallic ball
Hence, Option 3 is the correct option.
A hemi-spherical bowl (as shown) has external radius R and internal radius r, the outer surface area of the bowl is :
2πR2 + πr2
3πR2 - πr2
2πR2 + 2πr2
2πR2 - πr2

Answer
Outer surface area of the hemi-spherical bowl = Surface area of outer hemisphere + Area of outer cross-section - Area of inner cross-section
= 2πR2 + πR2 - πr2
= 3πR2 - πr2.
Hence, Option 2 is the correct option.
The ratio between the volumes of two spherical solids is 27 : 8. The ratio between their curved surface areas is :
27 : 8
8 : 27
3 : 2
9 : 4
Answer
Let radius of two spherical solids be R and r.
Given,
The ratio between the volumes of two spherical solids is 27 : 8.
The ratio between the curved surface area of two spherical solids :
Hence, Option 4 is the correct option.
A solid metallic sphere of radius 8 cm is melted and recast into 64 identical solid spheres. The diameter of each smaller sphere formed is :
4 cm
2 cm
8 cm
1 cm
Answer
Given,
Radius of larger metallic sphere (R) = 8 cm
Let radius of each smaller sphere be r cm.
Given,
A solid metallic sphere of radius 8 cm is melted and recast into 64 identical solid spheres.
∴ Volume of larger metallic sphere = 64 × Volume of smaller metallic sphere
Diameter of smaller sphere = 2 × 2 = 4 cm.
Hence, Option 1 is the correct option.
r1, r2 and r3 are the radii of three metallic spheres. If these spheres are melted to form a single solid sphere, the radius of sphere formed is :
r1 + r2 + r3
Answer
Given,
r1, r2 and r3 are the radii of three metallic spheres. These spheres are melted to form a single solid sphere.
Let the radius of sphere formed be R.
∴ Volume of sphere formed = Sum of volume of three smaller spheres
Hence, Option 4 is the correct option.
The volume of a sphere is 38808 cm3; find its diameter and the surface area.
Answer
Given,
Volume of the sphere = 38808 cm3
Let the radius of the sphere = r
By formula,
Volume of sphere =
∴ Diameter = 2r = 21 x 2 = 42 cm.
Surface area = 4πr2 =
= 5544 cm2.
Hence, diameter of ball = 42 cm and surface area = 5544 cm2.
A spherical ball of lead has been melted and made into identical smaller balls with radius equal to half the radius of the original one. How many such balls can be made?
Answer
Let the radius of the spherical ball be r cm.
So, the volume =
Radius of smaller ball = cm
According to question,
The volume of large spherical balls = Volume of all small balls
Let no. of small spherical balls that can be made be n.
Hence, 8 balls can be made.
How many balls each of radius 1 cm can be made by melting a bigger ball whose diameter is 8 cm.
Answer
Given,
Diameter of bigger ball = 8 cm
So, radius of bigger ball (R) = = 4 cm.
Volume of bigger ball =
=
= .
Radius of small ball (r) = 1 cm
Volume of each smaller ball =
=
Let n smaller balls can be made by, melting bigger ball.
Volume of bigger ball = n × Volume of each smaller ball
Hence, 64 balls can be made.
The volume of one sphere is 27 times that of another sphere. Calculate the ratio of their:
(i) radii
(ii) surface areas
Answer
Given,
Volume of first sphere = 27 x volume of second sphere
Let the radius of the first sphere = r1 and, radius of second sphere = r2
(i) According to the question, we have :
Hence, r1 : r2 = 3 : 1.
(ii) Surface area of the first sphere = 4π(r1)2
Surface area of second sphere = 4π(r2)2
Hence, the ratio of surface areas = 9 : 1.
If the number of square centimeters on the surface of a sphere is equal to the number of cubic centimeters in its volume, what is the diameter of the sphere ?
Answer
Let r be the radius of the sphere.
According to question,
Surface area of sphere = Volume of sphere
Diameter of sphere = 2r = 2 × 3 = 6 cm.
Hence, diameter of sphere = 6 cm.
A solid metal sphere is cut through its center into 2 equal parts. If the diameter of the sphere is cm, find the total surface area of each part correct to two decimal places.
Answer
Diameter of sphere = cm.
Radius of sphere (r) = cm.
Total surface area of each hemisphere = Curved surface area of sphere + Area of circular base
=
= 2πr2 + πr2
= 3πr2
Hence, total surface area of each hemisphere 28.88 cm2.
The internal and external diameters of a hollow hemispherical vessel are 21 cm and 28 cm respectively. Find :
(i) internal curved surface area,
(ii) external curved surface area,
(iii) total surface area,
(iv) volume of material of the vessel.
Answer
(i) Given,
Internal diameter = 21 cm
Internal radius (r) = cm.
By formula,
Internal curved surface area = 2πr2.
Hence, internal curved surface area = 693 cm2.
(ii) Given,
Internal diameter = 28 cm
Internal radius (R) = = 14 cm.
By formula,
External curved surface area = 2πR2.
Hence, external curved surface area = 1232 cm2.
(iii) By formula,
Total surface area of hemisphere = 2πr2 + 2πR2 + π(R2 - r2)
Hence, total surface area of hemisphere = 2194.5 cm2.
(iv) By formula,
Volume of hemispherical vessel =
Hence, volume of vessel = 3323.83 cm3.
A solid sphere and a solid hemi-sphere have the same total surface area. Find the ratio between their volumes.
Answer
Let radius of sphere be R cm and hemi-sphere be r cm.
Given,
Solid sphere and a solid hemi-sphere have the same total surface area.
Calculating ratio between volumes,
Hence, ratio between volumes = .
Metallic spheres of radii 6 cm, 8 cm and 10 cm respectively are melted and recasted into a single solid sphere. Taking π = 3.1, find the surface area of the solid sphere formed.
Answer
Let radius of spheres be r1, r2 and r3 cm respectively.
Let r be the radius of new sphere formed.
Volume of new sphere formed = Total volume of the three spheres melted
By formula,
Surface area of sphere = 4πr2
= 4 × 3.1 × 122
= 1785.6 cm2.
A cone and a sphere have equal volumes. Their radii are also equal each being 10 cm; the height of the cone is :
70 cm
40 cm
50 cm
20 cm
Answer
Let radius of cone and sphere be r cm and height of cone be h cm.
Given,
A cone and a sphere have equal volumes and their radius are equal.
∴ Volume of cone = Volume of sphere
Hence, Option 2 is the correct option.
A sphere and a cone have equal volumes and equal radii. The ratio between the radius and height of the cone is :
3 : 4
4 : 3
4 : 1
1 : 4
Answer
Let radius of cone and sphere be r cm and height of cone be h cm.
Given,
A cone and a sphere have equal volumes and their radius are equal.
∴ Volume of cone = Volume of sphere
Hence, Option 4 is the correct option.
The radius and the height of a cone are in the ratio 2 : 1. The ratio between the volumes of a sphere and this cone (both having equal radii) is :
1 : 4
4 : 1
8 : 1
1 : 8
Answer
Given,
The radius and the height of a cone are in the ratio 2 : 1.
Let radius of cone be 2x and height of cone be x.
Let radius f sphere be r.
Given,
Radius of cone and sphere are equal.
∴ r = 2x.
Hence, Option 3 is the correct option.
A solid metallic cylinder is melted and formed into identical solid cones each having same radius and same height as that of the cylinder. The number of cones formed is :
3
6
9
2
Answer
Given,
A solid metallic cylinder is melted and formed into identical solid cones.
Let no. of cones formed be n.
As, radius and height of cones formed is equal to the cylinder.
Let radius of cylinder and cone be r units, height of cylinder and cone be h units.
∴ Volume of cylinder = n × Volume of each cone
⇒ πr2h = n ×
⇒ n = = 3.
Hence, Option 1 is the correct option.
A solid metallic cone of radius 10 cm and height 12 cm is melted to form a wire of uniform cross-section 1 cm2. The length of wire formed is :
40 × π cm
4 × π m
400 × π m
2 × π m
Answer
Given,
A solid metallic cone of radius (r) 10 cm and height (h) 12 cm is melted to form a wire of uniform cross-section 1 cm2.
Let length of wire formed be l cm.
∴ Volume of cone = Volume of wire
Hence, Option 2 is the correct option.
A solid sphere of radius 15 cm is melted and recast into solid right circular cones of radius 2.5 cm and height 8 cm. Calculate the number of cones recast.
Answer
Given,
Radius of the sphere (R) = 15 cm
So, the volume of sphere melted =
= 4500π cm3.
Radius of each cone formed (r) = 2.5 cm
Height of each cone (h) = 8 cm
So, volume of each cone =
=
Let no. of cones formed be n.
Volume of sphere = n × Volume of cone
Hence, no. of cones formed = 270.
A hollow sphere of internal and external diameters 4 cm and 8 cm, respectively is melted into a cone of base diameter 8 cm. Find the height of the cone.
Answer
Given,
External diameter of the hollow sphere = 8 cm
So, external radius (R) = = 4 cm
Internal diameter of the hollow sphere = 4 cm
So, internal radius (r) = = 2 cm
Diameter of cone = 8 cm
Radius of cone (r1) = 4 cm
Let height of the cone = h cm.
Since, hollow sphere is melted and recasted into cone.
∴ Volume of sphere = Volume of cone
Hence, the height of the cone = 14 cm.
The radii of the internal and external surfaces of a metallic spherical shell are 3 cm and 5 cm respectively. It is melted and recast into a solid right circular cone of height 32 cm. Find the diameter of the base of the cone.
Answer
Given,
Height of the solid right circular cone (h) = 32 cm
Internal radius of metallic spherical shell (r) = 3 cm
External radius of metallic spherical shell (R) = 5 cm
Let radius of cone be r1 cm.
As, metallic spherical shell is recasted into right circular cone.
∴ Volume of spherical shell = Volume of cone.
Diameter = 2r = = 7 cm.
Hence, diameter = 7 cm.
Total volume of three identical cones is the same as that of a bigger cone whose height is 9 cm and diameter 40 cm. Find the radius of the base of each smaller cone, if height of each is 108 cm.
Answer
Let the radius of the smaller cone be r cm.
Given,
Height of smaller cone (h) = 108 cm
Diameter of bigger cone = 40 cm
So, radius (R) = = 20 cm
Height of bigger cone (H) = 9 cm.
According to question,
Volume of big cone = 3 × Volume of each smaller cone.
Hence, radius of base of each cone = cm.
A solid rectangular block of metal 49 cm by 44 cm by 18 cm is melted and formed into a solid sphere. Calculate the radius of the sphere.
Answer
Let radius of sphere be r cm.
Since,
A solid rectangular block of metal is melted and formed into a solid sphere.
∴ Volume of rectangular block = Volume of sphere
Hence, the radius of sphere = 21 cm.
A hemispherical bowl of internal radius 9 cm is full of liquid. This liquid is to be filled into conical shaped small containers each of diameter 3 cm and height 4 cm. How many containers are necessary to empty the bowl?
Answer
Given,
Internal radius of hemispherical bowl (R) = 9 cm
Diameter of each conical container = 3 cm
So, radius (r) = = 1.5 cm and height of conical container(h) = 4 cm
Let no. of conical containers needed be n.
∴ Volume of hemispherical bowl = n × Volume of each conical shaped container
Hence, 162 containers are necessary to empty the bowl.
The total area of a solid metallic sphere is 1256 cm3. It is melted and recast into solid right circular cones of radius 2.5 cm and height 8 cm. Calculate :
(i) the radius of the solid sphere,
(ii) the number of cones recast.
[Take π = 3.14]
Answer
(i) Given,
Total area of solid metallic sphere = 1256 cm3
Let R be the radius of metallic sphere.
By formula,
Total area of solid metallic sphere = 4πR2
∴ 4πR2 = 1256
Hence, radius of sphere = 10 cm.
(ii) Given,
Radius of cone (r) = 2.5 cm
Height of cone (h) = 8 cm.
Let no. of cones formed be n.
Since, sphere is recasted into n cones.
∴ Volume of sphere = n × Volume of cones
Hence, no. of cones formed = 80.
The surface area of a solid metallic sphere is 2464 cm2. It is melted and recast into solid right circular cones of radius 3.5 cm and height 7 cm. Calculate :
(i) the radius of the sphere.
(ii) the number of cones recast.
Answer
(i) Given,
Surface area of solid metallic sphere = 2464
Let radius of solid metallic sphere be R cm.
By formula,
Surface area of solid metallic sphere = 4πR2
∴ 4πR2 = 2464
⇒
⇒
⇒
⇒ R2 = 196
⇒ R =
⇒ R = 14 cm.
Hence, the radius of sphere = 14 cm.
(ii) Given,
Radius of cones (r) = 3.5 cm
Height of cones (h) = 7 cm.
Let no. of cones formed be n.
Since,
Sphere is melted and recasted into cones.
∴ Volume of sphere = n × Volume of cone
Hence, no. of cones formed = 128.
In the given figure, the radius of the cone is same as its height equal to 2 cm each. The sum of the volumes of the whole body is :
8π cm3
16 cm3
32π cm3
32 cm3

Answer
Given,
Radius of cone (r) = 2 cm
Height of cone (h) = 2 cm
From figure,
Radius of hemisphere = Radius of cone = 2 cm.
⇒ Volume of body = Volume of cone + Volume of hemisphere
⇒ Volume of body =
Hence, Option 1 is the correct option.
In the given figure, height of the conical part is 3 cm. The radius and the height of the cylindrical part are 1 cm each. The total volume of the body is :
9π cm3
18π cm3
2π cm3
4π cm3

Answer
Given,
Radius of cylindrical part (r) = 1 cm
Height of cylindrical part (h) = 1 cm
Height of conical part (H) = 3 cm
From figure,
Radius of conical part = Radius of cylindrical part (r) = 1 cm
Volume of body = Volume of conical part + Volume of cylindrical part
Hence, Option 3 is the correct option.
The given figure shows a solid cylinder of height h cm and radius r cm. If the slant height of the conical cavity is l cm, the total surface area of the remaining solid is :
πrl + 2πrh + 2πr2
πr2 + πrl + 2πrh
2πr2 - πrl + 2πrh
(πrl + πr2) + 2πr2 + 2πrh

Answer
From figure,
Total surface area of remaining solid = Curved surface area of cylinder + Area of upper surface of cylinder + Curved surface area of cone
= 2πrh + πr2 + πrl.
Hence, Option 2 is the correct option.
In the given figure, a solid cone is kept inverted in a closed cylindrical container such that the height of cone = height of cylinder = h, radius of cone = radius of cylinder = r and slant height of cone = l. If the remaining of cylinder is completely filled with water, the wetted surface area of the whole body is :
2πrh + πr2 + πrl
2πrh + πrl
2πrh + 2πr2 + πrl
2πrh - πr2 + πrl

Answer
From figure,
Total wetted surface area of body = Curved surface area of cylinder + Area of upper surface of cylinder + Curved surface area of cone
= 2πrh + πr2 + πrl.
Hence, Option 1 is the correct option.
The given figure shows a solid sphere and a closed cylindrical container, both having the same heights and same radii. The volume of air left in the cylinder is :
6πr3
4πr3

Answer
From figure,
Radius of sphere = Radius of cylinder = r
Height of cylinder (h) = 2r
Volume of air left = Volume of cylinder - Volume of sphere
Hence, Option 3 is the correct option.
A cone of height 15 cm and diameter 7 cm is mounted on a hemisphere of same diameter. Determine the volume of the solid thus formed.
Answer
Given,
Height of the cone (h) = 15 cm
Diameter of the cone = 7 cm

Radius of cone (r) = = 3.5 cm
So, radius of the hemisphere (R) = 3.5 cm
From figure,
Volume of the solid (V) = Volume of the cone + Volume of the hemisphere
Hence, volume of solid formed = 282.33 cm3.
A buoy is made in the form of a hemisphere surmounted by a right cone whose circular base coincides with the plane surface of the hemisphere. The radius of the base of the cone is 3.5 metres and its volume is two-third of the hemisphere. Calculate the height of the cone and the surface area of the buoy, correct to two places of decimal.
Answer
From figure,
Radius of hemisphere (r) = Radius of cone (R) = 3.5 m.
Volume of hemisphere =
=
=
= m3.
Let height of the cone = h.
By formula,
Volume of conical part = ........(1)
Given,
Volume of cone = Volume of hemisphere
= m3 ...........(2)
From (1) and (2), we get :
By formula,
⇒ l2 = R2 + h2
⇒ l2 = (3.5)2 + (4.67)2
⇒ l2 = 12.25 + 21.81
⇒ l2 = 34.06
⇒ l =
⇒ l = 5.83 cm.
Surface area of buoy = Surface area of hemisphere + Surface area of cone = 2πr2 + πRl
Hence, height = 4.67 and surface area of buoy = 141.13 m2.
From a rectangular solid of metal 42 cm by 30 cm by 20 cm, a conical cavity of diameter 14 cm and depth 24 cm is drilled out. Find:
(i) the surface area of the remaining solid
(ii) the volume of remaining solid
(iii) the weight of the material drilled out if it weighs 7 gm per cm3.
Answer
Given,
Dimensions of rectangular solid are:
l = 42 cm, b = 30 cm and h = 20 cm.
Conical cavity’s diameter = 14 cm
So, its radius (r) = 7 cm
Depth (h) = 24 cm

(i) Total surface area of cuboid = 2(lb + bh + lh)
= 2 (42 x 30 + 30 x 20 + 20 x 42)
= 2 (1260 + 600 + 840)
= 2 (2700)
= 5400 cm2
Area of circular base of conical cavity = πr2 = x 7 x 7 = 154 cm2.
By formula,
⇒ l2 = r2 + h2
⇒ l2 = (7)2 + (24)2
⇒ l2 = 49 + 576
⇒ l2 = 625
⇒ l =
⇒ l = 25 cm.
Area of curved surface area of cone = πrl
= = 22 x 25 = 550 cm2
Surface area of remaining part = Surface area of rectangular solid + Surface area of cone - Area of base of conical cavity
= 5400 + 550 - 154
= 5796 cm2.
Hence, surface area of remaining part = 5796 cm2.
(ii) Volume of the rectangular solid = lbh
= (42 x 30 x 20) cm3
= 25200 cm3
Radius of conical cavity (r) = 7 cm
Depth (h) = 24 cm
Volume of cone =
=
= 22 × 7 × 8
= 1232 cm3.
Volume of remaining solid = Volume of rectangular solid - Volume of cone
= 25200 - 1232
= 23968 cm3.
Hence, volume of remaining solid = 23968 cm3.
(iii) Volume of material drilled out = Volume of cone = 1232 cm3.
Weight of material drilled out = 1232 × 7 = 8624 g = 8.624 kg.
Hence, weight of material drilled out = 8.624 kg.
The cubical block of side 7 cm is surmounted by a hemisphere of the largest size. Find the surface area of the resulting solid.
Answer
It’s known that, the diameter of the largest hemisphere that can be placed on the face of a cube of side 7 cm will be 7 cm.
So, it’s radius (r) = = 3.5 cm
Curved surface area = 2πr2
= = 77 cm2.
Area of base of hemisphere = πr2
=
= 38.5 cm2.
From figure,
Surface area of the resulting solid = Surface area of the cube – Area of the base of the hemisphere + Curved surface area of hemisphere
= 6(side)2 - 38.5 + 77
= 6(7)2 + 38.5
= 294 + 38.5
= 332.5 cm2.
Hence, surface area of resulting solid = 332.5 cm3.
A vessel is in the form of an inverted cone. Its height is 8 cm and the radius of the top which is open is 5 cm. It is filled with water up to the rim. When lead shots, each of which is a sphere of radius 0.5 cm, are dropped into the vessel, one-fourth of the water flows out. Find the number of lead shots dropped in the vessel.
Answer
Given,
Height of cone (H) = 8 cm
Radius of cone (R) = 5 cm
Radius of sphere (r) = 0.5 cm.

Let no. of lead shots dropped in vessel be n.
According to question,
One-fourth of the water flows out after dropping lead shots.
∴ x Volume of cone = n × Volume of each sphere
Hence, no. of shots dropped = 100.
A hemi-spherical bowl has negligible thickness and the length of its circumference is 198 cm. Find the capacity of the bowl.
Answer
Given,
Circumference = 198 cm
∴ 2πr = 198
⇒ r = = 31.5 cm.
By formula,
Hence, capacity of bowl = 65488.5 cm3.
Find the maximum volume of a cone that can be carved out of a solid hemisphere of radius r cm.
Answer
The max height and radius of cone, inside a hemisphere of radius r cm can be r cm.

Volume of cone =
=
=
Hence, maximum volume of cone that can be carved out of solid hemisphere of radius r cm = cm3.
The radii of the bases of two right circular cones of same height are r1 and r2 respectively. The cones are melted and recast into a solid sphere of radius R. Find the height of each cone in terms of r1, r2 and R.
Answer
Let height of each cone be h cm.
Given,
Cones are melted and recasted into a sphere.
∴ Volume of cone with radii r1 + Volume of cone with radii r2 = Volume of sphere
Hence, h =
A cone and a hemisphere have the same base and the same height. Find the ratio of their volumes.
Answer
Let radius and height of cone and hemisphere be a cm.
Volume of cone =
Volume of hemisphere =
Hence, ratio between volumes = 1 : 2.
The volume of a solid cylinder and a solid cone are same. If their radii are also same, the ratio between the heights of cylinder and cone is :
3 : 1
2 : 3
1 : 3
3 : 2
Answer
Radii of cylinder = Radii of cone = r (let)
Let height of cylinder be h1 and height of cone be h2.
Given,
Volume of a solid cylinder and a solid cone are same.
⇒ πr2h1 = πr2h2
⇒ h1 = h2
⇒
⇒ h1 : h2 = 1 : 3.
Hence, Option 3 is the correct option.
The volume of the given solid is :
2πr3
4πr3

Answer
From figure,
Height of cone (h) = r
Height of cylinder (H) = r
Radius of hemispherical portion = Radius of cylindrical portion = Radius of conical portion = r.
From figure,
Volume of body = Volume of conical portion + Volume of cylindrical portion + Volume of hemispherical portion
Hence, Option 3 is the correct option.
Eight identical metallic spheres, each of radius 1 cm are melted and recast into a solid sphere. The radius of the solid sphere formed is :
3 cm
2 cm
1.5 cm
2.5 cm
Answer
Given,
Radius of small metallic sphere (r) = 1 cm
Eight identical metallic spheres, each of radius 1 cm are melted and recast into a solid sphere.
Let radius of solid sphere formed be R.
∴ Volume of large metallic sphere = 8 × Volume of each smaller sphere
Hence, Option 2 is the correct option.
The ratio between the heights of two solid cones is 2 : 3 and ratio between their radii is 9 : 8. The ratio between their volumes is :
27 : 32
32 : 27
3 : 2
2 : 3
Answer
Given,
Ratio between the heights of two solid cones is 2 : 3.
Let height of first (h1) and second cone (h2) be 2a and 3a.
Ratio between the radii of two solid cones is 9 : 8.
Let radii of first (r1) and second cone (r2) be 9x and 8x.
Hence, Option 1 is the correct option.
The radius of a solid cylinder is doubled keeping the height same. The percentage increase in its volume is :
200%
100%
400%
300%
Answer
Before change :
Radius of cylinder = r
Height of cylinder = h
Volume of cylinder = πr2h
After change :
Radius of cylinder = 2r
Height of cylinder = h
Volume of cylinder = π(2r)2h = 4πr2h
Difference in volume = Volume after change - Volume before change
= 4πr2h - πr2h
= 3πr2h.
Percentage increase in volume
Hence, Option 4 is the correct option.
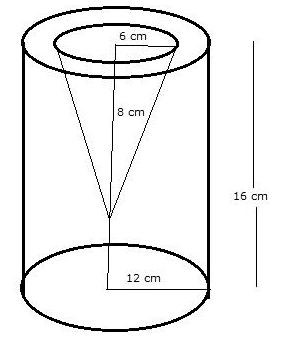
From a solid right circular cylinder with height 10 cm and radius of the base 6 cm, a right circular cone of the same height and same base are removed. Find the volume of the remaining solid.
Answer
Given,
Height of the cylinder (H) = 10 cm
Radius of the base of cylinder (R) = 6 cm
Height of the cone (h) = 10 cm
Radius of the base of cone (r) = 6 cm
Volume of remaining part (V) = Volume of cylinder - Volume of cone
Hence, volume of remaining solid = cm3.
From a solid cylinder whose height is 16 cm and radius is 12 cm, a conical cavity of height 8 cm and of base radius 6 cm is hollowed out. Find the volume and total surface area of the remaining solid.
Answer
Given,
Height of the cylinder (H) = 16 cm
Radius of the base of cylinder (R) = 12 cm
Height of the cone (h) = 8 cm
Radius of the base of cone (r) = 6 cm
(i) Volume of remaining part (V) = Volume of cylinder - Volume of cone
Hence, volume of remaining part = 6939.43 cm3.
(ii) By formula,
⇒ l2 = r2 + h2
⇒ l2 = 62 + 82
⇒ l2 = 36 + 64
⇒ l2 = 100
⇒ l2 = 102
⇒ l = 10 cm.
Thus,
Total surface area of remaining solid (T) = Curved surface area of cylinder + Curved surface area of cone + Base area of cylinder + Area of circular ring on upper side of cylinder
(T) = 2πRH + πrl + πR2 + π(R2 - r2)
Hence, total surface area of remaining solid = 2187.43 cm2.
A circus tent is cylindrical to a height of 4 m and conical above it. If its diameter is 105 m and its slant height is 80 m, calculate the total area of canvas required. Also, find the total cost of canvas used at ₹ 15 per meter if the width is 1.5 m.
Answer
Given,
Radius of the cylindrical part of the tent (R) = m
Radius of conical part (r) = m.
Slant height (l) = 80 m
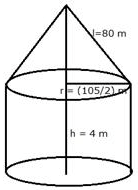
So, the total curved surface area of the tent = 2πRh + πrl
Width of canvas used = 1.5 m
Length of canvas =
Hence,
Total cost of canvas at the rate of ₹ 15 per meter = 9680 x 15 = ₹ 145200.
Hence, total area of canvas required = 9680 m2 and cost = ₹ 145200.
A circus tent is cylindrical to a height of 8 m surmounted by a conical part. If total height of the tent is 13 m and the diameter of its base is 24 m; calculate:
(i) total surface area of the tent
(ii) area of canvas, required to make this tent allowing 10% of the canvas used for folds and stitching.
Answer
Given,
Height of the cylindrical part (H) = 8 m
Height of the conical part (h) = (13 - 8) m = 5 m
Diameter of base = 24 m
From figure,
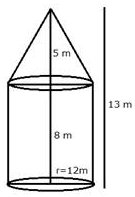
Radius of cone and cylinder are equal (r) = = 12 m.
By formula,
⇒ (l)2 = r2 + h2
⇒ l2 = 122 + 52
⇒ l2 = 144 + 25
⇒ l2 = 169
⇒ l =
⇒ l = 13 m.
(i) Total surface area of the tent = 2πrH + πrl = πr(2H + l)
= x 12 x (2 x 8 + 13)
= (16 + 13)
= m2
= 1093.71 m2.
Hence, total surface area of tent = 1093.71 m2.
(ii) According to question,
Area of canvas used in stitching = Total area of canvas
⇒ Total area of canvas required = Total surface area of tent + Area of canvas used in stitching
⇒ Total area of canvas = Total area of canvas
⇒ Total area of canvas - Total area of canvas =
⇒ Total area of canvas =
⇒ Total area of canvas =
⇒ Total area of canvas = 1215.23 m2.
Hence, the total area of canvas required = 1215.23 m2.
A cylindrical container with diameter of base 42 cm contains sufficient water to submerge a rectangular solid of iron with dimensions 22 cm × 14 cm × 10.5 cm. Find the rise in level of the water when the solid is submerged.
Answer
Given,
Diameter of base of cylindrical container = 42 cm
Radius of base of cylindrical container (r) = = 21 cm.
Let rise in level of water be h cm.
∴ Volume of solid submerged = Volume of increased water
⇒ 22 cm × 14 cm × 10.5 cm = πr2h
⇒ 3234 =
⇒ h =
⇒ h = cm.
Hence, water rises by cm in container.
Spherical marbles of diameter 1.4 cm are dropped into a beaker containing some water and are fully submerged. The diameter of the beaker is 7 cm. Find how many marbles have been dropped in it if the water rises by 5.6 cm?
Answer
Given,
Diameter of spherical marbles = 1.4 cm
Radius (r) = = 0.7 cm.
Diameter of beaker = 7 cm
Radius of beaker (R) = = 3.5 cm
Increase in water level (h) = 5.6 cm.
Let n marbles are dropped.
⇒ Volume of water increased in beaker = n × Volume of one marble (sphere)
⇒ πR2h =
Hence, 150 marbles are dropped in the beaker.
The given figure shows the cross-section of a water channel consisting of a rectangle and a semi-circle. Assuming that the channel is always full, find the volume of water discharged through it in one minute if water is flowing at the rate of 20 cm per second. Give your answer in cubic meters correct to one place of decimal.
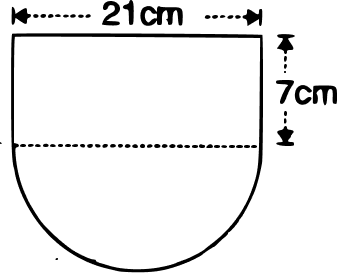
Answer
Let radius of semi-circle be r cm.
From figure,
⇒ 2r = 21 cm
⇒ r = cm.
Area of cross-section of water channel = l × b +
= 21 × 7 +
= 147 +
=
= 320.25 cm2.
Length of water column = Water flowing rate × Time
= 20 cm/s × 60 s
= 1200 cm.
Volume of water discharged = Area of cross-section of water channel × Length of water column
= 320.25 × 1200
= 384300 cm3
= m3
= 0.3843
≈ 0.4 m3.
Hence, volume of water discharged in one minute = 0.4 m3.
An open cylindrical vessel of internal diameter 7 cm and height 8 cm stands on a horizontal table. Inside this is placed a solid metallic right circular cone, the diameter of whose base is cm and height 8 cm. Find the volume of water required to fill the vessel.
If this cone is replaced by another cone, whose height is cm and the radius of whose base is 2 cm, find the drop in the water level.
Answer
Given,
Diameter of cylindrical vessel = 7 cm
Radius of cylindrical vessel (R) = = 3.5 cm
Height of cylindrical vessel (H) = 8 cm
Diameter of base of cone = cm
Radius of base of cone (r) = cm
Height of cone (h) = 8 cm
Volume of cylindrical vessel =
=
= 308 cm3.
Volume of original cone =
=
=
= cm3
Volume of water required to fill the vessel = Volume of cylindrical vessel - Volume of original cone
Given,
Radius of new cone (r1) = 2 cm
Height of new cone (h1) = cm
Volume of new cone =
Volume of water which comes down = Volume of original cone - Volume of new cone
=
= cm3.
Let drop in height of water be h2 cm.
Drop in volume of water = cm3
Hence, volume of water required to fill the vessel = 282.33 cm3 and drop in level of water = cm.
A cylindrical can, whose base is horizontal and of radius 3.5 cm, contains sufficient water so that when a sphere is placed in the can, the water just covers the sphere. Given that the sphere just fits into the can, calculate :
(i) the total surface area of the can in contact with water when the sphere is in it;
(ii) the depth of water in the can before the sphere was put into the can.
Answer
(i) Given,
Radius of base of cylindrical can (R) = 3.5 cm
Since,
When a sphere is placed in the can, the water just covers the sphere.
∴ Height (H) = 2R = 7 cm.
Total surface area = 2πRH + πR2
= πR(2H + R)
=
= 22 × 0.5 × (14 + 3.5)
= 192.5 cm2.
Hence, the total surface area of the can in contact with water when the sphere is in it = 192.5 cm2.
(ii) Let the depth of the water be h cm in the can.
Volume of water = Volume of cylinder - Volume of sphere
Hence, depth of water in the can before the sphere was put into the can = cm.
A hollow cylinder has solid hemisphere inward at one end and on the other end it is closed with a flat circular plate. The height of water is 10 cm when flat circular surface is downward. Find the level of water, when it is inverted upside down, common diameter is 7 cm and height of cylinder is 20 cm.
Answer
Given,
For Cylinder :
Height (H) = 20 cm, Radius (R) = 3.5 cm
For Hemisphere :
Radius (r) = Radius of cylinder (R) = 3.5 cm
When flat surface is downward, then height of water (h) = 10 cm.
So, when circular surface part will be downward then,
Let height upto which water fills be h1.
Volume of cylinder (upto height h1) = Volume of cylinder (upto height h) + Volume of hemisphere
Hence, the level of water, when cylinder is inverted upside down = 12.33 cm.
The given figure shows a solid cylinder and a solid cone on it according to the given measurement, the total surface area of the solid in terms of π and r is :
4πr2
5πr2
6πr2
7πr2
Answer
From figure,
Total surface area of solid = Curved surface area of cylinder + Curved surface area of cone + Area of cross-section
= 2πrh + πrl + πr2
= 2πr.r + πr.2r + πr2
= 2πr2 + 2πr2 + πr2
= 5πr2.
Hence, Option 2 is the correct option.
The radii of two solid spheres are 10 cm and 20 cm. The ratio between their volumes is :
3 : 8
1 : 4
1 : 8
8 : 3

Answer
Radius of first solid sphere (r) = 10 cm
Radius of second solid sphere (R) = 20 cm
Ratio of volumes of two spheres :
Hence, Option 3 is the correct option.
A cone and a sphere have equal volumes. If height of the cone = radius of the sphere = 10 cm, the radius of the cone is :
40 cm
10 cm
30 cm
20 cm
Answer
Given,
Height of the cone (H) = radius of the sphere (r) = 10 cm
Volume of cone and sphere are equal.
Let radius of cone be R cm.
Hence, Option 4 is the correct option.
By applying force on an uniform metallic wire, the wire is extended four times along its length with same width all around. Then :
(i) The volume of metal in both the cases is same.
(ii) The surface area of solid wires in both the cases is same.
Which of the above statements is/are true?
only (i)
only (ii)
both (i) and (ii)
neither (i) nor (ii)
Answer
On transforming a solid from one shape to another by any external force, the volume of solid remains same.
Let initial length of wire be l and radius be r.
After extension,
Length of wire = 4l and Radius be R.
Since, volume is equal in both the cases :
∴ πr2h = πR2H
⇒ πr2l = πR2.4l
⇒ r2 = 4R2
⇒ r =
⇒ r = 2R
⇒ R =
Surface area in first case :
⇒ 2πrh
⇒ 2πrl
Surface area in second case :
⇒ 2πRh
⇒
⇒ 4πrl.
∴ Surface area of solid wires in both the cases are different.
Hence, Option 1 is the correct option.
A solid metal cuboid with dimension 10 cm, 11 cm and 8 cm is melted and identical solid spheres, each of radius 1 cm, are formed. The number of sphere formed is :
105
210
315
420
Answer
Given,
A solid metal cuboid with dimensions 10 cm, 11 cm and 8 cm is melted and identical solid spheres, each of radius 1 cm, are formed. Let no. of spheres formed be n.
∴ Volume of metal cuboid = n × Volume of sphere
⇒ l × b × h = n ×
⇒ 10 × 11 × 8 = n ×
⇒ 880 = n ×
⇒ n =
⇒ n = 10 x 21 = 210.
Hence, option 2 is the correct option.
The given figure shows a toy made of very thin metal sheet. The toy has the hemisphere, a cylinder and a cone all of the same radius.

Assertion(A): The minimum area of metal sheet required is:
Curved surface area of conical part + curved surface area of cylinder part - curved surface area of hemispherical part
Reason(R): Metal sheet required = curved surface area of (conical part + cylindrical part + hemispherical part)
A is true, R is false.
A is false, R is true.
Both A and R are true and R is correct reason for A.
Both A and R are true and R is incorrect reason for A.
Answer
The toy has the hemisphere, a cylinder and a cone all of the same radius.
Metal sheet required = minimum area of metal sheet required
= curved surface area of conical part + curved surface area of cylinder part + curved surface area of hemisphere part
= curved surface area of (conical part + cylindrical part + hemispherical part)
∴ A is false, R is true.
Hence, option 2 is the correct option.
The base radius of two right circular cone of the same height are in ratio 3 : 5.
Assertion(A): The ratio between their volume is 9 : 25.
Reason(R): As
A is true, R is false.
A is false, R is true.
Both A and R are true and R is correct reason for A.
Both A and R are true and R is incorrect reason for A.
Answer
Given, the base radius of two right circular cone of the same height are in ratio 3 : 5.
As we know that volume of cone =
∴ Both A and R are true and R is correct reason for A.
Hence, option 3 is the correct option.
A solid cone of height 3 cm and radius 3 cm is recast into solid cylinder each of height 1 cm and radius 1 cm.
Assertion(A): Number of cylinders formed = x 3 x 3 x 3
Reason(R): Number of cylinders formed =
A is true, R is false.
A is false, R is true.
Both A and R are true and R is correct reason for A.
Both A and R are true and R is incorrect reason for A.
Answer
Given, radius of solid cone, R = 3 cm
Height of solid cone, H = 3 cm
Radius of solid cylinder, r = 1 cm
Height of solid cylinder, h = 1 cm
By formula,
Volume of cone =
Volume of cylinder = .
Given,
Solid cone is recasted into cylinders. Let no. of cylinders formed be n.
∴ Volume of cone = n × Volume of cylinder
∴ Both A and R are true and R is correct reason for A.
Hence, option 3 is the correct option.
A solid wooden cylinder is of height h cm and radius r cm. A conical cavity of same height and the same radius is drill out of the solid cylinder.
Statement (1): The volume of the remaining wood = volume of the solid cylinder - volume of the cone drilled.
Statement (2): The volume of the remaining wood = πr2h - πr2h = πr2h
Both the statement are true.
Both the statement are false.
Statement 1 is true, and statement 2 is false.
Statement 1 is false, and statement 2 is true.
Answer
The volume of the remaining wood is the volume of the original solid cylinder minus the volume of the conical cavity drilled out.
Let radius and height of cylinder and conical cavity (both are equal) be r and h units.
Volume of the cylinder : πr2h
Volume of the cone : πr2h
The volume of the remaining wood = Volume of the solid cylinder - Volume of the cone drilled.
= πr2h - πr2h
= πr2h
= πr2h
= πr2h.
∴ Both the statements are true.
Hence, option 1 is the correct option.
A solid sphere of radius 6 cm is melted and recast into solid spheres of diameter 2 cm each.
Statement (1): The number of solid sphere formed is 6 x 6 x 6 = 216.
Statement (2): If the smaller spheres formed are identical, the number of solid sphere formed =
Both the statement are true.
Both the statement are false.
Statement 1 is true, and statement 2 is false.
Statement 1 is false, and statement 2 is true.
Answer
Given, radius of solid sphere, R = 6 cm
Diameter of new sphere, d = 2 cm
Radius of new sphere, r = cm = 1 cm
Volume of the sphere: πr3
Given,
A solid sphere of radius 6 cm is melted and recast into solid spheres of diameter 2 cm each. Let no. of spheres formed be n.
∴ Volume of sphere = n × Volume of sphere recasted.
⇒ n =
∴ Statement 2 is true.
∴ Statement 1 is true.
Thus, both the statements are true.
Hence, option 1 is the correct option.
Water in a canal 6 m wide and 2 m deep, is flowing with the speed of 18 km/h.
Statement (1): The volume of water that flows through the canal in 20 minutes = 6 x 2 x x 20 x 60 m3.
Statement (2): The volume of water that flows through the canal = 6 x 2 x 18 x 20 m3.
Both the statement are true.
Both the statement are false.
Statement 1 is true, and statement 2 is false.
Statement 1 is false, and statement 2 is true.
Answer
Given, water in a canal 6 m wide and 2 m deep, is flowing with the speed of 18 km/h.
Volume of water flowing through the canal = Area of cross-section x speed x time
Area of cross-section = width × depth = (6 × 2) m2
Speed = 18 km/h = 18 × = m/sec
Time = 20 minutes = 20 × 60 sec
∴ Volume = 6 × 2 x 18 × x 20 × 60 m3
Thus, Statement 1 is true, and statement 2 is false.
Hence, option 3 is the correct option.
What is the least number of solid metallic spheres, each of 6 cm diameter, that should be melted and recast to form a solid metal cone whose height is 45 cm and diameter 12 cm ?
Answer
Given,
Diameter of metallic spheres = 6 cm
Radius of metallic spheres (r) = = 3 cm.
Height of cone (H) = 45 cm
Diameter of cone = 12 cm
Radius of cone (R) = = 6 cm.
Let no. of spheres melted to form a solid metal cone be n.
∴ n × Volume of each sphere = Volume of solid metal cone
Hence, 15 solid metallic spheres need to be melted.
A largest sphere is to be carved out of a right circular cylinder of radius 7 cm and height 14 cm. Find the volume of the sphere.
(Answer correct to the nearest integer)
Answer
Radius of largest sphere from a right circular cylinder will be equal to radius of circular cylinder = 7 cm.
Volume of sphere =
Hence, volume of sphere = 1437 m3.
A right circular cylinder having diameter 12 cm and height 15 cm is full of ice-cream. The ice-cream is to be filled in identical cones of height 12 cm and diameter 6 cm having a hemi-spherical shape on the top. Find the number of cones required.
Answer
Given,
Diameter of the cylinder = 12 cm
So, its radius (r) = = 6 cm
Height of the cylinder (h) = 15 cm
Diameter of the cone = 6 cm
So, its radius (R) = = 3 cm
Height of the cone (H) = 12 cm
Radius of the hemisphere = Radius of cone = R = 3 cm
Now,
Let the number of cones be n.
Volume of the cylinder = πr2h
= π × (6)2 × 15
= 540π cm2.
Volume of an ice-cream cone with ice-cream = Volume of cone + Volume of hemisphere
Let no. of cones required be n.
Volume of cylinder = n × Volume of each cone
n = = 10.
Hence, the number of cones required = 10.
A solid is in the form of a cone standing on a hemisphere with both their radii being equal to 8 cm and the height of cone is equal to its radius. Find in terms of π, the volume of the solid.
Answer
Given,
Radius of both cone and hemisphere (r) = 8 cm
Height of cone (h) = 8 cm
From figure,
Volume of the solid = Volume of cone + Volume of hemisphere
Hence, volume of solid = 512π cm3.
The diameter of a sphere is 6 cm. It is melted and drawn into a wire of diameter 0.2 cm. Find the length of wire.
Answer
Given,
Diameter of the sphere = 6 cm
So, its radius (R) = = 3 cm
Diameter of cylindrical wire = 0.2 cm
So, the radius of the wire (r) = = 0.1 cm
Let length of wire = h
Since, sphere is melted and recasted into a wire.
∴ Volume of sphere = Volume of wire
Hence, length of the wire = 36 m.
Determine the ratio of the volume of a cube to that of a sphere which will exactly fit inside the cube.
Answer
Let edge of the cube = a units.
Then, Volume of the cube = a x a x a = a3
The sphere that exactly fits in the cube will have diameter a units.
Radius of sphere (r) = units.
Hence, ratio of volume of cube to volume of sphere = 21 : 11.
An iron pole consisting of a cylindrical portion 110 cm high and of base diameter 12 cm is surmounted by a cone 9 cm high. Find the mass of the pole, given that 1 cm3 of iron has 8 gm of mass (approx). (Take π = )
Answer
Given,
Diameter of cylindrical portion = 12 cm
Radius of cylindrical portion (r) = = 6 cm
Height of the cylindrical part (H) = 110 cm
Height of the conical part (h) = 9 cm
From figure,

Radius of conical part = Radius of cylindrical portion = r = 6 cm.
Volume of iron pole = Volume of cylindrical portion + Volume of conical portion
Given,
Weight of 1 cm3 of iron = 8 gm.
Total weight = 12780 x 8 gm = 102240 gm
= kg = 102.24 kg.
Hence, mass of pole = 102.24 kg
The cross-section of a tunnel is a square of side 7 m surmounted by a semicircle as shown in the adjoining figure. The tunnel is 80 m long. Calculate:
(i) its volume,
(ii) the surface area of the tunnel (excluding the floor) and
(iii) its floor area.

Answer
Given,
Side of square (a) = 7 m
Let radius of semi-circle be r metres.
⇒ 2r = 7
⇒ r = m.
Length of the tunnel (h) = 80 m
Area of cross section of the front part = Area of square + Area of semi-circle
= a2 +
= 7 x 7 +
= 49 +
= m2.
(i) By formula,
Volume of the tunnel = Area of cross section x length of the tunnel
= x 80
= 5460 m3.
Hence, volume of tunnel = 5460 m3.
(ii) Surface area of the tunnel (excluding the floor) =
= Surface area of upper semi-circle portion + Surface area of square portion
= πrh + ah + ah
=
= 880 + 560 + 560
= 2000 m2.
Hence, the surface area of the tunnel = 2000 m2.
(iii) Area of floor = Breadth x Length of tunnel
= b x h = 80 x 7 = 560 m2.
Hence, area of floor = 560 m2.
A cylindrical water tank of diameter 2.8 m and height 4.2 m is being fed by a pipe of diameter 7 cm through which water flows at the rate of 4 m s-1. Calculate, in minutes, the time it takes to fill the tank.
Answer
Given,
Diameter of cylindrical tank = 2.8 m
So, its radius (R) = = 1.4 m
Height (H) = 4.2 m
Volume of water filled in it = πr2h
= x 1.4 x 1.4 x 4.2
= 25.872 m3
= 25.872 × (100)3 cm3
Given,
Diameter of the pipe = 7 cm
Radius (r) = = 3.5 cm
Area of cross section of pipe = πr2
=
= 22 × 0.5 × 3.5
= 38.5 cm2.
Volume of water discharged per second = 38.5 cm2 × 4 m s-1
= 38.5 × 400 cm s-1
Let the pipe fill the tank in n seconds.
∴ n × Volume of water discharged per second = Volume of tank
Hence, it takes 28 minutes to fill the tank.
Water flows, at 9 km per hour, through a cylindrical pipe of cross-sectional area 25 cm2. If this water is collected into a rectangular cistern of dimensions 7.5 m by 5 m by 4 m; calculate the rise in level in the cistern in 1 hour 15 minutes.
Answer
Given,
Rate of water flow = 9 km/hr
= 9 × 105 cm/hr. [As, 1 km = 105 cm.]
1 hour 15 minutes = hours.
Volume of water flowing in hours = Area of cross-section of pipe × Rate of water flow × hours
= 25 cm2 × 9 km/hr × hr
= 25 cm2 × (9 × 105) cm/hr × hr
= cm3.
Let increase in level of water be h cm.
Given,
Length of rectangular cistern = 7.5 m = 750 cm
Breadth of rectangular cistern = 5 m = 500 cm
Volume of water increase in cistern = 750 × 500 × h cm3
We know that,
Volume of water increase in cistern = Volume of water flowing in hours
Hence, there is an increase of 75 cm in level of water in cistern.
The given figure shows the cross-section of a cone, a cylinder and a hemisphere all with the same diameter 10 cm, and the other dimensions are as shown.
Calculate :
(i) the total surface area,
(ii) the total volume of the solid and
(iii) the density of the material if its total weight is 1.7 kg.

Answer
(i) Given,
Diameter of cone, cylinder and hemisphere = 10 cm
Radius of cone, cylinder and hemisphere (r) = = 5 cm.
From figure,
Height of cone (h) = 12 cm
By formula,
⇒ l2 = r2 + h2
⇒ l2 = 52 + 122
⇒ l2 = 25 + 144
⇒ l2 = 169
⇒ l = = 13 cm.
Total surface area = Surface area of cone + Surface area of cylinder + Surface area of hemisphere
= πrl + 2πrh + 2πr2
= πr(l + 2h + 2r)
=
=
=
= 738.57 cm2.
Hence, surface area of figure = 738.57 cm2.
(ii) From figure,
Volume of figure = Volume of cone + Volume of cylinder + Volume of hemisphere
Hence, volume of figure = 1519.05 cm3.
(iii) By formula,
Density =
Given,
Mass = 1.7 kg = 1700 gm
Substituting values we get,
Density = = 1.12 g/cm3.
Hence, density of material = 1.12 g/cm3.
A solid, consisting of a right circular cone standing on a hemisphere, is placed upright in a right circular cylinder, full of water, and touches the bottom. Find the volume of water left in the cylinder, having given that the radius of the cylinder is 3 cm and its height is 6 cm; the radius of the hemisphere is 2 cm and the height of cone is 4 cm. Give your answer to the nearest cubic centimeter.
Answer
Given,
Height of cylinder (H) = 6 cm
Radius of cylinder (R) = 3 cm
Height of cone (h) = 4 cm
Radius of cone = Radius of hemisphere = r = 2 cm

Volume of water left in cylinder = Volume of cylinder - Volume of cone - Volume of hemisphere
Hence, volume of water left in cylinder = 136 cm3.
A metal container in the form of a cylinder is surmounted by a hemisphere of the same radius. The internal height of the cylinder is 7 m and the internal radius is 3.5 m. Calculate :
(i) the total area of the internal surface, excluding the base;
(ii) the internal volume of the container in m3.
Answer
Given,
Radius of cylindrical portion = Radius of hemispherical portion = r = 3.5 m.
Height of cylinder (h) = 7 m.
(i) Area of internal surface = Surface area of cylinder + Surface area of hemisphere
= 2πrh + 2πr2
= 2πr(h + r)
=
= 2 × 22 × 0.5 × 10.5
= 231 m2.
Hence, the total area of the internal surface = 231 m2.
(ii) Internal volume of container = Volume of hemisphere + Volume of cylinder
Hence, volume of container = 359.33 m3.
An exhibition tent is in the form of a cylinder surmounted by a cone. The height of the tent above ground is 85 m and height of the cylindrical part is 50 m. If the diameter of the base is 168 m, find the quantity of canvas required to make the tent. Allow 20% extra for fold and for stitching. Give your answer to the nearest m2.
Answer
Given,
Diameter of base = 168 m
From figure,
Diameter of cylindrical base = Diameter of cone
Radius of cylindrical base = Radius of conical base = r = = 84 m.
Height of cylindrical part (H) = 50 m
Height of conical part (h) = 35 m
By formula,
⇒ l2 = r2 + h2
⇒ l2 = 842 + 352
⇒ l2 = 7056 + 1225
⇒ l2 = 8281
⇒ l = = 91 m.
Surface area of exhibition tent = Surface area of cylindrical part + Surface area of conical part
= 2πrH + πrl
Area required for folds and stitching = = 10084.8 m2.
Total area of canvas required = 50424 + 10084.8 = 60508.8 m2 ≈ 60509 m2 (to the nearest m2).
Hence, area of canvas required = 60509 m2.
A test tube consists of a hemisphere and a cylinder of the same radius. The volume of the water required to fill the whole tube is cm3, and cm3 of water is required to fill the tube to a level which is 4 cm below the top of the tube. Find the radius of the tube and the length of its cylindrical part.
Answer
Given,
Let radius of hemisphere be r cm and height of cylindrical portion be h cm.
Total volume of test tube = Volume of hemisphere + Volume of cylinder
Given,
cm3 of water is required to fill the tube to a level which is 4 cm below the top of the tube.
Substituting value of πr2(2r + 3h) from equation 1 in above equation.
Substituting value of r in equation 1, we get :
Hence, radius of cylindrical part = 3.5 cm and height = 20 cm.
A solid is in the form of a right circular cone mounted on a hemisphere. The diameter of the base of the cone, which exactly coincides with hemisphere, is 7 cm and its height is 8 cm. The solid is placed in a cylindrical vessel of internal radius 7 cm and height 10 cm. How much water, in cm3, will be required to fill the vessel completely?
Answer
Given,
Diameter of cone = 7 cm
Radius of cone (r) = = 3.5 cm
Height of cone (h) = 8 cm
Radius of hemisphere = radius of cone = r = 3.5 cm
Radius of cylindrical vessel (R) = 7 cm
Height of cylindrical vessel (H) = 10 cm.

Volume of solid = Volume of cone + Volume of hemisphere
By formula,
Volume of cylindrical vessel = πR2H
Volume of water required to fill the vessel completely = Volume of cylindrical vessel - Volume of solid
= 1540 - 192.5
= 1347.5 cm3.
Hence, volume of water required to fill the vessel completely = 1347.5 cm3.
A certain number of metallic cones, each of radius 2 cm and height 3 cm, are melted and recast into a solid sphere of radius 6 cm. Find the number of cones used.
Answer
Given,
Radius of cone (r) = 2 cm,
Height of cone (h) = 3 cm,
Radius of sphere (R) = 6 cm.
Let n cones be melted to recast into a solid sphere.
∴ n × Volume of each cone = Volume of sphere
Hence, 72 cones need to be melted to recast into a solid sphere.
A conical tent is to accommodate 77 persons. Each person must have 16 m3 of air to breathe. Given the radius of the tent as 7 m, find the height of the tent and also its curved surface area.
Answer
Given,
Each person must have 16 m3 of air to breathe.
∴ 77 persons need 77 × 16 m3 = 1232 m3.
Radius of tent (r) = 7 m.
Let height of conical tent be h meters.
Since, conical tent needs to accommodate 77 persons, so its volume will be equal to volume of air required for 77 persons.
By formula,
⇒ l2 = r2 + h2
⇒ l2 = 72 + 242
⇒ l2 = 49 + 576
⇒ l2 = 625
⇒ l = = 25 m.
Curved surface area of tent = πrl
=
= 22 × 25
= 550 m2.
Hence, height of tent = 24 m and curved surface area of tent = 550 m2.