Calculate the arithmetic mean of 5.7, 6.6, 7.2, 9.3, 6.2.
Answer
The sum of terms = 5.7 + 6.6 + 7.2 + 9.3 + 6.2 = 35
Number of terms = 5
Arithmetic mean (A.M.) =
Hence, the mean of 5.7, 6.6, 7.2, 9.3, 6.2 is 7.
The marks obtained by 15 students in a class test are 12, 14, 07, 09, 23, 11, 08, 13, 11, 19, 16, 24, 17, 03, 20. Find :
(i) the mean of their marks.
(ii) the mean of their marks when the marks of each student are increased by 4.
(iii) the mean of their marks when 2 marks are deducted from the marks of each student.
(iv) the mean of their marks when the marks of each student are doubled.
Answer
(i) The sum of marks of all students = 12 + 14 + 07 + 09 + 23 + 11 + 08 + 13 + 11 + 19 + 16 + 24 + 17 + 03 + 20 = 207.
Hence, the mean of marks of 15 students is 13.8
(ii) When the marks of each student are increased by 4, then the sum of their marks increases by 15 × 4 i.e. by 60.
∴ The new sum of marks of all students = 207 + 60 = 267.
Hence, the mean of marks of 15 students, when the marks of each student are increased by 4 is 17.8
(iii) When the marks of each student is decreased by 2, then the sum of their marks decreases by 15 × 2 i.e. by 30.
∴ The new sum of marks of all students = 207 - 30 = 177.
Hence, the mean of marks of 15 students, when the marks of each student is decreased by 2 is 11.8
(iv) When the marks of each student are doubled, then the sum of their marks will also be doubled.
∴ The new sum of marks of all students = 207 × 2 = 414.
Hence, the mean of marks of 15 students, when the marks of each student is doubled is 27.6
The mean of the numbers 6, y, 7, x, 14 is 8. Express y in terms of x.
Answer
Arithmetic mean (A.M.) =
Hence, the value of y = 13 - x.
The mean of 9 variates is 11. If eight of them are 7, 12, 9, 14, 21, 3, 8 and 15, find the 9th variate.
Answer
Let 9th variate be x.
Sum of terms = 7 + 12 + 9 + 14 + 21 + 3 + 8 + 15 + x = 89 + x
Number of terms = 9.
Arithmetic mean (A.M.) =
Given, A.M. = 11
Hence, the value of 9th variate is 10.
The mean age of 33 students of a class is 13 years. If one girl leaves the class, the mean becomes years. What is the age of the girl ?
Answer
Let the age of girl that leaves the class be x. So, sum of age of students becomes 429 - x and total no of students = 32. Given, new mean = .
Hence, the age of girl is 15 years.
In a class test, the mean of marks scored by a class of 40 students was calculated as 18.2. Later on, it was detected that the marks of one student was wrongly copied as 21 instead of 29. Find the correct mean.
Answer
As the marks of one student was wrongly copied as 21 instead of 29, correct sum of marks = 728 - 21 + 29 = 736.
Hence, the correct mean is 18.4.
Find the mean of 25 given numbers when the mean of 10 of them is 13 and the mean of the remaining numbers is 18.
Answer
Given, mean of 10 numbers is 13.
∴ Sum of 10 terms = 13 × 10 = 130.
Given, mean of 15 numbers is 18.
∴ Sum of 15 terms = 15 × 18 = 270.
Sum of 25 terms = 130 + 270 = 400.
Hence, the mean of 25 numbers is 16.
Find the mean of the following distribution :
| Number | Frequency |
|---|---|
| 5 | 1 |
| 10 | 2 |
| 15 | 5 |
| 20 | 6 |
| 25 | 3 |
| 30 | 2 |
| 35 | 1 |
Answer
We construct the following table:
| xi | fi | fixi |
|---|---|---|
| 5 | 1 | 5 |
| 10 | 2 | 20 |
| 15 | 5 | 75 |
| 20 | 6 | 120 |
| 25 | 3 | 75 |
| 30 | 2 | 60 |
| 35 | 1 | 35 |
| Total | 20 | 390 |
Mean = = 19.5
Hence, the mean of the following distribution is 19.5
The contents of 100 matchboxes were checked to determine the number of matches they contained.
| No. of matches | No. of boxes |
|---|---|
| 35 | 6 |
| 36 | 10 |
| 37 | 18 |
| 38 | 25 |
| 39 | 21 |
| 40 | 12 |
| 41 | 8 |
(i) Calculate, correct to one decimal place, the mean number of matches per box.
(ii) Determine how many extra matches would have to be added to the total contents of the 100 boxes to bring the mean upto exactly 39 matches.
Answer
(i) We construct the following table:
| xi | fi | fixi |
|---|---|---|
| 35 | 6 | 210 |
| 36 | 10 | 360 |
| 37 | 18 | 666 |
| 38 | 25 | 950 |
| 39 | 21 | 819 |
| 40 | 12 | 480 |
| 41 | 8 | 328 |
| Total | 100 | 3813 |
Mean = = 38.1
Hence, the mean of number of matches per box is 38.1
(ii) Mean =
Let the no. of matches added to total contents of 100 boxes be x in order to bring mean to 39. So, total matches becomes 3813 + x.
Hence, 87 extra matches need to added to bring the mean upto exactly 39 matches.
Find the mean for the following distribution by short cut method:
| Numbers | Cumulative Frequency |
|---|---|
| 60 | 8 |
| 61 | 18 |
| 62 | 33 |
| 63 | 40 |
| 64 | 49 |
| 65 | 55 |
| 66 | 60 |
Answer
We construct the following table as under taking the assumed mean, a = 63.
| xi | Cumulative frequency | fi | Deviation (di = xi - a) | fidi |
|---|---|---|---|---|
| 60 | 8 | 8 | -3 | -24 |
| 61 | 18 | 18 - 8 = 10 | -2 | -20 |
| 62 | 33 | 33 - 18 = 15 | -1 | -15 |
| 63 | 40 | 40 - 33 = 7 | 0 | 0 |
| 64 | 49 | 49 - 40 = 9 | 1 | 9 |
| 65 | 55 | 55 - 49 = 6 | 2 | 12 |
| 66 | 60 | 60 - 55 = 5 | 3 | 15 |
| Total | 60 | -23 |
Mean = = 62.62.
Hence, the mean of the following distribution is 62.62.
| Category | Wages in ₹ per day | No. of workers |
|---|---|---|
| A | 500 | 2 |
| B | 600 | 4 |
| C | 700 | 8 |
| D | 800 | 12 |
| E | 900 | 10 |
| F | 1000 | 6 |
| G | 1100 | 8 |
(i) Calculate done mean wages correct to the nearest rupees.
(ii) If the number of workers in each categories double what would be the new mean wage?
Answer
(i) We construct the following table:
| Category | Wages in ₹ per day (xi) | No. of workers (fi) | fixi |
|---|---|---|---|
| A | 500 | 2 | 1000 |
| B | 600 | 4 | 2400 |
| C | 700 | 8 | 5600 |
| D | 800 | 12 | 9600 |
| E | 900 | 10 | 9000 |
| F | 1000 | 6 | 6000 |
| G | 1100 | 8 | 8800 |
| Total | Σfi = 50 | Σfixi = 42400 |
Mean =
=
= 848.
Hence, the mean wage is ₹ 848.
(ii) If the number of workers in each category is doubled then total wage will also be doubled.
New total wage = 42400 × 2 = 84800 and number of workers = 50 × 2 = 100.
Mean =
=
= = 848.
Hence, the new mean wage is also ₹ 848.
The mean of the following data is 16. Calculate the value of f.
| Marks | No. of students |
|---|---|
| 5 | 3 |
| 10 | 7 |
| 15 | f |
| 20 | 9 |
| 25 | 6 |
Answer
| Marks (xi) | No. of students (fi) | fixi |
|---|---|---|
| 5 | 3 | 15 |
| 10 | 7 | 70 |
| 15 | f | 15f |
| 20 | 9 | 180 |
| 25 | 6 | 150 |
| Total | Σfi = 25 + f | Σfixi = 415 + 15f |
By formula; Mean =
Substituting the values, we get
Hence, the value of f = 15.
Marks obtained by 40 students in a short assessment is given below, where a and b are two missing data :
| Marks | No. of students |
|---|---|
| 5 | 6 |
| 6 | a |
| 7 | 16 |
| 8 | 13 |
| 9 | b |
If the mean of the distribution is 7.2, find a and b.
Answer
We construct the following table:
| Marks (xi) | No. of students (fi) | fixi |
|---|---|---|
| 5 | 6 | 30 |
| 6 | a | 6a |
| 7 | 16 | 112 |
| 8 | 13 | 104 |
| 9 | b | 9b |
| Total | 35 + a + b | 246 + 6a + 9b |
Given, total no. of students = 40 and mean = 7.2
∴ 35 + a + b = 40
⇒ a + b = 5
⇒ a = 5 - b .....(i)
Putting value of a from Eq (i)
a = 5 - b = 5 - 4 = 1.
Hence, the value of a = 1 and b = 4.
Calculate the mean of the following distribution:
| Class interval | Frequency |
|---|---|
| 5 - 15 | 2 |
| 15 - 25 | 6 |
| 25 - 35 | 4 |
| 35 - 45 | 8 |
| 45 - 55 | 4 |
Answer
| Class | Class-mark (yi) | Frequency (fi) | fiyi |
|---|---|---|---|
| 5 - 15 | 10 | 2 | 20 |
| 15 - 25 | 20 | 6 | 120 |
| 25 - 35 | 30 | 4 | 120 |
| 35 - 45 | 40 | 8 | 320 |
| 45 - 55 | 50 | 4 | 200 |
| Total | Σfi = 24 | Σfiyi = 780 |
Hence, mean of the following distribution is 32.5.
Calculate the mean of the following distribution :
| Class interval | Frequency |
|---|---|
| 0 - 10 | 8 |
| 10 - 20 | 5 |
| 20 - 30 | 12 |
| 30 - 40 | 35 |
| 40 - 50 | 24 |
| 50 - 60 | 16 |
Answer
We construct the following table:
| Classes | Class mark (yi) | Frequency (fi) | fiyi |
|---|---|---|---|
| 0 - 10 | 5 | 8 | 40 |
| 10 - 20 | 15 | 5 | 75 |
| 20 - 30 | 25 | 12 | 300 |
| 30 - 40 | 35 | 35 | 1225 |
| 40 - 50 | 45 | 24 | 1080 |
| 50 - 60 | 55 | 16 | 880 |
| Total | 100 | 3600 |
∴ Mean = = 36.
Hence, mean of the following distribution is 36.
Calculate the mean of the following distribution using step deviation method :
| Marks | Number of students |
|---|---|
| 0 - 10 | 10 |
| 10 - 20 | 9 |
| 20 - 30 | 25 |
| 30 - 40 | 30 |
| 40 - 50 | 16 |
| 50 - 60 | 10 |
Answer
We construct the following table, taking assumed mean a = 25.
Here, c (width of each class) = 10.
| Marks (Classes) | Class mark (yi) | No. of students (Frequency (fi)) | fiui | |
|---|---|---|---|---|
| 0 - 10 | 5 | -2 | 10 | -20 |
| 10 - 20 | 15 | -1 | 9 | -9 |
| 20 - 30 | 25 | 0 | 25 | 0 |
| 30 - 40 | 35 | 1 | 30 | 30 |
| 40 - 50 | 45 | 2 | 16 | 32 |
| 50 - 60 | 55 | 3 | 10 | 30 |
| Total | 100 | 63 |
Hence, mean of the following distribution is 31.3
The data on the number of patients attending a hospital in a month is given below. Find the average (mean) number of patients attending the hospital in a month using the short cut method.
Take assumed mean as 45. Give your answer correct to 2 decimal places.
| Number of patients | Number of days |
|---|---|
| 10 - 20 | 5 |
| 20 - 30 | 2 |
| 30 - 40 | 7 |
| 40 - 50 | 9 |
| 50 - 60 | 2 |
| 60 - 70 | 5 |
Answer
Construct table as under, taking assumed mean a = 45.
| Number of patients (Classes) | Class mark (yi) | Deviation (di = yi - a) | Number of days (Frequency (fi)) | fidi |
|---|---|---|---|---|
| 10 - 20 | 15 | -30 | 5 | -150 |
| 20 - 30 | 25 | -20 | 2 | -40 |
| 30 - 40 | 35 | -10 | 7 | -70 |
| 40 - 50 | 45 | 0 | 9 | 0 |
| 50 - 60 | 55 | 10 | 2 | 20 |
| 60 - 70 | 65 | 20 | 5 | 100 |
| Total | 30 | -140 |
Hence, mean of the following distribution is 40.33
The following table keep the daily wages of worker in a factory
| Wages in ₹ | No. of workers |
|---|---|
| 450 - 500 | 5 |
| 500 - 550 | 8 |
| 550 - 600 | 30 |
| 600 - 650 | 25 |
| 650 - 700 | 14 |
| 700 - 750 | 12 |
| 750 - 800 | 6 |
Calculate the mean by short cut method.
Answer
We construct the following table as under taking the assumed mean, a = 625.
| Class | Class - mark (xi) | Frequency (fi) | Deviation (di = xi - a) | fidi |
|---|---|---|---|---|
| 450 - 500 | 475 | 5 | -150 | -750 |
| 500 - 550 | 525 | 8 | -100 | -800 |
| 550 - 600 | 575 | 30 | -50 | -1500 |
| 600 - 650 | 625 | 25 | 0 | 0 |
| 650 - 700 | 675 | 14 | 50 | 700 |
| 700 - 750 | 725 | 12 | 100 | 1200 |
| 750 - 800 | 775 | 6 | 150 | 900 |
| Total | Σfi = 100 | Σfidi = -250 |
By formula,
Hence, mean of the following distribution is ₹622.5.
Calculate the mean of the distribution given below using the short cut method.
| Marks | No. of students |
|---|---|
| 11 - 20 | 2 |
| 21 - 30 | 6 |
| 31 - 40 | 10 |
| 41 - 50 | 12 |
| 51 - 60 | 9 |
| 61 - 70 | 7 |
| 71 - 80 | 4 |
Answer
Construct the table as under, taking assumed mean as 45.5
| Marks (Classes) | Class mark (yi) | Deviation (di = yi - a) | No. of students (Frequency (fi)) | fidi |
|---|---|---|---|---|
| 11 - 20 | 15.5 | -30 | 2 | -60 |
| 21 - 30 | 25.5 | -20 | 6 | -120 |
| 31 - 40 | 35.5 | -10 | 10 | -100 |
| 41 - 50 | 45.5 | 0 | 12 | 0 |
| 51 - 60 | 55.5 | 10 | 9 | 90 |
| 61 - 70 | 65.5 | 20 | 7 | 140 |
| 71 - 80 | 75.5 | 30 | 4 | 120 |
| Total | 50 | 70 |
Hence, mean of the following distribution is 46.9 marks
A class teacher has the following absentee record of 40 students of a class for the whole term. Find the mean number of days a student was absent.
| No. of days | No. of students |
|---|---|
| 0 - 6 | 11 |
| 6 - 10 | 10 |
| 10 - 14 | 7 |
| 14 - 20 | 4 |
| 20 - 28 | 4 |
| 28 - 38 | 3 |
| 38 - 40 | 1 |
Answer
We construct the following table :
| No. of days (Classes) | Class mark (yi) | No. of students (Frequency (fi)) | fiyi |
|---|---|---|---|
| 0 - 6 | 3 | 11 | 33 |
| 6 - 10 | 8 | 10 | 80 |
| 10 - 14 | 12 | 7 | 84 |
| 14 - 20 | 17 | 4 | 68 |
| 20 - 28 | 24 | 4 | 96 |
| 28 - 38 | 33 | 3 | 99 |
| 38 - 40 | 39 | 1 | 39 |
| Total | 40 | 499 |
∴ Mean = = 12.475
Hence, mean of the following distribution is 12.475
If the mean of the following distribution is 24, find the value of a :
| Marks | Number of students |
|---|---|
| 0 - 10 | 7 |
| 10 - 20 | a |
| 20 - 30 | 8 |
| 30 - 40 | 10 |
| 40 - 50 | 5 |
Answer
We construct the following table :
| Marks (Classes) | Class mark (yi) | Number of students (Frequency (fi)) | fiyi |
|---|---|---|---|
| 0 - 10 | 5 | 7 | 35 |
| 10 - 20 | 15 | a | 15a |
| 20 - 30 | 25 | 8 | 200 |
| 30 - 40 | 35 | 10 | 350 |
| 40 - 50 | 45 | 5 | 225 |
| Total | 30 + a | 810 + 15a |
Hence, the value of a = 10.
The mean of the following distribution is 50. Find the unknown frequency.
| Class Interval | Frequency |
|---|---|
| 0 - 20 | 6 |
| 20 - 40 | f |
| 40 - 60 | 8 |
| 60 - 80 | 12 |
| 80 - 100 | 8 |
Answer
| Class Interval | Class mark (xi) | Frequency (fi) | fixi |
|---|---|---|---|
| 0 - 20 | 10 | 6 | 60 |
| 20 - 40 | 30 | f | 30f |
| 40 - 60 | 50 | 8 | 400 |
| 60 - 80 | 70 | 12 | 840 |
| 80 - 100 | 90 | 8 | 720 |
| Total | Σfi = 34 + f | Σfixi = 2020 + 30f |
By formula,
Mean =
Substituting values we get :
Hence, the value of f = 16.
The mean of the following frequency distribution is 57.6 and the sum of all the frequencies is 50. Find the values of p and q :
| Classes | Frequency |
|---|---|
| 0 - 20 | 7 |
| 20 - 40 | p |
| 40 - 60 | 12 |
| 60 - 80 | q |
| 80 - 100 | 8 |
| 100 - 120 | 5 |
Answer
We construct the following table :
| Marks (Classes) | Class mark (yi) | Number of students (Frequency (fi)) | fiyi |
|---|---|---|---|
| 0 - 20 | 10 | 7 | 70 |
| 20 - 40 | 30 | p | 30p |
| 40 - 60 | 50 | 12 | 600 |
| 60 - 80 | 70 | q | 70q |
| 80 - 100 | 90 | 8 | 720 |
| 100 - 120 | 110 | 5 | 550 |
| Total | 32 + p + q | 1940 + 30p + 70q |
Given,
The sum of frequencies = 50.
∴ 32 + p + q = 50
⇒ p + q = 18
⇒ p = 18 - q .....(i)
Putting value of p from (i) in above equation,
Using (i),
⇒ p = 18 - q = 18 - 10 = 8.
Hence, the value of p = 8 and q = 10.
The following table gives the life time in days of 100 electricity tubes of a certain make :
| Lifetime in days | No. of tubes |
|---|---|
| less than 50 | 8 |
| less than 100 | 23 |
| less than 150 | 55 |
| less than 200 | 81 |
| less than 250 | 93 |
| less than 300 | 100 |
Find the mean lifetime of electricity tubes.
Answer
We construct the following table :
| Lifetime in days (Classes) | Class mark (yi) | No. of tubes (Cumulative frequency) | Frequency (fi)) | fiyi |
|---|---|---|---|---|
| 0 - 50 | 25 | 8 | 8 | 200 |
| 50 - 100 | 75 | 23 | 23 - 8 = 15 | 1125 |
| 100 - 150 | 125 | 55 | 55 - 23 = 32 | 4000 |
| 150 - 200 | 175 | 81 | 81 - 55 = 26 | 4550 |
| 200 - 250 | 225 | 93 | 93 - 81 = 12 | 2700 |
| 250 - 300 | 275 | 100 | 100 - 93 = 7 | 1925 |
| Total | 100 | 14500 |
∴ Mean = = 145
Hence, mean of the following distribution is 145 days
The following table gives the duration of movies in minutes.
| Duration (in minutes) | No. of movies |
|---|---|
| 100-110 | 5 |
| 110-120 | 10 |
| 120-130 | 17 |
| 130-140 | 8 |
| 140-150 | 6 |
| 150-160 | 4 |
Using step–deviation method, find the mean duration of the movies.
Answer
In the given table i is the class interval which is equal to 10.
| Class | Class mark (x) | d = (x - A) | u = d/i | Frequency (f) | fu |
|---|---|---|---|---|---|
| 100-110 | 105 | -30 | -3 | 5 | -15 |
| 110-120 | 115 | -20 | -2 | 10 | -20 |
| 120-130 | 125 | -10 | -1 | 17 | -17 |
| 130-140 | A = 135 | 0 | 0 | 8 | 0 |
| 140-150 | 145 | 10 | 1 | 6 | 6 |
| 150-160 | 155 | 20 | 2 | 4 | 8 |
| Total | Σf = 50 | Σfu = -38 |
Mean = A +
=
= 135 - 7.6
= 127.4
Hence, mean = 127.4
Shown below is a table illustrating the monthly income distribution in a company with 100 employees.
| Monthly income (in ₹ 10,000) | Number of employees |
|---|---|
| 0-4 | 55 |
| 4-8 | 15 |
| 8-12 | 06 |
| 12-16 | 08 |
| 16-20 | 12 |
| 20-24 | 4 |
Using step-deviation method, find the mean monthly income of an employee.
Answer
In the given table,
Class size (i) = 4.
| Monthly income | No.of employees (f) | Class mark | d = x - A | u = d/i | fu |
|---|---|---|---|---|---|
| 0-4 | 55 | 2 | -4 | -1 | -55 |
| 4-8 | 15 | A = 6 | 0 | 0 | 0 |
| 8-12 | 06 | 10 | 4 | 1 | 06 |
| 12-16 | 08 | 14 | 8 | 2 | 16 |
| 16-20 | 12 | 18 | 12 | 3 | 36 |
| 20-24 | 4 | 22 | 16 | 4 | 16 |
| Total | Σf = 100 | Σfu = 19 |
By formula,
Mean = A +
= 6 +
= 6 +
= 6 + 0.76
= 6.76
Hence, mean = 6.76
Using the information given in the adjoining histogram, calculate the mean correct to one decimal place.

Answer
We construct the following table :
| Class interval | Class mark (yi) | Frequency (fi) | fiyi |
|---|---|---|---|
| 20 - 30 | 25 | 3 | 75 |
| 30 - 40 | 35 | 5 | 175 |
| 40 - 50 | 45 | 12 | 540 |
| 50 - 60 | 55 | 9 | 495 |
| 60 - 70 | 65 | 4 | 260 |
| Total | 33 | 1545 |
∴ Mean = = 46.8
Hence, mean of the following distribution is 46.8
A student scored the following marks in 11 questions of a question paper :
3, 4, 7, 2, 5, 6, 1, 8, 2, 5, 7.
Find the median marks.
Answer
On arranging the marks in ascending order, we get
1, 2, 2, 3, 4, 5, 5, 6, 7, 7, 8.
Here, n (no. of observations) = 11, which is odd.
6th observation = 5.
Hence, the median marks are 5.
For the following set of numbers, find the median :
10, 75, 3, 81, 17, 27, 4, 48, 12, 47, 9, 15.
Answer
On arranging the numbers in ascending order we get,
3, 4, 9, 10, 12, 15, 17, 27, 47, 48, 75, 81.
Here, n (no. of observations) = 12, which is even.
Hence, median = 16.
Calculate the mean and the median of the numbers : 2, 1, 0, 3, 1, 2, 3, 4, 3, 5.
Answer
On arranging the numbers in ascending order we get,
0, 1, 1, 2, 2, 3, 3, 3, 4, 5.
Sum of terms = 0 + 1 + 1 + 2 + 2 + 3 + 3 + 3 + 4 + 5 = 24.
By definition,
Here, n (no. of observations) = 10, which is even.
Hence, mean = 2.4 and median = 2.5
The median of the observations 11, 12, 14, (x - 2), (x + 4), (x + 9), 32, 38, 47 arranged in ascending order is 24. Find the value of x and hence find the mean.
Answer
Observations arranged in ascending order are :
11, 12, 14, (x - 2), (x + 4), (x + 9), 32, 38, 47.
Here, n (no. of observations) = 9, which is odd.
Given, median = 24 = 5th observation = x + 4.
⇒ 24 = x + 4
⇒ x = 24 - 4 = 20.
Putting the value of x in observations :
11, 12, 14, 18, 24, 29, 32, 38, 47.
Sum of terms = 11 + 12 + 14 + 18 + 24 + 29 + 32 + 38 + 47 = 225.
By definition,
Hence, the value of x = 20 and mean = 25.
The mean of the numbers 1, 7, 5, 3, 4, 4 is m. The numbers 3, 2, 4, 2, 3, 3, p have mean m - 1 and median q. Find (i) p (ii) q (iii) the mean of p and q.
Answer
(i) Given, the mean of the numbers 1, 7, 5, 3, 4, 4 is m.
Sum of terms = 1 + 7 + 5 + 3 + 4 + 4 = 24.
By definition,
Given, the mean of the numbers 3, 2, 4, 2, 3, 3, p is (m - 1) i.e. 3.
Sum of terms = 3 + 2 + 4 + 2 + 3 + 3 + p = 17 + p.
By definition,
Hence, the value of p is 4.
(ii) Given, the median of the numbers 3, 2, 4, 2, 3, 3, 4 is q.
Arranging the numbers in ascending order we get,
2, 2, 3, 3, 3, 4, 4.
Here, n (no. of observations ) = 7, which is odd.
Given, median = q = 4th observation = 3.
⇒ q = 3.
Hence, the value of q is 3.
(iii) Mean of p and q i.e. 4 and 3 is,
Hence, mean of p and q is 3.5
Find the median for the following distribution:
| Wages per day (in ₹) | No. of workers |
|---|---|
| 380 | 14 |
| 450 | 8 |
| 480 | 7 |
| 550 | 10 |
| 620 | 6 |
| 650 | 2 |
Answer
The given variates (wages) are already in ascending order. We construct the cumulative frequency table as under :
| Wages per day (in ₹) | Frequency (No. of workers) | Cumulative frequency (fi) |
|---|---|---|
| 380 | 14 | 14 |
| 450 | 8 | 22 |
| 480 | 7 | 29 |
| 550 | 10 | 39 |
| 620 | 6 | 45 |
| 680 | 2 | 47 |
Here, n (total no. of workers) = 47, which is odd.
All observations from 23rd to 29th are equal, each = 480.
Median = ₹480
Hence, median = ₹480.
Marks obtained by 70 students are given below :
| Marks | No. of students |
|---|---|
| 20 | 8 |
| 70 | 12 |
| 50 | 18 |
| 60 | 6 |
| 75 | 9 |
| 90 | 5 |
| 40 | 12 |
Calculate the median marks.
Answer
On arranging the given variates (marks) in ascending order, we construct the cumulative frequency table as under :
| Variate (Marks) | Frequency (No. of students) | Cumulative frequency |
|---|---|---|
| 20 | 8 | 8 |
| 40 | 12 | 20 |
| 50 | 18 | 38 |
| 60 | 6 | 44 |
| 70 | 12 | 56 |
| 75 | 9 | 65 |
| 90 | 5 | 70 |
Here, n (total no. of students) = 70, which is even.
All observations from 21st to 38th are equal, each = 50.
Hence, median
Hence, median marks = 50.
Calculate the mean and the median for the following distribution :
| Number | Frequency |
|---|---|
| 5 | 1 |
| 10 | 2 |
| 15 | 5 |
| 20 | 6 |
| 25 | 3 |
| 30 | 2 |
| 35 | 1 |
Answer
The given numbers are already in ascending order. We construct the cumulative frequency table as under :
| Number (fi) | Frequency (xi) | Cumulative frequency | fixi |
|---|---|---|---|
| 5 | 1 | 1 | 5 |
| 10 | 2 | 3 | 20 |
| 15 | 5 | 8 | 75 |
| 20 | 6 | 14 | 120 |
| 25 | 3 | 17 | 75 |
| 30 | 2 | 19 | 60 |
| 35 | 1 | 20 | 35 |
| Total | 20 | 390 |
Here, n (no. of observations) = 20, which is even.
All observations from 9th to 14th are equal, each = 20.
Hence, median
Now calculating mean,
Hence, mean = 19.5 and median = 20.
The daily output of 19 workers are :
41, 21, 38, 27, 31, 45, 23, 26, 29, 30, 28, 25, 35, 42, 47, 53, 29, 31, 35.
Find :
(i) the median
(ii) lower quartile
(iii) upper quartile
(iv) inter quartile range
Answer
On arranging the given wages in ascending order we get,
21, 23, 25, 26, 27, 28, 29, 29, 30, 31, 31, 35, 35, 38, 41, 42, 45, 47, 53.
Here, n (no. of observations) = 19, which is odd.
(i) As n is odd,
∴ Median = 10th observation = 31.
Hence, median = 31.
(ii) As n is odd,
∴ Lower quartile (Q1) = 5th observation = 27.
Hence, lower quartile = 27.
(iii) As n is odd,
∴ Upper quartile (Q3) = 15th observation = 41.
Hence, upper quartile = 41.
(iv) Inter quartile range = Q3 - Q1 = 41 - 27 = 14.
Hence, inter quartile range = 14.
From the following frequency distribution, find :
(i) the median
(ii) lower quartile
(iii) upper quartile
(iv) inter quartile range
| Variate | Frequency |
|---|---|
| 15 | 4 |
| 18 | 6 |
| 20 | 8 |
| 22 | 9 |
| 25 | 7 |
| 27 | 8 |
| 30 | 6 |
Answer
The given variates are already in ascending order. We construct the cumulative frequency table as under
| Variate | Frequency | Cumulative frequency |
|---|---|---|
| 15 | 4 | 4 |
| 18 | 6 | 10 |
| 20 | 8 | 18 |
| 22 | 9 | 27 |
| 25 | 7 | 34 |
| 27 | 8 | 42 |
| 30 | 6 | 48 |
Here, n (no. of observations) = 48, which is even.
(i) As n is even,
All observations from 19th to 27th are equal, each = 22.
Hence, median
Hence, median = 22.
(ii) As n is even,
∴ Lower quartile (Q1) = 12th observation = 20.
Hence, lower quartile = 20.
(iii) As n is even,
∴ Upper quartile (Q3) = 36th observation = 27.
Hence, upper quartile = 27.
(iv) Inter quartile range = Q3 - Q1 = 27 - 20 = 7.
Hence, inter quartile range = 7.
For the following frequency distribution, find :
(i) the median
(ii) lower quartile
(iii) upper quartile
| Variate | Frequency |
|---|---|
| 25 | 3 |
| 31 | 8 |
| 34 | 10 |
| 40 | 15 |
| 45 | 10 |
| 48 | 9 |
| 50 | 6 |
| 60 | 2 |
Answer
The given numbers are already in ascending order. We construct the cumulative frequency table as under
| Variate | Frequency | Cumulative frequency |
|---|---|---|
| 25 | 3 | 3 |
| 31 | 8 | 11 |
| 34 | 10 | 21 |
| 40 | 15 | 36 |
| 45 | 10 | 46 |
| 48 | 9 | 55 |
| 50 | 6 | 61 |
| 60 | 2 | 63 |
Here, n (no. of observations) = 63, which is odd.
(i) As n is odd,
∴ Median = 32nd observation = 40.
Hence, median = 40.
(ii) As n is odd,
∴ Lower quartile (Q1) = 16th observation = 34.
Hence, lower quartile = 34.
(iii) As n is odd,
∴ Upper quartile (Q3) = 48th observation = 48.
Hence, upper quartile = 48.
Find the mode of the following sets of numbers :
(i) 5, 7, 6, 8, 9, 0, 6, 8, 1, 8
(ii) 9, 0, 2, 8, 5, 3, 5, 4, 1, 5, 2, 7
Answer
(i) In the given data : 5, 7, 6, 8, 9, 0, 6, 8, 1, 8
8 is repeated more number of times than any other number,
∴ mode = 8.
(ii) In the given data : 9, 0, 2, 8, 5, 3, 5, 4, 1, 5, 2, 7
5 is repeated more number of times than any other number,
∴ mode = 5.
Find the mean, median and mode of the following distribution :
8, 10, 7, 6, 10, 11, 6, 13, 10.
Answer
Arithmetic mean (A.M.) =
Sum of terms = 8 + 10 + 7 + 6 + 10 + 11 + 6 + 13 + 10 = 81.
∴ Mean = 9.
On arranging the marks in ascending order, we get
6, 6, 7, 8, 10, 10, 10, 11, 13.
Here, n (no. of observations) = 9, which is odd.
5th observation = 10.
∴ Median = 10.
In the given data : 8, 10, 7, 6, 10, 11, 6, 13, 10
10 is repeated more number of times than any other number,
∴ Mode = 10.
Hence, mean = 9, median = 10 and mode = 10.
Calculate the mean, median and the mode of the following numbers :
3, 1, 5, 6, 3, 4, 5, 3, 7, 2.
Answer
Arithmetic mean (A.M.) =
Sum of terms = 3 + 1 + 5 + 6 + 3 + 4 + 5 + 3 + 7 + 2 = 39
∴ Mean = 3.9
On arranging the numbers in ascending order we get,
1, 2, 3, 3, 3, 4, 5, 5, 6, 7.
Here, n (no. of observations) = 10, which is even.
∴ Median = 3.5
In the given data : 3, 1, 5, 6, 3, 4, 5, 3, 7, 2.
3 is repeated more number of times than any other number,
∴ Mode = 3.
Hence, mean = 3.9, median = 3.5 and mode = 3.
The marks of 10 students of a class in an examination arranged in ascending order are as follows :
13, 35, 43, 46, x, x + 4, 55, 61, 71, 80.
If the median marks is 48, find the value of x. Hence, find the mode of the given data.
Answer
Here, n (no. of observations) = 10, which is even.
Given, median marks = 48.
∴ x + 2 = 48
⇒ x = 46.
Putting value of x in data we get,
13, 35, 43, 46, 46, 50, 55, 61, 71, 80.
In the given data 46 is repeated more number of times than any other number.
Hence, the value of x = 46 and mode = 46.
Find the mode and median of the following frequency distribution :
| x | f |
|---|---|
| 10 | 1 |
| 11 | 4 |
| 12 | 7 |
| 13 | 5 |
| 14 | 9 |
| 15 | 3 |
Answer
The variates are already in ascending order. We construct the cumulative frequency table as under :
| x | f | Cumulative frequency (C.F.) |
|---|---|---|
| 10 | 1 | 1 |
| 11 | 4 | 5 |
| 12 | 7 | 12 |
| 13 | 5 | 17 |
| 14 | 9 | 26 |
| 15 | 3 | 29 |
Total number of observations = 29, which is odd.
All observations from 13th to 17th are equal, each = 13, so median = 13.
As the variate 14 has maximum frequency 9, so mode = 14.
Hence, median = 13 and mode = 14.
In a class of 40 students marks obtained by the students in a class test (out of 10) are given below :
| Marks | Number of students |
|---|---|
| 1 | 1 |
| 2 | 2 |
| 3 | 3 |
| 4 | 3 |
| 5 | 6 |
| 6 | 10 |
| 7 | 5 |
| 8 | 4 |
| 9 | 3 |
| 10 | 3 |
Calculate the following for the given distribution :
(i) median
(ii) mode.
Answer
(i) The variates are already in ascending order. We construct the cumulative frequency table as under :
| Marks | Number of students | Cumulative frequency (C.F.) |
|---|---|---|
| 1 | 1 | 1 |
| 2 | 2 | 3 |
| 3 | 3 | 6 |
| 4 | 3 | 9 |
| 5 | 6 | 15 |
| 6 | 10 | 25 |
| 7 | 5 | 30 |
| 8 | 4 | 34 |
| 9 | 3 | 37 |
| 10 | 3 | 40 |
Total number of observations = 40, which is even.
All observations from 16th to 25th are equal, each = 6.
Hence, median
Hence, median = 6.
(ii) As the variate 6 has maximum frequency 10, so mode = 6.
Hence, mode = 6.
The marks obtained by 30 students in a class assessment of 5 marks is given below :
| Marks | No. of students |
|---|---|
| 0 | 1 |
| 1 | 3 |
| 2 | 6 |
| 3 | 10 |
| 4 | 5 |
| 5 | 5 |
Calculate the mean, median and mode of the above distribution.
Answer
The variates (marks) are already in ascending order. We construct the cumulative frequency table as under :
| Marks (xi) | No. of students (fi) | Cumulative frequency (C.F.) | fixi |
|---|---|---|---|
| 0 | 1 | 1 | 0 |
| 1 | 3 | 4 | 3 |
| 2 | 6 | 10 | 12 |
| 3 | 10 | 20 | 30 |
| 4 | 5 | 25 | 20 |
| 5 | 5 | 30 | 25 |
| Total | 30 | 90 |
Mean = = 3.
Total number of observations = 30, which is even.
All observations from 11th to 20th are equal, each = 3.
Hence, median
As the variate 3 has maximum frequency 10, so mode = 3.
Hence, mean = 3, median = 3 and mode = 3.
The distribution table given below shows the marks obtained by 25 students in an aptitude test. Find the mean, median and mode of the distribution.
| Marks obtained | No. of students |
|---|---|
| 5 | 3 |
| 6 | 9 |
| 7 | 6 |
| 8 | 4 |
| 9 | 2 |
| 10 | 1 |
Answer
The variates (marks) are already in ascending order. We construct the cumulative frequency table as under :
| Marks (xi) | No. of students (fi) | Cumulative frequency (C.F.) | fixi |
|---|---|---|---|
| 5 | 3 | 3 | 15 |
| 6 | 9 | 12 | 54 |
| 7 | 6 | 18 | 42 |
| 8 | 4 | 22 | 32 |
| 9 | 2 | 24 | 18 |
| 10 | 1 | 25 | 10 |
| Total | 25 | 171 |
Mean = = 6.84.
Total number of observations = 25, which is odd.
All observations from 13th to 18th are equal, each = 7, so median = 7.
As the variate 6 has maximum frequency 9, so mode = 6.
Hence, mean = 6.84, median = 7 and mode = 6.
The following table gives the weekly wages (in ₹) of workers in a factory:
| Weekly wages (in ₹) | No. of workers |
|---|---|
| 500 - 550 | 5 |
| 550 - 600 | 20 |
| 600 - 650 | 10 |
| 650 - 700 | 10 |
| 700 - 750 | 9 |
| 750 - 800 | 6 |
| 800 - 850 | 12 |
| 850 - 900 | 8 |
Calculate:
(i) the mean.
(ii) the modal class.
(iii) the number of workers getting weekly wages below ₹800
(iv) the number of workers getting ₹650 or more but less than ₹850 as weekly wages.
Answer
(i) We construct the following table :
| Weekly wages (xi) | No. of workers (fi) | Class mark (ui) | Cumulative frequency (C.F.) | fi.ui |
|---|---|---|---|---|
| 500 - 550 | 5 | 525 | 5 | 2625 |
| 550 - 600 | 20 | 575 | 25 | 11500 |
| 600 - 650 | 10 | 625 | 35 | 6250 |
| 650 - 700 | 10 | 675 | 45 | 6750 |
| 700 - 750 | 9 | 725 | 54 | 6525 |
| 750 - 800 | 6 | 775 | 60 | 4650 |
| 800 - 850 | 12 | 825 | 72 | 9900 |
| 850 - 900 | 8 | 875 | 80 | 7000 |
| Total | Σfi = 80 | Σfiui = 55200 |
By formula,
Hence, mean = ₹ 690.
(ii) The class 550 - 600 has maximum frequency 20.
Hence, modal class = 550-600.
(iii) From table,
The number of workers getting weekly wages below ₹800 = 60.
(iv) From table,
The number of workers getting ₹650 or more but less than ₹850 as weekly wages = 72 - 35 = 37.
Draw a histogram for the following frequency distribution and find the mode from the graph :
| Class | Frequency |
|---|---|
| 0 - 5 | 2 |
| 5 - 10 | 5 |
| 10 - 15 | 18 |
| 15 - 20 | 14 |
| 20 - 25 | 8 |
| 25 - 30 | 5 |
Answer
Steps :
- Take 1 cm along x-axis = 5 units and 1 cm along y-axis = 4 units.
- Construct rectangles corresponding to the given data.
- In highest rectangle, draw two st. lines AC and BD from corners of the rectangles on either side of the highest rectangle to the opposite corners of the highest rectangle. Let P be the point of intersection of AC and BD.
- Through P, draw a vertical line to meet the x-axis at M. The abscissa of the point M represents 14.

Hence, the required mode = 14.
A mathematics aptitude test of 50 students was recorded as follows :
| Marks | No. of students |
|---|---|
| 50 - 60 | 4 |
| 60 - 70 | 8 |
| 70 - 80 | 14 |
| 80 - 90 | 19 |
| 90 - 100 | 5 |
Draw a histogram for the above data using a graph paper and locate the mode.
Answer
Steps :
- Take 1 cm along x-axis = 10 marks and 1 cm along y-axis = 4 (students).
- Since, the scale on x-axis starts at 50, a break (zig-zag curve) is shown near the origin along x-axis to indicate that the graph is drawn to scale beginning at 50 and not at origin itself.
- Construct rectangles corresponding to the given data.
- In highest rectangle, draw two st. lines AC and BD from corners of the rectangles on either side of the highest rectangle to the opposite corners of the highest rectangle. Let P be the point of intersection of AC and BD.
- Through P, draw a vertical line to meet the x-axis at M. The abscissa of the point M represents 82.5.

Hence, the required mode = 82.5
Draw a histogram and estimate the mode for the following frequency distribution :
| Classes | Frequency |
|---|---|
| 0 - 10 | 2 |
| 10 - 20 | 8 |
| 20 - 30 | 10 |
| 30 - 40 | 5 |
| 40 - 50 | 4 |
| 50 - 60 | 3 |
Answer
Steps :
- Take 1 cm along x-axis = 10 units and 1 cm along y-axis = 2 units.
- Construct rectangles corresponding to the given data.
- In highest rectangle, draw two st. lines AC and BD from corners of the rectangles on either side of the highest rectangle to the opposite corners of the highest rectangle. Let P be the point of intersection of AC and BD.
- Through P, draw a vertical line to meet the x-axis at M. The abscissa of the point M represents 23.

Hence, the required mode = 23.
Using a graph paper, draw a histogram for the given distribution showing the number of runs scored by 50 batsmen. Estimate the mode of the data :
| Runs scored | No. of batsmen |
|---|---|
| 3000 - 4000 | 4 |
| 4000 - 5000 | 18 |
| 5000 - 6000 | 9 |
| 6000 - 7000 | 6 |
| 7000 - 8000 | 7 |
| 8000 - 9000 | 2 |
| 9000 - 10000 | 4 |
Answer
Steps :
- Take 1 cm along x-axis = 1000 runs and 1 cm along y-axis = 4 (batsman).
- Construct rectangles corresponding to the given data.
- In highest rectangle, draw two st. lines AC and BD from corners of the rectangles on either side of the highest rectangle to the opposite corners of the highest rectangle. Let P be the point of intersection of AC and BD.
- Through P, draw a vertical line to meet the x-axis at M. The abscissa of the point M represents 4600.

Hence, the required mode = 4600.
Draw a histogram for the given data, using a graph paper:
| Weekly Wages (in ₹) | No. of people |
|---|---|
| 3000 - 4000 | 4 |
| 4000 - 5000 | 9 |
| 5000 - 6000 | 18 |
| 6000 - 7000 | 6 |
| 7000 - 8000 | 7 |
| 8000 - 9000 | 2 |
| 9000 - 10000 | 4 |
Estimate the mode from the graph.
Answer
Steps :
Take 1 cm along x-axis = 1000 rupees and 1 cm along y-axis = 2 (No. of people).
Construct rectangles corresponding to the given data.
In highest rectangle, draw two st. lines AD and BC from corners of the rectangles on either side of the highest rectangle to the opposite corners of the highest rectangle. Let P be the point of intersection of AD and BC.
Through P, draw a vertical line to meet the x-axis at M. The abscissa of the point M represents 5400.
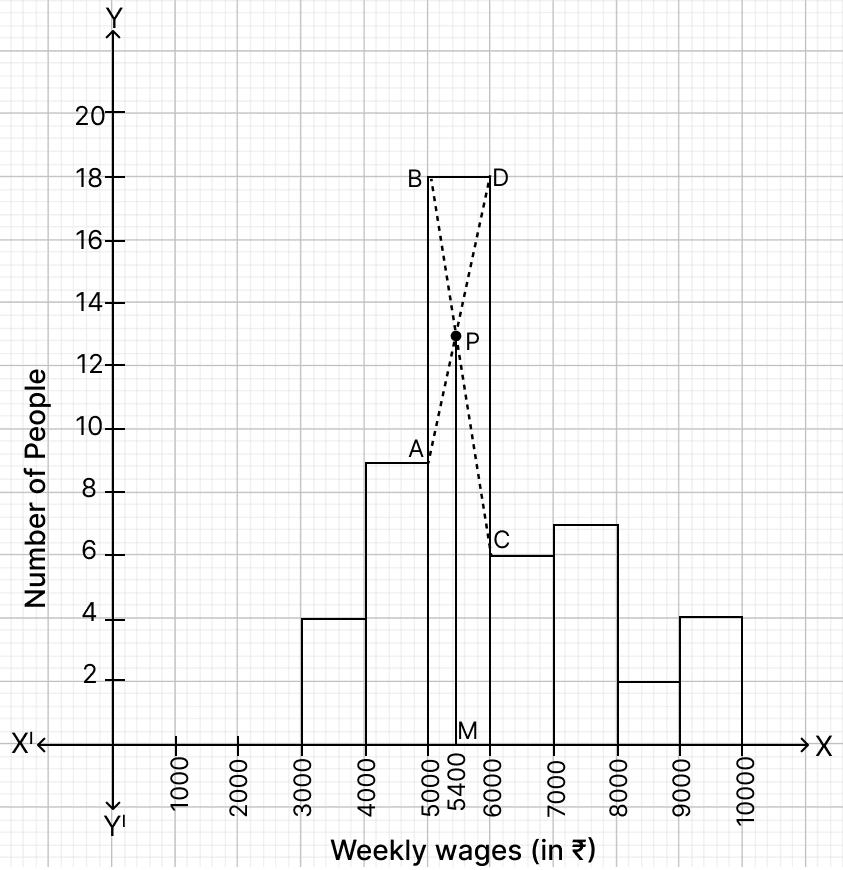
Hence, mode = ₹ 5,400.
Use a graph paper for this question. The daily pocket expenses of 200 students in a school are given below :
| Pocket expenses (in ₹) | No. of students (frequency) |
|---|---|
| 0 - 5 | 10 |
| 5 - 10 | 14 |
| 10 - 15 | 28 |
| 15 - 20 | 42 |
| 20 - 25 | 50 |
| 25 - 30 | 30 |
| 30 - 35 | 14 |
| 35 - 40 | 12 |
Draw a histogram representing the above distribution and estimate the mode from the graph.
Answer
Steps :
- Take 1 cm along x-axis = ₹5 and 1 cm along y-axis = 5 students.
- Construct rectangles corresponding to the given data.
- In highest rectangle, draw two st. lines AC and BD from corners of the rectangles on either side of the highest rectangle to the opposite corners of the highest rectangle. Let P be the point of intersection of AC and BD.
- Through P, draw a vertical line to meet the x-axis at M. The abscissa of the point M represents ₹21.50.

Hence, the required mode = ₹21.50.
Draw a histogram for the following distribution :
| Wt. (in kg) | No. of students |
|---|---|
| 40 - 44 | 2 |
| 45 - 49 | 8 |
| 50 - 54 | 12 |
| 55 - 59 | 10 |
| 60 - 64 | 6 |
| 65 - 69 | 4 |
Hence, estimate the modal weight.
Answer
Steps :
- The given frequency distribution is discontinuous, to convert it into continuous distribution,
Adjustment factor = = 0.5
We construct the continuous frequency table for the given data :
| Classes before adjustment | Classes after adjustment | No. of students |
|---|---|---|
| 40 - 44 | 39.5 - 44.5 | 2 |
| 45 - 49 | 44.5 - 49.5 | 8 |
| 50 - 54 | 49.5 - 54.5 | 12 |
| 55 - 59 | 54.5 - 59.5 | 10 |
| 60 - 64 | 59.5 - 64.5 | 6 |
| 65 - 69 | 64.5 - 69.5 | 4 |
Take 2 cm along x-axis = 5 kg and 1 cm along y-axis = 2 (students).
Since, the scale on x-axis starts at 39.5, a break (zig-zag curve) is shown near the origin along x-axis to indicate that the graph is drawn to scale beginning at 39.5 and not at origin itself.
Construct rectangles corresponding to the given data.
In highest rectangle, draw two st. lines AC and BD from corners of the rectangles on either side of the highest rectangle to the opposite corners of the highest rectangle. Let P be the point of intersection of AC and BD.
Through P, draw a vertical line to meet the x-axis at M. The abscissa of the point M represents 52.75 kg.
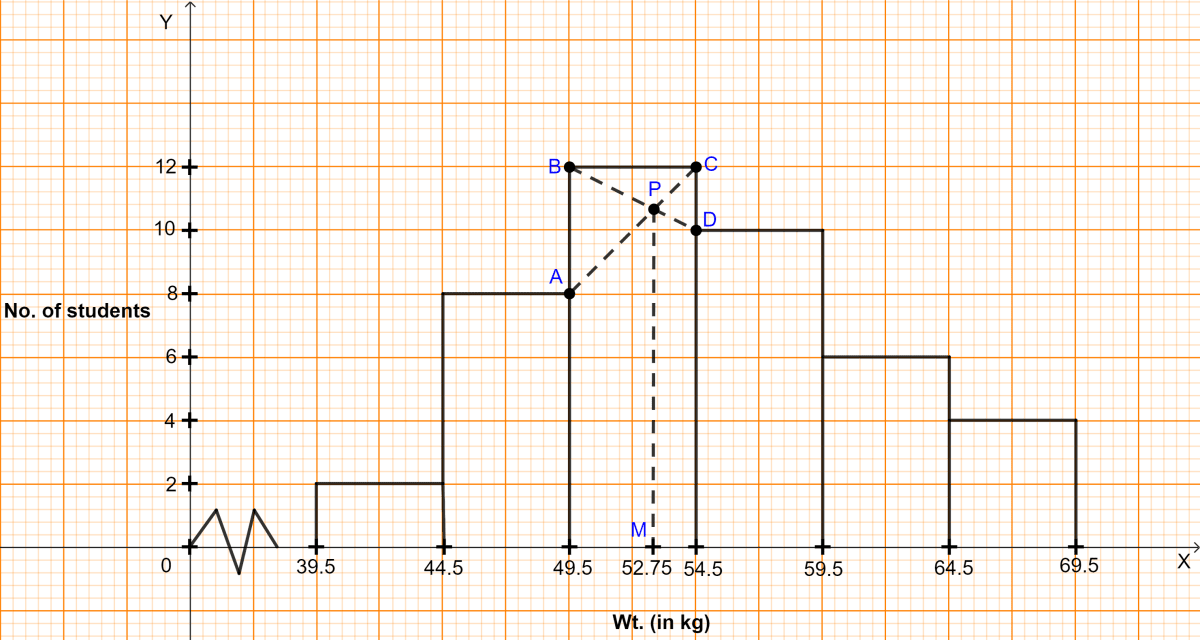
Hence, the required mode = 52.75 kg.
Find the mode of the following distribution by drawing a histogram.
| Mid value | Frequency |
|---|---|
| 12 | 20 |
| 18 | 12 |
| 24 | 8 |
| 30 | 24 |
| 36 | 16 |
| 42 | 8 |
| 48 | 12 |
Also state the modal class.
Answer
Size of each class = difference between two consecutive mid-values = 18 - 12 = 6.
Constructing the table as under :
| Mid value | Class | Frequency |
|---|---|---|
| 12 | 9 - 15 | 20 |
| 18 | 15 - 21 | 12 |
| 24 | 21 - 27 | 8 |
| 30 | 27 - 33 | 24 |
| 36 | 33 - 39 | 16 |
| 42 | 39 - 45 | 8 |
| 48 | 45 - 51 | 12 |
Steps :
Take 1 cm along x-axis = 6 units and 1 cm along y-axis = 4 units.
Since, the scale on x-axis starts at 9, a break (zig-zag curve) is shown near the origin along x-axis to indicate that the graph is drawn to scale beginning at 9 and not at origin itself.
Construct rectangles corresponding to the given data.
In highest rectangle, draw two st. lines AC and BD from corners of the rectangles on either side of the highest rectangle to the opposite corners of the highest rectangle. Let P be the point of intersection of AC and BD.
Through P, draw a vertical line to meet the x-axis at M. The abscissa of the point M represents 30.5.
∴ Mode = 30.5
As the class 27 - 33 has the highest frequency, hence modal class = 27 - 33.

Hence, the required mode = 30.5 and modal class = 27 - 33.
The table given below shows the runs scored by a cricket team during the overs of a match.
| Overs | Runs scored |
|---|---|
| 20-30 | 37 |
| 30-40 | 45 |
| 40-50 | 40 |
| 50-60 | 60 |
| 60-70 | 51 |
| 70-80 | 35 |
Use graph sheet for this question. Take 2 cm = 10 overs along one axis and 2 cm = 10 runs along the other axis.
(a) Draw a histogram representing the above distribution.
(b) Estimate the modal runs scored.
Answer
Steps :
Take 2 cm along x-axis = 10 overs and 1 cm along y-axis = 10 runs.
Since, the scale on x-axis starts at 20, a break (zig-zag curve) is shown near the origin along x-axis to indicate that the graph is drawn to scale beginning at 20 and not at origin itself.
Construct rectangles corresponding to the given data.
In highest rectangle, draw two st. lines KN and LI from corners of the rectangles on either side of the highest rectangle to the opposite corners of the highest rectangle. Let Z be the point of intersection of KN and LI.
Through Z, draw a vertical line to meet the x-axis at A. The abscissa of the point A represents 57.
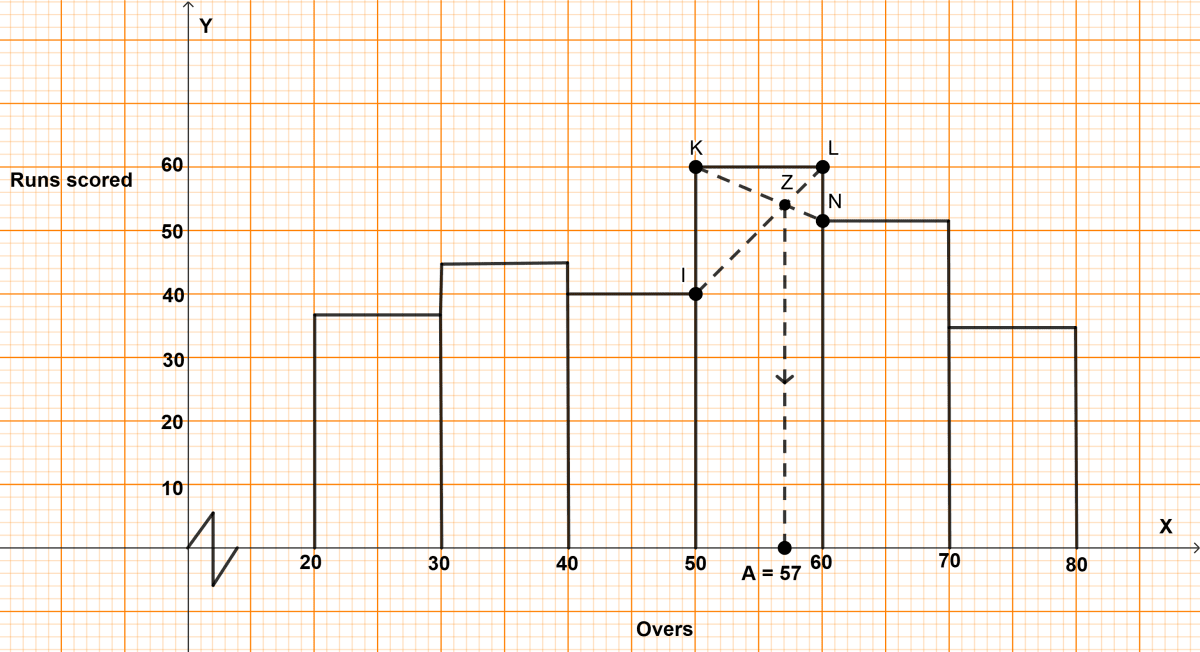
Hence, mode = 57.
Draw an ogive for the following frequency distribution :
| Height (in cm) | No. of students |
|---|---|
| 150 - 160 | 8 |
| 160 - 170 | 3 |
| 170 - 180 | 4 |
| 180 - 190 | 10 |
| 190 - 200 | 2 |
Answer
To draw an ogive :
- The cumulative frequency table for the given continuous distribution is :
| Height (in cm) | No. of students | Cumulative frequency |
|---|---|---|
| 150 - 160 | 8 | 8 |
| 160 - 170 | 3 | 11 |
| 170 - 180 | 4 | 15 |
| 180 - 190 | 10 | 25 |
| 190 - 200 | 2 | 27 |
Since, the scale on x-axis starts at 150, a kink is shown near the origin on x-axis to indicate that the graph is drawn to scale beginning at 150.
Take 2 cm along x-axis = 10 cm (height)
Take 1 cm along y-axis = 5 students

Plot the points (160, 8), (170, 11), (180, 15), (190, 25), (200, 27) representing upper class limits and the respective cumulative frequencies.
Also plot the point representing lower limit of the first class i.e. 150 - 160.Join these points by a freehand drawing.
The required ogive is shown in figure above.
Draw an ogive for the following frequency distribution :
| Class-intervals | Frequency |
|---|---|
| 1 - 10 | 3 |
| 11 - 20 | 5 |
| 21 - 30 | 8 |
| 31 - 40 | 7 |
| 41 - 50 | 6 |
| 51 - 60 | 2 |
Answer
To draw an ogive :
- The given frequency distribution is discontinuous, to convert it into continuous distribution,
Adjustment factor = (Lower limit of one class - Upper limit of previous class) / 2
The cumulative frequency table for the given data is :
| Classes before adjustment | Classes after adjustment | Frequency | Cumulative frequency |
|---|---|---|---|
| 1 - 10 | 0.5 - 10.5 | 3 | 3 |
| 11 - 20 | 10.5 - 20.5 | 5 | 8 |
| 21 - 30 | 20.5 - 30.5 | 8 | 16 |
| 31 - 40 | 30.5 - 40.5 | 7 | 23 |
| 41 - 50 | 40.5 - 50.5 | 6 | 29 |
| 51 - 60 | 50.5 - 60.5 | 2 | 31 |
Since, the scale on x-axis starts at 0.5, a kink is shown near the origin on x-axis to indicate that the graph is drawn to scale beginning at 0.5
Take 2 cm along x-axis = 10
Take 1 cm along y-axis = 5

- Plot the points (10.5, 3), (20.5, 8), (30.5, 16), (40.5, 23), (50.5, 29), (60.5, 31) representing upper class limits and the respective cumulative frequencies.
Also plot the point representing lower limit of the first class i.e. 0.5 - 10.5
- Join these points by a freehand drawing.
The required ogive is shown in figure above.
Draw a cumulative frequency curve for the following data :
| Marks obtained | No. of students |
|---|---|
| 24 - 29 | 1 |
| 29 - 34 | 2 |
| 34 - 39 | 5 |
| 39 - 44 | 6 |
| 44 - 49 | 4 |
| 49 - 54 | 3 |
| 54 - 59 | 2 |
Answer
To draw an ogive :
- The cumulative frequency table for the given continuous distribution is :
| Marks obtained | No. of students | Cumulative frequency |
|---|---|---|
| 24 - 29 | 1 | 1 |
| 29 - 34 | 2 | 3 |
| 34 - 39 | 5 | 8 |
| 39 - 44 | 6 | 14 |
| 44 - 49 | 4 | 18 |
| 49 - 54 | 3 | 21 |
| 54 - 59 | 2 | 23 |
Since, the scale on x-axis starts at 24, a kink is shown near the origin on x-axis to indicate that the graph is drawn to scale beginning at 24.
Take 1 cm along x-axis = 5 marks
Take 1 cm along y-axis = 5 (students)

- Plot the points (29, 1), (34, 3), (39, 8), (44, 14), (49, 18), (54, 21) and (59, 23) representing upper class limits and the respective cumulative frequencies.
Also plot the point representing lower limit of the first class i.e. 24 - 29.
- Join these points by a freehand drawing.
The required cumulative frequency curve is shown in figure above.
The weight of 50 workers is given below :
| Weight (in kg) | No. of workers |
|---|---|
| 50 - 60 | 4 |
| 60 - 70 | 7 |
| 70 - 80 | 11 |
| 80 - 90 | 14 |
| 90 - 100 | 6 |
| 100 - 110 | 5 |
| 110 - 120 | 3 |
Draw an ogive of the given distribution using a graph sheet. Take 2 cm = 10 kg on one axis and 2 cm = 5 workers along the other axis. Use a graph to estimate the following :
(i) the upper and lower quartiles.
(ii) if weighing 95 kg and above is considered overweight find the number of workers who are overweight.
Answer
- The cumulative frequency table for the given continuous distribution is :
| Weight (in kg) | No. of workers | Cumulative frequency |
|---|---|---|
| 50 - 60 | 4 | 4 |
| 60 - 70 | 7 | 11 |
| 70 - 80 | 11 | 22 |
| 80 - 90 | 14 | 36 |
| 90 - 100 | 6 | 42 |
| 100 - 110 | 5 | 47 |
| 110 - 120 | 3 | 50 |
Take 1 cm along x-axis = 10 kg
Take 1 cm along y-axis = 5 (workers)
Since, scale on x-axis starts at 50, a kink is shown near the origin on x-axis to indicate that the graph is drawn to scale beginning at 50.
Plot the points (60, 4), (70, 11), (80, 22), (90, 36), (100, 42), (110, 47) and (120, 50) representing upper class limits and the respective cumulative frequencies.
Also plot the point representing lower limit of the first class i.e. 50 - 60.

- Join these points by a freehand drawing.
The required ogive is shown in figure above.
(i) To find lower quartile :
Let A be the point on y-axis representing frequency = = 12.5
Through A, draw a horizontal line to meet the ogive at P. Through P, draw a vertical line to meet the x-axis at M. The abscissa of the point M represents 71 kg.
To find upper quartile :
Let B be the point on y-axis representing frequency = = 37.5
Through B, draw a horizontal line to meet the ogive at Q. Through Q, draw a vertical line to meet the x-axis at N. The abscissa of the point N represents 93 kg.
Hence, lower quartile = 71 kg and upper quartile = 93 kg.
(ii) Let O be the point on x-axis representing 95 kg. Through O draw a vertical line to meet the ogive R. Through R, draw a horizontal line to meet the y-axis at point C. The ordinate of the point C represents 39.
So, the number of people whose weight is less than 95 kg = 39. So, overweight people = 50 - 39 = 11 kg.
Hence, the number of workers who are overweight are 11.
The table shows the distribution of scores obtained by 160 shooters in a shooting competition. Use a graph sheet and draw an ogive for the distribution.
(Take 2 cm = 10 scores on the x-axis and 2 cm = 20 shooters on the y-axis)
| Scores | No. of shooters |
|---|---|
| 0 - 10 | 9 |
| 10 - 20 | 13 |
| 20 - 30 | 20 |
| 30 - 40 | 26 |
| 40 - 50 | 30 |
| 50 - 60 | 22 |
| 60 - 70 | 15 |
| 70 - 80 | 10 |
| 80 - 90 | 8 |
| 90 - 100 | 7 |
Use your graph to estimate the following :
(i) The median.
(ii) The inter quartile range.
(iii) The number of shooters who obtained a score of more than 85%.
Answer
- The cumulative frequency table for the given continuous distribution is :
| Scores | No. of shooters | Cumulative frequency |
|---|---|---|
| 0 - 10 | 9 | 9 |
| 10 - 20 | 13 | 22 |
| 20 - 30 | 20 | 42 |
| 30 - 40 | 26 | 68 |
| 40 - 50 | 30 | 98 |
| 50 - 60 | 22 | 120 |
| 60 - 70 | 15 | 135 |
| 70 - 80 | 10 | 145 |
| 80 - 90 | 8 | 153 |
| 90 - 100 | 7 | 160 |
Take 2 cm along x-axis = 10 scores
Take 2 cm along y-axis = 20 (shooters)
Plot the points (10, 9), (20, 22), (30, 42), (40, 68), (50, 98), (60, 120), (70, 135), (80, 145), (90, 153) and (100, 160) representing upper class limits and the respective cumulative frequencies.
Also plot the point representing lower limit of the first class i.e. 0 - 10.Join these points by a freehand drawing.
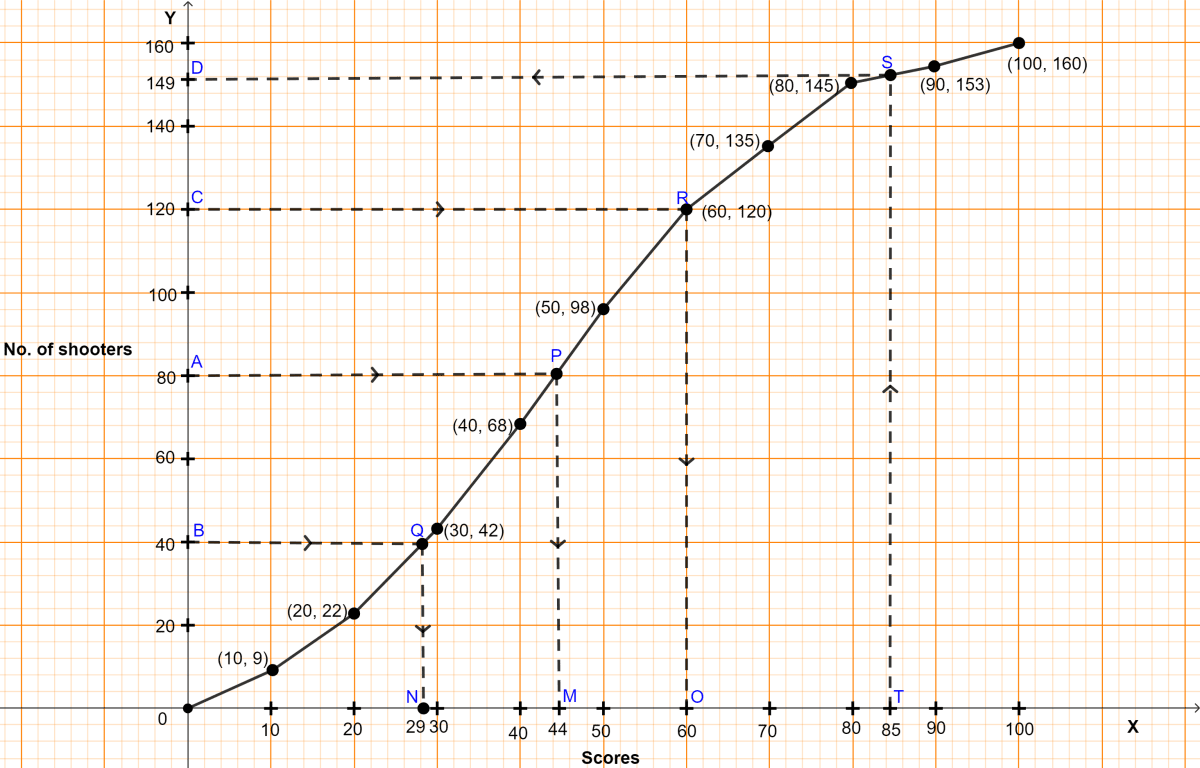
The required ogive is shown in figure above.
(i) Here, n (no. of students) = 160.
To find the median :
Let A be the point on y-axis representing frequency = = 80.
Through A draw a horizontal line to meet the ogive at P. Through P, draw a vertical line to meet the x-axis at M. The abscissa of the point M represents 44.
Hence, the required median score = 44.
(ii) To find lower quartile :
Let B be the point on y-axis representing frequency = = 40
Through B, draw a horizontal line to meet the ogive at Q. Through Q, draw a vertical line to meet the x-axis at N. The abscissa of the point N represents 29.
To find upper quartile :
Let C be the point on y-axis representing frequency = = 120
Through C, draw a horizontal line to meet the ogive at R. Through R, draw a vertical line to meet the x-axis at O. The abscissa of the point O represents 60.
Inter quartile range = Upper quartile - Lower quartile = 60 - 29 = 31.
Hence, the inter quartile range = 31 scores.
(iii) Total marks = 100.
So, more than 85% marks mean more than 85 marks.
Let T be the point on x-axis representing marks = 85.
Through T, draw a vertical line to meet the ogive at S. Through S, draw a horizontal line to meet the y-axis at D. The ordinate of the point D represents 149.
Students who have scored less than 85% = 149.
So, students scoring more than 85% = Total students - Students who have scored less = 160 - 149 = 11.
Hence, there are 11 shooters who obtained a score of more than 85%.
The daily wages of 80 workers in a project are given below :
| Wages (in ₹) | No. of workers |
|---|---|
| 400 - 450 | 2 |
| 450 - 500 | 6 |
| 500 - 550 | 12 |
| 550 - 600 | 18 |
| 600 - 650 | 24 |
| 650 - 700 | 13 |
| 700 - 750 | 5 |
Use a graph paper to draw an ogive for the above distribution. (Use a scale of 2 cm = ₹ 50 on x-axis and 2 cm = 10 workers on y-axis). Use your ogive to estimate :
(i) the median wage of the workers.
(ii) the lower quartile wage of the workers.
(iii) the number of workers who earn more than ₹625 daily.
Answer
- The cumulative frequency table for the given continuous distribution is :
| Wages (in ₹) | No. of workers | Cumulative frequency |
|---|---|---|
| 400 - 450 | 2 | 2 |
| 450 - 500 | 6 | 8 |
| 500 - 550 | 12 | 20 |
| 550 - 600 | 18 | 38 |
| 600 - 650 | 24 | 62 |
| 650 - 700 | 13 | 75 |
| 700 - 750 | 5 | 80 |
Take 2 cm along x-axis = 50 rupees
Take 1 cm along y-axis = 10 workers
Since, scale on x-axis starts at 400, a kink is shown near the origin on x-axis to indicate that the graph is drawn to scale beginning at 400.
Plot the points (450, 2), (500, 8), (550, 20), (600, 38), (650, 62), (700, 75) and (750, 80) representing upper class limits and the respective cumulative frequencies.
Also plot the point representing lower limit of the first class i.e. 400 - 450.Join these points by a freehand drawing.
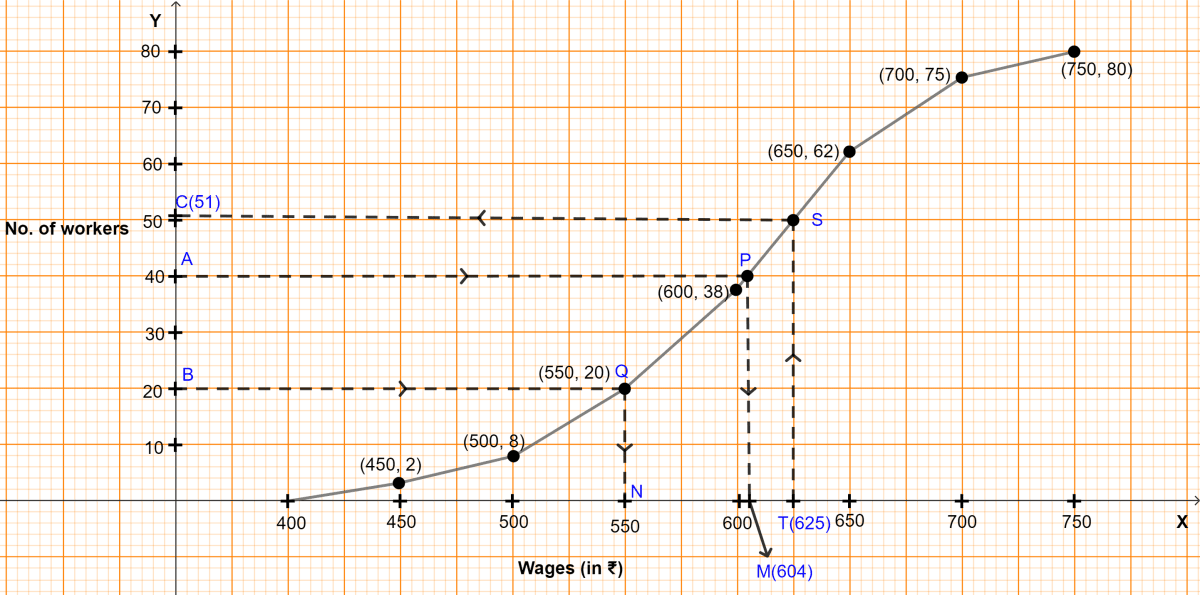
The required ogive is shown in figure above.
(i) Here, n (no. of students) = 80.
To find the median :
Let A be the point on y-axis representing frequency = = 40.
Through A draw a horizontal line to meet the ogive at P. Through P, draw a vertical line to meet the x-axis at M. The abscissa of the point M represents 604.
Hence, the required median wage = ₹604.
(ii) To find lower quartile :
Let B be the point on y-axis representing frequency = = 20
Through B, draw a horizontal line to meet the ogive at Q. Through Q, draw a vertical line to meet the x-axis at N. The abscissa of the point N represents 550.
Hence, lower quartile wage = ₹550.
(iii) Let T be the point on x-axis representing wage = ₹625.
Through T, draw a vertical line to meet the ogive at S. Through S, draw a horizontal line to meet the y-axis at C. The ordinate of the point C represents 51.
Workers who earn less than ₹625 = 51.
So, workers earning more than ₹625 = Total workers - workers who earn less than ₹625 = 80 - 51 = 29.
Hence, there are 29 workers earning more more than ₹625 daily.
Marks obtained by 200 students in an examination are given below :
| Marks | No. of students |
|---|---|
| 0 - 10 | 5 |
| 10 - 20 | 11 |
| 20 - 30 | 10 |
| 30 - 40 | 20 |
| 40 - 50 | 28 |
| 50 - 60 | 37 |
| 60 - 70 | 40 |
| 70 - 80 | 29 |
| 80 - 90 | 14 |
| 90 - 100 | 6 |
Draw an ogive for the given distribution taking 2 cm = 10 marks on one axis and 2 cm = 20 students on the other axis. Using the graph, determine :
(i) The median marks
(ii) The number of students who failed if minimum marks required to pass is 40.
(iii) If scoring 85 and more marks is considered as grade one, find the number of students who secured grade one in the examination.
Answer
- The cumulative frequency table for the given continuous distribution is :
| Marks | No. of students | Cumulative frequency |
|---|---|---|
| 0 - 10 | 5 | 5 |
| 10 - 20 | 11 | 16 |
| 20 - 30 | 10 | 26 |
| 30 - 40 | 20 | 46 |
| 40 - 50 | 28 | 74 |
| 50 - 60 | 37 | 111 |
| 60 - 70 | 40 | 151 |
| 70 - 80 | 29 | 180 |
| 80 - 90 | 14 | 194 |
| 90 - 100 | 6 | 200 |
Take 1 cm along x-axis = 10 scores
Take 1 cm along y-axis = 20 (students)
Plot the points (10, 5), (20, 16), (30, 26), (40, 46), (50, 74), (60, 111), (70, 151), (80, 180), (90, 194) and (100, 200) representing upper class limits and the respective cumulative frequencies.
Also plot the point representing lower limit of the first class i.e. 0 - 10.Join these points by a freehand drawing.
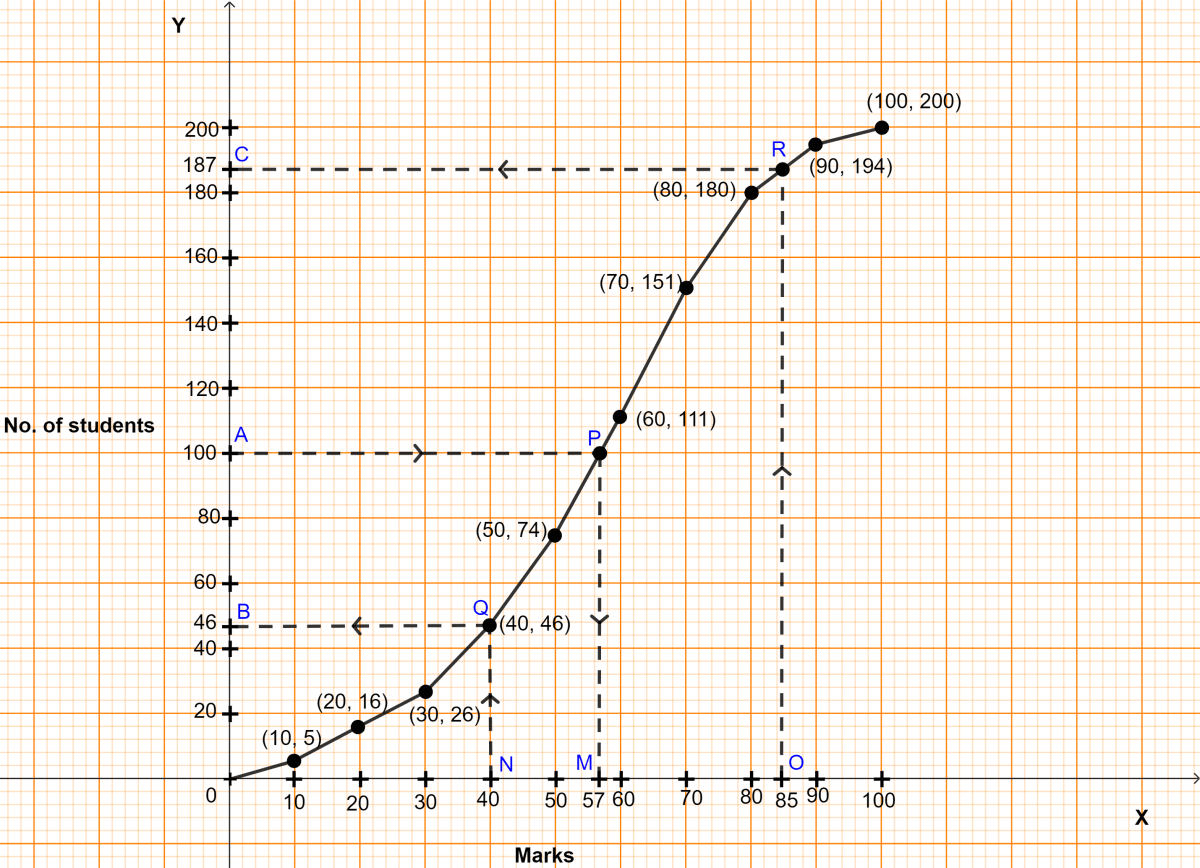
The required ogive is shown in figure above.
(i) Here, n (no. of students) = 200.
To find the median :
Let A be the point on y-axis representing frequency = = 100.
Through A draw a horizontal line to meet the ogive at P. Through P, draw a vertical line to meet the x-axis at M. The abscissa of the point M represents 57.
Hence, the required median marks = 57.
(ii) Let N be the point on x-axis representing marks = 40.
Through N, draw a vertical line to meet the ogive at Q. Through Q, draw a horizontal line to meet the y-axis at B. The ordinate of the point B represents 46.
Students who scored less than 40 = 46.
Hence, 46 students failed in the examination.
(iii) Let O be the point on x-axis representing marks = 85.
Through O, draw a vertical line to meet the ogive at R. Through R, draw a horizontal line to meet the y-axis at C. The ordinate of the point C represents 187.
Students who scored less than 85 = 187.
So, students scoring more than 85 = Total students - students scoring less than 85 = 200 - 187 = 13.
Hence, 13 students secured grade one in examination.
Use graph paper for this question.
A survey regarding height (in cm) of 60 boys belonging to class 10 of a school was conducted. The following data was recorded :
| Height (in cm) | No. of boys |
|---|---|
| 135 - 140 | 4 |
| 140 - 145 | 8 |
| 145 - 150 | 20 |
| 150 - 155 | 14 |
| 155 - 160 | 7 |
| 160 - 165 | 6 |
| 165 - 170 | 1 |
Taking 2 cm = height of 10 cm on one axis and 2 cm = 10 boys along the other axis, draw an ogive of the above distribution. Use the graph to estimate the following :
(i) median
(ii) lower quartile
(iii) if above 158 is considered as the tall boy of the class, find the number of boys in the class who are tall.
Answer
- The cumulative frequency table for the given continuous distribution is :
| Height (in cm) | No. of boys | Cumulative frequency |
|---|---|---|
| 135 - 140 | 4 | 4 |
| 140 - 145 | 8 | 12 |
| 145 - 150 | 20 | 32 |
| 150 - 155 | 14 | 46 |
| 155 - 160 | 7 | 53 |
| 160 - 165 | 6 | 59 |
| 165 - 170 | 1 | 60 |
Take 2 cm along x-axis = 5 cm
Take 2 cm along y-axis = 10 (boys)
Since, scale on x-axis starts at 135, a kink is shown near the origin on x-axis to indicate that the graph is drawn to scale beginning at 135.
Plot the points (140, 4), (145, 12), (150, 32), (155, 46), (160, 53), (165, 59) and (170, 60) representing upper class limits and the respective cumulative frequencies.
Also plot the point representing lower limit of the first class i.e. 135 - 140.Join these points by a freehand drawing.

The required ogive is shown in figure above.
(i) Here, n (no. of students) = 60.
To find the median :
Let A be the point on y-axis representing frequency = = 30.
Through A draw a horizontal line to meet the ogive at P. Through P, draw a vertical line to meet the x-axis at M. The abscissa of the point M represents 149.5.
Hence, the median height = 149.5 cm.
(ii) To find lower quartile :
Let B be the point on y-axis representing frequency = = 15.
Through B, draw a horizontal line to meet the ogive at Q. Through Q, draw a vertical line to meet the x-axis at N. The abscissa of the point N represents 146.
Hence, lower quartile = 146 cm.
(iii) Let O be the point on x-axis representing height = 158 cm.
Through O, draw a vertical line to meet the ogive at R. Through R, draw a horizontal line to meet the y-axis at C. The ordinate of the point C represents 51.
No. of boys shorter than 158 cm = 51
So, no. of boys taller than 158 cm = Total boys - boys shorter than 158 cm = 60 - 51 = 9.
Hence, there are 9 tall boys in the class.
40 students enter for a game of a shot put competition. The distance thrown in metre is recorded below:
| Distance in m | Number of students |
|---|---|
| 12 - 13 | 3 |
| 13 - 14 | 9 |
| 14 - 15 | 12 |
| 15 - 16 | 9 |
| 16 - 17 | 4 |
| 17 - 18 | 2 |
| 18 - 19 | 1 |
Use a graph paper to draw an ogive for the above distribution.
Uses scale of 2 cm = 1 m on one axis and 2 cm = 5 students on other axis.
Hence, using your graph, find:
(i) the median
(ii) the quartile
(iii) no. of student who cover a distance which is above m.
Answer
Cumulative frequency distribution table :
| Distance in m | Frequency | Cumulative frequency |
|---|---|---|
| 12 - 13 | 3 | 3 |
| 13 - 14 | 9 | 12 |
| 14 - 15 | 12 | 24 |
| 15 - 16 | 9 | 33 |
| 16 - 17 | 4 | 37 |
| 17 - 18 | 2 | 39 |
| 18 - 19 | 1 | 40 |
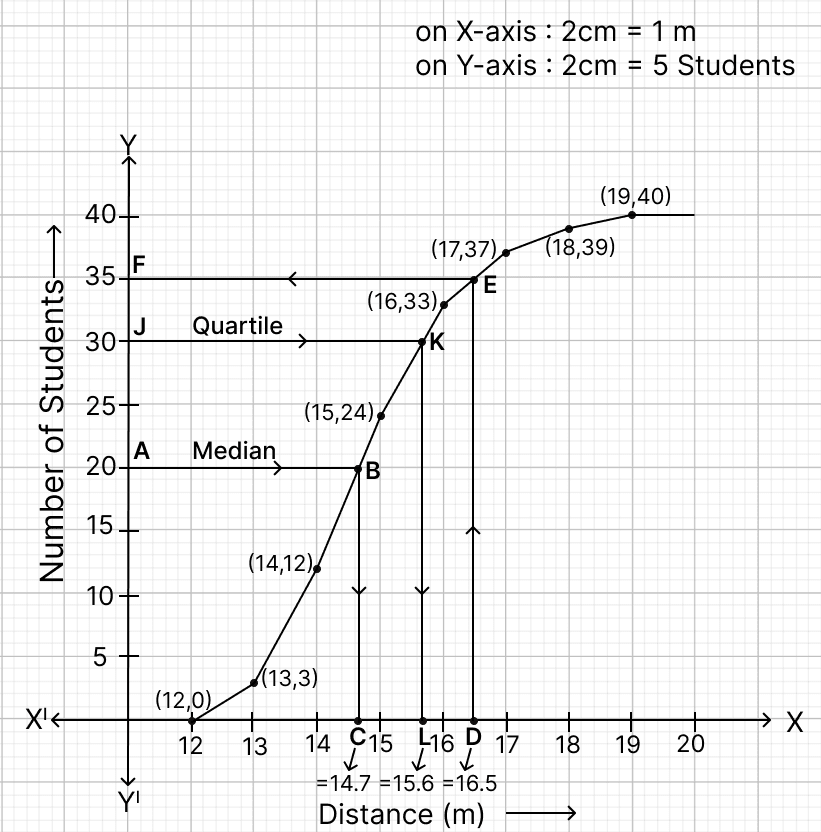
Steps of construction :
Since, the scale on x-axis starts at 12, a break (kink) is shown near the origin on x-axis to indicate that the graph is drawn to scale beginning at 12.
Take 2 cm along x-axis = 1 m.
Take 2 cm along y-axis = 5 students.
Plot the point (12, 0) as ogive starts from x-axis representing lower limit of first class.
Plot the points (13, 3), (14, 12), (15, 24), (16, 33), (17, 37), (18, 39) and (19, 40).
Join the points by a free hand curve.
(i) The total number of students is N = 40. The median position is found at .
Draw a line parallel to x-axis from point A (number of students) = 20, touching the graph at point B. From point B draw a line parallel to y-axis touching x-axis at point C.
From graph, C = 14.7
The median = 14.7 m.
(ii) Here, n = 40, which is even.
By formula,
Quartile = = 30.
Draw a line parallel to x-axis from point J (number of students) = 30, touching the graph at point K. From point K draw a line parallel to y-axis touching x-axis at point L.
From graph, L = 15.6
The quartile = 15.6 m.
(iii) Draw a line parallel to y-axis from point D (Distance) = m = 16.5 m, touching the graph at point E. From point E draw a line parallel to x-axis touching y-axis at point F.
From graph, F = 35.
It means that 35 students who cover a distance either less or equal to m.
Number of student who cover a distance which is above m = 40 - 35 = 5.
Number of students who cover a distance above m = 5.
The marks obtained by 100 students in a Mathematics test are given below :
| Marks | No. of students |
|---|---|
| 0 - 10 | 3 |
| 10 - 20 | 7 |
| 20 - 30 | 12 |
| 30 - 40 | 17 |
| 40 - 50 | 23 |
| 50 - 60 | 14 |
| 60 - 70 | 9 |
| 70 - 80 | 6 |
| 80 - 90 | 5 |
| 90 - 100 | 4 |
Draw an ogive on a graph sheet and from it determine the :
(i) median
(ii) lower quartile
(iii) number of students who obtained more than 85% marks in the test
(iv) number of students who did not pass in the test if the pass percentage was 35.
Answer
- The cumulative frequency table for the given continuous distribution is :
| Marks | No. of students | Cumulative frequency |
|---|---|---|
| 0 - 10 | 3 | 3 |
| 10 - 20 | 7 | 10 |
| 20 - 30 | 12 | 22 |
| 30 - 40 | 17 | 39 |
| 40 - 50 | 23 | 62 |
| 50 - 60 | 14 | 76 |
| 60 - 70 | 9 | 85 |
| 70 - 80 | 6 | 91 |
| 80 - 90 | 5 | 96 |
| 90 - 100 | 4 | 100 |
Take 1 cm along x-axis = 10 (marks)
Take 1 cm along y-axis = 10 (students)
Plot the points (10, 3), (20, 10), (30, 22), (40, 39), (50, 62), (60, 76), (70, 85), (80, 91), (90, 96) and (100, 100) representing upper class limits and the respective cumulative frequencies. Also plot the point representing lower limit of the first class i.e. 0 - 10.
Join these points by a freehand drawing.
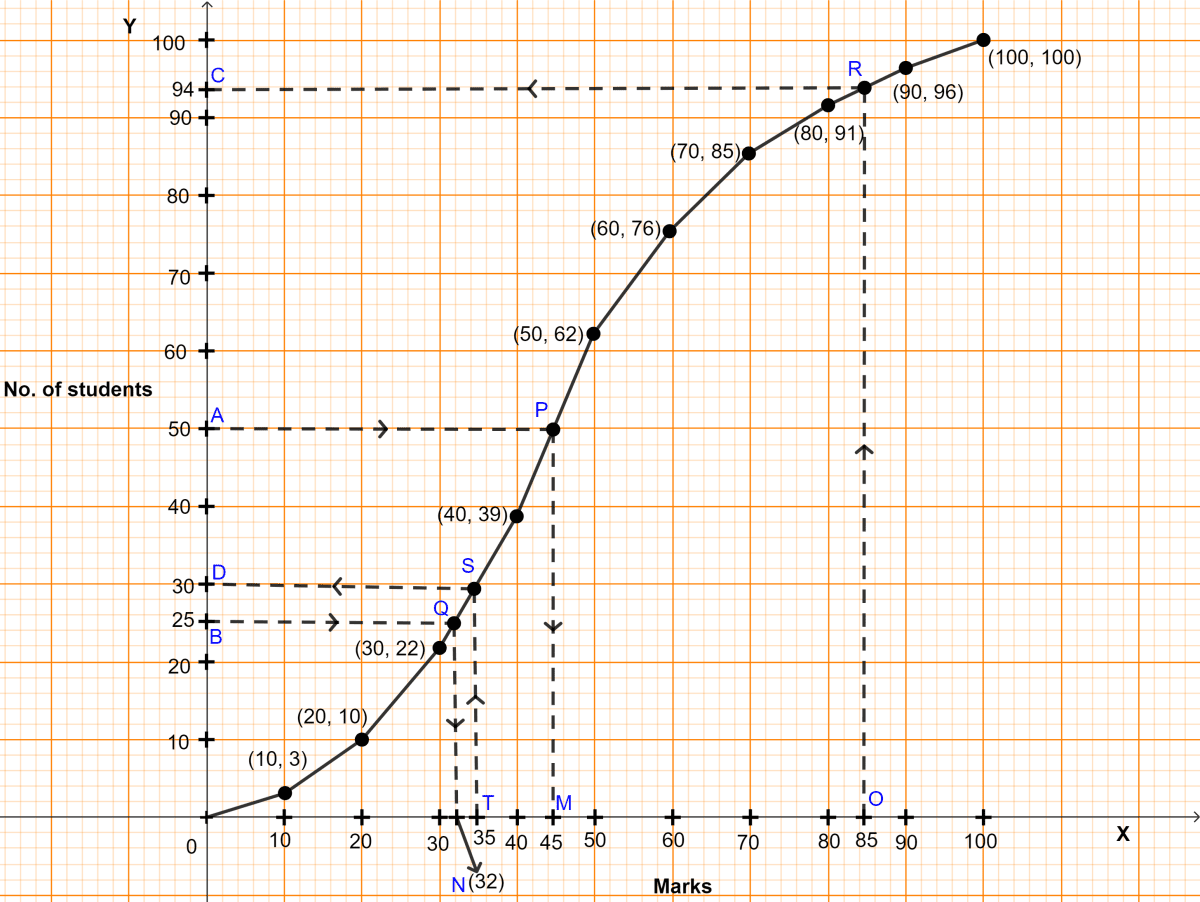
The required ogive is shown in figure above.
(i) Here, n (no. of students) = 100.
To find the median :
Let A be the point on y-axis representing frequency = = 50.
Through A draw a horizontal line to meet the ogive at P. Through P, draw a vertical line to meet the x-axis at M. The abscissa of the point M represents 45
Hence, the median marks = 45.
(ii) To find lower quartile :
Let B be the point on y-axis representing frequency = = 25.
Through B, draw a horizontal line to meet the ogive at Q. Through Q, draw a vertical line to meet the x-axis at N. The abscissa of the point N represents 32.
Hence, lower quartile = 32.
(iii) Total marks = 100.
85% marks = 85 numbers.
Let O be the point on x-axis representing marks = 85.
Through O draw a vertical line to meet the ogive at R. Through R, draw a horizontal line to meet the y-axis at C. The ordinate of the point C represents 94.
Hence, 94 students score less than 85 so students scoring ,ore than 85 = 100 - 94 = 6.
Hence, 6 students score more than 85% in the test.
(iv) 35% of 100 = 35.
Let T be the point on x-axis representing marks = 35.
Through T, draw a vertical line to meet the ogive at S. Through S, draw a horizontal line to meet the y-axis at D. The ordinate of the point D represents 30.
No. of students who scored less than 35 marks = 30.
Hence, 30 students were failed in the examination.
The marks obtained by 120 students in a Mathematics test are given below:
| Marks | No. of students |
|---|---|
| 0 - 10 | 5 |
| 10 - 20 | 9 |
| 20 - 30 | 16 |
| 30 - 40 | 22 |
| 40 - 50 | 26 |
| 50 - 60 | 18 |
| 60 - 70 | 11 |
| 70 - 80 | 6 |
| 80 - 90 | 4 |
| 90 - 100 | 3 |
Draw an ogive for the given distribution on a graph sheet. Use a suitable scale for ogive to estimate the following :
(i) the median
(ii) the number of students who obtained more than 75% marks in the test.
(iii) the number of students who did not pass in the test if the pass percentage was 40.
Answer
- The cumulative frequency table for the given continuous distribution is :
| Marks | No. of students | Cumulative frequency |
|---|---|---|
| 0 - 10 | 5 | 5 |
| 10 - 20 | 9 | 14 |
| 20 - 30 | 16 | 30 |
| 30 - 40 | 22 | 52 |
| 40 - 50 | 26 | 78 |
| 50 - 60 | 18 | 96 |
| 60 - 70 | 11 | 107 |
| 70 - 80 | 6 | 113 |
| 80 - 90 | 4 | 117 |
| 90 - 100 | 3 | 120 |
Take 1 cm along x-axis = 10 marks
Take 1 cm along y-axis = 10 students
Plot the points (10, 5), (20, 14), (30, 30), (40, 52), (50, 78), (60, 96), (70, 107), (80, 113), (90, 117) and (100, 120) representing upper class limits and the respective cumulative frequencies.
Also plot the point representing lower limit of the first class i.e. 0 - 10.Join these points by a freehand drawing.

The required ogive is shown in figure above.
(i) Here, n (no. of students) = 120.
To find the median :
Let A be the point on y-axis representing frequency = = 60.
Through A draw a horizontal line to meet the ogive at P. Through P, draw a vertical line to meet the x-axis at M. The abscissa of the point M represents marks = 43.5
Hence, the median marks = 43.5.
(ii) Total marks = 100.
75% marks = 75 numbers.
Let O be the point on x-axis representing marks = 75.
Through O draw a vertical line to meet the ogive at R. Through R, draw a horizontal line to meet the y-axis at C. The ordinate of the point C represents 110.
Hence, 110 students score less than 75 so students scoring more than 75 = 120 - 110 = 10.
Hence, 10 students score more than 75% in the test.
(iii) 40% of 100 = 40.
Let T be the point on x-axis representing marks = 40.
Through T, draw a vertical line to meet the ogive at S. Through S, draw a horizontal line to meet the y-axis at D. The ordinate of the point D represents 52.
No. of students who scored less than 40 marks = 52.
Hence, 52 students failed in the examination.
The following distribution represents the height of 160 students of a school.
| Height (in cm) | No. of students |
|---|---|
| 140 - 145 | 12 |
| 145 - 150 | 20 |
| 150 - 155 | 30 |
| 155 - 160 | 38 |
| 160 - 165 | 24 |
| 165 - 170 | 16 |
| 170 - 175 | 12 |
| 175 - 180 | 8 |
Draw an ogive for the given distribution taking 2 cm = 5 cm of height on one axis and 2 cm = 20 students on the other axis. Using the graph, determine :
(i) The median height.
(ii) The inter quartile range.
(iii) The number of students whose height is above 172 cm.
Answer
- The cumulative frequency table for the given continuous distribution is :
| Height (in cm) | No. of students | Cumulative frequency |
|---|---|---|
| 140 - 145 | 12 | 12 |
| 145 - 150 | 20 | 32 |
| 150 - 155 | 30 | 62 |
| 155 - 160 | 38 | 100 |
| 160 - 165 | 24 | 124 |
| 165 - 170 | 16 | 140 |
| 170 - 175 | 12 | 152 |
| 175 - 180 | 8 | 160 |
Take 2 cm along x-axis = 5 cm (height)
Take 1 cm along y-axis = 20 (students)
Since, scale on x-axis starts at 140, a kink is shown near the origin on x-axis to indicate that the graph is drawn to scale beginning at 140.
Plot the points (145, 12), (150, 32), (155, 62), (160, 100), (165, 124), (170, 140), (175, 152) and (180, 160) representing upper class limits and the respective cumulative frequencies. Also plot the point representing lower limit of the first class i.e. 140 - 145.
Join these points by a freehand drawing.

The required ogive is shown in figure above.
(i) Here, n (no. of students) = 160.
To find the median :
Let A be the point on y-axis representing frequency = = 80.
Through A draw a horizontal line to meet the ogive at P. Through P, draw a vertical line to meet the x-axis at M. The abscissa of the point M represents height = 157.5 cm.
Hence, the median height = 157.5 cm.
(ii) To find lower quartile :
Let B be the point on y-axis representing frequency = = 40
Through B, draw a horizontal line to meet the ogive at Q. Through Q, draw a vertical line to meet the x-axis at N. The abscissa of the point N represents 151.5.
To find upper quartile :
Let C be the point on y-axis representing frequency = = 120
Through C, draw a horizontal line to meet the ogive at R. Through R, draw a vertical line to meet the x-axis at O. The abscissa of the point O represents 164.
Inter quartile range = Upper quartile - Lower quartile = 164 - 151.5 = 12.5.
Hence, the inter quartile range = 12.5 cm.
(iii) Let T be the point on x-axis representing height = 172 cm.
Through T, draw a vertical line to meet the ogive at S. Through S, draw a horizontal line to meet the y-axis at D. The ordinate of the point D represents 144.
No. of students shorter than 172 cm = 144.
So, no. of students taller than 172 cm = Total students - No. of students shorter than 172 cm = 160 - 144 = 16.
Hence, there are 16 students taller than 172 cm.
Study the graph and answer each of the following :
(a) Name the curve plotted
(b) Total number of students
(c) The median marks
(d) Number of students scoring between 50 and 80 marks.

Answer
(a) From graph,
The curve plotted is a cumulative frequency curve (ogive).
(b) From graph,
The total number of students = 40.
(c) From graph,
The median marks = 56.
(d) From graph,
No of students scoring below 80 = 37
No of students scoring below 50 = 12
∴ No. of students scoring between 50 and 80 = 37 - 12 = 25.
Hence, the no. of students scoring between 50 and 80 = 25.
Choose the correct answer from the given four options (1 to 8) :
If the classes of a frequency distribution are 1 - 10, 11 - 20, 21 - 30, ...., 51 - 60, then the size of each class is
9
10
11
5.5
Answer
On converting the class from discontinuous intervals into continuous intervals.
Adjustment factor = (Lower limt of one class - Upper limit of previous class) / 2
| Classes before adjustment | Classes after adjustment |
|---|---|
| 1 - 10 | 0.5 - 10.5 |
| 11 - 20 | 10.5 - 20.5 |
| 21 - 30 | 20.5 - 30.5 |
| 31 - 40 | 30.5 - 40.5 |
| 41 - 50 | 40.5 - 50.5 |
| 51 - 60 | 50.5 - 60.5 |
Class interval = 10.5 - 0.5 = 10.
Hence, Option 2 is the correct option.
If the classes of a frequency distribution are 1 - 10, 11 - 20, 21 - 30, ....., 61 - 70, then the upper limit of the class 11 - 20 is
20
21
19.5
20.5
Answer
On converting the class from discontinuous intervals into continuous intervals.
Adjustment factor = (Lower limt of one class - Upper limit of previous class) / 2
| Classes before adjustment | Classes after adjustment |
|---|---|
| 1 - 10 | 0.5 - 10.5 |
| 11 - 20 | 10.5 - 20.5 |
| 21 - 30 | 20.5 - 30.5 |
| 31 - 40 | 30.5 - 40.5 |
| 41 - 50 | 40.5 - 50.5 |
| 51 - 60 | 50.5 - 60.5 |
| 61 - 70 | 60.5 - 70.5 |
From table, the upper limit of the class 11 - 20 is 20.5
Hence, Option 4 is the correct option.
In a grouped frequency distribution, the mid-values of the classes are used to measure which of the following central tendency?
median
mode
mean
all of these
Answer
In a grouped frequency distribution, the mid-values of the classes are used to measure mean.
Hence, Option 3 is the correct option.
In the formula : x̄ = a + for finding the mean of the grouped data, di's are deviations from a (assumed mean) of
lower limits of the classes
upper limits of the classes
mid-points of the classes
frequencies of the classes
Answer
In the formula : x̄ = a + for finding the mean of the grouped data, di's are deviations from a (assumed mean) of mid-points of the classes.
Hence, Option 3 is the correct option.
Construction of a cumulative frequency distribution table is useful in determining the
mean
median
mode
all the three measures
Answer
Cumulative frequency distribution table is useful in determining the median.
Hence, Option 2 is the correct option.
The median class for the given distribution is:
| Class Interval | Frequency |
|---|---|
| 0 - 10 | 2 |
| 10 - 20 | 4 |
| 20 - 30 | 3 |
| 30 - 40 | 5 |
0 - 10
10 - 20
20 - 30
30 - 40
Answer
The given class intervals are already in ascending order. We construct the cumulative frequency table as under :
| Class Interval | Frequency | Cumulative frequency |
|---|---|---|
| 0 - 10 | 2 | 2 |
| 10 - 20 | 4 | 6 |
| 20 - 30 | 3 | 9 |
| 30 - 40 | 5 | 14 |
Here, Cumulative frequency = 14, which is even.
By formula,
All observations from 7th to 8th are equal, each lies in the interval 20 - 30.
So, median class = 20 - 30
Hence, option 3 is the correct option.
Construct the following frequency distribution :
| Class | Frequency |
|---|---|
| 0 - 5 | 13 |
| 6 - 11 | 10 |
| 12 - 17 | 15 |
| 18 - 23 | 8 |
| 24 - 29 | 11 |
The upper limit of the median class is
17
17.5
18
18.5
Answer
Converting the discontinuous interval into continuous interval.
Adjustment factor = (Lower limt of one class - Upper limit of previous class) / 2
We construct the cumulative frequency distribution table as under :
| Classes before adjustment | Classes after adjustment | Frequency | Cumulative frequency |
|---|---|---|---|
| 0 - 5 | 0 - 5.5 | 13 | 13 |
| 6 - 11 | 5.5 - 11.5 | 10 | 23 |
| 12 - 17 | 11.5 - 17.5 | 15 | 38 |
| 18 - 23 | 17.5 - 23.5 | 8 | 46 |
| 24 - 29 | 23.5 - 29.5 | 11 | 57 |
Here n (total no. of observations) = 57.
As n is odd,
As observation from 24th to 38th lies in the class 11.5 - 17.5
∴ Median class = 11.5 - 17.5, with upper limit = 17.5
Hence, Option 2 is the correct option.
For the following distribution :
| Class | Frequency |
|---|---|
| 0 - 5 | 10 |
| 5 - 10 | 15 |
| 10 - 15 | 12 |
| 15 - 20 | 20 |
| 20 - 25 | 9 |
The sum of lower limits of the median class and modal class is
15
25
30
35
Answer
We construct the cumulative frequency distribution table as under :
| Class | Frequency | Cumulative frequency |
|---|---|---|
| 0 - 5 | 10 | 10 |
| 5 - 10 | 15 | 25 |
| 10 - 15 | 12 | 37 |
| 15 - 20 | 20 | 57 |
| 20 - 25 | 9 | 66 |
Here n (total no. of observations) = 66.
As n is even,
∴ Median = (th observation + ()th observation) / 2
As observation from 26th to 37th lie in the class 10 - 15,
∴ Median class = 10 - 15.
Since the class 15 - 20 has highest frequency i.e. 20.
∴ Modal class = 15 - 20.
Sum of lower limit of median and modal class = 10 + 15 = 25.
Hence, Option 2 is the correct option.
The modal class of a given distribution always corresponds to the:
Interval with highest frequency
Interval with lowest frequency
The first interval
The last interval
Answer
The "modal class" refers to the interval in a frequency distribution that has the highest number of observations, meaning it's the class with the most occurrences.
Hence, option 1 is the correct option.
An ogive curve is used to determine
range
mean
mode
median
Answer
An ogive curve is used to determine median.
Hence, Option 4 is the correct option.
The median of the following observations arranged in ascending order is 64. Find the value of x :
27, 31, 46, 52, x, x + 4, 71, 79, 85, 90
60
61
62
66
Answer
No. of observations = 10, which is even.
Median = = 5th term.
Given,
Median = 64
∴ x + 4 = 64
⇒ x = 64 - 4 = 60.
Hence, Option 1 is the correct option.
Assertion (A): Mean of the prime number lying between 5 and 20 is 13.4.
Reason (R): Mean =
Assertion (A) is true, but Reason (R) is false.
Assertion (A) is false, but Reason (R) is true.
Both Assertion (A) and Reason (R) are correct, and Reason (R) is the correct reason for Assertion (A).
Both Assertion (A) and Reason (R) are correct, and Reason (R) is incorrect reason for Assertion (A).
Answer
The prime numbers between 5 and 20 are: 7, 11, 13, 17, 19 .
There are 5 such primes.
By formula,
Mean =
∴ Reason (R) is true.
Mean = = 13.4
∴ Assertion (A) is true.
∴ Both Assertion (A) and Reason (R) are correct, and Reason (R) is the correct reason for Assertion (A).
Hence, option 3 is the correct option.
Assertion (A): A survey was conducted by a group of student as a part of their environment awareness program in which they collected the following data regarding the number of plants in 10 houses in a locality.
| Number of plants | Number of houses |
|---|---|
| 2 - 4 | 2 |
| 4 - 6 | 3 |
| 6 - 8 | 1 |
| 8 - 10 | 3 |
| 10 - 12 | 1 |
The mean of the data is 6.9.
Reason (R): If the observation x1, x2, x3,........., xk has frequencies f1, f2, f3, ........, fk, then mean =
Assertion (A) is true, but Reason (R) is false.
Assertion (A) is false, but Reason (R) is true.
Both Assertion (A) and Reason (R) are correct, and Reason (R) is the correct reason for Assertion (A).
Both Assertion (A) and Reason (R) are correct, and Reason (R) is incorrect reason for Assertion (A).
Answer
| Number of plants | Class mark(xi) | Number of houses(fi) | fi.xi |
|---|---|---|---|
| 2 - 4 | 3 | 2 | 6 |
| 4 - 6 | 5 | 3 | 15 |
| 6 - 8 | 7 | 1 | 7 |
| 8 - 10 | 9 | 3 | 27 |
| 10 - 12 | 11 | 1 | 11 |
| Total | Σfi = 10 | Σfixi = 66 |
Mean =
∴ Reason (R) is true.
Mean = = 6.6
∴ Assertion (A) is false.
∴ Assertion (A) is false, but Reason (R) is true.
Hence, option 2 is the correct option.
Assertion (A): The number of goals scored by a football team in a series of matches are 3, 1, 0, 7, 5, 3, 3, 4, 1, 2, 0, 2
The median of the data is 2.5.
Reason (R): Median of an ungrouped data is the variate which has maximum frequency.
Assertion (A) is true, but Reason (R) is false.
Assertion (A) is false, but Reason (R) is true.
Both Assertion (A) and Reason (R) are correct, and Reason (R) is the correct reason for Assertion (A).
Both Assertion (A) and Reason (R) are correct, and Reason (R) is incorrect reason for Assertion (A).
Answer
Given goals: 3, 1, 0, 7, 5, 3, 3, 4, 1, 2, 0, 2
Arrange the data in ascending order: 0, 0, 1, 1, 2, 2, 3, 3, 3, 4, 5, 7
There are 12 values (even).
By formula,
∴ Assertion (A) is true.
The median is a measure of central tendency that splits your ordered data into two equal parts—half the observations lie below it, and half lie above it.
∴ Reason (R) is false.
∴ Assertion (A) is true, but Reason (R) is false.
Hence, option 1 is the correct option.
For the given 25 variables : x1, x2, x3,........., x25.
Assertion (A): To find median of the given data, the variate need to be arranged in ascending or descending order.
Reason (R): The median is the central most term of the arranged data.
Assertion (A) is true, but Reason (R) is false.
Assertion (A) is false, but Reason (R) is true.
Both Assertion (A) and Reason (R) are correct, and Reason (R) is the correct reason for Assertion (A).
Both Assertion (A) and Reason (R) are correct, and Reason (R) is incorrect reason for Assertion (A).
Answer
For the given 25 variables : x1, x2, x3,........., x25.
To compute the median, you must first arrange the data in either ascending or descending order. Only with ordered data, the middle value can be identified.
∴ Assertion (A) is true.
The median is a measure of central tendency that splits your ordered data into two equal parts—half the observations lie below it, and half lie above it.
Thus, the median is the central most term of the arranged data.
∴ Reason (R) is true.
∴ Both Assertion (A) and Reason (R) are correct, and Reason (R) is the correct reason for Assertion (A).
Hence, option 3 is the correct option.
The mean of 20 numbers is 18. If 3 is added to each of the first ten numbers, find the mean of new set of 20 numbers.
Answer
Mean =
∴ Sum of observations = Mean × No. of observations
⇒ Sum of observations = 18 × 20 = 360.
Since 3 is added to first ten numbers then total sum increases by 10 × 3 = 30.
New sum = 360 + 30 = 390.
Mean = = 19.5
Hence, the mean of new set of 20 numbers is 19.5
The average height of 30 students is 150 cm. It was detected later that one value of 165 cm was wrongly copied as 135 cm for the computation of mean. Find the correct mean.
Answer
Mean =
∴ Sum of observations = Mean × No. of observations
⇒ Sum of observations = 150 × 30 = 4500.
Since, one value of 165 cm was wrongly copied as 135 cm,
∴ Correct sum of observations = 4500 - 135 + 165 = 4530.
Correct mean = = 151.
Hence, the correct mean is 151 cm.
There are 50 students in a class of which 40 are boys and the rest girls. The average weight of the students in the class is 44 kg and the average weight of the girls is 40 kg. Find the average weight of boys.
Answer
No. of girls = Total - No. of boys = 50 - 40 = 10.
Average weight of class =
∴ Total weight = Average weight × No. of students
⇒ Total weight = 44 × 50 = 2200
Average weight of girls =
∴ Weight of girls = Average weight of girls × No. of girls
⇒ Weight of girls = 40 × 10 = 400.
Total weight of boys = Total weight - Weight of girls = 2200 - 400 = 1800.
Average weight of boys = = 45.
Hence, the average weight of boys is 45 kg.
The heights of 50 children were measured (correct to the nearest cm) giving the following results :
| Height (in cm) | No. of children |
|---|---|
| 65 | 1 |
| 66 | 4 |
| 67 | 5 |
| 68 | 7 |
| 69 | 11 |
| 70 | 10 |
| 71 | 6 |
| 72 | 4 |
| 73 | 2 |
Calculate the mean height for this distribution correct to one place of decimal.
Answer
We construct the table as under :
| Height (xi) | No. of children (fi) | fixi |
|---|---|---|
| 65 | 1 | 65 |
| 66 | 4 | 264 |
| 67 | 5 | 335 |
| 68 | 7 | 476 |
| 69 | 11 | 759 |
| 70 | 10 | 700 |
| 71 | 6 | 426 |
| 72 | 4 | 288 |
| 73 | 2 | 146 |
| Total | 50 | 3459 |
Mean = = 69.2 cm.
Hence, mean height = 69.2 cm.
Find the value of p, if the mean of the following distribution is 18.
| Variate (x) | Frequency (f) |
|---|---|
| 13 | 8 |
| 15 | 2 |
| 17 | 3 |
| 19 | 4 |
| 20 + p | 5p |
| 23 | 6 |
Answer
We construct the table as under :
| Variate (x) | Frequency (f) | fx |
|---|---|---|
| 13 | 8 | 104 |
| 15 | 2 | 30 |
| 17 | 3 | 51 |
| 19 | 4 | 76 |
| 20 + p | 5p | 5p2 + 100p |
| 23 | 6 | 138 |
| Total | 5p + 23 | 5p2 + 100p + 399 |
⇒ 5p - 5 = 0 or p + 3 = 0
⇒ 5p = 5 or p = -3
⇒ p = 1 or p = -3.
Since, frequency cannot be negative so p = 1.
Hence, the value of p = 1.
Find the mean age in years from the frequency distribution given below :
| Age in years | No. of persons |
|---|---|
| 25 - 29 | 4 |
| 30 - 34 | 14 |
| 35 - 39 | 22 |
| 40 - 44 | 16 |
| 45 - 49 | 6 |
| 50 - 54 | 5 |
| 55 - 59 | 3 |
Answer
The above data is discontinuous converting in continuous data we get,
Adjustment factor = (Lower limt of one class - Upper limit of previous class) / 2
| Classes before adjustment | Classes after adjustment | Class mark (ui) | No. of persons (fi) | fiui |
|---|---|---|---|---|
| 25 - 29 | 24.5 - 29.5 | 27 | 4 | 108 |
| 30 - 34 | 29.5 - 34.5 | 32 | 14 | 448 |
| 35 - 39 | 34.5 - 39.5 | 37 | 22 | 814 |
| 40 - 44 | 39.5 - 44.5 | 42 | 16 | 672 |
| 45 - 49 | 44.5 - 49.5 | 47 | 6 | 282 |
| 50 - 54 | 49.5 - 54.5 | 52 | 5 | 260 |
| 55 - 59 | 54.5 - 59.5 | 57 | 3 | 171 |
| Total | 70 | 2755 |
Mean = = 39.36 years
Hence, the mean age = 39.36 years.
The mean of the following frequency distribution is 62.8. Find the value of p :
| Classes | Frequency |
|---|---|
| 0 - 20 | 5 |
| 20 - 40 | 8 |
| 40 - 60 | p |
| 60 - 80 | 12 |
| 80 - 100 | 7 |
| 100 - 120 | 8 |
Answer
We construct the following table :
| Classes | Class mark (ui) | Frequency (fi) | fiui |
|---|---|---|---|
| 0 - 20 | 10 | 5 | 50 |
| 20 - 40 | 30 | 8 | 240 |
| 40 - 60 | 50 | p | 50p |
| 60 - 80 | 70 | 12 | 840 |
| 80 - 100 | 90 | 7 | 630 |
| 100 - 120 | 110 | 8 | 880 |
| Total | 40 + p | 2640 + 50p |
Hence, the value of p = 10.
The daily expenditure of 100 families are given below. Calculate f1 and f2, if the mean daily expenditure is ₹188.
| Expenditure (in ₹) | No. of families |
|---|---|
| 140 - 160 | 5 |
| 160 - 180 | 25 |
| 180 - 200 | f1 |
| 200 - 220 | f2 |
| 220 - 240 | 5 |
Answer
We construct the table as under :
| Expenditure (in ₹) | Class mark (ui) | No. of families (fi) | fiui |
|---|---|---|---|
| 140 - 160 | 150 | 5 | 750 |
| 160 - 180 | 170 | 25 | 4250 |
| 180 - 200 | 190 | f1 | 190f1 |
| 200 - 220 | 210 | f2 | 210f2 |
| 220 - 240 | 230 | 5 | 1150 |
| Total | 35 + f1 + f2 | 6150 + 190f1 + 210f2 |
As there are 100 families,
∴ 35 + f1 + f2 = 100
⇒ f1 + f2 = 100 - 35 = 65
⇒ f1 = 65 - f2 ......(i)
Using (i),
⇒ f1 = 65 - f2 = 65 - 15 = 50.
Hence, f1 = 50 and f2 = 15.
The median of the following numbers, arranged in ascending order, is 25. Find x :
11, 13, 15, 19, x + 2, x + 4, 30, 35, 39, 46.
Answer
Here, n (no. of observations) = 10, which is even.
Given, median = 25.
∴ x + 3 = 25
⇒ x = 22.
Hence, the value of x = 22.
If the median of 5, 9, 11, 3, 4, x, 8 is 6, find the value of x.
Answer
Arranging the numbers in ascending order we get,
3, 4, 5, x, 8, 9, 11.
Here n (no. of observations) = 7
Given, median = 6.
∴ 6 = 4th observation = x.
Hence, the value of x = 6.
The marks scored by 16 students in a class test are :
3, 6, 8, 13, 15, 5, 21, 23, 17, 10, 9, 1, 20, 21, 18, 12.
Find :
(i) the median
(ii) lower quartile
(iii) upper quartile
(iv) inter quartile range.
Answer
On arranging the numbers in ascending order we get,
1, 3, 5, 6, 8, 9, 10, 12, 13, 15, 17, 18, 20, 21, 21, 23.
(i) Here, n (no. of observations) = 16, which is even.
Hence, the median of following data = 12.5.
(ii) Here, n (no. of observations) = 16, which is even.
Hence, lower quartile = 6.
(iii) Here, n (no. of observations) = 16, which is even.
Hence, upper quartile = 18.
(iv) Inter quartile range = Upper quartile - Lower quartile = 18 - 6 = 12.
Hence, inter quartile range = 12.
Calculate the mean, the median and the mode of the following distribution :
| Age in years | No. of students |
|---|---|
| 12 | 2 |
| 13 | 3 |
| 14 | 5 |
| 15 | 6 |
| 16 | 4 |
| 17 | 3 |
| 18 | 2 |
Answer
We construct the table as under :
| Age in years (xi) | No. of students (fi) | Cumulative frequency | fixi |
|---|---|---|---|
| 12 | 2 | 2 | 24 |
| 13 | 3 | 5 | 39 |
| 14 | 5 | 10 | 70 |
| 15 | 6 | 16 | 90 |
| 16 | 4 | 20 | 64 |
| 17 | 3 | 23 | 51 |
| 18 | 2 | 25 | 36 |
| Total | 25 | 374 |
Mean = = 14.96
Here, n (no. of observations) = 25, which is odd
The age of observation from 11th to 16th = 15.
∴ Median = 15.
Highest no. of students are 15 years old.
∴ Mode = 15.
Hence, mean = 14.96, median = 15 and mode = 15.
The daily canteen bill of 30 employees in an establishment are distributed as follows :
| Daily canteen bill (in ₹) | No. of employees |
|---|---|
| 0 - 10 | 1 |
| 10 - 20 | 8 |
| 20 - 30 | 10 |
| 30 - 40 | 5 |
| 40 - 50 | 4 |
| 50 - 60 | 2 |
Estimate the modal daily Canteen bill for this distribution by a graphical method.
Answer
Steps :
Take 2 cm along x-axis = 10 rupees and 1 cm along y-axis = 1 employee.
Construct rectangles corresponding to the given data.
In highest rectangle, draw two st. lines AC and BD from corners of the rectangles on either side of the highest rectangle to the opposite corners of the highest rectangle. Let P be the point of intersection of AC and BD.
Through P, draw a vertical line to meet the x-axis at M. The abscissa of the point M represents 23.

Hence, the required mode = ₹23.
Draw a cumulative frequency curve for the following data :
| Marks obtained | No. of students |
|---|---|
| 0 - 10 | 8 |
| 10 - 20 | 10 |
| 20 - 30 | 22 |
| 30 - 40 | 40 |
| 40 - 50 | 20 |
Hence, determine :
(i) the median
(ii) the pass marks if 85% of the students pass.
(iii) the marks which 45% of the students exceed.
Answer
- The cumulative frequency table for the given continuous distribution is :
| Marks obtained | No. of students | Cumulative frequency |
|---|---|---|
| 0 - 10 | 8 | 8 |
| 10 - 20 | 10 | 18 |
| 20 - 30 | 22 | 40 |
| 30 - 40 | 40 | 80 |
| 40 - 50 | 20 | 100 |
Take 2 cm along x-axis = 10 marks
Take 1 cm along y-axis = 10 (students)
Plot the points (10, 8), (20, 18), (30, 40), (40, 80) and (50, 100) representing upper class limits and the respective cumulative frequencies.
Also plot the point representing lower limit of the first class i.e. 0 - 10.Join these points by a freehand drawing.

The required ogive is shown in figure above.
(i) Here, n (no. of students) = 100.
To find the median :
Let A be the point on y-axis representing frequency = = 50.
Through A draw a horizontal line to meet the ogive at P. Through P, draw a vertical line to meet the x-axis at M. The abscissa of the point M represents 32.5 marks.
(ii) Total no. of students = 100.
85% of students pass i.e. 85 students pass.
Remaining no. of students = 15.
Let B be the point on y-axis representing frequency 15.
Through B draw a horizontal line to meet the ogive at Q. Through Q, draw a vertical line to meet the x-axis at N. The abscissa of the point N represents 18 marks.
Hence, passing marks = 18 if 85% students pass.
(iii) Total no. of students = 100.
45% of students i.e. 45 students.
Remaining no. of students = 55.
Let C be the point on y-axis representing frequency 55.
Through C draw a horizontal line to meet the ogive at R. Through R, draw a vertical line to meet the x-axis at O. The abscissa of the point O represents 34 marks.
Hence, 45% of students exceed 34 marks.
The given graph with a histogram represents the number of plants of different heights grown in a school campus. Study the graph carefully and answer the following questions :

(a) Make a frequency table with respect to the class boundaries and their corresponding frequencies.
(b) State the modal class.
(c) Identify and note down the mode of the distribution.
(d) Find the number of plants whose height range is between 80 cm to 90 cm.
Answer
(a) Frequency table :
| Height (class) | Number of plants |
|---|---|
| 30-40 | 4 |
| 40-50 | 2 |
| 50-60 | 8 |
| 60-70 | 12 |
| 70-80 | 6 |
| 80-90 | 3 |
| 90-100 | 4 |
(b) From graph,
The modal class is 60-70.
(c) From graph,
The mode = 64.
(d) From graph,
The number of plants whose height range is between 80 cm to 90 cm are 3.