Heights and Distances

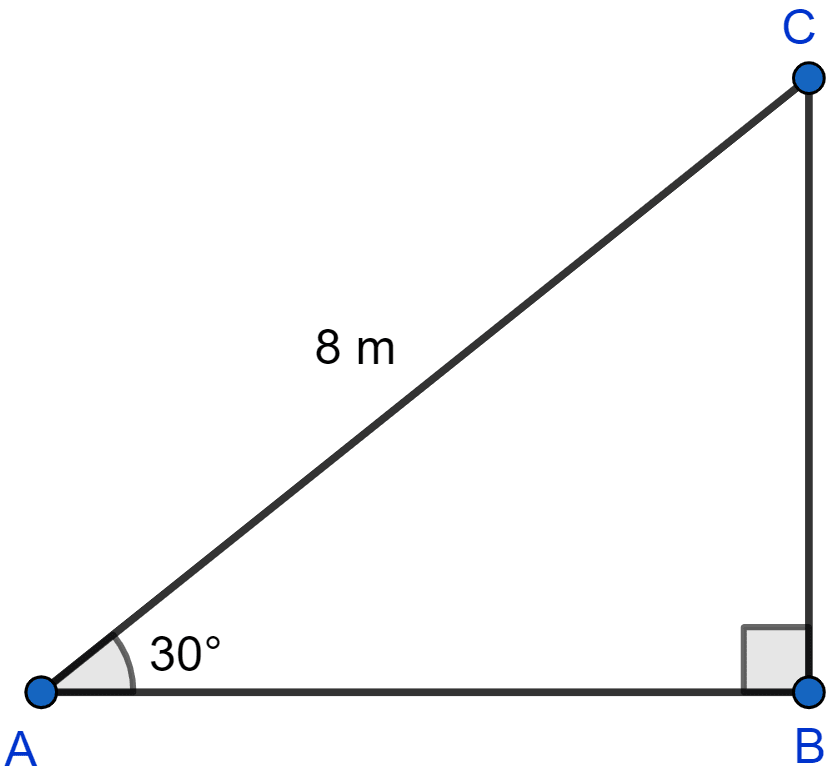
An electric pole is 10 metres high. If its shadow is $10\sqrt{3}$ metres in length, find the elevation of the sun.

Answer

Let the angle of elevation be θ as shown in the figure below:

Consider △ABC, AB be the height of electric pole and BC be the shadow. Since pole and it's shadow are perpendicular, ∠ABC = 90°.

From △ABC, we get

$\Rightarrow \text{tan θ} = \dfrac{\text{AB}}{\text{BC}} \\[1em] \Rightarrow \text{tan θ} = \dfrac{10}{10\sqrt{3}} \\[1em] \Rightarrow \text{tan θ} = \dfrac{1}{\sqrt{3}} \\[1em] \Rightarrow \text{tan θ} = \text{tan 30°} \\[1em] \therefore \text {θ} = 30°.$

Hence, the elevation of the sun is 30°.

The angle of elevation of the top of a tower, from a point on the ground and at a distance of 150 m from its foot, is 30°. Find the height of the tower correct to one place of decimal.

Answer

Let MP be the tower of height h metres and O be the point on the ground 150 m away from the foot of the tower.

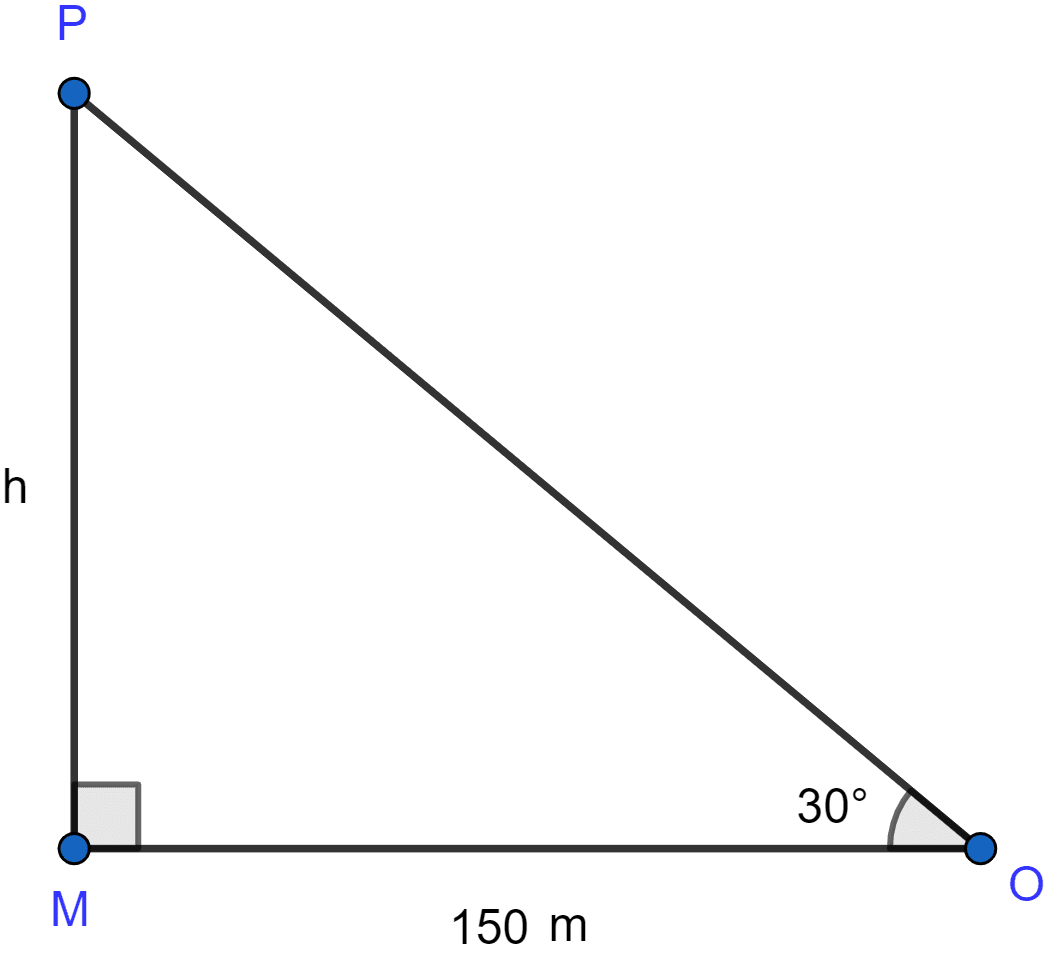
Then, the angle of elevation = ∠MOP = ∠30° (given).

In △OMP, ∠OMP = 90°.

From △OMP, we get

$\Rightarrow \text{tan 30°} = \dfrac{MP}{OM} \\[1em] \Rightarrow \dfrac{1}{\sqrt{3}} = \dfrac{h}{150} \\[1em] \Rightarrow h = \dfrac{150}{\sqrt{3}} \\[1em] \Rightarrow h = 86.6$

Hence, the height of the tower = 86.6 m.

A ladder is placed against a wall such that it just reaches the top of the wall. The foot of the ladder is 1.5 metres away from the wall and the ladder is inclined at an angle of 60° with the ground. Find the height of the wall.

Answer

Let MP be the wall of height h metres and O be the point on the ground 1.5 m away from the foot of the wall.

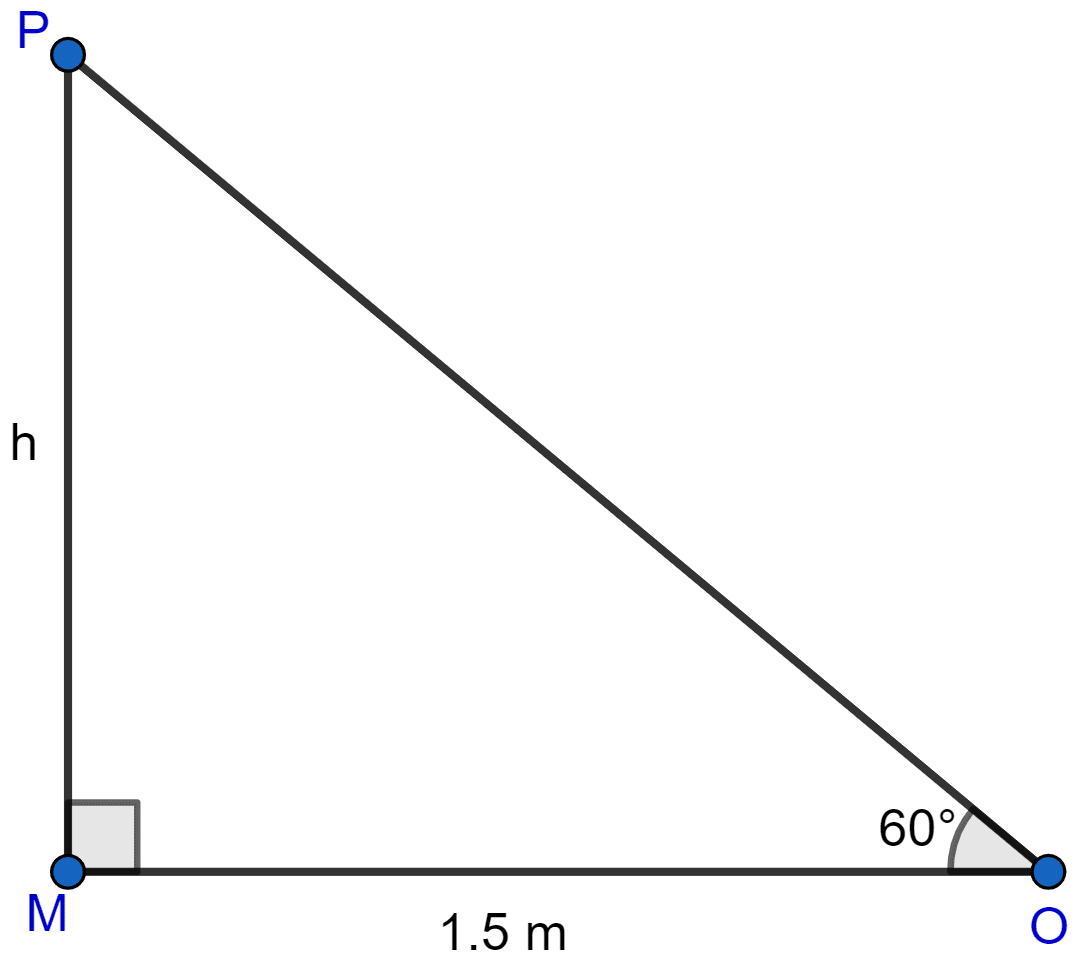
Then, the angle of elevation = ∠MOP = ∠60° (given).

In △OMP, ∠OMP = 90°.

From △OMP, we get

$\Rightarrow \text{tan 60°} = \dfrac{MP}{OM} \\[1em] \Rightarrow \sqrt{3} = \dfrac{h}{1.5} \\[1em] \Rightarrow h = 1.5 \times \sqrt{3} \\[1em] \Rightarrow h = 2.598 \approx 2.6$

Hence, the height of the tower = 2.6 m.

What is the angle of elevation of sun when the length of shadow of a vertical pole is equal to its height?

Answer

Let MP be the height of pole and OM be the length of shadow of pole.

Given, height of pole (MP) = shadow of pole (OM) = h metres.

Let the angle of elevation be θ

In △OMP, ∠OMP = 90°.

From △OMP, we get

$\Rightarrow \text{tan θ} = \dfrac{MP}{OM} \\[1em] \Rightarrow \text{tan θ} = \dfrac{h}{h} \\[1em] \Rightarrow \text{tan θ} = 1 \\[1em] \Rightarrow \text{tan θ} = \text{tan } 45° \\[1em] \therefore θ = 45°.$

Hence, the angle of elevation of sun is 45°.

From a point P on level ground, the angle of elevation of the top of a tower is 30°. If the tower is 100m high, how far is P from the foot of the tower ?

Answer

Let MO be the tower with O being the foot of tower.

Given, angle of elevation of the top of a tower is 30° and height of tower is 100m.

∴ ∠MPO = 30° and OM = 100 m.

In △POM, ∠POM = 90°.

From △POM, we get

$\Rightarrow \text{tan 30°} = \dfrac{OM}{OP} \\[1em] \Rightarrow \dfrac{1}{\sqrt{3}} = \dfrac{100}{OP} \\[1em] \Rightarrow OP = 100 \times \sqrt{3} \\[1em] \Rightarrow OP = 173.2$

Hence, the point P is at a distance of 173.2 metres from the foot of the tower.

From the top of a cliff 92 m high, the angle of depression of a buoy is 20°. Calculate to the nearest metre, the distance of the buoy from the foot of the cliff.

Answer

Let MP be the cliff and O be the buoy.

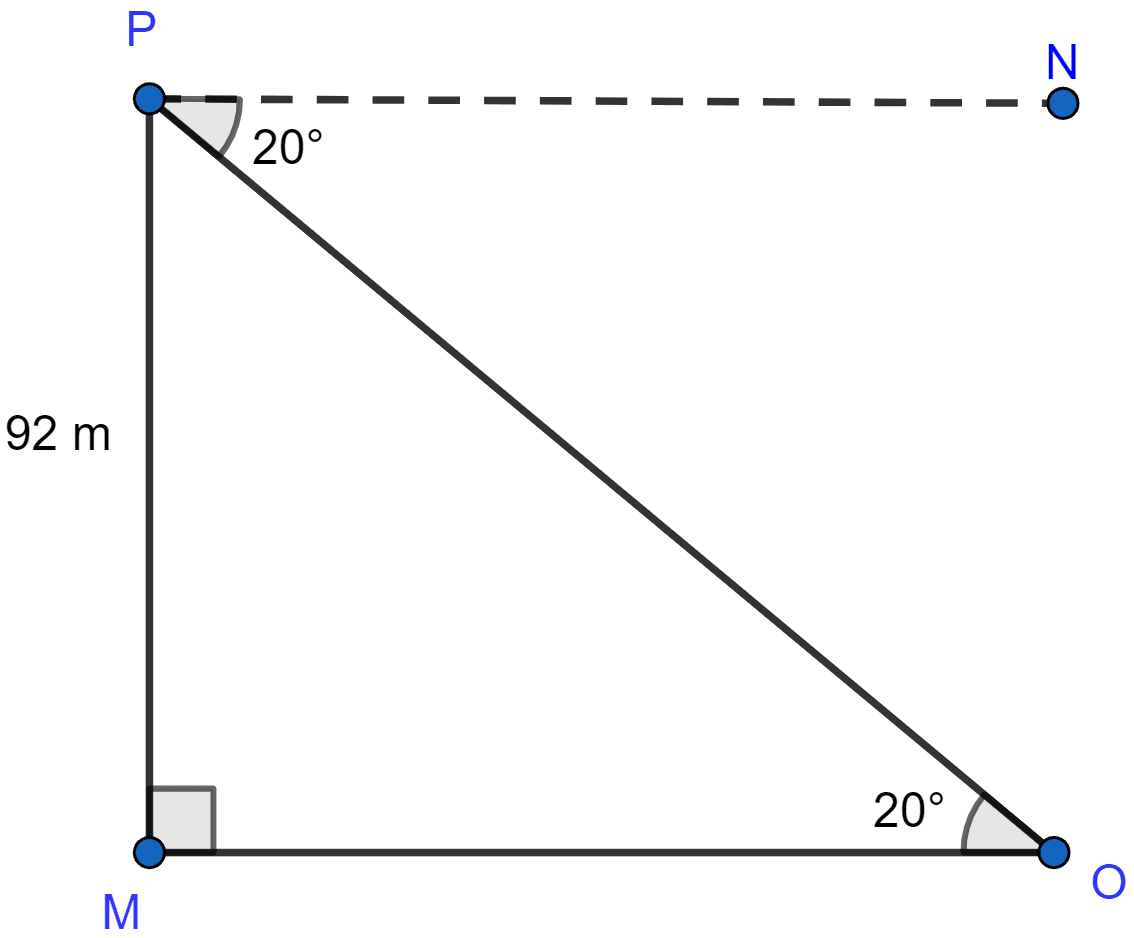
From figure,

Given angle of depression of a buoy is 20°.

∴ ∠POM = ∠OPN = 20° (Alternate angles are equal).

In △POM, ∠PMO = 90°.

From △POM, we get

$\Rightarrow \text{tan 20°} = \dfrac{PM}{OM} \\[1em] \Rightarrow 0.3640 = \dfrac{92}{OM} \\[1em] \Rightarrow OM = \dfrac{92}{0.3640} \\[1em] \Rightarrow OM = 252.74 \approx 253$

Hence, the distance of buoy from the foot of cliff is 253 metres.

A boy is flying a kite with a string of length 100 m. If the string is tight and the angle of elevation of the kite is 26° 32', find the height of the kite correct to one decimal place (ignore the height of the boy).

Answer

Suppose boy is at point O and the kite is at point P.

Considering △POM,

∠PMO = 90°, ∠POM = 26° 32', OP = 100 m and MP = height of kite.

From △POM, we get

$\Rightarrow \text{sin 26° 32}' = \dfrac{MP}{OP} \\[1em] \Rightarrow 0.4467 = \dfrac{MP}{100} \\[1em] \Rightarrow MP = 0.4467 \times 100 \\[1em] \Rightarrow MP = 44.67 \approx 44.7.$

Hence, the height of the kite is 44.7 metres.

An electric pole is 10 m high. A steel wire tied to the top of the pole is affixed at a point on the ground to keep the pole upright. If the wire makes an angle of 45° with the horizontal through the foot of the pole, find the length of the wire.

Answer

Let MP be the pole and string is tied from point P on the pole to point O on the ground.

Considering △POM,

∠PMO = 90°, ∠POM = 45° (given) and MP = 10 m.

From △POM, we get

$\Rightarrow \text{sin 45°} = \dfrac{MP}{OP} \\[1em] \Rightarrow \dfrac{1}{\sqrt{2}} = \dfrac{10}{OP} \\[1em] \Rightarrow OP = 10 \times \sqrt{2} \\[1em] \Rightarrow OP = 10 \times 1.414 \\[1em] \Rightarrow OP = 14.14$

Hence, the length of wire is 14.14 metres.

A vertical tower is 20 m high. A man standing at some distance from the tower knows that the cosine of the angle of elevation of the top of the tower is 0.53. How far is he standing from the foot of the tower ?

Answer

Let θ be the angle of elevation,

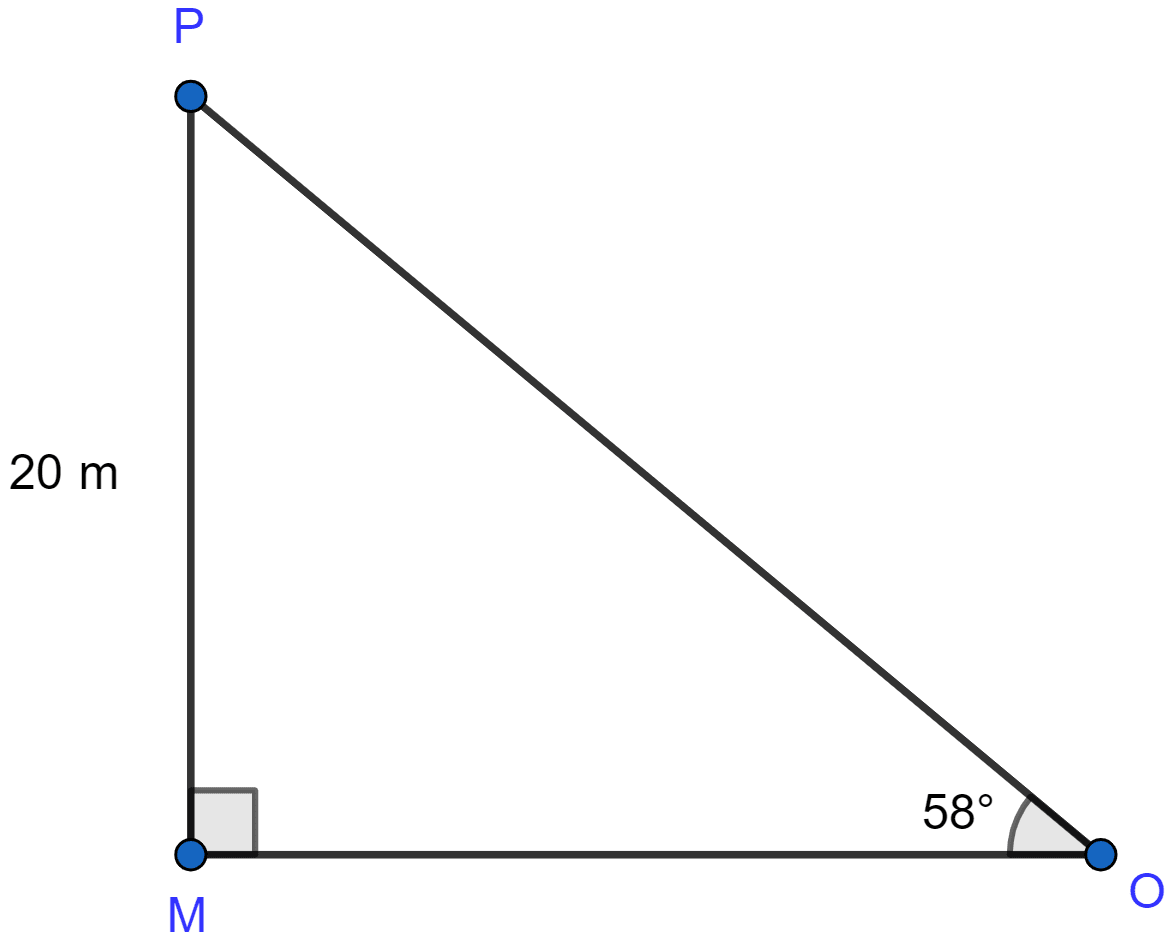
Given, cos θ = 0.53

∴ cos θ = cos 58°

⇒ θ = 58°

Let MP be the vertical tower and the man be standing at point O.

Considering △POM,

∠PMO = 90°, ∠POM = 58° and MP = 20 m.

From △POM, we get

$\Rightarrow \text{tan 58°} = \dfrac{MP}{OM} \\[1em] \Rightarrow 1.6003 = \dfrac{20}{OM} \\[1em] \Rightarrow OM = \dfrac{20}{1.6003} \\[1em] \Rightarrow OM = 12.49 \approx 12.5$

Hence, the man is at a distance of 12.5 metres from the foot of tower.

The upper part of a tree broken by wind, falls to the ground without being detached. The top of the broken part touches the ground at an angle of 38° 30' at a point 6 m from the foot of the tree. Calculate :

(i) the height at which the tree is broken.

(ii) the original height of the tree correct to two decimal places.

Answer

(i) Let ACB be the tree. When broken at point C by the storm, let its top A touch the ground so that ∠CAB = 38° 30' and AB = 6 m.

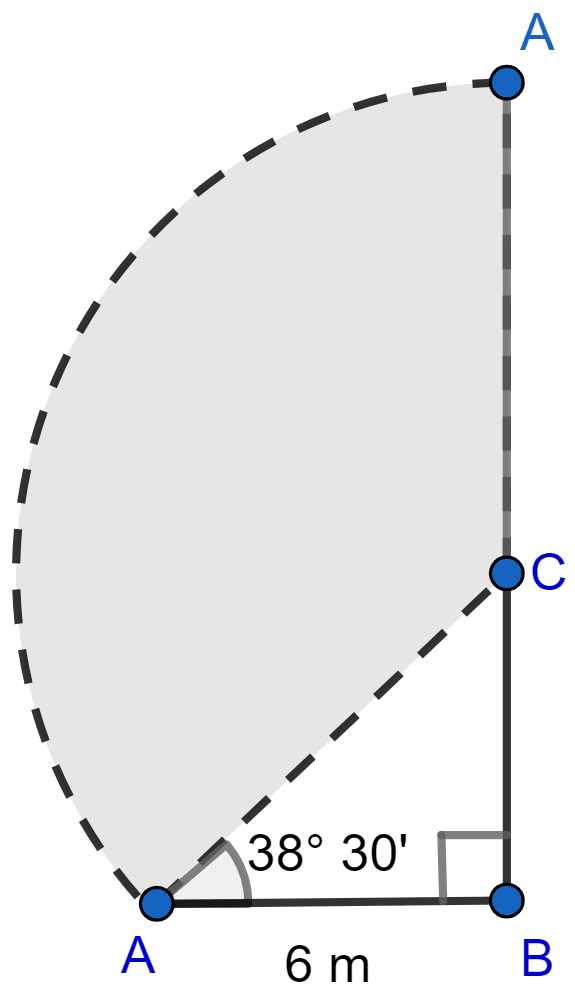
From right angled △ABC, we get

$\Rightarrow \text{tan 38° 30'} = \dfrac{BC}{AB} \\[1em] \Rightarrow 0.7954 = \dfrac{BC}{6} \\[1em] \Rightarrow BC = 0.7954 \times 6 \\[1em] \Rightarrow BC = 4.77$

Hence, the tree is broken at a height of 4.77 m

(ii) From right angled △ABC, we get

$\Rightarrow \text{cos 38° 30}' = \dfrac{AB}{AC} \\[1em] \Rightarrow 0.7826 = \dfrac{6}{AC} \\[1em] \Rightarrow AC = \dfrac{6}{0.7826} \\[1em] \Rightarrow AC = 7.67$

∴ The height of the tree = BC + AC = 4.77 + 7.67 = 12.44

Hence, the original height of the tree is 12.44 metres.

An observer 1.5 m tall is 20.5 meters away from a tower 22 metres high. Determine the angle of elevation of the top of the tower from the eye of the observer.

Answer

Let CD be an observer of height 1.5 m which is 20.5 m away from a tower AB of height 22 m.

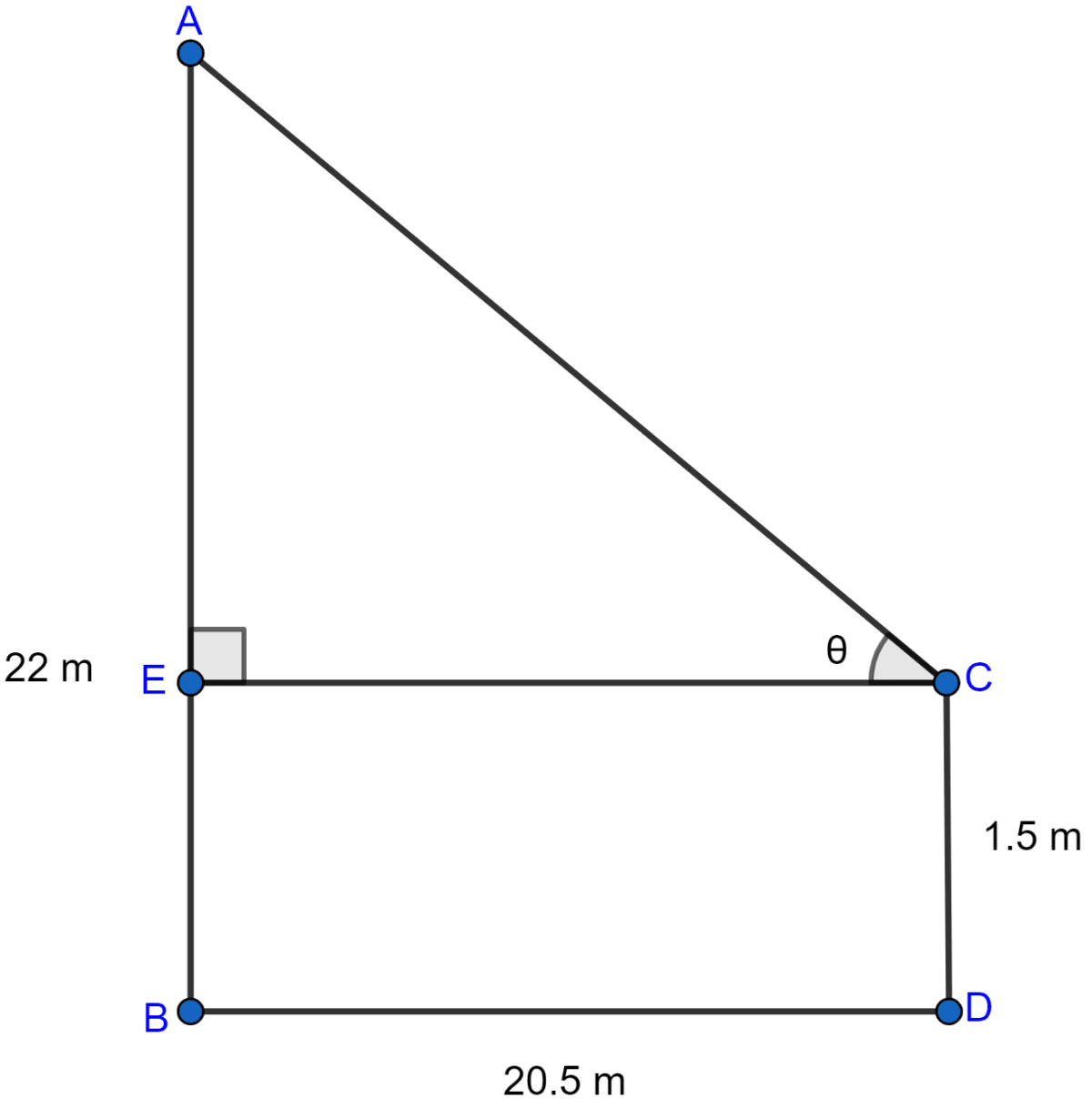
CD = 1.5 m and DB = 20.5 m

From C, draw CE ⊥ AB, then CDBE is a rectangle.

AE = AB - BE = AB - CD = 22 - 1.5 = 20.5 m
CE = DB = 20.5 m.

Let angle of elevation be θ,

From right angled △ACE, we get

$\Rightarrow \text{tan θ} = \dfrac{AE}{CE} \\[1em] \Rightarrow \text{tan θ} = \dfrac{20.5}{20.5} \\[1em] \Rightarrow \text{tan θ} = 1 \\[1em] \Rightarrow \text{tan θ} = \text{tan 45°} \\[1em] \therefore \text{θ} = 45°.$

Hence, the angle of elevation of the top of the tower from the eye of the observer is 45°.

In the adjoining figure, the angle of elevation from a point P of the top of a tower QR, 50 m high is 60° and that of the tower PT from a point Q is 30°. Find the height of the tower PT, correct to the nearest metre.

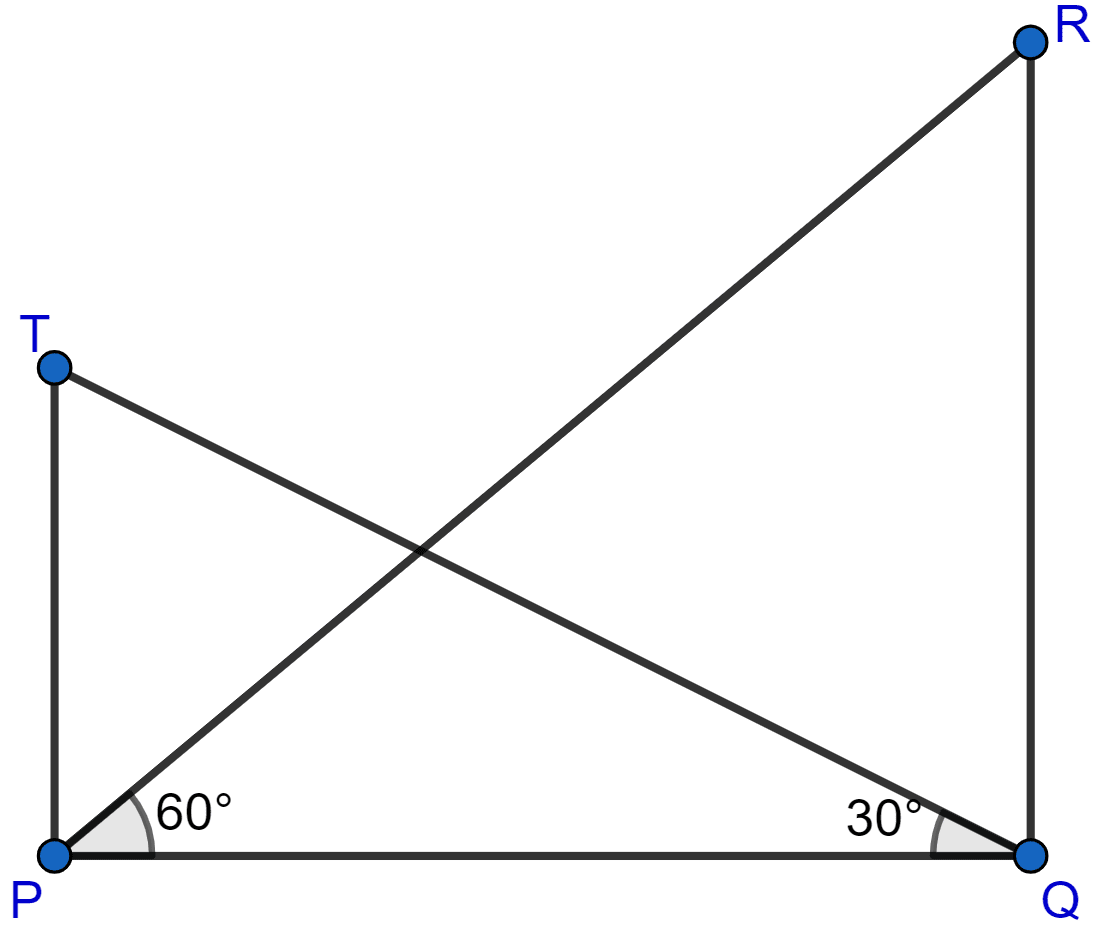
Answer

Let height of tower PT be h meters.

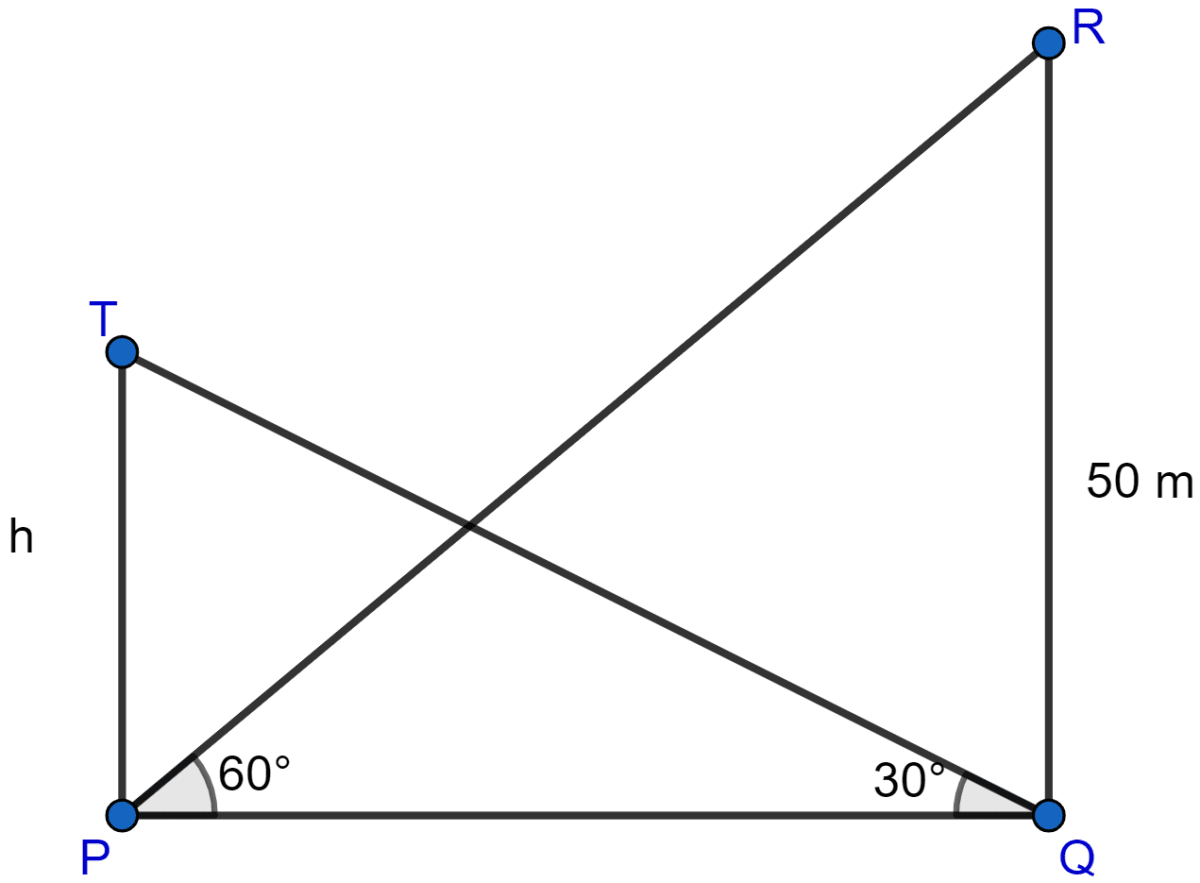
Considering right angled △PQR, we get

$\Rightarrow \text{tan 60°} = \dfrac{QR}{PQ} \\[1em] \Rightarrow \text{tan 60°} = \dfrac{50}{PQ} \\[1em] \Rightarrow \sqrt{3} = \dfrac{50}{PQ} \\[1em] \Rightarrow PQ = \dfrac{50}{\sqrt{3}} \\[1em]$

Now considering right angled △PQT, we get

$\Rightarrow \text{tan 30°} = \dfrac{h}{PQ} \\[1em] \Rightarrow \dfrac{1}{\sqrt{3}} = \dfrac{h}{\dfrac{50}{\sqrt{3}}} \\[1em] \Rightarrow \dfrac{1}{\sqrt{3}} = \dfrac{\sqrt{3} \times h}{50} \\[1em] \Rightarrow h = \dfrac{50}{\sqrt{3} \times \sqrt{3}} \\[1em] \Rightarrow h = \dfrac{50}{3} \\[1em] \Rightarrow h = 16.7.$

On correcting to nearest meter, h = 17 m.

Hence, the height of the tower PT = 17 m.

From a point P on the ground, the angle of elevation of the top of a 10 m tall building and a helicopter, hovering over the top of the building are 30° and 60° respectively. Find the height of the helicopter above the ground.

Answer

Let QR be the tall building and S be the point at which helicopter is present.

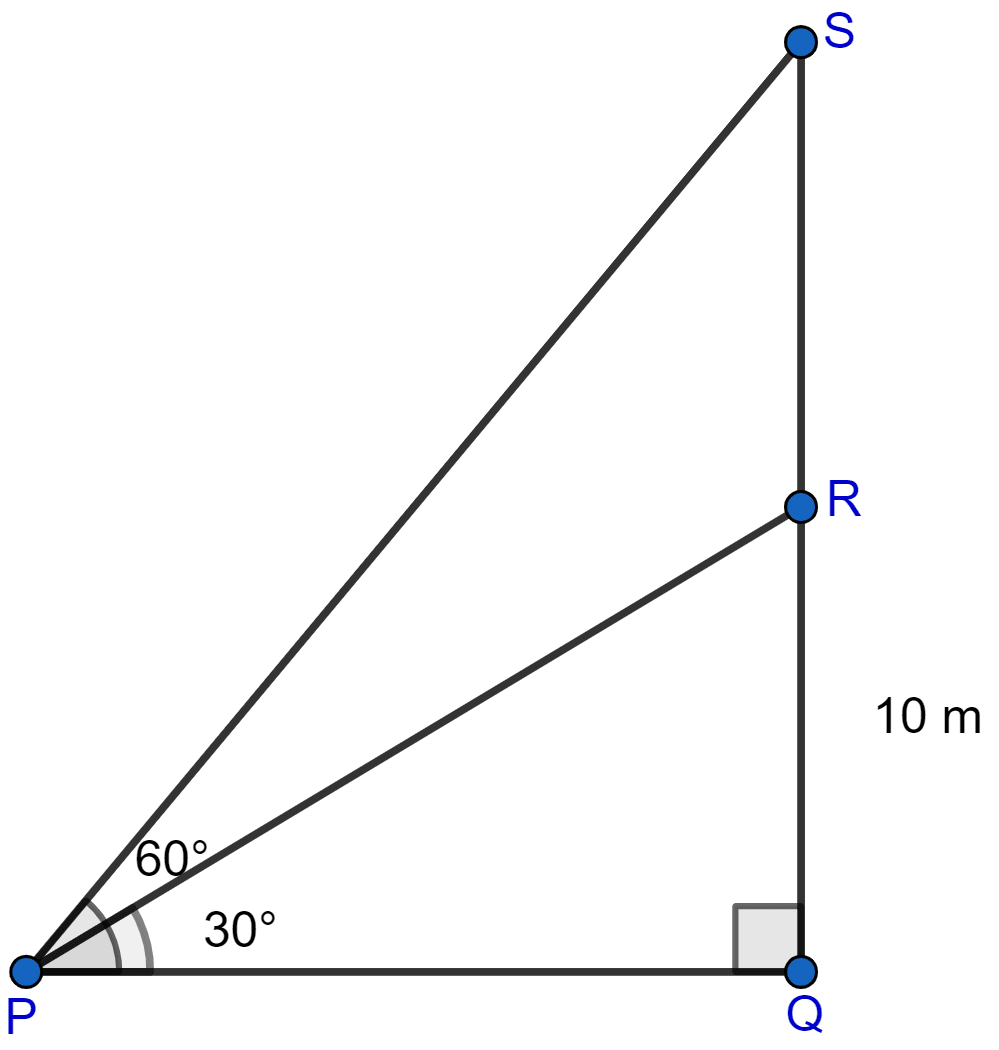
Considering right angled △PQR, we get

$\Rightarrow \text{tan 30°} = \dfrac{QR}{PQ} \\[1em] \Rightarrow \text{tan 30°} = \dfrac{10}{PQ} \\[1em] \Rightarrow \dfrac{1}{\sqrt{3}} = \dfrac{10}{PQ} \\[1em] \Rightarrow PQ = 10\sqrt{3}$

Now considering right angled △PQS, we get

$\Rightarrow \text{tan 60°} = \dfrac{QS}{PQ} \\[1em] \Rightarrow \sqrt{3} = \dfrac{QS}{10\sqrt{3}} \\[1em] \Rightarrow QS = 10\sqrt{3} \times \sqrt{3} \\[1em] \Rightarrow QS = 30.$

Hence, the height of helicopter above the ground is 30 m.

An aeroplane when flying at a height of 3125 m from the ground passes vertically below another plane at an instant when the angles of elevation of the two planes from the same point on the ground are 30° and 60° respectively. Find the distance between the two planes at the instant.

Answer

Let the aeroplane at a height of 3125 m be at a point R and the plane above be at point S.

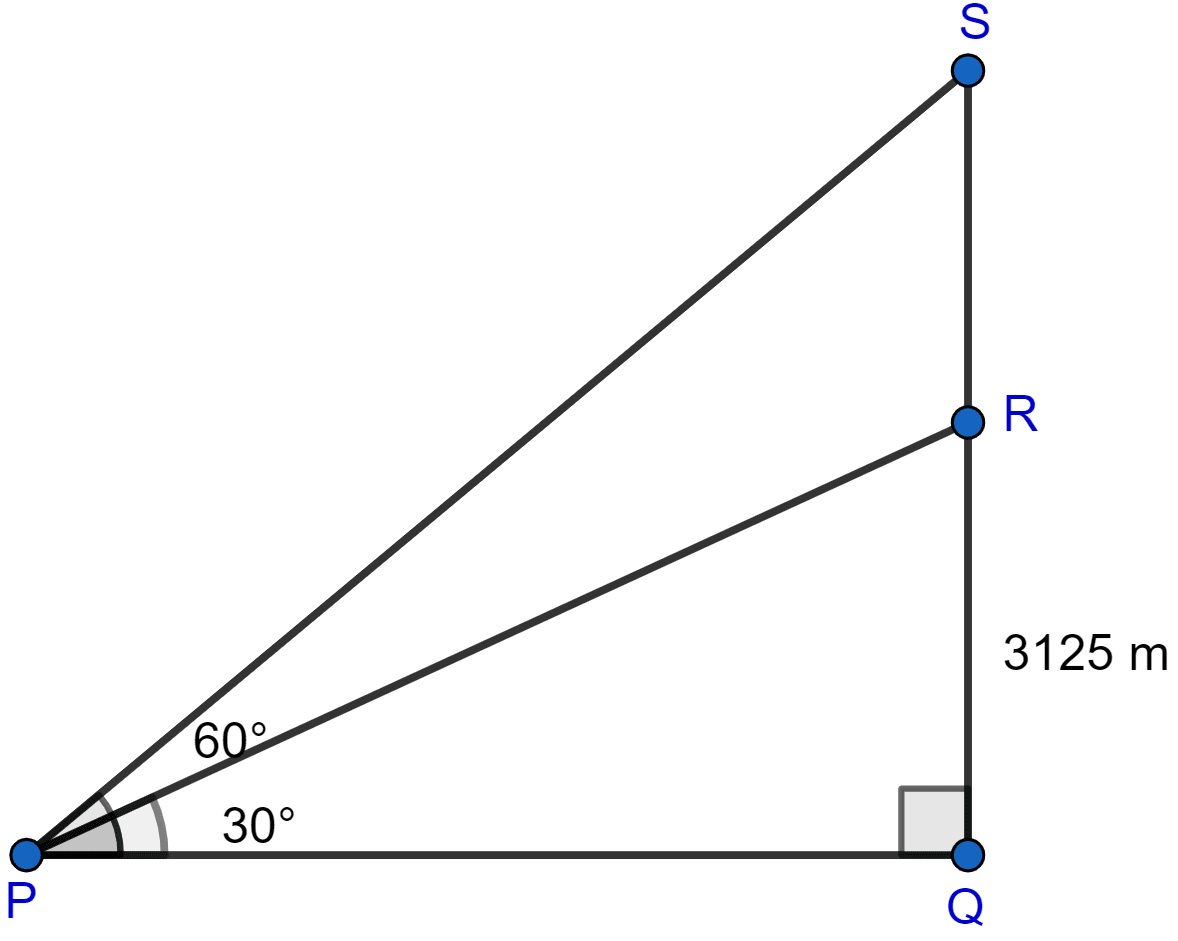
Considering right angled △PQR, we get

$\Rightarrow \text{tan 30°} = \dfrac{QR}{PQ} \\[1em] \Rightarrow \text{tan 30°} = \dfrac{3125}{PQ} \\[1em] \Rightarrow \dfrac{1}{\sqrt{3}} = \dfrac{3125}{PQ} \\[1em] \Rightarrow PQ = 3125\sqrt{3}$

Now considering right angled △PQS, we get

$\Rightarrow \text{tan 60°} = \dfrac{QS}{PQ} \\[1em] \Rightarrow \sqrt{3} = \dfrac{QS}{3125\sqrt{3}} \\[1em] \Rightarrow QS = 3125\sqrt{3} \times \sqrt{3} \\[1em] \Rightarrow QS = 9375$

Distance between two aeroplanes = QS - QR = 9375 - 3125 = 6250 m.

Hence, the distance between two planes = 6250 m.

A man observes the angle of elevation of the top of a tower to be 45°. He walks towards it in a horizontal line through its base. On covering 20 m, the angle of elevation changes to be 60°. Find the height of the tower correct to 2 significant figures.

Answer

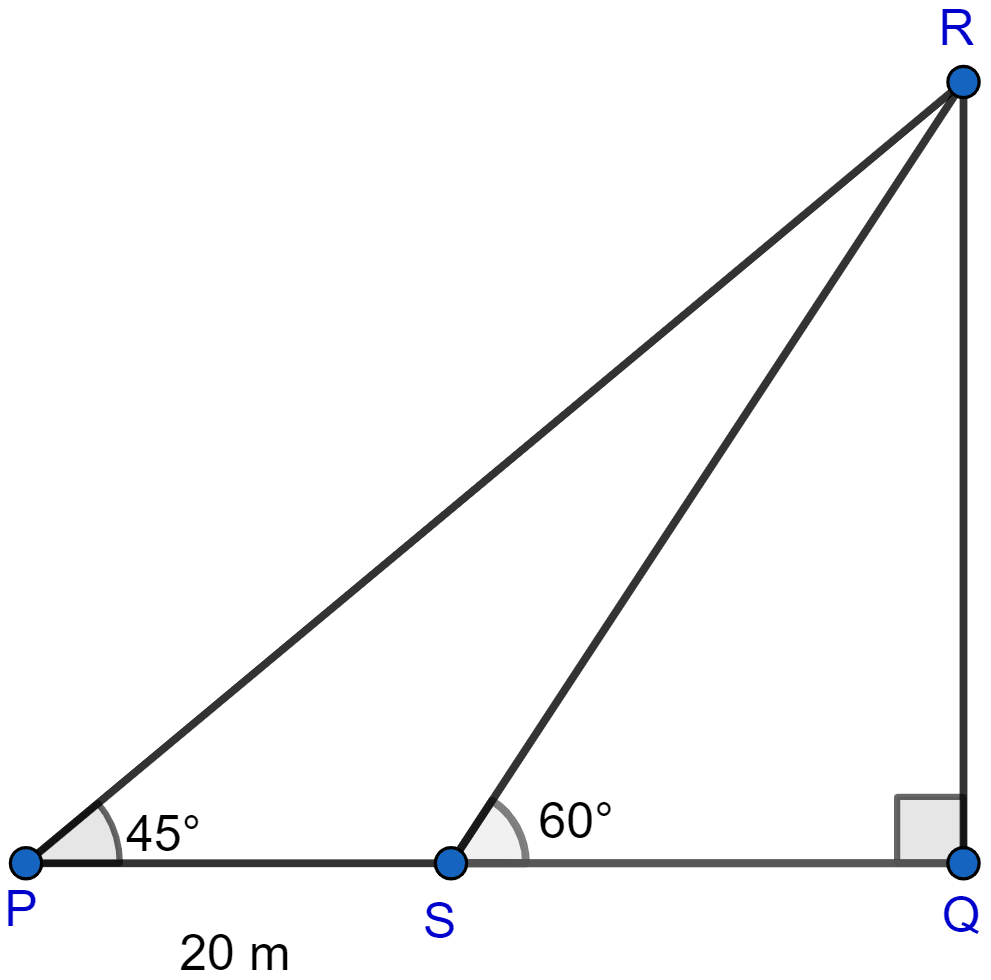
Let tower be QR and initial position of man be P, since the initial angle of elevation is 45°, considering right angled △PQR we get,

$\Rightarrow \text{tan 45°} = \dfrac{QR}{PQ} \\[1em] \Rightarrow 1 = \dfrac{QR}{PQ} \\[1em] \Rightarrow PQ = QR.$

After covering 20 m let the man be at point S, so PS = 20 m and SQ = PQ - PS = PQ - 20 = QR - 20.

Now considering right angled △SQR we get,

$\Rightarrow \text{tan 60°} = \dfrac{QR}{SQ} \\[1em] \Rightarrow \sqrt{3} = \dfrac{QR}{QR - 20} \\[1em] \Rightarrow \sqrt{3}(QR - 20) = QR \\[1em] \Rightarrow \sqrt{3}QR - 20\sqrt{3} = QR \\[1em] \Rightarrow \sqrt{3}QR - QR = 20\sqrt{3}\\[1em] \Rightarrow QR(1.732 - 1) = 20 \times 1.732 \\[1em] \Rightarrow 0.732\text{ QR} = 34.64 \\[1em] \Rightarrow QR = \dfrac{34.64}{0.732} \\[1em] \Rightarrow QR = 47.32$

On correcting to 2 significant figures QR = 47.

Hence, the height of the tower is 47 m.

The shadow of a vertical tower on a level ground increases by 10 m when the altitude of the sun changes from 45° to 30°. Find the height of the tower, correct to two decimal places.

Answer

Let the height of the tower BD be h metres and the length of its shadow be d metres when the sun's altitude is 45°. When the sun's altitude is 30°, then the length of shadow of tower is 10 m longer,
i.e., BD = h meters, AB = d meters and CA = 10 metres.

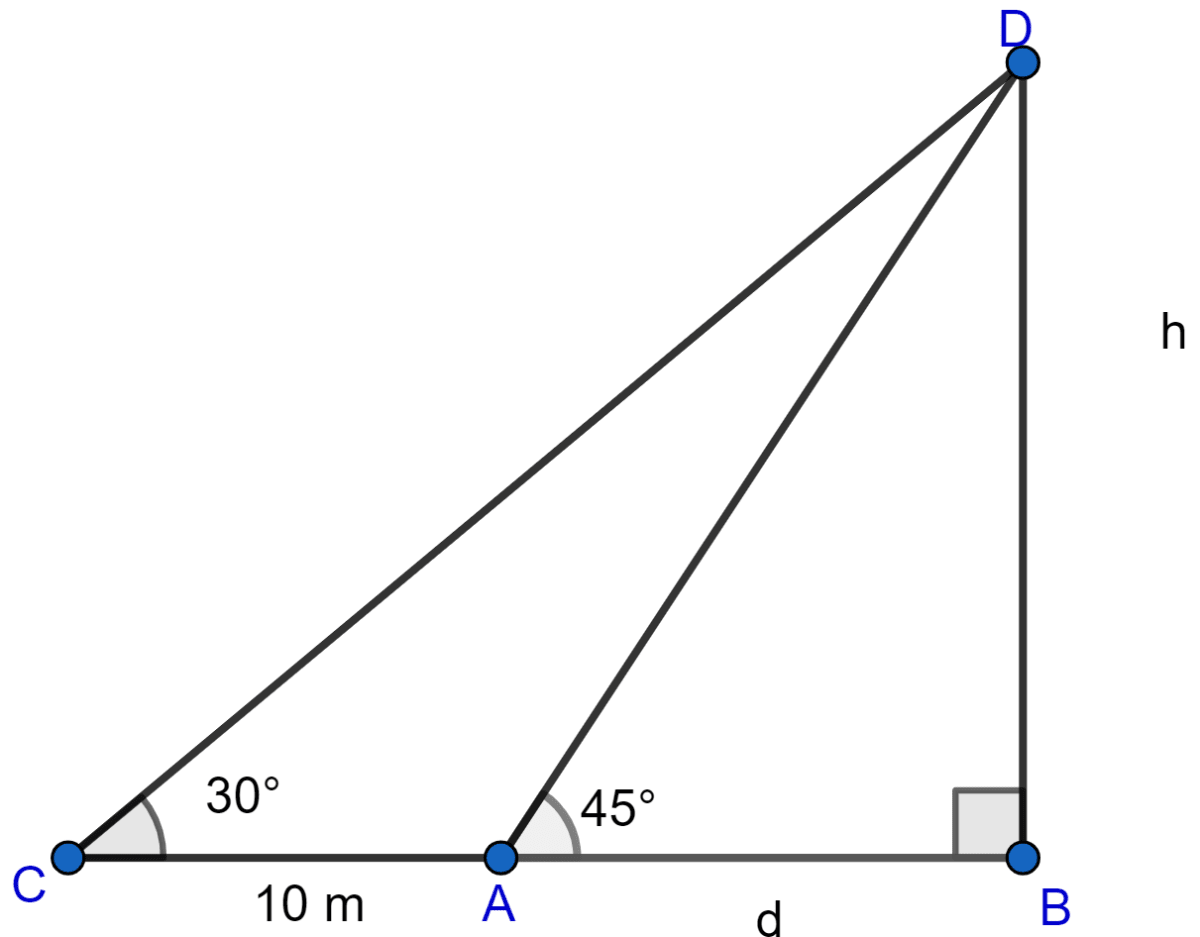
From right angled △ABD, we get

$\Rightarrow \text{tan 45°} = \dfrac{BD}{AB} \\[1em] \Rightarrow 1 = \dfrac{h}{d} \\[1em] \Rightarrow h = d$

From right angled △BCD, we get

$\Rightarrow \text{tan 30°} = \dfrac{BD}{BC} \\[1em] \Rightarrow \dfrac{1}{\sqrt{3}} = \dfrac{h}{AC + AB} \\[1em] \Rightarrow \dfrac{1}{\sqrt{3}} = \dfrac{h}{10 + d} \\[1em] \Rightarrow \dfrac{1}{\sqrt{3}} = \dfrac{h}{10 + h} [\because h = d] \\[1em] \Rightarrow 10 + h = \sqrt{3}h \\[1em] \Rightarrow \sqrt{3}h - h = 10 \\[1em] \Rightarrow h(\sqrt{3} - 1) = 10 \\[1em] \Rightarrow 0.732\text{ h} = 10 \\[1em] \Rightarrow h = \dfrac{10}{0.732} \\[1em] \Rightarrow h = 13.66$

Hence, the height of the tower is 13.66 meters.

From the top of a hill, the angles of depression of two consecutive kilometer stones, due east are found to be 30° and 45° respectively. Find the distance of two stones from the foot of the hill.

Answer

Let R be the top of the tower and Q the foot. P and T be two consecutive kilometer stones with depression angles 30° and 45° respectively.

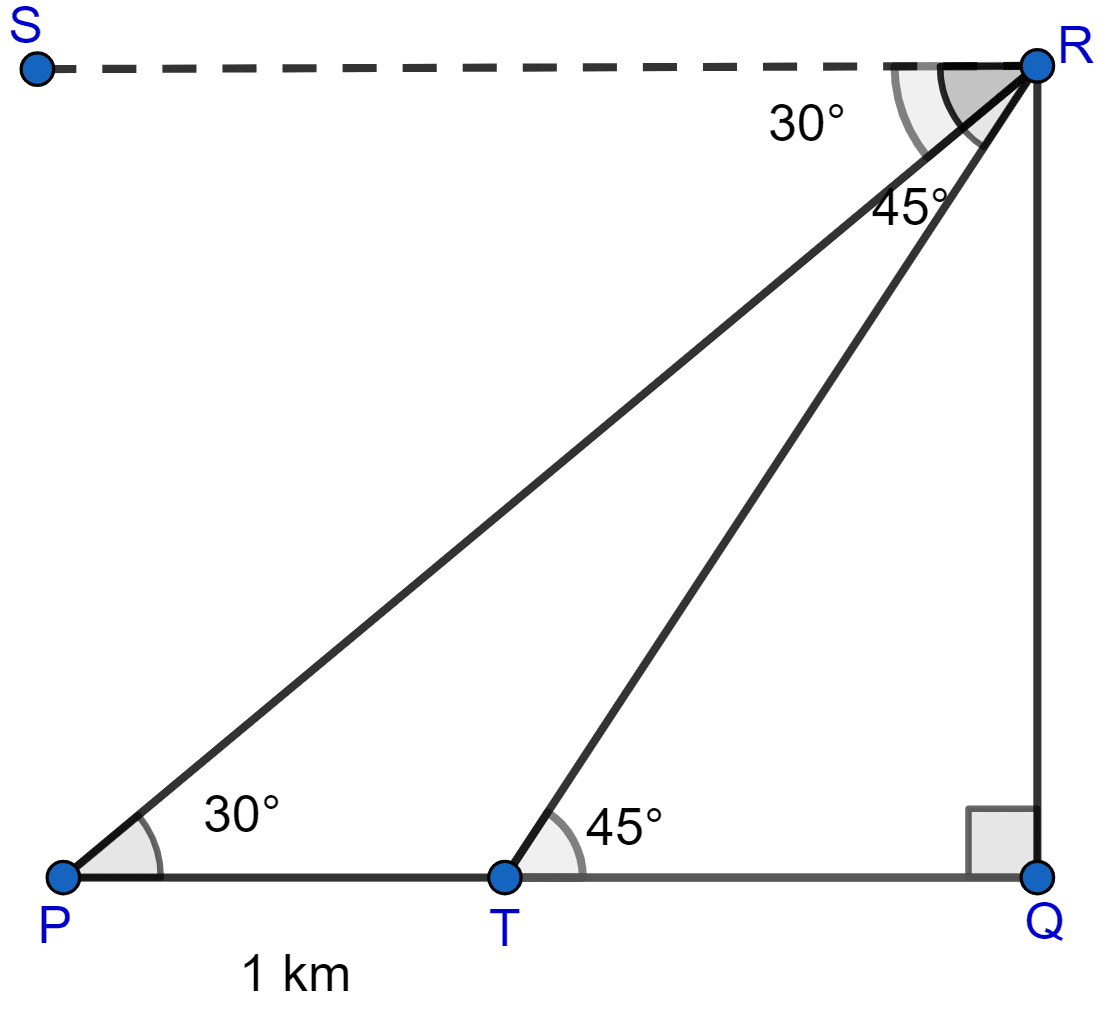
Since stones are consecutive kilometer stones hence distance between them = 1 km.

From figure,

∠RPQ = ∠SRP = 30°      (Alternate angles are equal)
∠RTQ = ∠SRT = 45°      (Alternate angles are equal)
PT = 1 km
TQ = PQ - PT = PQ - 1      (Eq 1)

From right angled △PQR, we get

$\Rightarrow \text{tan 30°} = \dfrac{QR}{PQ} \\[1em] \Rightarrow \dfrac{1}{\sqrt{3}} = \dfrac{QR}{PQ} \\[1em] \Rightarrow PQ = \sqrt{3} \text{ QR} \\[1em] \Rightarrow QR = \dfrac{PQ}{\sqrt{3}}\text{ ......(Eq 2)}$

From right angled △TQR, we get

$\Rightarrow \text{tan 45°} = \dfrac{QR}{TQ} \\[1em] \Rightarrow 1 = \dfrac{QR}{TQ} \\[1em] \Rightarrow TQ = QR \\[1em] \Rightarrow PQ - 1 = QR \text{ (Using Eq 1)}\\[1em] \Rightarrow PQ - 1 = \dfrac{PQ}{\sqrt{3}} \text{ (Using Eq 2)}\\[1em] \Rightarrow \sqrt{3}PQ - \sqrt{3} = PQ \\[1em] \Rightarrow \sqrt{3}PQ - PQ = \sqrt{3} \\[1em] \Rightarrow 0.732PQ = 1.732 \\[1em] \Rightarrow PQ = \dfrac{1.732}{0.732} \\[1em] \Rightarrow PQ = 2.366$

Using Eq 1,

TQ = PQ - 1 = 2.366 - 1 = 1.366.

Hence, the distance of two stones from hill are 1.366 km and 2.366 km.

A man observes the angle of elevation of the top of a building to be 30°. He walks towards it in a horizontal line through its base. On covering 60 m, the angle of elevation changes to 60°. Find the height of the building correct to the nearest metre.

Answer

Let QR be the tower and man be initially at point P after moving 60 m let it reach point S.

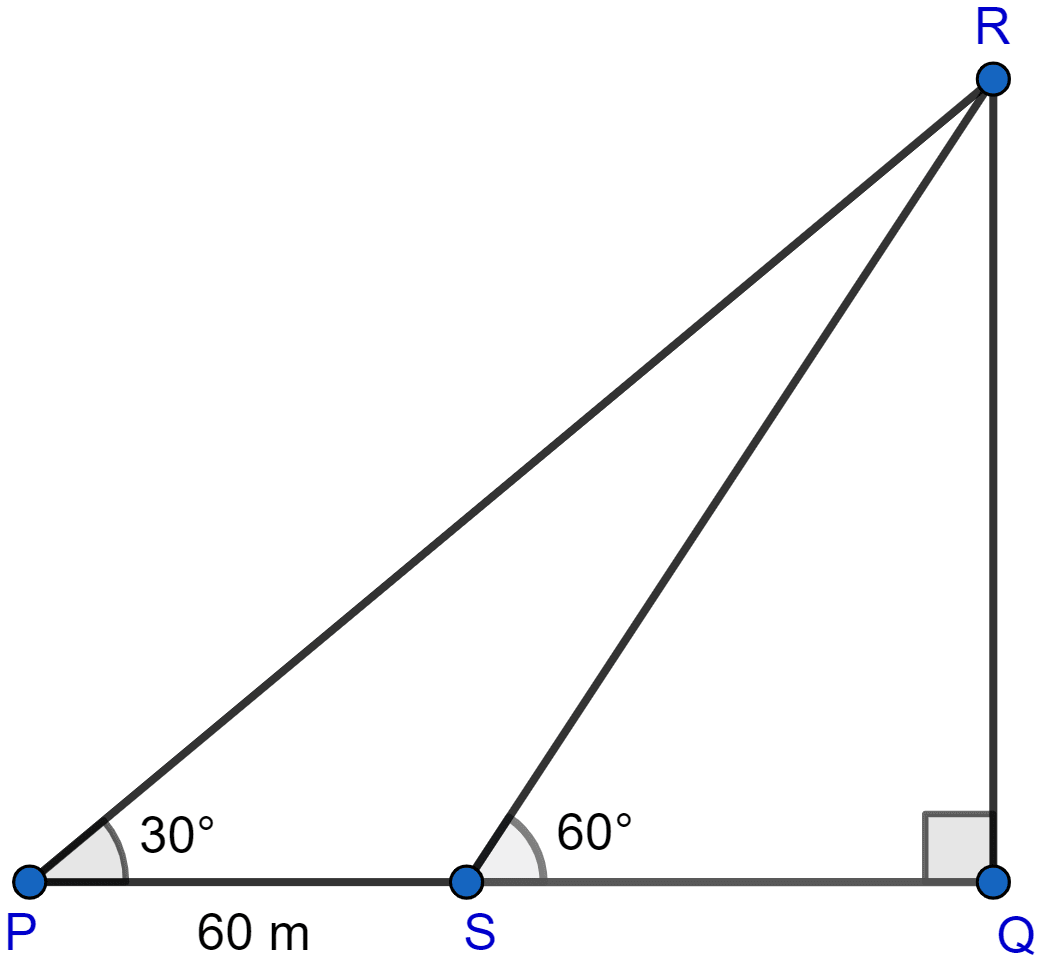
PS = 60 m

From figure,

PQ = PS + SQ = (SQ + 60) m.     (Eq 1)

Considering right angled △SQR, we get

$\Rightarrow \text{tan 60°} = \dfrac{QR}{SQ} \\[1em] \Rightarrow \sqrt{3} = \dfrac{QR}{SQ} \\[1em] \Rightarrow QR = \sqrt{3} \text{ SQ} \text{ .....(Eq 2)}$

Considering right angled △PQR, we get

$\Rightarrow \text{tan 30°} = \dfrac{QR}{PQ} \\[1em] \Rightarrow \dfrac{1}{\sqrt{3}} = \dfrac{QR}{PQ} \\[1em] \Rightarrow PQ = \sqrt{3} \text{ QR} \\[1em] \Rightarrow SQ + 60 = \sqrt{3} \text{ QR} \text{ ........(Eq 3)} \\[1em]$

Putting value of QR from Eq 2, in Eq 3 we get,

$\Rightarrow SQ + 60 = \sqrt{3} \times \sqrt{3} \text{ SQ} \\[1em] \Rightarrow SQ + 60 = 3 SQ \\[1em] \Rightarrow 2SQ = 60 \\[1em] \Rightarrow SQ = 30.$

From Eq 2,

$\Rightarrow QR = \sqrt{3}SQ \\[1em] \Rightarrow QR = \sqrt{3} \times 30 \\[1em] \Rightarrow QR = 51.96$

Correcting upto nearest meter QR = 52.

Hence, the height of building is 52 meters.

At a point on level ground, the angle of elevation of a vertical tower is found to be such that its tangent is $\dfrac{5}{12}$. On walking 192 m towards the tower, the tangent of the angle is found to be $\dfrac{3}{4}$. Find the height of the tower.

Answer

Let the height of tower QR be h meters and the angle of elevation be θ₁ and θ₂ at points P and S respectively.

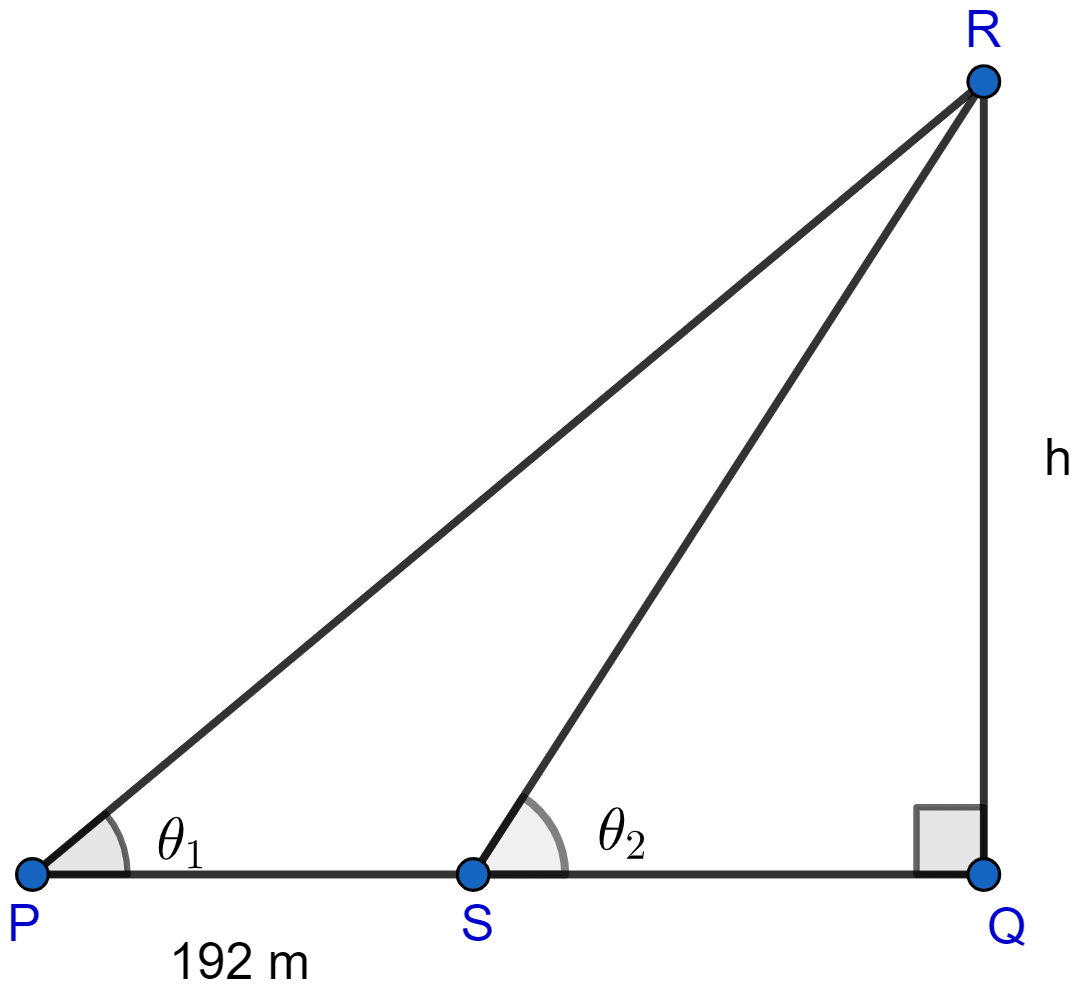
So,

$\text{tan }θ_1 = \dfrac{5}{12} \text{ and } \text{tan }θ_2 = \dfrac{3}{4}$

From figure,

QR = h meters
PQ = PS + QS = (192 + QS) meters.

Considering right angled △PQR, we get

$\Rightarrow \text{tan }θ_1 = \dfrac{QR}{PQ} \\[1em] \Rightarrow \dfrac{5}{12} = \dfrac{h}{192 + QS} \\[1em] \Rightarrow 5(192 + QS) = 12h \\[1em] \Rightarrow 5QS + 960 = 12h \text{ .......(Eq 1)}$

Considering right angled △SQR, we get

$\Rightarrow \text{tan }θ_2 = \dfrac{QR}{QS} \\[1em] \Rightarrow \dfrac{3}{4} = \dfrac{h}{QS} \\[1em] \Rightarrow 3QS = 4h \\[1em] \Rightarrow QS = \dfrac{4h}{3}\text{ .......(Eq 2)}$

Putting value of QS from Eq 2 in Eq 1 we get,

$\Rightarrow 5 \times \dfrac{4h}{3} + 960 = 12h \\[1em] \Rightarrow \dfrac{20h}{3} + 960 = 12h \\[1em] \Rightarrow \dfrac{20h + 2880}{3} = 12h \\[1em] \Rightarrow 20h + 2880 = 36h \\[1em] \Rightarrow 36h - 20h = 2880 \\[1em] \Rightarrow 16h = 2880 \\[1em] \Rightarrow h = \dfrac{2880}{16} \\[1em] \Rightarrow h = 180.$

Hence, the height of the tower is 180 meters.

In the figure, not drawn to scale, TF is a tower. The elevation of T from A is x° where tan x = $\dfrac{2}{5}$ and AF = 200 m. The elevation of T from B, where AB = 80 m, is y°. Calculate :

(i) the height of the tower TF.

(ii) the angle y, correct to the nearest degree.

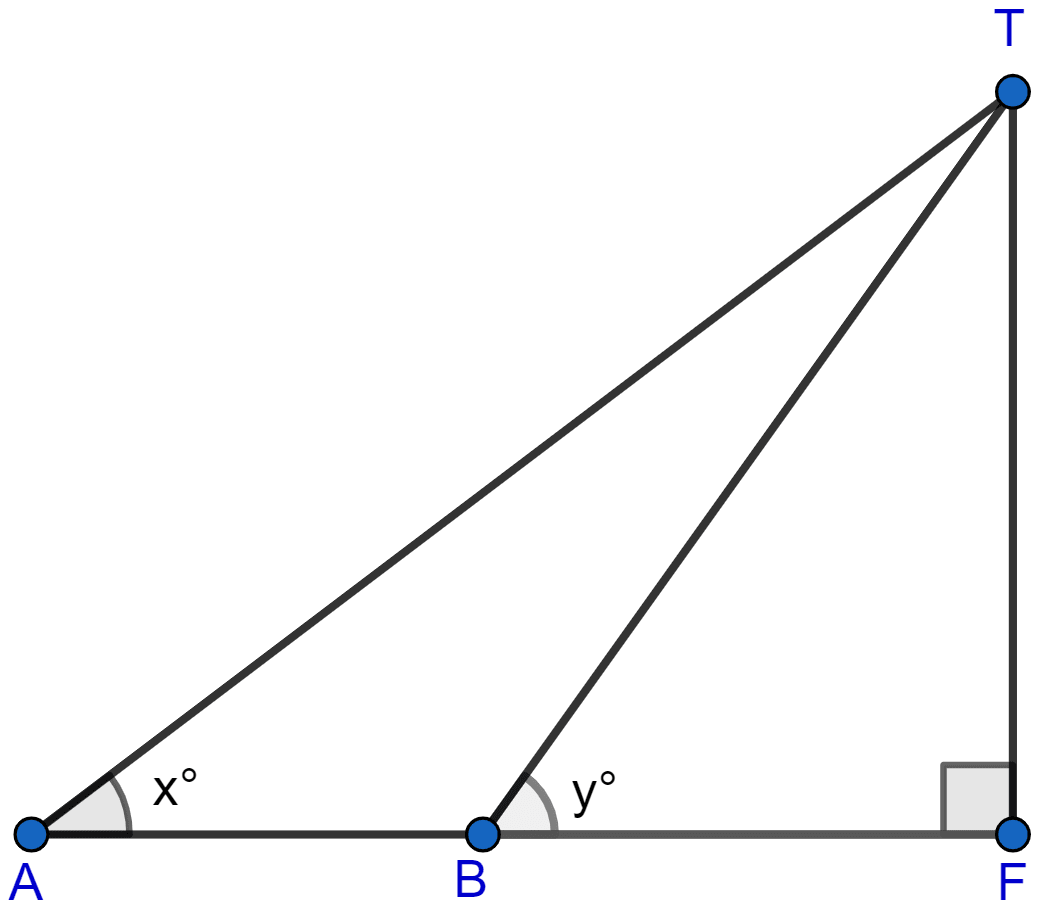
Answer

(i) From figure,

Considering right angled △AFT, we get

$\Rightarrow \text{tan x°} = \dfrac{TF}{AF} \\[1em] \Rightarrow \dfrac{2}{5} = \dfrac{TF}{200} \\[1em] \Rightarrow TF = \dfrac{2 \times 200}{5} \\[1em] \Rightarrow TF = 80$

Hence, the height of the tower is 80 meters.

(ii) From figure,

BF = AF - AB = 200 - 80 = 120 meters.

Considering right angled △BFT, we get

$\Rightarrow \text{tan y°} = \dfrac{TF}{BF} \\[1em] \Rightarrow \text{tan y°} = \dfrac{80}{120} \\[1em] \Rightarrow \text{tan y°} = 0.667 \\[1em] \Rightarrow \text{tan y°} = \text{tan 33° 41}' \\[1em] \Rightarrow \text{y°} = 33° 41'$

Rounding off to nearest degree, y = 34°.

Hence, angle y = 34°.

In the adjoining figure, not drawn to the scale, AB is a tower and two objects C and D are located on the ground, on the same side of AB. When observed from the top A of the tower, their angles of depression are 45° and 60°. Find the distance between the two objects, if the height of the tower is 300 m. Give your answer to the nearest meter.

Answer

From figure,

∠ACB = ∠EAC = 45° (Alternate angles are equal)
∠ADB = ∠EAD = 60° (Alternate angles are equal)

Considering right angled △ABC, we get

$\Rightarrow \text{tan 45°} = \dfrac{AB}{CB} \\[1em] \Rightarrow 1 = \dfrac{300}{CB} \\[1em] \Rightarrow CB = 300$

Considering right angled △ADB, we get

$\Rightarrow \text{tan 60°} = \dfrac{AB}{DB} \\[1em] \Rightarrow \sqrt{3} = \dfrac{300}{DB} \\[1em] \Rightarrow DB = \dfrac{300}{\sqrt{3}} \\[1em] \Rightarrow DB = 173.2$

Distance between two objects (CD) = CB - DB = 300 - 173.2 = 126.8.

Rounding off to nearest meter CD = 127 m.

Hence, the distance between two objects = 127 meters.

The horizontal distance between two towers is 140 m. The angle of elevation of the top of the first tower, when seen from the top of the second tower is 30°. If the height of the second tower is 60 m, find the height of the first tower.

Answer

Let AB be the first tower and CD be the second tower. From C draw a line parallel to AD and perpendicular to AB meeting AB at point E.

Now ADCE forms a rectangle,

EC = AD = 140
AE = DC = 60.

Considering right angled △BCE, we get

$\Rightarrow \text{tan 30°} = \dfrac{BE}{EC} \\[1em] \Rightarrow \dfrac{1}{\sqrt{3}} = \dfrac{BE}{140} \\[1em] \Rightarrow BE = \dfrac{140}{\sqrt{3}} \\[1em] \Rightarrow BE = 80.83$

From figure,

AB = AE + BE = 60 + 80.83 = 140.83

Hence, the height of the first tower is 140.83 meters.

As observed from the top of a 80 m tall light house, the angles of depression of two ships on the same side of the light house in horizontal line with its base are 30° and 40° respectively. Find the distance between the two ships. Give your answer correct to nearest meter.

Answer

Let AB be the tower of length 80 m and the ships be at point C and D.

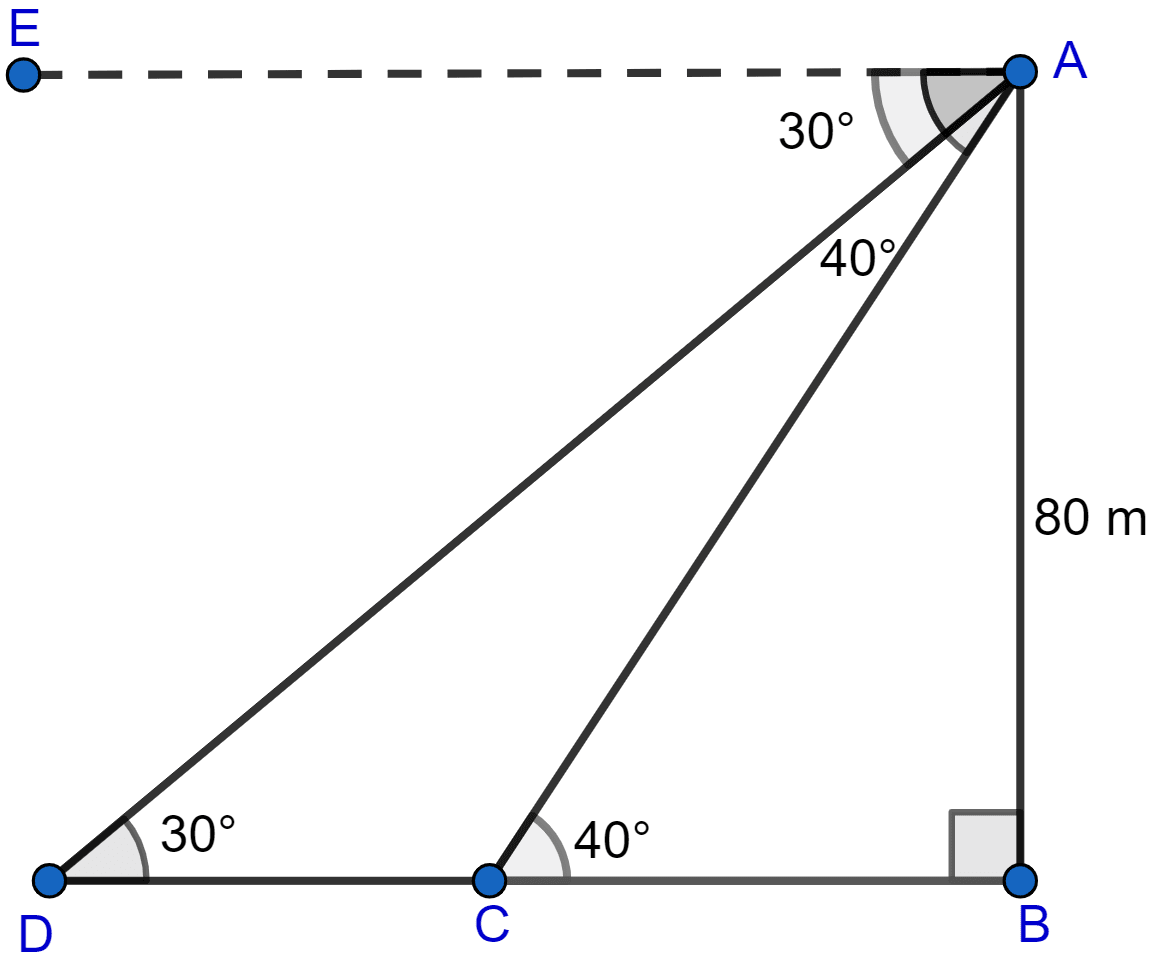
From figure,

∠ADB = ∠EAD = 30° (Alternate angles are equal)
∠ACB = ∠EAC = 40° (Alternate angles are equal)

Considering right angled △ADB, we get

$\Rightarrow \text{tan 30°} = \dfrac{AB}{DB} \\[1em] \Rightarrow \dfrac{1}{\sqrt{3}} = \dfrac{80}{DB} \\[1em] \Rightarrow DB = 80 \times \sqrt{3} = 138.56$

Considering right angled △ACB, we get

$\Rightarrow \text{tan 40°} = \dfrac{AB}{BC} \\[1em] \Rightarrow 0.8391 = \dfrac{80}{BC} \\[1em] \Rightarrow BC = \dfrac{80}{0.8391} \\[1em] \Rightarrow BC = 95.34$

Distance between two ships (DC) = DB - BC = 138.56 - 95.34 = 43.22 meters.

Rounding off to nearest meter DC = 43 meters.

Hence, the distance between two ships is 43 meters.

The angle of elevation of a pillar from a point A on the ground is 45° and from a point B diametrically opposite to A and on the other side of the pillar is 60°. Find the height of the pillar, given that the distance between A and B is 15 m.

Answer

Let the height of pillar (CD) be h meters.

Considering right angled △ACD, we get

$\Rightarrow \text{tan 45°} = \dfrac{CD}{AC} \\[1em] \Rightarrow 1 = \dfrac{h}{AC} \\[1em] \Rightarrow AC = h$

From figure,

BC = AB - AC = (15 - h) meters

Considering right angled △BCD, we get

$\Rightarrow \text{tan 60°} = \dfrac{CD}{BC} \\[1em] \Rightarrow \sqrt{3} = \dfrac{h}{15 - h} \\[1em] \Rightarrow \sqrt{3}(15 - h) = h \\[1em] \Rightarrow 15\sqrt{3} - \sqrt{3}h = h \\[1em] \Rightarrow 15\sqrt{3} = \sqrt{3}h + h \\[1em] \Rightarrow 25.98 = 2.732h \\[1em] \Rightarrow h = \dfrac{25.98}{2.732} \\[1em] \Rightarrow h = 9.51$

Hence, the height of the pillar is 9.51 meters.

From two points A and B on the same side of a building, the angles of elevation of the top of the building are 30° and 60° respectively. If the height of the building is 10 m, find the distance between A and B correct to two decimal places.

Answer

From figure,

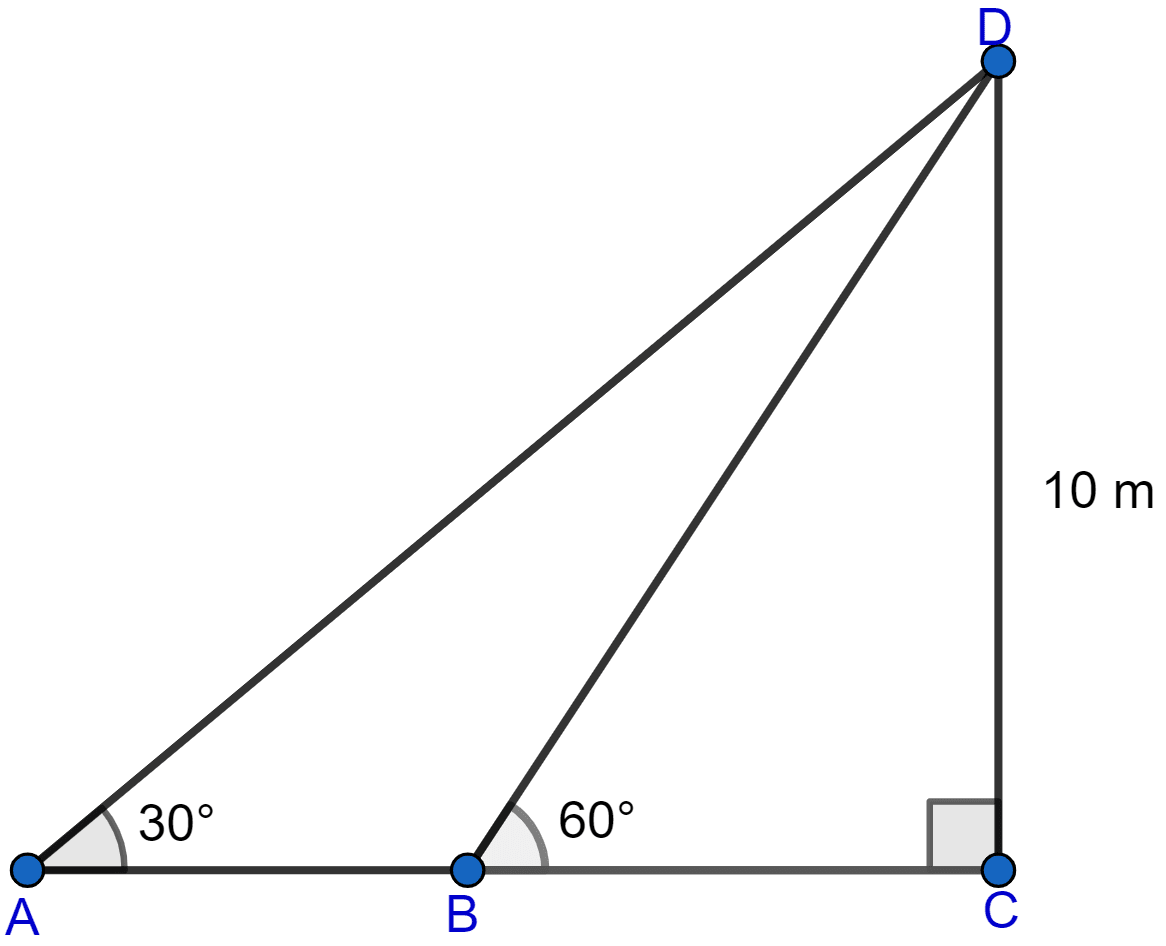
Considering right angled △ACD, we get

$\Rightarrow \text{tan 30°} = \dfrac{CD}{AC} \\[1em] \Rightarrow \dfrac{1}{\sqrt{3}} = \dfrac{10}{AC} \\[1em] \Rightarrow AC = 10 \times \sqrt{3} = 17.32$

Considering right angled △BCD, we get

$\Rightarrow \text{tan 60°} = \dfrac{CD}{BC} \\[1em] \Rightarrow \sqrt{3} = \dfrac{10}{BC} \\[1em] \Rightarrow BC = \dfrac{10}{\sqrt{3}} \\[1em] \Rightarrow BC = 5.77$

AB = AC - BC = 17.32 - 5.77 = 11.55 meters.

Hence, the distance between A and B = 11.55 meters.

The angles of depression of two ships A and B as observed from the top of a light house 60 m high are 60° and 45° respectively. If the two ships are on the opposite sides of the light house, find the distance between the two ships. Give your answer correct to the nearest whole number.

Answer

Let CD be the light house, 60 m tall and ships at point A and B.

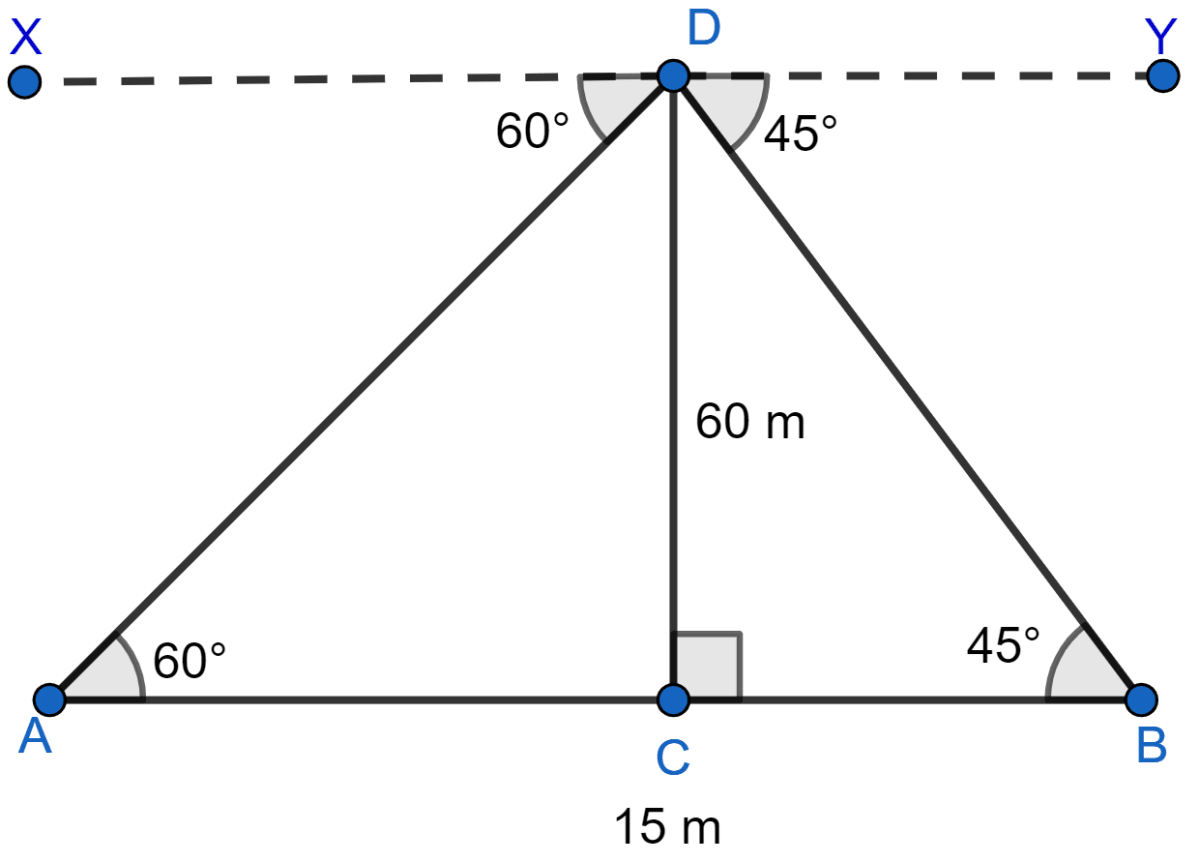
From figure,

∠DAC = ∠XDA = 60° (Alternate angles are equal)
∠DBC = ∠YDB = 45° (Alternate angles are equal)

Considering right angled △ACD, we get

$\Rightarrow \text{tan 60°} = \dfrac{CD}{AC} \\[1em] \Rightarrow \sqrt{3} = \dfrac{60}{AC} \\[1em] \Rightarrow AC = \dfrac{60}{\sqrt{3}} = 34.64$

Considering right angled △BCD, we get

$\Rightarrow \text{tan 45°} = \dfrac{CD}{BC} \\[1em] \Rightarrow 1 = \dfrac{60}{BC} \\[1em] \Rightarrow BC = 60$

Distance between two ships (AB) = AC + BC = 34.64 + 60 = 94.64 meters.

Rounding off to nearest meter, AB = 95 meters.

Hence, the distance between two ships is 95 meters.

An aeroplane at an altitude of 250 m observes the angle of depression of two boats on the opposite banks of a river to be 45° and 60° respectively. Find the width of the river. Write the answer correct to the nearest whole number.

Answer

Let aeroplane be at point D and boats be at point A and B. Since, aeroplane is at an altitude of 250 m therefore,

∴ CD = 250 m.

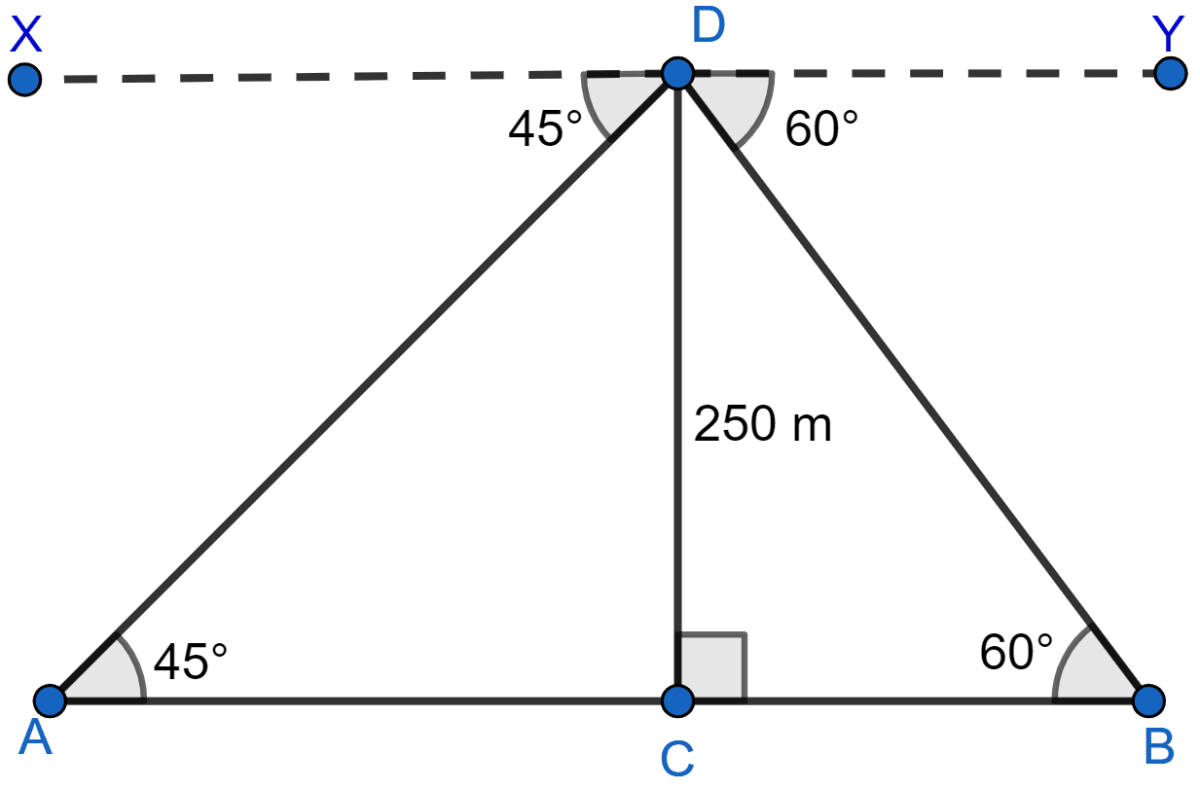
From figure,

∠DAC = ∠XDA = 45° (Alternate angles are equal)
∠DBC = ∠YDB = 60° (Alternate angles are equal)

Considering right angled △BCD, we get

$\Rightarrow \text{tan 60°} = \dfrac{CD}{BC} \\[1em] \Rightarrow \sqrt{3} = \dfrac{250}{BC} \\[1em] \Rightarrow BC = \dfrac{250}{\sqrt{3}} = 144.34$

Considering right angled △ACD, we get

$\Rightarrow \text{tan 45°} = \dfrac{CD}{AC} \\[1em] \Rightarrow 1 = \dfrac{250}{AC} \\[1em] \Rightarrow AC = 250$

Width of the river (AB) = AC + BC = 144.34 + 250 = 394.34 meters.

Rounding off to nearest meter AB = 394 meters.

Hence, the width of the river is 394 meters.

From a tower 126 m high, the angles of depression of two rocks which are in a horizontal line through the base of the tower are 16° and 12° 20'. Find the distance between the rocks if they are on

(i) the same side of the tower

(ii) the opposite sides of the tower.

Answer

(i) Let the rocks be at point A and D.

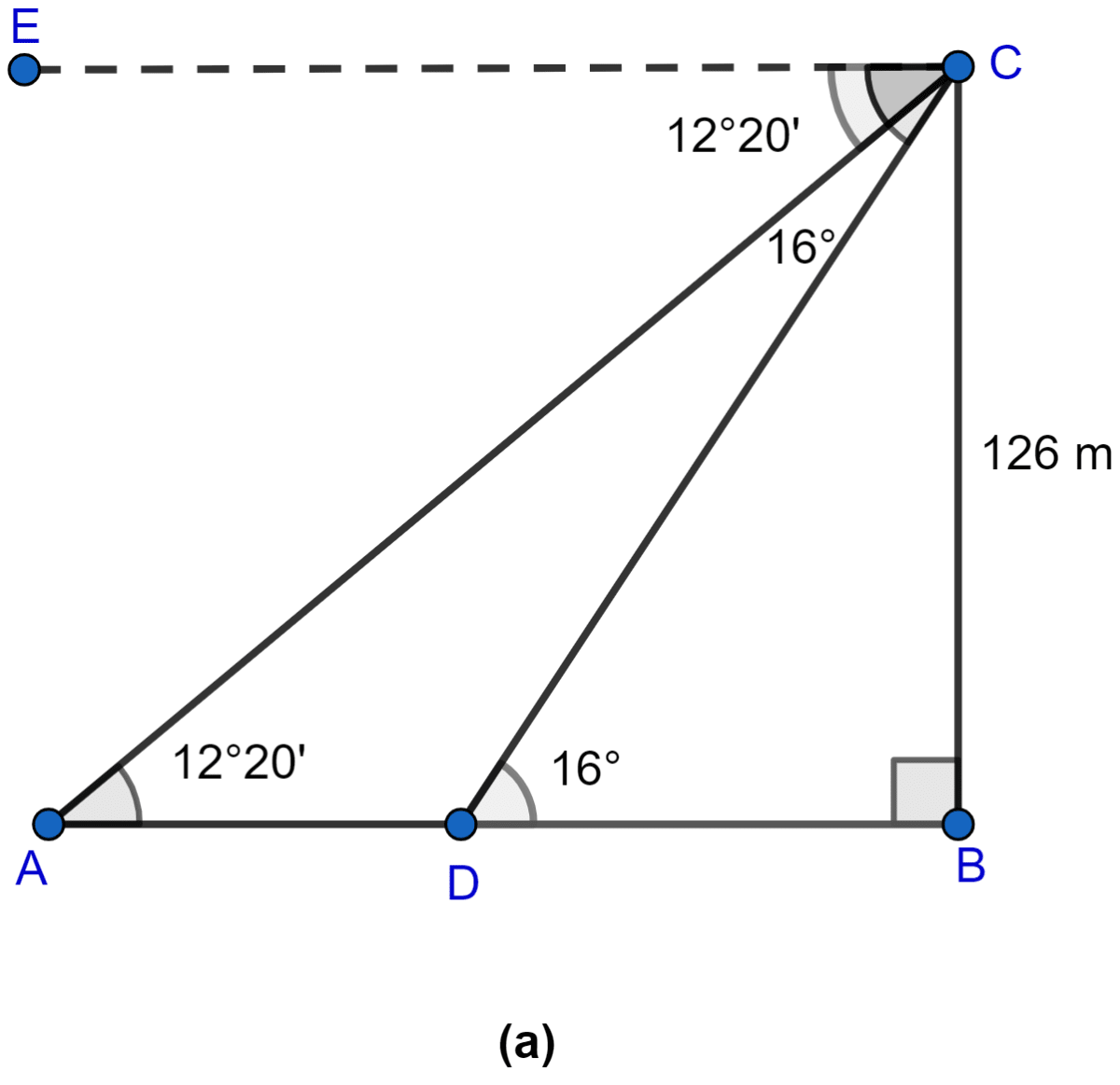
From figure a,

∠CAB = ∠ECA = 12° 20' (Alternate angles are equal)
∠CDB = ∠ECD = 16° (Alternate angles are equal)

Considering right angled △ABC, we get

$\Rightarrow \text{tan 12° 20}' = \dfrac{BC}{AB} \\[1em] \Rightarrow 0.2186 = \dfrac{126}{AB} \\[1em] \Rightarrow AB = \dfrac{126}{0.2186} = 576.29$

Considering right angled △BCD, we get

$\Rightarrow \text{tan 16°} = \dfrac{BC}{BD} \\[1em] \Rightarrow 0.2867 = \dfrac{126}{BD} \\[1em] \Rightarrow BD = \dfrac{126}{0.2867} = 439.48$

Distance between two rocks (AD) = AB - BD = 576.29 - 439.48 = 136.81

Hence, the distance between two rocks when they are on same side of the tower is 136.81 meters.

(ii) Let the rocks be at point A and B.

From figure b,

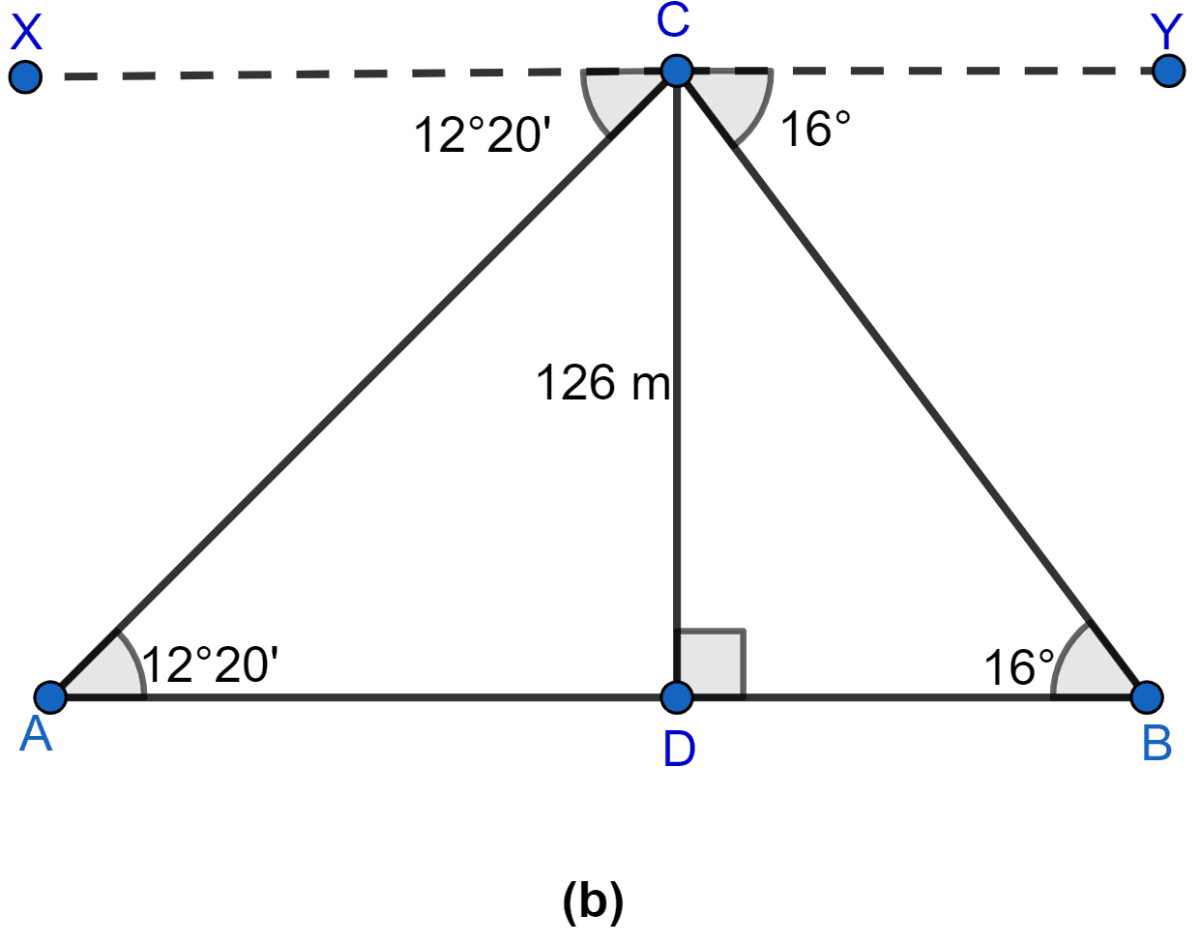
∠CAD = ∠XCA = 12° 20' (Alternate angles are equal)
∠CBD = ∠YCB = 16° (Alternate angles are equal)

Considering right angled △ADC, we get

$\Rightarrow \text{tan 12° 20}' = \dfrac{CD}{AD} \\[1em] \Rightarrow 0.2186 = \dfrac{126}{AD} \\[1em] \Rightarrow AD = \dfrac{126}{0.2186} = 576.29$

Considering right angled △BCD, we get

$\Rightarrow \text{tan 16°} = \dfrac{CD}{DB} \\[1em] \Rightarrow 0.2867 = \dfrac{126}{DB} \\[1em] \Rightarrow DB = \dfrac{126}{0.2867} = 439.48$

Distance between two rocks (AB) = AD + DB = 576.29 + 439.48 = 1015.7

Hence, the distance between two rocks when they are on opposite sides of the tower is 1015.7 meters.

A man 1.8 m high stands at a distance of 3.6 m from a lamp post and casts a shadow of 5.4 m on the ground. Find the height of the lamp post.

Answer

Let AB be the lamp post and CD the height of man.

BD is the distance of man from the foot of the lamp and FD is the shadow of man.

CE || DB.

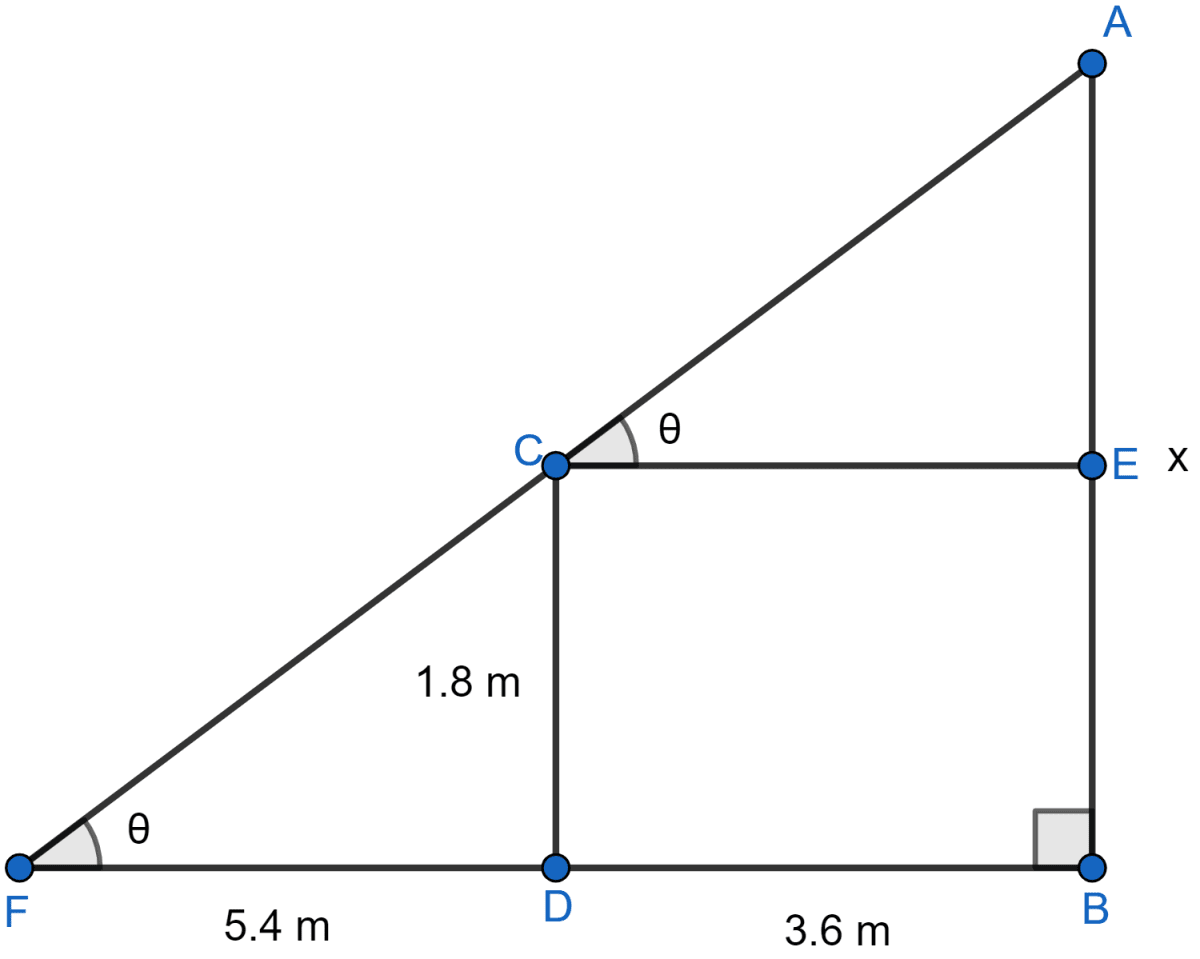
Take AB = x and CD = 1.8 m
EB = CD = 1.8 m
CE = DB = 3.6 m
AE = (x - 1.8) m
Shadow (FD) = 5.4 m

Considering right angled △ACE, we get

$\Rightarrow \text{tan θ} = \dfrac{AE}{CE} \\[1em] \Rightarrow \text{tan θ} = \dfrac{x - 1.8}{3.6} \text{ ......(Eq 1)}$

Considering right angled △CFD, we get

$\Rightarrow \text{tan θ} = \dfrac{CD}{FD} \\[1em] \Rightarrow \text{tan θ} = \dfrac{1.8}{5.4} = \dfrac{1}{3} \text{ ......(Eq 2)}$

Comparing Eq 1 and Eq 2 we get,

$\Rightarrow \dfrac{x - 1.8}{3.6} = \dfrac{1}{3} \\[1em] \Rightarrow 3x - 5.4 = 3.6 \\[1em] \Rightarrow 3x = 5.4 + 3.6 \\[1em] \Rightarrow 3x = 9 \\[1em] \Rightarrow x = 3.$

Hence, the height of the lamp post is 3 meters.

From top of a cliff, angle of depression of the top and bottom of a tower observed to be 45° and 60° respectively. If the height of the tower is 20 m. Find:

(i) the height of the cliff.

(ii) the distance between the cliff and the tower.

Answer

(i) Let AB be the cliff and CD be the tower.

From figure,

∠ACE = ∠FAC = 45° (Alternate angles are equal)

∠ADB = ∠FAD = 60° (Alternate angles are equal)

Let BD = x meters.

From figure,

EC = BD = x meters.

EB = CD = 20 meters.

In △ AEC,

⇒ tan 45° = $\dfrac{AE}{EC}$

⇒ 1 = $\dfrac{AE}{x}$

⇒ AE = x meters.

In △ ABD,

⇒ tan 60° = $\dfrac{AB}{BD}$

$\Rightarrow \sqrt{3} = \dfrac{AE + EB}{BD} \\[1em] \Rightarrow \sqrt{3} = \dfrac{x + 20}{x} \\[1em] \Rightarrow x\sqrt{3} = x + 20 \\[1em] \Rightarrow x\sqrt{3} - x = 20 \\[1em] \Rightarrow x(\sqrt{3} - 1) = 20 \\[1em] \Rightarrow x = \dfrac{20}{(\sqrt{3} - 1)} \\[1em] \Rightarrow x = \dfrac{20}{1.732 - 1} \\[1em] \Rightarrow x = \dfrac{20}{0.732} \\[1em] \Rightarrow x = 27.32 \text{ meters}$

From figure,

Height of cliff (AB) = AE + EB

= x + 20

= 27.32 + 20

= 47.32 meters.

Hence, the height of cliff = 47.32 meters.

(ii) From figure,

Distance between cliff and tower (BD) = x meters = 27.32 meters.

Hence, distance between cliff and tower = 27.32 meters.

A pole of height 5 m is fixed on the top of a tower. The angle of elevation of the top of pole as observed from a point A on the ground is 60° and the angle of depression of the point A from the top of the tower is 45°. Find the height of the tower. (Take $\sqrt{3} = 1.732$)

Answer

Let the height of tower (BC) be h meters and BD be the pole of height 5 meters above it.

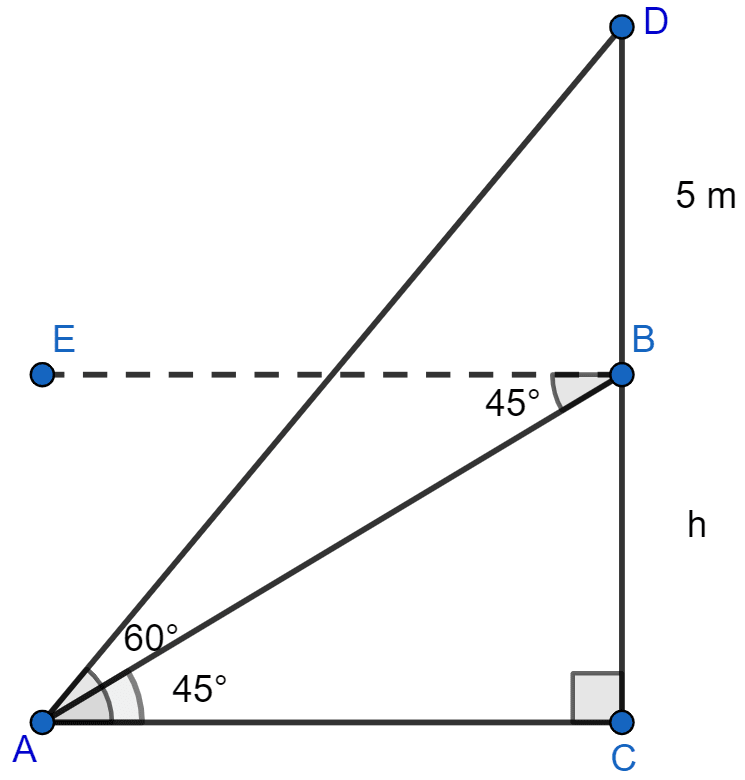
From figure,

∠BAC = ∠EBA = 45° (Alternate angles are equal)

DC = DB + BC = 5 + h.

Considering right angled △BCA, we get

$\Rightarrow \text{tan 45°} = \dfrac{BC}{AC} \\[1em] \Rightarrow 1 = \dfrac{h}{AC} \\[1em] \Rightarrow AC = h \text{ ......(Eq 1)}$

Considering right angled △DCA, we get

$\Rightarrow \text{tan 60°} = \dfrac{DC}{AC} \\[1em] \Rightarrow \sqrt{3} = \dfrac{h + 5}{AC}$

Putting value of AC from Eq 1 in above equation we get,

$\Rightarrow \sqrt{3} = \dfrac{h + 5}{h} \\[1em] \Rightarrow \sqrt{3}h = h + 5 \\[1em] \Rightarrow \sqrt{3}h - h = 5 \\[1em] \Rightarrow 0.732\text{ h} = 5 \\[1em] \Rightarrow h = \dfrac{5}{0.732} \\[1em] \Rightarrow h = 6.83$

Hence, the height of the tower is 6.83 meters.

A vertical pole and a vertical tower are on the same level ground. From the top of the pole, the angle of elevation of the top of the tower is 60° and the angle of depression of the foot of tower is 30°. Find the height of the tower if the height of the pole is 20 m.

Answer

Let AB be the pole and CD be the tower. Let length of tower (CD) be h metres.

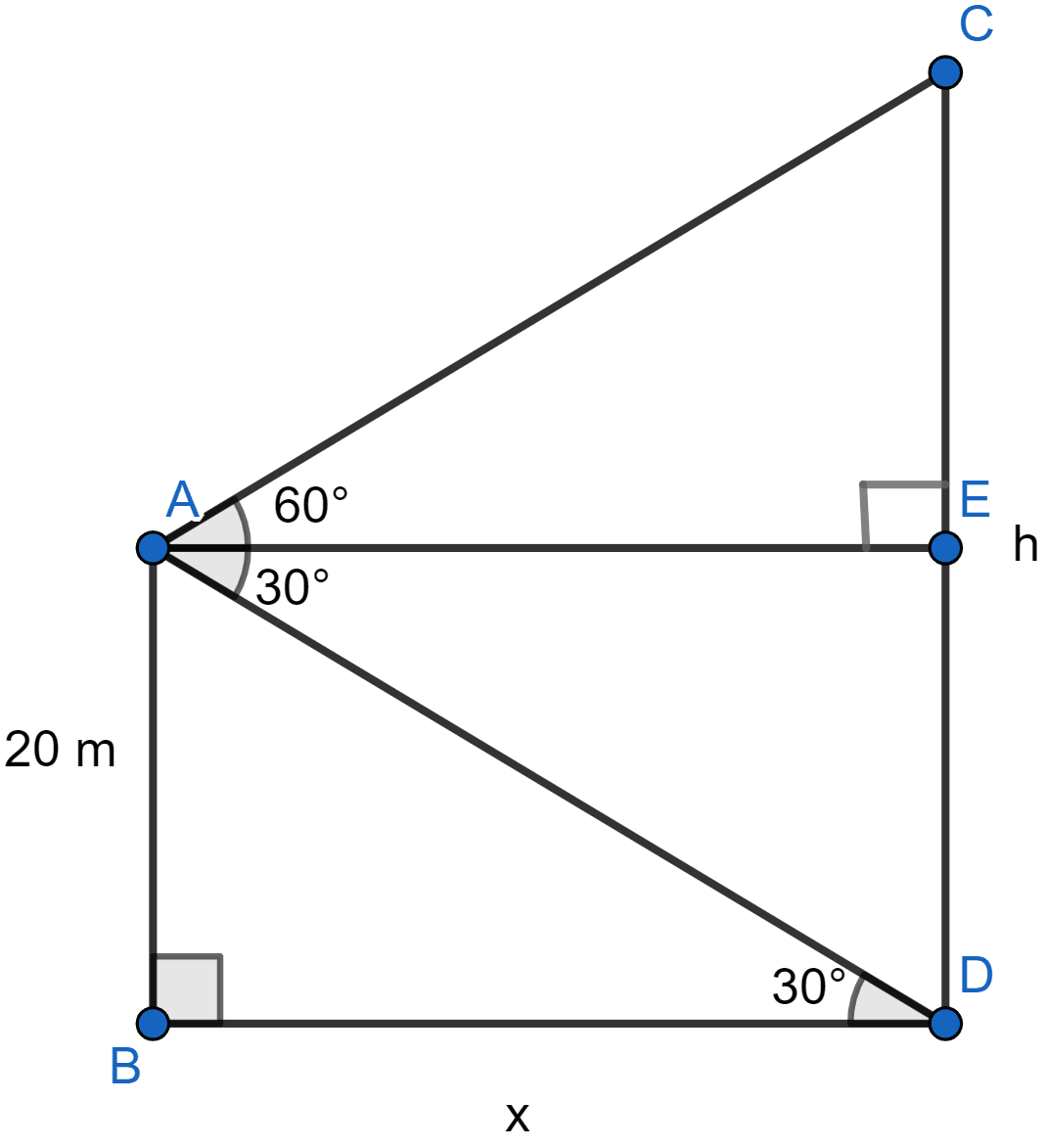
Let distance between pole and tower (BD) be x meters.

From figure,

ABDE is a rectangle so,

DE = AB = 20 meters
AE = BD = x meters
CE = CD - DE = (h - 20) meters
∠EAD = ∠ADB = 30° (Alternate angles are equal)

Considering right angled △ABD we get,

$\Rightarrow \text{tan 30°} = \dfrac{AB}{BD} \\[1em] \Rightarrow \dfrac{1}{\sqrt{3}} = \dfrac{20}{x} \\[1em] \Rightarrow x = 20\sqrt{3}$

Considering right angled △ACE we get,

$\Rightarrow \text{tan 60°} = \dfrac{CE}{AE} \\[1em] \Rightarrow \sqrt{3} = \dfrac{h - 20}{BD} \\[1em] \Rightarrow \sqrt{3} = \dfrac{h - 20}{x} \\[1em] \Rightarrow \sqrt{3} = \dfrac{h - 20}{20\sqrt{3}} \\[1em] \Rightarrow 20\sqrt{3} \times \sqrt{3} = h - 20 \\[1em] \Rightarrow 60 = h - 20 \\[1em] \Rightarrow h = 80.$

Hence, the height of the tower is 80 meters.

From the top of a building 20 m high, the angle of elevation of the top of a monument is 45° and the angle of depression of its foot is 15°. Find the height of the monument.

Answer

Let AB be the building and CD be the monument. Let length of monument (CD) be h metres.

Let distance between building and monument (BD) be x meters.

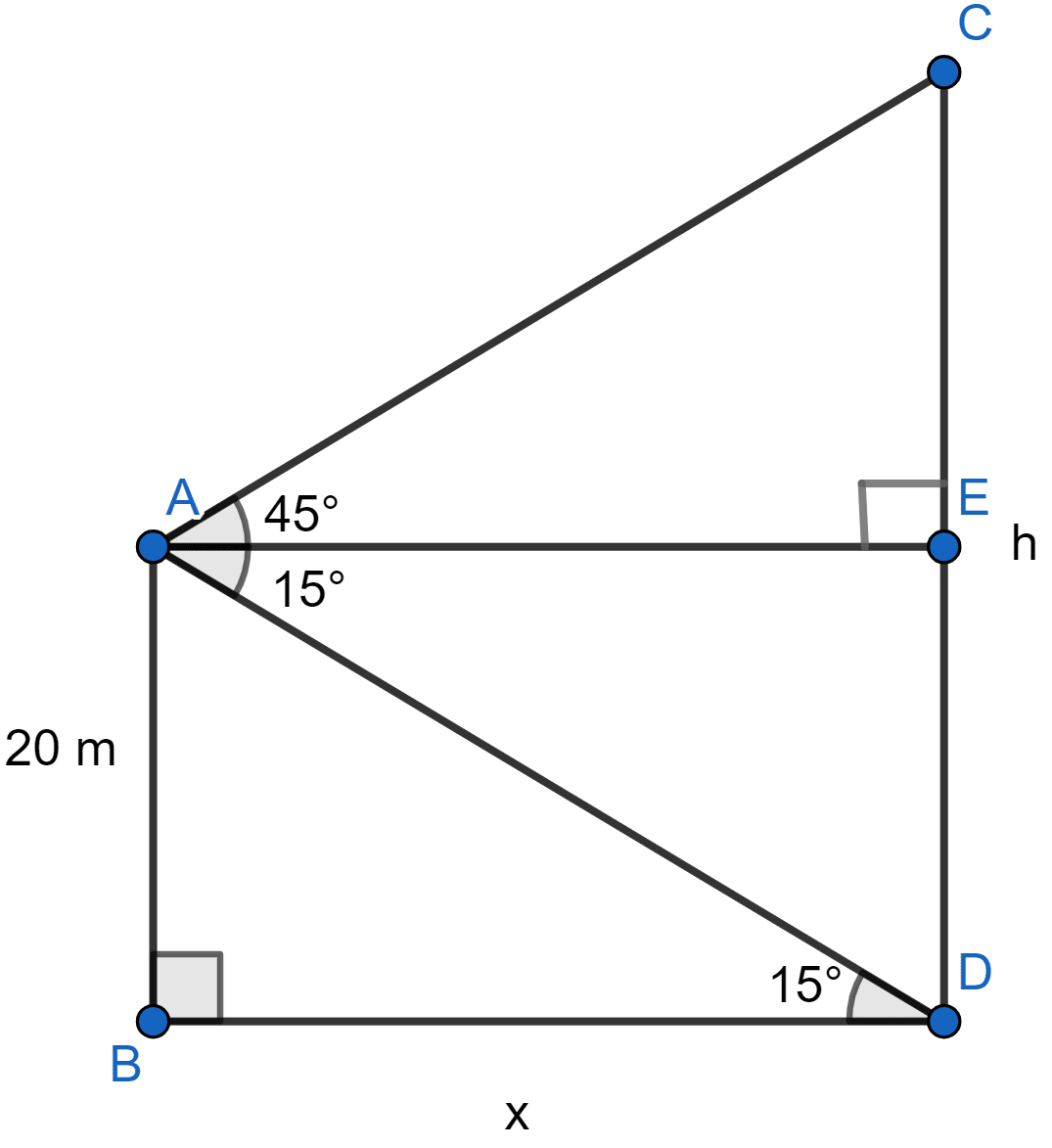
From figure,

ABDE is a rectangle so,

DE = AB = 20 meters
AE = BD = x meters
CE = CD - DE = (h - 20) meters
∠EAD = ∠ADB = 15°

Considering right angled △ABD we get,

$\Rightarrow \text{tan 15°} = \dfrac{AB}{BD} \\[1em] \Rightarrow 0.2679 = \dfrac{20}{x} \\[1em] \Rightarrow x = \dfrac{20}{0.2679} \\[1em] \Rightarrow x = 74.65$

Considering right angled △ACE we get,

$\Rightarrow \text{tan 45°} = \dfrac{CE}{AE} \\[1em] \Rightarrow 1 = \dfrac{h - 20}{x} \\[1em] \Rightarrow x = h - 20 \\[1em] \Rightarrow 74.65 = h - 20 \\[1em] \Rightarrow h = 74.65 + 20 \\[1em] \Rightarrow h = 94.65$

Hence, the height of the monument is 94.65 meters.

In the adjoining figure, the shadow of a vertical tower on the level ground increases by 10 m, when the altitude of the sun changes from 45° to 30°. Find the height of the tower and give your answer, correct to $\dfrac{1}{10}$ of a metre.

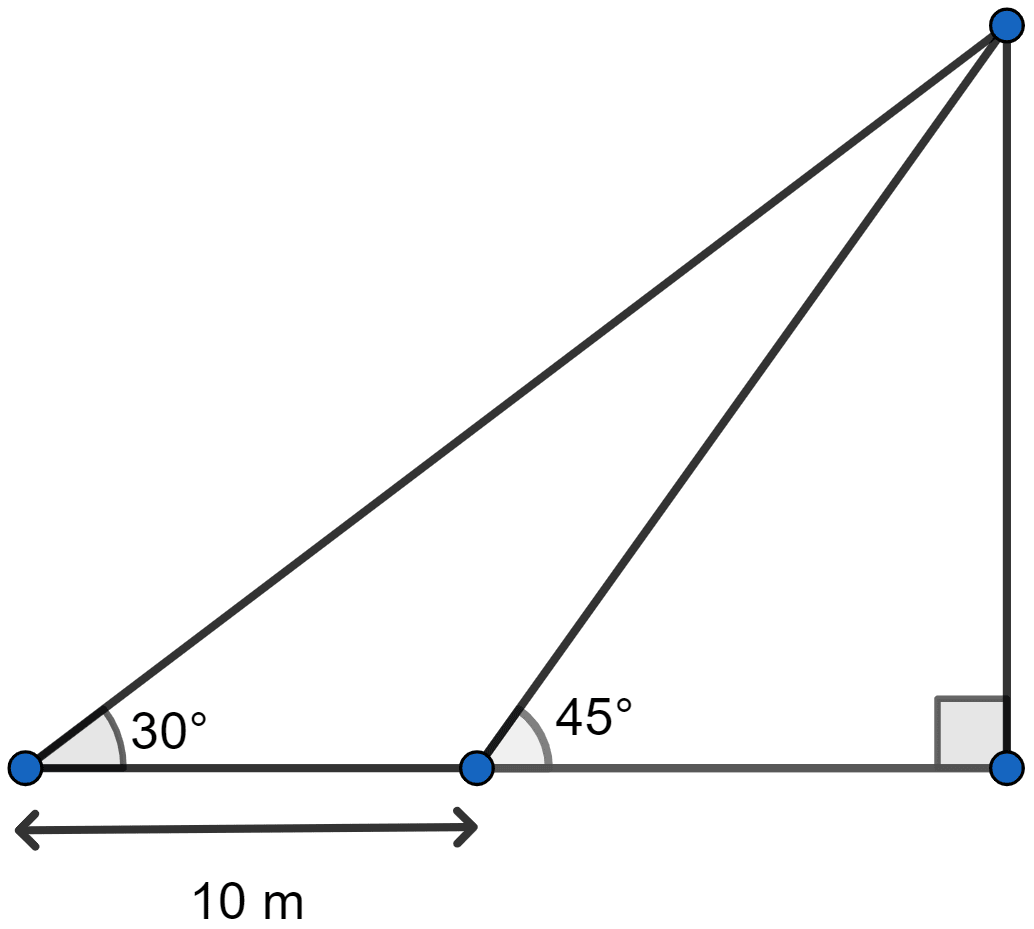
Answer

Let the initial length of shadow be x meters and height of tower be h meters.

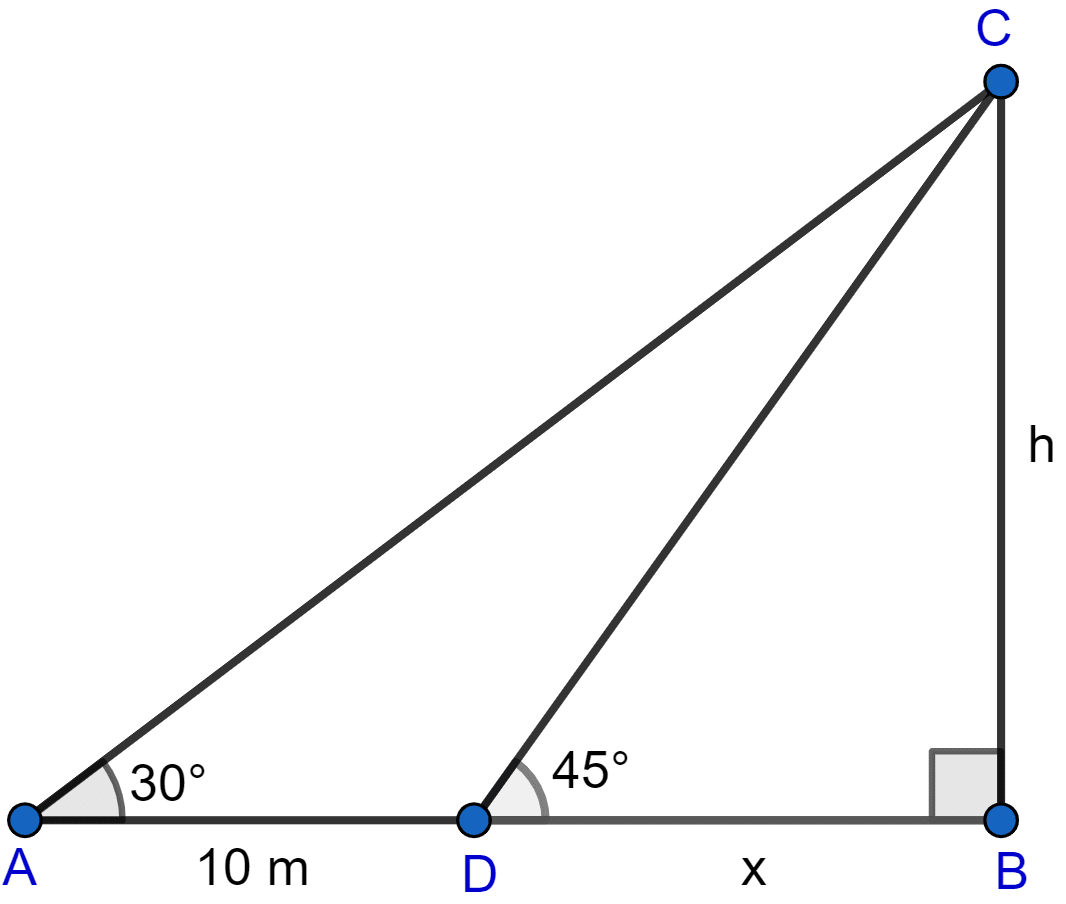
Considering right angled △DBC, we get

$\Rightarrow \text{tan 45°} = \dfrac{BC}{DB} \\[1em] \Rightarrow 1 = \dfrac{h}{x} \\[1em] \Rightarrow x = h \text{ ......(Eq 1)}$

Considering right angled △ABC we get,

$\Rightarrow \text{tan 30°} = \dfrac{BC}{AB} \\[1em] \Rightarrow \dfrac{1}{\sqrt{3}} = \dfrac{h}{x + 10} \\[1em] \Rightarrow x + 10 = \sqrt{3}h \\[1em] \Rightarrow h + 10 = \sqrt{3}h \text{ .....(Using Eq 1)} \\[1em] \Rightarrow \sqrt{3}h - h = 10 \\[1em] \Rightarrow 0.732h = 10 \\[1em] \Rightarrow h = \dfrac{10}{0.732} \\[1em] \Rightarrow h = 13.7$

Hence, the height of tower is 13.7 meters.

An aircraft is flying at a constant height with a speed of 360 km/h. From a point on the ground, the angle of elevation of the aircraft at an instant was observed to be 45°. After 20 seconds, the angle of elevation was observed to be 30°. Determine the height at which the aircraft is flying (use $\sqrt{3}$ = 1.732).

Answer

Speed of aircraft = 360 km/h

Distance covered in 20 seconds = $\dfrac{360 \times 20}{60 \times 60} = 2$ km

Let aeroplane be flying at a hight of h km.

E is the fixed point on ground and A is the initial position of aircraft and C is the position after 20 seconds.

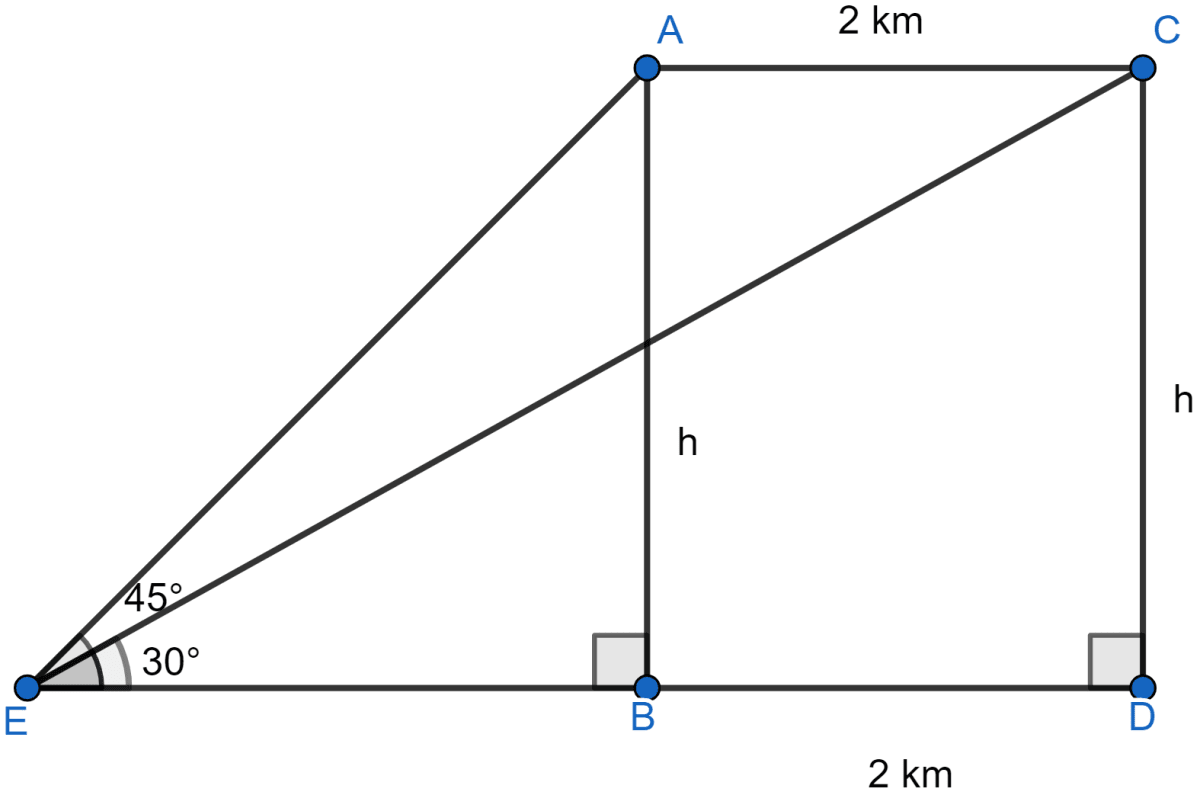
Considering right angled △EDC we get,

$\Rightarrow \text{tan 30°} = \dfrac{CD}{ED} \\[1em] \Rightarrow \dfrac{1}{\sqrt{3}} = \dfrac{h}{ED} \\[1em] \Rightarrow ED = h\sqrt{3}$

From figure,

$\Rightarrow ED = EB + BD \\[1em] \Rightarrow h\sqrt{3} = EB + 2 \\[1em] \Rightarrow EB = h\sqrt{3} - 2 \text{ .......(Eq 1)}$

Considering right angled △AEB we get,

$\Rightarrow \text{tan 45°} = \dfrac{AB}{EB} \\[1em] \Rightarrow 1 = \dfrac{h}{EB} \\[1em] \Rightarrow EB = h \text{ .......(Eq 2)}$

Comparing Eq 1 and Eq 2 we get,

$h = h\sqrt{3} - 2 \\[1em] \sqrt{3}h - h = 2 \\[1em] 0.732h = 2 \\[1em] h = \dfrac{2}{0.732} \\[1em] h = 2.732 \text{ km} = 2732 \text{ m}$

Hence, the aircraft is flying at a height of 2732 meters.

The angles of depression of two ships A and B on opposite sides of a light house of height 100 m are respectively 42° and 54°. The line joining the two ships passes through the foot of the light house.

(a) Find the distance between the two ships A and B.

(b) Give your final answer correct to the nearest whole number.

(Use mathematical tables for this question)

Answer

Let ∠BCP = α and ∠ACP = β

From figure,

⇒ α + 54° = 90°

⇒ α = 90° - 54° = 36°.

⇒ β + 42° = 90°

⇒ β = 90° - 42° = 48°.

⇒ tan α = $\dfrac{BP}{CP}$

⇒ tan 36° = $\dfrac{BP}{100}$

⇒ 0.7265 = $\dfrac{BP}{100}$

⇒ BP = 0.7265 × 100 = 72.65 m

⇒ tan β = $\dfrac{AP}{CP}$

⇒ tan 48° = $\dfrac{AP}{100}$

⇒ 1.1106 = $\dfrac{AP}{100}$

⇒ AP = 1.1106 × 100 = 111.06 m

(a) From figure,

AB = AP + BP = 72.65 + 111.06 = 183.71 m

Hence, the distance between two ships = 183.71 m.

(b) On rounding off,

AB = 184 m.

Hence, the distance between two ships = 184 m.

The angle of elevation of the top of a 100 m high tree from two points A and B on the opposite side of the tree are 52° and 45° respectively. Find the distance AB, to the nearest metre.

Answer

From figure,

⇒ tan 52° = $\dfrac{CD}{AC}$

⇒ 1.28 = $\dfrac{100}{AC}$

⇒ AC = $\dfrac{100}{1.28}$ = 78.125 m

⇒ tan 45° = $\dfrac{CD}{BC}$

⇒ 1 = $\dfrac{100}{BC}$

⇒ BC = 100 m

⇒ AB = AC + BC = 78.125 + 100 = 178.125 m

Hence, AB = 178.125 m

If a kite is flying at a height of $40\sqrt{3}$ meters from the level ground, attached to a string inclined at 60° to the horizontal, then the length of the string is

1. 80 m

2. $60 \sqrt{3}$ m

3. $80\sqrt{3}$ m

4. 120 m.

Answer

Let the kite be at point B.

Considering right angled △ABC we get,

$\text{sin 60} = \dfrac{BC}{AB} \\[1em] \dfrac{\sqrt{3}}{2} = \dfrac{40\sqrt{3}}{AB} \\[1em] AB = \dfrac{40 \sqrt{3} \times 2}{\sqrt{3}} \\[1em] AB = 80$

Hence, Option 1 is the correct option.

If the angle of depression of an object from a 75 m high tower is 30°, then the distance of the object from the tower is

1. $25\sqrt{3}$ m

2. $50\sqrt{3}$ m

3. $75\sqrt{3}$ m

4. 150 m

Answer

From figure,

∠ACB = ∠DAC = 30° (Alternate angles are equal)

Considering right angled △ABC we get,

$\Rightarrow \text{tan 30°} = \dfrac{AB}{BC} \\[1em] \Rightarrow \dfrac{1}{\sqrt{3}} = \dfrac{75}{BC} \\[1em] \Rightarrow BC = 75\sqrt{3}$

Hence, Option 3 is the correct option.

A ladder 14 m long rests against a wall. If the foot of ladder is 7 m from the wall, then the angle of elevation is

1. 15°

2. 30°

3. 45°

4. 60°

Answer

Let AB be the ladder and θ be the angle of elevation.

Considering right angled △ABC we get,

$\Rightarrow \text{cos θ} = \dfrac{7}{14} \\[1em] \Rightarrow \text{cos θ} = \dfrac{1}{2} \\[1em] \Rightarrow \text{cos θ} = \text{cos 60°} \\[1em] \Rightarrow θ = 60°.$

Hence, Option 4 is the correct option.

A light house is 80 m high. The angle of elevation of its top from a point 80 m away from its foot along the same horizontal line is

1. 60°

2. 45°

3. 30°

4. 90°

Answer

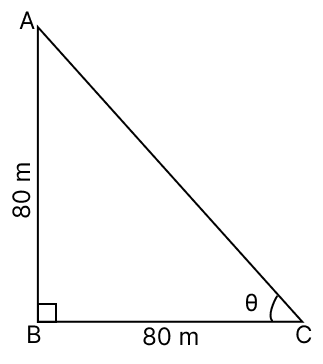
Let AB be the lighthouse and C be the point 80 m away from its foot.

Given, AB = 80 m

BC = 80 m

⇒ tan θ = $\dfrac{\text{AB}}{\text{BC}}$

⇒ tan θ = $\dfrac{80}{80}$

⇒ tan θ = 1

⇒ tan θ = tan 45°

⇒ θ = 45°.

Hence, option 2 is the correct option.

If a pole 6 m high casts shadow $2\sqrt{3}$ m long on the ground, then the sun's elevation is

1. 60°

2. 45°

3. 30°

4. 90°

Answer

Let the angle of elevation be θ and AB be the pole.

Considering right angled △ABC we get,

$\Rightarrow \text{tan θ} = \dfrac{6}{2\sqrt{3}} \\[1em] \Rightarrow \text{tan θ} = \dfrac{3}{\sqrt{3}} \\[1em] \Rightarrow \text{tan θ} = \sqrt{3} \\[1em] \Rightarrow \text{tan θ} = \text{tan 60°} \\[1em] \Rightarrow θ = 60°.$

Hence, Option 1 is the correct option.

If the length of the shadow of a tower is $\sqrt{3}$ times that of its height, then the angle of elevation of the sun is

1. 15°

2. 30°

3. 45°

4. 60°

Answer

Let the angle of elevation be θ and height of tower be h meters.

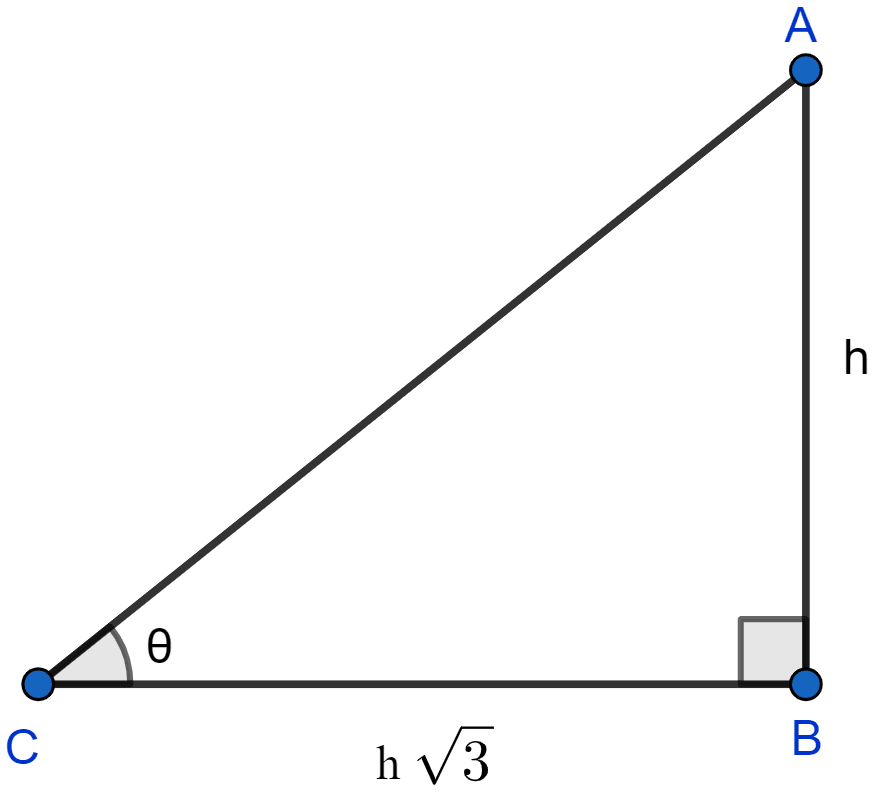
So, shadow of tower = h$\sqrt{3}$ meters

Considering right angled △ABC we get,

$\Rightarrow \text{tan θ} = \dfrac{AB}{BC} \\[1em] \Rightarrow \text{tan θ} = \dfrac{h}{h\sqrt{3}} \\[1em] \Rightarrow \text{tan θ} = \dfrac{1}{\sqrt{3}} \\[1em] \Rightarrow \text{tan θ} = \text{tan 30°} \\[1em] \Rightarrow θ = 30°.$

Hence, Option 2 is the correct option.

In △ABC, ∠A = 30° and ∠B = 90°. If AC = 8 cm, then its area is

1. $16\sqrt{3}$ cm²

2. 16 cm²

3. $8\sqrt{3}$ cm²

4. $6\sqrt{3}$ cm²

Answer

Considering right angled △ABC we get,

$\Rightarrow \text{sin 30°} = \dfrac{BC}{AC} \\[1em] \Rightarrow \dfrac{1}{2} = \dfrac{BC}{8} \\[1em] \Rightarrow BC = 4 \text{ cm}$

Similarly,

$\Rightarrow \text{cos 30°} = \dfrac{AB}{AC} \\[1em] \Rightarrow \dfrac{\sqrt{3}}{2} = \dfrac{AB}{8} \\[1em] \Rightarrow AB = 4\sqrt{3} \text{ cm}$

Area of right angle triangle = A

$\therefore A = \dfrac{1}{2} \times \text{ base} \times \text{ height} \\[1em] \Rightarrow A = \dfrac{1}{2} \times 4\sqrt{3} \times 4 \\[1em] \Rightarrow A = 8\sqrt{3}\text{ cm}^2$

Hence, Option 3 is the correct option.

An observer at point E, which is at a certain distance from the lamp post AB, finds the angle of elevation of top of lamp post from positions C, D and E as α, β and γ. It is given that B, C, D and E are along a straight line.

Which of the following conditions is satisfied ?

1. tan α > tan β

2. tan β < tan γ

3. tan γ > tan α

4. tan α < tan β

Answer

From figure,

⇒ tan α = $\dfrac{AB}{BC}$

⇒ tan β = $\dfrac{AB}{BD}$

⇒ tan γ = $\dfrac{AB}{BE}$

Since, BC < BD < BE.

∴ tan α > tan β > tan γ.

∴ tan α > tan β.

Hence, Option 1 is the correct option.

In the adjoining diagram the length of PR is :

1. $3\sqrt{3}$ cm

2. $6\sqrt{3}$ cm

3. $9\sqrt{3}$ cm

4. 18 cm

Answer

From figure,

⇒ sin 60° = $\dfrac{QR}{PR}$

⇒ $\dfrac{\sqrt{3}}{2} = \dfrac{9}{PR}$

⇒ PR = $\dfrac{9 \times 2}{\sqrt{3}} = 3\sqrt{3} \times 2 = 6\sqrt{3}$ cm.

Hence, Option 2 is the correct option.

The angle of elevation of the top of a tower from a point A (on the ground) is 30°. On walking 50 m towards the tower, the angle of elevation is found to be 60°. Calculate :

(i) the height of the tower (correct to one decimal place)

(ii) the distance of the tower from A.

Answer

Consider the below figure:

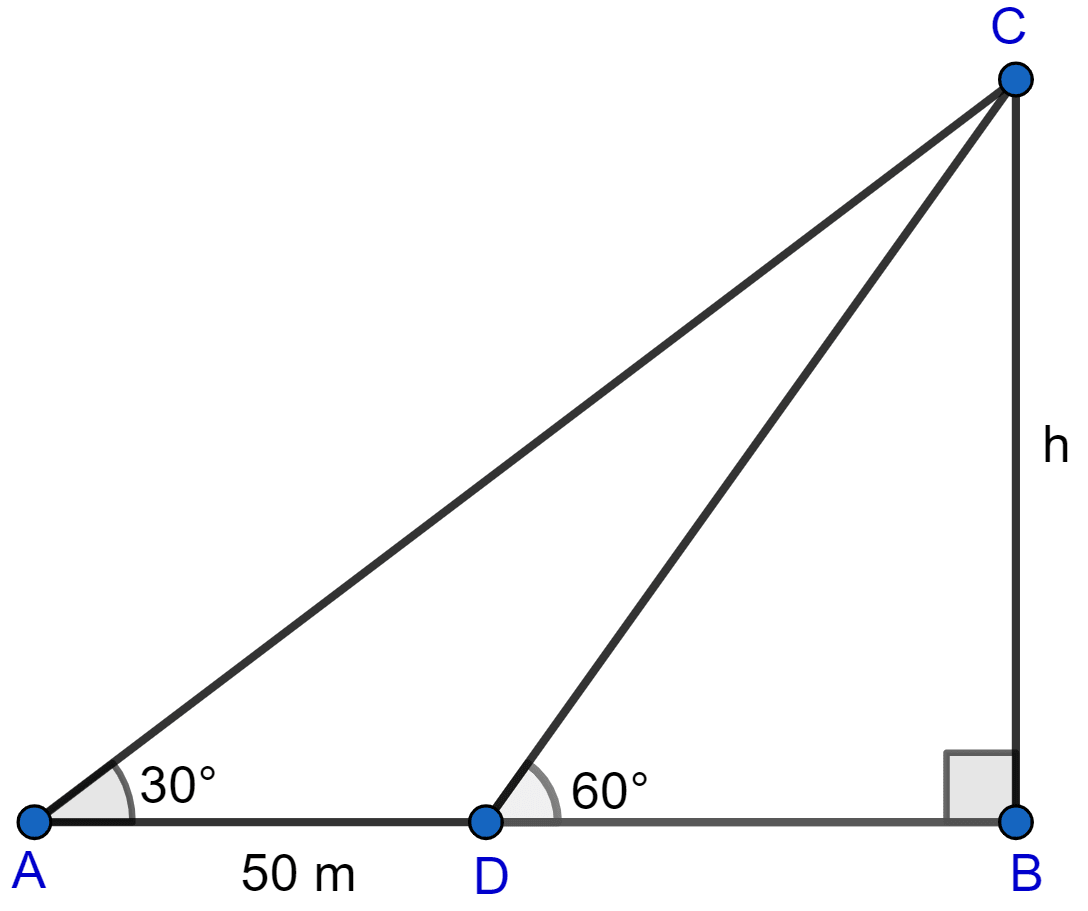
(i) Let after moving 50 m towards tower from point A, the person reaches point D and height of tower be h meters.

From figure,

AD = 50 m, AB = AD + DB = (50 + DB) m

Considering right angled triangle △ABC,

$\Rightarrow \text{tan 30°} = \dfrac{BC}{AB} \\[1em] \Rightarrow \dfrac{1}{\sqrt{3}} = \dfrac{h}{50 + DB} \\[1em] \Rightarrow 50 + DB = h\sqrt{3} \text{ .......( Eq 1)}$

Considering right angled triangle △BCD,

$\Rightarrow \text{tan 60°} = \dfrac{BC}{DB} \\[1em] \Rightarrow \sqrt{3} = \dfrac{h}{DB} \\[1em] \Rightarrow h = DB\sqrt{3} \text{ .......( Eq 2)}$

Putting value of h from Eq 2 in Eq 1 we get,

$\Rightarrow 50 + DB = DB\sqrt{3} \times \sqrt{3} \\[1em] \Rightarrow 50 + DB = 3DB \\[1em] \Rightarrow 2DB = 50 \\[1em] \Rightarrow DB = 25 \\[1em] \therefore h = DB\sqrt{3} = 25 \times 1.732 = 43.3 \text{ m}$

Hence, the height of tower is 43.3 m.

(ii) From figure,

Distance of tower from A (AB) = AD + DB = 50 + 25 = 75 m.

Hence, the distance of tower from A is 75 m.

An aeroplane 3000 m high, passes vertically above another aeroplane at an instant when the angles of elevation of the two aeroplanes from the same point on the ground are 60° and 45° respectively. Find the vertical distance between the two planes.

Answer

Let the plane 3000 m high be at point B and plane below it be at point D.

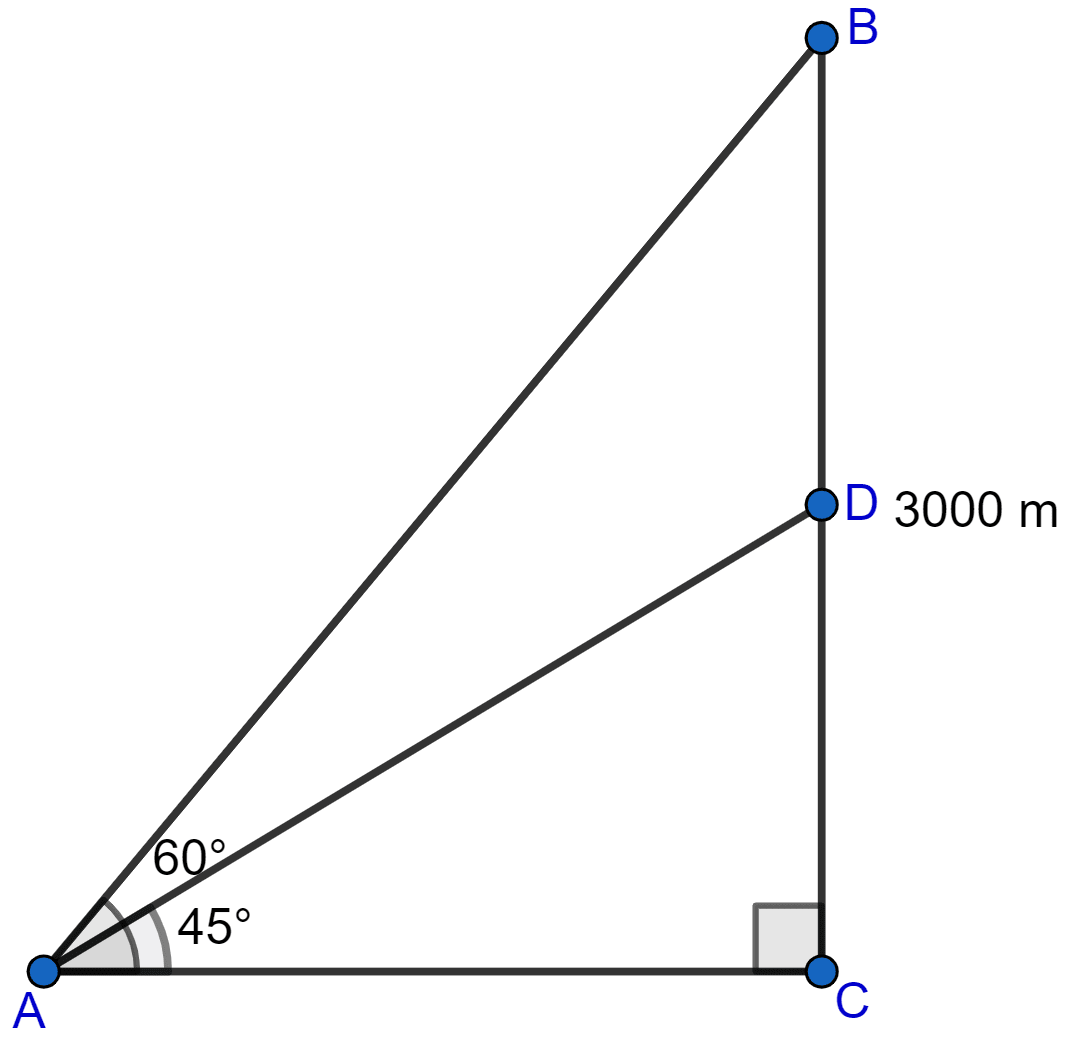
From figure,

Considering right angled triangle △ABC,

$\Rightarrow \text{tan 60°} = \dfrac{BC}{AC} \\[1em] \Rightarrow \sqrt{3} = \dfrac{3000}{AC} \\[1em] \Rightarrow AC = \dfrac{3000}{\sqrt{3}} \\[1em] \Rightarrow AC = 1732 \text{ m}.$

Considering right angled triangle △ADC,

$\Rightarrow \text{tan 45°} = \dfrac{DC}{AC} \\[1em] \Rightarrow 1 = \dfrac{DC}{1732} \\[1em] \Rightarrow DC = 1732 \text{ m}.$

Distance between two planes (BD) = BC - DC = 3000 - 1732 = 1268 m.

Hence, the distance between two planes is 1268 m.

A 7 m long flagstaff is fixed on the top of a tower. From a point on the ground, the angles of elevation of the top and bottom of the flagstaff are 45° and 36° respectively. Find the height of the tower correct to one place of decimal.

Answer

Let CD be the tower of height h meters and BD the flagstaff.

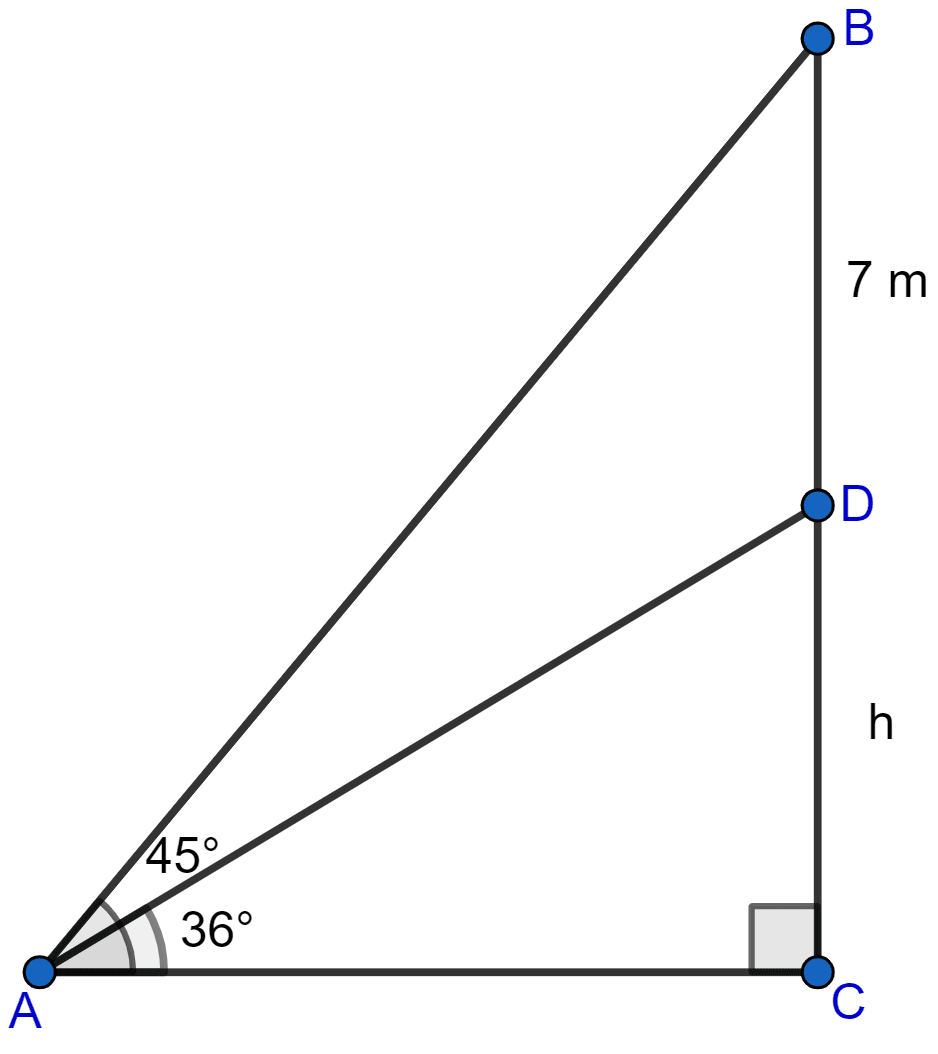
A be point on the ground from where the angles of elevation of the top and bottom of the flagstaff are 45° and 36° respectively.

From figure,

BC = BD + DC = (7 + h) meters.

Considering right angled triangle △ABC,

$\Rightarrow \text{tan 45°} = \dfrac{BC}{AC} \\[1em] \Rightarrow 1 = \dfrac{7 + h}{AC} \\[1em] \Rightarrow AC = h + 7 \text{ ......(Eq 1)}.$

Considering right angled triangle △ADC,

$\Rightarrow \text{tan 36°} = \dfrac{DC}{AC} \\[1em] \Rightarrow 0.7265 = \dfrac{h}{AC} \\[1em] \Rightarrow AC = \dfrac{h}{0.7265}$

Putting value of AC in Eq 1 we get,

$\Rightarrow \dfrac{h}{0.7265} = h + 7 \\[1em] \Rightarrow h = 0.7265(h + 7) \\[1em] \Rightarrow h = 0.7265h + 5.0855 \\[1em] \Rightarrow h - 0.7265\text{ h} = 5.0855 \\[1em] \Rightarrow 0.2735\text{ h} = 5.0855 \\[1em] \Rightarrow h = \dfrac{5.0855}{0.2735} \\[1em] \Rightarrow h = 18.6 \text{ m}.$

Hence, the height of tower is 18.6 m.

A boy, 1.6 m tall, is 20 m away from a tower and observes that the angle of elevation of the top of the tower is 60. Find the height of the tower.

Answer

Let AD be man and BC be tower of height h meters.

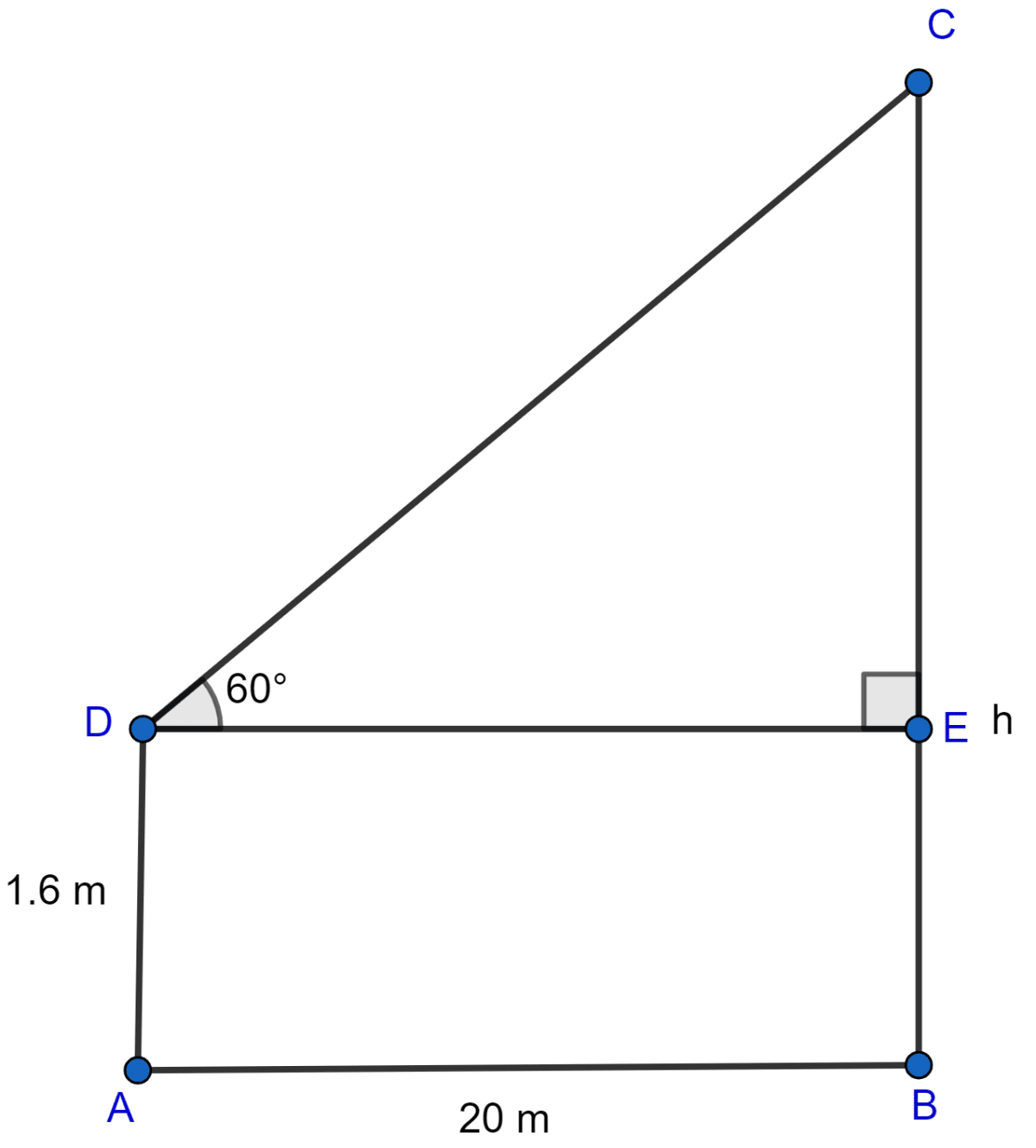
From figure,

ABED is a rectangle.

BE = AD = 1.6 m
DE = AB = 20 m.

CE = BC - BE = (h - 1.6) m.

Considering right angled triangle △DCE,

$\Rightarrow \text{tan 60°} = \dfrac{CE}{DE} \\[1em] \Rightarrow \sqrt{3} = \dfrac{h - 1.6}{20} \\[1em] \Rightarrow h - 1.6 = 20\sqrt{3} \\[1em] \Rightarrow h - 1.6 = 34.64 \\[1em] \Rightarrow h = 36.24 \text{ m}.$

Hence, the height of tower is 36.24 m.

A boy 1.54 m tall can just see the sun over a wall 3.64 m high which is 2.1 m away from him. Find the angle of elevation of the sun.

Answer

Let AD be man, BC be tower and θ be the angle of elevation.

From figure,

ABED is a rectangle.

BE = AD = 1.54 m
DE = AB = 2.1 m.

CE = BC - BE = (3.64 - 1.54) = 2.1 m.

Considering right angled triangle △DCE,

$\Rightarrow \text{tan θ} = \dfrac{CE}{DE} \\[1em] \Rightarrow \text{tan θ} = \dfrac{2.1}{2.1} \\[1em] \Rightarrow \text{tan θ} = 1 \\[1em] \Rightarrow \text{tan θ} = \text{tan 45°} \\[1em] \Rightarrow θ = 45°$

Hence, the angle of elevation is 45°.

An aeroplane flying horizontally 1 km above the ground is observed at an elevation of 60°. After 10 seconds, its elevation is observed to be 30°. Find the speed of the aeroplane in km/h.

Answer

Let initially aeroplane be at point B and after 10 seconds it is at point C.

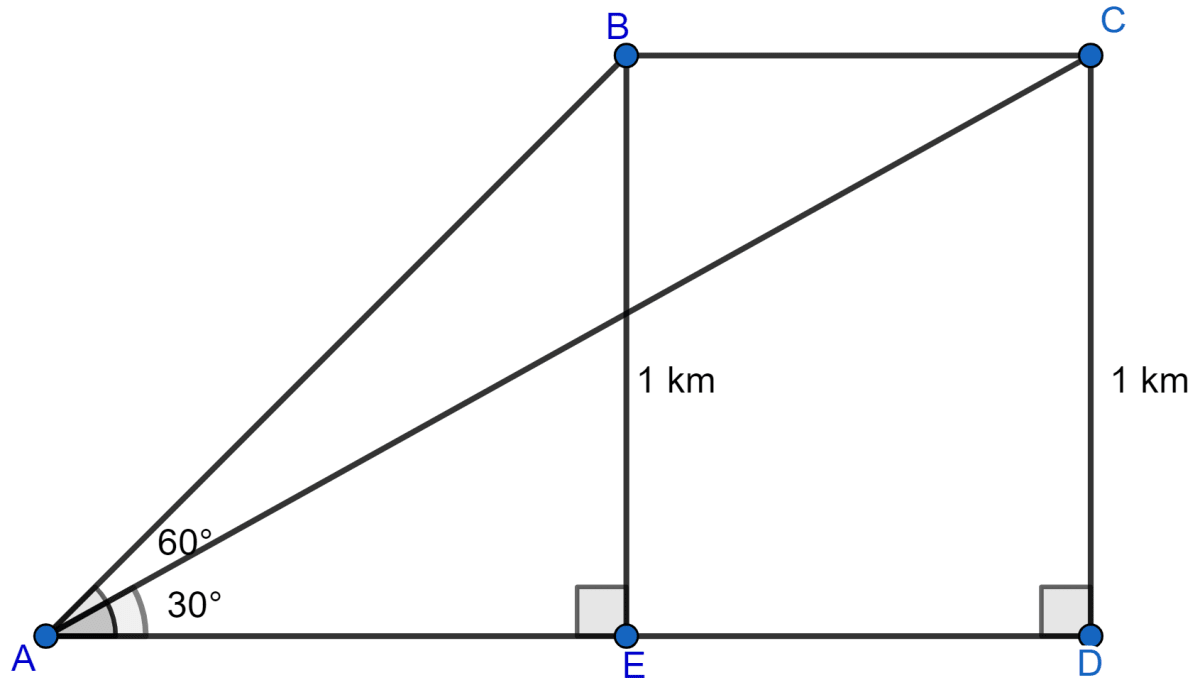
Since, aeroplane is flying horizontally 1 km above the ground so, BE = CD = 1 km.

Considering right angled triangle △ABE,

$\Rightarrow \text{tan 60°} = \dfrac{BE}{AE} \\[1em] \Rightarrow \sqrt{3} = \dfrac{1}{AE} \\[1em] \Rightarrow AE = \dfrac{1}{\sqrt{3}} \\[1em] \Rightarrow AE = 0.557 \text{ km}.$

From figure,

AD = AE + ED = (0.577 + ED) km.

Considering right angled triangle △ACD,

$\Rightarrow \text{tan 30°} = \dfrac{CD}{AD} \\[1em] \Rightarrow \dfrac{1}{\sqrt{3}} = \dfrac{1}{0.577 + ED} \\[1em] \Rightarrow 0.577 + ED = \sqrt{3} \\[1em] \Rightarrow ED = 1.732 - 0.577 \\[1em] \Rightarrow ED = 1.155 \text{ km}.$

Aeroplane covers 1.155 km in 10 seconds.

Time = 10 seconds = $\dfrac{10}{60 \times 60} = \dfrac{10}{3600} = \dfrac{1}{360}$ hours.

Speed = $\dfrac{\text{Distance}}{\text{Time}} = \dfrac{1.155}{\dfrac{1}{360}} = 1.155 \times 360 =$ 415.66 km/h.

Hence, the speed of aeroplane is 415.66 km/h.

A man on the deck of a ship is 16 m above the water level. He observes that the angle of elevation of the top of a cliff is 45° and the angle of depression of the base is 30°. Calculate the distance of the cliff from the ship and the height of the cliff.

Answer

Let A be the man on the deck of the ship B and CE is the cliff.

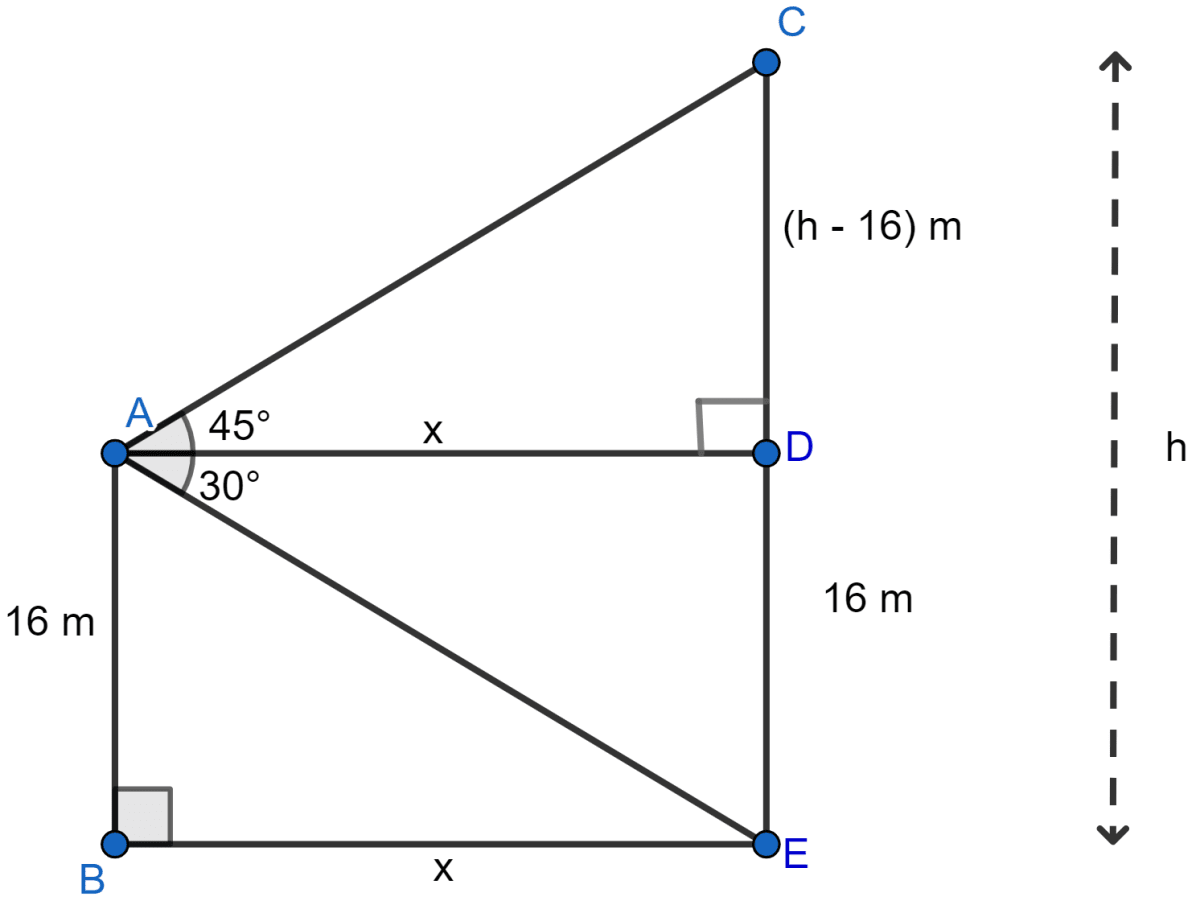
AB = 16 m and angle of elevation of the top of cliff is 45° and angle of depression of base of cliff is 30°.

Let CE = h, AD = x, then
CD = h - 16, AD = BE = x.

Now in right angled triangle △CAD,

$\text{tan 45°} = \dfrac{CD}{AD} \\[1em] 1 = \dfrac{h - 16}{x} \\[1em] x = h - 16 \text{ ......(i)}$

Again in right angled triangle △ADE,

$\text{tan 30°} = \dfrac{DE}{AD} = \dfrac{16}{x} \\[1em] \dfrac{1}{\sqrt{3}} = \dfrac{16}{x} \\[1em] x = 16\sqrt{3} = 27.71 \text{ m}$

From (i) and (ii),

$\Rightarrow h - 16 = 27.71 \\[1em] \Rightarrow h = 27.71 + 16 \\[1em] \Rightarrow h = 43.71 \text{ m}$

Hence, the distance of cliff from the ship is 27.71 m and height of cliff is 43.71 m.

There is a small island in between a river 100 meters wide. A tall tree stands on the island. P and Q are points directly opposite to each other on the two banks, and in line with the tree. If the angles of elevation of the top of the tree from P and Q are 30° and 45° respectively, find the height of the tree.

Answer

Let XY be tree of h meters.

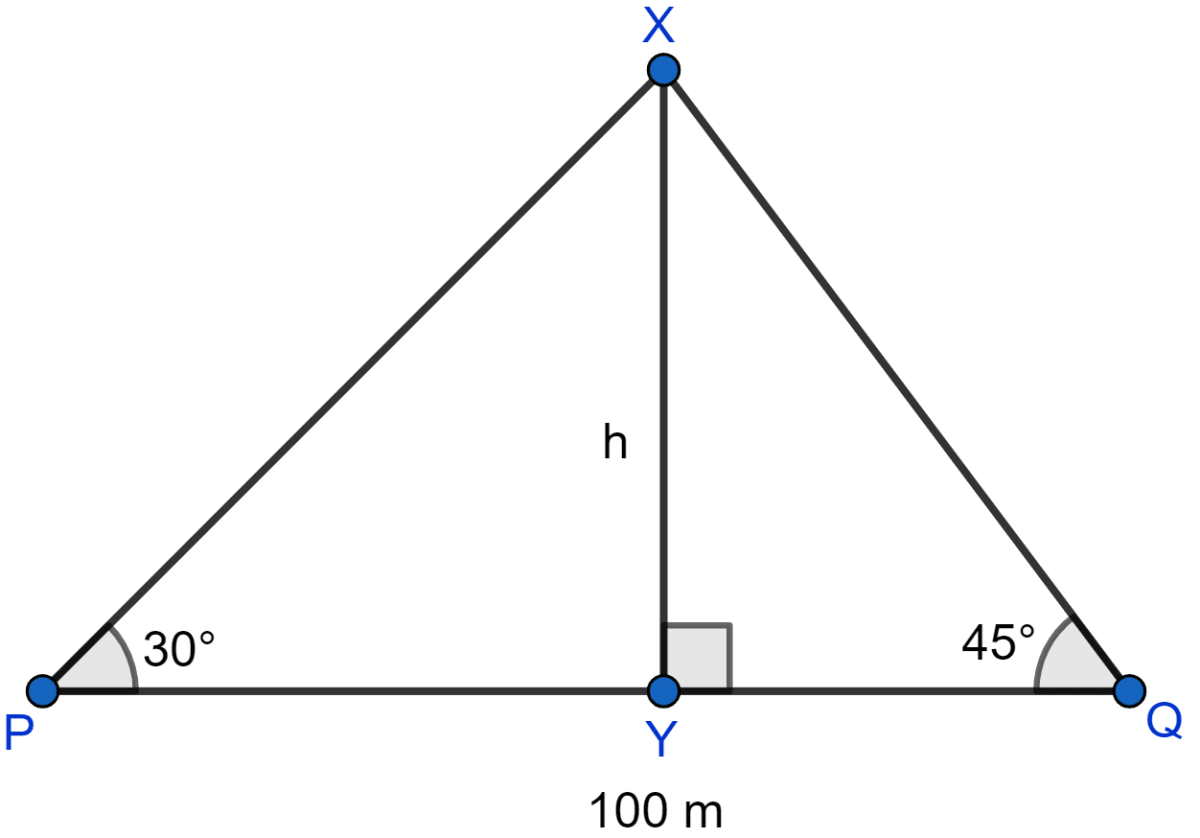
From figure,

Considering right angled triangle △XQY,

$\Rightarrow \text{tan 45°} = \dfrac{XY}{YQ} \\[1em] \Rightarrow 1 = \dfrac{h}{YQ} \\[1em] \Rightarrow YQ = h \text{ ....(Eq 1)}$

Considering right angled triangle △XPY,

$\Rightarrow \text{tan 30°} = \dfrac{XY}{PY} \\[1em] \Rightarrow \dfrac{1}{\sqrt{3}} = \dfrac{h}{100 - YQ} \\[1em] \Rightarrow 100 - YQ = h\sqrt{3}$

Putting value of YQ from Eq 1 in above equation,

$\Rightarrow 100 - h = 1.732h \\[1em] \Rightarrow 1.732h + h = 100 \\[1em] \Rightarrow 2.732h = 100 \\[1em] \Rightarrow h = \dfrac{100}{2.732} = 36.6 \text{ m}.$

Hence, the height of tree is 36.6 m.

A man standing on the deck of the ship which is 20 m above the sea level, observes the angle of elevation of a bird as 30° and the angle of depression of its reflection in the sea as 60°. Find the height of the bird.

Answer

Let P be the man standing on the deck of the ship which is 20 m above sea level and B is the bird.

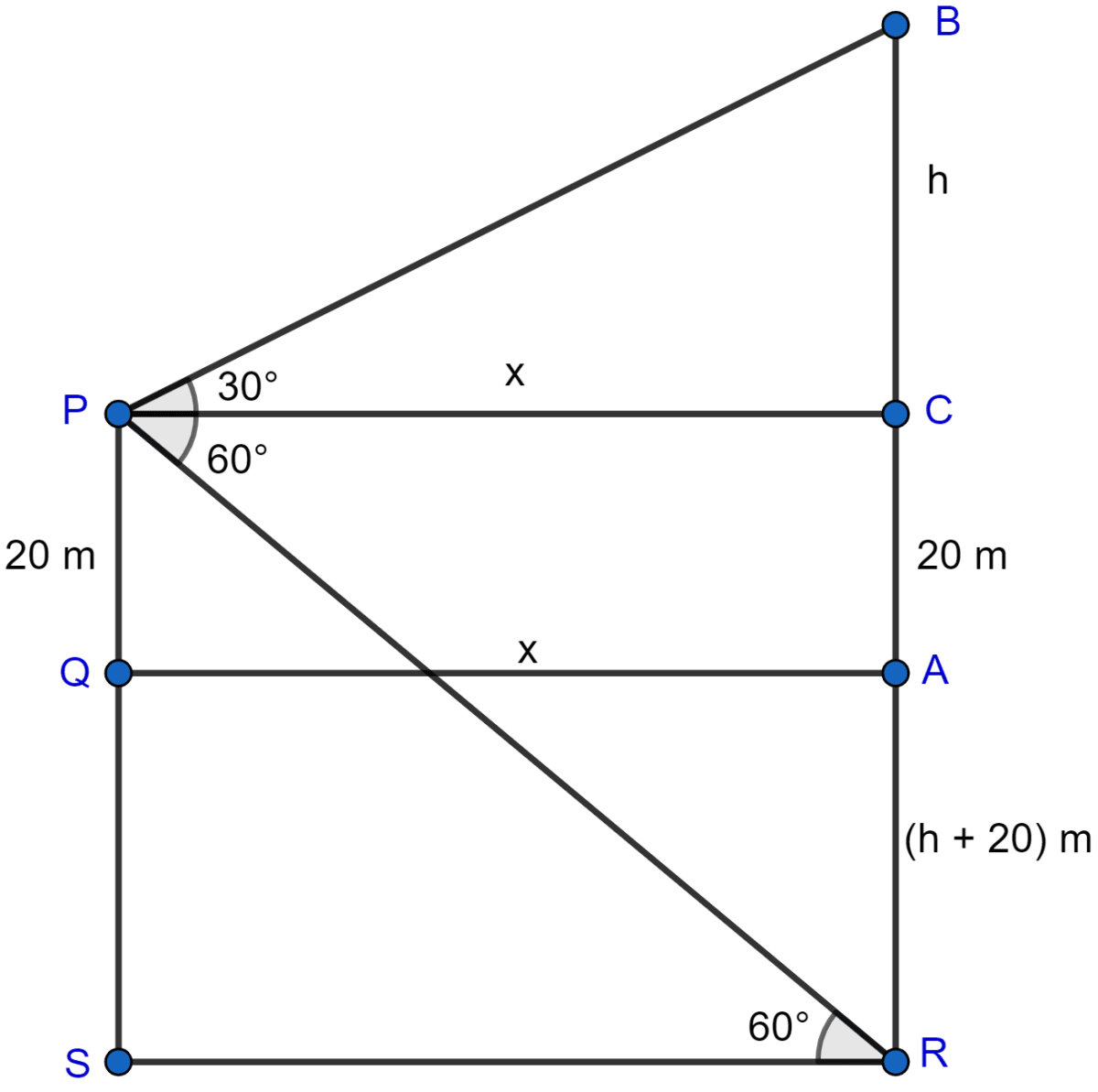
Let bird be flying above h meters from deck of the ship.

∴ BC = h

Let the shadow be created at point R, the shadow will be created vertically opposite at same distance as bird is from ship.

∴ AR = AB = AC + BC = h + 20.

From figure,

In right angled triangle △PCB,

$\Rightarrow \text{tan 30°} = \dfrac{BC}{PC} \\[1em] \Rightarrow \dfrac{1}{\sqrt{3}} = \dfrac{h}{x} \\[1em] \Rightarrow x = h\sqrt{3} ......(i)$

In right angled triangle △PCR,

$\Rightarrow \text{tan 60°} = \dfrac{CR}{CP} \\[1em] \Rightarrow \sqrt{3} = \dfrac{h + 40}{x} \\[1em] \Rightarrow \dfrac{h + 40}{h\sqrt{3}} = \sqrt{3} \quad \text{ [From (i)]}\\[1em] \Rightarrow h + 40 = \sqrt{3} \times \sqrt{3}h \\[1em] \Rightarrow h + 40 = 3h \\[1em] \Rightarrow 3h - h = 40 \\[1em] \Rightarrow 2h = 40 \\[1em] \Rightarrow h = 20.$

From sea level, height of bird (AB) = h + 20 = 20 + 20 = 40 m.

Hence, from sea level the height of bird is 40 m.

A vertical tower standing on a horizontal plane is surmounted by a vertical flagstaff. At a point 100 m away from the foot of the tower, the angle of elevation of the top and bottom of the flagstaff are 54° and 42° respectively. Find the height of the flagstaff. Give your answer correct to nearest metre.

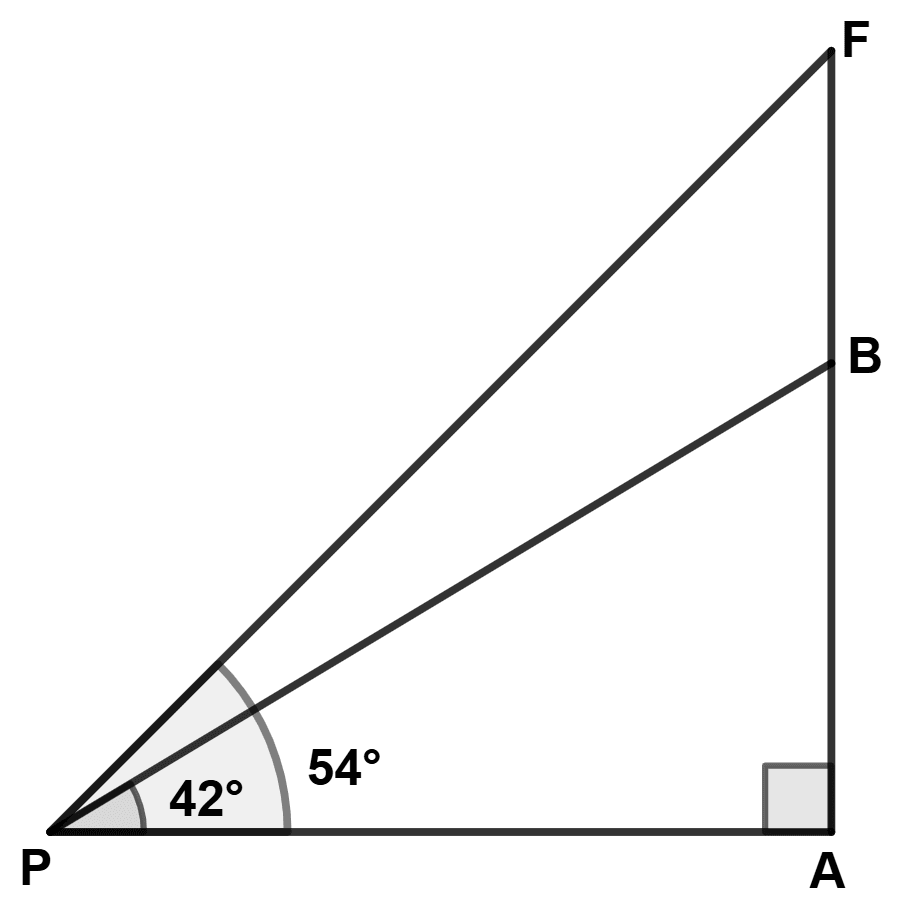
Answer

In △APB,

⇒ tan 42° = $\dfrac{AB}{AP}$

⇒ 0.9004 = $\dfrac{AB}{100}$

⇒ AB = 0.9004 × 100 = 90.04 m

In △APF,

⇒ tan 54° = $\dfrac{AF}{AP}$

⇒ 1.3764 = $\dfrac{AF}{100}$

⇒ AF = 1.3764 × 100 = 137.64 m

From figure,

BF = AF - AB = 137.64 - 90.04 = 47.60 ≈ 48 m.

Hence, height of flagstaff = 48 m.